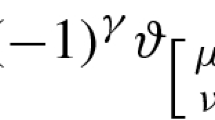Quaternionic loci in Siegel’s modular threefold

Abstract

Let $\mathcal {Q}_D$ be the set of moduli points on Siegel’s modular threefold whose corresponding principally polarized abelian surfaces have quaternionic multiplication by a maximal order $\mathcal {O}$ in an indefinite quaternion algebra of discriminant D over $\mathbb {Q}$ such that the Rosati involution coincides with a positive involution of the form $\alpha \mapsto \mu ^{-1}\overline{\alpha }\mu$ on $\mathcal {O}$ for some $\mu \in \mathcal {O}$ with $\mu ^2+D=0$. In this paper, we first give a formula for the number of irreducible components in $\mathcal {Q}_D$, strengthening an earlier result of Rotger. Then for each irreducible component of genus 0, we determine its rational parameterization in terms of a Hauptmodul of the associated Shimura curve.

Appendices

Appendix A: List of Shimura curves and their quadratic forms

Here we list all Shimura curves of discriminant $<100$ and Shimura curves of genus zero and discriminant $>100$ on $\mathscr {A}_2$, characterized by their quadratic forms. Here D is the discriminant of the quaternion algebra, k is the numbering of the curves, W is the stable group of the Shimura curve, as defined in Definition 11, and g is the genus of the Shimura curve. We let [a, b, c] represent the quadratic form $ax^2+bxy+cy^2$. The quadratic forms are enumerated first in the ascending order of b and then in the ascending order of a.

Appendix B: Modular parameterizations of Shimura curves

Let $s_k$, $k=2,3,5,6$, be the Siegel modular forms defined in (14). In this appendix, we give modular parameterizations for Shimura curves of genus zero on $\mathscr {A}_2$. Here we only list Shimura curves of discriminant D up to 50 and refer the reader to the arXiv version of the paper for a complete list.

Our choices of Hauptmoduls for $X_0^D(1)/W_D$ and $X_0^D(1)/w_D$ are given in 2 and 3, respectively. Note that the description of Hauptmoduls is given by specifying the values of the Hauptmodul at three certain CM-points $z_{d_1}$, $z_{d_2}$, and $z_{d_3}$. In the case of $X_0^D(1)/W_D$, this uniquely determines the Hauptmodul since for each $d_i$, there is only one CM-point of discriminant $d_i$. In the case of $X_0^D(1)/w_D$, we have two different CM-points of discriminant $d_3$. Thus, there are two possible choices of Hauptmoduls, related by the Atkin–Lehner involution $w_q$, q|D. In the table, we also describe their relations (Tables 1, 2, 3).

$\mathfrak {X}_{6}^1$$\quad [ 5, 2, 5 ]$
$s_2$	j
$s_3$	$j^2$
$s_5$	$j^3$
$s_6$	$j^3(j+1)$
$\mathfrak {X}_{10}^1$$\quad [ 5, 0, 8 ]$
$s_2$	$5^2(j-1)^2$
$s_3$	$2^1(j-1)^2(49j+5)$
$s_5$	$2^23^5(j-1)^4$
$s_6$	$3^5(j-1)^4(3j^2+10j+35)$
$\mathfrak {X}_{14}^1$$\quad [ 5, 4, 12 ]$
$s_2$	$(3j+5)^2$
$s_3$	$7^1(27j^2+36j+14)$
$s_5$	$3^5(j-1)^2j^2$
$s_6$	$3^5(3j^6-6j^5+4j^4+4j^3+j^2-6j+3)$
$\mathfrak {X}_{15}^1$$\quad [ 5, 0, 12 ]$
$s_2$	$5^2$
$s_3$	$4j^2+64j+121$
$s_5$	$2^6(j-1)^2j$
$s_6$	$2^4(j^4+72j^3+174j^2+8j+1)$
$\mathfrak {X}_{15}^2$$\quad [ 8, 4, 8 ]$
$s_2$	$5^1(4j+1)$
$s_3$	$4j^2+190j-5$
$s_5$	$2^4(j-1)^2(j+3)$
$s_6$	$2^4(j^4+15j^3+105j^2+125j+10)$
$\mathfrak {X}_{21}^1$$\quad [ 5, 2, 17 ]$
$s_2$	$(5j^2-16j-5)^2$
$s_3$	$7^1(j-1)(j+1)(27j^4-144j^3+394j^2-624j+603)$
$s_5$	$2^{12}(j-1)(j+1)(j+3)^2(j^2-5)^2$
$s_6$	$2^{12}(j^{12}+6j^{11}-9j^{10}-108j^9-28j^8+708j^7+406j^6-2016j^5+17j^4+3846j^3-2637j^2 -2436j+6346)$
$\mathfrak {X}_{22}^1$$\quad [ 8, 8, 13 ]$
$s_2$	$(j-1)^2(9j+64)$
$s_3$	$(j-1)^2(351j^2-782j+539)$
$s_5$	$3^5(j-1)^4j(j+1)^2$
$s_6$	$3^5(j-1)^4(3j^5+5j^4+23j^3+10j^2+4j+3)$
$\mathfrak {X}_{26}^1$$\quad [ 8, 0, 13 ]$
$s_2$	$25j^2-306j+1305$
$s_3$	$2^1(49j^3+27j^2-5913j+23085)$
$s_5$	$2^23^5(j-1)^2(j+3)^2$
$s_6$	$3^5(3j^6-2j^5+13j^4-92j^3+2733j^2+7038j+2595)$
$\mathfrak {X}_{26}^2$$\quad [ 5, 2, 21 ]$
$s_2$	$(5j^2+12j+15)^2$
$s_3$	$2^1(7j^2+12j+9)(7j^4+60j^3+144j^2+108j+297)$
$s_5$	$2^23^5(j-3)^2(j-1)^2(j^2-5)^2$
$s_6$	$3^5(3j^{12}-24j^{11}+22j^{10}+280j^9-651j^8-880j^7+3348j^6-848j^5-2819j^4+3336j^3+2166j^2-34632j+42987)$

$\mathfrak {X}_{33}^1$$\quad [ 8, 4, 17 ]$
$s_2$	$288j^6-360j^5-295j^4+240j^3+238j^2+120j+25$
$s_3$	$(j-1)(j+1)(324j^8-4536j^7+9216j^6+4284j^5+3373j^4+4704j^3+3350j^2+924j+121)$
$s_5$	$2^6(j-1)j^2(j+1)(3j-1)^2(3j^2+1)^2(3j^3+7j^2-3j+1)^2$
$s_6$	$2^4(6561j^{20}+26244j^{19}+275562j^{18}+26244j^{17}+279693j^{16}+863136j^{15}-190440j^{14}-779904j^{13}+700018j^{12}-123384j^{11}-72484j^{10}+20328j^9+35570j^8-28416j^7+12888j^6-3936j^5+1133j^4-300j^3+74j^2-12j+1)$
$\mathfrak {X}_{34}^1$$\quad [ 5, 4, 28 ]$
$s_2$	$j^2(11j^2-20j+1)^2$
$s_3$	$j^2(27j^8-926j^7+9096j^6-10998j^5+8186j^4-4122j^3+1032j^2-82j+27)$
$s_5$	$3^5j^4(j+1)^2(j+3)^2(j^2+2j-1)^2(j^2+4j-1)^2$
$s_6$	$3^5j^4(3j^{16}+68j^{15}+683j^{14}+3836j^{13}+12666j^{12}+23708j^{11}+21565j^{10}+6724j^9+8838j^8+13276j^7-12811j^6-9628j^5+13338j^4-5180j^3+771j^2-36j+3)$
$\mathfrak {X}_{35}^1$$\quad [ 5, 0, 28 ]$
$s_2$	$5^2(3j^2+10j+51)^2$
$s_3$	$7^1(27j^2+178j+243)(27j^4-36j^3-502j^2-1044j+9747)$
$s_5$	$2^{14}3^5(j-1)^2j(j^3+13j^2+51j-1)^2$
$s_6$	$2^{12}3^5(3j^{12}+96j^{11}+2014j^{10}+35808j^9+389869j^8+2509312j^7+9837156j^6+21020288j^5+17081069j^4-730208j^3+186334j^2-96j+3)$
$\mathfrak {X}_{35}^2$$\quad [ 12, 4, 12]$
$s_2$	$5^1(45j^4+876j^3-2002j^2-3924j+909)$
$s_3$	$7^1(729j^6-9126j^5+34119j^4+490604j^3+124119j^2+642330j+27945)$
$s_5$	$2^{12}3^5(j+3)^2(j+7)(j^3+13j^2+51j-1)^2$
$s_6$	$2^{12}3^5(3j^{12}+141j^{11}+3019j^{10}+39267j^9+339240j^8+1967522j^7+7421414j^6+16970566j^5+20814403j^4+14639425j^3+19460895j^2+2222055j+8130)$
$\mathfrak {X}_{35}^3$$\quad [ 12, 8, 13]$
$s_2$	$5^1(45j^8+288j^7+1356j^6+1824j^5+5390j^4+1632j^3+13644j^2-3744j+45)$
$s_3$	$7^1(729j^{12}+3888j^{11}+18090j^{10}+79056j^9+277623j^8+649440j^7+1230476j^6+819360j^5+1037367j^4-1563408j^3+1089450j^2+11664j+16281)$
$s_5$	$2^{12}3^5(j-1)^2(j+1)^2(j^2-2j+5)^2(j^2+3)^2(j^3-j^2+7j+1)^2$
$s_6$	$2^{12}3^5(3j^{24}-18j^{23}+147j^{22}-576j^{21}+2635j^{20}-7266j^{19}+23897j^{18}-48084j^{17}+132420j^{16}-194660j^{15}+536174j^{14}-563952j^{13}+1917622j^{12}-1570836j^{11}+6456226j^{10}-4274680j^9+15283435j^8-4052682j^7+16219183j^6+6354768j^5+7786095j^4+4437942j^3+1954773j^2-79956j+19038)$

$\mathfrak {X}_{38}^1$$\quad [ 12, 4, 13]$
$s_2$	$9j^6-60j^5+346j^4-240j^3+153j^2-180j+36$
$s_3$	$675j^8-2016j^7+2600j^6-8064j^5+11610j^4-6048j^3+3240j^2+243$
$s_5$	$3^5(j+1)^2(j^2+1)^2(j^2+3)^2(j^2+j+2)^2$
$s_6$	$3^5(3j^{18}+12j^{17}+61j^{16}+160j^{15}+525j^{14}+1068j^{13}+2612j^{12}+4032j^{11}+7533j^{10}+8548j^9+12532j^8+9984j^7+11971j^6+6180j^5+6792j^4+2208j^3+2592j^2+576j+435)$
$\mathfrak {X}_{38}^2$$\quad [ 8, 8, 21 ]$
$s_2$	$9j^3+46j^2+393j+576$
$s_3$	$81j^4-836j^3-6822j^2-13068j-13851$
$s_5$	$-3^5(j-1)^2j(j+1)^2(3j+1)^2$
$s_6$	$3^5(3j^9+153j^8+1077j^7+2848j^6+4149j^5+2872j^4+987j^3+172j^2+24j+3)$
$\mathfrak {X}_{39}^1$$\quad [ 5, 4, 32 ]$
$s_2$	$(5j^4+4j^3-10j^2+4j+5)^2$
$s_3$	$189j^{12}-180j^{11}+514j^{10}-708j^9-45j^8+24j^7-68j^6+2328j^5-45j^4-2148j^3-158j^2+684j+189$
$s_5$	$2^{10}(j-2)^2j^2(j^2-2j-1)^2(j^2-j-1)^2(j^3-j^2-2j-1)^2$
$s_6$	$2^{10}(4j^{24}-60j^{23}+363j^{22}-1056j^{21}+1088j^{20}+1680j^{19}-4884j^{18}+210j^{17}+8824j^{16}-3396j^{15}-10122j^{14}+3522j^{13}+8843j^{12}-348j^{11}-5640j^{10}-2082j^9+2134j^8+1632j^7$
	$-537j^6-642j^5+275j^4+492j^3+228j^2+48j+4)$
$\mathfrak {X}_{39}^2$$\quad [ 8, 4, 20 ]$
$s_2$	$25j^8-40j^7-4j^6-200j^5-58j^4+520j^3+556j^2+200j+25$
$s_3$	$189j^{12}-684j^{11}-998j^{10}+5340j^9+2139j^8-13752j^7-9308j^6+9384j^5+17931j^4+14148j^3+6562j^2+1692j+189$
$s_5$	$2^{10}(j-1)^2j^2(j^2-j-1)^2(j^3-2j^2+j+1)^2(j^4-j^3-j^2+j+1)$
$s_6$	$2^{10}(4j^{24}-48j^{23}+243j^{22}-639j^{21}+773j^{20}+219j^{19}-1875j^{18}+1560j^{17}+1642j^{16}-3300j^{15}-255j^{14}+3855j^{13}-1018j^{12}-3420j^{11}+1593j^{10}+2352j^9-1301j^8-1260j^7+639j^6+516j^5-172j^4-147j^3+15j^2+24j+4)$

Table 1 Modular parameterizations of Shimura curves

Table 2 Choice of Hauptmoduls for $X_0^D(1)/W_D$

Table 3 Choice of Hauptmoduls for $X_0^D(1)/w_D$

Table 4 Mestre obstruction for $\mathfrak {X}$

Appendix C: Mestre obstructions

In [23], Mestre gave an algorithm to generate a hyperelliptic curve of genus 2 with given Igusa invariants $J=[J_2,J_4,J_6,J_{10}]$. In the process, he considered a certain ternary quadratic form

$$\begin{aligned} L(J)=\sum _{1\le i,j\le 3}A_{ij}(J)x_ix_j, \end{aligned}$$

constructed from J. He showed that if L(J) is degenerate, then there is always a curve C of genus 2 defined over $\mathbb {Q}(J):=\mathbb {Q}(J_2,J_4,J_6,J_{10})$. In such a case, the curve C has a nontrivial automorphism different from the hyperelliptic involution. (For the case of curves over $\mathbb {C}$, this means that the Jacobian of C lies on the Humbert surface of discriminant 4. See [2].) Furthermore, he showed that when L(J) is nondegenerate, there is a curve C of genus 2 defined over a field K with Igusa invariants J if and only if L(J) is isotropic over K. In other words, there is a quaternion algebra $\mathcal {B}$ over $\mathbb {Q}(J)$ such that there is a curve over K with Igusa invariants J if and only if K splits $\mathcal {B}$. (In the case when L(J) is diagonal, say, $L(J)=a_1x_1^2+a_2x_2^2+a_3x_3^2$, $\mathcal {B}$ is simply $\left( \frac{-a_1a_3,-a_2a_3}{\mathbb {Q}(J)}\right)$). In literature, this quaternion algebra $\mathcal {B}$ is called the Mestre obstruction for J. In the case of the unique Shimura curve $\mathfrak {X}_6$ of discriminant 6, using the parameterization given in (2), Baba and Granath [1] exhibited a matrix $M\in M(3,\mathbb {Z}[j])$ such that

Therefore, for a point on $\mathfrak {X}_6$ that is not on $H_4$, the Mestre obstruction is $\left( \frac{-6j,-2(27j+16)}{\mathbb {Q}(j)}\right)$. For the case of $D=10$, Baba and Granath [1] found that the Mestre obstruction is $\left( \frac{-10j,-5(2j+25)}{\mathbb {Q}(j)}\right)$. (Note that their choice of Hauptmodul is different from ours.) In this section, we conduct a similar computation and determine Mestre obstructions for Shimura curves of genus 0 and discriminant less than 50 (80 in the arXiv version). The results are given in Table 4.

Remark 44

Note that when $X_0^D(1)/w_D$ has genus 0 and j is a Hauptmodul for $X_0^D(1)/w_D$, a canonical model for $X_0^D(1)$ has the form $y^2=f(x)$, where the roots of f(x) are the values of j at the fixed points of the Atkin-Lehner involution $w_D$. Our computation shows that in all cases where the Shimura curve $\mathfrak {X}$ is isomorphic to $X_0^D(1)/w_D$, the Mestre obstruction for $\mathfrak {X}$ is given by

$$\begin{aligned} \left( \frac{-D,mf(j)}{\mathbb {Q}(j)}\right) , \end{aligned}$$

where m is an integer such that $r^2m$ is representable by the quadratic form associated to $\mathfrak {X}$ for some rational number r. For instance, the quadratic form for $\mathfrak {X}_{51}^2$ is $5x^2+2xy+41y^2$, which clearly represents 5. Also, a canoncal model for $X_0^{51}(1)$ is $y^2=f(x)$, where $f(x)=-(x^2+3)(243x^6+235x^4-31x^2+1)$ (see [13, 15]). Our computation shows that the Mestre obstruction for $\mathfrak {X}_{51}^2$ is $\left( \frac{-51,5f(j)}{\mathbb {Q}(j)}\right)$. If this phenomenon holds in general, there should be a deep arithmetic meaning.

Note also that it is well-known that the Shimura curve $X_0^D(1)$ has no real points when $D>1$ (see [26]). In other words, the polynomial f(x) above is negative for any real x. It follows that the quaternion algebra $\left( \frac{-D,mp(j)}{\mathbb {Q}}\right)$ always ramifies at the infinite place whenever $j\in \mathbb {R}$. Therefore, we have the following proposition.

Proposition 45

Let $\mathfrak {X}$ be a Shimura curve in Table 4 that is isomorphic to $X_0^D(1)/w_D$. (I.e., the quadratic form associated to $\mathfrak {X}$ is not ambiguous.) Then there are only a finite number of isomorphism classes of genus 2 curves over $\mathbb {R}$ such that their Jacobians lie on $\mathfrak {X}$. To be more precise, these exceptional moduli points are the real points that lie on the intersection of $\mathfrak {X}$ and $H_4$, but not on $H_1$.

Example 46

Consider $\mathfrak {X}=\mathfrak {X}_{14}^1$. Using (15) and the modular parameterization in Appendix B, we find that the only real points lying on $\mathfrak {X}\cap H_4$ have j-values $j=\infty$,0,$\pm 1$,5 / 9,$\pm \sqrt{5}$. Among these points, the points corresponding to $j=\infty ,0,1$ also lie on $H_1$. Thus, there are precisely four genus 2 curves over $\mathbb {R}$ whose Jacobians belong to $\mathfrak {X}$, two of them defined over $\mathbb {Q}$ and the other two defined over $\mathbb {Q}(\sqrt{5})$. The point with $j=-1$ is a CM-point of discriminant $-11$ with

$$\begin{aligned}{}[s_2,s_3,s_5,s_6]=[4,35,972,4617], \end{aligned}$$

or equivalently,

$$\begin{aligned}{}[J_2,J_4,J_6,J_{10}]=[-76, 198, 188, -4096]. \end{aligned}$$

Its ternary quadratic form

represents $4x^2+4xy+4y^2$. Thus, it also lies on the modular curve $\mathfrak {Y}_3'$, defined in Sect. 5. Since $\mathfrak {Y}_3'$ parameterizes curves of genus 2 with an automorphism group containing the dihedral group $D_6$ of order 12 (see [7, Theorem 2.1]), a curve of genus 2 with these invariants can be obtained using a result of Cardona and Quer [8, Proposition 2.2]. We find that

$$\begin{aligned} y^2=11x^6+11x^3-4 \end{aligned}$$

is a curve with $[s_2,s_3,s_5,s_6]=[4,35,972,4617]$.

The point with $j=5/9$ is a CM-point of discriminant $-43$ with

$$\begin{aligned}{}[s_2,s_3,s_5,s_6]=[400/9, 889/3, 400/27, 144001/729] \end{aligned}$$

or equivalently,

$$\begin{aligned} {[}J_2,J_4,J_6,J_{10}]=\left[ -\frac{144001}{10800}, \frac{15552288001}{2799360000}, \frac{46655567999}{544195584000000}, -\frac{25}{419904}\right] . \end{aligned}$$

A curve of genus 2 over $\mathbb {Q}$ with these invariants is

$$\begin{aligned} y^2=ax^6+bx^5+cx^4+dx^3-43cx^2-43^2bx-43^3a, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} a&=55263257981868963587850953171983151, \\ b&=17933188094622164053062876274057062, \\ c&=2377689006459293602182305511758203269, \\ d&=1274547562528177370745959571323659332. \end{aligned} \end{aligned}$$

An extra involution is given by $(x,y)\mapsto (-43/x,\sqrt{-43^3}y/x^3)$.