A multi-fidelity RBF surrogate-based optimization framework for computationally expensive multi-modal problems with application to capacity planning of manufacturing systems

Abstract

This paper presents a multi-fidelity RBF (radial basis function) surrogate-based optimization framework (MRSO) for computationally expensive multi-modal optimization problems when multi-fidelity (high-fidelity (HF) and low-fidelity (LF)) models are available. The HF model is expensive and accurate while the LF model is cheaper to compute but less accurate. To exploit the correlation between the LF and HF models and improve algorithm efficiency, in MRSO, we first apply the DYCORS (dynamic coordinate search algorithm using response surface) algorithm to search on the LF model and then employ a potential area detection procedure to identify the promising points from the LF model. The promising points serve as the initial start points when we further search for the optimal solution based on the HF model. The performance of MRSO is compared with 6 other surrogate-based optimization methods (4 are using a single-fidelity surrogate and the rest 2 are using multi-fidelity surrogates). The comparisons are conducted on a multi-fidelity optimization test suite containing 10 problems with 10 and 30 dimensions. Besides the benchmark functions, we also apply the proposed algorithm to a practical and computationally expensive capacity planning problem in manufacturing systems which involves discrete event simulations. The experimental results demonstrate that MRSO outperforms all the compared methods.

1 Introduction

Computationally expensive multi-modal black-box optimization problems arise in many science and engineering areas. For example, in the field of complex products design optimization, the optimization analysis is driven by expensive computer simulation codes (e.g., finite element analysis (FEA) and computational fluid dynamics (CFD)), which are used to simulate the physical processes and to evaluate the design solutions (Simpson et al. 2004). Another example can be found in the hyper-parameter tuning process of machine learning algorithms. Each evaluation of the hyper-parameter configuration needs to run the whole training and testing process, which may take minutes or hours (Ilievski et al. 2017). A computationally expensive multi-modal black-box optimization problem can be formulated as follows:

$$ \begin{array}{@{}rcl@{}} &&\text{minimize: \quad} f(\boldsymbol{x})\\ &&\text{subject to:\quad } L_{i} \leq x_{i} \leq U_{i}, 1\leq i\leq d \end{array} $$

(1)

where x = (x₁,x₂,⋯ ,x_d) is the decision vector, d is the number of decision variables, and x_i (1 ≤ i ≤ d) is the i th decision variable. L_i and U_i are the lower and upper bounds on x_i. Computationally expensive multi-modal black-box optimization problems have the following challenges: (1) Every single evaluation of the objective function is expensive, which may take minutes, hours, or even days. Thus, in these cases only a relatively small number of evaluations are possible; (2) no derivative information can be obtained from the problem. Therefore, the gradient-based optimization methods cannot be directly applied. (3) The problem may have multiple local minima.

In recent years, surrogate-assisted global optimization (SAGO) methods have become very popular for computationally expensive black-box optimization problems. The basic idea of SAGO is to build a cheap approximate model (called a surrogate model or metamodel) for the expensive objective function and use this cheap model to replace some of the expensive evaluations, in the optimization search this can dramatically reduce the computational cost. Depending on the ways of using the surrogates, the SAGO methods can be classified into two categories: the offline mode and the online mode. In the offline mode, a surrogate is built at the beginning of the optimization process and will not be updated. In contrast, the online model keeps updating the surrogate when new evaluations are available. The majority of SAGO methods fall into the second category. More details about SAGO methods can be found in the literature reviews (Jin 2011; Haftka et al. 2016).

The surrogates used in the aforementioned SAGO methods are built solely on the high-fidelity (HF) models. Here, the term “fidelity” means how accurate or how close the model is for describing the original objective function. If a model is accurate and highly trusted, then it is an HF model. Otherwise, it is a low-fidelity (LF) model. Although these SAGO methods have been proved to be effective in various applications (Li et al. 2017; Liu et al. 2017, 2018; Han et al. 2018; Ali et al. 2018; Redouane et al. 2019), their shortcomings appear when dealing with extremely expensive problems, or medium- to high-dimensional decision vectors. To ensure higher prediction accuracy of the surrogate model, the search space should be space-filling sampled by sufficient sample points. However, it is impractical for both extremely expensive and medium- to high-dimensional decision vectors due to the limitation of computational budgets and the “curse of dimensionality.” Therefore, there are still limitations for the SAGO to tackle these kinds of computationally expensive problems.

To fill this gap, the multi-fidelity optimization (MFO) methods have received much attention in recent years and have been applied to various fields (Liu et al. 2016; Kandasamy et al. 2016; Bonfiglio et al. 2018; Habib et al. 2019; Liu et al. 2019; Yi et al. 2019; Zhang et al. 2019a; Yong et al. 2019; Zhang et al. 2018; Ding and Kareem 2018; Tao and Sun 2019). Instead of only building a single-fidelity surrogate-based on the HF model, MFO methods also utilize a LF model, which is less accurate but much cheaper and easier to compute. By using a large number of cheap LF evaluations and a small number of expensive HF evaluations, MFO can obtain better solutions with less computational cost. In addition, the LF models are easy to access. For example, the LF models of the airfoil shape optimization can be created by using coarse meshes (Zhou et al. 2017). There are two strategies among common MFO methods. In the first strategy, a variable-fidelity surrogate model is built to minimize the discrepancy between the LF model and the HF model. A lot of previous studies discussed how to build accurate variable-fidelity models (Zheng et al. 2015; Zhou et al. 2017; Durantin et al. 2017; Liu et al. 2018; Zheng 2018; Song et al. 2019). Zhang et al. (2018) proposed a variable-fidelity expected improvement criterion on a hierarchical Gaussian process model, which can adaptively select new samples on both LF and HF models. Yi et al. (2019) proposed a variable-fidelity RBF surrogate-assisted harmony search algorithm, where a multi-level screening mechanism based on non-dominated sorting is used to strictly control the numbers of LF and HF evaluations. In the second strategy, multiple surrogates are built for models of different fidelity levels and some recent research follows this line. Liu et al. (2016) developed a multi-fidelity surrogate model-assisted memetic differential evolution (DE) method, where the Gaussian process models are built based on both the LF and HF models. Kandasamy et al. (2016) formulated the MFO task as a multi-fidelity bandit problem and proposed a multi-fidelity Bayesian optimization method with the upper confident bound criterion.

We propose MRSO, a multi-fidelity RBF surrogate-based optimization framework that utilizes the original RBF surrogate-assisted dynamic coordinate search algorithm (DYCORS) (Regis and Shoemaker 2013), in which the surrogate is built on single-fidelity models. This study aims to further improve the performance and speed-up the optimization process for computationally expensive multi-modal black-box problems.

The proposed MFO framework has three main steps: In the first step, the original DYCORS algorithm is used to search on the LF model. Secondly, a potential area detection procedure is adopted to identify the potential points. Finally, the obtained potential points serve as the initial starting points for the DYCORS algorithm to further search on the HF model. The effectiveness of the proposed approach is validated by the comparison with 6 other surrogate-assisted global optimization methods include both single-fidelity and multi-fidelity methods. A capacity planning problem in manufacturing systems involving discrete event simulations is also used to demonstrate the superior performance of the proposed approach.

The main contributions of this study are as follows:

• (1) MRSO starts the search from the LF model and quickly identifies the potential search area. Then, it further searches on the HF model from the potential area. With the help of LF model, MRSO can further save the computational budget and speed-up the optimization process.

• (2) To link the search on LF and HF models, we innovatively develop a potential area detection procedure to identify the guesses for local optimal locations, which serve as the starting points for the HF run.

• (3) Empirically, we demonstrate that the proposed MRSO approach outperforms 6 other surrogate-assisted global optimization methods including both single-fidelity and multi-fidelity surrogate-based methods on a series of problems, including 10 numerical benchmark problems from the MFO test suite. Moreover, MRSO has been successfully applied to a complex capacity planning problem in manufacturing systems involving discrete event simulations.

The remainder of this paper is organized as follows. The prior research related to this research is given in Section 2. Section 3 introduces the proposed MRSO approach. Section 4 presents the numerical experiments. An application on the capacity planning problem is discussed in Section 5. Finally, Section 6 gives the concluding remarks.

2 Surrogate-assisted global optimization and DYCORS algorithm

2.1 Surrogate-assisted global optimization

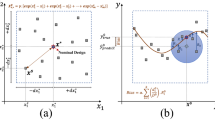
Most of the surrogate-assisted global optimization methods have the same framework shown in Fig. 1. Note that all methods here are single-fidelity surrogate-based methods (with the surrogate built solely on HF model). At the start of the optimization, a space-filling experimental design procedure (e.g., Latin hyper-cube design (Kenny et al. 2000)) is carried out to generate initial samples over the whole domain, and these initial samples are evaluated by the expensive HF models. Once this step is finished, a surrogate model is built based on the collected initial data A (i.e., a set of input-output pairs A). In the next step, a user-defined acquisition function is used to decide the next evaluation point x_E based on the surrogate information. Once the next evaluation point is found, it will be further evaluated by the expensive HF model, and this new data will be added into the database A. When the stopping criterion is not satisfied, the algorithms will go back to step 2 to update the surrogate model and repeat step 2 to step 4 (Fig. 1); otherwise, the algorithms will terminate and output the current best solution. Usually, the maximum number of HF evaluations is used as the stopping criterion since the surrogate-assisted global optimization methods are targeted for computationally expensive problems with a limited computational budget.

Fig. 1

Basic flowchart of surrogate-assisted global optimization

The key ingredients of surrogate-assisted optimization methods for expensive multi-modal functions are in step 2 and step 3 (Fig. 1), which are (a) surrogate model, (b) optimization algorithm used to search on the surrogate, and (c) its corresponding acquisition function. There are several different choices for each of the key ingredients. For the choice of the surrogate model, the most widely used models are Gaussian process model (or Kriging model) (Shahriari et al. 2015; Zhang et al. 2019b) and radial basis function model (RBF) (Regis and Shoemaker 2007; 2013; Regis 2014). Other methods that could also be used include the multivariate adaptive regression splines (MARS) (Friedman et al. 1991), support vector regression (SVM) (Smola and Schölkopf 2004), artificial neural networks (ANN) (Villarrubia et al. 2018), and random forest (RF) (Wang and Jin 2018). There are papers showing that MARS regression is not efficient as an RBF surrogate on the specific tested problems (Müller and Shoemaker 2014). For the optimization algorithm used to search on the surrogate surface, the popular methods are under three big categories: (a) global optimization methods, (b) local optimization methods, and (c) random sampling. For global optimization methods, a genetic algorithm (GA) (Whitley 1994) or a particle swarm optimization (PSO) (Kennedy 2010) can be used. Since the f(x) is multi-modal, the surrogate can also be multi-modal so the second approach is to use local optimization methods and combine with a multi-start strategy. The local optimization methods can include Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm (Battiti and Masulli 1990), Nelder-Mead simplex algorithm, and Newton conjugate gradient algorithm. In addition to these two methods, some previous researches applied random sampling to generate a fixed number of random candidates that are sorted on basis of the value of acquisition function, and the best candidate is selected for the next evaluation (Regis and Shoemaker 2007, 2013; Hutter et al. 2009). For the acquisition function, some popular options are expected improvement (EI) (Jones et al. 1998), probability of improvement (POI) (Snoek et al. 2012), upper bound of confidence (UCB), entropy search (ES) (Hennig and Schuler 2012), and the weighted score criterion (Regis and Shoemaker 2013), which will be introduced in the next subsection).

2.2 The DYCORS algorithm

The DYCORS algorithm proposed by Regis and Shoemaker (2013) is an efficient surrogate-assisted global optimization algorithm for computationally expensive problems. Algorithm 1 gives the pseudo-code of DYCORS algorithm. DYCORS has three main features: (1) it adopts the RBF model as the surrogate, (2) it generates the candidate points by perturbing the current best solution with a predefined probability, and (3) it uses the weighted score of the surrogate prediction (i.e., exploitation) and the minimum distance to previous evaluated points (i.e., exploration) as the acquisition function. Details are given in the following sections.

2.2.1 The RBF model

The RBF model serves as the surrogate in DYCORS algorithm. The RBF is a real-valued function whose value depends only on the distance between the input point to some fixed given point.

Given a set of n sampling points $\boldsymbol {x}_{1},\boldsymbol {x}_{2},\ldots ,\boldsymbol {x}_{n}\in \mathbb {R}^{d}$ in d-dimensional space, and the vector (f(x₁),f(x₂),…,f(x_n)) are the corresponding objective function values, then the RBF approximation can be obtained by the following:

$$ s(\boldsymbol{x}) =\sum\limits_{i=1}^{n}\lambda_{i}\phi(\parallel\boldsymbol{x}-\boldsymbol{x}_{i}\parallel) + p(\boldsymbol{x}) $$

(2)

where ∥⋅∥ is the Euclidean norm, $\lambda _{i}\in \mathbb {R}^{d}$, p(x) is the linear polynomial, and ϕ(⋅) is the basis function. ϕ(⋅) has several different forms, and in this study, we use the cubic form (ϕ(r) = r³) since previous study suggested that cubic RBFs might be more suitable than other forms of RBFs for surrogate-based optimization (Wild and Shoemaker 2013).

To determine the parameters (λ and c) of the RBF model in (2), we define the matrix $\boldsymbol {\Phi }\in \mathbb {R}^{n\times n}: {\Phi }_{ij}=\phi (\parallel \boldsymbol {x}_{i}-\boldsymbol {x}_{j}\parallel ),i,j=1,2,\ldots ,n$, and matrix $\boldsymbol P\in \mathbb {R}^{n\times (d+1)}$. The vector in the i th row of P is [1,x_i]. Then, λ and c can be obtained by solving the following equation (Powell M 1992):

$$ \left[ \begin{array}{cc} \boldsymbol {\Phi} &\boldsymbol P \\ \boldsymbol P^{T} &\boldsymbol 0_{(d+1)\times(d+1)} \end{array} \right]\left[ \begin{array}{c} \boldsymbol \lambda \\ \boldsymbol c \end{array} \right]=\left[ \begin{array}{c} \boldsymbol F \\ \boldsymbol 0_{(d+1)\times1} \end{array} \right] $$

(3)

where $\boldsymbol \lambda =(\lambda _{1},\lambda _{2},\ldots ,\lambda _{n})\in \mathbb {R}^{n}$, F = (f(x₁),f(x₂),…,f(x_n))^T, $\boldsymbol 0_{(d+1)\times (d+1)}\in \mathbb {R}^{(d+1)\times (d+1)}$ is a zero matrix, $\boldsymbol c=(c_{1},c_{2},\ldots ,c_{(d+1)})\in \mathbb {R}^{(d+1)}$ is the coefficient vector of the linear polynomial p(x), $\boldsymbol 0_{(d+1)}\in \mathbb {R}^{(d+1)}$ is a zero vector.

2.2.2 Candidate points generating

Lines 8 to 14 outlined in Algorithm 1 give the procedure of generating candidate points. The basic idea is to randomly perturb on some or all the coordinates of the best solution found so far (x_best). The perturbing process is controlled by a probability p_n = ϕ(n). ϕ(n) is defined by the following equation:

$$ \phi(n) = \phi_{0} \cdot \frac{1- \ln (n-n_{0}+1)}{ \ln (\max \_n-n_{0})}, \quad n_{0} \leq n \leq \max \_n-1. $$

(4)

where $\phi _{0}=\min \limits (20/d,1)$. It can be found from (4) that p_n will be smaller when n is larger, which means DYCORS perturbs most of the coordinates at the beginning but perturbs less dimensions at the end of the optimization process. Line 11 in Algorithm 1 is the perturbation operation, where z(δ) is a randomly generated number by a normal distribution $\mathcal {N}(0,\delta ^{2})$.

2.2.3 Selection of the next evaluation point

Line 15 in Algorithm 1 is the procedure for selecting the next evaluation point. The working steps are shown in Algorithm 2. In this procedure, the next evaluation point is selected according to the weighted score of the RBF prediction and the minimum distance to previously evaluated points. Based on line 13 of Algorithm 2, a larger value of ω encourages exploitation while a smaller value of ω encourages exploration. To maintain the balance between exploration and exploitation, the ω in DYCORS is cycling through a set of weights, which is denoted as γ = {γ₁,⋯ ,γ_s}, where 0 ≤ γ₁ ≤⋯ ≤ γ_s ≤ 1. Note that this procedure is computationally efficient and its computational complexity is only O(n ⋅ N_can).

3 Proposed MRSO algorithm

In this section, we introduce an efficient MRSO framework that uses some features from a single-fidelity surrogate-based global optimization algorithm but can further reduce the number of expensive objective function evaluations required for accurate solutions, beyond what is achievable with single-fidelity methods. First, the main steps of the proposed MRSO are given, and then some important features of MRSO are introduced in detail. For the convenience of explaining the algorithm, we define several notations, as shown in Table 8 from the Appendix.

3.1 The framework of MRSO

The flowchart of MRSO is depicted in Fig. 2 and the main steps are as follows:

Fig. 2

Flowchart of the proposed MRSO approach using LF and HF models

Step 1::

Space-filling experiment design for the LF model. Generate a sampling set $\mathcal {D}_{L}=\{\boldsymbol {x}_{1}, \boldsymbol {x}_{2},\ldots ,\boldsymbol {x}_{n_{0}}\}$ using a Latin hyper-cube design for the LF model.

Step 2::

Run LF model to obtain the LF response values f_L(x_i), $\boldsymbol {x}_{i}\in \mathcal {D}_{L}, i=1,2,\ldots ,n_{L}$. Set LF model evaluation number n_L as n_L = n₀. Initialize the database Θ_L, set Θ_L = {(x_i,f_L(x_i)),i = 1,2,…,n_L}. Let $\boldsymbol {x}^{*}_{L}$ be the best solution found so far on the LF model and $f^{L}_{\text {best}}=f^{L}(\boldsymbol {x}^{*}_{L})$.

Step 3::

While the termination condition is not satisfied. (e.g., $n_{L}< {\max \limits } \_n_{L}$) do

Step 3.1::

Build (or update) the RBF surrogate S_L(x) for the LF model using database Θ_L.

Step 3.2::

Randomly generate N_can candidate points denote as $C_{L}=\left \{\boldsymbol {x^{L}_{1}},\boldsymbol {x^{L}_{2}},..,\boldsymbol {x}^{L}_{N_{\text {can}}}\right \}$ around the current best solution $\boldsymbol {x}^{*}_{L}$ on the LF model by perturbing on part of the dimensions.

Step 3.3::

Select the next evaluation point x_nl from C_L by the weighted score criterion. The weight cycling pattern is denoted as γ.

Step 3.4::

Evaluate x_nl using the LF model and update the current best solution. If $f^{L}(\boldsymbol {x}_{\text {nl}})<f^{L}_{\text {best}}$, then $\boldsymbol {x}^{*}_{L}=\boldsymbol {x}_{\text {nl}}$ and $f^{L}_{\text {best}}=f^{L}(\boldsymbol {x}_{\text {nl}})$.

Step 3.5::

Update Information. Set Θ_L = Θ_L ∪{x_nl} and set n_L := n_L + 1.

Step 4::

Potential area detection procedure.

Step 4.1::

Run an optimizer on surrogate S_L(x) (i.e., run BFGS or GA for multiple trials, or run a multi-modal estimation of distribution algorithm). Store the final solutions into set $\mathcal {A}$, let $\mathcal {A}=\{(\boldsymbol {x}_{i},S_{L}(\boldsymbol {x}_{i})), i=1,2,\cdots ,m\}$, m is the number of solutions.

Step 4.2::

Use a cluster algorithm to classify the points from $\mathcal {A}$ into N_g groups. Identify the point with the best surrogate prediction value in each group and they are denoted as {x_k,k = 1,2,⋯ ,N_g}.

Step 4.3::

Re-evaluate the obtained points in step 4.2 with the actual LF function and keep the top Q% points with best LF objective function values. Then, store these points and the best solution from the LF run into a set $\mathcal {D}_{H}$, let $\mathcal {D}_{H}=\{\boldsymbol {x}^{*}_{L}\} \cup \left \{\boldsymbol {x}_{k}, k=1,2,\cdots ,\left \lfloor {N_{g} \cdot Q\%}\right \rfloor \right \}$. Set n_L := n_L + N_g

Step 5::

Run HF model to obtain the HF response values f_H(x_i), $\boldsymbol {x}_{i}\in \mathcal {D}_{H}, i=1,2,\ldots ,1+ \left \lfloor N_{g}\cdot Q\%\right \rfloor$. Set HF model evaluation number n_H as n_H = N_g. Initialize the database Θ_H, set Θ_H = {(x_i,f_H(x_i)),i = 1,2,…,n_H}. Let $\boldsymbol {x}^{*}_{H}$ be the best solution on the HF model and $f^{H}_{\text {best}}=f^{H}_{\text {best}}(\boldsymbol {x}^{*}_{H})$.

Step 6::

While the termination condition is not satisfied. (e.g., $n_{H}< {\max \limits } \_n_{E}-n_{L}/R$, R is the computational cost ratio between HF and LF models) do

Step 6.1::

Build (or update) the RBF surrogate S_H(x) for the HF model using database Θ_H.

Step 6.2::

Randomly generate N_can candidate points denote as $C_{H}=\{\boldsymbol {x^{H}_{1}},\boldsymbol {x^{H}_{2}},..,\boldsymbol {x}^{H}_{N_{\text {can}}}$ around the current best solution $\boldsymbol {x}^{*}_{H}$ on the HF model by perturbing on part of the dimensions.

Step 6.3::

Select the next evaluation point x_nh from C₂ by the weighted score criterion. The weight cycling pattern is denoted as γ.

Step 6.4::

Evaluate x_nh using the HF model and update the current best solution. If $f^{H}(\boldsymbol {x}_{\text {nh}})<f^{H}_{\text {best}}$, then $\boldsymbol {x}^{*}_{H}=\boldsymbol {x}_{\text {nh}}$ and $f^{H}_{\text {best}}=f^{H}(\boldsymbol {x}_{\text {nh}})$.

Step 6.5::

Update Information. Set Θ_H = Θ_H ∪{x_nh} and set n_H := n_H + 1.

Step 7::

Return the best solution $\boldsymbol {x}^{*}_{H}$ found so far.

3.2 Potential area detection procedure

A potential area detection procedure is proposed in MRSO. Its eventual aim is to identify multiple local optima, which might be in different area on the LF model and use them as the initial samples to drive the HF run. The motivation behind is that the LF and HF share some similarities; therefore, a better guess of the global optimum location using LF model could accelerate the optimization process on the HF model significantly.

Fig. 3

An illustration of the potential area detection process on 2-D Styblinski-Tang function. a Shows the landscape of LF model; b shows the landscape of HF model; c shows some points near multi-peaks are obtained by running GA to find maximum of the LF surrogate over multiple trials; d shows that all the peaks on the LF model are identified by the clustering algorithm

The potential area detection procedure has three main steps. In the first step (Fig. 2, part II, step 4.1), an optimizer is used to search on the RBF surrogate S_L(x) and identify the multiple local optimal solutions. In this study, three different methods have been utilized to complete this task. The first choice is to run a gradient-based algorithm (i.e., BFGS (Zhu et al. 1997)) for multiple trials from different start points. The second choice is to run a metaheuristic method (i.e., GA) for multiple trials. The third option is to run a multi-modal optimization method (i.e., multi-modal estimation of distribution algorithm (Yang et al. 2016)) for a single trial. In the second step (Fig. 2, part II, step 4.2), a cluster algorithm is used to classify the final solutions obtained in step one into several different groups. Here, the number of groups is the same as the number of local optima, and hence it is problem-dependent. In this study, the DBSCAN (density-based spatial clustering of applications with noise) algorithm (Schubert et al. 2017) is selected as the clustering algorithm since it does not require specifying the number of groups in advance of the clustering. In the third step (Fig. 2, part II, step 4.3), the best point in each group is re-evaluated by the LF model and the top Q% (Q is set to 50 in this study) points are selected. This step is necessary because the LF surrogate is less trusted and it helps filter those points that have nice LF surrogate prediction but bad actual LF model values.

To better demonstrate the potential area detection procedure, we take the 2-D Styblinski-Tang function as example. In this case, the aim is to maximize the function objective, and the HF and LF models are defined as follows:

$$ f_{H}(\boldsymbol{x}) = -\frac{1}{2} \sum\limits_{i=1}^{d} ({x^{4}_{i}}-16{x^{2}_{i}}+5x_{i}). $$

(5)

$$ f_{L}(\boldsymbol{x}) = f_{h}(\boldsymbol{x}) + f_{e}(\boldsymbol{x}). $$

(6)

where f_e(x) = η ⋅ f_h(x) is the error function and η is a uniform distributed random number between − 0.1 and 0.1.

Figure 3 shows the potential area detection process. Figure 3 a and b show the landscapes of the LF and HF models, respectively. It can be seen that the HF and LF models have similar landscapes. However, the HF model is smoother while the LF model is rougher. In the first step, a multi-modal metaheuristic/evolutionary algorithm is used to search on the RBF surrogate S_L(x), and the final solutions are shown in Fig. 3c. Then, the DBSCAN algorithm is applied to divide these points into different groups, and the best points from different groups, which is shown in Fig. 3d, are selected as the initial samples for the HF run.

3.3 Restart strategy

The restart strategy is applied to our proposed MRSO. Based on the previous study, the restart strategy is simple but efficient (Regis and Shoemaker 2007). In MRSO, the restart operation is triggered if the step size δ in Algorithm 1 is smaller than a threshold value $\delta _{ {\min \limits } }$. Once the restart strategy is triggered, all previously evaluated points will be abandoned and the algorithm starts over the whole optimization process of DYCORS from the experiment design.

4 Experimental results

In this section, the performance of proposed MRSO is validated on 10 benchmark functions with 10 and 30 dimensions and compared with 6 other surrogate-assisted optimization methods that include both single-fidelity and multi-fidelity methods.

4.1 Test problems

The benchmark functions adopted in this study are from the MFO test suite (Wang et al. 2017). In the test suite, a parameter α ranging from 0 to 10000 is introduced to describe the level of fidelity, where 0 represents the lowest level and 10000 represents the highest level. If the exact function is f(x), then the approximation of f(x) at fidelity level α can be formulated as follows:

$$ \hat{f}(\boldsymbol{x},\alpha) = f(\boldsymbol{x}) + f_{e}(\boldsymbol{x},\alpha) $$

(7)

where f_e(x,α) is the error function. The value of f_e(x,α) is smaller if fidelity level α is higher. For example, the error will be zero if α = 10000. In this study, we set α = 1000 for the LF model, and α = 10000 for the HF model. Three different types of error sources are introduced in the MFO test suite, including resolution errors, stochastic errors, and instability errors. The original test suite has 13 problems, but some of the problems have exactly the same expressions of HF and LF models. So, we choose the unique 10 problems as the test problems, which include P₁–P₃ and P₇–P₁₃ from the MFO test suite. The detailed information of the test problems is given in Table 1.

Table 1 Information about the test problems

4.2 Methods in comparison and experimental setup

The proposed MRSO is compared with 6 well-known surrogate-assisted optimization methods under two categories: single-fidelity methods and multi-fidelity methods. The single-fidelity methods include the DYCORS algorithm (Regis and Shoemaker 2013), the surrogate-assisted hierarchical particle swarm optimization (SHPSO) (Yu et al. 2018), the hybrid surrogate-based optimization using space reduction (HSOSR) (Dong et al. 2018), and the surrogate-guided differential evolution algorithm (S-JADE) (Cai et al. 2019). The multi-fidelity methods include the multi-fidelity Gaussian process and radial basis function-model-assisted memetic differential evolution (MGPMDE) (Liu et al. 2016), and the multi-fidelity Bayesian optimization (MF-GP-UCB) (Kandasamy et al. 2016). The MRSO and DYCORS are implemented based on the pySOT framework,¹ which is written in Python (Eriksson et al. 2019). The other methods are implemented in MATLAB. The code of MF-GP-UCB can be found from the GitHub website² and the code of S-JADE is provided by the original authors (Cai et al. 2019). Other algorithms are re-implemented by the authors of this paper according to the descriptions in the literature. The experiments are run on the high-performance computing platform at National University of Singapore.

Table 2 presents the parameter settings of the compared methods following the recommendations from the original literature. For a fair comparison, here we assume that the computational time of 10 LF evaluations is equal to one HF evaluation, as is common in industry (Liu et al. 2016; Koziel et al. 2014). Note that MRSO, MGPMDE, and MF-GP-UCB involve both HF and LF evaluations, while other methods only have HF evaluations. To ensure fair comparisons, among algorithms, the maximum number of the equivalent HF evaluations ${\max \limits } \_nE$ is limited to (15d + 350) for all algorithms, where d is problem dimension. The number of equivalent HF evaluations is the sum of the HF evaluations and discounted LF evaluations. For example, if an algorithm has 100 LF evaluations and 10 HF evaluations, and since 10 LF evaluations equals 1 HF evaluation, then the total number of equivalent HF evaluations is 10 + 100/10 = 20. Each of the algorithms is repeated for 30 independent trials and their average performances are compared.

Table 2 Parameter setting of compared algorithms

For our proposed MRSO approach, the parameter setting for the DYCORS component is the same as the original DYCORS shown in Table 2. Here, we implement three different variants of the MRSO by using different optimizers (BFGS, GA, and multi-modal estimation of distribution algorithm (MEDA)) in the potential area detection procedure, named MRSO-BFGS, MRSO-GA, and MRSO-MEDA. The number of multi-trials on BFGS and GA is set to 100. For the BFGS, the algorithm will stop when the gradient norm is less than 1.0e − 05. For GA, the population size is set to 100, the maximum number of iterations is set to 100, and the crossover and mutation rate are set to 0.9 and 1/d, respectively. For MEDA, the population size is set to 100, the maximum number of iterations is set to 200, and other parameter settings are taken from the original literature (Yang et al. 2016).

4.3 Impacts of different LF budget ratios on MRSO performance

One of the important issues in MFO is the allocation of the computational budgets between LF and HF runs. Too much search on LF model may cause an insufficient budget for further improving the solution on HF model. However, too little search on LF model is also unwise because not enough of the cheaply obtained useful information from the LF model will be used. In this section, the impacts of different LF budget ratios (i.e., the percentage of the LF computational budget on the total computational budget) on MRSO performance are analyzed. We vary the LF budget ratio from 10 to 90% and run the three MRSO variants on the 10- and 30-dimensional test problems. Figure 4 depicts the trend of average algorithm performance over different LF budget ratio. The Y -axis values are the average final function values over 10 problems. Based on Fig. 4a, the MRSO algorithms tend to have better performance with mediate LF budget ratio for 10-dimensional problems. The trend becomes much apparent on 30-dimensional problems, and Fig. 4b shows that the performances are the best when LF budget ratio is 40%. Therefore, the LF budget ratio of 40% is used in the following comparison.

Fig. 4

Comparison on the average performance of MRSO variants with different LF budget ratio. a 10-dimensional problems. b 30 dimensional problems

4.4 Comparison with other surrogate-assisted optimization methods

Tables 3 and 4 outline the statistical results achieved by all the compared methods including the mean values over 30 trials and the standard deviations for 10- and 30-dimensional problems. It can be observed from Table 3 that both of the best mean and standard deviation are achieved by MRSO variants on the 10-dimensional problems. Among the three MRSO variants, the performance of MRSO-MEDA is slightly better than the other two MRSO variants. A similar situation can be observed from Table 4 where MRSO variants also outperform other methods on the 30-d problems except for F₂. For F₂, the original DYCORS has the best performance.

Table 3 Mean and standard deviation of optimized HF function values found by each algorithm after 500 equivalent HF evaluations on 10-dimensional problems

Table 4 Mean and standard deviation of optimized HF function values found by each algorithm after 800 equivalent HF evaluations on 30-dimensional problems

Figures 5, 6, 7, and 8 present the convergence profiles of all the compared methods on 10- and 30-dimensional problems. Recall that all the convergence curves of MRSO variants start from the 201th evaluation for 10-dimensional problems and 321th evaluation for 30-dimensional problems because the first 40% equivalent evaluations are spent on the LF models. The convergence curves show that all of the MRSO variants start from very low HF function values benefit from the sufficient exploration on the cheap LF models. For some problems, MRSO can achieve better solutions than other methods at the very beginning of the HF run (i.e., F₇ and F₈ of the 10-dimensional problems, F₂, F₃, F₄, F₇, and F₈ of the 30-dimensional problems).

Fig. 5

Convergence curves of the alternative optimization methods on 10-dimensional benchmark functions (F₁–F₆)

Fig. 6

Convergence curves of the alternative optimization methods on 10-dimensional benchmark functions (F₇–F₁₀)

Fig. 7

Convergence curves of the alternative optimization methods on 30-dimensional benchmark functions. (F₁–F₆)

Fig. 8

Convergence curves of the alternative optimization methods on 30-dimensional benchmark functions (F₇–F₁₀)

For the 10-dimensional problems, all of our three MRSO variants have superior convergence performance on 9 problems (F₂ to F₁₀). For F₁, MRSO-BFGS and MRSO-MEDA have better convergence performance than other methods, and the performance of MRSO-GA is slightly worse than MGPMDE but better than the rest algorithms.

For the 30-dimensional problems, all of the three MRSO variants have superior convergence performance on 5 problems (F₁, F₃, F₄, F₇, F₈). For F₅, F₆, and F₁₀, the convergence performances of MRSO variants are worse than the original DYCORS. For F₂ and F₉, the convergence performances of DYCORS and the MRSO are similar and both of them are better than the rest 5 methods.

4.5 Performance and data profiles

To have an overall performance evaluation on all the test problems for all compared algorithms, the performance and data profiles are used (Moré and Wild 2009; Regis 2014). The performance and data profiles provide an effective approach to analyze how well and how fast of a specific algorithm is at solving a set of problem instances. Let P be the set of problems, and p is one of the instances in P. Since there are 10 optimization problems on both 10- and 30-dimensional problems, and 30 independent trials are repeated on each of the problems, there are 2 × 10 × 30 = 600 problem instances to produce the performance and data profiles. In addition, let S be the set of compared algorithms. In this study, S contains 9 compared algorithms (HSOSR, SHPSO, S-JADE, BRF-DYCORS, MF-GP-UCB, MGPMDE, MRSO-BFGS, MRSO-GA, and MRSO-MEDA). For any pair (p, s) of a problem instance p and an algorithm s, the performance ratio is defined to be Moré and Wild (2009):

$$ r_{p,s}=\frac{t_{p,s}}{ \min (t_{p,s}:s\in S)} $$

(8)

where t_p,s is the minimum number of function evaluations required by an algorithm to successfully pass the convergence test that is defined in Eq. 10. Clearly, r_p,s ≥ 1 for any p ∈ P and s ∈ S. Moreover, for problem p, the best algorithm s for this problem attains r_p,s = 1. Furthermore, when algorithm s fails to find a solution that satisfies the convergence test, then $r_{p,s}=\infty$.

For any algorithm s ∈ S and α ≥ 1, the performance profile of algorithm s with respect to α shows the fraction over all problem instances where its performance ratio is no greater than α,

$$ \rho_{s}(\alpha)=\frac{1}{|P|}|{p\in P:r_{p,s}\leq \alpha}| $$

(9)

In this study, the convergence test proposed by More and Wild (2009) with a tolerance τ = 0.05 is adopted. Let f_L be the minimum obtained function value among all the algorithms on a particular problem within a given number of function evaluations, the convergence test for an algorithm s is passed if the following condition is satisfied:

$$ f(\boldsymbol{x}_{0})-f(\boldsymbol{x})\geq (1-\tau)(f(\boldsymbol{x}_{0})-f_{L}) $$

(10)

where x₀ is a starting search point on a particular problem instance. Here, the point with the worst fitness value among all the first evaluated points of all methods is selected as the starting search point.

Similarly, the data profile of an algorithm for the indicator of the optimization progress β (i.e., how much of the budget is consumed; β is in the range of [0.0%,100.0%]), is defined by the following:

$$ d_{s}(\beta)=\frac{1}{|P|}|{p\in P:t_{p,s}\leq \beta}| $$

(11)

where t_p,s is the minimum number of objective function evaluations required by an algorithm to successfully pass the convergence test on problem p. For any algorithm s ∈ S, the data profile curve of s shows its growth of successful rate over all problem instances with the increasing of β.

Figure 9 shows the performance and data profiles. Note that for both performance profiles and data profiles the best results are the highest curves. The data profiles are especially important for expensive optimization problems because the horizontal axis indicate the optimization progress (it is positively correlated to the consumed number of equivalent HF function evaluations). Figure 9 a shows that the MRSO variants, followed by the original DYCORS and MGPMDE, have dramatically better performance profiles than other methods. Similarly, as shown by Fig. 9b, MRSO variants have better data profile values than other methods. In particular, the performance profile curves indicate that MRSO variants obtain the best solutions for about 72% to 80% out of 600 problem instances. The corresponding percentage of the original DYCORS is about 46%, and the corresponding percentage for MGPMDE is below 40%. For the remaining 4 methods (HSOSR, SHPSO, S-JADE, and MF-GP-UCB), the corresponding percentage is close to zero, which means they failed to pass the convergence tests. The data profile curves indicate that the MRSO variants obtain better performance than other methods since 50% of the whole optimization process. Notice that MGPMDE has better performance at the earlier stage of the optimization process but drops behind DYCORS and MRSO variants at the later stage. It is probably because that MGPMDE is trapped in local optimums and cannot further improve the solutions while DYCORS and MRSO variants have the restart strategy so that they are more likely to jump out the local optima.

Fig. 9

a Performance and b data profiles on all the problems (LF budget ratio = 40%, and highest curves are the best)

4.6 Discussion

According to the impact analysis of LF budget ratio to MRSO’s performance in Fig. 4, it is sensible to use about 40% of the computational budget for the search on LF model. The LF budget ratio of 40% is also used in the comparison to other methods. It should be recalled that the results in Fig. 9 for all methods assume that the maximum computational budget and the percentage of budget to be used for LF evaluations is fixed in advance of any optimization. Hence, one should not interpret the results in Fig. 9b to indicate that other methods outperform MRSO options when the evaluation budget is less. What Fig. 9b indicates is that MRSO is using (the less accurate) LF evaluation in those early iterations in contrast to DYCORS (that uses no LF computation) so it is not surprising the those objective values are lower in early computation. Also, MRSO methods would change their search method (which is a function of the computational budget allocated, see (4)) if the maximum evaluation effort were reduced. Hence, the fact that curves in Fig. 9b are lower than the MRSO for some other algorithms when fewer than 50% of the evaluation budget is expended just indicates MRSO is searching differently in early evaluations than the other methods. The valid number to look at is the performance at 100% of budget, where the MRSO algorithms have excellent performance in comparison to others.

It is also interesting to know if MRSO variants still outperform other methods when using other settings on the LF budget ratio. Hence, we use the results of MRSO variants with LF budget ratio of 10% to plot the performance and data profiles again. Interestingly, it can be observed from Fig. 10a, although there is a drop in the performance of MRSO variants, they still outperform other methods. In addition, it can be seen from the data profiles in Fig. 10b that MRSO variants keep ahead from the very beginning of the optimization process. Therefore, it demonstrates the high robustness of MRSO’s performance.

Fig. 10

a Performance and b data profiles on all the problems. (LF budget ratio = 10%, and highest curves are the best)

5 Applications on capacity planning for manufacturing systems

To further demonstrate the effectiveness of the proposed MRSO, in this section, we apply MRSO to the capacity planning problem in manufacturing systems. Capacity planning is of critical importance because investment in facility is very high in manufacturing systems. For example, the cost of new wafer fabs in a semiconductor factory can be more than US$1.0 billion (Hopp et al. 2002). A manufacturing system usually consists of different types of machines, and the managers have to determine the optimal capacity of each type of machine to minimize the system cost. This problem is challenging because the system performance is analytically intractable and accurate performance analysis of the system relies on running expensive simulation models. In other words, the problem can be recognized as a computationally expensive black-box optimization problem. In the following, we will introduce the detailed problem settings and compare the performance of the proposed MRSO with other algorithms in the literature.

5.1 The capacity planning problem

For simplicity, we model the manufacturing system with a queuing network and follow the outline given in Hopp et al. (2002). Jobs (or products) arrive to the system with the rate λ and need to be processed by the machines based on a deterministic sequence of procedures. Note that a product can visit one station multiple times (i.e., re-entry allowed) (Kumar 1993). There are N types of machines in the system and capacity planning involves determining the optimal capacity for these machines. We denote the decision variables, i.e., the capacity of each type of machine, by μ = (μ₁,μ₂,...,μ_N). The objective function (i.e., system cost) is comprised of two parts: the capacity cost and waiting cost. The capacity cost (CC) includes the machine purchasing operations cost and is an increasing function with respect to each μ_i, i = 1,2,...,N. The waiting cost (WC) is the function of jobs’ average cycle times (CT) in the manufacturing system. The reason for introducing the WT is that the CT can represent the service level and large cycle time generally means large volume of work in process (Little’s Law, Little and Graves (2008)), which will induce inventory cost. Depending on the practical situations, the relationship between the WT and CT can have different forms. CT depends on (μ₁,μ₂,...,μ_N) and its accurate evaluation relies on the simulation model for the manufacturing systems.

Hence, the capacity planning problem can be formulated as follows:

$$ \min_{\mu \in \mathcal{D}} f(\mu)=\text{WC}(\text{CT}(\mu))+\text{CC}(\mu). $$

(12)

Here, $\mathcal {D}$ is the feasible solution space. For stability, the capacity of each type of station should be greater than the effective arrival rate at the station (Shen and Wu 2018; Hopp et al. 2002). Note that f(μ) is a black-box function since the evaluation for CT(μ) relies on expensive simulation models.

In this context, an HF model means we run the simulation model for a sufficiently long period to get an accurate estimate for the average cycle and then the objective function can be calculated accordingly. The LF model may be created in different ways. For example, one can employ the approximation models in queuing theory to estimate CT(μ) (Whitt 1983; Wu and McGinnis 2013; Wu et al. 2018). These approximations are inaccurate but their computation is very inexpensive. Alternatively, an LF model can also be created by running the simulation model with less computing effort, which will provide an inaccurate estimate for CT(μ). To be consistent with the numerical studies in previous sections, we use the latter method as the LF model.

5.2 An illustration example of two stations

To better visualize the HF and LF models in a manufacturing system, we first present an example consisting of only two types of stations (i.e., a 2-d problem). As shown by Fig. 11, jobs arrive from outside with rate λ = 1 and need to be processed by station 1 and station 2 sequentially. The CC is assumed be of the form CC(μ) = c₁(μ₁ − 1.2)³ + c₁(μ₁ − 1.2)³. The waiting cost is assumed to be proportional to the average cycle time WC = h CT(μ₁,μ₂).

Fig. 11

A two-station tandem queue

Under the above setting, it follows that

$$ f(\mu_{1},\mu_{2}) = c_{1}(\mu_{1}-1.2)^{3}+c_{2}(\mu_{2}-1.2)^{3}+h\text{CT}(\mu_{1},\mu_{2}), $$

(13)

where c₁ = 3500, c₂ = 4000, and h = 0.2 are the cost parameters. For stability, the domain of (μ₁,μ₂) is (1,1.4] × (1,1.4]. We assume Gamma distributions for the inter-arrival time of jobs and service times at each stations. The squared coefficient of variation (SCVs) of the arrival process, service at station 1, and service at station 2 are 10, 0.1, 1.5 respectively.

To visualize the similarities and differences between the LF model and HF model, we produce the surface plot and contour plot of f(μ₁,μ₂) for the two models respectively. As shown in Fig. 12, although there is a performance gap between the LF model and HF model, they share a similar structure. Hopefully, we can exploit this property to improve the efficiency of determining the optimal capacity.

Fig. 12

Comparison between the LF and HF models on the two-station tandem queue problem

5.3 Experimental results on a 12-d capacity planning problem

In this section, the proposed MRSO is applied to a 12-d capacity planning problem, and we compare its performance with other methods (the same methods in Section 4). We use a simplified version of the example given by Hopp et al. (2002). We consider a semiconductor line with 12 types of machines and 1 type of job. Jobs arrive to the system with the rate λ = 1, and need to be processed based a deterministic sequence of procedures given in Table 5. In this case, the system cost is assumed to take the following form:

$$ f(\mu) = \sum\limits_{i=1}^{i=12} c_{i}\mu_{i}+e^{h\text{CT}(\mu)}, $$

(14)

where c_i is the unit cost for each type of machine and h is a constant. In other words, the CC is proportional to μ and the waiting cost increases exponentially with respect to the average cycle time CT(μ). The CC information and feasible space of each decision variable is given in Table 6 and the constant h is set as 2.

Table 5 Processing procedures of jobs

Table 6 Capacity cost information at each station and feasible space for each decision variable

To evaluate the average cycle time and then calculate the objective function, the HF model simulates the manufacturing system for 2 million hours and the LF model simulates the system for 0.2 million hours. A single run of the HF model takes about 30 min and a single run of the LF model takes about 3 min. Hence, the computational cost ratio between HF and LF model is also 10.0. Since the HF evaluation is expensive, thus we set the maximum number of equivalent HF evaluation as 150 and each of the compared methods is repeated for 10 trials. Each run of the whole optimization process (with 150 equivalent HF evaluations) takes more than 3 days of computing time.

Table 7 presents the statistic results from 10 trials of all the compared methods on this problem. The results show that MRSO-BFGS obtains the best results. Figure 13 presents the progress plots of all the methods on the capacity planning problem. It can be found that the MRSO variants find excellent solutions within a small number of evaluations. In addition, compared with the original DYCORS, the MRSO variants, especially MRSO-GA and MRSO-BFGS, converge to the optimal solution much faster. This validates that the proposed MFO framework can further speed-up the optimization process compared with the original DYCORS. In summary, the superior performance of MRSO variants in the capacity planning problem has demonstrated its potential to efficiently solve practical expensive optimization problems.

Table 7 Statistics of the results obtained by different methods on the 12-d capacity planning problem. The best value on each metric is in italic

Fig. 13

Progress plots of the compared methods on the capacity planning problem

6 Conclusions

In this paper, a multi-fidelity RBF surrogate-based optimization framework called MRSO is developed for computationally expensive black-box optimization problems. The proposed MRSO approach has three main steps: (1) search on the LF model, (2) potential area detection procedure, and (3) the search on the HF model. The proposed MRSO approach is tested and compared with other 6 recent surrogate-based optimization methods on 10 test problems from the MFO test suite with 10 and 30 dimensions. Experimental results show that MRSO can speed-up the optimization process and further improve the performance of the original DYCORS algorithm. Furthermore, it outperforms other compared single-fidelity and multi-fidelity surrogate-based optimization methods. Besides the results on test functions, MRSO is successfully applied to a complex, computationally expensive real-world capacity planning problem in manufacturing systems involving discrete event simulations. Therefore, the proposed MRSO can be considered as a promising approach for solving real-life computationally expensive optimization problems.

In the future, we will apply the proposed MRSO to other complex, computationally expensive optimization problems in real life.

Appendix

Table 8 List of notation used in the proposed MRSO