Skip to main content
SpringerLink
Log in

Active vibration control of rotating laminated composite truncated conical shells through magnetostrictive layers based on first-order shear deformation theory

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

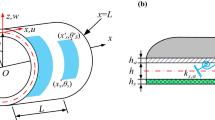
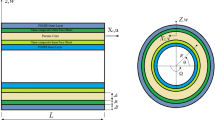
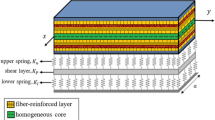
In this paper, for the first time active vibration control of rotating laminated composite truncated conical shells containing magnetostrictive layers by employing first-order shear deformation theory is investigated. The active vibration control task is done through magnetostrictive layers employing velocity feedback control law. The effects of initial hoop tension and centrifugal and Coriolis forces are considered in extraction of the partial differential equations through Hamilton principle. The ordinary differential equations are derived by employing modified Galerkin method. This study agrees with the mentioned results of the literature. Finally, the effects of several parameters on the vibration suppression are investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Chopra I, Sirohi J (2013) Smart structures theory, vol 35. Cambridge University Press, Cambridge

    Book  Google Scholar 

  2. Goodfriend MJ, Shoop KM (1992) Adaptive characteristics of the magnetostrictive alloy, Terfenol-D, for active vibration control. J Intell Mater Syst Struct 3(2):245–254

    Article  Google Scholar 

  3. Olabi AG, Grunwald A (2008) Design and application of magnetostrictive materials. Mater Des 29(2):469–483

    Article  Google Scholar 

  4. Li H, Chen ZB, Tzou HS (2010) Distributed actuation characteristics of clamped-free conical shells using diagonal piezoelectric actuators. Smart Mater Struct 19(11):115015

    Article  Google Scholar 

  5. Li H, Chen ZB, Hu SD, Tzou HS (2011) Optimal control of clamped-free conical shell using diagonal piezoelectric sensor and actuator. ASME Int Mech Eng Cong Expos. https://doi.org/10.1115/IMECE2011-63028

    Article  Google Scholar 

  6. Shah PH, Ray MC (2012) Active control of laminated composite truncated conical shells using vertically and obliquely reinforced 1–3 piezoelectric composites. Eur J Mech A Solids 32:1–12

    Article  MathSciNet  MATH  Google Scholar 

  7. Li FM, Song ZG, Chen ZB (2012) Active vibration control of conical shells using piezoelectric materials. J Vib Control 18(14):2234–2256

    Article  MathSciNet  Google Scholar 

  8. Li H, Hu SD, Tzou HS, Chen ZB (2012) Optimal vibration control of conical shells with collocated helical sensor/actuator pairs. J Theor Appl Mech 50(3):769–784

    Google Scholar 

  9. Kumar A, Ray MC (2014) Control of smart rotating laminated composite truncated conical shell using ACLD treatment. Int J Mech Sci 89:123–141

    Article  Google Scholar 

  10. Fan J, Huang J, Ding J, Zhang J (2017) Free vibration of functionally graded carbon nanotube-reinforced conical panels integrated with piezoelectric layers subjected to elastically restrained boundary conditions. Adv Mech Eng 9(7):1687814017711811

    Google Scholar 

  11. Sun L, Li W, Wu Y, Lan Q (2017) Active vibration control of a conical shell using piezoelectric ceramics. J Low Freq Noise Vib Act Control 36(4):366–375

    Article  Google Scholar 

  12. Hajmohammad MH, Farrokhian A, Kolahchi R (2018) Smart control and vibration of viscoelastic actuator-multiphase nanocomposite conical shells-sensor considering hygrothermal load based on layerwise theory. Aerosp Sci Technol 78:260–270

    Article  Google Scholar 

  13. Chan DQ, Quan TQ, Kim SE, Duc ND (2019) Nonlinear dynamic response and vibration of shear deformable piezoelectric functionally graded truncated conical panel in thermal environments. Eur J Mech A Solids 77:103795

    Article  MathSciNet  MATH  Google Scholar 

  14. Mohammadrezazadeh S, Jafari AA (2019) Vibration suppression of truncated conical shells embedded with magnetostrictive layers based on first order shear deformation theory. J Theor Appl Mech 57(4):957–972. https://doi.org/10.15632/jtam-pl/112419

    Article  Google Scholar 

  15. Moghaddam SMF, Ahmadi H (2020) Active vibration control of truncated conical shell under harmonic excitation using piezoelectric actuator. Thin Walled Struct 151:106642

    Article  Google Scholar 

  16. Lam KY, Hua L (1997) Vibration analysis of a rotating truncated circular conical shell. Int J Solids Struct 34(17):2183–2197

    Article  MATH  Google Scholar 

  17. Hua L (2000) Frequency characteristics of a rotating truncated circular layered conical shell. Compos Struct 50(1):59–68

    Article  MathSciNet  Google Scholar 

  18. Ng TY, Li H, Lam KY (2003) Generalized differential quadrature for free vibration of rotating composite laminated conical shell with various boundary conditions. Int J Mech Sci 45(3):567–587

    Article  MATH  Google Scholar 

  19. Civalek Ö (2006) An efficient method for free vibration analysis of rotating truncated conical shells. Int J Press Vessels Pip 83(1):1–12

    Article  Google Scholar 

  20. Talebitooti M, Ghayour M, Ziaei-Rad S, Talebitooti R (2010) Free vibrations of rotating composite conical shells with stringer and ring stiffeners. Arch Appl Mech 80(3):201–215

    Article  MATH  Google Scholar 

  21. Malekzadeh P, Heydarpour Y (2013) Free vibration analysis of rotating functionally graded truncated conical shells. Compos Struct 97:176–188

    Article  Google Scholar 

  22. Heydarpour Y, Aghdam MM, Malekzadeh P (2014) Free vibration analysis of rotating functionally graded carbon nanotube-reinforced composite truncated conical shells. Compos Struct 117:187–200

    Article  MATH  Google Scholar 

  23. Nejati M, Asanjarani A, Dimitri R, Tornabene F (2017) Static and free vibration analysis of functionally graded conical shells reinforced by carbon nanotubes. Int J Mech Sci 130:383–398

    Article  Google Scholar 

  24. Civalek Ö (2017) Discrete singular convolution method for the free vibration analysis of rotating shells with different material properties. Compos Struct 160:267–279

    Article  Google Scholar 

  25. Sarkheil S, Foumani MS (2017) An improvement to motion equations of rotating truncated conical shells. Eur J Mech A Solids 62:110–120

    Article  MathSciNet  MATH  Google Scholar 

  26. Dai Q, Cao Q, Chen Y (2018) Frequency analysis of rotating truncated conical shells using the Haar wavelet method. Appl Math Model. https://doi.org/10.1016/j.apm.2017.06.025

    Article  MATH  MathSciNet  Google Scholar 

  27. Shekari A, Ghasemi FA, Malekzadehfard K (2017) Free damped vibration of rotating truncated conical sandwich shells using an improved high-order theory. Latin Am J Solids Struct 14(12):2291–2323

    Article  Google Scholar 

  28. Talebitooti M (2018) Thermal effect on free vibration of ring-stiffened rotating functionally graded conical shell with clamped ends. Mech Adv Mater Struct 25(2):155–165

    Article  Google Scholar 

  29. Dung DV, Anh LTN, Hoa LK (2018) Analytical investigation on the free vibration behavior of rotating FGM truncated conical shells reinforced by orthogonal eccentric stiffeners. Mech Adv Mater Struct 25(1):32–46

    Article  Google Scholar 

  30. Shakouri M (2019) Free vibration analysis of functionally graded rotating conical shells in thermal environment. Compos B Eng 163:574–584

    Article  Google Scholar 

  31. Singha TD, Rout M, Bandyopadhyay T, Karmakar A (2020) Free vibration analysis of rotating pretwisted composite sandwich conical shells with multiple debonding in hygrothermal environment. Eng Struct 204:110058

    Article  Google Scholar 

  32. Rao SS (2007) Vibration of continuous systems. Wiley, New York

    Google Scholar 

  33. Pradhan SC, Reddy JN (2004) Vibration control of composite shells using embedded actuating layers. Smart Mater Struct 13(5):1245

    Article  Google Scholar 

  34. Reddy JN (2003) Mechanics of laminated composite plates and shells: theory and analysis, 2nd edn. CRC Press, Boca Raton

    Google Scholar 

  35. Lee SJ, Reddy JN (2004) Vibration suppression of laminated shell structures investigated using higher order shear deformation theory. Smart Mater Struct 13(5):1176

    Article  Google Scholar 

  36. Talebitooti M (2013) Three-dimensional free vibration analysis of rotating laminated conical shells: layerwise differential quadrature (LW-DQ) method. Arch Appl Mech 83(5):765–781

    Article  MATH  Google Scholar 

  37. Li H, Lam KY, Ng TY (2005) Rotating shell dynamics. Elsevier, Amsterdam

    MATH  Google Scholar 

  38. Qatu MS (2004) Vibration of laminated shells and plates. Elsevier, Amsterdam

    MATH  Google Scholar 

  39. Sun S, Liu L, Cao D (2018) Nonlinear travelling wave vibrations of a rotating thin cylindrical shell. J Sound Vib 431:122–136

    Article  Google Scholar 

  40. Irie T, Yamada G, Tanaka K (1984) Natural frequencies of truncated conical shells. J Sound Vib 92(3):447–453

    Article  Google Scholar 

  41. Li FM, Kishimoto K, Huang WH (2009) The calculations of natural frequencies and forced vibration responses of conical shell using the Rayleigh-Ritz method. Mech Res Commun 36(5):595–602

    Article  MATH  Google Scholar 

  42. Lam KY, Hua L (1999) Influence of boundary conditions on the frequency characteristics of a rotating truncated circular conical shell. J Sound Vib 223(2):171–195

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mechanical Engineering, K. N. Toosi University of Technology, Tehran, Iran

    Shahin Mohammadrezazadeh & Ali Asghar Jafari

Authors
  1. Shahin Mohammadrezazadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ali Asghar Jafari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shahin Mohammadrezazadeh.

Additional information

Technical Editor: Wallace Moreira Bessa, D.Sc..

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The differential operators of matrix L which is introduced in Eq. (29) are defined as the following for symmetric cross-ply lamination scheme:

$$\begin{aligned} L_{11} & = A_{11} R(x)\frac{{\partial^{2} }}{{\partial x^{2} }} + A_{11} \sin \alpha \frac{\partial }{\partial x} - \frac{{A_{22} \sin^{2} \alpha }}{R(x)} + \frac{{A_{66} }}{R(x)}\frac{{\partial^{2} }}{{\partial \theta^{2} }} - I_{1} R(x)\frac{{\partial^{2} }}{{\partial t^{2} }} \\ & \quad + I_{1} \varOmega^{2} R(x)\sin^{2} \alpha + I_{1} \varOmega^{2} R(x)\frac{{\partial^{2} }}{{\partial \theta^{2} }} \\ \end{aligned}$$
(46)
$$L_{12} = A_{12} \frac{{\partial^{2} }}{\partial x\partial \theta } - \frac{{A_{22} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + A_{66} \frac{{\partial^{2} }}{\partial x\partial \theta } - \frac{{A_{66} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + 2I_{1} \varOmega R(x)\sin \alpha \frac{\partial }{\partial t}$$
(47)
$$\begin{aligned} L_{13} & = A_{12} \cos \alpha \frac{\partial }{\partial x} - A_{31} R(x)\frac{{\partial^{2} }}{\partial x\partial t} - A_{31} \sin \alpha \frac{\partial }{\partial t} - \frac{{A_{22} \sin \alpha \cos \alpha }}{R(x)} + A_{32} \sin \alpha \frac{\partial }{\partial t} \\ & \quad + I_{1} \varOmega^{2} R(x)\sin \alpha \cos \alpha - I_{1} (R(x))^{2} \varOmega^{2} \cos \alpha \frac{\partial }{\partial x} \\ \end{aligned}$$
(48)
$$L_{14} = 0$$
(49)
$$L_{15} = 0$$
(50)
$$\begin{aligned} L_{21} & = A_{12} \frac{{\partial^{2} }}{\partial x\partial \theta } + \frac{{A_{22} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + A_{66} \frac{{\partial^{2} }}{\partial x\partial \theta } + \frac{{A_{66} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } - 2I_{1} \varOmega R(x)\sin \alpha \frac{\partial }{\partial t} \\ & \quad + I_{1} \varOmega^{2} (R(x))^{2} \frac{{\partial^{2} }}{\partial x\partial \theta } + I_{1} \varOmega^{2} R(x)\sin \alpha \frac{\partial }{\partial \theta } \\ \end{aligned}$$
(51)
$$\begin{aligned} L_{22} & = \frac{{A_{22} }}{R(x)}\frac{{\partial^{2} }}{{\partial \theta^{2} }} + A_{66} R(x)\frac{{\partial^{2} }}{{\partial x^{2} }} + A_{66} \sin \alpha \frac{\partial }{\partial x} - \frac{{A_{66} }}{R(x)}\sin^{2} \\ & \quad\alpha - \frac{{K_{s} A_{44} \cos^{2} \alpha }}{R(x)} - I_{1} R(x)\frac{{\partial^{2} }}{{\partial t^{2} }} + I_{1} \varOmega^{2} R(x)\\ & \quad + I_{1} \varOmega^{2} (R(x))^{2} \sin \alpha \frac{\partial }{\partial x} - I_{1} \varOmega^{2} R(x)\sin^{2} \alpha \\ \end{aligned}$$
(52)
$$L_{23} = \frac{{A_{22} \cos \alpha }}{R(x)}\frac{\partial }{\partial \theta } - A_{32} \frac{{\partial^{2} }}{\partial \theta \partial t} + \frac{{K_{s} A_{44} \cos \alpha }}{R(x)}\frac{\partial }{\partial \theta } - 2I_{1} \varOmega R(x)\cos \alpha \frac{\partial }{\partial t}$$
(53)
$$L_{24} = 0$$
(54)
$$L_{25} = K_{\text{s}} A_{44} \cos \alpha$$
(55)
$$\begin{aligned} L_{31} & = - A_{12} \cos \alpha \frac{\partial }{\partial x} - \frac{{A_{22} \sin \alpha \cos \alpha }}{R(x)} + I_{1} \varOmega^{2} R(x)\sin \alpha \cos \alpha \\ & \quad - m_{kh} I_{1} \varOmega^{2} (R(x))^{2} \cos \alpha \frac{\partial }{\partial x} \\ \end{aligned}$$
(56)
$$ \begin{aligned}L_{32} &= - \frac{{A_{22} \cos \alpha }}{R(x)}\frac{\partial }{\partial \theta } - \frac{{K_{\text{s}} A_{44} \cos \alpha }}{R(x)}\frac{\partial }{\partial \theta } \\ &\quad+ 2I_{1} \varOmega R(x)\cos \alpha \frac{\partial }{\partial t} - I_{1} os\varOmega^{2} R(x)\frac{\partial }{\partial \theta }\end{aligned} $$
(57)
$$\begin{aligned} L_{33} & = - \frac{{A_{22} \cos^{2} \alpha }}{R(x)} + A_{32} \cos \alpha \frac{\partial }{\partial t} + K_{\text{s}} A_{55} R(x)\frac{{\partial^{2} }}{{\partial x^{2} }} + K_{s} A_{55} \sin \alpha \frac{\partial }{\partial x} \\ & \quad + \frac{{K_{\text{s}} A_{44} }}{R(x)}\frac{{\partial^{2} }}{{\partial \theta^{2} }} - I_{1} R(x)\frac{{\partial^{2} }}{{\partial t^{2} }} + I_{1} \varOmega^{2} R(x)\cos^{2} \alpha + I_{1} \varOmega^{2} R(x)\frac{{\partial^{2} }}{{\partial \theta^{2} }} \\ \end{aligned}$$
(58)
$$L_{34} = K_{\text{s}} A_{55} R(x)\frac{\partial }{\partial x} + K_{\text{s}} A_{55} \sin \alpha$$
(59)
$$L_{35} = K_{\text{s}} A_{44} \frac{\partial }{\partial \theta }$$
(60)
$$L_{41} = 0$$
(61)
$$L_{42} = 0$$
(62)
$$L_{43} = - K_{\text{s}} A_{55} R(x)\frac{\partial }{\partial x}$$
(63)
$$\begin{aligned} L_{44} & = D_{11} R(x)\frac{{\partial^{2} }}{{\partial x^{2} }} + D_{11} \sin \alpha \frac{\partial }{\partial x} - \frac{{D_{22} \sin^{2} \alpha }}{R(x)} + \frac{{D_{66} }}{R(x)}\frac{{\partial^{2} }}{{\partial \theta^{2} }} - K_{\text{s}} A_{55} R(x) \\ & \quad - I_{3} R(x)\frac{{\partial^{2} }}{{\partial t^{2} }} + I_{3} \varOmega^{2} R(x)\sin^{2} \alpha \\ \end{aligned}$$
(64)
$$ \begin{aligned}L_{45} &= D_{12} \frac{{\partial^{2} }}{\partial x\partial \theta } - \frac{{D_{22} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + D_{66} \frac{{\partial^{2} }}{\partial x\partial \theta } \\ &\quad- \frac{{D_{66} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + 2I_{3} \varOmega R(x)\sin \alpha \frac{\partial }{\partial t}\end{aligned} $$
(65)
$$L_{51} = 0$$
(66)
$$L_{52} = K_{\text{s}} A_{44} \cos \alpha$$
(67)
$$L_{53} = - K_{\text{s}} A_{44} \frac{\partial }{\partial \theta }$$
(68)
$$ \begin{aligned}L_{54} &= D_{12} \frac{{\partial^{2} }}{\partial x\partial \theta } + \frac{{D_{22} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + D_{66} \frac{{\partial^{2} }}{\partial x\partial \theta } \\ &\quad+ \frac{{D_{66} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } - 2I_{3} \varOmega R(x)\sin \alpha \frac{\partial }{\partial t}\end{aligned} $$
(69)
$$\begin{aligned} L_{55} & = \frac{{D_{22} }}{R(x)}\frac{{\partial^{2} }}{{\partial \theta^{2} }} + D_{66} R(x)\frac{{\partial^{2} }}{{\partial x^{2} }} + D_{66} \sin \alpha \frac{\partial }{\partial x} \\ & \quad - \frac{{D_{66} \sin^{2} \alpha }}{R(x)} - K_{\text{s}} A_{44} R(x) - I_{3} R(x)\frac{{\partial^{2} }}{{\partial t^{2} }} + I_{3} \varOmega^{2} R(x) \\ \end{aligned}$$
(70)

The elements of matrix P which is presented in Eq. (32) can be obtained in the following types for cross-ply symmetric laminate scheme:

$$P_{11} = - A_{11} R(x)\frac{\partial }{\partial x} - A_{12} \sin \alpha$$
(71)
$$P_{12} = - A_{12} \frac{\partial }{\partial \theta }$$
(72)
$$P_{13} = - A_{12} \cos \alpha + A_{31} R(x)\frac{\partial }{\partial t}$$
(73)
$$P_{44} = - D_{11} R(x)\frac{\partial }{\partial x} - D_{12} \sin \alpha$$
(74)
$$P_{45} = - D_{12} \frac{\partial }{\partial \theta }$$
(75)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mohammadrezazadeh, S., Jafari, A.A. Active vibration control of rotating laminated composite truncated conical shells through magnetostrictive layers based on first-order shear deformation theory. J Braz. Soc. Mech. Sci. Eng. 42, 304 (2020). https://doi.org/10.1007/s40430-020-02363-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-020-02363-w

Keywords

Search

Navigation