Since the seminal papers of Evans and Ritchie about two decades ago [1, 2], based on previous theoretical models of bond rupture by Bell [3], dynamic force spectroscopy (DFS) has been widely used as a tool to measure the thermodynamics and kinetics of bonds between a wide variety of ligand-receptor pairs, providing very detailed information regarding important biological processes [4]. The power of this experiment stems from the fact that it allows to prove binding at the level of a single ligand-receptor pair, without the averaging implicit in bulk binding essays as ELISA. In DFS, the kinetics of binding is inferred by measuring the probability distribution of rupture forces at breakage, and fitting this quantity to model distribution functions, such as the Dudko-Hummer-Szabo’s [5, 6] or Bell’s [3] models. In this way, microscopic quantities such as the free-energy barrier for bond rupture and the equilibrium bond lifetime can be recovered.

DFS experiments can be carried out in various ways, but the general procedure can be exemplified in the following way: In a typical experiment, a ligand (receptor) is tethered to a substrate via a linking construct, typically another small molecule, a protein or a polymer. Colloids controlled via optical tweezers are a prominent example of a substrate [7, 8], although the tip of an AFM cantilever, or just a simple planar surface, has also often been used in this type of experiments [9]. Starting from afar, ligand and receptor are brought to a distance where bonding can occur at time t = 0, and retracted after a certain time t = tobs, which will be referred to as the observation time. If a bond is present within the ligand-receptor pair, a resisting force is measured, and none otherwise. In a typical DFS experiment, the ligand bound is retracted from the receptor and the exact value of the force at rupture is recorded and analysed. Here, instead of looking at the distribution of rupture forces, we will look at the probability to observe a certain number of binding and unbinding events as a function of time during an experiment where the ligand-receptor distance is kept fixed. We will derive a mathematical model to describe this probability and see that this quantity provides us with another root to extract kon and koff from a DFS experiment. As we shall see, it turns out that such probability is connected to the bond energy ΔGbond for a tethered ligand-receptor pair. The statistical mechanical interpretation of such bond energy, its dependence on microscopic details of the ligand-receptor pair and its connection to the binding constant of such pair will be the other main concern of this paper.

Let us first imagine a thought experiment, the practical realisation of which will be discussed later. The system of concern is schematically depicted in Fig. 1. We have a ligand and a receptor, both tethered via a linker to a substrate, the relative position of which is fixed. At time t = 0, as the ligand-receptor pair was brought to binding distance from afar, the system is in an unbound state. What is the number of binding and unbinding events measured within a time tobs? Using the same setup typically employed in DFS, this is equivalent to measuring the number of times that a non-zero attractive force (bond formation) and its subsequent disappearance (bond rupture) is recorded within tobs. Unlike in normal DFS, however, where after formation the bond is stretched until rupture, in this case, the ligand-receptor pair must be kept at a fixed distance during the measurement. In this sense, this setup restricts this potential experiment to ligand-receptor pairs where a dynamic equilibrium between bound and unbound states exist, or in other words to reversible bonds. In the following, I present a general but simple microscopic model to connect the outcome of this measurement to the binding, kon, and unbinding, koff, rate of the bond between the ligand-receptor pair. Before doing any calculation, let us think about this problem for a second to see what we should expect. In fact, instead of concentrating on the number of binding and unbinding events observed, let us consider the probability PB for the system to be found in a bound state at a certain time tobs. If the system was initially unbound at t = 0, it means the system must have gone through N binding and N − 1 unbinding events. This probability is thus given by:

$$ P_{\mathrm{B}}(t_{\text{obs}}) = \sum\limits_{N=1}^{\infty} P_{N,N-1}\left( t_{\text{obs}}\right), $$
(1)

where \(P_{N,N-1}\left (t_{\text {obs}}\right )\) is the probability to observe exactlyN binding and N − 1 unbinding events. Similarly, the probability to find the system in an unbound state \(P_{\bar {\text {B}}} = 1 - P_{\mathrm {B}} = {\sum }_{N=1}^{\infty } P_{N,N}\left (t_{\text {obs}}\right )\), \(P_{N,N}\left (t_{\text {obs}}\right )\) now being the probability to observe an equal number N of binding and unbinding events. If one waits long enough for the system to equilibrate before making an observation, i.e. formally for \(t_{\text {obs}}\rightarrow \infty \), the probability for the ligand-receptor pair to be found in a bound state must reach its equilibrium value. The system we describe can be regarded as a two-state system, where the bond is formed, or not. In a two-state system, the equilibrium value for the bonding probability is trivially given by:

$$ P_{\mathrm{B}}^{\text{eq}} = \frac{\exp(-\upbeta{\Delta} G^{\text{bond}})}{1+\exp(-\upbeta{\Delta} G^{\text{bond}})} $$
(2)
Fig. 1
figure 1

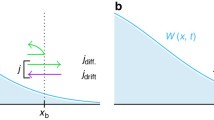
Schematic representation of the system and the proposed experiment. Ligand and receptor (white and red circle) are grafted via a linker to a substrate (e.g. a colloid). (1) At time t = 0, the unbound ligand-receptor pair is brought to a distance where binding can occur. In this state, binding from an unbound state can occur at each time interval with probability kondt. The opposite process starting from a bound state occurs with probability koffdt. Upon bond formation (breakage), a force on the substrate is measured, signalling a binding event

Full size image

β = 1/kBT being the inverse of the thermal energy and ΔGbond the difference in free-energy between the bound and unbound state, i.e. the bond free-energy. Whereas this result is only valid at equilibrium, or in other words at very long times, we should expect for finite times this probability to depend on both kon and koff, the rates for bond formation and bond breakage, respectively. Qualitatively, for example, since the system starts in an unbound state, it will typically be found in a bound state after a time \(t\approx k_{\text {on}}^{-1}\). If we wait a bit more, the bond can dissociate again, in a time dictated by koff. In general, however, we should expect the long-time limit of any kinetic model to converge to the equilibrium value. This will allow us to connect kon,koff and ΔGbond.

In order to calculate a general expression for \(P_{N,N}\left (t\right )\) and \(P_{N,N-1}\left ({t}\right )\), and thus PB(t), valid for all timescales, one should consider the stochastic nature of the binding and unbinding process. The key ingredients are the conditional binding(unbinding) probabilities. Given the over-damped nature of the bond formation and breaking in a typical biological environment, i.e. in solution, we can consider its description using a simple Markov model, with a constant rate for these two processes. Thus, if kondt is the probability that an unbound system becomes bound in a time interval dt, and koffdt the probability for the reverse process, the probabilities that given that one start with an unbound(bound) state at time t = 0 this state will persist up to a later time \(t^{\prime }\) can be given as:

$$ \begin{array}{@{}rcl@{}} P_{\text{on}} &=& \exp(-k_{\text{on}} t^{\prime}) \end{array} $$
(3)
$$ \begin{array}{@{}rcl@{}} P_{\text{off}} &= &\exp(-k_{\text{off}} t^{\prime}) \end{array} $$
(4)

Using Eqs. 3 and 4, \(P_{N,N}\left (t_{\text {obs}}\right )\) and \(P_{N,N-1}\left (t_{\text {obs}}\right )\) can be written in terms of a convolution as:

$$ \begin{array}{@{}rcl@{}} P_{N,N}\left( t_{\text{obs}}\right) & = & {\int}_{0}^{t_{\text{obs}}} dt_{1} P_{N,N-1}\left( t_{1}\right) k_{\text{off}} P_{\text{on}}(t_{\text{obs}} - t_{1}) \end{array} $$
(5)
$$ \begin{array}{@{}rcl@{}} P_{N,N-1}\left( t_{\text{obs}}\right) & = & {\int}_{0}^{t_{\text{obs}}} dt_{1} P_{N - 1,N - 1}\left( t_{1}\right) k_{\text{on}} P_{\text{off}}(t_{\text{obs}} - t_{1}). \end{array} $$
(6)

In other words, the probability that the system has made exactly N binding and N unbinding transitions within an observation time tobs is equal to the sum over all possible times t1 < tobs that the system has made exactly N binding transitions and N − 1 unbinding transitions within t1, makes an unbinding transition at time t = t1 and then remains in this state for the remaining time tobs − t1, when the state of the system is observed via a measurement. A similar interpretation can be given to the expression for \(P_{N,N-1}\left ({t}\right )\). Because Eqs. 5 and 6 have the structure of a convolution, one can take their Laplace transform \(f(s) \equiv {\mathscr{L}} f(t) = {\int \limits }_{0}^{\infty } f(t) \exp (- s t ) dt \) to obtain the following, equivalent representation in terms of two recurrence relations:

$$ \begin{array}{@{}rcl@{}} P_{N,N}\left( s\right) &=& P_{N,N-1}\left( s\right) k_{\text{off}} \frac{1}{k_{\text{on}} + s} \end{array} $$
(7)
$$ \begin{array}{@{}rcl@{}} P_{N,N-1}\left( s\right) &=& P_{N-1,N-1}\left( s\right) k_{\text{on}} \frac{1}{k_{\text{off}} + s} \end{array} $$
(8)

where we used the fact that \({\mathscr{L}} \{\exp (- k t )\} = \frac {1}{k+s}\) and \({\mathscr{L}} (f * g ) = f(s)g(s)\). Starting from \(P_{0,0} = P_{\text {on}} \Rightarrow P_{0,0}(s) = \frac {1}{k_{\text {on}} + s}\), Eqs. 7 and 8 can be used to recursively calculate \(P_{N,N}\left (s\right )\) and \(P_{N,N-1}\left (s\right )\) for every N, leading to the closed form expressions:

$$ \begin{array}{@{}rcl@{}} P_{N,N}\left( s\right) &=& k_{\text{on}}^{N} k_{\text{off}}^{N} \left( \frac{1}{k_{\text{on}}+s}\right)^{N+1}\left( \frac{1}{k_{\text{off}}+s}\right)^{N} \end{array} $$
(9)
$$ \begin{array}{@{}rcl@{}} P_{N,N-1}\left( s\right) &=& k_{\text{on}}^{N} k_{\text{off}}^{N-1} \left( \frac{1}{k_{\text{on}}+s}\right)^{N}\left( \frac{1}{k_{\text{off}}+s}\right)^{N}, \end{array} $$
(10)

which can then be used to obtain the equivalent formula in time domain by applying the inverse Laplace transform, given for every N > 0:

$$ \begin{array}{@{}rcl@{}} P_{N,N}\left( t\right) &=& \frac{\sqrt{\pi t |k_{\text{off}}-k_{\text{on}}|}}{2 N!}e^{-\frac{1}{2}(k_{\text{on}}+k_{\text{off}})t} \left( \frac{k_{\text{off}}k_{\text{on}} t}{|k_{\text{off}}-k_{\text{on}}|}\right)^{N}\\ &&\times \left[ I_{N-\frac{1}{2}}\left( \frac{|k_{\text{off}}-k_{\text{on}}|t}{2}\right)\right.\\ &&\left.\pm I_{N+\frac{1}{2}}\left( \frac{|k_{\text{off}}-k_{\text{on}}|t}{2}\right) \right] \end{array} $$
(11)
$$ \begin{array}{@{}rcl@{}} P_{N,N-1}\left( t\right) &=& \frac{\sqrt{\pi}}{ (N-1)!}e^{-\frac{1}{2}(k_{\text{on}}+k_{\text{off}})t} \left( \frac{k_{\text{off}}k_{\text{on}} t}{|k_{\text{off}}-k_{\text{on}}|}\right)^{N}\\ &&\times\left( \frac{|k_{\text{off}}-k_{\text{on}}|}{k_{\text{off}}^{2} t }\right)^{1/2}I_{N-\frac{1}{2}}\left( \frac{|k_{\text{off}}-k_{\text{on}}| t}{2}\right), \\ \end{array} $$
(12)

where Iν(x) is the modified Bessel function of the first kind [10] and P0,0 = Pon. The + sign in Eq. 11 corresponds to the case koff > kon, whereas the − sign should be used in the opposite case. Notice that these formulas can be simplified to somewhat simpler but less compact expressions containing only exponentials and powers of kon,koff and t, which can be derived by inverting (9) and (10) for a specific value of N.

Equations 11 and 12 are the most general result and can be used to fit the number of observed binding and unbinding events during the previously described experiments to provide an estimate of kon and koff. It should be noted that all the various \(P_{N,N}\left (t\right )\) and \(P_{N,N-1}\left (t\right )\) are connected and to fully use all the information recorded during an experiment one should fit all of them concurrently to get the best statistical estimate for kon and koff. Notably, more specialised models appeared in the literature, where a given number of binding and unbinding events is assumed based on physical constraints of the system, can be derived from the previous expressions. For example, Fritz et al. [11] in their experiments on P-selectin bindings used the fact that for their system kon ≫ koff and that a single unbinding event can be measured at most due to their settings during the observation time. This is equivalent to using \(P_{1,0} = k_{\text {on}} \frac {\exp (-k_{\text {off}} t)-\exp (-k_{\text {on}} t)}{k_{\text {on}}-k_{\text {off}}}\), which indeed for kon ≫ koff reduces to \(P_{\mathrm {B}} \approx \exp (- k_{\text {off}} t )\) (but all information regarding kon is then lost). Combined with Eq. 1, use of Eqd. 11 and 12 allows to calculate the probability to find the system in a bound state after a certain observation time tobs, regardless of the number of potential binding and unbinding events. In this case, however, it is easier to first take the Laplace transform of the right hand side of Eq. 1 and sum the resulting infinite series:

$$ \begin{array}{@{}rcl@{}} P_{\mathrm{B}}(s)&=&\sum\limits_{N=1}^{\infty} \frac{1}{k_{\text{off}}}\left( \frac{k_{\text{on}}k_{\text{off}}}{(k_{\text{on}}+s)(k_{\text{off}}+s)}\right)^N\\ &=& \frac{k_{\text{on}}}{(k_{\text{on}}+k_{\text{off}})s + s^2,} \end{array} $$
(13)

where we have used the fact that \({\sum }_{i=1}^{\infty }x^{i}= \frac {x}{1-x}\) (for |x| < 1), which after performing the inverse Laplace transform, reads:

$$ P_{\mathrm{B}} = \frac{\left( 1-e^{-(k_{\text{off}} + k_{\text{on}}) t}\right) k_{\text{on}}}{k_{\text{off}} + k_{\text{on}}} $$
(14)

and thus for \(P_{\bar {\text {B}}}\):

$$ P_{\bar{\text{B}}} = \frac{k_{\text{off}}+e^{-(k_{\text{off}} + k_{\text{on}}) t} k_{\text{on}}}{k_{\text{off}} + k_{\text{on}}}, $$
(15)

which could have also been derived in a simpler way by solving the Master equation for this two-state model:

$$ \frac{d P_B}{dt} = -k_{\text{off}} P_B + k_{\text{on}} (1 - P_B ) $$
(16)

with the boundary conditions PB(0) = 0.

Before we delve into the connection between kon, koff and the ligand-receptor bond energy, let us now discuss how these could be determined from experiments applying either Eqs. 14 or 11, 12, as well as the associated challenges. First of all, let us discuss how the measurement of PB. In practice, this can be extracted using the typical setting employed in single-molecule pulling experiment, see, e.g. [11]. Starting with an unbound ligand at \(t^{\prime }=0\), the ligand is subsequently pulled away from the receptor at a later time \(t^{\prime }=t\). The fraction of times that a non-zero retraction force is measured is our estimate of PB(t). In this regard, it should be noticed that pulling the ligand away from the receptor takes a finite time τpull. In order to have a correct interpretation of PB(t), the system must not be able to spontaneously change its state from bound to unbound (or vice versa) during this time, hence one needs \(\tau _{\text {pull}} \ll \min \limits (k_{\text {on}}^{-1},k_{\text {off}}^{-1})\). This requirement can be restated in terms of the minimum retraction speed necessary, vpull, which should obey vpull ≫ δ/τpull, δ being the distance at which a ligand-receptor pair cannot rebind anymore, which to first approximation will be of the order of the size of the ligand-receptor interaction range. Whether this speed is achievable depends on the specifics of the experimental apparatus used and could be challenging when the on and off rates are high, as typical for reversible bonds. Assuming this retraction speed can be achieved, determining kon and koff from Eq. 14 can be done by measuring both the short- and long-time limit of PB. This is easy to see because in the short-time limit one has:

$$ P_{B}(t\rightarrow 0 ) \approx k_{\text{on}} t + \mathcal{O}(t^{2} ) $$
(17)

whereas at long times:

$$ P_{B}(t\rightarrow \infty ) = k_{\text{on}} / \left( {k_{\text{on}} + k_{\text{off}} }\right). $$
(18)

In this way, Eqs. 17 and 18 provide two equations for the two unknown. The need to measure PB at this two time limits tells us about other requirements of the experimental apparatus. First, because measuring kon means measuring the short-time behaviour of PB, the time resolution of the force τf, i.e. the inverse of the frequency νf at which the force is experimentally sampled, needs to be smaller than \(k_{\text {on}}^{-1}\). Note that this is a separate requirement from that on τpull. Finally, an accurate measurement of the plateau value of PB can also be challenging, especially in the case of strong bonds, i.e. when (kon ≫ koff). This is because in this regime the plateau value \(P_{B}(t\rightarrow \infty )\) will be always very close to 1 and measuring its deviation from this number with good statistical accuracy requires taking a number of measurements \(N_{\text {samples}} \gg \frac {1}{1-P_{B}} \approx k_{\text {on}} / k_{\text {off}}\). A smaller number of samples will likely result in estimating PB = 1, which will translate in an estimate of zero for koff, or an infinite value for kon, if koff was somehow known and kon could not be estimated from the slope at short timescales.

Estimating kon and koff from Eqs. 11 and 12 requires a slightly different experiment, which can be summarised in the following steps: (1) As for measuring PB(t), we start with an unbound ligand at time \(t^{\prime }=0\), which at all times should be kept at a fixed position with respect to the receptor. If at some point a bond is formed, a non-zero force will appear. In practice, this is the thermodynamic average of the instantaneous force over all microscopic configurations of the bound ligand-receptor pair. A force of opposite value will thus be required to keep the ligand fixed, which can be done via a feedback mechanism using the same apparatus used to maintain a fixed retraction velocity in a ligand during a standard pulling experiment. This feedback force is measured and recorded. The appearance of a force (its disappearance) at a certain time thus signals a binding (unbinding) event. (2) The time series of the force is collected for analysis for a certain time \(t_{\max \limits }\). (3) \(t_{\max \limits }\) is divided in sub-intervals of time t1 and used to make an histogram of the number of observed binding and unbinding events within it. In this way, one has experimentally measured the values of PN,N(t1) and PN,N− 1(t1). (4) Using any preferred optimisation algorithm to minimise the difference between the experimentally measured PN,N, PN,N− 1 and those in Eqs. 11 and 12 in the paper for a certain value of kon and koff, one can find those that best fit the measured distribution, which will represent our estimate. Using this second approach comes with its own experimental requirements. One is that the total observation time must be \(t_{\max \limits } \gg t_{1} \gg \max \limits (k_{\text {on}}^{-1},k_{\text {off}}^{-1})\) to obtain good statistics. Also, similarly to what occurs for the measurement of PB, the frequency at which the force is recorded, νf, should be much higher than both kon and koff to be able not to miss any binding or unbinding event. However, use of Eqs. 11 and 12 might be easier because no retraction of the ligand is required; hence, there is no minimum pulling velocity to deal with. This could be an advantage in particular when reversible ligand-receptor pairs, for which both kon and koff can be quite high, are involved. At the same time, however, it is important to recognise that in this second type of experiment one would require an apparatus able to accurately measure relatively lower forces compared with those involved in measuring PB. The reason is that in a normal pulling experiment the force becomes higher, and thus more easily detectable, once the ligand-receptor pair is sufficiently stretched. This does not necessarily occur instead in the case where the ligand is kept fixed, because in this case the thermodynamic force can be arbitrarily small, in fact, even zero if no stretching of the ligand is at all required to form a bond with the receptor. Eventually, whether measuring the distributions PNN,PN,N− 1 or PB provides a more accurate estimate of kon and koff for a given ligand-receptor pair should be evaluated on a system by system basis, as well as on the specifics of the experimental apparatus available, in light of the above requirements and limitations. In any case, however, it is important to highlight that the measurement of PN,N,PN,N− 1 provides a second, independent route towards the estimation of the binding and unbinding rates, a fact that can be used to check for consistency of other experiments.

Let us now turn back again to Eq. 14 to discuss its connection with physical quantities related to the ligand-receptor pair. In practice, it has the form of an exponential, describing the approach to equilibrium with a typical time teq = 1/(kon + koff). The long-time limit of PB, Eq. 18, can be compared with the equilibrium behaviour described by Eq. 2 in terms of ΔGbond, which allows us to identify the following relation:

$$ k_{\text{on}}/k_{\text{off}} = e^{-\upbeta{\Delta} G^{\text{bond}}} \equiv K^{\text{bind}}_{\text{tether}}. $$
(19)

At this point, one should stop and consider an important point regarding kon,koff and ΔGbond. Given their definition here via Eq. 16, kon and koff have both the dimension of a rate and thus \(K^{\text {bind}}_{\text {tether}} \equiv k_{\text {on}} / k_{\text {off}} \) is a non-dimensional quantity. In describing ligand-receptor bonds, however, kon is often provided with the dimension of a rate times an inverse number density (i.e. in units of 1/s M), or, equivalently, as a rate times a (molar) volume. To avoid confusion, let us call this second quantity \(k_{\text {on}}^{\text {sol}}\). The binding constant of the ligand-receptor pair is then defined as \(K^{\text {bind}}_{\text {solution}} = k_{\text {on}}^{\text {sol}} / k_{\text {off}}\), which has the dimension of a molar volume, exactly the dimension in which ligand-receptor binding constants are typically reported in the literature. Clearly, kon and \(k_{\text {on}}^{\text {sol}}\), and thus \(K^{\text {bind}}_{\text {tether}}\) and \(K^{\text {bind}}_{\text {solution}}\), cannot be the same quantity and a question arises: what is their connection, if any? The difference between the two actually arises from the exact definition of the equilibrium binding constant. For free ligand and receptor in solutions, the equilibrium constant is typically defined as \(K^{\text {bind}}_{\text {solution}} = \frac {[LR]}{[L][R]}\), where [LR],[L] and [R] are the equilibrium concentration of bound ligand receptor pairs, free ligands and free receptors, respectively. This \(K^{\text {bind}}_{\text {solution}}\) has the familiar dimension of an inverse density. However, \(K^{\text {bind}}_{\text {solution}}\) is derived considering free ligand and receptors in solution, whereas single-molecule experiments probe binding of tethered ligands to tethered receptors. Tethering has important consequences in both the kinetics and thermodynamics of bond formation, and some of its effects in the context of DFS experiments have already been discussed, albeit using simplified models, as we will discuss later.

Generally speaking, to fully quantify and understand the role of tethering, a microscopic description of the linker is required. Models of this sort have already appeared in the soft matter literature, where the concern has been to understand the role of different tethers on colloidal self-assembly mediated by grafted ligand-receptor pairs [12,13,14,15]. These works, however, do not seem to have yet reached the full attention of the community of single-molecule experiments. Since they are important for the correct interpretation of ΔGbond, and to shed some light on its microscopic origins, we will briefly discuss them here, focusing on highlighting the correct statistical mechanical definition of the quantities measured when tethered ligands and receptors are involved and highlight the approximations one must use to connect \({\Delta } G^{\text {bond}},K^{\text {bind}}_{\text {tether}}\) and \(K^{\text {bind}}_{\text {solution}}\). In the following, we will thus follow the derivation first provided in [12] and later generalised in [13], trying to put their arguments in the context of the single-molecule experiments discussed here. The first step is to look at the binding between ligand-receptor pairs in solution. From a statistical mechanics point of view, the chemical potential for a free ligand(receptor) L(R) in solution in a volume V is given by [13, 15]:

$$ \mu_{L(R)} = -k_{\mathrm{B}} T \log{\frac{N_{L(R)} {\Lambda}^3}{V \mathcal{Z}_{L(R)}} } = -k_{\mathrm{B}} T \log{\frac{[L(R)] {\Lambda}^3}{\mathcal{Z}_{L(R)}} } $$
(20)

whereas that for a bound ligand-receptor pair is:

$$ \mu_{LR} = -k_{\mathrm{B}} T \log{\frac{N_{LR} {\Lambda}^3}{V \mathcal{Z}_{LR}} } = -k_{\mathrm{B}} T \log{\frac{[LR] {\Lambda}^3}{\mathcal{Z}_{LR}} }, $$
(21)

where \(\mathcal {Z}_{L(R)}\) and \(\mathcal {Z}_{LR}\) are the so-called molecular partition function of the free ligand(receptor) and of the bound ligand-receptor pair in solution [13], or in other words the partition function of a single ligand(receptor), or that of a bound ligand-receptor pair, at fixed centre of mass. These expressions simply describe an ideal gas of particles with an internal structure, quantified by the molecular partition function \(\mathcal {Z}\)s. At equilibrium \(\mu _{LR} - \left (\mu _{F} + \mu _{R}\right ) = 0\), leading to \(\frac {[LR]}{[L][R]} = \frac {\mathcal {Z}_{LR}}{\mathcal {Z}_{L} \mathcal {Z}_{R}}\). This should be compared with the classical thermodynamic expression \(\frac {[LR]}{[L][R]} = K^{\mathrm {e}} = \exp (-\frac {\Delta G^{\o }}{k_{\mathrm {B}} T}) / \rho ^{\o }\) (where, importantly a reference density ρø appears), leading to:

$$ \frac{\mathcal{Z}_{LR}}{\mathcal{Z}_L \mathcal{Z}_R} = \exp(-\frac{\Delta G^{\o}}{k_{\mathrm{B}} T}) / \rho^{\o} = K^{\text{bind}}_{\text{solution}}. $$
(22)

One important thing to notice is the correct identification of \(K^{\text {bind}}_{\text {solution}}\) as the exponential of the bonding energy scaled by the reference densityρø, at which ΔGø is measured. In practice, ΔGø measures detail about how upon binding molecular interactions change. Equation 22 has been obtained by treating ligands and receptors as an ideal gas of structured particles floating in solution. In a DFS experiment, however, both ligands and receptors are tethered: What is the equivalent of the bond energy for a tethered ligand-receptor pair? Similar statistical mechanical considerations in this case lead to a definition of the bond energy as [13]:

$$ \exp(-\upbeta{\Delta} G^{\text{bond}}) = \frac{Q_{LR}}{Q_{R}Q_{L}} $$
(23)

where now QL(R) and QLR are the partition functions of the tethered and unbound bound ligand(receptor) and of the bound ligand-receptor pair, respectively. What is the connection between the bond energy ΔGbond, as defined by Eq. 23, and the bond energy ΔGø (or the equilibrium binding constant \(K^{\text {bind}}_{\text {solution}}\)) for binding between free ligands and receptors in solution? In the general case, although one expects ΔGbond to have contributions from both ligand-receptor binding and from their linkers, its value cannot be expressed simply as the sum of two separate and well defined contributions. In this case, a simple connection between ΔGbond, ΔGø and \(K^{\text {bind}}_{\text {solution}}\) cannot be established. However, a good approximation in many cases is to assume that the linker does not change appreciably the molecular structure of the ligands and receptors [13]. This allows to factorise the partition functions as \(Q_{L(R)} = {\Omega }_{T_{L(R)}} \mathcal {Z}_{L(R)}\) and \(Q_{LR} = {\Omega }_{T_{L}T_{R}} \mathcal {Z}_{LR}\). Hence, with this approximation, and further using Eq. 22, we have that:

$$ \begin{array}{@{}rcl@{}} \exp(-\upbeta{\Delta} G^{\text{bond}}) &=& \frac{\mathcal{Z}_{LR}}{\mathcal{Z}_{L} \mathcal{Z}_{R}} \frac{{\Omega}_{T_{L},T_{R}}}{{\Omega}_{T_{L}}{\Omega}_{T_{R}}} \\ &=& \frac{\exp(-\upbeta{\Delta} G^{\o}) }{ \rho^{\o}} \frac{{\Omega}_{T_{L},T_{R}}}{{\Omega}_{T_{L}}{\Omega}_{T_{R}}} \\ &=& K^{\text{bind}}_{\text{solution}} \frac{{\Omega}_{T_{L},T_{R}}}{{\Omega}_{T_{L}}{\Omega}_{T_{R}}} \end{array} $$
(24)

where \({\Omega }_{T_{L},T_{R}}\) and \({\Omega }_{T_{L}(T_{R})}\) are now the partition functions of the linker only, when the ligand and receptors are bound to each other, or not, respectively. These partition functions account for the fact that the linker is constrained from being grafted, and additionally that in the bound state the linkers of the ligand and that of the receptor must assume microscopic configurations compatible with the presence of a bond, or in other words that allow ligand and receptors to be at binding distance. Examples of how to calculate or compute these quantities using specific molecular models for the linkers (for example, treated as rigid rods or gaussian chains) are reported in [13]. For a general Monte Carlo formalism to compute this quantity for realistic polymer models see [13] and [16].

An alternative and revealing form of Eq. 24 can also be given by re-adjusting terms,

$$ \begin{array}{@{}rcl@{}} {\Delta} G^{\text{bond}} &=& -k_{\mathrm{B}} T \log\left( K^{\mathrm{e}} \rho^{\o}\right) - k_{\mathrm{B}} T \log\left( \frac{1}{\rho^{\o}}\frac{{\Omega}_{T_{L},T_{R}}}{{\Omega}_{T_{L}}{\Omega}_{T_{R}}}\right) \\ &=& {\Delta} G^{\o} + {\Delta} G^{\text{cnf}}. \end{array} $$
(25)

Equations 24 and 25 suggest a few important points regarding the study of ligand-receptor interactions and their quantification via single-molecule experiments such as DFS, which will now be discussed. The first is that the bond energy measured in any experiment using tethered ligands and receptors has an additional contribution ΔGcnf compared with that of free ligands and receptors in solution. This point has previously been made by others, albeit using specific microscopic models, whereas the generalisation discussed allows a broader applicability of these results. For example, Nguyen-Duong et al. [17] showed that if one treats the linker as a spring, an additional positive contribution to the bond free-energy destabilising the bond arises. Generally speaking, this contribution, usually referred to as “configurational free-energy” [13], can be several kBT in magnitude depending on the type of tether [13, 14], and should thus always be properly taken into account in comparing experiments with the same ligand-receptor pairs but different linkers. It should be noted that since ΔGbond contains the non-negligible effect of tethering, this augmented bond energy ΔGbond, and not ΔGø, is the relevant quantity determining binding in various biological settings, where often the ligands and receptors which mediate binding are attached to the surface of a cell, and not free in solution. The definition of ΔGcnf given by Eq. 25 shows that this quantity is strongly influenced by both the molecular architecture of the linker as well as the specifics of the grafting geometry, e.g. the distance between ligand and receptor grafting points [13], the mobility of the grafting points [18] as well as the rigidity of the grafting surface to which grafting occurs [19], since all these quantities affect the molecular partition functions. Indirectly, this also means that the values of kon and koff depend on the same quantities, suggesting that the proposed experiments to measure them must be performed keeping these quantities fixed. Just to make a relevant example, this means that during the measurements of the binding or unbinding events suggested here, the distance between the ligand receptor pair must be kept fixed, since \({\Omega }_{T_{L},T_{R}}\) depends on it [13]. On a more general note, the presence of ΔGcnf in the definition of the bond free-energy suggests that, at least potentially, changes in binding energies might sometimes be dominated by changes in ΔGcnf, and hence to the linker, rather than the specific ligand or receptor used. For example, it is tempting to speculate that some adhesion phenomena, e.g. leukocyte rolling on the epithelium, might be controlled by changing simply the length or rigidity of that part of the selectin molecules acting as a linker to the epithelium’s surface. In fact, this might represent a competitive evolutionary strategy with respect to changing instead the binding site (i.e. what we call the ligand) for specific receptors. Another field where exploration of the change in ΔGcnf as a function of linker’s features is quite important is that of DNA and DNA-mediated self-assembly [20, 21], where knowledge of this quantity would lead to increased designability of these systems, as well as exploitation of geometrical effects to change binding properties. In this regard, whereas normally single-molecule experiments aim at measuring ΔGø for specific ligand-receptor pairs, and ΔGcnf is only considered a nuisance to account for, similar experiments can instead be used to measure this latter quantity. In fact, the second point suggested by Eqs. 24 and 25 is that one can combine known values of \(K^{\text {bind}}_{\text {solution}}\) for different ligand-receptor pairs determined in solution to measure ΔGcnf for specific linkers. Until now, this has only been measured indirectly by fitting melting curves of DNA-coated colloids, or directly but via computer simulations that must necessarily make assumptions built into the molecular force-field employed [13, 16]. It is suggested here that the use of single-molecule experiments can instead provide a direct experimental measurement for this quantity, by simply taking the ratio of \(K^{\text {bind}}_{\text {tether}}\) measured with the same ligand-receptor pairs, but different linkers. This procedure would provide a systematic way to explore the connection between ΔGcnf and the microscopic parameters it is linked to. However, it should be pointed out that in this way only the relative value of ΔGcnf can be measured, which nevertheless can provide an accurate measurement of trends within a range of linkers. For similar reasons, Eq. 24 also suggests that a direct comparison of the absolute values of the binding constants measured from single-molecule experiments with that measured by essays measuring binding in solution, e.g. ELISA, cannot be done unless a proper estimate of ΔGcnf is available. Similarly to the previous case illustrated for ΔGcnf, however, ratios between binding constants measured consistently (i.e. with the same type of experiment and keeping the same types of linkers, while only changing the ligand-receptor pair) will cancel out these configurational effects, and can be directly compared. This is not a minor point, for the following reason. In DFS experiments, \(K^{\text {bind}}_{\text {solution}}\) is typically estimated via the empirical expression [22]:

$$ K^{\text{bind}}_{\text{solution}} = \frac{k_{\text{on}} n / V_{\text{eff}}}{k_{\text{off}}}, $$
(26)

where n is the number of potential binding receptors within the effective volume Veff spanned by the linker. Considering surface densities of receptors low enough so that a single ligand-receptor bond can occur, i.e. using n = 1 in Eq. 26, we can directly compare with our model, where only a single binding partner was considered (a generalisation to many receptors, however, is trivial, one simply replaces \(k_{\text {on}}\rightarrow k_{\text {on}} n\) in all the previous expressions, and the total partition function for the bound state must also be multiplied by n). Using the general statistical mechanical definition, one obtains:

$$ \begin{array}{@{}rcl@{}} K^{\text{bind}}_{\text{solution}} &=& \frac{\exp(-\upbeta{\Delta} G^{\text{bond}})}{\frac{{\Omega}_{T_L,T_R}}{{\Omega}_{T_L}{\Omega}_{T_R}}} \\ &=& \frac{\exp(-\upbeta{\Delta} G^{\text{bond}})}{\rho^{\o} \exp(-\upbeta{\Delta} G^{\text{cnf}})}\equiv \frac{\exp(-\upbeta{\Delta} G^{\text{bond}})}{ \bar{V}_{\text{eff,model}} }. \end{array} $$
(27)

Crucially, although \(\bar {V}_{\text {eff, model}}\) has indeed the dimensions of a volume, it is not equal to the definition used to calculate Veff when interpreting DFS experiments. In fact, estimating Veff as the volume spanned by the linker is an approximation that one can arrive at only by making two approximations. The first is that the linker confines the ligand to reside at points within a volume Veff, which is quite reasonable. The second approximation is that each point in this volume is equally likely to be occupied by the ligand and does not depend on the actual microscopic configuration the linker must assume given to put the ligand in that position. This is a very rough approximation. In fact, it is not even valid using a very simple model for a tether, i.e. treating it as a spring [17]. For this reason, one should expect this empirical definition of Veff to provide at best a correct order of magnitude for its real value, and its use to determine \(K^{\text {bind}}_{\text {solution}}\) from \(K^{\text {bind}}_{\text {tether}}\) should be taken carefully, with more than a pinch of salt.

In conclusion, we presented a mathematical model for the calculation of the probability to observe a certain number of binding and unbinding transitions in a single-molecule experiment, which can be used in different ways to extract the binding and unbinding rates for tethered ligand-receptor pairs. Furthermore, we discussed the exact connection between these rates and the bond (free-)energy for tethered ligands and receptors, and elucidated the difference with bond energies, and equilibrium binding constants, measured in solution.

We have used a statistical mechanical model to show that, under well-defined assumptions, the bond free-energy for tethered constructs can be split into two parts. The first is the bond energy measured from binding experiments of free ligand and receptors in solution (or when at least one species is free), ΔGø. The other, ΔGcnf, is a configurational penalty term that depends both on molecular characteristics of the linker, as measured by its molecular partition function, and on details of the grafting geometry and substrate, like the relative position of the grafting points, or the shape and rigidity of the grafting surface. By a proper combination of available information regarding binding between ligand-receptor pairs in solution, it is suggested how single-molecule experiments can be used to systematically investigate tethering effects and the role of ΔGcnf. This latter fact seems quite important, considering that ΔGcnf is currently being exploited for the rational design of nanotechnology applications, in particular for self-assembly purposes. It would be peculiar, indeed, if similar effects were not already exploited by nature to tune the large variety of biological interactions also mediated by ligand-receptor binding between tethered species, and their understanding could thus be further exploited for a large variety of applications connected to them, e.g. in drug-design.