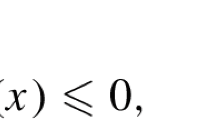Adaptive regularization with cubics on manifolds

Abstract

Adaptive regularization with cubics (ARC) is an algorithm for unconstrained, non-convex optimization. Akin to the trust-region method, its iterations can be thought of as approximate, safe-guarded Newton steps. For cost functions with Lipschitz continuous Hessian, ARC has optimal iteration complexity, in the sense that it produces an iterate with gradient smaller than $\varepsilon$ in $O(1/\varepsilon ^{1.5})$ iterations. For the same price, it can also guarantee a Hessian with smallest eigenvalue larger than $-\sqrt{\varepsilon }$. In this paper, we study a generalization of ARC to optimization on Riemannian manifolds. In particular, we generalize the iteration complexity results to this richer framework. Our central contribution lies in the identification of appropriate manifold-specific assumptions that allow us to secure these complexity guarantees both when using the exponential map and when using a general retraction. A substantial part of the paper is devoted to studying these assumptions—relevant beyond ARC—and providing user-friendly sufficient conditions for them. Numerical experiments are encouraging.

Appendices

A Proofs from Section 2: mechanical lemmas

Lemma 1 characterizes the conditions under which the subproblem solver is allowed to return $s_k = 0$ at iteration k.

Proof of Lemma 1

By definition of the model $m_k$ (1) and by properties of retractions (17),

$$\begin{aligned} \nabla m_k(0) = \nabla \hat{f}_k(0) = \mathrm {grad}f(x_k), \end{aligned}$$

where $\hat{f}_k = f \circ \mathrm {R}_{x_k}$. Thus, if $\mathrm {grad}f(x_k) = 0$, the first-order condition (2) allows $s_k = 0$. The other way around, if $s_k = 0$ is allowed, then $\Vert \nabla m_k(0)\Vert = 0$, so that $\mathrm {grad}f(x_k) = 0$.

Now assume the second-order condition (3) is enforced. If $s_k = 0$ is allowed, then we already know that $\mathrm {grad}f(x_k) = 0$. Combined with (32), we deduce that

$$\begin{aligned} \nabla ^2 m_k(0) = \nabla ^2 \hat{f}_k(0) = \mathrm {Hess}f(x_k), \end{aligned}$$

for any retraction. Then, condition (3) at $s_k = 0$ indicates $\nabla ^2 m_k(0)$ is positive semidefinite, hence $\mathrm {Hess}f(x_k)$ is positive semidefinite. The other way around, if $\mathrm {grad}f(x_k) = 0$ and $\mathrm {Hess}f(x_k)$ is positive semidefinite, then $\nabla m_k(0) = \mathrm {grad}f(x_k)$ and $\nabla ^2 m_k(0) = \mathrm {Hess}f(x_k)$, so that indeed $s_k = 0$ is allowed $\square$

The two supporting lemmas presented in Sect. 2 follow from the regularization parameter update mechanism of Algorithm 1. The standard proofs are not affected by the fact we here work on a manifold. We provide them for the sake of completeness.

Proof of Lemma 2

Using the definition of $\rho _k$ (4), $m_k(0) = f(x_k)$ (1) and $m_k(0) - m_k(s_k) \ge 0$ by condition (2):

$$\begin{aligned} 1 - \rho _k = 1 - \frac{f(x_k) - f(\mathrm {R}_{x_k}(s_k))}{m_k(0) - m_k(s_k) + \frac{\varsigma _k}{3} \Vert s_k\Vert ^3} \le \frac{f(\mathrm {R}_{x_k}(s_k)) - m_k(s_k) + \frac{\varsigma _k}{3} \Vert s_k\Vert ^3}{\frac{\varsigma _k}{3} \Vert s_k\Vert ^3}. \end{aligned}$$

Owing to A2, the numerator is upper bounded by $(L/6)\Vert s_k\Vert ^3$. Hence, $1 - \rho _k \le \frac{L}{2\varsigma _k}$. If $\varsigma _k \ge \frac{L}{2(1-\eta _2)}$, then $1-\rho _k \le 1-\eta _2$ so that $\rho _k \ge \eta _2$, meaning step k is very successful. The regularization mechanism (5) then ensures $\varsigma _{k+1} \le \varsigma _k$. Thus, $\varsigma _{k+1}$ may exceed $\varsigma _k$ only if $\varsigma _k < \frac{L}{2(1-\eta _2)}$, in which case it can grow at most to $\frac{L\gamma _3}{2(1-\eta _2)}$, but cannot grow beyond that level in later iterations. $\square$

Proof of Lemma 3

Partition iterations $0, \ldots , \bar{k} - 1$ into successful or very successful ($\mathcal {S}_{\bar{k}}$) and unsuccessful ($\mathcal {U}_{\bar{k}}$) ones. Following the update mechanism (5), for $k \in \mathcal {S}_{\bar{k}}$, $\varsigma _{k+1} \ge \gamma _1 \varsigma _k$, while for $k \in \mathcal {U}_{\bar{k}}$, $\varsigma _{k+1} \ge \gamma _2 \varsigma _k$. Thus, by induction, $\varsigma _{\bar{k}} \ge \varsigma _0 \gamma _1^{|\mathcal {S}_{\bar{k}}|} \gamma _2^{|\mathcal {U}_{\bar{k}}|}$. By assumption, $\varsigma _{\bar{k}} \le \varsigma _{\max }$ so that

$$\begin{aligned} \log \left( \frac{\varsigma _{\max }}{\varsigma _0}\right) \ge |\mathcal {S}_{\bar{k}}| \log (\gamma _1) + |\mathcal {U}_{\bar{k}}| \log (\gamma _2) = |\mathcal {S}_{\bar{k}}|\left[ \log (\gamma _1) - \log (\gamma _2)\right] + \bar{k} \log (\gamma _2), \end{aligned}$$

where we also used $|\mathcal {S}_{\bar{k}}| + |\mathcal {U}_{\bar{k}}| = \bar{k}$. Isolating $\bar{k}$ using $\gamma _2> 1 > \gamma _1$ allows to conclude. $\square$

B Proofs from Section 3: first-order analysis, exponentials

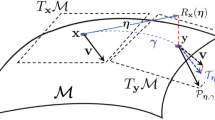
Certain tools from Riemannian geometry are useful throughout the appendices—see for example [46, pp 59–67]. To fix notation, let $\nabla$ denote the Riemannian connection on $\mathcal {M}$ (not to be confused with $\nabla$ and $\nabla ^2$ which denote gradient and Hessian of functions on linear spaces, such as pullbacks). With this notation, the Riemannian Hessian [3, Def. 5.5.1] is defined by $\mathrm {Hess}f = \nabla \mathrm {grad}f$. Furthermore, $\frac{\mathrm {D}}{\mathrm {d}t}$ denotes the covariant derivative of vector fields along curves on $\mathcal {M}$, induced by $\nabla$. With this notation, given a smooth curve $c :{\mathbb {R}}\rightarrow \mathcal {M}$, the intrinsic acceleration is defined as $c''(t) = \frac{\mathrm {D}^2}{\mathrm {d}t^2} c(t)$. For example, for a Riemannian submanifold of a Euclidean space, $c''(t)$ is obtained by orthogonal projection of the classical acceleration of c in the embedding space to the tangent space at c(t). Geodesics are those curves which have zero intrinsic acceleration.

We first state and prove a partial version of Proposition 2 which applies for general retractions. Right after this, we prove Proposition 2. The purpose of this detour is to highlight how crucial properties of geodesics and of their interaction with parallel transports allow for the more direct guarantees of Sect. 3. In turn, this serves as motivation for the developments in Sect. 4.

Proposition 6

Let $f :\mathcal {M}\rightarrow {\mathbb {R}}$ be twice differentiable on a Riemannian manifold $\mathcal {M}$ equipped with a retraction $\mathrm {R}$. Given $(x, s) \in \mathrm {T}\mathcal {M}$, assume there exists $L \ge 0$ such that, for all $t \in [0, 1]$,

$$\begin{aligned} \left\| P_{t s}^{-1}\left( \mathrm {Hess}f(c(t))[c'(t)]\right) - \mathrm {Hess}f(x)[s] \right\| \le L \Vert s\Vert \cdot \ell (c|_{[0, t]}), \end{aligned}$$

where $P_{ts}$ is parallel transport along $c(t) = \mathrm {R}_x(ts)$ from c(0) to c(t) (note the retraction instead of the exponential) and $\ell (c|_{[0, t]}) = \int _{0}^{t} \Vert c'(\tau )\Vert \mathrm {d}\tau$ is the length of c restricted to the interval [0, t]. Then,

$$\begin{aligned} \left\| P_{s}^{-1}\mathrm {grad}f(\mathrm {R}_x(s)) - \mathrm {grad}f(x) - \mathrm {Hess}f(x)[s] \right\| \le L \Vert s\Vert \int _{0}^{1} \ell (c|_{[0, t]}) \,\mathrm {d}t. \end{aligned}$$

Proof

Pick a basis $v_1, \ldots , v_d$ for $\mathrm {T}_x\mathcal {M}$, and define the parallel vector fields $V_i(t) = P_{ts}(v_i)$ along c(t). Since parallel transport is an isometry, $V_1(t), \ldots , V_d(t)$ form a basis for $\mathrm {T}_{c(t)}\mathcal {M}$ for each $t \in [0, 1]$. As a result, we can express the gradient of f along c(t) in these bases,

$$\begin{aligned} \mathrm {grad}f(c(t)) = \sum _{i = 1}^{d} \alpha _i(t) V_i(t), \end{aligned}$$

(40)

with $\alpha _1(t), \ldots , \alpha _d(t)$ differentiable. Using properties of the Riemannian connection $\nabla$ and its associated covariant derivative $\frac{\mathrm {D}}{\mathrm {d}t}$ [46, pp 59–67], we find on one hand that

$$\begin{aligned} \frac{\mathrm {D}}{\mathrm {d}t}\mathrm {grad}f(c(t)) = \nabla _{c'(t)} \mathrm {grad}f = \mathrm {Hess}f(c(t))[c'(t)], \end{aligned}$$

and on the other hand that

$$\begin{aligned} \frac{\mathrm {D}}{\mathrm {d}t}\sum _{i = 1}^{d} \alpha _i(t) V_i(t) = \sum _{i = 1}^{d} \alpha _i'(t) V_i(t) = P_{ts} \sum _{i = 1}^{d} \alpha _i'(t) v_i, \end{aligned}$$

where we used that $\frac{\mathrm {D}}{\mathrm {d}t}V_i(t) = 0$, by definition of parallel transport. Furthermore,

$$\begin{aligned} c'(t) = \mathrm {D}\mathrm {R}_x(ts)[s] = T_{ts}(s), \end{aligned}$$

where $T_{ts} = \mathrm {D}\mathrm {R}_x(ts)$ is a linear operator from the tangent space at x to the tangent space at c(t)—just like $P_{ts}$. Combining, we deduce that

$$\begin{aligned} \sum _{i = 1}^d \alpha _i'(t) v_i = \left( P_{ts}^{-1} \circ \mathrm {Hess}f(c(t)) \circ T_{ts}\right) [s]. \end{aligned}$$

Going back to (40), we also see that

$$\begin{aligned} G(t) \triangleq P_{ts}^{-1} \mathrm {grad}f(c(t)) = \sum _{i = 1}^{d} \alpha _i(t) v_i \end{aligned}$$

is a map from (a subset of) ${\mathbb {R}}$ to $\mathrm {T}_x\mathcal {M}$—two linear spaces—so that we can differentiate it in the usual way:

$$\begin{aligned} G'(t) = \sum _{i = 1}^{d} \alpha _i'(t) v_i. \end{aligned}$$

We conclude that

$$\begin{aligned} G'(t) = \frac{\mathrm {d}}{\mathrm {d}t}\left[ P_{ts}^{-1} \mathrm {grad}f(c(t)) \right] = \left( P_{ts}^{-1} \circ \mathrm {Hess}f(c(t)) \circ T_{ts}\right) [s]. \end{aligned}$$

(41)

Since $G'$ is continuous,

$$\begin{aligned} P_{ts}^{-1}\mathrm {grad}f(c(t)) = G(t)&= G(0) + \int _{0}^{t} G'(\tau ) \mathrm {d}\tau \\&= \mathrm {grad}f(x) + \int _{0}^{t} \left( P_{\tau s}^{-1} \circ \mathrm {Hess}f(c(\tau )) \circ T_{\tau s}\right) [s] \mathrm {d}\tau . \end{aligned}$$

Moving $\mathrm {grad}f(x)$ to the left-hand side and subtracting $\mathrm {Hess}f(x)[ts]$ on both sides, we find

$$\begin{aligned}&P_{ts}^{-1}\mathrm {grad}f(c(t)) - \mathrm {grad}f(x) - \mathrm {Hess}f(x)[ts] \\&\quad = \int _{0}^{t} \left( P_{\tau s}^{-1} \circ \mathrm {Hess}f(c(\tau )) \circ T_{\tau s} - \mathrm {Hess}f(x)\right) [s] \mathrm {d}\tau . \end{aligned}$$

Using the main assumption on $\mathrm {Hess}f$ along c, it easily follows that

$$\begin{aligned} \left\| P_{ts}^{-1}\mathrm {grad}f(c(t)) - \mathrm {grad}f(x) - \mathrm {Hess}f(x)[ts] \right\| \le \Vert s\Vert L \int _{0}^{t} \ell (c|_{[0, \tau ]}) \mathrm {d}\tau . \end{aligned}$$

(42)

For $t = 1$, this is the announced inequality. $\square$

Proof of Proposition 2

In this proposition we work with the exponential retraction, so that instead of a general retraction curve c(t) we work along a geodesic $\gamma (t) = \mathrm {Exp}_x(ts)$. By definition, the velocity vector field $\gamma '(t)$ of a geodesic $\gamma (t)$ is parallel, meaning

$$\begin{aligned} \gamma '(t) = P_{ts}(\gamma '(0)) = P_{ts}(s). \end{aligned}$$

(43)

This elegant interplay of geodesics and parallel transport is crucial. In particular,

$$\begin{aligned} \ell (\gamma |_{[0, t]}) = \int _{0}^{t} \Vert \gamma '(\tau )\Vert \mathrm {d}\tau = t \Vert s\Vert , \end{aligned}$$

and the condition in Proposition 6 becomes

$$\begin{aligned} \left\| P_{t s}^{-1}\left( \mathrm {Hess}f(\gamma (t))[P_{ts}(s)]\right) - \mathrm {Hess}f(x)[s] \right\|&\le t L \Vert s\Vert ^2, \end{aligned}$$

which is indeed guaranteed by our own assumptions. We deduce that (42) holds:

$$\begin{aligned} \left\| P_{ts}^{-1}\mathrm {grad}f(\gamma (t)) - \mathrm {grad}f(x) - \mathrm {Hess}f(x)[ts] \right\|&\le \Vert s\Vert L \int _{0}^{t} \ell (\gamma |_{[0, \tau ]}) \mathrm {d}\tau = \frac{L}{2} \Vert s\Vert ^2 t^2. \end{aligned}$$

(44)

The relation (43) also yields the scalar inequality. Indeed, since $f \circ \gamma :[0, 1] \rightarrow {\mathbb {R}}$ is continuously differentiable,

$$\begin{aligned} f(\mathrm {Exp}_x(s)) = f(\gamma (1))&= f(\gamma (0)) + \int _{0}^{1} (f \circ \gamma )'(t) \mathrm {d}t\\&= f(x) + \int _{0}^{1} \left\langle {\mathrm {grad}f(\gamma (t))},{\gamma '(t)}\right\rangle \mathrm {d}t\\&= f(x) + \int _{0}^{1} \left\langle {P_{ts}^{-1}\mathrm {grad}f(\gamma (t))},{s}\right\rangle \mathrm {d}t, \end{aligned}$$

where on the last line we used (43) and the fact that $P_{ts}$ is an isometry. For a general retraction curve c(t), instead of s as the right-most term we would find $P_{ts}^{-1}(c'(t))$ which may vary with t: this would make the next step significantly more difficult. Move f(x) to the left-hand side and subtract terms on both sides to get

$$\begin{aligned}&f(\mathrm {Exp}_x(s)) - f(x) - \left\langle {\mathrm {grad}f(x)},{s}\right\rangle - \frac{1}{2} \left\langle {s},{\mathrm {Hess}f(x)[s]}\right\rangle \\&\quad = \int _{0}^{1} \left\langle {P_{ts}^{-1}\mathrm {grad}f(\gamma (t)) - \mathrm {grad}f(x) - \mathrm {Hess}f(x)[ts]},{s}\right\rangle \mathrm {d}t. \end{aligned}$$

Using (44) and Cauchy–Schwarz, it follows immediately that

$$\begin{aligned} \left| f(\mathrm {Exp}_x(s)) - f(x) - \left\langle {s},{\mathrm {grad}f(x)}\right\rangle - \frac{1}{2} \left\langle {s},{\mathrm {Hess}f(x)[s]}\right\rangle \right| \le \int _{0}^{1} \frac{L}{2} \Vert s\Vert ^3 t^2 \mathrm {d}t= \frac{L}{6} \Vert s\Vert ^3, \end{aligned}$$

as announced. $\square$

Next, we provide an argument for the last claim in Theorem 3.

Proof of Theorem 3

We argue that $\lim _{k \rightarrow \infty } \Vert \mathrm {grad}f(x_k)\Vert = 0$. The first claim of the theorem states that, for every $\varepsilon > 0$, there is a finite number of successful steps k such that $x_{k+1}$ has gradient larger than $\varepsilon$. Thus, for any $\varepsilon > 0$, there exists K: the last successful step such that $x_{K+1}$ has gradient larger than $\varepsilon$. Furthermore, there is a finite number of unsuccessful steps directly after $K+1$. Indeed, $\varsigma _{K+1} \ge \varsigma _{\min }$, and failures increase $\varsigma$ exponentially; additionally, $\varsigma$ cannot outgrow $\varsigma _{\max }$ by Lemma 2. Thus, after a finite number of failures, a new success arises, necessarily producing an iterate with gradient norm at most $\varepsilon$ since K was the last successful step to produce a larger gradient. By the same argument, all subsequent iterates have gradient norm at most $\varepsilon$. In other words: for any $\varepsilon > 0$, there exists $K'$ finite such that for all $k \ge K'$, $\Vert \mathrm {grad}f(x_k)\Vert \le \varepsilon$, that is: $\lim _{k\rightarrow \infty } \Vert \mathrm {grad}f(x_k)\Vert = 0$. $\square$

C Proofs from Section 5: second-order analysis

Proof of Corollary 3

Consider these subsets of the set of successful iterations $\mathcal {S}$:

$$\begin{aligned} \mathcal {S}^1 \triangleq \{k \in \mathcal {S}: \Vert \mathrm {grad}f(x_{k + 1})\Vert > \varepsilon _g\},&\text { and }\quad&\mathcal {S}^2&\triangleq \{k \in \mathcal {S}: \lambda _{\min }(\mathrm {Hess}f(x_{k})) < - \varepsilon _{{H}}\}. \end{aligned}$$

These sets are finite: for $K_1 = K_1(\varepsilon _g)$ as provided by either Theorem 3 or Theorem 4, and for $K_2 = K_2(\varepsilon _{{H}})$ as provided by Theorem 5, we know that

$$\begin{aligned} |\mathcal {S}^1|&\le K_1,&\text { and } \quad&|\mathcal {S}^2|&\le K_2. \end{aligned}$$

Note that successful steps are in one-to-one correspondence with the distinct points in the sequence of iterates $x_1, x_2, x_3, \ldots$.² The first inequality states at most $K_1$ of the distinct points in that list have large gradient. The second inequality states at most $K_2$ of the distinct points in that same list have significantly negative Hessian eigenvalues. Thus, if more than $K_1+K_2+1$ distinct points appear among $x_0, x_1, \ldots , x_{\bar{k}}$ (note the $+1$ as we added $x_0$ to the list), then at least one of these points has both a small gradient and an almost positive semidefinite Hessian.

In particular, as long as the number of successful iterations among $0, \ldots , \bar{k}-1$ exceeds $K_1 + K_2 + 1$ (strictly), there must exist $k \in \{0, \ldots , \bar{k}\}$ such that

$$\begin{aligned} \Vert \mathrm {grad}f(x_{k})\Vert&\le \varepsilon _g&\text { and }\quad&\lambda _{\min }(\mathrm {Hess}f(x_{k}))&\ge - \varepsilon _{{H}}. \end{aligned}$$

Lemma 3 allows to conclude. $\square$

D Proofs from Section 6: regularity assumptions

Proof of Lemma 4

Since $\hat{f}$ is a real function on a linear space, standard calculus applies:

$$\begin{aligned}&\hat{f}(s) - \left[ \hat{f}(0) + \langle {s},{\nabla \hat{f}(0)}\rangle + \frac{1}{2} \langle {s},{\nabla ^2 \hat{f}(0)[s]}\rangle \right] \\&\quad = \int _{0}^{1}\int _{0}^{1} t_1 \left\langle {\left[ \nabla ^2 \hat{f}(t_1t_2 s) - \nabla ^2 \hat{f}(0) \right] [s]},{s}\right\rangle \mathrm {d}t_1 \mathrm {d}t_2, \\&\nabla \hat{f}(s) - \left[ \nabla \hat{f}(0) + \nabla ^2 \hat{f}(0)[s]\right] = \int _{0}^{1} \left[ \nabla ^2 \hat{f}(ts) - \nabla ^2 \hat{f}(0) \right] [s] \, \mathrm {d}t. \end{aligned}$$

Taking norms on both sides, by a triangular inequality to pass the norm through the integral and integrating respectively $t_1^2 t_2^{}$ and $t$, we find using our main assumption (27) that

$$\begin{aligned} \left| \hat{f}(s) - \left[ \hat{f}(0) + \langle {s},{\nabla \hat{f}(0)}\rangle + \frac{1}{2} \langle {s},{\nabla ^2 \hat{f}(0)[s]}\rangle \right] \right|&\le \frac{1}{6} L \Vert s\Vert ^3, \text { and } \\ \left\| \nabla \hat{f}(s) - \left[ \nabla \hat{f}(0) + \nabla ^2 \hat{f}(0)[s]\right] \right\|&\le \frac{1}{2} L \Vert s\Vert ^2. \end{aligned}$$

$\square$

Proof of Lemma 5

For an arbitrary $\dot{s} \in \mathrm {T}_x\mathcal {M}$, consider the curve $c(t) = \mathrm {R}_x(s + t\dot{s})$, and let $g = f \circ c :{\mathbb {R}}\rightarrow {\mathbb {R}}$. We compute the derivatives of g in two different ways. On the one hand, $g(t) = \hat{f}(s + t\dot{s})$ so that

$$\begin{aligned} g'(t)&= \mathrm {D}\hat{f}(s+t\dot{s})[\dot{s}] = \langle {\nabla \hat{f}(s+t\dot{s})},{\dot{s}}\rangle , \\ g''(t)&= \left\langle { \frac{\mathrm {d}}{\mathrm {d}t}\nabla \hat{f}(s+t\dot{s})},{\dot{s}}\right\rangle = \langle {\nabla ^2 \hat{f}(s+t\dot{s})[\dot{s}]},{\dot{s}}\rangle . \end{aligned}$$

On the other hand, $g(t) = f(c(t))$ so that, using properties of $\frac{\mathrm {D}}{\mathrm {d}t}$ [46, pp 59–67]:

$$\begin{aligned} g'(t)&= \mathrm {D}f(c(t))[c'(t)] = \langle {\mathrm {grad}f(c(t))},{c'(t)}\rangle , \\ g''(t)&= \frac{\mathrm {d}}{\mathrm {d}t}\left\langle {(\mathrm {grad}f \circ c)(t))},{c'(t)}\right\rangle \\&= \left\langle {\nabla _{c'(t)} \mathrm {grad}f},{c'(t)}\right\rangle + \left\langle {(\mathrm {grad}f \circ c)(t))},{\frac{\mathrm {D}}{\mathrm {d}t} c'(t)}\right\rangle \\&= \left\langle {\mathrm {Hess}f(c(t))[c'(t)]},{c'(t)}\right\rangle + \left\langle {\mathrm {grad}f(c(t))},{c''(t)}\right\rangle . \end{aligned}$$

Equating the different identities for $g'(t)$ and $g''(t)$ at $t = 0$ while using $c'(0) = T_s \dot{s}$, we find for all $\dot{s} \in \mathrm {T}_x\mathcal {M}$:

$$\begin{aligned} \langle {\nabla \hat{f}(s)},{\dot{s}}\rangle&= \left\langle {\mathrm {grad}f(\mathrm {R}_x(s))},{T_s \dot{s}}\right\rangle , \\ \langle {\nabla ^2 \hat{f}(s)[\dot{s}]},{\dot{s}}\rangle&= \left\langle {\mathrm {Hess}f(\mathrm {R}_x(s))[T_s \dot{s}]},{T_s \dot{s}}\right\rangle + \left\langle {\mathrm {grad}f(\mathrm {R}_x(s))},{c''(0)}\right\rangle . \end{aligned}$$

The last term, $\left\langle {\mathrm {grad}f(\mathrm {R}_x(s))},{c''(0)}\right\rangle$, is seen to be the difference of two quadratic forms in $\dot{s}$, so that it is itself a quadratic form in $\dot{s}$. This justifies the definition of $W_s$ through polarization. The announced identities follow by identification. $\square$

Proof of Proposition 3

With $\mathrm {R}_x(s) = \frac{x+s}{\sqrt{1+\Vert s\Vert ^2}}$, it is easy to derive

$$\begin{aligned} T_s \dot{s} \triangleq \mathrm {D}\mathrm {R}_x(s)[\dot{s}]&= \left[ \frac{1}{\sqrt{1+\Vert s\Vert ^2}} I_n - \frac{1}{\sqrt{1+\Vert s\Vert ^2}^3} (x+s)s^\top \right] \dot{s} \nonumber \\&= \frac{1}{\sqrt{1+\Vert s\Vert ^2}} \left[ I_n - \mathrm {R}_x(s) \mathrm {R}_x(s)^\top \right] \dot{s}, \end{aligned}$$

(45)

where we used $x^\top \dot{s} = 0$ in between the two steps to replace $s^\top$ with $(x+s)^\top$. The matrix between brackets is the orthogonal projector from ${\mathbb {R}^n}$ to $\mathrm {T}_{\mathrm {R}_x(s)}\mathcal {M}$. Thus, its singular values are upper bounded by 1. Since $T_s$ is an operator on $\mathrm {T}_x\mathcal {M}\subset {\mathbb {R}^n}$,

$$\begin{aligned} \left\| {T_s}\right\| _\mathrm {op} \le \frac{1}{\sqrt{1+\Vert s\Vert ^2}} \le 1. \end{aligned}$$

This secures the first property with $c_1 = 1$.

For the second property, consider $U(t) = T_{ts} \dot{s}$ and

$$\begin{aligned} U'(t) \triangleq \frac{\mathrm {D}}{\mathrm {d}t} U(t) = \mathrm {Proj}_{c(t)} \frac{\mathrm {d}}{\mathrm {d}t}U(t), \end{aligned}$$

where $\mathrm {Proj}_y(v) = v - y (y^\top v)$ is the orthogonal projector to $\mathrm {T}_y\mathcal {M}$ and $c(t) = \mathrm {R}_x(ts)$. Define $g(t) = \frac{1}{\sqrt{1+t^2\Vert s\Vert ^2}}$. Then, from (45), we have

$$\begin{aligned} U(t) = \left[ g(t) I_n - t g(t)^3 (x+ts)s^\top \right] \dot{s}. \end{aligned}$$

(46)

This is easily differentiated in the embedding space ${\mathbb {R}^n}$:

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}U(t) = \left[ g'(t) I_n - (t g(t)^3)' (x+ts)s^\top - t g(t)^3 ss^\top \right] \dot{s}. \end{aligned}$$

The projection at c(t) zeros out the middle term, as it is parallel to $x+ts$. This offers a simple expression for $U'(t)$, where in the last equality we use $g'(t) = -t g(t)^3 \Vert s\Vert ^2$:

$$\begin{aligned} U'(t) = \mathrm {Proj}_{c(t)}\left( \left[ g'(t) I_n - t g(t)^3 ss^\top \right] \dot{s} \right) = -t g(t)^3 \cdot \mathrm {Proj}_{c(t)}\left( \left[ \Vert s\Vert ^2 I_n + ss^\top \right] \dot{s} \right) . \end{aligned}$$

The norm can only decrease after projection, so that, for $t \in [0, 1]$,

$$\begin{aligned} \Vert U'(t)\Vert \le 2 t g(t)^3 \Vert s\Vert ^2 \Vert \dot{s}\Vert . \end{aligned}$$

Let $h(t) = 2 t g(t)^3 \Vert s\Vert ^2 = \frac{2t\Vert s\Vert ^2}{(1+t^2 \Vert s\Vert ^2)^{1.5}}$. For $s = 0$, h is identically zero. Otherwise, h attains its maximum $h\left( t = \frac{1}{\sqrt{2} \Vert s\Vert }\right) = \frac{4 \sqrt{3}}{9} \Vert s\Vert$. It follows that $\Vert U'(t)\Vert \le c_2 \Vert s\Vert \Vert \dot{s}\Vert$ for all $t \in [0, 1]$ with $c_2 = \frac{4\sqrt{3}}{9}$.

Finally, we establish the last property. Given $s, \dot{s} \in \mathrm {T}_x\mathcal {M}$, consider $c(t) = \mathrm {R}_x(s + t\dot{s})$. Simple calculations yield:

$$\begin{aligned} c'(t) = \frac{\mathrm {d}}{\mathrm {d}t}c(t) = \frac{1}{\sqrt{1 + \Vert s + t\dot{s}\Vert ^2}} \left[ \dot{s} - \left\langle {\dot{s}},{c(t)}\right\rangle c(t) \right] = \frac{1}{\sqrt{1 + \Vert s + t\dot{s}\Vert ^2}} \mathrm {Proj}_{c(t)} \dot{s}. \end{aligned}$$

(47)

This is indeed in the tangent space at c(t). The classical derivative of $c'(t)$ is given by

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}c'(t)&= - \frac{1}{\sqrt{1 + \Vert s + t\dot{s}\Vert ^2}}\\&\quad \left[ \left\langle {\dot{s}},{c'(t)}\right\rangle c(t) + \left\langle {\dot{s}},{c(t)}\right\rangle c'(t) + \frac{\left\langle {s + t\dot{s}},{\dot{s}}\right\rangle }{1 + \Vert s + t \dot{s}\Vert ^2} \mathrm {Proj}_{c(t)} \dot{s} \right] \\&= - \frac{1}{\sqrt{1 + \Vert s + t\dot{s}\Vert ^2}} \left[ \left\langle {\dot{s}},{c'(t)}\right\rangle c(t) + 2\frac{\left\langle {s + t\dot{s}},{\dot{s}}\right\rangle }{1 + \Vert s + t \dot{s}\Vert ^2} \mathrm {Proj}_{c(t)} \dot{s} \right] , \end{aligned}$$

where we used (47) and orthogonality of x and $\dot{s}$ in $\left\langle {c(t)},{\dot{s}}\right\rangle = \frac{1}{\sqrt{1+\Vert s+t\dot{s}\Vert ^2}} \left\langle {x + s + t \dot{s}},{\dot{s}}\right\rangle$. The acceleration of c is $c''(t) = \frac{\mathrm {D}}{\mathrm {d}t} c'(t) = \mathrm {Proj}_{c(t)}\left( \frac{\mathrm {d}}{\mathrm {d}t}c'(t) \right)$. The first term vanishes after projection, while the second term is unchanged. Overall,

$$\begin{aligned} c''(t) = -\frac{2\left\langle {s + t\dot{s}},{\dot{s}}\right\rangle }{\sqrt{1 + \Vert s + t \dot{s}\Vert ^2}^3} \mathrm {Proj}_{c(t)} \dot{s} = -\frac{2\left\langle {c(t)},{\dot{s}}\right\rangle }{1 + \Vert s + t \dot{s}\Vert ^2} \mathrm {Proj}_{c(t)} \dot{s}. \end{aligned}$$

(48)

In particular, $c''(0) = -2 \frac{\left\langle {s},{\dot{s}}\right\rangle }{\sqrt{1+\Vert s\Vert ^2}^3} \mathrm {Proj}_{c(0)} \dot{s}$, so that $\Vert c''(0)\Vert \le 2 \min (\Vert s\Vert , 0.4) \Vert \dot{s}\Vert ^2$ and the property holds with $c_3 = 2$. (Peculiarly, if s and $\dot{s}$ are orthogonal, $c''(0) = 0$.) $\square$

In order to prove Theorem 6, we introduce two supporting lemmas (needed only for the case where $\mathcal {M}$ is not compact) and one key lemma. The first lemma below is similar in spirit to [23, Lem. 2.2].

Lemma 6

Let $f :\mathcal {M}\rightarrow {\mathbb {R}}$ be twice continuously differentiable. Let $\{ (x_0, s_0), (x_1, s_1), \ldots \}$ be the points and steps generated by Algorithm 1. Each step has norm bounded as:

$$\begin{aligned} \Vert s_k\Vert \le \sqrt{\frac{3 \Vert \nabla \hat{f}_k(0)\Vert }{\varsigma _{\min }}} + \frac{3}{2\varsigma _{\min }} \max \left( 0, -\lambda _{\mathrm{min}}(\nabla ^2 \hat{f}_k(0))\right) , \end{aligned}$$

(49)

where $\hat{f}_k = f \circ \mathrm {R}_{x_k}$ is the pullback, as in (6).

Proof

Owing to the first-order progress condition (2), using Cauchy–Schwarz and the fact that $\varsigma _k \ge \varsigma _{\min }$ for all k by design of the algorithm, we find

$$\begin{aligned} \varsigma _{\min } \Vert s_k\Vert ^3 \le \varsigma _{k} \Vert s_k\Vert ^3&\le -3\left\langle {s_k},{\nabla \hat{f}_k(0) + \frac{1}{2}\nabla ^2 \hat{f}_k(0)[s_k]}\right\rangle \\&\le 3 \Vert s_k\Vert \left( \Vert \nabla \hat{f}_k(0)\Vert + \frac{1}{2} \max \left( 0, -\lambda _{\mathrm{min}}(\nabla ^2 \hat{f}_k(0))\right) \Vert s_k\Vert \right) . \end{aligned}$$

This defines a quadratic inequality in $\Vert s_k\Vert$:

$$\begin{aligned} \varsigma _{\min } \Vert s_k\Vert ^2 - h_k \Vert s_k\Vert - g_k \le 0, \end{aligned}$$

where to simplify notation we let $h_k = \frac{3}{2} \max (0, -\lambda _{\mathrm{min}}(\nabla ^2 \hat{f}_k(0)))$ and $g_k = 3 \Vert \nabla \hat{f}_k(0)\Vert$. Since $\Vert s_k\Vert$ must lie between the two roots of this quadratic, we know in particular that

$$\begin{aligned} \Vert s_k\Vert \le \frac{h_k + \sqrt{h_k^2 + 4\varsigma _{\min }g_k}}{2\varsigma _{\min }} \le \frac{h_k + \sqrt{\varsigma _{\min } g_k}}{\varsigma _{\min }}, \end{aligned}$$

where in the last step we used $\sqrt{u+v} \le \sqrt{u} + \sqrt{v}$ for any $u, v \ge 0$. $\square$

Lemma 7

Let $f :\mathcal {M}\rightarrow {\mathbb {R}}$ be twice continuously differentiable. Let $\{ (x_0, s_0), (x_1, s_1), \ldots \}$ be the points and steps generated by Algorithm 1. Consider the following subset of $\mathcal {M}$, obtained by collecting all curves generated by retracted steps (both accepted and rejected):

$$\begin{aligned} \mathcal {N}= \bigcup _{k} \left\{ \mathrm {R}_{x_k}(ts_k) : t \in [0, 1] \right\} . \end{aligned}$$

(50)

If the sequence $\{x_0, x_1, x_2, \ldots \}$ remains in a compact subset of $\mathcal {M}$, then $\mathcal {N}$ is included in a compact subset of $\mathcal {M}$.

Proof

If $\mathcal {M}$ is compact, the claim is clear since $\mathcal {N}\subseteq \mathcal {M}$. Otherwise, we use Lemma 6. Specifically, considering the upper bound in that lemma, define

$$\begin{aligned} \alpha (x) = \sqrt{\frac{3 \Vert \nabla \hat{f}_x(0)\Vert }{\varsigma _{\min }}} + \frac{3}{2\varsigma _{\min }} \max \left( 0, -\lambda _{\mathrm{min}}(\nabla ^2 \hat{f}_x(0))\right) , \end{aligned}$$

where $\hat{f}_x = f \circ \mathrm {R}_x$. This is a continuous function of x, and $\Vert s_k\Vert \le \alpha (x_k)$. Since by assumption $\{x_0, x_1, \ldots \} \subseteq \mathcal {K}$ with $\mathcal {K}$ compact, we find that

$$\begin{aligned} \forall k, \quad \Vert s_k\Vert \le \sup _{k'} \alpha (x_{k'}) \le \max _{x \in \mathcal {K}} \alpha (x) \triangleq r, \end{aligned}$$

where r is a finite number. Consider the following subset of the tangent bundle $\mathrm {T}\mathcal {M}$:

$$\begin{aligned} \mathcal {K}' = \{ (x, s) \in \mathrm {T}\mathcal {M}: x \in \mathcal {K}, \Vert s\Vert _x \le r \}. \end{aligned}$$

Since $\mathcal {K}$ is compact, $\mathcal {K}'$ is compact. Furthermore, since the retraction is a continuous map, $\mathrm {R}(\mathcal {K}')$ is compact, and it contains $\mathcal {N}$. $\square$

Lemma 8

Let $f :\mathcal {M}\rightarrow {\mathbb {R}}$ be three times continuously differentiable, and consider the points and steps $\{(x_0, s_0), (x_1, s_1), \ldots \}$ generated by Algorithm 1. Assume the retraction is second-order nice on this set (see Definition 4). If the set $\mathcal {N}$ as defined by (50) is contained in a compact set $\mathcal {K}$, then A2 and A4 are satisfied.

Proof

For some k and $\bar{t} \in [0, 1]$, let $(x, s) = (x_k, \bar{t} s_k)$ and define the pullback $\hat{f} = f \circ \mathrm {R}_x$. Notice in particular that $\mathrm {R}_x(s) \in \mathcal {N}\subseteq \mathcal {K}$. Combine the expression for the Hessian of the pullback (29) with (27) to get:

$$\begin{aligned}&\left\| \nabla ^2 \hat{f}(s) - \nabla ^2 \hat{f}(0) \right\| _{\mathrm {op}}\\&\qquad \le \left\| T_{s}^* \circ \mathrm {Hess}f(\mathrm {R}_x(s)) \circ T_{s} - \mathrm {Hess}f(x) \right\| _{\mathrm {op}} + \left\| W_{s} - W_0 \right\| _{\mathrm {op}}. \end{aligned}$$

By definition of $W_s$ (31), using the third condition on the retraction, we find that $W_0 = 0$ and

$$\begin{aligned} \Vert W_s\Vert _\mathrm {op} = \max _{\begin{array}{c} \dot{s} \in \mathrm {T}_x\mathcal {M}\\ \Vert \dot{s}\Vert \le 1 \end{array}} \left| \left\langle {W_s[\dot{s}]},{\dot{s}}\right\rangle \right| \le \Vert \mathrm {grad}f(\mathrm {R}_x(s))\Vert \cdot \max _{\begin{array}{c} \dot{s} \in \mathrm {T}_x\mathcal {M}\\ \Vert \dot{s}\Vert \le 1 \end{array}} \Vert c''(0)\Vert \le c_3 G \Vert s\Vert , \end{aligned}$$

where $G = \max _{y \in \mathcal {K}} \Vert \mathrm {grad}f(y)\Vert$ is finite by compactness of $\mathcal {K}$ and continuity of the gradient norm. Thus, it remains to show that

$$\begin{aligned} \left\| T_s^* \circ \mathrm {Hess}f(\mathrm {R}_x(s)) \circ T_s - \mathrm {Hess}f(x) \right\| _{\mathrm {op}}&\le c' \Vert s\Vert \end{aligned}$$

for some constant $c'$. For an arbitrary $\dot{s} \in \mathrm {T}_x\mathcal {M}$, owing to differentiability properties of f,

$$\begin{aligned}&\left\langle {\big [T_s^* \circ \mathrm {Hess}f(\mathrm {R}_x(s)) \circ T_s - \mathrm {Hess}f(x)\big ][\dot{s}]},{\dot{s}}\right\rangle \nonumber \\&\quad = \int _{0}^{1} \frac{\mathrm {d}}{\mathrm {d}t} \left\langle {T_{ts}^* \circ \mathrm {Hess}f(\mathrm {R}_x(ts)) \circ T_{ts} [\dot{s}]},{\dot{s}}\right\rangle \mathrm {d}t. \end{aligned}$$

(51)

We aim to upper bound the above by $c' \Vert s\Vert \Vert \dot{s}\Vert ^2$. Consider the curve $c(t) = \mathrm {R}_{x}(ts)$ and a tangent vector field $U(t) = T_{ts} \dot{s}$ along c. Then, define

$$\begin{aligned} h(t)&= \left\langle {T_{ts}^* \circ \mathrm {Hess}f(c(t)) \circ T_{ts} [\dot{s}]},{\dot{s}}\right\rangle \\&= \left\langle {\mathrm {Hess}f(c(t))[T_{ts} \dot{s}]},{T_{ts} \dot{s}}\right\rangle \\&= \left\langle {\mathrm {Hess}f(c(t))[U(t)]},{U(t)}\right\rangle . \end{aligned}$$

The integrand in (51) is the derivative of the real function h:

$$\begin{aligned} h'(t)&= \frac{\mathrm {d}}{\mathrm {d}t} \left\langle {\mathrm {Hess}f(c(t))[U(t)]},{U(t)}\right\rangle \\&= \left\langle {\frac{\mathrm {D}}{\mathrm {d}t}\Big [\mathrm {Hess}f(c(t))[U(t)]\Big ]},{U(t)}\right\rangle + \left\langle {\mathrm {Hess}f(c(t))[U(t)]},{\frac{\mathrm {D}}{\mathrm {d}t} U(t)}\right\rangle \\&= \left\langle {\left( \nabla _{c'(t)} \mathrm {Hess}f \right) [U(t)]},{U(t)}\right\rangle + 2\left\langle {\mathrm {Hess}f(c(t))[U(t)]},{U'(t)}\right\rangle , \end{aligned}$$

where $U'(t) \triangleq \frac{\mathrm {D}}{\mathrm {d}t} U(t)$ and we used that the Hessian is symmetric. Here, $\nabla _{c'(t)} \mathrm {Hess}f$ is the Levi–Civita derivative of the Hessian tensor field at $c(t)$ along $c'(t)$—see [28, Def. 4.5.7, p 102] for the notion of derivative of a tensor field. For every $t$, the latter is a symmetric linear operator on the tangent space at $c(t)$. By Cauchy–Schwarz,

$$\begin{aligned} |h'(t)| \le \Vert \nabla _{c'(t)} \mathrm {Hess}f\Vert _{\mathrm {op}} \Vert U(t)\Vert ^2 + 2 \Vert \mathrm {Hess}f(c(t))\Vert _{\mathrm {op}} \Vert U(t)\Vert \Vert U'(t)\Vert . \end{aligned}$$

By compactness of $\mathcal {K}$ and continuity of the Hessian, we can define

$$\begin{aligned} H = \max _{y \in \mathcal {K}} \Vert \mathrm {Hess}f(y)\Vert _{\mathrm {op}}. \end{aligned}$$

By linearity of the connection $\nabla$, if $c'(t) \ne 0$,

$$\begin{aligned} \nabla _{c'(t)} \mathrm {Hess}f = \Vert c'(t)\Vert \cdot \nabla _{\frac{c'(t)}{\Vert c'(t)\Vert }} \mathrm {Hess}f. \end{aligned}$$

Furthermore, $c'(t) = T_{ts} s$ has norm bounded by the first assumption on the retraction: $\Vert c'(t)\Vert \le c_1 \Vert s\Vert$. Thus, in all cases, by compactness of $\mathcal {K}$ and continuity of the function $v \rightarrow \nabla _v \mathrm {Hess}f$ on the tangent bundle $\mathrm {T}\mathcal {M}$, there is a finite J as follows:

$$\begin{aligned} \Vert \nabla _{c'(t)} \mathrm {Hess}f \Vert _{\mathrm {op}} \le c_1 \Vert s\Vert \cdot \overbrace{\max _{\begin{array}{c} y \in \mathcal {K}, v \in \mathrm {T}_y\mathcal {M}\\ \Vert v\Vert \le 1 \end{array}} \Vert \nabla _v \mathrm {Hess}f \Vert _{\mathrm {op}}}^{J}. \end{aligned}$$

Of course, $\Vert U(t)\Vert \le c_1 \Vert \dot{s}\Vert$. Finally, we bound $\Vert U'(t)\Vert$ using the second property of the retraction: $\Vert U'(t)\Vert \le c_2\Vert s\Vert \Vert \dot{s}\Vert$. Collecting what we learned about $|h'(t)|$ and injecting in (51),

$$\begin{aligned}&\left| \left\langle {\big [T_s^* \circ \mathrm {Hess}f(\mathrm {R}_x(s)) \circ T_s - \mathrm {Hess}f(x)\big ][\dot{s}]},{\dot{s}}\right\rangle \right| \\&\quad \le \int _{0}^{1} |h'(t)| \mathrm {d}t\le \left[ c_1^3 J + 2 c_1 c_2 H \right] \Vert s\Vert \Vert \dot{s}\Vert ^2. \end{aligned}$$

Finally, it follows from Lemma 4 that A2 and A4 hold with $L = L' = c_3G + 2 c_1 c_2 H + c_1^3 J$ and $q \equiv 0$. We note in closing that the constants G, H, J can be related to the Lipschitz properties of f, $\mathrm {grad}f$ and $\mathrm {Hess}f$, respectively. $\square$

The theorem we wanted to prove now follows as a direct corollary.

Proof of Theorem 6

For the main result, simply combine Lemmas 7 and 8. To support the closing statement, it is sufficient to verify that Algorithm 1 is a descent method owing to the step acceptance mechanism and the first part of condition (2). $\square$

E Proofs from Section 7: differential of retraction

1.1 Stiefel manifold

Proposition 4 regarding the Stiefel manifold is a corollary of the following statement.

Lemma 9

For the Stiefel manifold $\mathcal {M}= \mathrm {St}(n,p)$ with the Q-factor retraction $\mathrm {R}$, for all $X \in \mathcal {M}$ and $S \in \mathrm {T}_X\mathcal {M}$,

$$\begin{aligned} \sigma _{\mathrm{min}}(\mathrm {D}\mathrm {R}_X(S)) \ge 1 - 3\Vert S\Vert _{\mathrm {F}} - \frac{1}{2}\Vert S\Vert _{\mathrm {F}}^2, \end{aligned}$$

where $\Vert \cdot \Vert _{\mathrm {F}}$ denotes the Frobenius norm. Moreover, for the special case $p = 1$ (the unit sphere in ${\mathbb {R}^n}$), the retraction reduces to $\mathrm {R}_x(s) = \frac{x+s}{\Vert x+s\Vert }$ and we have for all $x \in \mathcal {M}, s \in \mathrm {T}_x\mathcal {M}$:

$$\begin{aligned} \sigma _{\mathrm{min}}(\mathrm {D}\mathrm {R}_x(s)) = \frac{1}{1 + \Vert s\Vert ^2}. \end{aligned}$$

Proof

Let $X \in \mathrm {St}(n, p)$ and $S \in \mathrm {T}_X \mathrm {St}(n, p) = \{ \dot{X} \in {\mathbb {R}^{n\times p}}: \dot{X}^\top X + X^\top \dot{X} = 0 \}$ be fixed. Define Q, R as the thin QR-decomposition of $X + S$, that is, Q is an $n \times p$ matrix with orthonormal columns and R is a $p \times p$ upper triangular matrix with positive diagonal entries such that $X+S = QR$: this decomposition exists and is unique since $X+S$ has full column rank, as shown below (53). By definition, we have that $\mathrm {R}_X(S) = Q$.

For a matrix M, define $\mathrm {tril}(M)$ as the lower triangular portion of the matrix M, that is, $\mathrm {tril}(M)_{ij} = M_{ij}$ if $i \ge j$ and 0 otherwise. Further define $\rho _{\mathrm {skew}}(M)$ as

$$\begin{aligned} \rho _{\mathrm {skew}}(M) \triangleq \mathrm {tril}(M) - \mathrm {tril}(M)^\top . \end{aligned}$$

As derived in [3, Ex. 8.1.5] (see also the erratum for the reference) we have a formula for the directional derivative of the retraction along any $Z \in \mathrm {T}_X \mathrm {St}(n, p)$:

$$\begin{aligned} \mathrm {D}\mathrm {R}_X(S)[Z] = Q\rho _{\mathrm {skew}}(Q^\top Z R^{-1}) + (I-QQ^\top ) Z R^{-1}. \end{aligned}$$

(52)

We first confirm that R is always invertible. To see this, note that S being tangent at X means $S^\top X + X^\top S = 0$ and therefore

$$\begin{aligned} R^\top R = \underbrace{(X+S)^\top (X + S)}_{\text {start reading here}} = X^\top X + X^\top S + S^\top X + S^\top S = I_p + S^\top S, \end{aligned}$$

(53)

which shows R is invertible. Moreover the above expression also implies that:

$$\begin{aligned} \sigma _k(R) = \sigma _k(X + S) = \sqrt{\lambda _k((X+S)^\top (X+S))} = \sqrt{1 + \lambda _k(S^\top S)} = \sqrt{1 + \sigma _k(S)^2}, \end{aligned}$$

where $\sigma _k(M)$ represents the kth singular value of M and $\lambda _k$ likewise extracts the kth eigenvalue (in decreasing order for symmetric matrices). In particular we have that

$$\begin{aligned} \sigma _{\mathrm{min}}(R^{-1})&= \frac{1}{\sqrt{1 + \sigma _{\mathrm{max}}(S)^2}} \ge \frac{1}{\sqrt{1 + \Vert S\Vert _{\mathrm {F}}^2}} \ge 1 - \frac{1}{2}\Vert S\Vert _{\mathrm {F}}^2, \nonumber \\ \sigma _{\mathrm{max}}(R^{-1})&= \frac{1}{\sqrt{1 + \sigma _{\mathrm{min}}(S)^2}} \le 1. \end{aligned}$$

(54)

Further note that since $QR = X + S$, we have that $Q = (X+S)R^{-1}$ and therefore

$$\begin{aligned} Q^\top Z R^{-1}&= (R^{-1})^\top (X+S)^\top Z R^{-1} \nonumber \\&= (R^{-1})^\top X^\top Z R^{-1} + (R^{-1})^\top S^\top Z R^{-1}. \end{aligned}$$

The first term above is always skew-symmetric since Z is tangent at X, so that $X^\top Z + Z^\top X = 0$. Furthermore, for any skew-symmetric matrix M, $\rho _{\mathrm {skew}}(M) = M$. Therefore, using (52),

$$\begin{aligned} \mathrm {D}\mathrm {R}_X(S)[Z]&= Q\rho _{\mathrm {skew}}(Q^\top Z R^{-1}) + (I-QQ^\top ) Z R^{-1} \nonumber \\&= Q\left( \rho _{\mathrm {skew}}(Q^\top Z R^{-1}) - Q^\top Z R^{-1} \right) + Z R^{-1} \nonumber \\&= Q\left( \rho _{\mathrm {skew}}((R^{-1})^\top S^\top Z R^{-1}) - (R^{-1})^\top S^\top Z R^{-1} \right) + Z R^{-1}, \end{aligned}$$

(55)

where in the last step we used $XR^{-1} - Q = -SR^{-1}$. Further note that for any matrix M of size $p \times p$,

$$\begin{aligned} \Vert Q(\rho _{\mathrm {skew}}(M) - M)\Vert _{\mathrm {F}} = \Vert \mathrm {tril}(M) - \mathrm {tril}(M)^\top - M\Vert _{\mathrm {F}} \le 3 \Vert M\Vert _{\mathrm {F}}. \end{aligned}$$

(56)

Hence, we have that,

$$\begin{aligned} \Vert \mathrm {D}\mathrm {R}_X(S)[Z] \Vert _{\mathrm {F}}&\ge \Vert ZR^{-1}\Vert _{\mathrm {F}} - 3\Vert (R^{-1})^\top S^\top Z R^{-1} \Vert _{\mathrm {F}} \nonumber \\&\ge \Vert Z\Vert _{\mathrm {F}} \left( \sigma _{\mathrm{min}}(R^{-1}) - 3 \sigma _{\mathrm{max}}(R^{-1})^2 \sigma _{\mathrm{max}}(S) \right) , \end{aligned}$$

(57)

where we have used $\Vert A\Vert _{\mathrm {F}}\sigma _{\mathrm{min}}(B) \le \Vert AB\Vert _{\mathrm {F}} \le \Vert A\Vert _{\mathrm {F}} \sigma _{\mathrm{max}}(B)$ multiple times. Using the bounds on the singular values of $R^{-1}$ (derived in (54)) we get that

$$\begin{aligned} \Vert \mathrm {D}\mathrm {R}_X(S)[Z] \Vert _{\mathrm {F}} \ge \Vert Z\Vert _{\mathrm {F}} \left( 1 - \frac{1}{2}\Vert S\Vert _{\mathrm {F}}^2 - 3 \Vert S\Vert _{\mathrm {F}} \right) . \end{aligned}$$

Since this holds for all tangent vectors Z, we get that

$$\begin{aligned} \sigma _{\mathrm{min}}(\mathrm {D}\mathrm {R}_X(S)) \ge 1 - 3 \Vert S\Vert _{\mathrm {F}} - \frac{1}{2}\Vert S\Vert _{\mathrm {F}}^2. \end{aligned}$$

To prove a better bound for the case of $p=1$ (the sphere), we improve the analysis of the expression derived in (55). Note that for $p = 1$, the matrix inside the $\rho _{\mathrm {skew}}$ operator is a scalar, whose skew-symmetric part is necessarily zero. Also note that Q is a single column matrix with value $\frac{x + s}{\Vert x + s\Vert }$ and $R = \Vert x + s\Vert$. Also, $X^\top S X^\top Z = 0$ since S, Z are tangent. Therefore,

$$\begin{aligned} \mathrm {D}\mathrm {R}_X(S)[Z]&= Z R^{-1} - Q(R^{-1})^\top S^\top Z R^{-1} \\&= \frac{1}{\Vert x+s\Vert } \left( z - \frac{s^\top z}{1+\Vert s\Vert ^2}(x+s)\right) \\&= \frac{1}{\Vert x+s\Vert } \left( z - \frac{s^\top z}{1+\Vert s\Vert ^2} s - \frac{s^\top z}{1+\Vert s\Vert ^2} x\right) . \end{aligned}$$

Since x is orthogonal to s and z,

$$\begin{aligned} \Vert \mathrm {D}\mathrm {R}_x(s)[z]\Vert ^2&= \frac{1}{1+\Vert s\Vert ^2} \left( \left\| z - \frac{s^\top z}{1+\Vert s\Vert ^2} s \right\| ^2 + \left( \frac{s^\top z}{1+\Vert s\Vert ^2}\right) ^2 \right) \\&= \frac{1}{1+\Vert s\Vert ^2} \left( \Vert z\Vert ^2 - 2\frac{(s^\top z)^2}{1+\Vert s\Vert ^2} + \left( \frac{s^\top z}{1+\Vert s\Vert ^2}\right) ^2 (1 + \Vert s\Vert ^2) \right) \\&= \frac{1}{1+\Vert s\Vert ^2} \left( \Vert z\Vert ^2 - \frac{(s^\top z)^2}{1+\Vert s\Vert ^2}\right) \\&\ge \Vert z\Vert ^2 \frac{1}{1+\Vert s\Vert ^2} \left( 1 - \frac{\Vert s\Vert ^2}{1+\Vert s\Vert ^2} \right) \\&= \Vert z\Vert ^2 \frac{1}{(1+\Vert s\Vert ^2)^2}. \end{aligned}$$

The worst-case scenario is achieved when z and s are aligned. Overall, we get

$$\begin{aligned} \Vert \mathrm {D}\mathrm {R}_x(s)[z]\Vert \ge \Vert z\Vert \frac{1}{1+\Vert s\Vert ^2}, \end{aligned}$$

which establishes the bound for the sphere. $\square$

1.2 Differential of exponential map for manifolds with bounded curvature

Proposition 5 regarding the differential of the exponential map on complete manifolds with bounded sectional curvature follows as a corollary of the following statement.

Lemma 10

Assume all sectional curvatures of $\mathcal {M}$, complete, are bounded above by C:

• If $C \le 0$, then $\sigma _{\mathrm{min}}(\mathrm {D}\mathrm {Exp}_x(s)) = 1$;

• If $C = \frac{1}{R^2} > 0$ and $\Vert s\Vert \le \pi R$, then $1 \ge \sigma _{\mathrm{min}}(\mathrm {D}\mathrm {Exp}_x(s)) \ge \frac{\sin (\Vert s\Vert /R)}{\Vert s\Vert /R}$.

As usual, we use the convention $\sin (t)/t = 1$ at $t = 0$.

Proof

This results from a combination of few standard facts in Riemannian geometry:

• 1. [42, Prop. 10.10] Given any two tangent vectors $s, \dot{s} \in \mathrm {T}_x\mathcal {M}$, $J(t) = \mathrm {D}\mathrm {Exp}_x(ts)[t\dot{s}]$ is the unique Jacobi field along the geodesic $\gamma (t) = \mathrm {Exp}_x(ts)$ satisfying $J(0) = 0$ and $\frac{\mathrm {D}}{\mathrm {d}t}J(0) = \dot{s}$.

• 2. In particular, if $\dot{s} = \alpha s$ for some $\alpha \in {\mathbb {R}}$ so that $\dot{s}$ and s are parallel, then

  $$\begin{aligned} J(t)&= \mathrm {D}\mathrm {Exp}_x(ts)][t\dot{s}] = \left. \frac{\mathrm {d}}{\mathrm {d}q}\mathrm {Exp}_x(ts + qt\dot{s}) \right| _{q=0} = \left. \frac{\mathrm {d}}{\mathrm {d}q}\gamma (t + q\alpha t) \right| _{q=0} \\&= \alpha t \gamma '(t) = t P_{ts}(\dot{s}), \end{aligned}$$

  using $\gamma '(t) = P_{ts}(s)$. It remains to understand the case where $\dot{s}$ is orthogonal to s.

• 3. [42, Prop. 10.12] If $\mathcal {M}$ has constant sectional curvature C, $\Vert s\Vert = 1$ and $\left\langle {s},{\dot{s}}\right\rangle = 0$, the Jacobi field above is given by:

  $$\begin{aligned} J(t) = s_C(t) P_{ts}(\dot{s}), \end{aligned}$$

  where $P_{ts}$ denotes parallel transport along $\gamma$ as in (13) and

  $$\begin{aligned} s_C(t) = {\left\{ \begin{array}{ll} t &{} \text { if } C = 0, \\ R \sin (t/R) &{} \text { if } C = \frac{1}{R^2} > 0, \text { and} \\ R \sinh (t/R) &{} \text { if } C = -\frac{1}{R^2}. \end{array}\right. } \end{aligned}$$

  This can be reparameterized to allow for $\Vert s\Vert \ne 1$. Evaluating at $t = 1$ and using linearity in $\dot{s}$, we find for any $s, \dot{s} \in \mathrm {T}_x\mathcal {M}$ that

  $$\begin{aligned} \mathrm {D}\mathrm {Exp}_x(s)[\dot{s}] = P_s\left( \dot{s}_\parallel + \frac{s_C(\Vert s\Vert )}{\Vert s\Vert } \dot{s}_\perp \right) , \end{aligned}$$

  (58)

  where $\dot{s}_\perp$ is the part of $\dot{s}$ which is orthogonal to s and $\dot{s}_\parallel$ is the part of $\dot{s}$ which is parallel to s—this corresponds to expression (20). By isometry of parallel transport, it is a simple exercise in linear algebra to deduce that

  $$\begin{aligned} \sigma _{\mathrm{min}}(\mathrm {D}\mathrm {Exp}_x(s)) = \min \left( 1, \frac{s_C(\Vert s\Vert )}{\Vert s\Vert } \right) . \end{aligned}$$

• 4. [42, Thm. 11.9(a)] Consider the case where $\dot{s}$ is orthogonal to s of unit norm once again: the Jacobi field comparison theorem states that if the sectional curvatures of $\mathcal {M}$ are upper-bounded by C, then $\Vert J(t)\Vert$ is at least as large as what it would be if $\mathcal {M}$ had constant sectional curvature C—with the additional condition that $\Vert s\Vert \le \pi R$ if $C = 1/R^2 > 0$. This leads to the conclusion through similar developments as above, using also [42, Prop. 10.7] to separate the components of J(t) that are parallel or orthogonal to $\gamma '(t)$. $\square$

1.3 Extending to general retractions

In order to prove Theorem 7, we first introduce a result from topology. We follow [7], including the blanket assumption that all encountered topological spaces are Hausdorff (page 65 in that reference)—this is the case for us so long as the topology of $\mathcal {M}$ itself is Hausdorff, which most authors require as part of the definition of a smooth manifold. Products of topological spaces are equipped with the product topology. Neighborhoods are open. A correspondence $\varGamma :Y \rightarrow Z$ maps points in Y to subsets of Z.

Definition 5

(Upper semicontinuous (u.s.c.) mapping) A correspondence $\varGamma :Y \rightarrow Z$ between two topological spaces Y, Z is a u.s.c. mapping if, for all y in Y, $\varGamma (y)$ is a compact subset of Z and, for any neighborhood V of $\varGamma (y)$, there exists a neighborhood U of y such that, for all $u \in U$, $\varGamma (u) \subseteq V$.

Theorem 8

(Bergé [7, Thm. VI.2, p 116]) If $\phi$ is an upper semicontinuous, real-valued function in $Y \times Z$ and $\varGamma$ is a u.s.c. mapping of Y into Z (two topological spaces) such that $\varGamma (y)$ is nonempty for each y, then the real-valued function M defined by

$$\begin{aligned} M(y) = \max _{z \in \varGamma (y)} \phi (y,z) \end{aligned}$$

is upper semicontinuous. (Under the assumptions, the maximum is indeed attained.)

We use the above theorem to establish our result. Manifolds (including tangent bundles) are equipped with the natural topology inherited from their smooth structure.

Proof of Theorem 7

It is sufficient to show that the function

$$\begin{aligned} t(r) = \inf _{(x, s) \in \mathrm {T}\mathcal {M}: x \in \mathcal {U}, \Vert s\Vert _x \le r} \sigma _{\mathrm{min}}(\mathrm {D}\mathrm {R}_x(s)) \end{aligned}$$

(59)

is lower semicontinuous from ${\mathbb {R}}^+ = \{r \in {\mathbb {R}}: r \ge 0 \}$ to ${\mathbb {R}}$, with respect to their usual topologies. Indeed, $t(0) = 1$ owing to the fact that $\mathrm {D}\mathrm {R}_x(0)$ is the identity map for all x, and t being lower semicontinuous means that it cannot “jump down”. Explicitly, lower semicontinuity at $r = 0$ implies that, for all $\delta > 0$, there exists $a > 0$ such that for all $r \le a$ we have $t(r) \ge t(0) - \delta = 1 - \delta \triangleq b$.

To this end, consider the correspondence $\varGamma :{\mathbb {R}}^+ \rightarrow \mathrm {T}\mathcal {M}$ defined by

$$\begin{aligned} \varGamma (r) = \{ (x, s) \in \mathrm {T}\mathcal {M}: x \in \mathcal {U}\text { and } \Vert s\Vert _x \le r \}. \end{aligned}$$

(60)

Further consider the function $\phi :{\mathbb {R}}^+ \times \mathrm {T}\mathcal {M}\rightarrow {\mathbb {R}}$ defined by $\phi (r, (x, s)) = -\sigma _{\mathrm{min}}(\mathrm {D}\mathrm {R}_x(s))$. Then, $t(r) = -M(r)$, where

$$\begin{aligned} M(r) = \sup _{(x, s) \in \varGamma (r)} \phi (r, (x, s)). \end{aligned}$$

(61)

Thus, we must show M is upper semicontinuous. By Theorem 8, this is the case if

• 1. $\phi$ is upper semicontinuous,

• 2. $\varGamma (r)$ is nonempty and compact for all $r \ge 0$, and

• 3. For any $r \ge 0$ and any neighborhood $\mathcal {V}$ of $\varGamma (r)$ in $\mathrm {T}\mathcal {M}$, there exists a neighborhood I of r in ${\mathbb {R}}^+$ such that, for all $r' \in I$, we have $\varGamma (r') \subseteq \mathcal {V}$.

The first condition holds a fortiori since $\phi$ is continuous, owing to smoothness of $\mathrm {R}:\mathrm {T}\mathcal {M}\rightarrow \mathcal {M}$. The second condition holds since $\mathcal {U}$ is nonempty and compact. For the third condition, we show in Lemma 11 below that there exists a continuous function $\varDelta :\mathcal {U}\rightarrow {\mathbb {R}}$ (continuous with respect to the subspace topology) such that $\{ (x, s) \in \mathrm {T}\mathcal {M}: x \in \mathcal {U}\text { and } \Vert s\Vert _x \le \varDelta (x) \} \subseteq \mathcal {V}$ and $\varDelta (x) > r$ for all $x \in \mathcal {U}$ (if $\mathcal {M}$ is not connected, apply the lemma to each connected component which intersects with $\mathcal {U}$). As a result, $\min _{x\in \mathcal {U}} \varDelta (x) = r + \varepsilon$ for some $\varepsilon > 0$ (using $\mathcal {U}$ compact), and $\varGamma (r+\varepsilon )$ is included in $\mathcal {V}$. We conclude that $I = [0, r+\varepsilon )$ is a suitable neighborhood of r to verify the condition. $\square$

We now state and prove the last piece of the puzzle, which applies above with r(x) constant ($L = 0$). Although the context is quite different, the first part of the proof is inspired by that of the tubular neighborhood theorem in [42, Thm. 5.25].

Lemma 11

Let $\mathcal {U}$ be any subset of a connected Riemannian manifold $\mathcal {M}$ and let $r :\mathcal {U}\rightarrow {\mathbb {R}}^+$ be L-Lipschitz continuous with respect to the Riemannian distance $\mathrm {dist}$ on $\mathcal {M}$, that is,

$$\begin{aligned} \forall x, x' \in \mathcal {U}, \quad |r(x) - r(x')| \le L\, \mathrm {dist}(x, x'). \end{aligned}$$

Consider this subset of the tangent bundle:

$$\begin{aligned} \left\{ (x, s) \in \mathrm {T}\mathcal {M}: x \in \mathcal {U}\text { and } \Vert s\Vert _x \le r(x) \right\} . \end{aligned}$$

For any neighborhood $\mathcal {V}$ of this set in $\mathrm {T}\mathcal {M}$, there exists an $(L+1)$-Lipschitz continuous function $\varDelta :\mathcal {U}\rightarrow {\mathbb {R}}^+$ such that $\varDelta (x) > r(x)$ for all $x \in \mathcal {U}$ and

$$\begin{aligned} \left\{ (x, s) \in \mathrm {T}\mathcal {M}: x \in \mathcal {U}\text { and } \Vert s\Vert _x \le \varDelta (x) \right\} \subseteq \mathcal {V}. \end{aligned}$$

Proof

Consider the following open subsets of the tangent bundle, defined for each $x \in \mathcal {M}$ and $\delta \in {\mathbb {R}}$:

$$\begin{aligned} V_\delta (x) = \left\{ (x', s') \in \mathrm {T}\mathcal {M}: \mathrm {dist}(x, x')< \delta - r(x) \text { and } \Vert s'\Vert _{x'} < \delta \right\} . \end{aligned}$$

Referring to these sets, define the function $\varDelta :\mathcal {U}\rightarrow {\mathbb {R}}$ as:

$$\begin{aligned} \varDelta (x) = \sup \left\{ \delta \in {\mathbb {R}}: V_\delta (x) \subseteq \mathcal {V}\right\} . \end{aligned}$$

This is well defined since $V_{r(x)}(x) = \emptyset$, so that $\varDelta (x) \ge r(x)$ for all x. If $\varDelta (x) = \infty$ for some x, then $\mathcal {V}= \mathrm {T}\mathcal {M}$ and the claim is clear (for example, redefine $\varDelta (x) = r(x) + 1$ for all x). Thus, we assume $\varDelta (x)$ finite for all x. The rest of the proof is in two parts.

Step 1: $\varDelta$ is Lipschitz continuous. Pick $x, x' \in \mathcal {U}$, arbitrary. We must show

$$\begin{aligned} \varDelta (x) - \varDelta (x') \le (L+1) \mathrm {dist}(x, x'). \end{aligned}$$

Then, by reversing the roles of x and $x'$, we get $|\varDelta (x) - \varDelta (x')| \le (L+1) \mathrm {dist}(x, x')$, as desired. If $\varDelta (x) \le (L+1) \mathrm {dist}(x, x')$, the claim is clear since $\varDelta (x') \ge 0$. Thus, we now assume $\varDelta (x) > (L+1) \mathrm {dist}(x, x')$. Define $\delta = \varDelta (x) - (L+1) \mathrm {dist}(x, x') > 0$. It is sufficient to show that $V_\delta (x') \subseteq \mathcal {V}$, as this implies $\varDelta (x') \ge \delta = \varDelta (x) - (L+1) \mathrm {dist}(x, x')$, allowing us to conclude. To this end, we show the first inclusion in:

$$\begin{aligned} V_\delta (x') \subseteq V_{\varDelta (x)}(x) \subseteq \mathcal {V}. \end{aligned}$$

Consider an arbitrary $(x'', s'') \in V_\delta (x')$. This implies two things: first, $\Vert s''\Vert _{x''} < \delta \le \varDelta (x)$, and second:

$$\begin{aligned} \mathrm {dist}(x'', x)&\le \mathrm {dist}(x'', x') + \mathrm {dist}(x', x) \\&< \delta - r(x') + \mathrm {dist}(x', x) \\&= \varDelta (x) - r(x) + r(x) - r(x') - L \mathrm {dist}(x, x') \\&\le \varDelta (x) - r(x), \end{aligned}$$

where in the last step we used $r(x) - r(x') \le L\mathrm {dist}(x, x')$ since r is L-Lipschitz continuous on $\mathcal {U}$. As a result, $(x'', s'')$ is in $V_{\varDelta (x)}(x)$, which concludes this part of the proof.

Step 2: $\varDelta (x) > r(x)$ for all $x \in \mathcal {U}$. Pick $x \in \mathcal {U}$, arbitrary: $\mathcal {V}$ is a neighborhood of

$$\begin{aligned} \left\{ (x, s) \in \mathrm {T}\mathcal {M}: \Vert s\Vert _x \le r(x) \right\} . \end{aligned}$$

(62)

The claim is that there exists $\varepsilon > 0$ such that

$$\begin{aligned} \left\{ (x', s') \in \mathrm {T}\mathcal {M}: \mathrm {dist}(x, x') \le \varepsilon \text { and } \Vert s'\Vert _{x'} \le r(x) + \varepsilon \right\} \end{aligned}$$

(63)

is included in $\mathcal {V}$. Indeed, that would show that $\varDelta (x) \ge r(x) + \varepsilon > r(x)$. To show this, we construct special coordinates on $\mathrm {T}\mathcal {M}$ around x.

The (inverse of the) exponential map at x restricted to tangent vectors of norm strictly less than $\mathrm {inj}(x)$ (the injectivity radius at x) provides a diffeomorphism $\varphi$ from $\mathcal {W}\subseteq \mathcal {M}$ (the open geodesic ball of radius $\mathrm {inj}(x)$ around x) to $B(0, \mathrm {inj}(x))$: the open ball centered around the origin in the Euclidean space ${\mathbb {R}^{d}}$, where $d = \dim \mathcal {M}$. Additionally, from the chart $(\mathcal {W}, \varphi )$, we extract coordinate vector fields on $\mathcal {W}$: a set of smooth vector fields $W_1, \ldots , W_d$ on $\mathcal {W}$ such that, at each point in $\mathcal {W}$, the corresponding tangent vectors form a basis for the tangent space. We further orthonormalize this local frame (see [42, Prop. 2.8]) into a new local frame, $E_1, \ldots , E_d$, so that for each $x' \in \mathcal {W}$ we have that $E_1(x'), \ldots , E_d(x')$ form an orthonormal basis for $\mathrm {T}_{x'}\mathcal {M}$ (with respect to the Riemannian metric at $x'$). Then, the map

$$\begin{aligned} \psi (x', s')&= \left( \varphi (x'), \zeta (x', s') \right)&\text { with }&\zeta (x', s')&= \left( \left\langle {E_1(x')},{s'}\right\rangle _{x'}, \ldots , \left\langle {E_d(x')},{s'}\right\rangle _{x'} \right) \end{aligned}$$

establishes a diffeomorphism between $\mathrm {T}\mathcal {W}$ and $B(0, \mathrm {inj}(x)) \times {\mathbb {R}^{d}}$, with the following properties:

• 1. $\mathrm {dist}(x, x') = \Vert \varphi (x')\Vert$ (in particular, $\varphi (x) = 0$), and

• 2. For any $s', v' \in \mathrm {T}_{x'}\mathcal {M}$, it holds $\left\langle {s'},{v'}\right\rangle _{x'} = \left\langle {\zeta (x', s')},{\zeta (x', v')}\right\rangle$.

(Here, $\left\langle {\cdot },{\cdot }\right\rangle$ and $\Vert \cdot \Vert$ denote the Euclidean inner product and norm in ${\mathbb {R}^{d}}$.)

Expressed in these coordinates (that is, mapped through $\psi$), the set in (62) becomes:

$$\begin{aligned} D_0 = \{ 0 \} \times \bar{B}(0, r(x)), \end{aligned}$$

where $\bar{B}(0, r(x))$ denotes the closed Euclidean ball of radius r(x) around the origin in ${\mathbb {R}^{d}}$. Of course, $\mathcal {V}\cap \mathrm {T}\mathcal {W}$ maps to a neighborhood of $D_0$ in ${\mathbb {R}^{d}}\times {\mathbb {R}^{d}}$: call it O. Similarly, the set in (63) maps to:

$$\begin{aligned} D_\varepsilon = \bar{B}(0, \varepsilon ) \times \bar{B}(0, r(x) + \varepsilon ). \end{aligned}$$

It remains to show that there exists $\varepsilon > 0$ such that $D_\varepsilon$ is included in O.

Use this distance on ${\mathbb {R}^{d}}\times {\mathbb {R}^{d}}$: $\mathrm {dist}((y, z), (y', z')) = \max (\Vert y - y'\Vert , \Vert z - z'\Vert )$. This distance is compatible with the usual topology. For each (0, z) in $D_0$, there exists $\varepsilon _z > 0$ such that

$$\begin{aligned} C(z, \varepsilon _z) = \left\{ (y', z') \in {\mathbb {R}^{d}}\times {\mathbb {R}^{d}}: \Vert y'\Vert< \varepsilon _z \text { and } \Vert z - z'\Vert < \varepsilon _z \right\} \end{aligned}$$

is included in O (this is where we use the fact that $\mathcal {V}$—hence O—is open). The collection of open sets $C(z, \varepsilon _z/2)$ forms an open cover of $D_0$. Since $D_0$ is compact, we may extract a finite subcover, that is, we select $z_1, \ldots , z_n$ such that the sets $C(z_i, \varepsilon _{z_i}/2)$ cover $D_0$. Now, define $\varepsilon = \min _{i = 1, \ldots , n} \varepsilon _{z_i}/2$ (necessarily positive), and consider any point $(y, z) \in D_\varepsilon$. We must show that (y, z) is in O. To this end, let $\bar{z}$ denote the point in $\bar{B}(0, r(x))$ which is closest to z. Since $(0, \bar{z})$ is in $D_0$, there exists i such that $(0, \bar{z})$ is in $C(z_i, \varepsilon _{z_i}/2)$. As a result,

$$\begin{aligned} \Vert z - z_i\Vert \le \Vert z - \bar{z}\Vert + \Vert \bar{z} - z_i\Vert < \varepsilon + \varepsilon _{z_i}/2 \le \varepsilon _{z_i}. \end{aligned}$$

Likewise, $\Vert y\Vert \le \varepsilon \le \varepsilon _{z_i}/2 < \varepsilon _{z_i}$. Thus, we conclude that (y, z) is in $C(z_i, \varepsilon _{z_i})$, which is included in O. This confirms $D_\varepsilon$ is in O, so that the set in (63) is in $\mathcal {V}$ for some $\varepsilon > 0$. $\square$