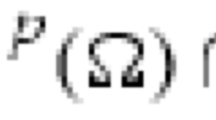Existence and multiplicity for an elliptic problem with critical growth in the gradient and sign-changing coefficients

Abstract

Let $\Omega \subset \mathbb {R}^{N}$, $N \ge 2$, be a smooth bounded domain. We consider the boundary value problem

where $c_{\lambda }$ and h belong to $L^q(\Omega )$ for some $q > N/2$, $\mu$ belongs to $\mathbb {R}{\setminus } \{0\}$ and we write $c_{\lambda }$ under the form $c_{\lambda }:= \lambda c_{+} - c_{-}$ with $c_{+} \gneqq 0$, $c_{-} \ge 0$, $c_{+} c_{-} \equiv 0$ and $\lambda \in \mathbb {R}$. Here $c_{\lambda }$ and h are both allowed to change sign. As a first main result we give a necessary and sufficient condition which guarantees the existence (and uniqueness) of solution to ($P_{\lambda }$) when $\lambda \le 0$. Then, assuming that $(P_0)$ has a solution, we prove existence and multiplicity results for $\lambda > 0$. Our proofs rely on a suitable change of variable of type $v = F(u)$ and the combination of variational methods with lower and upper solution techniques.

Appendix A. Hopf’s Lemma and SMP with unbounded lower order terms

In this section we prove Theorem 2.7 which can be seen as a combination of the Strong maximum principle and the Hopf’s Lemma. As said in Sect. 2, our proof is inspired by [35]. Let us begin with some preliminary results that will be needed to prove Theorem A.6. Throughout the appendix we assume $N \ge 2$.

Lemma A.1

[28, Lemma 4.2] Let $\Omega \subset \mathbb {R}^{N}$ be a bounded domain, $\beta \in (L^N(\Omega ))^N$ and $\xi \in L^{N/2}(\Omega )$ with $\xi \ge 0$. Then, for every $F \in H^{-1}(\Omega )$, there exists a unique solution $u \in H_0^1(\Omega )$ to

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u + \langle \beta (x), \nabla u\rangle + \xi (x)u = F, \quad &{} \text { in } \Omega ,\\ u = 0, \quad &{} \text { on } \partial \Omega . \end{array} \right. \end{aligned}$$

As a consequence of the previous lemma we obtain an existence result with inhomogeneous boundary conditions.

Corollary A.2

Let $\omega := B_1(0) {\setminus } \overline{B_{1/2}(0)}$, $\beta \in (L^p(\omega ))^N$ and $\xi \in L^p(\omega )$ for some $p > N$ and assume that $\xi \ge 0$. Then, there exists a unique solution $u \in \mathcal {C}^{1,\tau }(\overline{\omega })$ for some $\tau > 0$ to

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u + \langle \beta (x), \nabla u\rangle + \xi (x)u = 0, \quad &{} \text { in } \omega ,\\ u = 0, \quad &{} \text { on } \partial B_1(0),\\ u = 1, \quad &{} \text { on } \partial B_{1/2}(0), \end{array} \right. \end{aligned}$$

(A.1)

such that $0 \le u \le 1$ in $\overline{\omega }$.

Proof

Let us consider $\varphi \in C^{\infty }(\mathbb {R}^{N})$ given by $\varphi (x) = \frac{4}{3}(1-|x|^2),$ and observe that $\varphi (x) = 0$ for all $x \in \partial B_1(0)$ and $\varphi (x) = 1$ for all $x \in \partial B_{1/2}(0)$. Moreover, by direct computations it follows that

$$\begin{aligned} -\Delta \varphi + \langle \beta (x), \nabla \varphi \rangle + \xi (x) \varphi = \frac{8N}{3} - \frac{8}{3} \langle \beta (x), x \rangle + \frac{4}{3} \xi (x) (1-|x|^2) =: - F \in H^{-1}(\omega ). \end{aligned}$$

By Lemma A.1 we know that there exists a unique solution $w \in H_0^1(\omega )$ to

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta w + \langle \beta (x), \nabla w \rangle + \xi (x)w = F, \quad &{} \text { in } \omega ,\\ w = 0, \quad &{} \text { on } \partial \omega . \end{array} \right. \end{aligned}$$

Then, we define $u = w + \varphi$ and we observe that $u \in H^1(\omega )$ is a solution to (A.1). Next, by [28, Proposition 3.10] we deduce that $0 \le u \le 1$ in $\overline{\omega }$ and, by [29, Theorem II-15.1] we obtain that $u \in \mathcal {C}^{1,\tau }(\overline{\omega })$ for some $\tau > 0$. Finally, the uniqueness follow again from [28, Proposition 3.10]. $\square$

Lemma A.3

Let $\omega := B_1(0) {\setminus } \overline{B_{1/2}(0)}$, $\varepsilon \in (0,1/4)$, $x_0 \in \partial B_1(0)$ and $T: \mathbb {R}^{N}\rightarrow \mathbb {R}^{N}$ given by $T(x) = \varepsilon ^{-1}( x-x_0) + x_0$. Then, it follows that $\omega \subset T(\omega ):= \{T(x): x \in \omega \}$.

Proof

First of all, observe that

$$\begin{aligned} T(\omega ) = B_{1/\varepsilon } \left( \big (1-\frac{1}{\varepsilon }\big )x_0 \right) {\setminus } \overline{B_{1/2\varepsilon } \left( \big (1-\frac{1}{\varepsilon }\big )x_0 \right) } = \left\{ x \in \mathbb {R}^{N}: \frac{1}{2\varepsilon }< \big | x - \big ( 1 - \frac{1}{\varepsilon }\big )x_0 \big | < \frac{1}{\varepsilon } \right\} .\nonumber \\ \end{aligned}$$

(A.2)

Now, observe that, for all $x \in \omega$ and all $\varepsilon \in (0,1/4)$, it follows that

$$\begin{aligned} \big | x - \big ( 1 - \frac{1}{\varepsilon }\big )x_0 \big | \le |x| + \big | 1 - \frac{1}{\varepsilon }\big |\,|x_0| = |x| + \frac{1}{\varepsilon }-1 < 1 + \frac{1}{\varepsilon } - 1 = \frac{1}{\varepsilon }, \end{aligned}$$

(A.3)

and

$$\begin{aligned} \big | x - \big ( 1 - \frac{1}{\varepsilon }\big )x_0 \big | \ge \left| |x| - \big | 1 - \frac{1}{\varepsilon }\big |\,|x_0| \right| \ge \frac{1}{\varepsilon } - 1 - |x|> \frac{1}{\varepsilon } - 2 > \frac{1}{2\varepsilon }. \end{aligned}$$

(A.4)

Hence, the result follows from (A.2)–(A.4). $\square$

Lemma A.4

Let $\omega := B_1(0) {\setminus } \overline{B_{1/2}(0)}$, $B = (B^1, \ldots , B^N) \in (L^p(\omega ))^N$ and $a \in L^p(\omega )$, for some $p > N$, $\varepsilon \in [0,1/4]$, $B_{\varepsilon }(y) = (B_\varepsilon ^1, \ldots , B_{\varepsilon }^N) := \varepsilon B(\varepsilon (y-x_0) + x_0)$ and $a_{\varepsilon }(y) := \varepsilon ^2 a(\varepsilon (y-x_0) + x_0).$ Then, it follows that

• $\Vert B_{\varepsilon }^i \Vert _{L^p(\omega )} \le \varepsilon ^{1 - \frac{N}{p}} \Vert B^i\Vert _{L^p(\omega )},\qquad \forall \ i = 1, \ldots , N$;

• $\Vert a_{\varepsilon }\Vert _{L^p(\omega )} \le \varepsilon ^{2 - \frac{N}{p}} \Vert a\Vert _{L^p(\omega )}$.

Proof

Let $i \in \{1, \ldots , N\}$. We directly observe that

$$\begin{aligned} \Vert B_{\varepsilon }^{i}\Vert _{L^p(\omega )}^p = \int _{\omega } |B_{\varepsilon }^i(y)|^p dy = \varepsilon ^p \int _{\omega } |B^{i}(\varepsilon (y-x_0)+x_0)|^p dy = \varepsilon ^{p-N} \int _{S(\omega )} |B^i(z)|^p dz,\nonumber \\ \end{aligned}$$

(A.5)

where $z = S(y) = \varepsilon (y-x_0) + x_0$. Then, arguing as in Lemma A.3, we obtain that $S(\omega ) \subset \omega$, and so, taking into account (A.5), we deduce that

$$\begin{aligned} \Vert B_{\varepsilon }^{i}\Vert _{L^p(\omega )}^p \le \varepsilon ^{p-N} \int _{\omega } |B^{i}(z)|^p dz = \varepsilon ^{p-N} \Vert B^{i}\Vert _{L^p(\omega )}^p . \end{aligned}$$

The estimate for $a_{\varepsilon }$ follows arguing on the same way. $\square$

Using the rescaled functions $B_{\varepsilon }$ and $a_{\varepsilon }$ defined in Lemma A.4, we introduce the auxiliary boundary value problem

and we prove the following uniform a priori bound that will be crucial in the proof of Theorem A.6.

Lemma A.5

Let $\omega := B_1(0) {\setminus } \overline{B_{1/2}(0)}$, $B = (B_1, \ldots , B_N) \in (L^p(\omega ))^N$ and $a \in L^p(\omega )$ for some $p > N$. Then, there exists $M > 0$ such that, for all $\varepsilon \in [0,1/4]$, any solution u to ($P_{\varepsilon }$) satisfies $\Vert u\Vert _{\mathcal {C}^1(\overline{\omega })} \le M$.

Proof

We argue by contradiction. Assume the existence of sequences $\{\varepsilon _n\} \subset [0,1/4]$ and $\{u_n\}$ solutions to ($P_{\varepsilon }$) with $\varepsilon = \varepsilon _n$ such that

$$\begin{aligned} \Vert u_n\Vert _{\mathcal {C}^1(\overline{\omega })} \rightarrow + \infty , \quad \text { as } n \rightarrow \infty . \end{aligned}$$

Without loss of generality (up to a subsequence if necessary) we may assume that

$$\begin{aligned} 1 \le \Vert u_n\Vert _{\mathcal {C}^1(\overline{\omega })}, \quad \forall \ n \in \mathbb {N}. \end{aligned}$$

We consider then $v_n:= \frac{u_n}{\Vert u_n\Vert _{\mathcal {C}^1(\overline{\omega })}}$ and observe that $v_n$ solves

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta v_n + \langle B_{\varepsilon _n}(x), \nabla v_n \rangle + a_{\varepsilon _n}(x)v_n = 0, \quad &{} \text { in } \omega , \\ v_n = 0, \quad &{} \text { on } \partial B_1(0),\\ v_n = \frac{1}{\Vert v_n\Vert _{ \mathcal {C}^1(\overline{\omega }) }}, \quad &{} \text { on } \partial B_{1/2}(0). \end{array} \right. \end{aligned}$$

Now, for all $n \in \mathbb {N}$, let us define

$$\begin{aligned} \xi _n = \frac{4}{3\Vert u_n\Vert _{ \mathcal {C}^1(\overline{\omega }) }} (1-|x|^2) \in \mathcal {C}^{\infty }(\mathbb {R}^{N}) \quad \text { and } \quad w_n = v_n - \xi _n, \end{aligned}$$

and observe that $w_n$ solves

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta w_n = - \langle B_{\varepsilon _n}(x), \nabla v_n \rangle - a_{\varepsilon _n} (x) v_n - \frac{8N}{3\Vert u_n\Vert _{\mathcal {C}^1(\overline{\omega })}}, \quad &{} \text { in } \omega , \\ w_n = 0, &{} \text { on } \partial \omega . \end{array} \right. \end{aligned}$$

Then, by [19, Lemma 9.17], there exists $C (\omega , N) > 0$ such that

$$\begin{aligned} \Vert w_n\Vert _{W^{2,p}(\omega )} \le C\, \left\| \langle B_{\varepsilon _n}(x), \nabla v_n \rangle + a_{\varepsilon _n} (x) v_n + \frac{8N}{3\Vert u_n\Vert _{\mathcal {C}^1(\overline{\omega })}} \right\| _{L^p(\omega )}, \end{aligned}$$

and so, since $\Vert v_n\Vert _{\mathcal {C}^1(\overline{\omega })} = 1$ for all $n \in \mathbb {N}$, by Lemma A.4, there exists $C_1 = C_1 (\omega , N, \Vert B\Vert _{(L^p(\omega ))^N},$$\Vert a\Vert _{L^p(\omega )}) > 0$ such that

$$\begin{aligned} \Vert w_n\Vert _{W^{2,p}(\omega )} \le C_1.\end{aligned}$$

From the definition of $w_n$, we deduce the existence of $C_2 > 0$ (independent of n) such that

$$\begin{aligned} \Vert v_n\Vert _{W^{2,p}(\omega )} \le C_2.\end{aligned}$$

Since $p > N$, by the Sobolev compact embedding, we have that, up to a subsequence $v_n \rightarrow v$ in $\mathcal {C}^1(\overline{\omega })$ for some $v \in \mathcal {C}^1(\overline{\omega })$. Moreover, by Lemma A.4, we have ${\overline{a}} \in L^p(\omega )$ (resp. ${\overline{B}} \in (L^p(\omega ))^N$) with ${\overline{a}}\ge 0$ such that $a_{\varepsilon _n} \rightharpoonup {\overline{a}}$ weakly in $L^p(\omega )$ (resp. $B_{\varepsilon _n} \rightharpoonup {\overline{B}}$ weakly in $(L^p(\omega ))^N$). This implies that v is a weak solution to

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta v + \langle {\overline{B}}(x), \nabla v \rangle + {\overline{a}}(x) v = 0, \quad &{} \text { in } \omega ,\\ v = 0, &{} \text { on } \partial \omega . \end{array} \right. \end{aligned}$$

By [28, Proposition 3.10], we deduce that $v \equiv 0$. This contradicts the fact that $v_n \rightarrow v$ in $\mathcal {C}^1(\overline{\omega })$ and the result follows. $\square$

Having at hand all the needed ingredients, we prove the Hopf’s Lemma with unbounded lower order terms.

Theorem A.6

(Hopf’s Lemma) For $z \in \mathbb {R}^{N}$ and $R > 0$, let $B \in (L^p(B_R(z))^N$ and $a \in L^p(B_R(z))$ for some $p > N$ such that $a \ge 0$. Let $x_0 \in \partial B_R(z)$ and let $u \in \mathcal {C}^{1}(\overline{B_R(z)})$ be an upper solution to

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u + \langle B(x), \nabla u\rangle + a(x)u = 0, \quad &{} \text { in } B_R(z),\\ u = 0, \quad &{} \text { on } \partial B_R(z), \end{array} \right. \end{aligned}$$

such that $u(x) > u(x_0) = 0$ for all $x \in B_R(z)$. Then $\frac{\partial u}{\partial \nu }(x_0) < 0$, where $\nu$ denotes the exterior unit normal.

Proof

As it is well known, by the change of variable $y = T(x) = \frac{1}{R}(x-z)$, there is no loss of generality to consider the problem on $B_1(0)$ i.e. to assume that $x_0 \in \partial B_1(0)$ and that $u \in \mathcal {C}^{1}(\overline{B_1(0)})$ is an upper solution to

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u + \langle B(x), \nabla u\rangle + a(x)u = 0, \quad &{} \text { in } B_1(0),\\ u = 0, \quad &{} \text { on } \partial B_1(0). \end{array} \right. \end{aligned}$$

(A.6)

Let us fix $\omega := B_1(0) {\setminus } \overline{B_{1/2}(0)}$ and split the proof into several steps:

Step 1 Auxiliary regular barrier $\varphi$

Let us consider the problem

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta \varphi = 0, \quad &{} \text { in } \omega ,\\ \varphi = 0, \quad &{} \text { on } \partial B_1(0),\\ \varphi = 1, \quad &{} \text { on } \partial B_{1/2}(0). \end{array} \right. \end{aligned}$$

(A.7)

By [19, Theorem 6.14] we know that there exists $\varphi \in \mathcal {C}^{2,\tau }(\overline{\omega })$ for some $\tau > 0$ solution to (A.7). Moreover, by [19, Lemma 3.4 and Theorem 3.5], we know that

$$\begin{aligned} 0< \varphi (x)< 1, \quad \forall \ x \in \omega , \quad \text { and } \quad \frac{\partial \varphi }{\partial \nu } (x_0) < 0. \end{aligned}$$

(A.8)

Step 2Let$M > 0$given by LemmaA.5. For every$\varepsilon \in (0,1/4)$there exists$\varphi _{\varepsilon } \in \mathcal {C}^{1,\tau }(\overline{\omega })$for some$\tau > 0$solution to ($P_{\varepsilon }$) such that$\Vert \varphi _{\varepsilon }\Vert _{\mathcal {C}^1(\overline{\omega })} \le M.$

The existence follows from Corollary A.2 and the uniform bound from Lemma A.5.

Step 3Let$\varphi _{\varepsilon }$the solution to ($P_{\varepsilon }$) given by Step 2. There exists$\overline{\varepsilon } \in (0,1/4)$such that, for all$\varepsilon \in (0, \overline{\varepsilon })$, it follows that$\frac{\partial \varphi _{\varepsilon }}{\partial \nu } (x_0) < 0$.

Let us define $\psi _{\varepsilon } := \varphi _{\varepsilon } - \varphi$ and observe that $\psi _{\varepsilon } \in \mathcal {C}^{1,\tau }(\overline{\omega })$ for some $\tau > 0$ solves

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta \psi _{\varepsilon } = - \langle B_{\varepsilon }(x), \nabla \varphi _{\varepsilon } \rangle - a_{\varepsilon }(x) \varphi _{\varepsilon }, \quad &{} \text { in } \omega ,\\ \psi _{\varepsilon } = 0, &{} \text { on } \partial \omega . \end{array} \right. \end{aligned}$$

Then, by [19, Lemma 9.17] and Lemma A.4, there exists $C = C(\omega , N)> 0$ such that

$$\begin{aligned} \begin{aligned} \Vert \psi _{\varepsilon }\Vert _{W^{2,p}(\omega )}&\le C \left\| \langle B_{\varepsilon }(x), \nabla \varphi _{\varepsilon } \rangle + a_{\varepsilon }(x) \varphi _{\varepsilon } \right\| _{L^p(\omega )} \\&\le C \Vert \varphi _{\varepsilon }\Vert _{\mathcal {C}^{1}(\overline{\omega })} \varepsilon ^{1-\frac{N}{p}} \left( \sum _{i=1}^N \Vert B^{i}\Vert _{L^p(\omega )} + \varepsilon \Vert a\Vert _{L^p(\omega )} \right) \\&\le \varepsilon ^{1-\frac{N}{p}} C M \left( \sum _{i=1}^N \Vert B^{i}\Vert _{L^p(\omega )} + \Vert a\Vert _{L^p(\omega )} \right) =: \varepsilon ^{1-\frac{N}{p}} C_2 \end{aligned} \end{aligned}$$

for some $C_2$ independent of $\varepsilon$. Hence, by the Sobolev embedding, there exists $C_3 > 0$ independent of $\varepsilon$ such that

$$\begin{aligned} \Vert \psi _{\varepsilon }\Vert _{\mathcal {C}^{1,\tau }(\overline{\omega })} \le \varepsilon ^{1-\frac{N}{p}} C_3. \end{aligned}$$

We conclude that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} \left| \frac{\partial \varphi _{\varepsilon }}{\partial \nu }(x_0) - \frac{\partial \varphi }{\partial \nu }(x_0) \right| \le \lim _{\varepsilon \rightarrow 0} \Vert \psi _{\varepsilon }\Vert _{\mathcal {C}^{1,\tau }(\overline{\omega })} = 0, \end{aligned}$$

and the Step 3 follows by (A.8).

Step 4 Conclusion

Let $u \in \mathcal {C}^1(\overline{B_1(0))}$ be an upper solution to (A.6) such that $u(x) > u(x_0) = 0$ for all $x \in B_1(0)$. We fix $\varepsilon > 0$ small enough to ensure that the Step 3 holds and define

$$\begin{aligned} u_{\varepsilon }(y) = u( \varepsilon (y-x_0) + x_0). \end{aligned}$$

Since we know that $\omega \subset T(\omega )$ by Lemma A.3, we have that $u_{\varepsilon }$ is an upper solution to

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u_{\varepsilon } + \langle B_{\varepsilon }(x), \nabla u_{\varepsilon } \rangle + a_{\varepsilon }(x) u_{\varepsilon } = 0, \quad &{} \text { in } \omega , \\ u_{\varepsilon } = 0, &{} \text { on } \partial \omega . \end{array} \right. \end{aligned}$$

Then, we define ${\overline{u}}_{\varepsilon } = u_{\varepsilon } - \theta _{\varepsilon } \varphi _{\varepsilon }$ with

$$\begin{aligned} \theta _{\varepsilon } = \inf _{\partial B_{1/2}(0)} u_{\varepsilon } > 0, \end{aligned}$$

and we have that ${\overline{u}}_{\varepsilon }$ is an upper solution to

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta {\overline{u}}_{\varepsilon } + \langle B_{\varepsilon }(x), \nabla {\overline{u}}_{\varepsilon } \rangle + a_{\varepsilon }(x) {\overline{u}}_{\varepsilon } = 0, \quad &{} \text { in } \omega , \\ {\overline{u}}_{\varepsilon } = 0, &{} \text { on } \partial \omega . \end{array} \right. \end{aligned}$$

Applying then [28, Proposition 3.10] we deduce that $u_{\varepsilon } - \theta _{\varepsilon } \varphi _{\varepsilon } \ge 0,$ in $\overline{\omega },$ and so, by Step 3, we conclude that

$$\begin{aligned} \frac{\partial u }{\partial \nu }(x_0) = \frac{1}{\varepsilon } \frac{\partial u_{\varepsilon }}{\partial \nu } (x_0) \le \frac{\theta _{ \varepsilon }}{\varepsilon } \frac{\partial \varphi _{\varepsilon }}{\partial \nu }(x_0) < 0, \end{aligned}$$

as desired. $\square$

Proof of Theorem 2.7

The result follows from Theorem A.6 arguing as in [39, Theorem 3.27]. See also [19, Theorem 3.5]. $\square$