Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-24T18:27:58.346Z Has data issue: false hasContentIssue false
  • English
  • Français

On intrinsic and extrinsic rational approximation to Cantor sets

Part of: Geometry of numbers Diophantine approximation, transcendental number theory Classical measure theory

Published online by Cambridge University Press:  10 February 2020

JOHANNES SCHLEISCHITZ
JOHANNES SCHLEISCHITZ*
Affiliation:
Middle East Technical University, Northern Cyprus Campus, Kalkanli, Güzelyurt, Turkey email johannes.schleischitz@univie.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish various new results on a problem proposed by Mahler [Some suggestions for further research. Bull. Aust. Math. Soc.29 (1984), 101–108] concerning rational approximation to fractal sets by rational numbers inside and outside the set in question. Some of them provide a natural continuation and improvement of recent results of Broderick, Fishman and Reich, and Fishman and Simmons. A key feature is that many of our new results apply to more general, multi-dimensional fractal sets and require only mild assumptions on the iterated function system. Moreover, we provide a non-trivial lower bound for the distance of a rational number 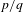$p/q$ outside the Cantor middle-third set 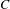$C$ to the set 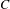$C$, in terms of the denominator $q$. We further discuss patterns of rational numbers in fractal sets. We highlight two of them: firstly, an upper bound for the number of rational (algebraic) numbers in a fractal set up to a given height (and degree) for a wide class of fractal sets; and secondly, we find properties of the denominator structure of rational points in ‘missing-digit’ Cantor sets, generalizing claims of Nagy and Bloshchitsyn.

Keywords

Cantor setsintrinsic/extrinsic Diophantine approximationcontinued fractions

MSC classification

Primary: 28A80: Fractals 11J13: Simultaneous homogeneous approximation, linear forms
Secondary: 11H06: Lattices and convex bodies
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 5 , May 2021 , pp. 1560 - 1589
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Álvarez-Samaniego, B., Álvarez-Samaniego, W. P. and Ortiz-Castro, J.. Some existence results on Cantor sets. J. Egyptian Math. Soc. 25(3) (2017), 326–330.CrossRefGoogle Scholar
Baker, S.. An analogue of Khintchine’s theorem for self-conformal sets. Math. Proc. Cambridge Philos. Soc. 167(3) (2019), 567–597.CrossRefGoogle Scholar
Bloshchitsyn, V. Ya.. Rational points in m-adic Cantor sets. J. Math. Sci. (N.Y.) 211(6) (2015), 747–751.10.1007/s10958-015-2630-zCrossRefGoogle Scholar
Boes, D., Darst, R. and Erdös, P.. Fat, symmetric, irrational Cantor sets. Amer. Math. Monthly 88(5) (1981), 340–341.10.1080/00029890.1981.11995266CrossRefGoogle Scholar
Broderick, R., Fishman, L. and Reich, A.. Intrinsic approximation on Cantor-like sets, a problem of Mahler. Mosc. J. Comb. Number Theory 1(4) (2011), 3–12.Google Scholar
Budarina, N., Dickinson, D. and Levesley, J.. Simultaneous Diophantine approximation on polynomial curves. Mathematika 56(1) (2010), 77–85.CrossRefGoogle Scholar
Bugeaud, Y.. Approximation by Algebraic Numbers (Cambridge Tracts in Mathematics, 160) . Cambridge University Press, Cambridge, 2004.CrossRefGoogle Scholar
Bugeaud, Y.. Diophantine approximation and Cantor sets. Math. Ann. 314 (2008), 677–684.10.1007/s00208-008-0209-4CrossRefGoogle Scholar
Dickinson, D. and Dodson, M. M.. Simultaneous Diophantine approximation on the circle and Hausdorff dimension. Math. Proc. Cambridge Philos. Soc. 130(3) (2001), 515–522.10.1017/S0305004101004984CrossRefGoogle Scholar
Druţu, C.. Diophantine approximation on rational quadrics. Math. Ann. 333(2) (2005), 405–469.CrossRefGoogle Scholar
Falconer, K.. Fractal Geometry, Mathematical Foundations and Applications, 3rd edn. John Wiley, Chichester, 2014.Google Scholar
Fishman, L., Kleinbock, D., Merrill, K. and Simmons, D.. Intrinsic Diophantine approximation on manifolds: general theory. Trans. Amer. Math. Soc. 370(1) (2018), 577–599.10.1090/tran/6971CrossRefGoogle Scholar
Fishman, L. and Simmons, D.. Intrinsic approximation for fractals defined by rational iterated function systems: Mahler’s research suggestion. Proc. Lond. Math. Soc. (3) 109(1) (2014), 189–212.CrossRefGoogle Scholar
Fishman, L. and Simmons, D.. Extrinsic Diophantine approximation on manifolds and fractals. J. Math. Pures Appl. (9) 104(1) (2015), 83–101.10.1016/j.matpur.2015.02.002CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers, 5th edn. Clarendon Press, Oxford, 1979.Google Scholar
Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J. 30(5) (1981), 713–747.CrossRefGoogle Scholar
Jarník, V.. Über die simultanen Diophantischen Approximationen. Math. Z. 33 (1931), 505–543.10.1007/BF01174368CrossRefGoogle Scholar
Khintchine, A. Y.. Über eine Klasse linearer Diophantischer Approximationen. Rend. Palermo 50 (1926), 170–195.CrossRefGoogle Scholar
Levesley, J., Salp, C. and Velani, S. L.. On a problem of K. Mahler: Diophantine approximation and Cantor sets. Math. Ann. 338(1) (2007), 97–118.10.1007/s00208-006-0069-8CrossRefGoogle Scholar
Liebeck, H. and Osborne, A.. The generation of all rational orthogonal matrices. Amer. Math. Monthly 98(2) (1991), 131–133.CrossRefGoogle Scholar
Mahler, K.. Some suggestions for further research. Bull. Aust. Math. Soc. 29 (1984), 101–108.Google Scholar
Marques, D. and Moreira, C. G.. On a variant of a question proposed by K. Mahler concerning Liouville numbers. Bull. Aust. Math. Soc. 91(1) (2015), 29–33.CrossRefGoogle Scholar
Mauldin, R. D. and Urbański, M.. Dimensions and measures in infinite iterated function systems. Proc. Lond. Math. Soc. (3) 73(1) (1996), 105–154.10.1112/plms/s3-73.1.105CrossRefGoogle Scholar
Nagy, J.. Rational points in Cantor sets. Fibonacci Quart. 39(3) (2001), 238–241.Google Scholar
Roy, D. and Schleischitz, J.. Numbers with almost all convergents in a Cantor set. Canad. Math. Bull. 62(4) (2019), 869–875.CrossRefGoogle Scholar
Schleischitz, J.. Generalizations of a result of Jarník on simultaneous approximation. Mosc. J. Comb. Number Theory 6(2–3) (2016), 253–287.Google Scholar
Schleischitz, J.. Rational approximation to algebraic varieties and a new exponent of simultaneous approximation. Monatsh. Math. 182(4) (2017), 941–956.CrossRefGoogle Scholar
Schmidt, W. and Summerer, L.. Parametric geometry of numbers and applications. Acta Arith. 140(1) (2009), 67–91.CrossRefGoogle Scholar
Sidorov, N.. Combinatorics of linear iterated function systems with overlaps. Nonlinearity 20(5) (2007), 1299–1312.CrossRefGoogle Scholar
Wall, C. R.. Terminating decimals in the Cantor ternary set. Fibonacci Quart. 28(2) (1990), 98–101.Google Scholar