Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-23T07:49:19.098Z Has data issue: false hasContentIssue false
  • English
  • Français

The Erdős–Moser Sum-free Set Problem

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  23 September 2019

Tom Sanders
Tom Sanders*
Affiliation:
Mathematical Institute, University of Oxford, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, United Kingdom Email: tom.sanders@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that there is an absolute 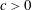$c>0$ such that if 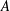$A$ is a finite set of integers, then there is a set 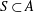$S\subset A$ of size at least 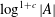$\log ^{1+c}|A|$ such that the restricted sumset 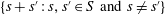$\{s+s^{\prime }:s,s^{\prime }\in S\text{ and }s\neq s^{\prime }\}$ is disjoint from 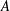$A$. (The logarithm here is to base 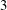$3$.)

Keywords

sum-freesummingFreiman’s theoremadditive energyhereditarily energetic

MSC classification

Primary: 11P70: Inverse problems of additive number theory, including sumsets
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 1 , February 2021 , pp. 63 - 107
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Behrend, F. A., On sets of integers which contain no three terms in arithmetical progression. Proc. Nat. Acad. Sci. USA 32(1946), 331–332. https://doi.org/10.1073/pnas.32.12.331CrossRefGoogle ScholarPubMed
Bloom, T. F., A quantitative improvement for Roth’s theorem on arithmetic progressions. J. Lond. Math. Soc. (2) 93(2016), 643–663. https://doi.org/10.1112/jlms/jdw010CrossRefGoogle Scholar
Bourgain, J., On triples in arithmetic progression. Geom. Funct. Anal. 9(1999), 968–984. https://doi.org/10.1007/s000390050105CrossRefGoogle Scholar
Baltz, A., Schoen, T., and Srivastav, A., Probabilistic construction of small strongly sum-free sets via large Sidon sets. In: Randomization, approximation, and combinatorial optimization. Algorithms and techniques, Berlin, Heidelberg, 1999. Springer, Berlin Heidelberg, 1999, pp. 138–143. https://doi.org/10.1007/978-3-540-48413-4_15.Google Scholar
Baltz, A., Schoen, T., and Srivastav, A., Probabilistic construction of small strongly sum-free sets via large Sidon sets. Colloq. Math. 86(2000), 171–176. https://doi.org/10.4064/cm-86-2-171-176Google Scholar
Bukh, B., Sums of dilates. Combin. Probab. Comput. 17(2008), 627–639. https://doi.org/10.1017/S096354830800919XCrossRefGoogle Scholar
Choi, S. L. G., On a combinatorial problem in number theory. Proc. London Math. Soc. (3) 23(1971), 629–642. https://doi.org/10.1112/plms/s3-23.4.629CrossRefGoogle Scholar
Croot, E. S., Lev, V. F., and Pach, P. P., Progression-free sets in ℤ4n are exponentially small. Ann. of Math. (2) 185(2017), 331–337. https://doi.org/10.4007/annals.2017.185.1.7CrossRefGoogle Scholar
Croot, E. S. and Sisask, O., A probabilistic technique for finding almost-periods of convolutions. Geom. Funct. Anal. 20(2010), 1367–1396. https://doi.org/10.1007/s00039-010-0101-8CrossRefGoogle Scholar
Dousse, J., On a generalisation of Roth’s theorem for arithmetic progressions and applications to sum-free subsets. Math. Proc. Cambridge Philos. Soc. 155(2013), 331–341. https://doi.org/10.1017/S0305004113000327CrossRefGoogle Scholar
Elkin, M., An improved construction of progression-free sets. In: Symposium on Discrete Algorithms. 2010, pp. 886–905. https://doi.org/10.1007/s11856-011-0061-1.Google Scholar
Erdős, P., Extremal problems in number theory. In: Proc. Sympos. Pure Math., Vol. VIII. Amer. Math. Soc., Providence, RI, 1965, pp. 181–189. https://pdfs.semanticscholar.org/6754/29cbb9a130028ce8af5380a0330bb9733d9b.pdf.Google Scholar
Green, B. J., Arithmetic progressions in sumsets. Geom. Funct. Anal. 2(2002), 584–597. https://doi.org/10.1007/s00039-002-8258-4CrossRefGoogle Scholar
Green, B. J., Counting sets with small sumset, and the clique number of random Cayley graphs. Combinatorica 25(2005), 307–326. https://doi.org/10.1007/s00493-005-0018-2CrossRefGoogle Scholar
Green, B. J., Finite field models in additive combinatorics. In: Surveys in combinatorics 2005. London Math. Soc. Lecture Note Ser., 327, Cambridge University Press, Cambridge, 2005, pp. 1–27. https://doi.org/10.1017/CBO9780511734885.002.Google Scholar
Green, B. J., A Szemerédi-type regularity lemma in abelian groups, with applications. Geom. Funct. Anal. 15(2005), 340–376. https://doi.org/10.1007/s00039-005-0509-8CrossRefGoogle Scholar
Green, B. J. and Konyagin, S. V., On the Littlewood problem modulo a prime. Canad. J. Math. 61(2009), 141–164. https://doi.org/10.4153/CJM-2009-007-4CrossRefGoogle Scholar
Green, B. J. and Sanders, T., A quantitative version of the idempotent theorem in harmonic analysis. Ann. of Math. (2) 168(2008), 1025–1054. https://doi.org/10.4007/annals.2008.168.1025CrossRefGoogle Scholar
Green, B. J. and Tao, T. C., An inverse theorem for the Gowers U 3(G) norm. Proc. Edinb. Math. Soc. (2) 51(2008), 73–153. https://doi.org/10.1017/S0013091505000325CrossRefGoogle Scholar
Green, B. J. and Tao, T. C., Linear equations in primes. Ann. of Math. (2) 171(2010), 1753–1850. https://doi.org/10.4007/annals.2010.171.1753CrossRefGoogle Scholar
Green, B. J. and Wolf, J., A note on Elkin’s improvement of Behrend’s construction. In: Additive number theory: Festschrift in honor of the sixtieth birthday of Melvyn B. Nathanson, First ed., Springer-Verlag, 2010, pp. 141–144. https://doi.org/10.1007/978-0-387-68361-4_9.CrossRefGoogle Scholar
Rudin, W., Fourier analysis on groups. Wiley Classics Library. John Wiley & Sons Inc., New York, 1990. https://doi.org/10.1002/9781118165621CrossRefGoogle Scholar
Ruzsa, I. Z., Sum-avoiding subsets. Ramanujan J. 9(2005), 77–82. https://doi.org/10.1007/s11139-005-0826-4CrossRefGoogle Scholar
Schoen, T., Near optimal bounds in Freiman’s theorem. Duke Math. J. 158(2011), 1–12. https://doi.org/10.1215/00127094-1276283CrossRefGoogle Scholar
Shao, X., Finding linear patterns of complexity one. Int. Math. Res. Not. 2015 2311–2327. https://doi.org/10.1093/imrn/rnu004Google Scholar
Shkredov, I. D., On one problem of Gowers. 2004. arxiv:math/0405406.Google Scholar
Shkredov, I. D., On a problem of Gowers. Izv. Ross. Akad. Nauk Ser. Mat. 70(2006), 179–221. https://doi.org/10.1070/IM2006v070n02ABEH002316Google Scholar
Shkredov, I. D., On sets of large trigonometric sums. Izv. Ross. Akad. Nauk Ser. Mat. 72(2008), 161–182. https://doi.org/10.1070/IM2008v072n01ABEH002396Google Scholar
Sudakov, B., Szemerédi, E., and Vu, V. H., On a question of Erdős and Moser. Duke Math. J. 129(2005), 129–155. https://doi.org/10.1215/S0012-7094-04-12915-XCrossRefGoogle Scholar
Tao, T. C. and Vu, V. H., Additive combinatorics. Cambridge Studies in Advanced Mathematics, 105, Cambridge University Press, Cambridge, 2006. https://doi.org/10.1017/CBO9780511755149CrossRefGoogle Scholar
Tao, T. C. and Vu, V. H., Sum-avoiding sets in groups. Discrete Anal. 31(2016), Paper No. 15. https://doi.org/10.19086/da.887.Google Scholar
Tao, T. C. and Vu, V. H., Sum-free sets in groups: a survey. J. Comb. 8(2017), 541–552. https://doi.org/10.4310/JOC.2017.v8.n3.a7Google Scholar
Wolf, J., Finite field models in arithmetic combinatorics—ten years on. Finite Fields Appl. 32(2015), 233–274. https://doi.org/10.1016/j.ffa.2014.11.003CrossRefGoogle Scholar