Abstract
This is the second part of a series of three strongly related papers in which three equivalent structures are studied:
Internal categories in categories of monoids; defined in terms of pullbacks relative to a chosen class of spans.
Crossed modules of monoids relative to this class of spans.
Simplicial monoids of so-called Moore length 1 relative to this class of spans.
The most important examples of monoids that are covered are small categories (treated as monoids in categories of spans) and bimonoids in symmetric monoidal categories (regarded as monoids in categories of comonoids). In this second part we define relative crossed modules of monoids and prove their equivalence with the relative categories of Part I.
Similar content being viewed by others
1 Introduction
Since their appearance in [25], crossed modules of groups have been intensively studied and applied in various contexts; see e.g. the reviews [19, 21, 22] and the references in them. They admit several different descriptions: a simplicial group whose Moore complex is concentrated in degrees 1 and 2 turns out to be the internal nerve of an internal category in the category of groups (which is necessarily an internal groupoid, a.k.a. strict 2-group or \(\mathsf {Cat} ^1\)-group) and the Moore complex yields a crossed module. These constructions establish, in fact, equivalences between these three notions.
The first (to our knowledge) proofs of the equivalence between crossed modules and strict 2-groups can be found in [6]—where it is referred also to the unpublished proof [7]—and in [17]. Based on the fact that groups constitute a semi-abelian category in the sense of [15], another short and deeply conceptual proof is due to Janelidze [14]. It also leads to a broad generalization describing the equivalent notions of crossed modules and internal categories of all of Lie algebras, \(\Omega \)-groups in the sense of [13], Heyting semi-lattices, the dual of the category of pointed sets and much more. Thus by working in an arbitrary semi-abelian category, not only a more transparent proof is obtained, but also a much wider generality, also unifying earlier results in [16, 23].
More recently, however, some results on, and certain applications of crossed modules of groups were extended to crossed modules of ordinary monoids [20], groupoids [5] and of Hopf algebras [1, 8, 9, 18, 25]. From this list only cocommutative Hopf algebras over a field are known to constitute a semi-abelian category [11, 12]. Hence Janelidze’s proof can not be applied directly to the rest of these generalizations. Our aim is therefore to develop a wider theory of crossed modules of monoids in more general monoidal categories which are not expected to have all pullbacks (not even along split epimorphisms). We have the above two main examples in mind:
Categories of spans whose monoids are small categories, including groupoids in particular.
Categories of comonoids in symmetric monoidal categories whose monoids are bimonoids including Hopf monoids in particular.
In the first part [3] of this series of papers we discussed classes of spans satisfying appropriate conditions; and relative pullbacks with respect to them. Assuming that such pullbacks exist—as they do in our key examples—we introduced a monoidal category with monoidal product provided by these pullbacks. We defined a relative (to the chosen class of spans) category as a monoid in this monoidal category. It is given by the usual data

where  is now a relative pullback.
is now a relative pullback.
In the current article we make the next step and prove the equivalence of the following categories for a fixed class of suitable spans in a monoidal category:
The category of relative categories in the category of monoids,
The category of relative crossed modules of monoids.
Our methodology is inspired by Janelidze’s paper [14]. In Sect. 1 we investigate first some category of the category of split epimorphisms of monoids. We obtain an equivalent description of a split epimorphism of monoids  in terms of a distributive law which allows for handy characterizations of possible morphisms t and d in (\(*\)). This is used in Sects. 2 and 3, respectively, to present equivalent descriptions of some reflexive graphs of monoids in terms of relative pre-crossed modules of monoids; and of relative category objects (\(*\)) in categories of monoids in terms of relative crossed modules of monoids. Applying our results to categories of spans and to categories of comonoids, respectively, we re-obtain the definitions of crossed modules of groupoids in [5] and of crossed modules of Hopf monoids in [25], respectively.
in terms of a distributive law which allows for handy characterizations of possible morphisms t and d in (\(*\)). This is used in Sects. 2 and 3, respectively, to present equivalent descriptions of some reflexive graphs of monoids in terms of relative pre-crossed modules of monoids; and of relative category objects (\(*\)) in categories of monoids in terms of relative crossed modules of monoids. Applying our results to categories of spans and to categories of comonoids, respectively, we re-obtain the definitions of crossed modules of groupoids in [5] and of crossed modules of Hopf monoids in [25], respectively.
Our next aim is to extend to our setting the equivalence of the category of strict 2-groups (that is, internal groupoids in the category of groups) and the category of crossed modules of groups to the further category of simplicial groups whose Moore complex has length 1. This will be achieved in Part III of this series [2].
2 Split Epimorphisms of Monoids Versus Distributive Laws
We freely use definitions, notation and results from [3]. Throughout, the composition of some morphisms  and
and  in an arbitrary category will be denoted by
in an arbitrary category will be denoted by  . Identity morphisms will be denoted by 1 (without any reference to the (co)domain object if it causes no confusion). In any monoidal category \(\mathsf C\) the monoidal product will be denoted by juxtaposition and the monoidal unit will be I. For the monoidal product of n copies of the same object A also the power notation \(A^n\) will be used. For any monoid A in \({\mathsf {C} }\), the multiplication and the unit morphisms will be denoted by
. Identity morphisms will be denoted by 1 (without any reference to the (co)domain object if it causes no confusion). In any monoidal category \(\mathsf C\) the monoidal product will be denoted by juxtaposition and the monoidal unit will be I. For the monoidal product of n copies of the same object A also the power notation \(A^n\) will be used. For any monoid A in \({\mathsf {C} }\), the multiplication and the unit morphisms will be denoted by  and
and  , respectively. If \({\mathsf {C} }\) is also braided, then for the braiding the symbol c will be used.
, respectively. If \({\mathsf {C} }\) is also braided, then for the braiding the symbol c will be used.
Recall that a class \({\mathcal {S}}\) of spans in an arbitrary category is said to be admissible if it satisfies the following two properties in [3, Definition 2.1].
- (POST)
If
 then
then  too, for any morphisms
too, for any morphisms 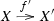 and
and  .
. - (PRE)
If
 then
then  , for any morphism
, for any morphism  .
.
The relative pullback of a cospan  with respect to such a class \(\mathcal S\) was introduced in [3, Definition 3.1] as a span
with respect to such a class \(\mathcal S\) was introduced in [3, Definition 3.1] as a span  in \({\mathcal {S}}\) satisfying the following properties.
in \({\mathcal {S}}\) satisfying the following properties.
Commutativity of the diagram

Universality. For any
 such that \(f\cdot f'=g\cdot g'\), there is a unique morphism
such that \(f\cdot f'=g\cdot g'\), there is a unique morphism  which satisfies \(p_A \cdot h =f'\) and \(p_C \cdot h =g'\).
which satisfies \(p_A \cdot h =f'\) and \(p_C \cdot h =g'\).Reflection. If both

belong to \({\mathcal {S}}\) then also
 belongs to \({\mathcal {S}}\); and symmetrically, if
belongs to \({\mathcal {S}}\); and symmetrically, if 
belong to \({\mathcal {S}}\) then also
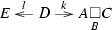 belongs to \({\mathcal {S}}\).
belongs to \({\mathcal {S}}\).
As in [3, Definition 2.10], we say that a cospan  has legs in a class \({\mathcal {S}}\) of spans if
has legs in a class \({\mathcal {S}}\) of spans if  and
and  belong to \({\mathcal {S}}\). [3, Assumption 4.1] asserts that there exists the \({\mathcal {S}}\)-relative pullback of those cospans whose legs are in an admissible class \({\mathcal {S}}\). Under this assumption it was proven in [3, Corollary 4.6] that for any object B for which
belong to \({\mathcal {S}}\). [3, Assumption 4.1] asserts that there exists the \({\mathcal {S}}\)-relative pullback of those cospans whose legs are in an admissible class \({\mathcal {S}}\). Under this assumption it was proven in [3, Corollary 4.6] that for any object B for which  , those spans
, those spans  over B whose legs
over B whose legs  and
and  are in \({\mathcal {S}}\), constitute a monoidal category with the monoidal product given by the \({\mathcal {S}}\)-relative pullback over B. An \({\mathcal {S}}\)-relative category (with object of objects B) is defined in [3, Definition 4.9] as a monoid therein. Explicitly, this means morphisms
are in \({\mathcal {S}}\), constitute a monoidal category with the monoidal product given by the \({\mathcal {S}}\)-relative pullback over B. An \({\mathcal {S}}\)-relative category (with object of objects B) is defined in [3, Definition 4.9] as a monoid therein. Explicitly, this means morphisms

subject to the following axioms.
The legs of
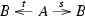 are in \({\mathcal {S}}\) (so that its \({\mathcal {S}}\)-relative pullback denoted by
are in \({\mathcal {S}}\) (so that its \({\mathcal {S}}\)-relative pullback denoted by  exists).
exists).i is a common section of s and t (that is,
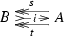 is a reflexive graph).
is a reflexive graph).\(t\cdot d=t\cdot p_1\) and \(s\cdot d=s\cdot p_2\).
\(d\cdot (i\,\Box \,1)=1=d\cdot (1\,\Box \,i)\).
\(d\cdot (d\,\Box \,1)=d\cdot (1\,\Box \,d)\).
A class \({{\mathcal {S}}}\) of spans in a monoidal category is said to be monoidal if it satisfies the following two conditions in [3, Definition 2.5].
- (UNITAL)
For any morphisms f and g whose domain is the monoidal unit I,
 .
. - (MULTIPLICATIVE)
If both
 and
and  then also
then also 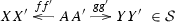 .
.
It is discussed in [3, Example 2.8] that a monoidal admissible class \({\mathcal {S}}\) of spans in a braided monoidal category \({\mathsf {C} }\) induces a monoidal admissible class of spans in the category of monoids in \({\mathsf {C} }\); and it is shown in [3, Example 4.4] that if \({\mathcal {S}}\) satisfies [3, Assumption 4.1] then so does the induced class in the category of monoids. This allows for the discussion of \(\mathcal S\)-relative categories in the category of monoids.
In this paper we will be interested mainly in these relative categories of monoids. They contain, in particular, a split epimorphism of monoids (consisting of the morphisms i and s of (\(*\)) in the Introduction). So we start with the analysis of the following category of split epimorphisms of monoids.
Theorem 1.1
Consider a monoidal admissible class \({\mathcal {S}}\) of spans in a monoidal category \({\mathsf {C} }\) for which [3, Assumption 4.1] holds. The following categories are equivalent.
\(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) are split epimorphisms
 of monoids in \({\mathsf {C} }\) subject to the following conditions.
of monoids in \({\mathsf {C} }\) subject to the following conditions. - (a):
 ; so that by the unitality of \({\mathcal {S}}\) and [3, Assumption 4.1], there exists the \(\mathcal S\)-relative pullback
; so that by the unitality of \({\mathcal {S}}\) and [3, Assumption 4.1], there exists the \(\mathcal S\)-relative pullback 
- (b):
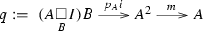 is invertible.
is invertible.
\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms
 such that \(s'\cdot a=b\cdot s\) and \(i'\cdot b=a\cdot i\).
such that \(s'\cdot a=b\cdot s\) and \(i'\cdot b=a\cdot i\).\(\mathsf {DistLaw} _{{\mathcal {S}}}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) consist of monoids B and Y, a monoid morphism
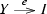 and a distributive law
and a distributive law  subject to the following conditions.
subject to the following conditions. - (a\(^\prime \)):
 and
and  . Then by the monoidality of \({\mathcal {S}}\) also
. Then by the monoidality of \({\mathcal {S}}\) also 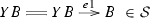 so by [3, Assumption 4.1] there exists the \({\mathcal {S}}\)-relative pullback
so by [3, Assumption 4.1] there exists the \({\mathcal {S}}\)-relative pullback  in the diagram below.
in the diagram below.- (b\(^\prime \)):
\(e1\cdot x=1e\).
- (c\(^\prime \)):
The morphism f occurring in the diagram below is invertible. (It is well-defined since by (a’) and condition (POST) in [3, Definition 2.1],
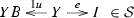 .)
.) 
\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms
 such that \(e'\cdot y=e\) and \(x'\cdot by=yb\cdot x\).
such that \(e'\cdot y=e\) and \(x'\cdot by=yb\cdot x\).
Proof
We prove the theorem by constructing mutually inverse equivalence functors. The first one \(\mathsf {SplitEpiMon} _{{\mathcal {S}}}(\mathsf C) \rightarrow \mathsf {DistLaw} _{{\mathcal {S}}}({\mathsf {C} })\) sends

Let us see that the object map is meaningful. By construction B is a monoid and  is a monoid morphism. By [3, Proposition 3.7 (1)]
is a monoid morphism. By [3, Proposition 3.7 (1)]  is a monoid and
is a monoid and  is a monoid morphism. By [3, Lemma 1.5]
is a monoid morphism. By [3, Lemma 1.5]  is a distributive law. Concerning property (a’),
is a distributive law. Concerning property (a’),  by the unitality of \({\mathcal {S}}\); hence by [3, Lemma 3.4 (2)]
by the unitality of \({\mathcal {S}}\); hence by [3, Lemma 3.4 (2)]  . By [3, Lemma 2.4 (1)]Footnote 1 also
. By [3, Lemma 2.4 (1)]Footnote 1 also  belongs to \( {\mathcal {S}}\). Condition (b’) holds since commutativity of the first diagram of
belongs to \( {\mathcal {S}}\). Condition (b’) holds since commutativity of the first diagram of

implies the commutativity of the second diagram. For condition (c’) observe that by the unitality of the monoid morphism i the equality \(q\cdot 1u= p_A\) holds, equivalently, \(q^{-1}\cdot p_A=1u\). With this identity in mind we see that the morphism f of condition (c’) is equal to \(q^{-1}\,\Box \,1\) in the first diagram of

Then by [3, Proposition 3.5 (2)] it is invertible with the inverse \(q\,\Box \,1\) in the second diagram. Both morphisms \(q^{-1}\,\Box \,1\) and \(q\,\Box \,1\) are well-defined by the commutativity of the first diagram of (1.1); see [3, Proposition 3.5 (1)]. This proves that the object map of our candidate functor is meaningful.
Concerning the morphism map, \(a\,\Box \,1\) is a well-defined morphism in \({\mathsf {C} }\) by the assumption that \(b\cdot s=s'\cdot a\) (see [3, Proposition 3.5 (1)]) and it is a monoid morphism by [3, Proposition 3.7 (2)]. Condition \(p_I\cdot (a\,\Box \,1)=p_I\) holds by construction and the other equality holds since the commutativity of the first diagram of

implies the commutativity of the second diagram.
In the opposite direction \(\mathsf {DistLaw} _{{\mathcal {S}}}({\mathsf {C} }) \rightarrow \mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\) we define a functor sending

Here YB is considered with the monoid structure induced by the distributive law x, see [3, Lemma 1.4]. Then  is a monoid morphism by [3, Lemma 1.4] again. By [3, Lemma 1.6] condition (b’) implies that
is a monoid morphism by [3, Lemma 1.4] again. By [3, Lemma 1.6] condition (b’) implies that  is a monoid morphism too. (For a more direct proof consider the commutative diagrams
is a monoid morphism too. (For a more direct proof consider the commutative diagrams

whose unlabelled regions commute since \(e:Y \rightarrow I\) is a monoid morphism.) The rows are split epimorphisms (of monoids) by the unitality of the monoid morphism e. By (a’) and the multiplicativity of \({\mathcal {S}}\),  so that condition (a) holds. For condition (b) note that the commutativity of
so that condition (a) holds. For condition (b) note that the commutativity of

implies that the bottom row is the inverse of the isomorphism f1 in the left column hence it is invertible. This proves that the object map is well defined.
Concerning the morphism map, it follows by the assumption \(yb\cdot x=x'\cdot by\) that yb is a monoid morphism, see

The monoid morphisms (b, yb) are compatible with the monomorphisms  and
and  by the unitality of y, and they are compatible with the epimorphisms
by the unitality of y, and they are compatible with the epimorphisms  and
and  by the assumption that \(e'\cdot y=e\).
by the assumption that \(e'\cdot y=e\).
So we have well-defined functors in both directions, it remains to see that their composites are naturally isomorphic to the identity functors. The composite
acts as

We claim that a natural isomorphism from this to the identity functor has the components  ,
,  . Since \(p_A\) is a monoid morphism by [3, Proposition 3.7 (1)], so is q by [3, Lemma 1.5]. The stated pair (1, q) is a morphism in \(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\) by the commutativity of the first diagram of (1.1) and by the fact that the unitality of \(p_A\) implies \(q\cdot 1u=i\). Naturality with respect to any morphism
. Since \(p_A\) is a monoid morphism by [3, Proposition 3.7 (1)], so is q by [3, Lemma 1.5]. The stated pair (1, q) is a morphism in \(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\) by the commutativity of the first diagram of (1.1) and by the fact that the unitality of \(p_A\) implies \(q\cdot 1u=i\). Naturality with respect to any morphism  in \(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\) follows by the commutativity of the first diagram of (1.2).
in \(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\) follows by the commutativity of the first diagram of (1.2).
Composing our functors in the opposite order
we obtain the functor sending

to

We claim that a natural isomorphism from this to the identity functor has the invertible components  . By construction f is a monoid morphism, see [3, Proposition 3.7 (2)]. The compatibility of the monoid morphisms (1, f) with
. By construction f is a monoid morphism, see [3, Proposition 3.7 (2)]. The compatibility of the monoid morphisms (1, f) with  and
and  holds by the definition of f and the compatibility with the distributive laws \(BY \rightarrow YB\) and
holds by the definition of f and the compatibility with the distributive laws \(BY \rightarrow YB\) and  holds by the commutativity of
holds by the commutativity of

Finally, the naturality with respect to an arbitrary morphism  in \(\mathsf {DistLaw} _{{\mathcal {S}}}({\mathsf {C} })\) follows by the commutativity of the diagrams
in \(\mathsf {DistLaw} _{{\mathcal {S}}}({\mathsf {C} })\) follows by the commutativity of the diagrams

using that the morphisms  are jointly monic in \({\mathsf {C} }\). \(\square \)
are jointly monic in \({\mathsf {C} }\). \(\square \)
Example 1.2
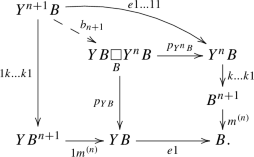
For any fixed set X, the category \({\mathsf {C} }\) of spans over X is monoidal via the pullback over X. A monoid in \({\mathsf {C} }\) is a small category with the object set X and a monoid morphism is a functor acting on the objects as the identity map. Moreover, \({\mathsf {C} }\) has all pullbacks (computed in the underlying category of sets). So taking as \({\mathcal {S}}\) the class of all spans in \({\mathsf {C} }\), from Theorem 1.1 we obtain the equivalence of the following categories (from now on we shall denote by s the source map and by t the target map of any category).
\(\mathsf {SplitEpiMon} ({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) are pairs of identity-on-objects functors
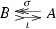 between categories of the common object set X such that the composite \(\sigma \iota \) is the identity functor, and the map
between categories of the common object set X such that the composite \(\sigma \iota \) is the identity functor, and the map 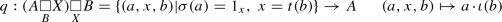 (1.3)
(1.3)is invertible. (The map of (1.3) is invertible e.g. if B is a groupoid; then its inverse takes a morphism a to \((a\cdot \iota (\sigma (a)^{-1}), t(a),\sigma (a))\). )
\({\underline{\text {morphisms}}}\) are pairs of identity-on-objects functors
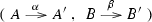 for which \(\alpha \iota =\iota '\beta \) and \(\beta \sigma =\sigma '\alpha \).
for which \(\alpha \iota =\iota '\beta \) and \(\beta \sigma =\sigma '\alpha \).\(\mathsf {DistLaw} ({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) consist of categories B and Y with the common object set X such that Y has no morphisms between non-equal objects (that is, its source map s and target map t coincide; using the terminology of [4] this means that Y is a totally disconnected category); and an action
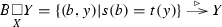 in the sense of [5, Definition 1.1]; meaning the following axioms for all morphisms \(b,b'\) in B and \(y,y'\) in Y for which \(s(b')=t(b)\) and \(s(b)=t(y)=s(y)=t(y')=s(y')\).
in the sense of [5, Definition 1.1]; meaning the following axioms for all morphisms \(b,b'\) in B and \(y,y'\) in Y for which \(s(b')=t(b)\) and \(s(b)=t(y)=s(y)=t(y')=s(y')\). - (i)
\(t(b\triangleright y)=t(b)\)
- (ii)
\(b\triangleright (y\cdot y')=(b\triangleright y)\cdot (b\triangleright y')\) and \(b\triangleright 1_{s(b)}=1_{t(b)}\)
- (iii)
\((b'\cdot b)\triangleright y = b'\triangleright (b\triangleright y)\) and \(1_{t(y)}\triangleright y =y\).
\({\underline{\text {morphisms}}}\) are pairs of identity-on-objects functors
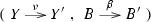 for which \(\nu (b\triangleright y)=\beta (b)\triangleright \nu (y)\) for all morphisms b in B and y in Y for which \(s(b)=t(y)\).
for which \(\nu (b\triangleright y)=\beta (b)\triangleright \nu (y)\) for all morphisms b in B and y in Y for which \(s(b)=t(y)\).- (i)
Only the above description of an object in \(\mathsf {DistLaw} (\mathsf C)\) requires some explanation.
The monoidal unit of \({\mathsf {C} }\) is the trivial span  . Its trivial monoid structure yields the discrete category \({\mathsf {D} } (X)\). An identity-on-objects functor
. Its trivial monoid structure yields the discrete category \({\mathsf {D} } (X)\). An identity-on-objects functor  as in Theorem 1.1 exists if and only if Y is totally disconnected. Then there is precisely one such functor sending any morphism to the identity morphism on its equal source and target objects. For this functor e, precisely those maps
as in Theorem 1.1 exists if and only if Y is totally disconnected. Then there is precisely one such functor sending any morphism to the identity morphism on its equal source and target objects. For this functor e, precisely those maps  satisfy \((e\,\Box \,1)\cdot x=1\,\Box \,e\) which are of the form \((b,y)\mapsto (b\triangleright y,b)\) in terms of some map \(\triangleright \) obeying condition (i). It is straightforward to see that x is then a distributive law if and only if conditions (ii) and (iii) hold.
satisfy \((e\,\Box \,1)\cdot x=1\,\Box \,e\) which are of the form \((b,y)\mapsto (b\triangleright y,b)\) in terms of some map \(\triangleright \) obeying condition (i). It is straightforward to see that x is then a distributive law if and only if conditions (ii) and (iii) hold.
The morphism f of Theorem 1.1 (c’) is invertible because the diagram

is clearly a pullback of X-spans for any span morphism g.
Example 1.3
Let \({\mathsf {M} }\) be a symmetric monoidal category in which equalizers exist and are preserved by taking the monoidal product with any object.
Take \({\mathsf {C} }\) to be the category of comonoids in \({\mathsf {M} }\) with the monoidal admissible class \({\mathcal {S}}\) in [3, Example 2.3] of spans in \({\mathsf {C} }\). This means that  belongs to \({\mathcal {S}}\) if and only if
belongs to \({\mathcal {S}}\) if and only if  is a comonoid morphism, which holds if and only if \(c\cdot fg \cdot \delta =gf\cdot \delta \). Thanks to the symmetry of \({\mathsf {M} }\), its monoidal structure is inherited by \({\mathsf {C} }\). A monoid A in \({\mathsf {C} }\) is known as a bimonoid in \({\mathsf {M} }\). Recall that the monoidal structure of \({\mathsf {M} }\) is lifted to the category of (left or right) modules over the monoid A in \({\mathsf {M} }\). A monoid (respectively, a comonoid) in the category of A-modules is known as an A-module monoid (respectively, A-module comonoid).
is a comonoid morphism, which holds if and only if \(c\cdot fg \cdot \delta =gf\cdot \delta \). Thanks to the symmetry of \({\mathsf {M} }\), its monoidal structure is inherited by \({\mathsf {C} }\). A monoid A in \({\mathsf {C} }\) is known as a bimonoid in \({\mathsf {M} }\). Recall that the monoidal structure of \({\mathsf {M} }\) is lifted to the category of (left or right) modules over the monoid A in \({\mathsf {M} }\). A monoid (respectively, a comonoid) in the category of A-modules is known as an A-module monoid (respectively, A-module comonoid).
Recall from [3, Example 3.3] that for a cospan  of comonoids whose legs are in \({\mathcal {S}}\), the \({\mathcal {S}}\)-relative pullback is given by the so-called cotensor product, defined as the equalizer
of comonoids whose legs are in \({\mathcal {S}}\), the \({\mathcal {S}}\)-relative pullback is given by the so-called cotensor product, defined as the equalizer

in \({\mathsf {M} }\) (where \(\delta \) denotes both comultiplications of the comonoids A and C.)
Below we describe the equivalent categories of Theorem 1.1 in this context.
\(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) are split epimorphisms
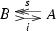 of bimonoids in \({\mathsf {M} }\) subject to the following conditions.
of bimonoids in \({\mathsf {M} }\) subject to the following conditions. - (a)
The comultiplication \(\delta \) of A satisfies \(c\cdot 1s\cdot \delta =s1\cdot \delta \).
- (b)
In terms of the morphism j of (1.5),
 is invertible.
is invertible.
\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms which are compatible with the epimorphisms s as well as their sections i.
- (a)
\(\mathsf {DistLaw} _{{\mathcal {S}}}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) consist of a cocommutative bimonoid B and a bimonoid Y in \({\mathsf {M} }\), together with a left B-action on Y which makes Y both a left B-module monoid and a left B-module comonoid.
\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms
 which are compatible with the actions
which are compatible with the actions 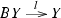 and
and 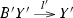 in the sense that \(l'\cdot by=y\cdot l\).
in the sense that \(l'\cdot by=y\cdot l\).
This concise description of \(\mathsf {DistLaw} _{{\mathcal {S}}}(\mathsf C)\) requires a proof. Note that the monoidal unit I is now a terminal object in \({\mathsf {C} }\); the unique morphism \(Y \rightarrow I\) is the counit \(\varepsilon \). It obviously satisfies  . The other condition
. The other condition  in (a’) of Theorem 1.1 reduces to the requirement that the comonoid B is cocommutative.
in (a’) of Theorem 1.1 reduces to the requirement that the comonoid B is cocommutative.
Next we establish a bijective correspondence between distributive laws \(BY \rightarrow YB\) satisfying property (b’) of Theorem 1.1 and left actions \(BY\rightarrow Y\) as in the description above. Starting with a distributive law  , put \(l:=1\varepsilon \cdot x\). It is a unital action by the left unitality of x and it is associative by the left multiplicativity of x:
, put \(l:=1\varepsilon \cdot x\). It is a unital action by the left unitality of x and it is associative by the left multiplicativity of x:

By the right unitality of x the unit  is a morphism of B-modules and by the right multiplicativity of x the multiplication
is a morphism of B-modules and by the right multiplicativity of x the multiplication  is a morphism of B-modules:
is a morphism of B-modules:

(note that here we also used the comultiplicativity of x). The condition that the counit  is a morphism of B-modules coincides with the counitality of l and also with the counitality of x. The comultiplication
is a morphism of B-modules coincides with the counitality of l and also with the counitality of x. The comultiplication  is a morphism of B-modules, equivalently, l is comultiplicative by the comultiplicativity of x:
is a morphism of B-modules, equivalently, l is comultiplicative by the comultiplicativity of x:

Conversely, given an action l as above, put  It clearly satisfies (b\(^\prime \)) by the counitality of l hence it is counital. It is comultiplicative by the comultiplicativity of l:
It clearly satisfies (b\(^\prime \)) by the counitality of l hence it is counital. It is comultiplicative by the comultiplicativity of l:

where the top-left region commutes by the coassociativity and cocommutativity of the comonoid B. This morphism x is a distributive law. Indeed, the left unitality and the left multiplicativity follow by the unitality and the associativity of the action l, respectively:

and the right unitality and the right multiplicativity of x follow using that the unit and the multiplication of Y are B-module morphisms:

The above correspondences between l and x are bijective by the commutativity of

for a comultiplicative morphism x satisfying (b’) and any morphism l.
Finally, we show that the morphism  in part (c’) of Theorem 1.1 is invertible without any further assumption; its inverse is constructed as
in part (c’) of Theorem 1.1 is invertible without any further assumption; its inverse is constructed as  . In order to see that it is the inverse, indeed, recall that by [3, Example 3.3] the morphism \(p_{YB}\) is the equalizer of
. In order to see that it is the inverse, indeed, recall that by [3, Example 3.3] the morphism \(p_{YB}\) is the equalizer of  and
and  . Hence the following diagrams commute.
. Hence the following diagrams commute.

This completes the characterization of the objects of \(\mathsf {DistLaw} _{{\mathcal {S}}}({\mathsf {C} })\). Concerning the morphisms  , the first condition in Theorem 1.1 is the counitality of the bimonoid morphism y hence it identically holds. The second condition in Theorem 1.1 is equivalent to \(y\cdot l=l'\cdot by\) by the commutativity of
, the first condition in Theorem 1.1 is the counitality of the bimonoid morphism y hence it identically holds. The second condition in Theorem 1.1 is equivalent to \(y\cdot l=l'\cdot by\) by the commutativity of

Example 1.4
We can apply Example 1.3 to the particular case of a finitely complete category \({\mathsf {M} }\) regarded with the cartesian monoidal structure. Then the category \({\mathsf {C} }\) of comonoids in \({\mathsf {M} }\) is isomorphic to \({\mathsf {M} }\).
Since in this case the monoidal unit I of \({\mathsf {M} }\) is a terminal object, with the trivial monoid structure it becomes the zero object in the category of monoids in \({\mathsf {M} }\). Then for any morphism  of monoids in \({\mathsf {M} }\), we may identify
of monoids in \({\mathsf {M} }\), we may identify  with the kernel of s.
with the kernel of s.
The equivalent categories of Theorem 1.1 reduce to the following ones.
\(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {M} })\) whose
\({\underline{\text {objects}}}\) are split epimorphisms
 of monoids in \({\mathsf {M} }\) such that in terms of the morphism j of (1.5),
of monoids in \({\mathsf {M} }\) such that in terms of the morphism j of (1.5),  is invertible.
is invertible.\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms which are compatible with the epimorphisms s as well as their sections i.
\(\mathsf {DistLaw} _{{\mathcal {S}}}({\mathsf {M} })\) whose
\({\underline{\text {objects}}}\) consist of monoids B and Y in \({\mathsf {M} }\), together with a left B-action on Y which makes the multiplication and the unit of the monoid Y left B-linear.
\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms
 which are compatible with the actions
which are compatible with the actions 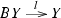 and
and  in the sense that \(l'\cdot by=y\cdot l\).
in the sense that \(l'\cdot by=y\cdot l\).
In particular, if \({\mathsf {M} }\) is the cartesian monoidal category of sets, then the morphism q in the above description of the objects of \(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {M} })\) is invertible if and only if  satisfies the Schreier property of [20]. That is, for each element a of A, there is a unique element \(z_a\) in the kernel of s such that \(a=z_a\cdot is(a)\). (Indeed, this condition clearly implies the surjectivity of q. For its injectivity assume \(z\cdot i(b)=z'\cdot i(b')\) for some \(z,z'\) in the kernel of s and \(b,b'\) in B. Applying the monoid morphism s we obtain \(b=b'\). From
satisfies the Schreier property of [20]. That is, for each element a of A, there is a unique element \(z_a\) in the kernel of s such that \(a=z_a\cdot is(a)\). (Indeed, this condition clearly implies the surjectivity of q. For its injectivity assume \(z\cdot i(b)=z'\cdot i(b')\) for some \(z,z'\) in the kernel of s and \(b,b'\) in B. Applying the monoid morphism s we obtain \(b=b'\). From
and the uniqueness part of the Schreier property we infer \(z=z'\). Conversely, if q is invertible then its inverse \(a\mapsto (z_a,s(a))\) defines the required element \(z_a\) of the kernel.) On the other hand, in this case an object of \(\mathsf {DistLaw} _{{\mathcal {S}}}({\mathsf {M} })\) reduces to a monoid morphism from B to the monoid of monoid endomorphisms of Y.
Recall that a bimonoid B—with monoid structure (m, u) and comonoid structure \((\delta ,\varepsilon )\)—is a Hopf monoid provided that there exists a morphism  —the so-called antipode—which renders commutative the diagram
—the so-called antipode—which renders commutative the diagram

If the antipode exists then it is unique. It is a monoid morphism from B to the monoid with the opposite multiplication \(m\cdot c\) and comonoid morphism from B to the comonoid with the opposite comultiplication \(c\cdot \delta \).
Proposition 1.5
-
(1)
The equivalent categories of Example 1.3 have equivalent full subcategories as follows.
The category whose
\({\underline{\text {objects}}}\) are split epimorphisms
 of bimonoids in \({\mathsf {M} }\) subject to the following conditions.
of bimonoids in \({\mathsf {M} }\) subject to the following conditions. - (a)
The comultiplication \(\delta \) of A satisfies \(c\cdot 1s \cdot \delta =s1 \cdot \delta \).
- (b)
B is a Hopf monoid.
\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms which are compatible with the epimorphisms s as well as their sections i.
- (a)
The category whose
\({\underline{\text {objects}}}\) consist of a cocommutative Hopf monoid B and a bimonoid Y in \({\mathsf {M} }\), together with a left B-action on Y which makes Y both a left B-module monoid and a left B-module comonoid.
\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms
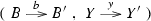 which are compatible with the actions
which are compatible with the actions  and
and  in the sense that \(l'\cdot by=y\cdot l\).
in the sense that \(l'\cdot by=y\cdot l\).
-
(2)
The equivalent categories of part (1) have equivalent full subcategories as follows.
The category whose
\({\underline{\text {objects}}}\) are split epimorphisms
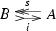 of cocommutative Hopf monoids.
of cocommutative Hopf monoids.\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms which are compatible with the epimorphisms s as well as their sections i.
The category whose
\({\underline{\text {objects}}}\) consist of cocommutative Hopf monoids B and Y in \({\mathsf {M} }\), together with a left B-action on Y which makes Y both a left B-module monoid and a left B-module comonoid.
\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms
 which are compatible with the actions
which are compatible with the actions 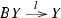 and
and  in the sense that \(l'\cdot by=y\cdot l\).
in the sense that \(l'\cdot by=y\cdot l\).
Proof
(1) The second listed category is obviously a full subcategory of \(\mathsf {DistLaw} _{{\mathcal {S}}}({\mathsf {C} })\) of Example 1.3; thus via the equivalence of Theorem 1.1 it is equivalent to some full subcategory of \(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\) of Example 1.3. Our task is to show that it is the first listed category above. For that we only need to show that it is a subcategory of \(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\); that is, that for any object  of it, the morphism q in part (b) of Example 1.3 is invertible. Following ideas in [24], we use the antipode z of B and the image of the equalizer (1.5) under the functor \(-B\) to construct the inverse:
of it, the morphism q in part (b) of Example 1.3 is invertible. Following ideas in [24], we use the antipode z of B and the image of the equalizer (1.5) under the functor \(-B\) to construct the inverse:

This definition works because the horizontal morphism equalizes the parallel morphisms of the fork on the right; see Fig. 1. The so constructed morphism \(q^{-1}\) is the inverse of q by the commutativity of the diagrams of Fig. 2 (in the second case we also need to use that the columns are equal monomorphisms).
(2) If both Y and B are cocommutative comonoids then clearly so is YB; and if both Y and B have antipodes z then  is the antipode of the Hopf monoid YB.
is the antipode of the Hopf monoid YB.
Conversely, if A is cocommutative then evidently so is its sub-comonoid  . If furthermore A has an antipode z then it restricts to
. If furthermore A has an antipode z then it restricts to  by the commutativity of the following diagram.
by the commutativity of the following diagram.

The top right region commutes by the Hopf monoid identity \(\delta \cdot z=zz\cdot c\cdot \delta \) and the assumed cocommutativity of A. The bottom right region commutes since any bimonoid morphism s commutes with the antipodes. \(\square \)
Example 1.6
Proposition 1.5 can be applied in particular to a finitely complete category \({\mathsf {M} }\), regarded as a cartesian monoidal category. From Proposition 1.5 we obtain equivalences between the following pairs of categories.
- (1)
The category whose
\({\underline{\text {objects}}}\) are split epimorphisms
 of monoids in \({\mathsf {M} }\) such that B is a group object.
of monoids in \({\mathsf {M} }\) such that B is a group object.\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms which are compatible with the epimorphisms s as well as their sections i.
The category whose
\({\underline{\text {objects}}}\) consist of a group object B and a monoid Y in \({\mathsf {M} }\), together with a left B-action on Y which makes Y a left B-module monoid.
\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms
 which are compatible with the actions
which are compatible with the actions 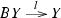 and
and  in the sense that \(l'\cdot by=y\cdot l\).
in the sense that \(l'\cdot by=y\cdot l\).
- (2)
The category whose
\({\underline{\text {objects}}}\) are split epimorphisms
 of group objects.
of group objects.\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms which are compatible with the epimorphisms s as well as their sections i.
The category whose
\({\underline{\text {objects}}}\) consist of group objects B and Y in \(\mathsf M\), together with a left B-action on Y which makes Y a left B-module group.
\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms
 which are compatible with the actions
which are compatible with the actions  and
and  in the sense that \(l'\cdot by=y\cdot l\).
in the sense that \(l'\cdot by=y\cdot l\).
Remark 1.7
There are particular symmetric monoidal categories \({\mathsf {M} }\) whose cocommutative Hopf monoids constitute semi-abelian categories \(\mathsf {Hopf} ({\mathsf {M} })\); e.g. the category of sets (which is cartesian monoidal hence the Hopf monoids are the groups, all of them cocommutative) or the category of vector spaces over an arbitrary field [12] (for the particular case of an algebraically closed field see [11]). In such cases the equivalence of Proposition 1.5 (2) is in fact the equivalence \(\mathsf {SplitEpi} (\mathsf {Hopf} ({\mathsf {M} }))\cong \mathsf {Act} (\mathsf {Hopf} ({\mathsf {M} }))\) discussed in [14, Section 1], see [14, Example 3.10].
3 Reflexive Graphs of Monoids Versus Pre-crossed Modules
Consider a monoidal admissible class \({\mathcal {S}}\) of spans in a monoidal category \({\mathsf {C} }\) for which [3, Assumption 4.1] holds. Take an object  in the category \(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\) of Theorem 1.1. Then by property (b) in Theorem 1.1, the induced morphism
in the category \(\mathsf {SplitEpiMon} _{{\mathcal {S}}}({\mathsf {C} })\) of Theorem 1.1. Then by property (b) in Theorem 1.1, the induced morphism  is invertible. Therefore by [3, Corollary 1.7] there is a bijective correspondence between the retractions t of the monoid morphism i and the monoid morphisms
is invertible. Therefore by [3, Corollary 1.7] there is a bijective correspondence between the retractions t of the monoid morphism i and the monoid morphisms  rendering commutative the diagram
rendering commutative the diagram

The correspondence is given by

Combining this observation with the equivalence of Theorem 1.1, next we present an equivalent description of a suitable category of reflexive graphs of monoids. This leads to the notion of pre-crossed module over a monoid.
Theorem 2.1
Consider a monoidal admissible class \({\mathcal {S}}\) of spans in a monoidal category \({\mathsf {C} }\) for which [3, Assumption 4.1] holds. The following categories are equivalent.
\(\mathsf {ReflGraphMon} _{{\mathcal {S}}}(\mathsf {C} )\) whose
\({\underline{\text {objects}}}\) are reflexive graphs
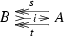 of monoids in \({\mathsf {C} }\) subject to the following conditions.
of monoids in \({\mathsf {C} }\) subject to the following conditions. - (a)
 (hence the \({\mathcal {S}}\)-relative pullback
(hence the \({\mathcal {S}}\)-relative pullback 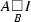 in Theorem 1.1 exists).
in Theorem 1.1 exists). - (b)
 is invertible.
is invertible.
\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms
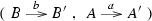 such that \(s'\cdot a=b\cdot s\), \(t'\cdot a=b\cdot t\) and \(i'\cdot b=a\cdot i\).
such that \(s'\cdot a=b\cdot s\), \(t'\cdot a=b\cdot t\) and \(i'\cdot b=a\cdot i\).- (a)
\({\mathsf {PreX} }_{\mathcal S}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) consist of monoids B and Y, monoid morphisms
 and
and  and a distributive law
and a distributive law  subject to the following conditions.
subject to the following conditions. - (a’)
 and
and  .
. - (b’)
\(e1\cdot x=1e\) and \(m\cdot k1\cdot x=m\cdot 1k\).
- (c’)
The morphism f of Theorem 1.1 (c’) is invertible.
\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms
 such that \(e'\cdot y=e\), \(k'\cdot y=b\cdot k\) and \(x'\cdot by=yb\cdot x\).
such that \(e'\cdot y=e\), \(k'\cdot y=b\cdot k\) and \(x'\cdot by=yb\cdot x\).- (a’)
Proof
We show that the equivalence functors of Theorem 1.1 lift to the equivalence of the claim. In the direction \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\rightarrow \mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\) we send

to

By [3, Proposition 3.7 (1)], \(p_A\) is a monoid morphism hence so is \(t\cdot p_A\). The second condition in (b’) holds by the considerations preceding the theorem. Hence in light of the proof of Theorem 1.1 the object map is well-defined. Concerning the morphisms, the second condition holds by the commutativity of

Thus using again the proof of Theorem 1.1 we conclude that this functor is well-defined.
In the opposite direction the functor \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} }) \rightarrow \mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\) is defined by

By [3, Lemma 1.6], it follows from the second equality of (b’) that \(m\cdot k1\) is a monoid morphism. It is a retraction of  by the unitality of k. The monoid morphisms (b, yb) are compatible with \(m\cdot k1\) by the compatibility of (b, y) with k and the multiplicativity of b. So using again the proof of Theorem 1.1 we conclude that this functor is well-defined too.
by the unitality of k. The monoid morphisms (b, yb) are compatible with \(m\cdot k1\) by the compatibility of (b, y) with k and the multiplicativity of b. So using again the proof of Theorem 1.1 we conclude that this functor is well-defined too.
By the commutativity of

the components (1, q) and (1, f) of the natural isomorphisms in the proof of Theorem 1.1 are morphisms in the appropriate category. This proves that the stated functors are mutually inverse equivalences. \(\square \)
Example 2.2
As in Example 1.2, take the (evidently admissible and monoidal) class of all spans in the monoidal category \({\mathsf {C} }\) of spans over a fixed set X. Then the equivalent categories of Theorem 2.1 take the following forms.
\(\mathsf {ReflGraphMon} ({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) are reflexive graphs
 of categories with the common object set X and identity-on-objects functors between them, such that the map (1.3) in Example 1.2 is invertible (recall that this holds e.g. if B is a groupoid).
of categories with the common object set X and identity-on-objects functors between them, such that the map (1.3) in Example 1.2 is invertible (recall that this holds e.g. if B is a groupoid).\({\underline{\text {morphisms}}}\) are pairs of compatible identity-on-objects functors.
\(\mathsf {PreX} ({\mathsf {C} })\) whose \({\underline{\text {objects}}}\) consist of categories B and Y of the common object set X such that Y is totally disconnected (in the sense of [4]); an action (cf. Example 1.2)
 and an identity-on-objects functor
and an identity-on-objects functor 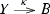 such that $$\begin{aligned} \kappa (b \triangleright y)\cdot b=b\cdot \kappa (y) \end{aligned}$$(2.2)
such that $$\begin{aligned} \kappa (b \triangleright y)\cdot b=b\cdot \kappa (y) \end{aligned}$$(2.2)for all morphisms b in B and y in Y for which \(s(b)=t(y)\). (If B is a groupoid then (2.2) has the equivalent form \(\kappa (b \triangleright y)=b\cdot \kappa (y)\cdot b^{-1}\); so when both B and Y are groupoids we recover the notion of pre-crossed module of groupoids in [5, Definition 1.2].)
\({\underline{\text {morphisms}}}\) are pairs of identity-on-objects functors
 such that \(\kappa '\nu =\beta \kappa \) and \(\nu (b \triangleright y)=\beta (b) \triangleright \nu (y)\) for all morphisms b in B and y in Y for which \(s(b)=t(y)\).
such that \(\kappa '\nu =\beta \kappa \) and \(\nu (b \triangleright y)=\beta (b) \triangleright \nu (y)\) for all morphisms b in B and y in Y for which \(s(b)=t(y)\).
Example 2.3
In the setting of Example 1.3, the equivalent categories of Theorem 2.1 take the following explicit forms.
\(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) are reflexive graphs
 of bimonoids in \({\mathsf {M} }\) subject to the following conditions.
of bimonoids in \({\mathsf {M} }\) subject to the following conditions. - (a)
The comultiplication \(\delta \) of A satisfies \(c\cdot 1s\cdot \delta =s1\cdot \delta \).
- (b)
In terms of the morphism j of (1.5),
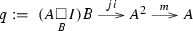 is invertible.
is invertible.
\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms
 such that \(s'\cdot a=b\,\cdot \,s\), \(t'\cdot a=b\cdot t\) and \(i'\cdot b=a\cdot i\).
such that \(s'\cdot a=b\,\cdot \,s\), \(t'\cdot a=b\cdot t\) and \(i'\cdot b=a\cdot i\).- (a)
\(\mathsf {PreX} _{\mathcal S}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) consist of a cocommutative bimonoid B and a bimonoid Y in \({\mathsf {M} }\), together with a left B-action l on Y which makes Y both a left B-module monoid and a left B-module comonoid, and a bimonoid morphism
 for which the following diagram commutes.
for which the following diagram commutes. 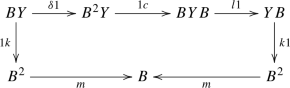 (2.3)
(2.3)\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms
 which are compatible with the actions
which are compatible with the actions  and
and  in the sense that \(l'\cdot by=y\cdot l\) and which satisfy \(k'\cdot y=b\cdot k\).
in the sense that \(l'\cdot by=y\cdot l\) and which satisfy \(k'\cdot y=b\cdot k\).
Proposition 2.4
The equivalent categories of Example 2.3 have equivalent full subcategories as follows.
The category whose
\({\underline{\text {objects}}}\) are reflexive graphs
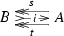 of bimonoids in \({\mathsf {M} }\) such that the comultiplication \(\delta \) of A satisfies \(c\cdot 1s\cdot \delta =s1\cdot \delta \) and B is a Hopf monoid.
of bimonoids in \({\mathsf {M} }\) such that the comultiplication \(\delta \) of A satisfies \(c\cdot 1s\cdot \delta =s1\cdot \delta \) and B is a Hopf monoid.\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms
 such that \(s'\cdot \,\, a=b\,\,\cdot \,\, s\), \(t'\cdot a=b\cdot t\) and \(i'\cdot b=a\cdot i\).
such that \(s'\cdot \,\, a=b\,\,\cdot \,\, s\), \(t'\cdot a=b\cdot t\) and \(i'\cdot b=a\cdot i\).The category whose
\({\underline{\text {objects}}}\) consist of a cocommutative Hopf monoid B and a bimonoid Y in \({\mathsf {M} }\), together with a left action
 which makes Y both a left B-module monoid and a left B-module comonoid, and a bimonoid morphism
which makes Y both a left B-module monoid and a left B-module comonoid, and a bimonoid morphism  for which the diagram
for which the diagram 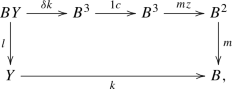 (2.4)
(2.4)occurring in [25, Definition 12 (iv)], commutes.
\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms
 for which \(l'\cdot by=y\cdot l\) and \(k'\cdot y=b\cdot k\).
for which \(l'\cdot by=y\cdot l\) and \(k'\cdot y=b\cdot k\).
Proof
For a reflexive graph  of bimonoids such that B is a Hopf monoid,
of bimonoids such that B is a Hopf monoid,  in part (b) of Example 2.3 is invertible by Example 1.5.
in part (b) of Example 2.3 is invertible by Example 1.5.
Whenever B has an antipode z, the commutative diagram (2.3) has an equivalent form (2.4). Their equivalence follows by the commutativity of the diagrams of Fig. 3. \(\square \)
Lemma 2.5
Consider a monoidal admissible class \({\mathcal {S}}\) of spans in a monoidal category \({\mathsf {C} }\) for which [3, Assumption 4.1] holds. For any object  of the category \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\) of Theorem 2.1, the following assertions are equivalent.
of the category \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\) of Theorem 2.1, the following assertions are equivalent.
- (i)
 .
. - (ii)
 .
.
Proof
Assertion (i) implies (ii) by [3, Lemma 3.4]. Conversely, since  is an object of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\), we have
is an object of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\), we have  . Then it follows by [3, Lemma 2.4]Footnote 2 that
. Then it follows by [3, Lemma 2.4]Footnote 2 that  , whence (ii) implies
, whence (ii) implies  by the multiplicativity of \({\mathcal {S}}\). Then by (PRE) also
by the multiplicativity of \({\mathcal {S}}\). Then by (PRE) also  . So using the identity \(t=m\! \cdot \! k1\! \cdot \! q^{-1}\) from (2.1), (i) follows by (POST) (composing by m on the left and by q on the right). \(\square \)
. So using the identity \(t=m\! \cdot \! k1\! \cdot \! q^{-1}\) from (2.1), (i) follows by (POST) (composing by m on the left and by q on the right). \(\square \)
4 Relative Categories of Monoids Versus Crossed Modules
Consider again a monoidal admissible class \({\mathcal {S}}\) of spans in a monoidal category \({\mathsf {C} }\) for which [3, Assumption 4.1] holds. Take an object  of the category \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathcal {C}})\) of Theorem 2.1 such that also
of the category \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathcal {C}})\) of Theorem 2.1 such that also  ; that is, the legs of the cospan
; that is, the legs of the cospan  are in \({\mathcal {S}}\) (hence there exists its \({\mathcal {S}}\)-relative pullback
are in \({\mathcal {S}}\) (hence there exists its \({\mathcal {S}}\)-relative pullback  ). Whenever the morphism
). Whenever the morphism

is invertible, we infer from [3, Corollary 1.7] that there exists at most one monoid morphism d rendering commutative

which is our candidate to serve as the composition morphism of a relative category. Note that if there is a monoid morphism d rendering commutative the diagram of (3.2), then it satisfies
So if \(q_2\) is invertible, then the only candidate is \(d=m\cdot p_A1\cdot q_2^{-1}\). By this motivation, in this section first we investigate the condition that \(q_2\) of (3.1) is invertible. Assuming so, next we show that whenever the morphism d of (3.2) exists, it makes the object  of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathcal {C}})\) to an \(\mathcal S\)-relative category. Finally, based on Theorem 2.1, we give an equivalent description of the category of \({\mathcal {S}}\)-relative categories in the category of monoids in \({\mathsf {C} }\), in terms of crossed modules introduced hereby.
of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathcal {C}})\) to an \(\mathcal S\)-relative category. Finally, based on Theorem 2.1, we give an equivalent description of the category of \({\mathcal {S}}\)-relative categories in the category of monoids in \({\mathsf {C} }\), in terms of crossed modules introduced hereby.
4.1 Invertibility of Some Canonical Morphisms
Lemma 3.1
Consider a monoidal admissible class \({\mathcal {S}}\) of spans in a monoidal category \({\mathsf {C} }\) for which [3, Assumption 4.1] holds. For any monoid B in \({\mathsf {C} }\) for which  is in \({\mathcal {S}}\), for any span of monoids
is in \({\mathcal {S}}\), for any span of monoids  with legs in \({\mathcal {S}}\), and for any natural number n, the following assertions hold. (Recall the convention
with legs in \({\mathcal {S}}\), and for any natural number n, the following assertions hold. (Recall the convention  from [3, Corollary 4.6].)
from [3, Corollary 4.6].)
- (1)
There exists the \({\mathcal {S}}\)-relative pullback
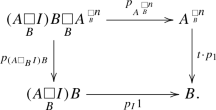
- (2)
There is a unique morphism \(h_n\) rendering commutative the diagram
- (3)
For a common section i of s and t, consider the morphism
 (3.4)
(3.4)(it is well-defined by [3, Proposition 3.5] and \(q_1\) is equal to q in Theorem 1.1 (b)). If \(q_{n+1}\) is invertible for some n, then \(q_k\) is invertible for all \(0<k\le n\).
- (4)
For a common section i of s and t the following are equivalent.
- (i)
\(h_n\) in part (2) and \(q_1\) in part (3) are invertible.
- (ii)
\(q_{n+1}\) in part (3) is invertible.
- (i)
Proof
(1) By assumption  and by the unitality of \({\mathcal {S}}\),
and by the unitality of \({\mathcal {S}}\),  . Then by [3, Lemma 3.4],
. Then by [3, Lemma 3.4],

By assumption also  hence by the second assertion in (3.5) and the multiplicativity of \({\mathcal {S}}\)
hence by the second assertion in (3.5) and the multiplicativity of \({\mathcal {S}}\)

The first assertion of (3.5) and (3.6) say that the legs of  are in \({\mathcal {S}}\) hence their \(\mathcal S\)-relative pullback exists by assumption.
are in \({\mathcal {S}}\) hence their \(\mathcal S\)-relative pullback exists by assumption.
(2) By (3.5) and the multiplicativity of \({\mathcal {S}}\),

Hence by the evident commutativity of the exterior of the diagram in part (2), universality of the \({\mathcal {S}}\)-relative pullback in its codomain implies the existence of the unique morphism \(h_n\).
(3) For some positive integer n assume that \(q_{n+1}\) is invertible. Then so is \(q_n\) with the inverse

Indeed, (3.7) renders commutative both diagrams

The leftmost region of the first diagram commutes by the explicit expression (3.4) of \(q_n\) and \(q_{n+1}\), multiplicativity of \(1\,\Box \,i\) and the functoriality of \(\Box \), see [3, Proposition 3.5 (2)]. The rightmost region of the second diagram commutes again by the explicit expression (3.4) of \(q_n\) and \(q_{n+1}\) and the multiplicativity of \(p_{1\dots n}\).
(4) Our strategy is to prove that \(q_{n+1}\) can be rewritten as

Then (i) obviously implies (ii) and in view of part (3) also the opposite implication holds.
The occurring morphism \(q\,\Box \,1\) is defined as the unique morphism rendering commutative the diagram

It is well-defined by the commutativity of the first diagram of (1.1); see [3, Proposition 3.5 (2)]. The morphism of (3.8) is equal to \(q_{n+1}\) by the commutativity of both diagrams


whose right vertical arrows are jointly monomorphic. \(\square \)
Example 3.2
In the category \({\mathsf {C} }\) of spans over a given set X from Example 1.2, the morphisms \(h_n\) of Lemma 3.1 (2) are isomorphisms, see the pullback (1.4). Hence for any reflexive graph  of categories with common object set X and identity-on-objects functors between them, all morphisms \(\{q_n\}_{n>0}\) in Lemma 3.1 (3) are invertible if and only if \(q_1\) is so; see Lemma 3.1 (4). The latter condition holds e.g. if B is a groupoid, see Example 1.2.
of categories with common object set X and identity-on-objects functors between them, all morphisms \(\{q_n\}_{n>0}\) in Lemma 3.1 (3) are invertible if and only if \(q_1\) is so; see Lemma 3.1 (4). The latter condition holds e.g. if B is a groupoid, see Example 1.2.
Example 3.3
In the context of Example 1.3 we know from [3, Example 4.3] that [3, Assumption 4.1] holds for the monoidal admissible class \({\mathcal {S}}\) in [3, Example 2.3] and [3, Example 2.7] of spans in \({\mathsf {C} }\).
In this situation, for any cocommutative comonoid B in \({\mathsf {M} }\) and any comonoid morphism  such that the comultiplication \(\delta \) of C satisfies \(f1\cdot \delta =f1\cdot c\cdot \delta \), there is a unique isomorphismh rendering commutative the diagram
such that the comultiplication \(\delta \) of C satisfies \(f1\cdot \delta =f1\cdot c\cdot \delta \), there is a unique isomorphismh rendering commutative the diagram

with the inverse  (where \(j=p_{AB}p_C\cdot \delta \) is the equalizer of \(1\delta 1\) and \(11f1\cdot 11\delta \) as in (1.5); and \(\varepsilon \) stands for both counits of A and B). Indeed, the following diagrams commute.
(where \(j=p_{AB}p_C\cdot \delta \) is the equalizer of \(1\delta 1\) and \(11f1\cdot 11\delta \) as in (1.5); and \(\varepsilon \) stands for both counits of A and B). Indeed, the following diagrams commute.



By [3, Example 2.8] there is an induced monoidal admissible class (also denoted by \({\mathcal {S}}\)) in the category of monoids in \({\mathsf {C} }\) (that is, the category of bimonoids in \({\mathsf {M} }\)) also satisfying [3, Assumption 4.1] by [3, Example 4.4]. So whenever the above morphism f is a monoid morphism as well, there is a bimonoid isomorphism h in the diagram, see [3, Proposition 3.7]. Consequently, in the category of bimonoids in \({\mathsf {M} }\), the morphisms \(h_n\) of Lemma 3.1 (2) are isomorphisms. Therefore \(q_n\) in Lemma 3.1 (3) is an isomorphism for all positive integer n if and only if it is invertible for \(n=1\); and this holds whenever B is a Hopf monoid, see Proposition 1.5.
Lemma 3.4
Let \({\mathcal {S}}\) be a monoidal admissible class of spans in a monoidal category \({\mathsf {C} }\) for which [3, Assumption 4.1] holds and let  be an object of the category \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\) in Theorem 2.1 such that
be an object of the category \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\) in Theorem 2.1 such that  . For any natural number n denote by
. For any natural number n denote by  the n-times iterated multiplication (unique by the associativity of m; by definition the identity morphism for \(n=0\)) and consider the span
the n-times iterated multiplication (unique by the associativity of m; by definition the identity morphism for \(n=0\)) and consider the span

For any natural number n the following assertions hold.
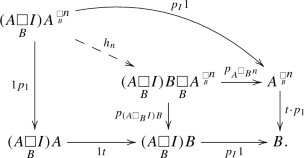
- (1)
The cospan
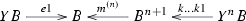 has its legs in \({\mathcal {S}}\) (hence there exists its \({\mathcal {S}}\)-relative pullback
has its legs in \({\mathcal {S}}\) (hence there exists its \({\mathcal {S}}\)-relative pullback  ).
). - (2)
There exists a unique morphism \(b_{n+1}\) of spans (for the spans (3.11)) rendering commutative
- (3)
If \(b_{n+1}\) in part (2) is an isomorphism then also \(b_k\) is an isomorphism for all \(0<k\le n\).
- (4)
For the morphism

the following diagram commutes
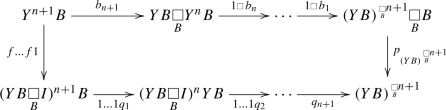
where f is the isomorphism in Theorem 1.1 (c’).
- (5)
\(b_{n+1}\) in part (2) is an isomorphism if and only if \(q_{n+1}\) in part (4) is an isomorphism.
Proof
(1) By definition the first two spans in

belong to \({\mathcal {S}}\) hence so does the last one by the multiplicativity of \({\mathcal {S}}\). Again, by definition the second and the third spans of (3.12) belong to \({\mathcal {S}}\) hence by the multiplicativity of \({\mathcal {S}}\) so does the first one in

Then the second span of (3.13) is in \({\mathcal {S}}\) by (POST).
(2) Since the first span of (3.12) and the second span of (3.13) are in \({\mathcal {S}}\), the multiplicativity of \({\mathcal {S}}\) implies that so is

So by the evident commutativity of the exterior of the diagram of part (2) the stated morphism \(b_{n+1}\) exists. It is a morphism of spans (for the spans (3.11)) by the commutativity of the following diagrams.

(3) Since for a positive integer n,  is a morphism between the spans of (3.11), the morphism in the top row of the following diagram is well-defined by [3, Proposition 3.5].
is a morphism between the spans of (3.11), the morphism in the top row of the following diagram is well-defined by [3, Proposition 3.5].

By their commutativity we infer \(b_{n+1}\cdot 1\dots 1u1=(1\,\Box \,1\dots 1u1)\cdot b_n\) Similarly, since for \(n>0\) also  is a morphism between the spans of (3.11), the morphism in the top row of the following diagram is well-defined by [3, Proposition 3.5].
is a morphism between the spans of (3.11), the morphism in the top row of the following diagram is well-defined by [3, Proposition 3.5].

By their commutativity, \(b_n\cdot 1\dots 1m1=(1\,\Box \,1\dots 1m1)\cdot b_{n+1}\). It follows from these identities and the unitality of the monoid Y that whenever \(b_{n+1}\) is invertible then so is \(b_n\) with the inverse

(4) We proceed by induction in n. For \(n=0\) the diagram in the claim reduces to the diagram

whose upper half part commutes by construction (see part (2)) and the lower half part commutes since f1 and \(q_1\) are mutual inverses (see the proof of Theorem 1.1).
For any positive value of n, denote the top-right path in the diagram of the claim by \({\widetilde{b}}_{n+1}\) and the bottom row by \({\widetilde{q}}_{n+1}\). Then the diagram takes the form

The region at the bottom left corner commutes if the claim holds for \(n-1\); and the commutativity of the large region is proven in Fig. 4.
(5) By Theorem 1.1\(q_1\) is an isomorphism without any further assumption; it is the inverse of the isomorphism  . Also \(b_1\) is an isomorphism; the inverse of the isomorphism
. Also \(b_1\) is an isomorphism; the inverse of the isomorphism  in [3, Proposition 3.6 (1)].
in [3, Proposition 3.6 (1)].
Assume that \(b_l\) is iso for some \(l>1\). Take the diagram of part (4) for \(n=1\); it says \(b_2=q_2\,\,\cdot \,\, f11\). Since f is an isomorphism by definition and \(b_2\) is an isomorphism by part (3), also \(q_2\) is an isomorphism. If \(l=2\) then this completes the proof. If \(l>2\) then take next the diagram of part (4) for \(n=2\); it says \((1\,\Box \,b_2)\,\,\cdot \,\, b_3=q_3\,\,\cdot \,\, 1q_2\,\,\cdot \,\, ff11\). All of the occurring morphisms but \(q_3\) are known to be isomorphisms proving that so is \(q_3\). Repeating this reasoning for all \(n\le l\) we conclude that \(q_n\) is an isomorphism for all \(0<n\le l\).
The opposite implication is proven by the same steps. Assume that \(q_l\) is iso for some \(l>1\). Take the diagram of part (4) for \(n=1\); it says \(b_2=q_2\cdot f11\). Since f is an isomorphism by definition and \(q_2\) is an isomorphism by Lemma 3.1 (3), also \(b_2\) is an isomorphism. If \(l=2\) then this completes the proof. If \(l>2\) then take next the diagram of part (4) for \(n=2\); it says \((1\,\Box \,b_2)\cdot b_3=q_3\cdot 1q_2\cdot ff11\). All of the occurring morphisms but \(b_3\) are known to be isomorphisms proving that so is \(b_3\). Repeating this reasoning for all \(n\le l\) we conclude that \(b_n\) is an isomorphism for all \(0<n\le l\). \(\square \)
Example 3.5
Take \({\mathcal {S}}\) to be the (monoidal and admissible) class of all spans in the monoidal category \({\mathsf {C} }\) of spans over a given set. For any object of the category \(\mathsf {ReflGraphMon} ({\mathsf {C} })\) of Example 2.2 and for any positive integer n, the morphism \(b_n\) in Lemma 3.4 (2) is invertible, see the pullback (1.4).
Example 3.6
In the setting of Example 1.3 we know from Example 3.3 that the morphism \(q_n\) of Lemma 3.1 (3) is invertible for any positive integer n and for any object of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\). By the isomorphism of Theorem 2.1 this means that the morphism \(q_n\) of Lemma 3.4 (4) is invertible for any object of \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\). Then also the morphism \(b_n\) of Lemma 3.4 (2) is invertible by Lemma 3.4 (5). Since the diagram

commutes, we conclude that the morphism in its bottom-right path—involving the equalizer j as in (1.5)—is the inverse of \(b_n\).
Let \({\mathcal {S}}\) be a monoidal admissible class of spans in a monoidal category \({\mathsf {C} }\) for which [3, Assumption 4.1] holds. For any object  of the category \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\) in Theorem 2.1, it follows by the conditions in (a’) and the multiplicativity of \({\mathcal {S}}\) that the span
of the category \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\) in Theorem 2.1, it follows by the conditions in (a’) and the multiplicativity of \({\mathcal {S}}\) that the span  belongs to \({\mathcal {S}}\). Then by [3, Proposition 3.6] the \({\mathcal {S}}\)-relative pullback in the first diagram of
belongs to \({\mathcal {S}}\). Then by [3, Proposition 3.6] the \({\mathcal {S}}\)-relative pullback in the first diagram of

exists and the left vertical of the first diagram is an isomorphism. If in addition  , then by (a’) and the multiplicativity of \({\mathcal {S}}\) also
, then by (a’) and the multiplicativity of \({\mathcal {S}}\) also  . Hence by (POST)
. Hence by (POST)  . We infer again by [3, Proposition 3.6] that the \({\mathcal {S}}\)-relative pullback in the second diagram of (3.14) exists and the top row of of the second diagram is an isomorphism.
. We infer again by [3, Proposition 3.6] that the \({\mathcal {S}}\)-relative pullback in the second diagram of (3.14) exists and the top row of of the second diagram is an isomorphism.
Lemma 3.7
Let \({\mathcal {S}}\) be a monoidal admissible class of spans in a monoidal category \({\mathsf {C} }\) for which [3, Assumption 4.1] holds and let  be an object of the category \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\) in Theorem 2.1 such that
be an object of the category \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\) in Theorem 2.1 such that  . The morphism \(b_2\) in Lemma 3.4 (2) satisfies the identities
. The morphism \(b_2\) in Lemma 3.4 (2) satisfies the identities
- (1)
\(b_2\cdot u11=u1\,\Box \,1\) and
- (2)
\(b_2\cdot 1u1=1\,\Box \,u1\),
whose right hand sides are defined as the unique fillers of the respective diagrams

Proof
Assertion (1) follows by the commutativity of the diagrams

and part (2) follows by the commutativity of the diagrams

\(\square \)
4.2 The Composition Morphism of a Relative Category of Monoids
Proposition 3.8
Consider a monoidal admissible class \({\mathcal {S}}\) of spans in a monoidal category \({\mathsf {C} }\) such that [3, Assumption 4.1] holds. Take an object  of the category \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\) of Theorem 2.1 such that the following properties hold.
of the category \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\) of Theorem 2.1 such that the following properties hold.
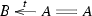 belongs to \({\mathcal {S}}\)
belongs to \({\mathcal {S}}\)the morphism \(q_3\) of Lemma 3.1 (3) is invertible.
The following assertions hold.
- (1)
There is at most one monoid morphism d rendering commutative

- (2)
The monoid morphism d of part (1) exists if and only if the following diagram commutes (recall that \(q_2\) is invertible by Lemma 3.1 (3)).

Moreover, in this case d is equal to

- (3)
Whenever the monoid morphism d of part (1) exists,
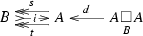 is an \({\mathcal {S}}\)-relative category in the category of monoids in \(\mathsf C\).
is an \({\mathcal {S}}\)-relative category in the category of monoids in \(\mathsf C\).
Proof
The proof is built on [3, Corollary 1.7].
(1) Since the morphism \(q_2\) in Lemma 3.1 (3) is invertible, we know from [3, Corollary 1.7] that there is at most one monoid morphism rendering commutative

Since a monoid morphism d as in part (1) obviously renders commutative (3.15), this proves its uniqueness.
(2) By [3, Corollary 1.7] commutativity of the diagram of part (2) is equivalent to the existence of a (unique) monoid morphism making (3.15) commute. Since a monoid morphism d in part (1) provides such a morphism, its existence implies commutativity of the diagram of part (2).
In order to prove the converse implication, we show that any monoid morphism d making (3.15) commute renders commutative also the diagram of part (1). Recall from [3, Lemma 1.2] that the invertibility of q in Theorem 2.1 (b) implies that \(p_A\) and i are jointly epic morphisms of monoids. Hence if d makes (3.15) commute then it does so the left hand side of the diagram of part (1) by \(d\cdot (1\,\Box \,i)\cdot i=d\cdot (i\,\Box \,1)\cdot i=i\).
The stated expression of d immediately follows from [3, Corollary 1.7] (see also (3.3)).
(3) In order to see that the monoid morphism d in part (1) is a morphism of spans, we use that by the invertibility of \(q_2\) there are unique morphisms rendering commutative the respective diagrams

see [3, Corollary 1.7]. Now \(s\cdot d\) obviously makes the first diagram commute and so does  by the commutativity of
by the commutativity of

Thus they are equal. Similarly, both \(t\cdot d\) and  render commutative the second diagram proving that they are equal.
render commutative the second diagram proving that they are equal.
The to-be composition morphism d in part (1) admits the unit i by construction. Its associativity follows again by [3, Corollary 1.7] since by the invertibility of \(q_3\) there is at most one morphism rendering commutative

Since both \(d\cdot (d\,\Box \,1)\) and \(d\cdot (1\,\Box \,d)\) do so by the commutativity of

this proves their equality (modulo the omitted associativity isomorphism in [3, Proposition 3.6]). \(\square \)
Proposition 3.9
Consider a monoidal admissible class \({\mathcal {S}}\) of spans in a monoidal category \({\mathsf {C} }\) such that [3, Assumption 4.1] holds. Between \({\mathcal {S}}\)-relative categories in the category of monoids in \({\mathsf {C} }\) for which the morphisms \(q_2\) in Lemma 3.1 (3) are invertible, any morphism of reflexive graphs of monoids is in fact an \({\mathcal {S}}\)-relative functor.
Proof
Take \({\mathcal {S}}\)-relative categories  and
and  as in the claim. We need to check the compatibility of any morphism of reflexive graphs
as in the claim. We need to check the compatibility of any morphism of reflexive graphs  with the composition morphisms d and \(d'\). The first diagram of
with the composition morphisms d and \(d'\). The first diagram of

commutes since \(a\,\Box \,a\) is multiplicative by [3, Proposition 3.7 (2)] and by the functoriality of \(\Box \); see [3, Proposition 3.5 (2)]. It is used to prove the commutativity of the second diagram. \(\square \)
4.3 The Equivalence Between Relative Categories and Crossed Modules of Monoids
Theorem 3.10
Consider a monoidal admissible class \({\mathcal {S}}\) of spans in a monoidal category \({\mathsf {C} }\) such that [3, Assumption 4.1] holds. Use the same notation \({\mathcal {S}}\) for the induced admissible class of spans in the category of monoids in \({\mathsf {C} }\) from [3, Example 2.8] (also satisfying [3, Assumption 4.1] by [3, Example 4.4]). The following categories are equivalent.
\(\mathsf {CatMon} _{{\mathcal {S}}}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) are \({\mathcal {S}}\)-relative categories
 in the category of monoids in \({\mathsf {C} }\) such that the morphisms \(q_n\) of (3.4) are invertible for any positive integer n.
in the category of monoids in \({\mathsf {C} }\) such that the morphisms \(q_n\) of (3.4) are invertible for any positive integer n.\({\underline{\text {morphisms}}}\) are \({\mathcal {S}}\)-relative functors in the category of monoids in \({\mathsf {C} }\).
\(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) consist of monoids B and Y, monoid morphisms
 and
and 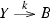 and a distributive law
and a distributive law  subject to the following conditions.
subject to the following conditions. - (a\(^\prime \)):
 ,
,  and
and  .
.- (b’):
\(e1\cdot x=1e\) and \(m\cdot k1\cdot x=m\cdot 1k\).
- (c’):
The morphism f of Theorem 1.1 (c’) is invertible and the morphisms \(b_n\) of Lemma 3.4 (2) are invertible for all positive integers n.
- (d’):
Regarding YB as a monoid via the structure induced by the distributive law x, the following diagram commutes.

\({\underline{\text {morphisms}}}\) are pairs of monoid morphisms
 such that \(e'\cdot y=e\), \(k'\cdot y=b\cdot k\) and \(x'\cdot by=yb\cdot x\).
such that \(e'\cdot y=e\), \(k'\cdot y=b\cdot k\) and \(x'\cdot by=yb\cdot x\).
Proof
It follows by Propositions 3.8 and 3.9 that \(\mathsf {CatMon} _{{\mathcal {S}}}({\mathsf {C} })\) is a full subcategory of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\) and obviously \(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\) is a full subcategory of \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\). Below we show that the mutually inverse functors of Theorem 2.1 restrict to functors between these subcategories thus establishing the stated equivalence.
Regarding an object  of \(\mathsf {CatMon} _{{\mathcal {S}}}({\mathsf {C} })\) as an object
of \(\mathsf {CatMon} _{{\mathcal {S}}}({\mathsf {C} })\) as an object  of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\), the functor in the proof of Theorem 2.1 takes it to the object
of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\), the functor in the proof of Theorem 2.1 takes it to the object  of the category \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\); we claim that it is in fact an object of \(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\).
of the category \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\); we claim that it is in fact an object of \(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\).
It satisfies the condition  by Lemma 2.5.
by Lemma 2.5.
From Lemma 3.4 (5) we know that the morphism \(b_n\) of Lemma 3.4 (2) is invertible if and only if the left column of the commutative diagram

is invertible. Recognize the isomorphism \(q_n\) of Lemma 3.1 (3) in the right column. Since also the rows are isomorphisms by assumption, so is the left column and hence \(b_n\). This also shows that the morphism of Lemma 3.1 (3) for the reflexive graph  , and the morphism of Lemma 3.4 (4) for the corresponding object
, and the morphism of Lemma 3.4 (4) for the corresponding object  of \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\), differ by the isomorphisms of the top and bottom rows (justifying our use of the same symbol \(q_n\) for them).
of \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\), differ by the isomorphisms of the top and bottom rows (justifying our use of the same symbol \(q_n\) for them).
The proof of the commutativity of the diagram in part (d’) requires some preparation. The commutativity of


proves \((q\,\Box \,q)\cdot b_2=q_2\cdot 1q\). (Here the bottom-right region of the first diagram commutes since the lower half of the diagram of (3.9) commutes and the bottom-right region of the second diagram commutes since the lower half of the diagram of (3.10) commutes.) By the associativity of the monoid A and the multiplicativity of  also the following diagram commutes.
also the following diagram commutes.

With the help of these identities and Lemma 3.7, and using that the region marked by \((*)\) commutes by Proposition 3.8 (2), the diagram of Fig. 5 is seen to commute. This proves that the stated object belongs to \(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\) indeed.
In the opposite direction, consider an object  of \(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\) as an object of \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\). The functor in the proof of Theorem 2.1 takes it to the object
of \(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\) as an object of \(\mathsf {PreX} _{{\mathcal {S}}}({\mathsf {C} })\). The functor in the proof of Theorem 2.1 takes it to the object  of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\); we claim that it can be seen as an object of \(\mathsf {CatMon} _{{\mathcal {S}}}({\mathsf {C} })\).
of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\); we claim that it can be seen as an object of \(\mathsf {CatMon} _{{\mathcal {S}}}({\mathsf {C} })\).
By Lemma 3.4 (1) the span  belongs to \({\mathcal {S}}\).
belongs to \({\mathcal {S}}\).
The morphism \(q_n\) of Lemma 3.4 (4) is invertible for all positive integers n by Lemma 3.4 (5).
By Proposition 3.8 (2) and (3), the reflexive graph of monoids  extends to an \({\mathcal {S}}\)-relative category in the category of monoids in \({\mathsf {C} }\) by the commutativity of
extends to an \({\mathcal {S}}\)-relative category in the category of monoids in \({\mathsf {C} }\) by the commutativity of

The region at the top-right corner is the commutative diagram of Lemma 3.4 (4) for \(n=1\). The region bounded from below by the curved arrows commutes by Lemma 3.7. The region marked by (d’) coincides with the diagram of part (d’) hence it commutes. \(\square \)
Example 3.11
As in Example 1.2, take the (evidently admissible and monoidal) class of all spans in the category \({\mathsf {C} }\) of spans over a given set X. Then the equivalent categories of Theorem 3.10 take the following forms.
\(\mathsf {CatMon} ({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) are the double categories with the object set X and only identity horizontal morphisms and such that the morphism (1.3) is invertible. (This last condition holds e.g. if the vertical edge category is a groupoid.)
\({\underline{\text {morphisms}}}\) are the double functors which are identities on the objects (and hence on the horizontal morphisms).
\(\mathsf {Xmod} ({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) consist of categories B and Y with the common object set X such that Y is totally disconnected (in the sense of [4]); an action (see Example 1.2)
 and an identity-on-objects functor
and an identity-on-objects functor 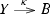 such that $$\begin{aligned} \kappa (b \triangleright y)\cdot b=b\cdot \kappa (y) \qquad \text {and}\qquad (\kappa (y) \triangleright y')\cdot y=y\cdot y' \end{aligned}$$
such that $$\begin{aligned} \kappa (b \triangleright y)\cdot b=b\cdot \kappa (y) \qquad \text {and}\qquad (\kappa (y) \triangleright y')\cdot y=y\cdot y' \end{aligned}$$for all morphisms b in B and \(y,y'\) in Y for which \(s(b)=t(y)=t(y')\).
\({\underline{\text {morphisms}}}\) are the same as the morphisms in \(\mathsf {PreXMon(C)} \), see Example 2.2.
Note that these equivalent categories have equivalent full subcategories whose objects are such that the category B is a groupoid; and other equivalent full subcategories whose objects are such that both of the occurring categories are groupoids. In the latter case these are the category of categories in the category of groupoids; and the category of crossed modules of groupoids in [5, Definition 1.2], respectively.
Example 3.12
In the setting of Example 1.3, the equivalent categories of Theorem 3.10 take the following explicit forms.
\(\mathsf {CatMon} _{{\mathcal {S}}}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) are \({\mathcal {S}}\)-relative categories
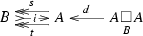 in the category of monoids in \({\mathsf {C} }\)—that is, in the category of bimonoids in \({\mathsf {M} }\)—such that the morphism q of Theorem 1.1 (b) is invertible.
in the category of monoids in \({\mathsf {C} }\)—that is, in the category of bimonoids in \({\mathsf {M} }\)—such that the morphism q of Theorem 1.1 (b) is invertible.\({\underline{\text {morphisms}}}\) are \({\mathcal {S}}\)-relative functors in the category of monoids in \({\mathsf {C} }\)—that is, in the category of bimonoids in \({\mathsf {M} }\).
\(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\) whose
\({\underline{\text {objects}}}\) consist of a bimonoid Y and a cocommutative bimonoid B together with a left action
 which makes Y both a B-module monoid and a B-module comonoid and a bimonoid morphism
which makes Y both a B-module monoid and a B-module comonoid and a bimonoid morphism  for which the following diagrams commute.
for which the following diagrams commute. 
The third condition appears in [25, Definition 12 (v)] under the name Peiffer condition (motivated by the terminology for groups).
\({\underline{\text {morphisms}}}\) are pairs of bimonoid morphisms
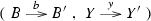 such that \(k'\cdot y=b\cdot k\) and \(l'\cdot by=y\cdot l\).
such that \(k'\cdot y=b\cdot k\) and \(l'\cdot by=y\cdot l\).
These equivalent categories are equivalent furthermore to the full subcategory of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\) of Example 2.3 for whose objects  the following diagrams commute.
the following diagrams commute.


The above description of \(\mathsf {CatMon} _{{\mathcal {S}}}({\mathsf {C} })\) requires no further explanation. In the description of \(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\) we need to show that the third diagram (the Peiffer condition) is equivalent to the diagram of Theorem 3.10 (d’) in the current setting. The path on the right hand side of the diagram of Theorem 3.10 (d’) appears as the left bottom path of the commutative diagram

(in which x stands for the distributive law  of Example 1.3). Hence it can be replaced by the top right path yielding the equivalent form
of Example 1.3). Hence it can be replaced by the top right path yielding the equivalent form

of the diagram of Theorem 3.10 (d’). The first diagram of Fig. 6 shows that if the diagram of (3.18) commutes then the Peiffer condition in the above presentation of \(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\) holds. The opposite implication is proven by the second diagram of Fig. 6.
In order to justify the further equivalent characterization of these categories as a full subcategory of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\), we need to see the equivalence of the diagram of Proposition 3.8 (2) in the current setting and the diagram of (3.17). This follows by noting that the top row of the diagram of Proposition 3.8 (2) in the current setting appears in the left-bottom path of the commutative diagram

hence it can be replaced by the top-right path. (The expression of \(h_1^{-1}\) in the bottom-right corner was computed in Example 3.3.)
In the particular case when \({\mathsf {M} }\) is the cartesian monoidal category of sets, the current example yields an equivalence between the category of those internal categories

in the category of ordinary monoids for which the split epimorphism (i, s) satisfies the Schreier property of [20] (see Example 1.3), and the category of crossed semimodules in [20]. Hence it extends the main result of [20].
Proposition 3.13
The equivalent categories of Example 3.12 have equivalent full subcategories as follows.
The full subcategory of \(\mathsf {CatMon} _{{\mathcal {S}}}({\mathsf {C} })\) for whose objects
 the bimonoid B in \({\mathsf {M} }\) is a Hopf monoid.
the bimonoid B in \({\mathsf {M} }\) is a Hopf monoid.The full subcategory of \(\mathsf {Xmod} _{{\mathcal {S}}}({\mathsf {C} })\) for whose objects
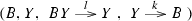 the bimonoid B in \({\mathsf {M} }\) is a Hopf monoid.
the bimonoid B in \({\mathsf {M} }\) is a Hopf monoid.The full subcategory of \(\mathsf {ReflGraphMon} _{{\mathcal {S}}}({\mathsf {C} })\) for whose objects
 the following conditions hold.
the following conditions hold.B is a Hopf monoid (with antipode z)
\(t1\cdot \delta =t1\cdot c\cdot \delta \)
for the morphisms

the following diagram commutes.
 (3.19)
(3.19)
Proof
The only ingredient that requires a proof is the equivalence of diagrams (3.17) and (3.19) in the case when B has an antipode z. The proof will repeatedly use the identity on \(\overrightarrow{s}\) encoded in the following commutative diagram.

Recall from [24] that if B has an antipode z then  is a split monomorphism in \({\mathsf {M} }\); a retraction is provided by
is a split monomorphism in \({\mathsf {M} }\); a retraction is provided by  . Indeed,
. Indeed,

On the other hand, since in Proposition 1.5 the inverse \(q^{-1}\) was constructed as the unique solution of \(p_A1\cdot q^{-1}=\overrightarrow{s} s\cdot \delta \), also the equality

holds, proving that \(\overrightarrow{s}\) is idempotent.
Pre-composing both paths around (3.17) with the split epimorphism \(1g_A\), we obtain the equivalent diagram

Its rightmost region commutes by (3.20) and the fact that \(\overrightarrow{s}\) is idempotent.
The morphism around the right hand side of (3.21) occurs as the left-bottom path of the commutative diagram

Hence it can be replaced by the top-right path yielding the equivalent form

of (3.21).
Finally, observe that for any morphisms  the following diagrams are equivalent:
the following diagrams are equivalent:

Indeed, the first diagram below shows that if the first diagram of (3.23) commutes then so does the second one; and the opposite implication follows by the second diagram below.

Applying the equivalence of the diagrams of (3.23) to  and
and  , we obtain from (3.22) the equivalent form
, we obtain from (3.22) the equivalent form

which is equivalent to (3.19) by the naturality of the symmetry c.
Note that by the equalities
the above morphism \(g_A\) in the splitting of the idempotent morphism \(\overrightarrow{s}\) can also be obtained as the unique filler of the first diagram in

The symmetrically constructed filler of the second diagram above yields a splitting of the idempotent morphism \(\overleftarrow{t}\) in the ambient category \({\mathsf {M} }\). So commutativity of the diagram of (3.19) is equivalent also to the commutativity of

\(\square \)
In the particular case of Proposition 3.13 when \({\mathsf {M} }\) is cartesian monoidal (e.g. it is the category of sets),  is the kernel of the monoid morphism s and
is the kernel of the monoid morphism s and  is the kernel of the monoid morphism t, see Example 1.4. Hence in this case the equivalent diagrams of (3.19) and (3.24) say precisely that the kernels of s and t commute in the monoid A.
is the kernel of the monoid morphism t, see Example 1.4. Hence in this case the equivalent diagrams of (3.19) and (3.24) say precisely that the kernels of s and t commute in the monoid A.
The equivalent categories of Proposition 3.13 have equivalent full subcategories in whose objects both occurring bimonoids are Hopf monoids, and other equivalent full subcategories in whose objects they are both cocommutative Hopf monoids. In this way, Proposition 3.13 includes [25, Proposition 11] and [25, Theorem 14] about the equivalence between the category of so-called \(\mathsf {Cat} ^1\)-Hopf algebras and the category of crossed modules over Hopf algebras; hence in particular the equivalence between the category of \(\mathsf {Cat} ^1\)-groups and the category of crossed modules over groups in [6, Theorem 1]—where it is also referred to unpublished works by Verdier and Duskin—, [17, Lemma 2.2] and [14, Section 3.9] (whose language is most similar to ours).
References
Aguiar, M.: Internal Categories and Quantum Groups. Ph.D. Thesis, Cornell University (1997)
Böhm, G.: Crossed modules of monoids III. Simplicial monoids of Moore length 1. arXiv:1803.04622
Böhm, G.: Crossed modules of monoids I. Relative categories. Appl. Categ. Struct. 27(6), 641–662 (2019)
Bourn, D.: Commutator theory, action groupoids, and an intrinsic Schreier–Mac Lane extension theorem. Adv. Math. 217(6), 2700–2735 (2008)
Brown, R., İçen, İ.: Homotopies and automorphisms of crossed modules of groupoids. Appl. Categ. Struct. 11(2), 185–206 (2003)
Brown, R., Spencer, C.B.: \({\cal{G}}\)-groupoids, crossed modules and the fundamental groupoid of a topological group. Indag. Math. (Proc.) 79(4), 296–302 (1976)
Duskin, J.W.: Preliminary remarks on groups, as quoted in [6]: Unpublished notes, Tulane University (1969)
Emir, K.: The Moore Complex of a Simplicial Cocommutative Hopf Algebra. arXiv:1905.09620
Faria Martins, J.: Crossed modules of Hopf algebras and of associative algebras and two-dimensional holonomy. J. Geom. Phys. 99, 68–110 (2016)
Fernández Vilaboa, J.M., López López, M.P., Villanueva Novoa, E.: Cat \(^1\)-Hopf algebras and crossed modules. Commun. Algebra 35(1), 181–191 (2006)
Gran, M., Kadjo, G., Vercruysse, J.: A torsion theory in the category of cocommutative Hopf algebras. Appl. Categ. Struct. 24(3), 269–282 (2016)
Gran, M., Sterck, F., Vercruysse, J.: A semi-abelian extension of a theorem by Takeuchi. J. Pure Appl. Algebra 223, 4171–4190 (2019)
Higgins, P.J.: Groups with multiple operators. Proc. Lond. Math. Soc. 3–6(6), 366–416 (1956)
Janelidze, G.: Internal crossed modules. Georgian Math. J. 10, 99–114 (2003)
Janelidze, G., Márki, L., Tholen, W.: Semi-abelian categories. J. Pure Appl. Algebra 168(2–3), 367–386 (2002)
Lavendhomme, R., Roisin, J.-R.: Cohomologie non abélienne de structures algébriques. J. Algebra 67, 385–414 (1980)
Loday, J.-L.: Spaces with finitely many homotopy groups. J. Pure Appl. Algebra 24, 179–202 (1982)
Majid, S.: Strict quantum 2-groups. arXiv:1208.6265
Paoli, S.: Internal categorical structures in homotopical algebra. In: Baez, J.C., May, J.P. (eds.) Towards Higher Categories. IMA Volumes in Mathematics and Its Applications, pp. 85–103. Springer, Berlin (2009)
Patchkoria, A.: Crossed semimodules and Schreier internal categories in the category of monoids. Georgian Math. J. 5(6), 575–581 (1998)
Porter, T.: Homotopy quantum field theories meets the crossed menagerie: an introduction to HQFTs and their relationship with things simplicial and with lots of crossed gadgetry. In: Notes Prepared for the Workshop and School on Higher Gauge Theory, TQFT and Quantum Gravity Lisbon, February, 2011. https://ncatlab.org/timporter/show/HQFTs+meet+the+Crossed+Menagerie
Porter, T.: The crossed menagerie: an introduction to crossed gadgetry and cohomology in algebra and topology. In: Notes Initially Prepared for the XVI Encuentro Rioplatense de Álgebra y Geometría Algebraica, in Buenos Aires, 12–15 December 2006, Extended for an M.Sc. Course (Summer 2007) at Ottawa. https://ncatlab.org/timporter/show/crossed+menagerie
Porter, T.: Extensions, crossed modules and internal categories in categories of groups with operations. Proc. Edinb. Math. Soc. 30, 373–381 (1987)
Radford, D.E.: The structure of Hopf algebras with a projection. J. Algebra 92(2), 322–347 (1985)
Whitehead, J.H.C.: Combinatorial homotopy II. Bull. Am. Math. Soc. 55, 453–496 (1949)
Acknowledgements
Open access funding provided by MTA Wigner Research Centre for Physics (MTA Wigner FK, MTA EK). The author’s interest in the subject was triggered by the excellent workshop ‘Modelling Topological Phases of Matter—TQFT, HQFT, premodular and higher categories, Yetter–Drinfeld and crossed modules in disguise’ in Leeds UK, 5–8 July 2016. It is a pleasure to thank the organizers, Zoltán Kádár, João Faria Martins, Marcos Calçada and Paul Martin for the experience and a generous invitation. Financial support by the Hungarian National Research, Development and Innovation Office—NKFIH (Grant K124138) is gratefully acknowledged. Special thanks to the Anonymous Referee for a thorough review and many helpful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by George Janelidze.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Böhm, G. Crossed Modules of Monoids II: Relative Crossed Modules. Appl Categor Struct 28, 601–653 (2020). https://doi.org/10.1007/s10485-020-09592-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10485-020-09592-z




 then
then  too, for any morphisms
too, for any morphisms 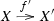 and
and  .
. then
then  , for any morphism
, for any morphism  .
.
 such that
such that  which satisfies
which satisfies 
 belongs to
belongs to 
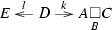 belongs to
belongs to 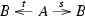 are in
are in  exists).
exists).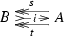 is a reflexive graph).
is a reflexive graph). .
. and
and  then also
then also 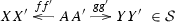 .
. of monoids in
of monoids in  ; so that by the unitality of
; so that by the unitality of 
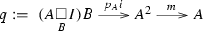 is invertible.
is invertible. such that
such that  and a distributive law
and a distributive law  subject to the following conditions.
subject to the following conditions.  and
and  . Then by the monoidality of
. Then by the monoidality of 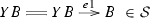 so by [
so by [ in the diagram below.
in the diagram below.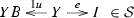 .)
.) 
 such that
such that 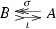 between categories of the common object set X such that the composite
between categories of the common object set X such that the composite 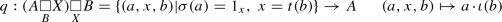
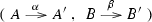 for which
for which 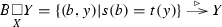 in the sense of [
in the sense of [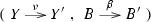 for which
for which 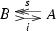 of bimonoids in
of bimonoids in  is invertible.
is invertible. which are compatible with the actions
which are compatible with the actions 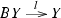 and
and 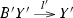 in the sense that
in the sense that  of monoids in
of monoids in  is invertible.
is invertible. which are compatible with the actions
which are compatible with the actions 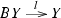 and
and  in the sense that
in the sense that  of bimonoids in
of bimonoids in 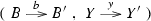 which are compatible with the actions
which are compatible with the actions  and
and  in the sense that
in the sense that  of cocommutative Hopf monoids.
of cocommutative Hopf monoids. which are compatible with the actions
which are compatible with the actions 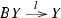 and
and  in the sense that
in the sense that 

 of monoids in
of monoids in  which are compatible with the actions
which are compatible with the actions 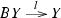 and
and  in the sense that
in the sense that  of group objects.
of group objects. which are compatible with the actions
which are compatible with the actions  and
and  in the sense that
in the sense that 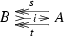 of monoids in
of monoids in  (hence the
(hence the 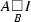 in Theorem
in Theorem  is invertible.
is invertible.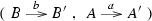 such that
such that  and
and  and a distributive law
and a distributive law  subject to the following conditions.
subject to the following conditions.  and
and  .
. such that
such that  of categories with the common object set X and identity-on-objects functors between them, such that the map (
of categories with the common object set X and identity-on-objects functors between them, such that the map ( and an identity-on-objects functor
and an identity-on-objects functor  such that
such that  such that
such that  of bimonoids in
of bimonoids in 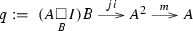 is invertible.
is invertible. such that
such that  for which the following diagram commutes.
for which the following diagram commutes. 
 which are compatible with the actions
which are compatible with the actions  and
and  in the sense that
in the sense that 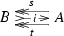 of bimonoids in
of bimonoids in 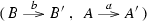 such that
such that  which makes Y both a left B-module monoid and a left B-module comonoid, and a bimonoid morphism
which makes Y both a left B-module monoid and a left B-module comonoid, and a bimonoid morphism  for which the diagram
for which the diagram 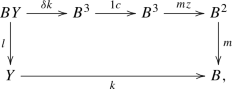
 for which
for which 
 .
. .
.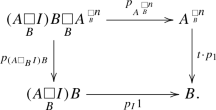


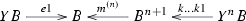 has its legs in
has its legs in  ).
).

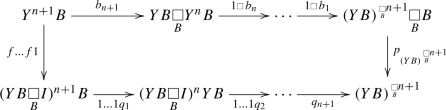

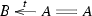 belongs to
belongs to 


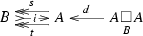 is an
is an  in the category of monoids in
in the category of monoids in  and
and 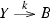 and a distributive law
and a distributive law  subject to the following conditions.
subject to the following conditions.  ,
,  and
and  .
.
 such that
such that 
 and an identity-on-objects functor
and an identity-on-objects functor 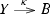 such that
such that 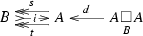 in the category of monoids in
in the category of monoids in  which makes Y both a B-module monoid and a B-module comonoid and a bimonoid morphism
which makes Y both a B-module monoid and a B-module comonoid and a bimonoid morphism  for which the following diagrams commute.
for which the following diagrams commute. 
 such that
such that 
 the bimonoid B in
the bimonoid B in  the bimonoid B in
the bimonoid B in  the following conditions hold.
the following conditions hold.
