Introduction

In many engineering applications materials are subjected to dynamic loads. For cases where materials are subjected to dynamic loads it is necessary to account for any strain rate dependent properties in the design. In order to characterise this rate dependence specific test methods are required. Moderate strain rate loading (1 to 102s− 1) is normally achieved with a high rate hyrdaulic machine or a drop tower system whereas high strain rate (102 to 103s− 1) loading is normally produced using a split Hopkinson pressure bar (SHPB). The main difficulty with all these systems is accurate measurement of the externally applied load.

When using fast hydraulic or drop tower machines ringing from wave reverberation in the load cell corrupts the force measurement. For the standard SHPB method it is also necessary to neglect inertial waves in the test sample and assume that the sample is in a state of quasi-static equilibrium. Materials that have low wave speeds and/or low strains to failure are particularly problematic for the SHPB test. For low wave speed materials a significant amount time is taken for multiple wave reverberations to occur eventually causing inertial effects to damp out. This means the usable portion of the test occurs after the specimen has already undergone significant elastic deformation making it difficult to accurately measure the stiffness of the material [1]. A similar problem occurs for brittle materials which can fail before the inertial effects have damped out corrupting the force measurement. Thus, there is a need for new test methods that can be used to investigate the elastic response of materials at high strain rates.

Recently, the coupling of ultra-high speed imaging (> 1Mfps) and full-field measurements has opened up new avenues for developing high strain rate testing techniques. This effort has mainly focused on applying full-field measurements to complement the analysis of existing methods such as the SHPB [2,3,4,5]. However, the use of full-field measurements combined with inverse identification techniques, such as the virtual fields method, provides an opportunity to create whole new test methods that do not required external load measurement [6,7,8]. This was first explored using the SHPB as a loading device in ref. [6]. The key idea of this new type of test is to use time resolved full-field displacement measurements to obtain acceleration fields. Then, through the virtual fields method (VFM) the acceleration fields are related to the stress state in the material, removing the need for external load measurement. This method was later refined to use an edge-on impact configuration with a first experimental validation on a non-rate sensitive material in [8]. Subsequently, this idea was further developed as the so-called ‘image-based inertial impact’ (IBII) test and has been successfully applied to a variety of materials in refs. [9,10,11].

Based on the same inertial loading concept the image-based ultrasonic shaking (IBUS) test was developed in [12]. In this case the loading is provided by an ultrasonic horn with the dimensions of the sample being selected such that the sample is excited in its first longitudinal resonant mode. This method is complementary to the IBII test providing stiffness information at more moderate strain rates (\(\sim 10^{2}~s^{-1}\)). The use of acceleration-based stress information in high rate testing has also been extended by others to hyper elastic materials [13] and compacting polymeric foams [14] demonstrating the potential for this type of test method to provide material information where traditional test methods are not well suited.

This paper presents a new image-based test which uses acceleration-based stress information for stiffness identification at high strain rates, in a similar manner to the IBII and IBUS tests. In this case the inertial loading is provided by the release wave produced when a sample breaks under a tensile load. Thus, this new test methodology is hereafter referred to as the image-based inertial release (IBIR) test. The general procedure for the IBIR test is to use a standard tensile testing machine to load a long thin sample until it fails. The sample is notched such that it will break near one of the grips of the test machine. This sends a release wave along the sample from the fracture point. Full-field displacement measurements of the release wave are then obtained using an ultra-high speed camera. From the displacement fields the strain and acceleration fields are obtained by numerical differentiation. The virtual fields method (VFM) is then used to extract the stiffness of the material from the kinematic fields with the dynamic loading information provided by the inertial acceleration.

This method of loading the sample is not dissimilar from early torsional split Hopkinson bar designs that used the fracture of a circular epoxy joint to create a torsional release wave to load the test specimen [15]. More modern Hopkinson bar designs for tension and torsional loading now use quick release hydraulic clamping mechanisms to statically pre-load the bar and send a release wave into the test sample [5, 16]. The advantage of this type of system is that it is not destructive allowing for repeated use. However, this type of specialist apparatus is not available in all mechanical testing laboratories.

One of the main advantages of the IBIR method is that it uses a standard mechanical test frame. Pre-loading the sample with a standard test frame also allows the quasi-static stiffness to be identified as part of the test. Once the sample breaks the loading provided by the release wave then allows for the dynamic stiffness to be identified for the same sample. This has the advantage of providing a strain rate stiffness sensitivity information on the same sample in a single test with the only specialist equipment being a camera capable of imaging at \(\sim 1 Mfps\). This article presents a description of the IBIR test method and a first experimental validation of the test on PMMA samples. This paper begins with an overview of the theory required to extract material properties from the full-field measurements using the IBIR test. The following section describes the experimental implementation of the method. The final section of the paper provides a discussion of the limitations along with suggested directions to further develop the method in the future.

Theory

The Virtual Fields Method

The virtual fields method (VFM) is a tool for extracting material properties from full-field measurements. A detailed overview of the VFM theory can be found in [17]. For use of the VFM in inertial tests the reader is referred to refs. [7,8,9,10,11]. Here, the VFM relating to inertial testing will be briefly revisited for completeness.

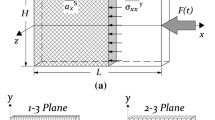
In order to identify material properties from full-field measurements the VFM uses the principle of virtual work, which is the weak form of the dynamic equilibrium equation. The goal here is to apply the VFM to the IBIR test configuration shown in Fig. 1 to derive equations linking the measured kinematic fields to the desired material properties. In the present case, the test can be considered to be 2D plane stress, so if body forces are neglected, the principle of virtual work can be written as follows:

$$ \underbrace{-{\int}_{S} {\sigma}\colon {\epsilon^{*}} dS}_{W_{int}^{*}} + \underbrace{{\int}_{\delta l} {T}\cdot {u^{*}}dl}_{W_{ext}^{*}} = \underbrace{\rho {\int}_{S} {a}\cdot {u^{*}} dS}_{W_{acc}^{*}} $$
(1)

where σ is the stress tensor, S is the surface of the specimen and T is the traction vector over the sample perimeter l. The virtual displacement field is given by u∗ and the virtual strain field 𝜖∗ is given by \(2\epsilon _{ij}^{*} = u_{i,j}^{*} + u_{j,i}^{*}\) where the comma indicates partial differentiation, and i,j are x and y for a plane stress problem. The density of the material is given by ρ and acceleration is a. Note that the kinematic fields are functions of both space and time however the function notation has been omitted for simplicity. The next part of the VFM procedure requires that virtual fields are substituted into Eq. 1. Two types of virtual fields are used in the present study, the first are rigid body virtual fields and the second are piece-wise special optimised virtual fields. Both of these are discussed below.

Fig. 1
figure 1

Schematic of an IBIR test sample showing the region of interest (ROI) that is imaged during the test

Full size image

Rigid body virtual fields

There are three different approaches for using rigid body virtual fields to produce stress-strain curves for stiffness identification. The most general approach is to use the generalized stress-strain curve procedure described in ref. [18]. However, the use of the generalized stress-strain curves requires that the kinematic fields are sufficiently heterogeneous to activate all terms in the equations. For the simple IBIR test configuration presented here this will not be the case so this approach will not be considered. In the future it would be interesting to use more heterogeneous test configurations which would enable the use of the generalized stress-strain curve procedure. This would need a more complex specimen shape in the field of view to generate wave propagation patterns leading to multi-axial stress states.

The second approach uses a rigid body virtual field describing a rigid translation along the axial direction of the sample: \(u_{x}^{*} = 1\), \(u_{y}^{*} = 0\) (for this case the virtual strains are zero). It has been previously shown in refs. [8,9,10,11] that this virtual field leads to an equation which relates the average axial stress directly to the acceleration as follows:

$$ \overline{\sigma_{xx}}^{y} = \rho x_{0} \overline{a_{x}}^{S_{0}} $$
(2)

where \(\overline {\sigma _{xx}}^{y}\) is the average axial stress along a horizontal slice of fixed x-coordinate, x0 is the distance from the bottom edge of the ROI to the section of interest and \(\overline {a_{x}}^{S_{0}}\) is the average axial acceleration over the surface between the considered section and the bottom edge of the ROI. The parameters for Eq. 2 are shown graphically in the inset of Fig. 1.

For the IBIR test presented here, Eq. 2 is valid as long as the bottom edge of the ROI (co-ordinate system origin in Fig. 1) can be considered stress free (i.e. until the release wave reaches the bottom edge). It should also be noted that the reference configuration is the fully stretched one here, so the release wave will be considered as a compressive wave. This is valid as long as the material remains in its linear elastic region (principle of superposition). The present paper is aimed at elastic stiffnesses only, but the IBIR test has also potential for non-linear materials. It would just require a more more complex VFM formulation as reported in [13] for instance. This is however beyond the scope of the current paper.

For the isotropic material considered here the x component of stress is given by σxx = Qxx(𝜖xx + ν𝜖yy). Therefore, the stiffness component Qxx can be obtained by plotting the average stress, \(\overline {\sigma _{xx}}^{y}\), against the average strain, \(\overline {\epsilon _{xx}+\nu \epsilon _{yy}}^{y}\), and linearly fitting the elastic response. The main drawback of this approach is that the Poisson’s ratio must be known beforehand. Previously, this problem has been solved by using the general VFM to first obtain the Poisson’s ratio and then use this to calculate the average strain [10, 11]. This method will be used in this paper.

The final approach is to assume that the test sample is in a state of uni-axial strain. In this case the y strains only come from the Poisson effect and the constitutive equation is simplified to σxx = E𝜖xx. For this case it is possible to plot \(\overline {\sigma _{xx}}^{y}\) against \(\overline {\epsilon _{xx}}^{y}\) and linearly fit the elastic response to obtain the elastic modulus. Given the sample geometry used here it is likely that the uni-axial assumption will hold. However, processing with the uni-axial assumption will be compared with the second approach in the dynamic stiffness identification section (“Dynamic Stiffness Identification”) in order to verify this.

The strength of using such rigid body virtual fields is that one can resolve stiffness spatially, as each transverse section provides a stiffness value. So in the case of heterogeneous materials, there is no need for parameterisation of the spatial stiffness variation. Further work is currently underway to extend this idea by obtaining spatially-resolved stress information [19].

Special optimised virtual fields

When processing the IBIR test data it is also possible to identify the stiffness using the more general VFM procedure where a constitutive law is substituted into the external virtual work term. This gives the stiffness components as a function of time averaged over the whole ROI. In this study the special optimised virtual fields method will be used in a similar manner to refs. [8,9,10,11, 20] where the virtual fields are formulated based on piece-wise functions similar to a finite element mesh. It should be noted that in this case, one needs to assume a distribution for the spatial stiffness variation of the material. Here, the material will be considered elastically homogeneous at the scale of the measurements. For heterogeneous materials, piecewise [21], polynomial [22] or harmonic [23] expansions have been considered in the past.

Another important consideration when using the general virtual fields procedure is the boundary conditions applied to the virtual fields themselves. In the IBII test described in refs. [9,10,11] all boundaries of the sample can be considered free apart from the impact edge. Therefore, a virtual boundary condition is applied to constrain virtual displacement in the impact direction to be zero. For the IBIR test configuration shown in Fig. 1 this type of virtual boundary condition will only be suitable until the point at which the wave starts to exit the ROI. Another approach for the IBIR configuration would be to constrain the axial or ‘x’ virtual displacement of the nodes at the top and bottom of the ROI. These two types virtual boundary conditions will be compared in the dynamic stiffness identification section of this article (“Dynamic Stiffness Identification”).

The Grid Method

The use of the VFM for material property identification requires full-field displacement measurements. One of the most common full-field displacement measurement techniques is digital image correlation (DIC). However, the grid method has been used for previous implementations of imaged-based inertial tests as it offers an improved trade-off between spatial and measurement resolution when compared to DIC for two dimensional problems [24]. This is especially important because of the low pixel count for current ultra-high speed cameras (e.g. the Shimadzu HPV-X and X2 with 400 × 250 pixels). A detailed review of the grid method theory and practical implementation is given in [25] so only the main features will be briefly described here.

The grid method uses a periodic ‘grid’ pattern bonded to the surface of the test sample. Phase maps are extracted from each image of the pattern using a windowed discrete Fourier transform. The phase is defined between between π and − π. Therefore, when the displacement is above one grid pitch discontinuous jumps occur in the phase in space or time. This is known as phase wrapping and can be corrected for using a suitable ‘unwrapping’ algorithm. Here, the spatial unwrapping algorithm described in [26] was used as well as an in-house temporal unwrapping algorithm as described in [9]. The basic form of the grid method relates the difference in phase between two images directly to the displacement. However, when using imperfect grids in a real experiment it is beneficial to use an iterative procedure which transforms the grid back to the reference configuration as described in [25, 27]. In this case the direct phase subtraction serves as an initial guess for the iterative procedure. This is the version that was used in this work.

Experimental Method

Material and Test Set-up

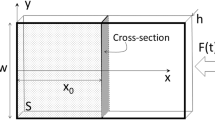
Three poly-methylmethacrylate (PMMA) samples were tested, the nominal geometry of each sample was 760 × 10 × 2.8 mm. The geometry of the cross section near the ROI was measured for each individual sample with a calliper. Each sample was notched across the width on the front and back face using a razor blade. The notch was located 100 mm from the top of the sample allowing 50 mm of the sample to be gripped and a 50 mm gap between the grip and the notch. The top of the ROI for each sample was located at Lwp = 250 mm from the notch. The ROI was spray painted black and a white transferable grid pattern was applied, similar to the grids described in ref. [12]. The density of the material was measured using a small section of the sample taken after the test. This analysis gave a density of 1185 ± 3 kg.m− 3.

The samples were loaded until failure in displacement control at 1 mm/min using an electromechanical load frame equipped with a 5 kN load cell. The maximum load at failure was recorded for each sample. An annotated photograph of the main components of the experimental set-up is shown in Fig. 2. The samples were imaged with a Shimadzu HPV-X camera with a Sigma 105mm macro lens and illumination was provided by a Bowens Gemini Pro flash. The relevant imaging and full-field measurement parameters are summarised in Table 1.

Fig. 2
figure 2

Experimental set-up with close up view of the break trigger mechanism used for triggering the camera

Full size image
Table 1 Imaging and full-field measurement parameters
Full size table

A particular challenge with dynamic image-based tests is triggering and synchronising the camera and the flash; that is, the flash must be triggered before the camera to ensure that the light level is usable over the test duration accounting for the rise time of the flash. The flash used in this study has a rise time of 100 μs to reach 50% of the peak intensity. For each sample the exact fracture load is not known a priori. Therefore, it is necessary to trigger the flash directly from the failure of the notch. Triggering the camera and flash using this method means that the ROI must be located far enough from the notch such that the release wave is not yet quite within the ROI when the camera begins recording. The required distance between the notch and the ROI was estimated using simple one dimensional wave mechanics. Calculation of the longitudinal wave speed of a material requires the elastic modulus and density. However, the elastic modulus of PMMA is expected to increase significantly with strain rate. Using previous data collected in our laboratory with the IBII and IBUS tests the modulus was expected to be \(\sim 5~GPa\) in the strain rate range between 102 and 103s− 1 [12, 28]. Taking the density of PMMA to be 1185 kg.m− 3 as measured, the longitudinal wave speed was calculated to be: \(c = \sqrt {E/\rho } = 2050~m.s^{-1}\). Using this wave speed the release wave will propagate a distance of 205 mm over the rise time of the flash. Therefore, a distance of 250 mm between the notch and the top of the ROI allows for the variability of the trigger mechanism with several undeformed frames before the wave enters the ROI. Note that the flash will not have reached peak intensity at the start of the test given that the rise time was chosen based on the flash reaching 50% of the peak intensity. This threshold was chosen based on minimising the distance between the notch and the ROI. To avoid the use of unfeasibly long specimens, the use of more flexible illumination sources (pulsed lasers, tunable flashes) would significantly relax this constraint and make the test easier to conduct.

A close up image of the ‘break’ trigger mechanism is shown in Fig. 2. The trigger is created using copper tape on either side of the notch with the gap being bridged using conductive graphite paint. The two graphite paint bridges across the notch are connected in series such that breaking either bridge will send a trigger signal. Two wires are soldered to the copper tape, these wires are then connected to the trigger port on the camera. It is recommended that some strain gauging tape is used to provide strain relief to the wires such that the copper tape does not accidentally debond from the sample under the weight of the trigger wires. Note that the graphite paint must be left to dry for at least a half hour before testing as the paint needs to be as brittle as possible to ensure reliability of the trigger. Once the ‘break’ trigger sends a signal to the camera the flash is immediately triggered and the camera is set to start recording after a 100 μs delay allowing for the rise time of the flash and the travel of the release waves, as detailed thereafter.

The frame rate for samples 1 and 2 was set to 1 Mfps and once the reliability of the trigger mechanism was established the frame rate was increased to 2 Mfps for sample 3 to maximise temporal resolution. Note that the integration (shutter) time was kept constant for all samples at 0.2 μs, which was good enough to prevent any significant image blurring. Two sequences of images were taken for each sample. The first set of images was taken once the sample was mounted in the test machine before any loading was applied, giving a static reference for the undeformed sample. This image sequence was used for the quasi-static stiffness identification and for the measurement resolution analysis. The second image sequence corresponded to the dynamic portion of the test and was used with the VFM for stiffness identification. Care was taken to ensure that the first few frames of the dynamic recording were taken before the release wave reached the ROI, so that these images contain information about the quasi-static deformation just before the fracture of the specimen.

Data Processing and Measurement Resolution

All grid method image analysis was implemented using the Matlab code made freely available as part of refs. [25, 27]Footnote 1. In order to determine the quasi-static stiffness the first image was taken from the static reference sequence and correlated with the first image in the dynamic sequence (before the release wave has entered the ROI) using the grid method. This allowed the displacement fields to be obtained from which the strain fields were derived using a centred finite difference method. For each sample the maximum load at failure was recorded and the average axial stress was calculated using the initial dimensions of the sample cross section. The axial strain was determined by taking the average over the whole ROI, no smoothing was applied to the strain prior to averaging. The elastic modulus was then calculated by taking the ratio between the stress and strain. The average transverse strain was determined in a similar manner to the axial strain and the Poisson’s ratio was calculated by taking the negative of the ratio between the transverse and axial strains. When using the grid method one pitch of data is lost on the borders of the sample. Thus, for the quasi-static analysis this data was not extrapolated and the averages over the ROI only included data inside one pitch of the sample edge. This is possible here as the strain field is nominally uniform in the field of view before the release wave reaches the ROI.

The dynamic portion of the test was processed using the same procedures developed for analysing IBII test data as in refs. [9,10,11]. A detailed description of the data processing procedures and code for IBII test analysis can be found in [29]. Note that the strain fields for the quasi-static tests were calculated using the same functions implemented in the IBII processing code. For the dynamic stiffness identification it was necessary to smooth the displacement fields prior to numerical differentiation to obtain the desired resolution for the strain and acceleration fields. The smoothing kernels used for each sample and the associated measurement resolutions are summarised in Table 2 The measurement resolution for each variable was taken as the standard deviation of the noise maps. Normally it would be necessary to perform an image deformation sweep to select optimal smoothing parameters and estimate the associated random and systematic error on the identification as in refs. [10, 11, 30,31,32]. However, previous experience with image deformation simulations for the IBII test has shown that the measurement error does not vary significantly with the selected smoothing kernels, as long as extreme values are not selected. Therefore, the smoothing kernels given in Table 2 were taken based on these results. Note that for specimen 1 it was found that part of the grid near the wave exit edge debonded from the sample during the dynamic portion of the test. Therefore, the ROI was limited to the top 62 mm of the sample.

Table 2 Smoothing parameters and measurement resolution analysis for all samples tested
Full size table

A copy of all raw image data can be found in the data repository detailed at the end of the manuscript. The data repository also includes a copy of the IBII processing code and the associated output for each sample.

Results and Discussion

Quasi-static Stiffness Identification

The results of the quasi-static stiffness identification for the three tested samples are summarised in Table 3. There is some variation in the fracture load for all samples which is a result of manually creating the notch using a razor blade. However, the stiffness identification is quite consistent between all samples tested. These stiffness results also compare well to the expected values for PMMA under quasi-static loading conditions previously obtained in our lab [12] and others [3, 33,34,35,36], where the quasi-static modulus is normally on the order of 3 GPa and the Poisson’s ratio is close to 0.35. One of the key assumptions of the quasi-static stiffness identification procedure used here is that the material within the ROI (i.e. material far from the notch) behaves linear elastically until the notch fractures. Based on comparison with previous data for PMMA it would appear that this assumption is mostly valid here [37].

Table 3 Quasi-static test results
Full size table

The main limitation on the quality the quasi-static results is due to the flash lighting system used. The trigger of the camera is set such that for the first frame in the sequence the flash is at 50% of its peak intensity. This means that the first image in the dynamic sequence is relatively dark and does not provide an optimal signal to noise ratio. One would also assume that the limited pixel array size of the ultra-high speed camera would impact the results. However, as the quasi-static strain fields are nominally uniform it is unlikely that this is the case. The main benefit of using a larger pixel array for the quasi-static portion of the test would be to have decreased sensitivity to noise through additional displacement smoothing.

For future use of this test method it is recommended that a standard machine vision camera system is set up in a back-to-back configuration with the ultra-high speed camera. This could be done using a single camera with the grid method or a stereo digital image correlation set-up. The use of a standard camera system will allow for multiple images to be taken during the loading process giving much more data redundancy and noise rejection in the elastic loading regime rather than the simple two image correlation used here. This will also remove the need to assume the material behaves linear elastically until failure as the whole quasi-static loading history will be available. The procedure described previously using the ultra-high speed camera images can still be used and would serve as a secondary verification for the value obtained with standard camera set-up.

Dynamic Fields

A sequence of the kinematic fields for specimen 1 is shown in Fig. 3. The time region shown in this figure corresponds to the time over which the longitudinal release wave propagates through the ROI. Analysis of the axial acceleration fields (middle column in Fig. 3) shows that the release wave starts to pass out of the ROI approximately 35 μs after the start of the test. The time point at which the wave passes outside the ROI is critical as this will determine the time period over which someFootnote 2 of the dynamic stiffness identification procedures can be used. A more precise analysis of the time at which the wave leaves the ROI can be gained by analysing the average axial acceleration over the width of the sample near the edge of the ROI, \(\overline {a_{x}}^{y}\), as a function of time as shown in Fig. 4. Once the acceleration signal rises above the noise this time point can be taken to indicate when the wave has begun to exit the ROI. This is shown in Fig. 4 giving a time of t = 32 μs for the wave to reach the end of the ROI for specimen 1. A similar analysis for specimen 2 gave a threshold time of 37 μs and for specimen 3, 30.5 μs. These thresholds will be used in the next section to constrain the time period over which some of the identification techniques are valid.

Fig. 3
figure 3

Time sequence of the kinematic fields for specimen 1 at 5 μs intervals. This corresponds to every fifth frame at 1 Mfps. The right-hand side of the maps corresponds to the top of the specimen as depicted in Figs. 1 and 2. Note that the colorbar range is constant for all images in the sequence

Full size image
Fig. 4
figure 4

Average axial acceleration at the exit edge of the ROI for all tested samples. The time point at which the wave begins to exit the ROI is indicated with a circle of the same colour as the average acceleration for that sample

Full size image

While it is not shown in Fig. 3 the axial strain rate maps show the same general pattern as the acceleration maps with a peak magnitude on the order of \(\sim 800~s^{-1}\) for this specimen. Note that image sequences of all kinematic fields for all samples can be found in the data repository detailed at the end of this manuscript.

Dynamic Stiffness Identification

The kinematic fields shown in the previous section were used to identify the stiffness components under dynamic loading for all tested samples using the VFM. The identification as a function of time using the special optimised virtual fields procedure is shown in Fig. 5. This includes the case where boundary conditions are only applied to the input edge of the ROI (1 BC, Fig. 5a and b) and the case where boundary conditions are applied to the input and exit edge (2 BCs, Fig. 5c and d). Note that a mesh sensitivity study was conducted and it was found that the stiffness identification was insensitive to the virtual mesh for mesh densities between 7 × 4 and 9 × 6 elements. A smaller number of elements was found to cause more instability in the early portion of the test. This type of response is typical of such virtual fields [17]. For the first 10 μs of the test the wave has not fully entered the ROI so the time axis in Fig. 5 has been truncated to this point. During the initial portion of the test there is not enough information encoded in the kinematic fields to identify the stiffness components. Eventually, the identification stabilises until the point at which the wave starts to exit the ROI.

Fig. 5
figure 5

Dynamic stiffness identified as a function of time using the special optimised virtual fields for all specimens using boundary conditions on one (1 BC) or two edges (2 BCs). a and cQxx and b and dQxy. The quasi-static stiffness is shown with a black dashed line and the average identified stiffness for each sample is shown as a dashed line with the same colour as the VFM identification over time. Note that the average identified stiffness was taken between the time at which the wave exits the ROI and 18 μs before this time

Full size image

Comparison of Fig. 5a and b shows that the identification of Qxy is noisier than Qxx. This is expected due to the difficulty in accurately resolving the small transverse strains. An average identified stiffness value can be obtained for each specimen by averaging over the time range for which the identification is stable and the wave has not reached the bottom end of the ROI. For all specimens the average was taken over an 18 μs window ending at the wave exit time previously provided for each specimen. The average identified stiffness for each specimen is given in Table 4 and shown as a dashed line in Fig. 5. The results are quite consistent between specimens, the main difference appears to be that the identification for specimen 3 (frame rate of 2 Mfps) is slightly noisier. This is a result of the difference in frame rate leading to a different level of regularisation for the acceleration (see Table 2). However, the average identified stiffness for sample 3 is consistent with the other two samples suggesting that a 1 Mfps frame rate is sufficient for stiffness identification in this case, though this would need to be confirmed by synthetic image deformation as presented in refs. [10, 11, 32]. This result was expected as the material wave speed is rather low here and the strain rates somewhat lower than in IBII tests, leading to less challenging acceleration reconstruction.

Table 4 Dynamic stiffness identification results for all methods
Full size table

Finally, comparison of the results for one or two virtual boundary conditions shows that the identified stiffness does not differ significantly for these cases. One would expect that the identification would be stable for a longer period of time when using both virtual boundary conditions as the acceleration passing outside the ROI does not violate the assumptions of the analysis. However, once the acceleration starts to exit the ROI there is less information to identify the stiffness parameters, regardless of the virtual boundary conditions. This explains why there is only a minimal difference between the two cases of virtual boundary conditions considered here.

The stiffness was also identified by linearly fitting stress-strain curves constructed using the stress-gauge (2) with and without the uni-axial assumption. A series of fitted stress-strain curves for each specimen is shown in Fig. 6. The Poisson’s ratio for calculating the average strain term was taken from the special optimised virtual fields procedure (see Table 4). Similarly, the stress-strain curves constructed using the uni-axial assumption are shown in Fig 7. The stress-strain curves in Figs. 6 and 7 have been truncated to only include data points before the wave starts to leave the ROI. As expected, the stress-strain curves near the point at which the wave leaves the ROI (x0 = 0.25l) contain significantly less data points than the curves near the wave entrance point (x0 = 0.75l). Therefore, it is expected that the stiffness identified near the wave exit edge will be not be as reliable. This is shown in Fig. 8 which gives the identified stiffness as function of position for all specimens. Averaging over the middle 50% of the specimen where the identification is stable gives a single representative stiffness value for each sample. The average stiffness for each sample is summarised in Table 4 and shown graphically on Fig. 8.

Fig. 6
figure 6

Dynamic stress-strain curves and linear fit for each specimen at 0.25l, 0.5l and 0.75l using the standard approach with the Poisson’s ratio taken from the optimised virtual fields. Each row of the figure corresponds to a different specimen and each column corresponds to a different position from the edge of the ROI. The number of points shown on each curve is only given up to the point at which the wave starts to move outside the ROI

Full size image
Fig. 7
figure 7

Dynamic stress-strain curves and linear fit for each specimen at 0.25l, 0.5l and 0.75l using the uni-axial assumption. Each row of the figure corresponds to a different specimen and each column corresponds to a different position from the edge of the ROI. The number of points shown on each curve is only given up to the point at which the wave starts to move outside the ROI

Full size image
Fig. 8
figure 8

Identified dynamic stiffness, Qxx, as a function of length for all specimens obtained by linearly fitting the stress-strain curves constructed with equation 2. The quasi-static value is shown as a black dashed line and the average identified for each sample is shown as a dashed line of the same colour

Full size image

Comparison of the stress-strain curves (Figs. 6 and 7) and identified stiffness as a function of position (Fig. 8a and b) shows essentially no difference between the uni-axial assumption and the standard approach including the Poisson effect. This is not surprising given the long thin sample geometry used here. In the future it would be interesting to use more complex geometry in the test section to obtain a more heterogeneous stress-state. In this case the uni-axial assumption will not hold but it should be possible to design the test sample to have enough information to use the generalized stress-strain curve procedure described in [18].

Another parameter of interest is the maximum strain rate achieved during the test. Thus, the maximum absolute value of the strain rate is reported for each specimen in Table 4. All specimens achieved a peak strain rate in the mid to high 100’ss− 1. It is interesting that the peak quasi-static load before fracture (Table 3) correlates with the peak strain rate achieved during the test. This would suggest that the strain rate could be controlled by more careful design of the notch geometry. This is an interesting area for future work and will be discussed further in the next section.

Comparing the identified stiffness values to the quasi-static results (Table 3) shows a significant rate dependence for both the elastic modulus and the Poisson’s ratio. This agrees well with previous studies analysing rate dependence of the stiffness of polymers such as PMMA [37]. The identified elastic modulus for the special optimised virtual fields and stress-strain curves is quite consistent. Both methods give an elastic modulus near 5 GPa under dynamic loading. This compares reasonably well with existing data in the literature for PMMA at strain rates between 102s− 1 and 103s− 1 [3, 33,34,35]. The IBUS test in [12] gives a storage modulus of \(\sim 5.5~GPa\) in the strain rate range between 50 − 150 s− 1. This strain-rate range is in the same order of magnitude as this and the identified modulus is similar. Differences between these results are possibly due to the fact that the samples for the IBUS tests in [12] were obtained from a different plate of source material. In the future, IBUS experiments will be run on the PMMA samples used in this study which will provide a comparison that does not include the effects of material variability.

It is much more difficult to find comparison data in the literature for the Poisson’s ratio reported here. In [38] there was an attempt to analyse the Poisson’s ratio for another amorphous polymer, polycarbonate, during SHPB tests. This study focused on analysing the Poisson’s ratio when the samples were subjected to large plastic strains. However, in [38] the measurements were relatively noisy in the elastic regime making it difficult to draw any comparisons with the data in the present study.

Further analysis of data previously collected in our laboratory using the IBUS methodology showed a Poisson’s ratio of 0.22 in the first part of the test (before the temperature had increased significantly). Note that this value was obtained using the data collected in [19] by taking the ratio of the strain components over the middle half of the sample where the strains are largest. The peak strain rate for this portion of the IBUS test was 170 s− 1, which is within the same order of magnitude as this study. As the Poisson’s ratio obtained with the IBUS test compares reasonably well to the values obtained in this study this would suggest that there is a rate dependence for the Poisson’s ratio of PMMA in the elastic regime. Further support for this conclusion can be obtained by considering models of polymer constitutive behaviour. The model outlined in ref. [39] predicts a decrease of Poisson’s ratio with decreasing temperature. If the time-temperature superposition principle holds then a decrease in temperature corresponds to an increase in strain rate indicating that the Poisson’s ratio may be expected to decrease with increasing strain rate. So overall, the stiffness identification results for PMMA obtained with the IBIR test are consistent and compare well with existing literature.

It could be argued that for this test configuration one could obtain the elastic modulus by using strain gauges on the test sample and one-dimensional wave theory in a similar manner to the SHPB. However, this would limit the analysis of the test to be one-dimensional preventing the use of more heterogeneous stress-states. For example, it would be possible to use the IBIR test on an off-axis open hole composite sample (as defined in [40]) to obtain all four stiffness components simultaneously at quasi-static and high strain rates. In this case one-dimensional wave analysis is not possible.

Limitations and Future Work

There are several assumptions made in the analysis of the IBIR test data. These mainly stem from the limitations of the imaging system used and the fact that only surface displacement measurements are collected during the test.

Quality of the quasi-static data:

A detailed discussion of the limitations of the quasi-static analysis is given in “Quasi-static Stiffness Identification”. Here, it is re-iterated that a standard camera system can be used (in a back-to-back configuration if needed, to mitigate the effects of possible out-of-plane bending during the loading) for the quasi-static portion of the test to alleviate the issues associated with using the ultra-high speed camera for the quasi-static stiffness identification.

Three-dimensional effects:

Identification of the stiffness from two dimensional surface measurements requires the assumption that the sample is in a state of plane stress and that the kinematic fields are uniform through-thickness. Three-dimensional effects are likely to be important near the notch or near the test machine grips. When the sample first fails near the notch it will not instantaneously release, it will take some short period of time for the crack to propagate through-thickness. Therefore close to the notch the kinematic fields may not be uniform through-thickness. However, as the wave propagates away from the notch location a dynamic St Venant effect will occur causing the wave front to become more uniform similar to ref. [41]. In the present study the ROI is located a relatively long distance from notch when compared to the thickness of the sample through which the crack must propagate (\(t/L_{wg} \sim 89\)). Therefore, it is highly likely that the assumption of through-thickness uniformity is valid. This could be experimentally verified using two back-to-back ultra-high speed cameras, a mirror arrangement with a single camera or even a strain gauge.

This is only a first proof-of-principle validation of the IBIR test and there are many possible avenues for future developments, including:

Pulsed laser illumination:

Compared to the photographic flash used in this work a pulsed laser has a very low rise time that allows it to directly synchronise with the camera as it is triggered. This would mean that the positioning of the ROI would not need to account for the rise time of the light system. The only major limitation on positioning the ROI would be based on three-dimensional effects as mentioned previously. Further work is needed with explicit dynamics finite element models to try and determine the minimum distance between the notch and ROI to ensure that three dimensional effects are not causing a significant error on the stiffness identification.

Test design:

The results of this study show that the fracture load correlated with the observed peak strain rate in each test sample. This means that it should be possible to design different mechanical ‘fuses’ to tune the applied strain and strain rate by changing either the geometry or material used. In this first implementation of the IBIR test the sample itself was used as the mechanical fuse for simplicity. However, it would also be possible to use different materials for the fuse and test sample with some sort of grip or attachment mechanism connecting them in series. Obviously, the fuse would need to be designed to fail before the sample in this case. The key issue with a gripping mechanism would be the presence of three dimensional effects, as previously discussed, but it should be possible to analyse this using back-to-back imaging and/or finite element modelling. Using a different material for the mechanical fuse and test sample would also allow materials that do not fail abruptly (e.g. materials that damage progressively before failure) to be tested with this method. In this case, PMMA could be used as the fuse with the notch designed to fail before significant damage formed in the test sample. Additionally, the IBIR test method is not limited to the simple uniform rectangular geometry considered here. In fact, it is possible to have any geometry within the ROI as long as the mechanical fuse which generates the release wave is designed to fail before the material in the ROI. The design process could be optimised using a parametric sweep of a suitable finite element model. A basic example of extending the IBIR test would be to use an off-axis unidirectional carbon fibre composite sample along with the analysis procedures described in [18, 42] to obtain the in-plane transverse and shear modulus in the same test. It could even be extended to the full set of orthotropic stiffness components using a short open-hole off-axis specimen as in [40].

Biological materials:

A major issue when testing biological tissue samples, such as bone, is that there can be significant variability between samples. This can be problematic as it is difficult to separate biological variability from rate dependence. The IBIR test has a significant advantage in that the quasi-static and dynamic stiffness can be identified on a single sample in a non-destructive manner. The sample could then be tested to failure using the IBII test method providing stiffness measurements at three different strain rates for a single test sample. This has the potential to cleanly separate strain rate dependence effects from specimen to specimen variability.

Rate-Sensitivity Identification:

In the first implementation of the IBIR test presented here, only a single elastic modulus and Poisson’s ratio was assigned to the high strain rate data. However, the inertial nature of this test means that the sample experiences a range of strains and strain rates. This is an advantage as it is possible that the test encodes enough information to identify a stiffness model that is a function of strain rate. To illustrate this, consider Fig. 9 which shows the histogram of data points for specimen S1 in terms of strain and strain rate. Here we observe that the IBIR test sweeps a range of data points in strain/strain rate space which may be enough to identify a rate sensitive material model. This would need to be investigated further using a finite element model and image deformation simulations to determine if the relevant material parameters could be identified with sufficient accuracy. The idea of identifying a rate sensitive material model using the heterogeneous strain rate fields from an inertial test has already been suggested in [12, 43] and a first attempt at identifying the rate sensitive parameter of a Johnson-Cook material model was made in [44, 45] for metallic materials. However, applying this type of analysis to the rate dependent stiffness of polymeric materials is an open and exciting research question.

Fig. 9
figure 9

Histogram of measured data points as a function of strain and strain rate for S1

Full size image

Conclusion

This work presents the first experimental validation of a new image-based inertial test method for measuring the stiffness of a material under both quasi-static and dynamic loading. The Image-Based Inertial Release (IBIR) test uses a standard tensile test machine to load a sample until failure. The release wave generated by the sample failing is used to identify the dynamic stiffness. The main outcomes of this study are summarised as follows:

  1. 1.

    An experimental validation of the IBIR test was performed demonstrating the identification of the quasi-static and dynamic stiffness using the same test sample.

  2. 2.

    The quasi-static elastic modulus of the PMMA samples was identified as 2.98 GPa and the dynamic elastic modulus was identified as 4.97 GPa at strain rates on the order of 450 − 800 s− 1.

  3. 3.

    The Poisson’s ratio of the PMMA samples was shown to be rate dependent with a quasi-static value of 0.37 and a dynamic value of 0.25.

  4. 4.

    The identified stiffness values under both quasi-static and dynamic loading were found to agree well with data in the literature and data obtained with the IBUS test.

  5. 5.

    The test is complementary to the IBUS and IBII methods providing stiffness data at quasi-static and moderate strain rates in the range of 102s− 1. Coupling this test method with the IBUS and IBII test would provide stiffness data spanning several orders of magnitude.

There is considerable room for developing the IBIR test method further by changing the notch geometry or material to tune the applied strain rate or by changing the geometry within the ROI to achieve more heterogeneous stress states. A major advantage of the IBIR test method is that it does not require any specialist equipment apart from an ultra high speed camera. Given that recent generations of standard high speed cameras are capable of imaging at 1 Mfps, this test method could be useful for those wanting a method for high rate stiffness identification without having to invest in specialist equipment. The main drawback of standard high speed cameras is the limited pixel array size with a high aspect ratio at the highest frame rates. Fortunately, this suits the long thin specimen geometry used here. An example system would be the 726 camera from iX. This camera can record at 1Mfps with a window of 336 × 42 pixels, which should be enough to obtain the stiffness components for an isotropic sample. Image deformation studies could be performed to explore the feasibility in more depth. In the future, ultra-high speed imaging technology will improve and reduce in cost opening up a large area for the development of new image-based inertial tests for high strain rate material property identification, providing data that has not been available previously.