Abstract
This paper discusses the fitting of linear state space models to given multivariate time series in the presence of constraints imposed on the four main parameter matrices of these models. Constraints arise partly from the assumption that the models have a block-diagonal structure, with each block corresponding to an ARMA process, that allows the reconstruction of independent source components from linear mixtures, and partly from the need to keep models identifiable. The first stage of parameter fitting is performed by the expectation maximisation (EM) algorithm. Due to the identifiability constraint, a subset of the diagonal elements of the dynamical noise covariance matrix needs to be constrained to fixed values (usually unity). For this kind of constraints, so far, no closed-form update rules were available. We present new update rules for this situation, both for updating the dynamical noise covariance matrix directly and for updating a matrix square-root of this matrix. The practical applicability of the proposed algorithm is demonstrated by a low-dimensional simulation example. The behaviour of the EM algorithm, as observed in this example, illustrates the well-known fact that in practical applications, the EM algorithm should be combined with a different algorithm for numerical optimisation, such as a quasi-Newton algorithm.
Similar content being viewed by others
1 Introduction
Linear state space (LSS) models represent a well-established class of predictive time-domain models for dynamic modelling of time series data [1, 2]. In numerous fields of science and engineering, LSS models have been applied successfully to a broad variety of tasks; in particular, many tasks requiring processing of multi-channel time series data recorded from complex natural or technical systems can be addressed by variants of LSS modelling. Usually, the core element of LSS modelling is an inversion algorithm like the famous Kalman filter or a numerically improved variant of it, such as a square-root Kalman filter [1, 3]. A Kalman filter performs a recursion through the given data in forward direction; afterwards, a second recursion through the data in backward direction may be performed by a smoother, yielding improved state estimates.
State space models contain a set of model parameters, describing the dynamical properties of the underlying system and of the observation process generating the data. These parameters usually form a set of four matrices, namely the state transition matrix, the observation matrix, and two covariance matrices pertaining to the two noise processes arising in state space models: dynamical noise and observation noise. The estimation of the parameters in these matrices from given data forms a central part of the process of system identification [4]. Since usually the sequence of states cannot be observed directly, estimating the parameters requires appropriate numerical approaches, based on the optimisation of some kind of quality function; the arguably most famous quality function is given by the likelihood of the data, as a function of the parameters, or by information criteria based on the likelihood [5]. Frequently chosen algorithms for maximising the likelihood are given by the expectation maximisation (EM) algorithm [6, 7], gradient-based algorithms of Newton-Raphson type, or the Nelder-Mead simplex algorithm [8].
In this paper, we discuss a particular class of LSS models, to be denoted as independent components linear state space (IC-LSS) models [9], which has been introduced for the task of Blind Signal Separation, i.e. for decomposing multivariate time series which are assumed to represent mixtures of (approximately) independent source signals. It is furthermore assumed that each source signal can be modelled by an autoregressive moving-average (ARMA) process of preselected order. These assumptions generate a particular structure of the parameter matrices of these LSS models which needs to be taken into account when estimating these parameters, i.e. specific constraints have to be imposed on these matrices.
While in previous work we have exclusively employed Newton-Raphson and Nelder-Mead simplex algorithms for the task of maximising the likelihood [9, 10], in this paper, we explore the EM algorithm, since it has become a standard tool for estimating parameters of LSS models. The concept of applying the EM algorithm, as introduced by Dempster et al. in 1977 [6], to this particular optimisation task, has been proposed by Shumway and Stoffer in 1982 [7]. Almost simultaneously, a similar suggestion was published by Watson and Engle [11].
Excellent presentations of the application of the EM algorithm to the task of estimating the parameters of LSS models have recently been provided by Gibson and Ninness [12] and by Särkkä [13], but these authors only discuss the unconstrained case. It is surprising that so far there are only few papers that would discuss the case of constrained estimation by the EM algorithm, since in a general LSS model any attempt to estimate the unconstrained parameter matrices simultaneously will suffer from identifiability issues. These issues arise due to the existence of a case of parameter redundancy between the observation matrix and the dynamical noise covariance matrix, which needs to be removed by a set of appropriate constraints.
We remark that Shumway and Stoffer in their seminal paper do provide an update equation for the case of applying column-wise constraints on the state transition equation, and in this paper, we will apply their update equation to our IC-LSS class of models. Shumway and Stoffer do not discuss estimation of the observation matrix, since they regard it as known (thereby avoiding the identifiability problem). However, as shown by Ghahramani and Hinton [14], the observation matrix can be estimated in almost the same way as the state transition matrix; therefore, the constrained EM update equation which Shumway and Stoffer have given for the state transition matrix can also be applied to the observation matrix.
Constrained EM estimation of the dynamical noise covariance matrix is more challenging, compared to the state transition matrix or the observation matrix, but for the class of IC-LSS models, we need to impose constraints on this matrix, in order to avoid the aforementioned identifiability problem. Therefore, the derivation of new update rules for constrained EM estimation of the dynamical noise covariance matrix forms the central topic of this paper. As a further concern, it has to be ensured that estimates of covariance matrices remain positive definite. For this reason, several authors have developed square-root variants of the EM algorithm [12, 15]. In this paper, we approach constrained EM estimation by the method of Lagrange multipliers, which in the case of covariance matrices yields cubic matrix equations. For both the non-square-root and square-root cases, we present analytic solutions of these equations.
Other authors who have worked on constrained EM estimation for LSS models include Wu et al. [16], Holmes [17], and Nemesin and Derrode [15, 18]. Both Holmes and Nemesin and Derrode have provided constrained update equations for all four parameter matrices of LSS models, allowing for more general constraints than Shumway and Stoffer. However, their update equations for the dynamical noise covariance matrix are limited to special cases which do not apply to the case needed for IC-LSS models.
The work of Nemesin and Derrode [15, 18] is embedded in the framework of a generalisation of LSS modelling, which is known as “pairwise Kalman filtering” [19]. While we are not interested in this generalisation itself, it offers us a very efficient formulation of LSS models which simplifies the equations arising in the EM algorithm; therefore, in this paper, we will make use of this generalisation. Nemesin and Derrode have also proposed a useful decomposition of the complete-data likelihood which we will employ in this paper.
The structure of this paper is as follows. In the second section, the main model classes and algorithms for state estimation are reviewed. Section 3 deals with parameter estimation by the EM algorithm and contains the main results of this paper. Section 4 demonstrates the algorithm derived in Section 3 by two numerical examples. Section 5 discusses several additional constraints that might be imposed on LSS models. A concluding discussion of the results of this paper is given in Section 6. Mathematical proofs are presented in the Appendix.
A note on notation In this paper, we refer to individual elements of a matrix M by writing [M]kl. Submatrices obtained from larger matrices by omitting certain rows and columns are written as \([\mathsf {M}]_{[k_{1},k_{2},\ldots ],[l_{1},l_{2},\ldots ]}\), where k1,k2,… and l1,l2,… denote the (sorted) indices of the rows and columns, respectively, that are not omitted. If a list of such indices forms a continuous sequence of integer numbers, we write in MATLAB-type notation k1 : k2 and omit the square brackets in the subscript, e.g. [M]1:k,1:l. The determinant of a (square) matrix is denoted by det(M) instead of the more traditional |M|. The trace of a (square) matrix is denoted by tr (M). The transpose of a matrix is denoted by \(\mathsf {M}^{\intercal }\) and the matrix square-root (defined through a Cholesky decomposition) is denoted by M1/2; then, the transpose of the matrix square-root is denoted by \(\mathsf {M}^{{}^{\intercal }\!/2}\).
2 Methods
The aim of this study is to discuss the fitting of LSS models to given multivariate time series, in the presence of constraints imposed on the four main parameter matrices of LSS models, and to introduce new update rules for applying the EM algorithm to this task. For this purpose, the method of Lagrange multipliers will be employed. In this section, we will first discuss LSS models, then briefly review the standard algorithms for state estimation, namely Kalman filtering and Rauch-Tung-Striebel (RTS) smoothing. The review of the EM algorithm itself and the presentation of the new update rules will follow in the next section.
2.1 Linear state space models: general formulation
Given a time series of n-dimensional data vectors \(\mathbf {y}_{t}=\left (y_{1}(t),\ldots,y_{n}(t)\right)^{\intercal }\,,\,t=1,\ldots,T\) where T denotes the length of the time series, a LSS model of this time series is given by two linear equations:
Here, \(\mathbf {x}_{t}=\left (x_{1}(t),\ldots,x_{m}(t)\right)^{\intercal }\) denotes a series of m-dimensional state vectors (which cannot be directly observed, but only indirectly via the observation equation), A denotes the (m×m) state transition matrix, C denotes the (n×m) observation matrix, ηt denotes a series of m-dimensional dynamical noise vectors, assumed to follow a Gaussian distribution with mean zero and (m×m) covariance matrix Q, and εt denotes a series of n-dimensional observational noise vectors, assumed to follow a Gaussian distribution with mean zero and (n×n) covariance matrix R. In this paper, we assume that the four matrices A, C, Q, and R do not depend on time, but rather represent the set of model parameters, which have to be estimated. Formally, the elements of these four matrices (except those fixed at 0 or 1, see below) may be collected in a vector of model parameters 𝜗. The initial state x1 and the corresponding covariance P1 may also be regarded as model parameters, but in this paper, we do not discuss their estimation.
In general, the covariance matrices Q and R must have the property of positive definiteness, i.e. they must fulfil
This property is equivalent to all eigenvalues of these matrices being positive. However, the case of one eigenvalue equal to zero (corresponding to positive semi-definiteness) may also be acceptable.
2.2 Independent components linear state space models
In this paper, we deal with a specific class of LSS models which is motivated by the task of Blind Signal Separation. In order to model a set of Nc mutually independent components, we assume the matrices A and Q to have a common block-diagonal structure as follows [20]:
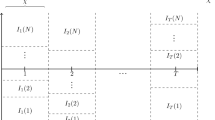
where A(j) and Q(j) denote two sets of (pj×pj) square matrices, such that \(\sum _{j=1}^{N_{c}} p_{j}=m\). Any combination of integer values may be chosen for the pj. The common block-diagonal structure of A and Q generates a corresponding partition of the state vector
and of the observation matrix
We remark that the block-diagonal structure proposed here represents a generalisation over the temporal factor analysis algorithm [21, 22] where the matrices A and Q were defined as diagonal.
For the independent components corresponding to the individual blocks, different structures may be chosen; in this paper, we choose a structure corresponding to ARMA (pj, pj−1) models, where pj denotes the model order; these model orders are chosen equal to the block sizes introduced above. For a univariate variable \(x^{(j)}_{t}\), an ARMA (pj,pj−1) model would be given by
where \(\eta ^{(j)}_{t}\) denotes a dynamical noise term, and \(a^{(j)}_{\tau }\,,\,\tau =1,\ldots,p_{j}\) and \(b^{(j)}_{\tau }\,,\,\tau =0,\ldots,p_{j}-1\) denote the sets of AR parameters and MA parameters, respectively. It is advisable to set \(b^{(j)}_{0}=1\) as a scaling convention for the dynamical noise term.
Various state space representations of ARMA (pj,pj−1) models exist; here, we choose the observer canonical form model [23]. Then, the block matrices A(j) and Q(j) of the state space model follow from the AR and MA parameters of the ARMA (pj,pj−1) models according to
However, according to the definition of Eq. (9), the matrices Qj would have pj−1 zero eigenvalues, i.e. be positive semidefinite. If it is required that Q be invertible, we consider a generalised definition, given by
where the \(\bar {b}^{(j)}_{ij}\) are additional model parameters that generalise the state space components corresponding to ARMA models. For further discussion on the case of singular state space models, we refer to [24].
According to the observer canonical form of state space models, the observation matrix corresponding to Eq. (2) is given by the (1×pj) matrix C(j)=(1 0 … 0). If the state space models of the individual ARMA (pj,pj−1) models, for j=1,…,Nc, are embedded within a single larger state space model, with block-diagonal structure, for the prediction of a data vector of dimension n, each of these (1×pj) observation matrices needs to be replaced by a (n×pj) block observation matrix
Note that in the univariate case n=1, as discussed by [20], it would suffice to use C(j)=(1 0 … 0) for all j, and to shift the corresponding scaling factor to the dynamical noise term, i.e. to the parameter [Q(j)]11; however, this is no longer possible in the multivariate case n>1 where we need a different observation parameter for each combination of a component within the data vector and an (independent) component within the state vector. In this case, the constraint [Q(j)]11=1 needs to be imposed, in order to avoid redundancy in the parametrisation.
The resulting state space model with block-diagonal structure, composed of independent ARMA models, has been called the Independent Components Linear State Space (IC-LSS) model [9].
2.3 The Kalman filter and the innovation likelihood
The task of estimating the states xt from given data yt by using a IC-LSS model represents a twofold estimation problem, since both the states xt and the model parameters A, C, Q, and R are unknown. For given estimates of the model parameters, the state estimation task is solved by the famous Kalman filter, given by the following recursion, to be applied during a forward loop over time:
where \(\mathbf {x}_{t_{1}|t_{2}}\) denotes an estimate of xt at time t=t1, using all information available at time t2, and \(\mathsf {P}_{t_{1}|t_{2}}\) denotes the corresponding state estimation covariance.
Based on the Kalman forward loop, the likelihood of the innovations for the given data and model parameters can be computed. Assuming a multivariate Gaussian density for the innovations, the logarithm of the likelihood is given by (omitting a constant term)
2.4 The Rauch-Tung-Striebel smoother
The Rauch-Tung-Striebel (RTS) smoother is a classical algorithm for smoothing, given by the following recursion, to be applied in a backward loop over time, after the forward loop of the Kalman filter [25]:
where the predicted and filtered covariances Pt+1|t and Pt|t have to be stored in the Kalman forward loop.
Due to numerical effects, the covariance matrices arising in the Kalman filter and the RTS smoother may fail to preserve the property of positive definiteness, see Eqs. (3,4). For this purpose, square-root variants of the forward and backward recursions have been introduced; such algorithms have been called “robust” variants of the conventional algorithms [12, 15]. Matrix square-roots can be defined either via the Cholesky decomposition, as done by the majority of authors (see, e.g. [1]), or via the singular value decomposition (SVD) [26, 27]. The numerical results reported in this paper were obtained from an implementation which defines matrix square-roots by Cholesky decompositions and computes them by using QR decompositions of suitably defined arrays [1].
3 Parameter estimation by the EM algorithm
Estimation of the model parameters could be performed by numerical maximisation of the innovation likelihood, as given by Eq. (19). As an alternative, it has been proposed to estimate parameters by employing the expectation maximisation (EM) algorithm [7, 11]. We will now briefly review the application of the EM algorithm to LSS models, with particular emphasis on constrained optimisation.
3.1 An augmented state equation
We begin by introducing an augmented state vector ξt and a corresponding augmented dynamic noise vector ζt, to be defined by
Here, the (delayed) data vector yt−1 is used in order to introduce additional components of an augmented state space. Then, the original state equation, Eq. (1), and the corresponding observation equation, Eq. (2), can be merged into a new augmented state equation
where we have defined an augmented state transition matrix
Since the augmented state equation Eq. (24) contains both the original state equation and the corresponding observation equation, it allows for new interaction effects between these two equations which are absent from standard state space modelling. In particular, there could be an interaction effect of past data yt−2 on the present state xt and an interaction effect of past data yt−2 on (delayed) present data yt−1. In Eq. (25), these effects are represented by the two submatrices of zeros on the right side of \(\mathcal {A}\); since such effects are absent in standard state space models, we have kept these submatrices at zero. However, such feedback of the data on the states, as well as on future data, are present within the framework of “pairwise Kalman filtering” [19], where the distinction between states and data is blurred.
We shall also introduce an augmented covariance matrix of the augmented dynamical noise vector ζt:
The off-diagonal submatrices of zeros in \(\mathcal {Q}\) represent cross-correlations between the noise terms ηt and εt, which again are usually absent in standard state space models, but present in the “pairwise Kalman filtering” framework. We will refer to the parameters in the three zero submatrices within \(\mathcal {A}\) and \(\mathcal {Q}\) as “pairwise KF” parameters.
Finally, we also need to introduce estimates for the augmented state vector ξt and the corresponding augmented state estimation covariance matrices. Let \(\boldsymbol {\xi }_{t_{1}|t_{2}}\) denote an estimate of ξt at time t=t1, using all information available at time t2, and let \(\mathcal {P}_{t_{1}|t_{2}}\) denote the corresponding covariance matrix. Since the data has zero covariance, we then have
3.2 Expectation step
In the EM approach to parameter estimation, instead of the innovation (log-)likelihood \(\mathcal {L}_{\nu }(\mathsf {A},\mathsf {C},\mathsf {Q},\mathsf {R})\), the so-called complete-data (log-)likelihood \(\mathcal {L}_{xy}(\mathsf {A},\mathsf {C},\mathsf {Q},\mathsf {R})\) is employed:
In this expression, through the augmented state approach, data terms, and state terms have been merged. Since the true states xt are unknown, the complete-data log-likelihood cannot be evaluated. The states are then regarded as “missing data”, and, as the first step of the EM algorithm, the expectation of the complete-data log-likelihood with respect to the states is computed; after some rearrangement, this gives us
where \(\mathsf {M}_{\mathcal {A}}\) represents the quantity
which is defined through the ((m+n)×(m+n)) matrices
In Eq. (32), \(\mathcal {P}_{t,t-1|T}\) represents a delayed covariance term which is usually not found in standard Kalman filter or smoother algorithms; however, this term can be computed by
where Jt represents the smoother gain, given by Eq. (20).
We add two remarks on the definition of the matrices Mij:
Many authors define these matrices without the factor 1/T [7, 18]; however, we feel that it is more natural to define them as actual averages, as also done, among others, by Gibson and Ninness [12] and by Särkkä [13]. As a benefit, the update equation for \(\mathcal {Q}\) becomes simpler.
It can be seen that the definitions of M00 and M11 are very similar, with the averages being shifted by just one time unit, and in the limit of infinite data these two quantities would become identical. One may then argue that in actual implementations M00 and M11 should not be distinguished.
3.2.1 Example
As an example, we consider the case of an IC-LSS model consisting of two ARMA(2,1) models and observed by two mixtures. Then, the matrix \(\mathcal {A}\) is given by
Note that the two columns of zeros on the right represent the “pairwise KF” parameters. The matrix \(\mathcal {Q}\) is given by
Here, we have assumed the observation noise covariance matrix R to be diagonal. In order to avoid singular \(\mathcal {Q}\), the blocks Q(i) have been defined with the additional parameters \(\bar {b}^{(i)}\). Note that the submatrix of (2×4) zeros in the lower left position of this matrix represents the “pairwise KF” parameters, as well as its symmetric counterpart in the upper right position.
3.3 Decomposition of expected complete-data log-likelihood
In the IC-LSS model, we have the special case of block-diagonal A and Q; if we assume ηt and εt to be independent of each other, as in Eq. (26), also \(\mathcal {Q}\) will be block-diagonal, with blocks denoted as \(\mathcal {Q}^{(i)}\) (given by R and the blocks of Q). If \(\mathcal {A}\) is defined as in Eq. (25), it will also be block-diagonal, except for the lowest block, corresponding to the observation matrix. Regardless of the shape of \(\mathcal {A}\), for block-diagonal \(\mathcal {Q}\), the expected complete-data log-likelihood can be decomposed into independent subfunctions. For this purpose, we decompose \(\mathcal {A}\) into row-wise blocks \(\mathcal {A}^{(i)}\), i=1,…,(Nc+1), with vertical block sizes corresponding to the sizes of the diagonal blocks of \(\mathcal {Q}\); note that in general, the \(\mathcal {A}^{(i)}\) will not be square, unlike the blocks A(i) of Eq. (5). Let \(\mathcal {V}_{i}\) denote the projector that extracts \(\mathcal {A}^{(i)}\) from \(\mathcal {A}\), i.e. \(\mathcal {A}^{(i)} = \mathcal {V}_{i}\mathcal {A}\); then, we have the decomposition [18]
where \(\mathsf {M}_{\mathcal {A}}^{(i)}\) represents the quantity
In the last line, we have defined \(\mathsf {M}_{10}^{(i)} = \mathcal {V}_{i}\mathsf {M}_{10}\) and \(\mathsf {M}_{11}^{(i)} = \mathcal {V}_{i}\mathsf {M}_{11}\mathcal {V}_{i}^{\intercal }\).
3.4 Maximisation step: unconstrained case
As the second step of the EM algorithm, the expected complete-data log-likelihood is maximised with respect to \(\mathcal {A}\) and \(\mathcal {Q}\). First, we show the results for the case without constraints. Using results from matrix calculus, maximisation yields the following update rules, which were already given by Shumway and Stoffer [7]:
The matrices \(\mathcal {A}_{\text {opt}}\) and \(\mathcal {Q}_{\text {opt}}\) resulting from this update will in general be full, i.e. not contain the zero submatrices shown in Eqs. (25) and (26); therefore, these updates correspond to the “pairwise Kalman filter” framework. In order to obtain updates for the standard Kalman filter, appropriate constraints have to be imposed. Further constraints are required in order to preserve the structure of the matrices A(i) and Q(i) according to Eqs. (9) or (10). Constrained optimisation by the EM algorithm will be discussed in the next section.
As already mentioned, Shumway and Stoffer did not discuss estimation of the observation matrix C; the update rule for C for the unconstrained case was later given by Ghahramani and Hinton [14]. However, with respect to C, the update rule of Eq. (41) does not exactly correspond to the rule given by Ghahramani and Hinton. Their update rule for C would be given by
while Eq. (41) gives
Despite the equivalence of the state space models, the corresponding maximisation tasks yield slightly different results, depending on whether we estimate A and C separately, or jointly via the combined matrix \(\mathcal {A}\). In practical applications, one can easily switch between both estimators for Copt, since the matrices M00, M10 and M10 are available anyway. We have already commented above on the similarity between the matrices M00 and M11. This point will be discussed further below.
3.5 Lagrange approach to the maximisation step in the presence of constraints
The study of parameter estimation for IC-LSS models under constraints represents the main topic of this paper. We approach this problem by the method of Lagrange multipliers.
First, we note that due to the decomposition of the expected complete-data log-likelihood into independent subfunctions, as given by Eq. (37), we can process each pair of blocks \(\mathcal {A}^{(i)}, \mathcal {Q}^{(i)}\) separately.
Constraints shall be defined by individual elements of \(\mathcal {A}^{(i)}\) and \(\mathcal {Q}^{(i)}\) being fixed to given values \(a_{\mu _{a}}\) and \(q_{\mu _{q}}\); the indices μa and μq shall label the constraints. Let ed;α denote a column vector of dimension d with a 1 at position α and zeros otherwise. Then, constraints for the elements \(\left [\mathcal {A}^{(i)}\right ]_{\alpha (\mu _{a}),\beta (\mu _{a})}\) and \(\left [\mathcal {Q}^{(i)}\right ]_{\gamma (\mu _{q}),\delta (\mu _{q})}\) can be written as
Then, the Lagrangian is given by
where \(\lambda _{\mu _{a}}\) and \(\phi _{\mu _{q}}\) denote two sets of Lagrange multipliers, and \(\mathsf {M}_{\mathcal {A}}^{(i)}\) has been defined in Eq. (38). Note that there needs to be a Lagrange multiplier for each position in \(\mathcal {A}^{(i)}\) we wish to keep at a value of 1 or of 0, including the “pairwise KF” positions.
3.5.1 Constraints on \(\mathcal {A}\)
In order to simplify notation, we will from now on omit the superscript (i), referring to the block we are processing. Taking the derivative of Eq. (44) with respect to \(\mathcal {A}\) (i.e. one of the row-wise blocks) and setting it zero yields
where we have defined
Positions in the (pi×(m+n)) matrix Λ for which no constraints were imposed on \(\mathcal {A}\) remain zero.
Equation (45) represents a system of m2 linear equations for the unknowns in \(\mathcal {A}\) and Λ. In case of IC-LSS models, constraints on \(\mathcal {A}\) will always apply to full columns of \(\mathcal {A}\): for the case of the row-wise blocks of the state transition matrix, columns outside the local autoregressive block A(i) and columns in the “pairwise KF” block are constrained to zero; within each A(i), the first left-hand column contains non-zero parameters, while the remaining pi−1 columns are constrained to the observer canonical form, consisting of zeros and ones, according to Eq. (9). For the case of the observation matrix C, for each autoregressive block, there is one column of non-zero parameters while the remaining pi−1 columns are constrained to zero; again, also the “pairwise KF” columns will be constrained to zero. In this situation, constraints can be written concisely as
where \(\mathcal {A}_{c}\) consists of the columns containing the fixed values (mostly zeros or ones), while Vc maps these columns into the corresponding positions within \(\mathcal {A}\). The general solution of Eq. (45) under constraints given by Eq. (47) has already been given by Shumway and Stoffer in their seminal paper from 1982 [7] (albeit without giving solutions for the Lagrange parameters):
We remark that Shumway and Stoffer discuss this solution only for the case of quadratic \(\mathcal {A}\); however, it remains valid for row-wise blocks, i.e. for rectangular \(\mathcal {A}\), if the matrices \(\mathcal {A}_{c}\) and Vc are defined accordingly.
An alternative version to solution Eq. (48) has been given by Nemesin and Derrode [18]; they write the constraints as
where \(\tilde {\mathcal {A}}_{c}\) contains both the columns with the fixed values and the columns with the values to be estimated (the latter containing just zeros); \(\tilde {\mathcal {A}}_{e}\) consists of the columns containing the values to be estimated, and \(\tilde {\mathsf {V}}_{e}\) maps the elements of \(\tilde {\mathcal {A}}_{e}\) into the corresponding positions within \(\mathcal {A}\). For the case \(\tilde {\mathcal {A}}_{c}=\mathsf {0}\) (which applies to the case of updating the block containing the observation matrix C), the solution is given by
This expression turns out to be more convenient for updating the observation matrix C than Eq. (48).
The general case of constraints which do not necessarily apply to full columns has recently been discussed by Holmes [17], who has derived a general solution using kron-vec notation, and also by Nemesin and Derrode [18].
From Eqs. (48) and (50), it can be seen that column-wise constraints on \(\mathcal {A}\) yield solutions that do not depend on (the local block of) the covariance matrix \(\mathcal {Q}\), thereby removing the need to keep this matrix invertible. This is no longer true for the general solutions given by Holmes and by Nemesin and Derrode: e.g. if some individual autoregressive parameters within \(\mathcal {A}\) would also be constrained to a fixed value, the corresponding update rule would depend on the inverse of \(\mathcal {Q}\) (see [17] for further discussion).
3.5.2 Example
We use again the example of an IC-LSS model consisting of two ARMA(2,1) models, and observed by two mixtures, as presented at the end of Section 3.2. Through block-wise application of Eq. (48), the following solution for the parameters in \(\mathcal {A}\) is obtained:
where the factor μ is given by
Solutions for the Lagrange parameters are somewhat complicated and will be omitted, since they are not needed for practical application.
The update rules of Eqs. (53 - 55) for the elements of the observation matrix C can conveniently be obtained from Eq. (50); for the case of more than two ARMA(2,1) models, they would turn out to be more complicated; however, they can always be interpreted as ratios of determinants, corresponding to Cramer’s rule.
Furthermore, we emphasise that the update rules of Eqs. (53 – 55) correspond to the case of estimating A and C jointly via the combined matrix \(\mathcal {A}\). As mentioned above in Section 3.4, these update rules differ slightly from the update rules found for the case of estimating A and C separately, as done by Ghahramani and Hinton [14] for the unconstrained case, and by Holmes [17] for the constrained case. In order to make Eqs. (53 - 55) consistent with the update rules derived by Holmes in kron-vec notation, one would have to replace both the matrices M00 and M10 by M11. In the simulation example presented below, we will employ both sets of update rules.
3.5.3 Constraints on \(\mathcal {Q}\)
After the state transition matrix A has been updated, the next step is the update of the dynamical noise covariance matrix Q, i.e. from now on, A shall denote the update according to Eq. (48). Strictly speaking, the entire forward Kalman filter and backward RTS smoother passes should be repeated when switching from the update of A to the update of Q [28], but in order to decrease the computational effort, this procedure is frequently simplified.
The case of constraints on the covariance matrix \(\mathcal {Q}\) is more complicated than the case of constraints on \(\mathcal {A}\). First, we note that the decomposition of the expected complete-data log-likelihood, according to Eq. (37), was based on the assumption of \(\mathcal {Q}\) being block-diagonal, i.e. the off-diagonal blocks describing correlations between different components within the dynamical noise vector ηt, or between ηt and the observation noise vector εt, need not be constrained explicitly to vanish. Therefore, we can work with square diagonal blocks \(\mathcal {Q}^{(i)}\), and we will again omit the block index (i).
Taking the derivative of Eq. (44) with respect to \(\mathcal {Q}\) (i.e. one of the diagonal blocks) and setting it zero yields
where we have defined
Equation (56) represents a system of m2 cubic equations for the unknowns in \(\mathcal {Q}\) and Φ. However, due to the symmetry of covariance matrices, m(m−1)/2 equations are redundant and should be omitted. The main constraint that needs to be imposed is given by the (block-wise) scaling convention, \([\mathcal {Q}]_{11}=1\) (see the discussion in Section 2.2). While both Holmes [17] and Nemesin and Derrode [18] discuss a number of special constraints on \(\mathcal {Q}\) and present corresponding closed-form solutions, none of their solutions applies to this kind of constraint.
We claim that a closed-form solution of Eq. (56) under the constraint \([\mathcal {Q}]_{11}=q_{11}\) is given as follows:
for k=1,…,pi, l=1,…,pi. A proof for this claim is given in the Appendix. Note that indices both of \(\mathcal {Q}\) and of \(\mathsf {M}_{\mathcal {A}}\) refer to the local block which we are processing. Since \(\mathsf {M}_{\mathcal {A}}\) is a symmetric matrix, this solution generates a symmetric covariance matrix.
3.5.4 Example
For the example of an IC-LSS model discussed above, Eq. (58) yields the following solution for the parameters in \(\mathcal {Q}\):
In Eq. (61), parameters r1 and r2 represent the observation noise covariance block, for which no constraint corresponding to \([\mathcal {Q}]_{11}=q_{11}\) was applied; instead, this block was assumed to be diagonal, representing a different type of constraint, see Eq. (36). The estimates of the parameters in \(\mathcal {Q}\) according to Eqs. (59,60) would remain valid, if we had allowed the observation noise covariance block to be non-diagonal, i.e. if we had introduced an off-diagonal parameter r12; in this case, for this parameter the solution \(r_{12}=\left [\mathsf {M}_{\mathcal {A}}\right ]_{56}\) would result.
3.5.5 Constraints on \(\mathcal {Q}\): square-root case
Following the work of Nemesin and Derrode [18], we will now present a square-root version of the constrained estimator for \(\mathcal {Q}\), given in the previous section. For this purpose, we will introduce a matrix square-root of the (block-wise) covariance matrix \(\mathcal {Q}\), using a Cholesky decomposition:
where \(\mathcal {Q}^{1/2}\) is a (pi×pi) upper triangular square matrix. Then, \(\mathcal {Q}^{1/2}\) replaces \(\mathcal {Q}\) as parameter matrix to be estimated. The benefit of this approach is that \(\mathcal {Q}\) is guaranteed to be positive definite.
Constraints are imposed directly on \(\mathcal {Q}^{1/2}\):
where \(s_{\mu _{s}}\) denotes the fixed values corresponding to the constraints. Note that \(\mathcal {Q}^{1/2}\) has upper triangular shape by definition; it is unnecessary to introduce constraints and Lagrange multipliers for the purpose of keeping the lower triangular matrix elements zero, and the indices γ(μs),δ(μs) should only refer to positions in the upper triangular matrix or on the diagonal. Lagrange multipliers relating to lower triangular matrix elements would always turn out to be zero.
Taking the derivative of Eq. (44) with respect to \(\mathcal {Q}^{1/2}\) (i.e. the matrix square-root of one of the diagonal blocks) and setting it zero yields
where we have defined
Equation (64) represents a system of m2 cubic equations for the unknowns in \(\mathcal {Q}^{1/2}\) and Φ; this system of equations slightly differs from the system of Eq. (56). But again, m(m−1)/2 equations are redundant and should be omitted. As before, the main constraint that needs to be imposed is given by the (block-wise) scaling convention, which now reads \([\mathcal {Q}^{1/2}]_{11}=1\).
We claim that a closed-form solution of Eq. (64) under the constraint \([\mathcal {Q}^{1/2}]_{11}=s_{11}\) is given as follows:
A proof for this claim is given in the Appendix. Again, indices refer to the local block which we are processing.
3.5.6 Example
For the example of the IC-LSS model discussed above, Eq. (66) yields the following solution for the parameters in \(\mathcal {Q}^{1/2}\):
Also, in this case, the estimates for the observation noise covariance block, given in Eq. (69), represent the constraint of a diagonal block; had we allowed this block to be non-diagonal, the estimates for the two blocks of the dynamical noise covariance, given in Eqs. (67,68), would remain valid, while the estimates for the observation noise covariance block would change according to
4 A numerical example
4.1 Simulation setup
We demonstrate the practical performance of the algorithm discussed in this paper by a simulation example. The simulation is a simplified version of the simulation used in [9]. Two time series are generated from two sets of deterministic nonlinear differential equations, namely the famous Lorenz system [29],
where σ=10, r=28, b=8/3, and Thomas’ cyclically symmetric system [30],
where b=0.18.
These differential equations are integrated by the “local linearisation” method [31]. Time discretisation is 0.01 time units for the Lorenz system and 0.1 time units for the Thomas system. After integration, the simulated time series are subsampled by factors of 4 (Lorenz) and 12 (Thomas). These values are chosen since they provide a sufficiently dense sampling of the chaotic trajectories, such that the power spectra of the source time series roughly coincide.
From the two time series of state variables (x1(t),x2(t),x3(t)), the first variable is stored, while the remaining variables are discarded; these two scalar time series form the mutually independent source time series. They are individually standardised to unit variance, then they are instantaneously mixed by a randomly chosen invertible (2×2) matrix, given by (0.8545 2.0789 ; 1.1874 0.1273). A fair amount (10%) of gaussian observation noise is added to each mixture, such that the two added gaussian noise time series are mutually independent. The length of the simulated data is 8192 points.
The setup of this simulation corresponds to the situation chosen for the example given above, i.e. there are two mixtures and two source processes, each of which shall be modelled by an ARMA (p,p−1) process. Therefore, we can apply constrained optimisation by the EM algorithm, using the update rules given in Eqs. (51-54) and Eqs. (59-61), or preferably Eqs. (67–69). For p=2 and diagonal R, the total number of parameters to be estimated is 14; for each additional ARMA(2,1) process which we would add to the model, 6 additional parameters would result. We refrain from optimising also the initial state and initialise it with zeros instead; the innovation likelihood is then evaluated only after a transient of 20 time steps has died out. The initial state covariance is arbitrarily initialised with 0.5 times a unity matrix.
In this simulation, we are trying to model deterministic nonlinear time series by ARMA processes, i.e. by stochastic linear processes; this represents the “wrong-model-class” scenario, i.e. the situation that the model class which we are using does not contain the true model structure. Due to this situation, there are no “correct” values for the parameters. This situation is typical for the analysis of real-world data recorded from complex natural or technical systems. Contrary to this situation, in a simulation, it would also be possible to work in the “true-model-class” scenario, and we will briefly present an example for this scenario below.
Another aspect related to the choice of the model class is the “correct” number of source processes. The need to determine this number represents a fundamental problem of all algorithms for Blind Signal Separation. In many cases, the number is simply chosen as the number of available mixtures. In principle, the number of components to be included in the model could be determined by a model comparison approach; however, such approach would cause considerable computational effort.
In the case of data recorded from complex natural or technical systems, unlike the case of simulated data, the concept of the “correct” number of components is probably ill-defined. Such data will contain contributions from a large number of structures, subsystems, and background sources, most of them at least weakly interacting. Then, any attempt to extract a moderate preselected number of components, assumed to be “independent,” will only be valid as an approximation.
For our simulation example, we will assume that the number of source processes is equal to the number of available mixtures, i.e. 2; however, we will also perform simulations with the (incorrect) assumptions of the presence of 1 and of 3 source processes.
4.2 Evaluation of performance
Since in a simulation setting the true source components are known, we can directly compare reconstructed and true source components by forming the cross-correlation matrix between these two sets of time series. The reconstructed source components are given by time series of smoothed state estimates. For this purpose, all individual components are standardised to zero mean and unit variance. For perfect reconstruction, we would expect this cross-correlation matrix to have in each row and in each column exactly one element with a value of ±1, while all other elements should vanish, i.e. we would expect this cross-correlation matrix to be a permutation matrix with an additional binary information corresponding to the possibility of a “phase flip.” This shape of the cross-correlation matrix corresponds to the residual indeterminacies with respect to polarity and ordering which cannot be resolved by any algorithm for Blind Signal Separation [32].
The actual reconstruction will not be perfect; therefore, the actual cross-correlation matrix will not have exactly this shape, but we can determine the closest permutation matrix, with ± 1 elements, and quantify the difference between these two matrices by the Frobenius norm of the difference matrix [9]. For perfect reconstruction, we would expect this Frobenius norm to be zero. The larger the actual value of the Frobenius norm, the poorer is the performance of the model, with respect to the reconstruction of the source components.
4.3 Choice of initial values
The initial values for the parameters of the IC-LSS model are chosen as follows. The \(a^{(j)}_{i}\) within the state transition matrix A (see Eq. (35)) are initialised by the corresponding eigenvalues, which for 2 ×AR(1) are rather arbitrarily chosen as (1/3),(2/3), and for 2 ×ARMA(p,p−1), p>1, as (1/(2p+1), (p+2)/(2p + 1), (p+3)/ (2p+1),…, (2p)/(2p+1)),(2/(2p + 1),3/(2p+1),…,(p+1)/(2p+1)), without any claim of “optimality.” For p=2, this gives us eigenvalues (0.2,0.8),(0.4,0.6). For all p, both AR/ARMA processes are stable and have only real eigenvalues. All \(c^{(j)}_{i}\) are initialised by 1.
The \(b^{(j)}_{i}\) within the dynamical noise covariance matrix Q (see Eq. (36)) are initialised by 1. The additional parameters \(\bar {b}^{(j)}_{ik}\) are initialised by small values chosen as min(i,k)/100. The diagonal values of the observation noise covariance matrix R are initialised by 0.01.
For the case 2×ARMA(2,1), this gives us as initial matrices
and
For the case of assuming the presence of just one ARMA process, the rows and columns corresponding to the second process are omitted from \(\mathcal {A}\) and \(\mathcal {Q}\); for p=2, the remaining ARMA process has eigenvalues (0.2,0.8). For the case of assuming the presence of three ARMA processes, additional rows and columns are inserted into both matrices, after the first two processes, such that the additional (p×p) block on the diagonal of \(\mathcal {A}\) corresponds to p real eigenvalues which are different from the eigenvalues of the first two processes; for p=2, the eigenvalues of the three ARMA processes are chosen as (0.1,0.9), (0.2,0.8), and (0.3,0.7). Additional \(c^{(j)}_{i}\) are again initialised by 1. The additional (p×p) block on the diagonal of \(\mathcal {Q}\) contains the same values as the other two blocks.
We remark that these choices of initial values are fairly arbitrary, based on only preliminary study. Superior ways of choosing initial parameters could be devised, but this is not the subject of the present paper.
4.4 Results of simulation
4.4.1 EM optimisation
We fit IC-LSS models with structure 2×AR(1) and 2×ARMA(p,p−1), p=2,3,…,10, to the data; furthermore we fit models with structure 1×ARMA(2,1) and 3×ARMA(2,1). The results are summarised in Table 1.
In all cases tested, the EM algorithm, when started for the initial model as described above, reaches a minimum value of (-2)log(likelihood) after a certain number of iterations (shown in the 4th column of Table 1); further iterations yield slowly increasing (−2)log(likelihood). The obtained minimum value of (−2)log(likelihood) is shown in the 5th column of Table 1.
For the initial models, values for (−2)log(likelihood) are very large, indicating poor predictions. For the case of p=2, we find initially a value of 1632738.63, which after 33 iterations is reduced to a minimal value of 27917.36; most of this improvement is achieved during the first two iterations, after which 58313.32 is reached. All values for (−2)log(likelihood) have been computed omitting the transient. Regarding the update rules for the covariance matrices, in this low-dimensional case, both the direct update of Eqs. (59-61), and the square-root update of Eqs. (67-69) yield the same result.
For the case of p=2, after optimisation eigenvalues of the two ARMA processes are (0.1146,0.9382) and (0.1603,0.9306); MA parameters are 0.9706 and 0.9791, while additional parameters \(\bar {b}^{(j)}_{ik}\) are 0.0095 and 0.0096 (all values rounded to 4 decimal places). The non-zero elements of the observation matrix are row-wise 0.1255,0.2845 and 0.1619,0.0247. The diagonal elements of the observation noise covariance matrix are 0.4904,0.1130. For higher model orders p>2, we also find cases where some pairs of the initial real eigenvalues turn into pairs of complex conjugated eigenvalues during optimisation by the EM algorithm.
If we quantify the performance of the model with the initially chosen parameters, for p=2 given by Eqs. (74,75), with respect to the reconstruction of the source components, we find a value of the Frobenius norm of 1.0641; for p>2, similar values are found. Therefore, values of this size represent a complete failure of the reconstruction of source components (cmp. Fig. 2). The values of the Frobenius norm after optimisation by the EM algorithm are shown in the 6th column of Table 1. For p=2, we find a value of 0.0331, a value which represents good performance of the reconstruction of the source components (cmp. Fig. 2). However, for other model orders, such as p=1 or p>2, according to Table 1, the values of the Frobenius norm after optimisation by the EM algorithm are not as small as for p=2.
4.4.2 Visualisation of results for p=2
We will now report some more results for the case p=2. In Fig. 1, the evolution of (−2)log(likelihood) and of the Frobenius norm during the EM iteration is displayed. Note that the evolution of the Frobenius norm does not necessarily behave monotonically.
Evolution of (−2)log(likelihood) (left) and the Frobenius norm (right) during the EM optimisation procedure, with joint updating of A and C, for a IC-LSS model with structure 2×ARMA(2,1) and one particular choice of initial parameter estimates; for the first two iterations the values of (−2)log(likelihood) fall outside of the figure
Scatterplots of true versus reconstructed source components, including corresponding cross-correlation coefficients, for the initial IC-LSS model (left) and the final IC-LSS model after EM optimisation with joint updating of A and C (right), for a IC-LSS model with structure 2×ARMA(2,1) and one particular choice of initial parameter estimates
In Fig. 2, the performance of the models is displayed, with respect to the reconstruction of the source components, both for the initially chosen model, containing parameters as given in Eqs. (74,75) (left), and for the model obtained after EM optimisation (right). The performance is visualised by perpendicular superpositions of the pairs of true and reconstructed source components, representing a graphical array of “scatterplots”. For perfectly reconstructed components, we would expect such scatterplots to form sharp diagonal lines, while for each pair of unrelated true and reconstructed component, we would expect a featureless erratic superposition pattern. In addition to the perpendicular superpositions, also the corresponding cross-correlation values are given. The scatterplots and the cross-correlation values confirm that the source components have been reconstructed successfully after EM optimisation, although further improvement would surely be possible. It is a coincidence that no cross-correlation values close to −1 occur, i.e. that no phase flips are present.
Replacing the non-zero values for the parameters \(\bar {b}^{(j)}_{ik}\) by zero, i.e. projecting the model onto the space of IC-LSS models which correspond exactly to block-wise ARMA(2,1) processes, improves the (−2)log(likelihood) slightly to a value of 27917.08. The performance, as quantified by the Frobenius norm, stays virtually unchanged.
We need to remark that the results of the EM algorithm display a strong dependence on the initial values chosen for the parameters. Of course, this remark applies to all algorithms for numerical optimisation. From 1000 initial models with randomly chosen eigenvalues within the interval (0,1), after EM optimisation, 146 models yield values below 0.1 for the Frobenius norm, representing good reconstructions, while 33 models yield values above 0.5, representing poor reconstructions.
Replacing the update rules for joint updating of A and C with the rules for separate updating (see Section 3.5.1) yields a value of 29376.86 for (−2)log(likelihood) after 33 iterations; the corresponding value of the Frobenius norm is 0.2560. Both values are worse than the values for joint updating; when comparing the models obtained after 33 iterations by joint updating with the models obtained by separate updating for 1000 initial models with randomly chosen eigenvalues within the interval (0,1), we find that without exception each single joint updating model has smaller (−2)log(likelihood) than the corresponding separate updating model. Regarding the Frobenius norm, we find for 985 of 1000 models smaller values for the joint updating models than for the corresponding separate updating models. Therefore, we believe that for small number of iterations, joint updating generically achieves faster improvement of the likelihood than separate updating.
However, in the case of separate updating, continuing the EM algorithm beyond the 33th iteration (or beyond any other iteration number obtained from joint updating) yields slowly decreasing values of (−2)log(likelihood), in contrast to the case of joint updating; this would be the theoretically expected behaviour of an EM algorithm. In our example for p=2, also the value of the Frobenius norm continues to decrease, until after 720 iterations it reaches a minimal value of 0.0287; afterwards, the Frobenius norm increases again at a linear rate, crossing 1.0 after 7955 iterations, a value that corresponds to complete failure of the source reconstruction task. The minimum value at 720 iterations cannot be detected from monitoring the decreasing values of (−2)log(likelihood).
4.4.3 EM optimisation with subsequent numerical optimisation
We also consider the case of using the model provided by EM optimisation (with joint updating of A and C) as initial model for a subsequent numerical optimisation step, to be performed by the BFGS quasi-Newton algorithm, thereby following a suggestion from Shumway and Stoffer [7].
For model orders \(p=1,\dots,10\) we apply the BFGS quasi-Newton algorithm to all parameters within the system matrices A, C, Q, and R which are not fixed to 0 or 1. The algorithm is terminated after converging to a minimum. The corresponding values of (−2)log(likelihood) are shown in the 7th column of Table 1. From the table, it can be seen that for most model orders the BFGS quasi-Newton algorithm substantially improves (−2)log(likelihood). The same is true for the Frobenius norm, which is shown in the 9th column of Table 1: most values are below 0.1, representing good reconstructions, while for most model orders, they were larger directly after the EM optimisation step. Notable exceptions are the model orders p=1, p=8, and p=10. For the case p=2, the Frobenius norm has slightly deteriorated during the BFGS quasi-Newton optimisation, although at a value of 0.0967 it still represents a good reconstruction.
For the case p=2, it takes the BFGS quasi-Newton algorithm about 750 function evaluations to converge to a model with a value of 13663.76 for (−2)log(likelihood). As an alternative to the BFGS quasi-Newton algorithm, we may choose to employ the Nelder-Mead simplex algorithm; we find that it converges after 4430 function evaluations, reaching a model with a value of 13742.67 for (−2)log(likelihood), which is worse than the value for BFGS. The Frobenius norm for this model is 0.1067, which is close to the value of 0.0967 for BFGS. We remark that these results display strong variation with respect to the particular realisation of the source components and to the values of the mixing matrix which were used for creating the simulated data.
4.4.4 Choice of model order
We will now briefly discuss what can be learned from our simulations regarding the choice of the model order p. For this purpose, we show in the 8th column of Table 1 the values of the Akaike Information Criterion (AIC) [5], defined as (−2)log(likelihood) plus 2 times the number of model parameters, denoted as dim(𝜗), the latter being shown in the 3rd column of the table. These values refer to the models resulting from optimisation by the EM algorithm with subsequent optimisation by the BFGS quasi-Newton algorithm.
From the table, it can be seen that a minimum of AIC occurs at p=4, so we might conclude that, at least for this particular data set, this was the optimum model order. However, such conclusion would be premature, since in general numerical optimisation, be it by the EM algorithm, by the BFGS quasi-Newton algorithm or by the Nelder-Mead simplex algorithm, yields only local minima. The larger the number of parameters, the more difficult it is to find the global minimum, or at least to reach values of the AIC close to the value of the global minimum. As the 3rd column of Table 1 shows, the number of parameters grows quadratically with the model order p. This fact explains the comparatively large values of AIC for p>7.
The results we report in Table 1 were obtained by simply applying the BFGS quasi-Newton algorithm to all parameters simultaneously until convergence; however, experience has shown that for larger number of parameters this approach becomes inappropriate. More effort has to be expended on this second step of the optimisation, such as sequentially optimising subsets of parameters, as it has been recommended already by Watson and Engle [11], who call this a “zigzag” approach. By using such approach, we were able to reach values of AIC as low as 12807.77 for model order p=9, and 12674.14 for model order p=10, both of which are lower than any other value reported in Table 1 for this particular data set. The corresponding values of the Frobenius norm are 0.0103 and 0.0109, which again are lower than any other value.
We therefore believe that in this case the optimal model order could be considerably larger than 4, apparently even larger than 10; however, due to the growing number of parameters, fitting such high-order models becomes increasing cumbersome and time-consuming. As we have demonstrated, for the mere purpose of Blind Signal Separation, such high model orders are not necessary, since already a low model order such as p=2 or p=3 achieves a sufficiently low value for the Frobenius norm (cmp. Table 1).
Strictly speaking, we would have to allow for the possibility that for different source components the optimal model order would be different, so it would not suffice to study the dependence of AIC on a single choice for the model order; instead, combinations of different model orders \(\left (p_{1},\ldots,p_{N_{c}}\right)\) would have to be explored, thereby further increasing the computational time consumption.
In many practical situations, the number of source components to be reconstructed and separated may be considerably larger than Nc=2, such that the number of parameters would become larger than given in Table 1. For such cases, we recommend to fix the model order to p=2 for all source components, in order to reduce the optimisation effort; this choice also offers advantages with respect to the choice of initial models, as we have argued elsewhere [10]. However, source components with drift-like behaviour may be modelled by AR(1) processes, i.e. by model order p=1.
4.4.5 Incorrect number of source processes
Finally, we briefly consider the case of fitting IC-LSS models with an incorrect number of source processes. For the model with a single ARMA(2,1) process, EM optimisation and subsequent BFGS quasi-Newton optimisation yield a value of 37955.71 for AIC, while for the model with three ARMA(2,1) processes, a value of 13529.03 is found. By comparing these values with the other values of AIC reported in Table 1, it can be seen that the model with a single ARMA(2,1) process is clearly inferior, while the model with three ARMA(2,1) processes performs almost as well as the models with Nc=2: it is superior with respect to the model with p=2, while it is still somewhat inferior with respect to the models with p=3,…,7.
It is again instructive to visualise the reconstructed source components through perpendicular superposition with the true source components, as shown in Fig. 3. For the model with three ARMA(2,1) processes, it can be seen that the Thomas source has been successfully reconstructed, while the Lorenz source has been split up into two source components, which clearly is a consequence of assuming too many source processes. By computing the cross-correlation coefficients between the reconstructed source components, it can still be detected that the two Lorenz source components belong together, as shown by a coefficient of 0.34725, while the coefficients between the two Lorenz source components and the Thomas source are close to zero, −0.0208 and −0.0129. We believe that the superiority of the model with three ARMA(2,1) processes over the model with two processes, in terms of AIC, is a consequence of working with a “wrong-model-class” scenario. We have already argued, that in most cases of analysis of real data, the concept of the “correct” number of source components has to be regarded as ill-defined.
Scatterplots of true versus reconstructed source components, including corresponding cross-correlation coefficients, for IC-LSS models with structure 1×ARMA(2,1) (left) and with structure 3×ARMA(2,1) (right), after EM optimisation with joint updating of A and C, and additional quasi-Newton optimisation
4.5 True-model-class scenario
We conduct a second simulation experiment, now working with the “true-model-class” scenario, i.e. we generate time series from Eqs. (1, 2), using a IC-LSS model composed of two ARMA(2,1) processes. The model parameters are chosen as
The eigenvalues of the ARMA(2,1) processes are (7±i)/10 and \((17\pm i \sqrt {11})/20\), where i denotes the imaginary unit. Again, the length of the simulated data is 8192 points. Processing this data by Kalman filtering with the correct IC-LSS model yields a value of 50975.22 for (−2)log(likelihood). Applying the BFGS quasi-Newton algorithm to the correct model as initial model yields a model with a value of 49287.43 for (−2)log(likelihood); the corresponding parameters are given by
The difference between the maximum-likelihood estimates of the parameters and the true values represents the effect of finite size of the simulated data set. We remark that, in contrast to the BFGS quasi-Newton algorithm, our EM algorithm is unable to find the model of Eqs. (78, 79), if Eqs. (76, 77) are used as initial parameters.
However, we may choose different initial parameters and then apply EM optimisation, followed by BFGS quasi-Newton optimisation, as also done in the “wrong-model-class” scenario. As an example, we may choose Eqs. (74, 75) as initial parameters. Optimisation then yields a model with a value of 49287.50 for (−2)log(likelihood), which is almost the same value as for the BFGS quasi-Newton algorithm, and parameters
It can be seen that the parameters in A, C, and R are estimated quite accurately, while the parameters in Q show larger deviations. The corresponding value of the Frobenius norm is 0.1349, indicating essentially successful reconstruction of source components.
The combination of EM optimisation with a different algorithm for numerical optimisation was suggested already by Shumway and Stoffer [7]. For this particular data set within the “true-model-class” scenario, it turns out that employing an algorithm for numerical optimisation, such as the BFGS quasi-Newton algorithm, is crucial for the success of the modelling, since application of the EM algorithm alone yields a value of 71656.79 for (−2)log(likelihood) and a value 1.2258 for the Frobenius norm, corresponding to complete failure of the reconstruction of source components.
However, in such cases, already slight modifications of the standard EM algorithm may lead to considerably improved results, without the need for an additional optimisation step. As an example, we employ the “adaptive over-relaxed bound” variant of the standard EM algorithm, as proposed by Salakhutdinov and Roweis [33], by which a successful reconstruction of source components is achieved, with a value of 49421.01 for (−2)log(likelihood) and a value of 0.1068 for the Frobenius norm.
5 Other constraints for LSS models
In this section, we will briefly discuss some further constraints that one might wish to impose on LSS models, depending on the application for which the models are created. These are two general properties of LSS models, namely observability and controllability [23], and two properties of the ARMA processes within our IC-LSS model structure, namely stability and invertibility [34].
5.1 Observability
Observability is a property of the matrices A and C, or rather, in our case, of the blocks A(j) and C(j). If this property is not given, the Kalman filter will be unable to estimate all components of the state vectors. Luckily, in our case, we do not need to worry about observability, since it is always given for LSS models in the observer canonical form (hence the name).
5.2 Controllability
Controllability is a property of the matrices A and Q, or rather of the blocks A(j) and Q(j). It has been shown that a LSS model that is both observable and controllable has minimal state dimension, i.e. it is a minimal realisation. From the viewpoint of the theory of maximum likelihood estimation, this is a desirable property for LSS models [35].
LSS models in the observer canonical form are not necessarily controllable. We could have avoided this problem by choosing the controller canonical form instead, but then, we would risk losing the observability property, which, with respect to application to Blind Signal Separation, is the more important of these two properties.
Commonly controllability is defined for state space models whose state equation reads as follows [23]:
When compared with Eq. (1), this equation contains an additional input gain matrixB. Within the setting of Blind Signal Separation of this paper, we have chosen to omit this additional matrix, since usually no information is available that would allow us to distinguish it from the dynamical noise covariance matrix Q, so we prefer to absorb B in Q. However, we can easily replace this choice by its opposite, i.e. we can form the Cholesky decomposition \(\mathsf {Q}=\mathsf {B}^{\intercal }\mathsf {B}\), thereby retrieving an input gain matrix B while replacing Q by a unity matrix.
For each block, we can then form the controllability matrix
The jth block is controllable, if and only if \(\mathcal {C}^{(j)}\) has rank m (a similar test exists for observability).
An equivalent test for controllability can be based on the transfer function of the (blockwise) ARMA representation of our IC-LSS models: the poles of this function are given by the roots of the characteristic polynomial of A(j),
while its zeros are given by the roots of the polynomial formed from the MA parameters \(b^{(j)}_{i}\),
Controllability requires that no pole-zero cancellations occur, i.e. that none of the roots of Eq. (84) coincides with any of the roots of Eq. (85).
During the fitting of IC-LSS models, either by the EM algorithm, or by algorithms for numerical optimisation, the parameters \(a^{(j)}_{i}\) and \(b^{(j)}_{i}\) are estimated based on the maximum-likelihood principle; no constraint regarding the roots of the two polynomials, Eqs. (84) and (85), is present. To the best of our knowledge, there exists currently no published work on introducing this kind of constraint into parameter estimation for LSS models by the EM algorithm. We doubt that an approach could be found that would take this constraint into account while retaining the closed-form update equations which are an attractive feature of the EM algorithm.
What can be done is explicitly testing the obtained models for cases of pole-zero cancellation. For the simulation studies reported in this paper, such testing has been done for all obtained models, but no case of pole-zero cancellation was found. This is to be expected since in the space of the autoregressive and moving-average model parameters, the set of points corresponding to exact pole-zero cancellations has measure zero.
However, it could happen that some pole-zero pairs have very small distance in the complex plane. The higher the model order p is chosen, the smaller these distances may become within the unit circle (if we force all zeros to lie within the unit circle, see section 5.4 below). The smallest distance between a pole and a zero which we have seen in our simulations was 0.00031, after EM optimisation and additional numerical optimisation; this occurred for p=10, i.e. a rather high model order. For a low model order of p=2, the smallest distance was 1.0852, after pure EM optimisation.
5.3 Stability
Stability, or lack thereof, is a fundamental property of dynamical models, such as ARMA models or LSS models. If the model is unstable, the states will diverge. An ARMA model is stable if the roots of its characteristic polynomial, Eq. (84), lie inside the unit circle; more generally, a LSS model is stable, if the eigenvalues of the state transition matrix A lie inside the unit circle.
Enforcing stability during model fitting would correspond to applying inequality constraints to functions of the autoregressive parameters \(a^{(j)}_{i}\). To the best of our knowledge, there exists currently no published work on introducing inequality constraints into parameter estimation for LSS models by the EM algorithm. On the other hand, within most algorithms for numerical optimisation, it is quite easy to prevent the roots of the autoregressive polynomial from leaving the unit circle.
Again, what can be done is explicitly testing the obtained models for roots outside the unit circle. For the simulation studies reported in this paper, no such case was found. This is to be expected since the simulated data was generated by stable dynamical systems. However, we could also have generated data from a slowly diverging system, and if we would fit a LSS model to such data, we would expect to obtain an unstable model, since this would be the correct result.
As an alternative, it would be possible to employ structures for LSS models which are intrinsically guaranteed to be stable, such as the ladder / lattice form models that have been developed for digital filtering [36, 37].
For our intended application of Blind Signal Separation, stability of the LSS model is less relevant, since we simply want to reconstruct mixed components, be they stable or diverging, but for control applications the situation would be different.
5.4 Invertibility
While stability is a property of the autoregressive parameters \(a^{(j)}_{i}\), there is a corresponding property of the moving average parameters \(b^{(j)}_{i}\), known as invertibility. The moving-average part of an ARMA model is invertible if the roots of Eq. (85) lie inside the unit circle. Invertibility is less important than stability, since there is no danger of divergence for non-invertible models; however, keeping the zeros of an ARMA model inside the unit circle may offer numerical benefits.
It can be shown ([34], chapter 3.7) that any non-invertible ARMA model can be transformed into an invertible model as follows. Let the roots of Eq. (85) be denoted by
such that the roots \(\lambda ^{(j)}_{i}\), i=1,…,k−1 lie inside the unit circle, while the remaining roots lie outside. Then, we replace the latter set of roots by their inverses, obtaining
The transformed moving average parameters are computed from these roots. Additionally, the variance of the process has to be multiplied by the factor
Since in our IC-LSS models, the variance of the stochastic term is normalised to unity for each ARMA model via a scale convention, instead the square root of Eq. (88) has to be multiplied to the corresponding block within the observation matrix C(j) (see Eq. (11)).
6 Discussion and conclusion
In this paper, we have discussed the fitting of LSS models to given multivariate time series; in particular, we have discussed the estimation of the parameters of such models in the presence of constraints imposed on the four main parameter matrices of LSS models. This study was motivated by the intention to apply LSS models to a task from the field of Blind Signal Separation, namely the reconstruction of independent components from linear mixtures. Each of these components was modelled as an ARMA(p,p−1) process, reformulated in the observer canonical form state space representation. In order to keep the dynamical noise covariance matrix invertible, for each component, a further parameter, or set of parameters, was introduced, thereby generalising the ARMA structure. Constraints arise partly from the choice of this generalised ARMA structure, within the assumption of mutually independent components, and partly from the need to avoid parameter redundancy which would render the model unidentifiable.
We have reviewed the available published work on constrained estimation of LSS parameters by the EM algorithm and found that it does not cover the particular kind of constraint which we need to impose on the dynamical noise covariance matrix. Consequently, we have derived a new closed-form EM update rule for this kind of constraints. Also, for the case of updating the matrix square-root of the dynamical noise covariance matrix, we have derived a corresponding closed-form update rule; this variant has the benefit of keeping the estimates of the dynamical noise covariance matrix always positive definite. The latter update rule contains determinants, and we have presented a proof based on recursive application of Sylvester’s determinantal identity.
The new update rules were formulated within the framework of a generalisation of LSS modelling, known as “pairwise Kalman filtering”; however, we have used this framework mainly for the purpose of attaining a more efficient formulation of the equations, while ignoring the actual generalisations offered by this framework. As a consequence of employing “pairwise Kalman filtering,” the two parameter matrices A and C are updated jointly, instead of separately; the update rule for this joint updating slightly differs from the update rule for separate updating. We have shown simulation results indicating that joint updating is superior to separate updating, with respect to increasing the likelihood within a given number of iterations.
We have explored the practical application of the proposed algorithm through two simulation examples, given by the task of unmixing two linear mixtures of two mutually independent source components. The source components were either given by time series integrated from two deterministic nonlinear dynamical systems (“wrong-model-class” scenario) or by time series generated by two stochastic linear ARMA(2,1) processes (“true-model-class” scenario). For both cases, LSS modelling was performed by two linear ARMA (p,p−1) processes, with generalisation. In the “wrong-model-class” scenario, the model order p was varied from 1 to 10, while in the “true-model-class” scenario, it was fixed to 2. Examples for the unmixing of real-world biomedical time series by using similar LSS methodology have been published elsewhere [10].
In the case of simulations, the correct source components are known, therefore other quantitative measures of performance are available, in addition to the likelihood. As a convenient example, we have employed a recently proposed measure based on the Frobenius norm of a difference of matrices [9].
In a “wrong-model-class” scenario, there is no correct value for the model order p. The choice of the model order represents a compromise between the complexity of the model, with more complex models allowing better modelling of the data, and the number of model parameters to be estimated, with larger number creating the risk of overfitting, and also entailing higher computational effort for numerical optimisation. In this paper, we have explored model orders larger than p=2, and our results indicate that optimal model orders for the mixtures of two deterministic nonlinear systems which represent our simulated data are probably considerably larger than 2. This should not be surprising, if we remember that, from a linear perspective, nonlinear systems would appear as infinitely-dimensional.
In principle, optimal model orders may be estimated by a model comparison approach, e.g. based on minimising the AIC. For this purpose, the values of AIC obtained for different model orders have to be compared. However, in an IC-LSS model composed of several ARMA components, the optimal model order of each component may be different; therefore such model comparison approach would require fitting a considerable number of individual models. Due to the large number of parameters, fitting IC-LSS models with high values for the number of components Nc and for the model order p can easily become very time-consuming.
As we have demonstrated, for the mere purpose of Blind Signal Separation, high model orders are not necessary; instead, we recommend to choose p=2 for all source components and possibly p=1 for source components with drift-like behaviour. This choice also offers advantages with respect to the choice of initial models [10]. Furthermore, the choice p=2 represents the simplest model which would be able to describe stochastic oscillations, via a pair of complex conjugated eigenvalues; therefore, it is often employed as a standard model for time series analysis [38].
We need to emphasise that the simulation examples presented in this paper merely serve for the purpose of proof-of-principle. In practical applications, such unmixing tasks could have been accomplished much faster by standard algorithms for Independent Component Analysis (ICA). At least, an ICA algorithm would have provided a much better initial model for the EM optimisation, as compared with the arbitrarily chosen initial models which we have used. On the other hand, LSS modelling does provide an attractive alternative to ICA in cases of underdetermined mixing (with the number of source components exceeding the number of mixtures) and in cases of large amounts of observation noise. The concept of combining ICA algorithms with LSS modelling has been explored in a recent paper [39].
The EM algorithm is supposed to converge to a local minimum, but it is well known that the convergence can be extremely slow. In our “wrong-model-class” scenario simulation example, (−2)log(likelihood) has either continued to decrease slowly without reaching a point with positive definite Hessian even after 25000 iterations (in case of separate updating of A and C), or it has started to rise again after a rather small number of iterations, having attained a minimum value of (−2)log(likelihood) (in case of joint updating of A and C), but also at this minimum value, the Hessian failed to be positive definite; therefore, also this point did not represent an actual local minimum. Even more surprising was the behaviour of the Frobenius norm which, in case of separate updating of A and C, after several hundreds of iterations started to rise towards values indicating a complete failure of the unmixing task, while (−2)log(likelihood) continued to decrease. Also in the “true-model-class” scenario simulation example, which would seemingly pose an easier task, the EM algorithm alone was often unable to reach a convincing minimum.
For practical applications, these phenomena and differences of behaviour are essentially irrelevant, because it would be unwise to run hundreds or thousands of iterations of the EM algorithm anyway. Usually, the EM algorithm achieves the main improvements of (−2)log(likelihood) during the first few iterations, maybe up to 20 or 30, but, as recommended already by Shumway and Stoffer [7], afterwards, one should switch to another algorithm for numerical optimisation, such as the BFGS quasi-Newton algorithm or the Nelder-Mead simplex algorithm. In our simulation examples, both algorithms have achieved considerable further improvements of (−2)log(likelihood), converging to points with positive definite Hessians. In general, we expect that improvement of (−2)log(likelihood) also leads to improvement of the Frobenius norm, i.e. of the performance of source component reconstruction, but we have also seen cases where this expectation turned out to be wrong. A systematic investigation of the relationship between the Frobenius norm and the likelihood would be an interesting topic for future work.
As a further topic for future work, we mention the filter-based EM algorithm for estimating the parameters of LSS models that has been developed by Elliott, Krishnamurty, and Hyndman [28, 40]. Their EM algorithm is based on update rules that can be applied without the need to run a smoother backwards through the data, thereby saving computational time and avoiding numerical issues that may result from the smoother pass. It would be interesting to develop a square-root version of this algorithm and compare its properties with the algorithm presented in this paper.
7 Appendix: Proofs
In this Appendix, we present proofs for the claims that Eq. (58) is a solution of Eq. (56), and that Eq. (66) is a solution of Eq. (64).
As a preparation for the proof of Eq. (66), we first need to establish a determinantal recursion that can be derived from Sylvester’s determinantal identity.
Consider the submatrix [M]1:k,1:k of a symmetric (m×m) matrix M, then according to Sylvester’s determinantal identity the following relationship holds for the determinant of this submatrix:
For the case k=3, this identity would be an example of Chió’s pivotal condensation. It is important to note that this identity also applies to submatrices which are defined by non-continuous subsets of indices, e.g. we might choose to ignore the kth column of M and use the jth column instead, where k<j≤m:
We start building up the desired recursion by using Eq. (90) for k=3, i.e.
This expression represents the first step of the recursion, but it will be convenient to label it as the third step, while the first two steps are omitted. Next, we employ Eq. (89) for k=4 which gives
Then, we insert j=4 into Eq. (91) and multiply the resulting expression with det([M]1:3,1:3); furthermore, we multiply Eq. (92) with det([M]1,1)≡m11. Then the term
in the latter equation can be replaced by the right-hand side of the former equation. In the resulting identity, we choose to ignore the 4th column of M and use the jth column instead (where j≥4), in the same way by which we derived Eq. (90) from Eq. (89); this gives the 4th step of the recursion:
where in the last two terms we have used the symmetry of M. The recursion continues by inserting j=5 into Eq. (93) and multiplying the resulting expression with det([M]1:4,1:4), then by employing Eq. (89) for k=5 and multiplying the resulting identity with m11 det([M]1:2,1:2). Then, the term
in the latter equation can be replaced by the right-hand side of the former equation. In the resulting identity, we choose to ignore the 5th column of M and use the jth column instead (where j≥5); this gives the 5th step of the recursion:
again by using symmetry of M. It becomes clear now that the ith step of this recursion can be derived by inserting j=i into the identity from the previous step, then multiplying the resulting expression with det([M]1:(i−1),1:(i−1)), then by employing Eq. (89) for k=i and by multiplying the resulting identity with \(\prod _{l=1}^{i-3}\det \left ([\mathsf {M}]_{1:l,1:l}\right)\). Then, the first term on the right-hand side of the latter equation (the only term with positive sign) is replaced by the right-hand side of the former equation. In the resulting identity, we ignore the ith column of M and use the jth column instead (where j≥i). With each step of the recursion the right-hand side of the identity grows by one further term. The general form of the identity is given by
We are now in a position to perform the actual proofs. We begin with Eq. (56). As argued above, it suffices to work with a single square block and to use only a single Lagrange multiplier ϕ which occupies position (1,1) of Φ while all other elements remain zero. Let nb denote the dimension of the given square block. For ease of notation, we define [Q]ij=qij and \([\mathsf {M}_{\mathcal {A}}]_{ij}=m_{ij}\). When we write the matrix \(\mathsf {M}_{\mathcal {A}}\), we omit the subscript \(\mathcal {A}\). Then, the set of equations to be solved is given by
for i=1,…,nb and j=i,…,nb. The choice (i=1,j=1) gives the Lagrange multiplier as
Then, all equations (i=1, j=2,…,m) can be solved, giving
Then, for all remaining equations, the terms ϕq1iq1j are known, and all qij, i>1 result as
This expressions also describes the solutions for the q1j. q.e.d.
Next, we turn to Eq. (64). For ease of notation, we define [Q1/2]ij=sij. Again, Φ contains only one non-zero element at position (1,1). Then, the set of equations to be solved is given by
for i=1,…,nb and j=i,…,nb. The choice (i=1,j=1) gives the Lagrange multiplier as
Then, all equations (i=1, j=2,…,nb) can be solved, giving
thus establishing the case k=1 of Eq. (66). Proving the general case k>1 requires more effort than in the non-square-root case. First, we note that the sij, i.e. the elements of Q1/2, can be computed consecutively column by column, from the left to the right, and within each column from top to the diagonal; elements below the diagonal are zero by definition. The choice (i=2,j=2) gives
which after inserting ϕ and s12 yields
The choice (i=2,j=3) gives
which after inserting ϕ, s12, s13 and s22 yields
These solutions for s22 and s23 agree with the expression given for k>1 in Eq. (66); therefore, they can serve as starting point of a proof by induction.
It is obvious from the structure of Eq. (64) that if we have the solution for the choice (i=2,j=3), we indeed have the solution for all j≥3, since in the solution for s23 we just have to replace the index 3 by j. In this fashion, we can solve entire rows of Q1/2. It therefore suffices to perform induction over the index i in sij with j>i. The case sii will be treated separately.
In order to perform the main induction step, we write Eq. (64) as
which after inserting ϕ, s1i and s1j yields
Note that due to the symmetry of M
Now, we assume that Eq. (66) is true for all skl with k=2,…,i, l=k,…,i. We intend to compute sij from Eq. (64) with j>i. Inserting the appropriate expressions from Eq. (66) yields
But, if we consider the diagonal elements, i.e. i=j, we get
By inserting Eq. (95) into Eq. (97), we obtain
in agreement with Eq. (66). Next, we return to the diagonal elements sii. For i=j Eq. (95) becomes
By inserting Eq. (99) into Eq. (98), we obtain
which again is in agreement with Eq. (66). q.e.d.
Availability of data and materials
Please contact author for data requests
Abbreviations
- AIC:
-
Akaike Information Criterion
- ARMA model:
-
autoregressive moving-average model
- BFGS algorithm:
-
Broyden-Fletcher-Goldfarb-Shanno algorithm
- EM algorithm:
-
Expectation maximisation algorithm
- ICA:
-
Independent Component Analysis
- IC-LSS model:
-
Independent components linear state space model
- KF:
-
Kalman filter/filtering
- LSS model:
-
Linear state space model
- RTS smoother:
-
Rauch-Tung-Striebel smoother
- SVD:
-
Singular value decomposition
References
T. Kailath, A. Sayed, B. Hassibi, Linear estimation (Prentice Hall, Englewood Cliffs, 2000).
J. Durbin, S. J. Koopman, Time series analysis by state space methods (Oxford University Press, Oxford, New York, 2001).
G. J. Bierman, Factorization methods for discrete sequential estimation (Academic Press, New York, 1977).
L. Ljung, System identification: theory for the user, 2. edn. (Prentice-Hall, Englewood Cliffs, 1999).
H. Akaike, A new look at the statistical model identification. IEEE Trans. Autom. Contr.19:, 716–723 (1974).
A. P. Dempster, N. M. Laird, D. B. Rubin, Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B. 39:, 1–38 (1977).
R. H. Shumway, D. S. Stoffer, An approach to time series smoothing and forecasting using the EM algorithm. J. Time Ser. Anal.3:, 253–264 (1982).
J. Nocedal, S. Wright, Numerical optimization, 2. edn. (Springer, Berlin, Heidelberg, New York, 2006).
A. Galka, K. F. K. Wong, U. Stephani, T. Ozaki, M. Siniatchkin, Blind signal separation of mixtures of chaotic processes: a comparison between independent component analysis and state space modeling. Int. J. Bifurcation Chaos. 23:, 1350165 (2013).
A. Galka, K. F. K. Wong, T. Ozaki, H. Muhle, U. Stephani, M. Siniatchkin, Decomposition of neurological multivariate time series by state space modelling. Bull. Math. Biology. 73:, 285–324 (2011).
M. Watson, R. Engle, Alternative algorithms for the estimation of dynamic factor, MIMIC and varying coefficient regression models. J. Econ.23:, 385–400 (1983).
S. Gibson, B. Ninness, Robust maximum-likelihood estimation of multivariable dynamic systems. Automatica. 41:, 1667–1682 (2005).
S. Särkkä, Bayesian filtering and smoothing (Cambridge University Press, Cambridge, 2013).
Z. Ghaharamani, G. E. Hinton, Parameter estimation for linear dynamical systems. Technical report CRG-TR-96-2 (Univ. of Toronto, Toronto, 1996).
V. Némesin, S. Derrode, Robust blind pairwise Kalman algorithms using QR decompositions. IEEE Trans. Sig. Process.61:, 5–9 (2013).
L. S. Wu, J. S. Pai, J. R. M. Hosking, An algorithm for estimating parameters of state-space models. Stat. Probab. Lett.28:, 99–106 (1996).
E. E. Holmes, Derivation of an EM algorithm for constrained and unconstrained multivariate autoregressive state-space (MARSS) models. arXiv:1302.3919 (2013).
V. Némesin, S. Derrode, Robust partial-learning in linear Gaussian systems. IEEE Trans. Autom. Contr.60:, 2518–2523 (2015).
W. Pieczynski, F. Desbouvries, in 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2003. Proceedings. (ICASSP ’03). Kalman filtering using pairwise gaussian models (IEEE, 2003). https://doi.org/10.1109/icassp.2003.1201617.
E. J. Godolphin, S. E. Johnson, Decomposition of time series dynamic linear models. J. Time Ser. Anal.24:, 513–527 (2003).
L. Xu, Temporal BYY learning for state space approach, hidden Markov model and blind source separation. IEEE Trans. Signal Process.48:, 2132–2144 (2000).
Y. M. Cheung, A maximum likelihood approach to temporal factor analysis in state-space model. Sig. Process.86:, 2966–2980 (2006).
G. F. Franklin, J. D. Powell, M. L. Workman, Digital control of dynamic systems, 3rd edn. (Prentice-Hall, Englewood Cliffs, 1998).
V. Solo, in 42nd IEEE Conference on Decision and Control (CDC). An EM algorithm for singular state space models (IEEEPiscataway, 2003), pp. 3457–3460.
H. E. Rauch, G. Tung, C. T. Striebel, Maximum likelihood estimates of linear dynamic systems. Am. Inst. Aeronaut. Aeronaut. (AIAA) J.3:, 1445–1450 (1965).
L. Wang, G. Libert, P. Manneback, Kalman filter algorithm based on singular value decomposition (IEEE, 1992). https://doi.org/10.1109/cdc.1992.371522.
M. V. Kulikova, J. V. Tsyganova, Improved discrete-time Kalman filtering within singular value decomposition. IET Control Theory Appl.11:, 2412–2418 (2017).
R. J. Elliott, C. B. Hyndman, Parameter estimation in commodity markets: a filtering approach. J. Econ. Dyn. Control. 31:, 2350–2373 (2007).
E. N. Lorenz, Deterministic nonperiodic flow. J. Atmos. Sci.20:, 130–141 (1963).
R. Thomas, Deterministic chaos seen in terms of feedback circuits: analysis, synthesis, ’labyrinth chaos’. Int. J. Bifurcation Chaos. 9:, 1889–1905 (1999).
T. Ozaki, A bridge between nonlinear time series models and nonlinear stochastic dynamical systems: a local linearization approach. Stat. Sin.2:, 113–135 (1992).
L. Tong, R. Liu, V. C. Soon, Y. Huang, Indeterminacy and identifiability of blind separation. IEEE Trans. Circuits Syst.38:, 499–509 (1991).
R. Salakhutdinov, S. Roweis, in 20th International Conference on Machine Learning (ICML). Adaptive overrelaxed bound optimization methods (AAAI PressMenlo Park, 2003), pp. 664–671.
J. D. Hamilton, Time series analysis (Princeton University Press, Princeton, 1994).
P. Caines, Linear stochastic systems (Wiley, New York, 1988).
S. Mitra, R. Sherwood, Digital ladder networks. IEEE Trans. Audio Electroacoust.21(1), 30–36 (1973). https://doi.org/10.1109/TAU.1973.1162423.
S. Horvath, in Proc. IEEE Int. Symp. Circuits Systems. Lattice form adaptive recursive digital filters: algorithms and applications, (1980), pp. 128–133.
M. West, R. Prado, A. D. Krystal, Evaluation and comparison of EEG traces: latent structure in nonstationary time series. J. Amer. Stat. Assoc.94:, 1083–1095 (1999).
A. Santillán Guzmán, U. Heute, U. Stephani, A. Galka, Comparison of different methods to suppress muscle artifacts in EEG signals. SIViP. 11:, 761–768 (2017).
R. J. Elliott, V. Krishnamurthy, New finite-dimensional filters for parameter estimation of discrete-time linear Gaussian models. IEEE Trans Autom. Contr.44:, 938–951 (1999).
Acknowledgements
This work was supported by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) through SFB 1261 “Magnetoelectric Sensors: From Composite Materials to Biomagnetic Diagnostics” and through the funding programme “Open Access Publizieren”. The authors would like to thank E.E. Holmes, S. Börm, and T. Ozaki for helpful discussions.
Funding
German Research Foundation (Deutsche Forschungsgemeinschaft, DFG): SFB 1261; “Open Access Publizieren”.
Author information
Authors and Affiliations
Contributions
AG wrote the paper and major parts of the code. SM contributed parts of the constrained EM code and worked on the numerical example. MS supervised the research work. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Galka, A., Moontaha, S. & Siniatchkin, M. Constrained expectation maximisation algorithm for estimating ARMA models in state space representation. EURASIP J. Adv. Signal Process. 2020, 23 (2020). https://doi.org/10.1186/s13634-020-00678-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13634-020-00678-3