Indentation of a Periodically Layered, Planar, Elastic Half-Space

Abstract

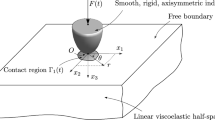
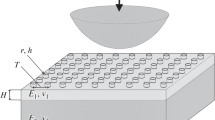
We investigate indentation by a smooth, rigid indenter of a two-dimensional half-space comprised of periodically arranged linear-elastic layers with different constitutive responses. Identifying the half-space’s material parameters as periodic functions in space, we utilize the theory of periodic homogenization to approximate the layered heterogeneous material by a linear-elastic, homogeneous, but anisotropic medium. This approximation becomes exact as the layer thickness becomes infinitesimal. In this way, we reduce the original problem to the indentation of an anisotropic, homogeneous, linear-elastic half-space by a smooth, rigid indenter. The latter is solved analytically by formulating and resolving the corresponding matrix Riemann–Hilbert boundary-value problem in complex analysis. Thus, we obtain an approximate, but analytical solution for the indentation of a layered heterogeneous medium. We then compare this solution with finite element computations of the indentation on the original layered, heterogenous half-space. We conclude that (a) the contact pressure on the layered, heterogenous half-space is well approximated by that obtained through homogenization, and the approximation improves as the layer thickness is decreased, or if the indentation force is increased; (b) the upper bound of the difference between the two contact pressures depends only upon the ratio of the Young’s moduli of the two materials constituting the heterogenous medium and their Poisson’s ratio; and (c) the average variation of the discontinuous von Mises stress in the layered half-space is well approximated by the one found in the homogenized half-space. The approach presented here can be utilized for a diverse array of indentation and contact problems of finely mixed heterogeneous media, and is also amenable to systematic improvements.

Appendices

Appendix A: Evaluation of $\mathbf{M}$ for Isotropic Materials

For cases when $\mathbf{S_{2}}^{-1}\mathbf{S_{1}}$ is not diagonalizable, which happens only if $\varLambda _{1}=\varLambda _{2}=\varLambda$, we can still find a nonsingular matrix $\hat{\mathbf{E}}$, such that

$$\begin{aligned} \hat{\mathbf{E}}^{-1}\mathbf{S_{2}}^{-1}\mathbf{S_{1}} \hat{\mathbf{E}}= \begin{bmatrix} \varLambda &1&0&0 \\ 0&\varLambda &0&0 \\ 0&0&\bar{\varLambda }&1 \\ 0&0&0&\bar{\varLambda } \end{bmatrix}, \end{aligned}$$

(74)

where the square matrix on the right is the Jordan normal form of $\mathbf{S_{2}}^{-1}\mathbf{S_{1}}$. We can then extend the definition of $\mathbf{M}$ to such cases by writing $\hat{\mathbf{E}}$ in terms of two $2\times 2$ nonsingular matrices $\mathbf{A}$ and $\mathbf{B}$, as done in (25). We let $\hat{\mathbf{E}}=\left[\begin{array}{cc}\mathbf{A}& \overline{\mathbf{A}}\\ \mathbf{B}& \overline{\mathbf{B}}\end{array}\right]$ and define $\mathbf{M}=i\mathbf{A}\mathbf{B}^{-1}$ as done in Sect. 3.

For an isotropic material with Lamé’s parameters $\lambda$ and $\mu$, we find matrices $\mathbf{Q}$, $\mathbf{R}$ and $\mathbf{W}$ using (10) and (19) to be

$$\begin{aligned} \mathbf{Q}= \begin{bmatrix} \lambda +2\mu &0 \\ 0&\mu \end{bmatrix},\quad \mathbf{R}= \begin{bmatrix} 0&\lambda \\ \mu &0 \end{bmatrix}\quad \text{and}\quad \mathbf{W}= \begin{bmatrix} \mu &0 \\ 0&\lambda +2\mu \end{bmatrix}. \end{aligned}$$

(75)

While diagonalizing $\mathbf{S_{2}}^{-1}\mathbf{S_{1}}$ with (75), we find $\varLambda _{1}=\varLambda _{2}=i$, corresponding to which we obtain only one independent eigenvector. Therefore, the matrix $\mathbf{S_{2}}^{-1}\mathbf{S_{1}}$ for an isotropic material, obtained using (75) is not diagonalizable. Hence, we use its Jordan normal form (74) to compute $\hat{\mathbf{E}}$, so that

$$\begin{aligned} &\mathbf{S_{2}}^{-1}\mathbf{S_{1}}=\hat{\mathbf{E}} \begin{bmatrix} i&1&0&0 \\ 0&i&0&0 \\ 0&0&-i&1 \\ 0&0&0&-i \end{bmatrix} \hat{\mathbf{E}}^{-1}, \\ &\quad \text{where}\quad \hat{\mathbf{E}}= \begin{bmatrix} -\dfrac{1}{2\mu }&i\dfrac{\lambda +2\mu }{2\mu (\lambda +\mu )}&- \dfrac{1}{2\mu }&-i\dfrac{\lambda +2\mu }{2\mu (\lambda +\mu )} \\ -\dfrac{i}{2\mu }&\dfrac{1}{2(\lambda +\mu )}&\dfrac{i}{2\mu }&\dfrac{1}{2(\lambda +\mu )} \\ -i&-1&i&-1 \\ 1&0&1&0 \end{bmatrix}. \end{aligned}$$

(76)

We now easily find $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{M}$, as done in (25) to obtain

$$\begin{aligned} &\mathbf{A}= \begin{bmatrix} -\dfrac{1}{2\mu }&i\dfrac{\lambda +2\mu }{2\mu (\lambda +\mu )} \\ -\dfrac{i}{2\mu }&\dfrac{1}{2(\lambda +\mu )} \end{bmatrix}, \,\mathbf{B}= \begin{bmatrix} -i&-1 \\ 1&0 \end{bmatrix} \\ &\quad \text{and}\quad \mathbf{M}= \dfrac{1}{2(\lambda +\mu )} \begin{bmatrix} \dfrac{\lambda +2\mu }{\mu }&i \\ -i&\dfrac{\lambda +2\mu }{\mu } \end{bmatrix}. \end{aligned}$$

(77)

In particular, we obtain from (77) that $M_{22}={(\chi +1)}/{4\mu }$, where we recall that $\chi ={(\lambda +3\mu )}/{(\lambda +\mu )}$. Thus, for an isotropic material, (41) reduces to (11), as it should.

We, however, cannot use the matrix $\mathbf{B}$ thus obtained in (44) when $\mathbf{S_{2}}^{-1}\mathbf{S_{1}}$ is not diagonalizable, because in such a case the general solutions (24), which crucially depend upon this diagonalization, no longer hold and need modification. Therefore, for indentation of an isotropic material, we require a different approach. We follow the results obtained by Muskhelishvili [19], which we compiled at the end of Sect. 2. Muskhelishvili employed a similar complex variables based approach as given in Sect. 3, but employing the structure of an isotropic material right from the beginning, thereby bypassing the problem of lack of diagonalization of $\mathbf{S_{2}}^{-1}\mathbf{S_{1}}$.

Appendix B: Solutions of the Auxiliary Periodic Problem

We solve auxiliary problem (49) for $\boldsymbol{\chi }^{lm}$, which are then used in (48) to find the components of the effective stiffness tensor of the homogenized material. For $l=1$, $m=1$ and $i=1$, the PDE

$$\begin{aligned} \dfrac{\partial }{\partial x_{j}}\left (a_{{ijkh}} \dfrac{\partial \chi _{k}^{lm}}{\partial x_{h}}\right )= \dfrac{\partial a_{{ijlm}}}{\partial x_{j}} \end{aligned}$$

in (49) transforms to

$$\begin{aligned} &\frac{\partial }{\partial x_{1}}\left (a_{1111} \frac{\partial \chi _{1}^{11}}{\partial x_{1}} +a_{1122} \frac{\partial \chi _{2}^{11}}{\partial x_{2}} +a_{1133} \frac{\partial \chi _{3}^{11}}{\partial x_{3}}\right )+ \frac{\partial }{\partial x_{2}}\left (a_{1212} \frac{\partial \chi _{1}^{11}}{\partial x_{2}} +a_{1221} \frac{\partial \chi _{2}^{11}}{\partial x_{1}}\right ) \\ &\quad {}+ \frac{\partial }{\partial x_{3}}\left (a_{1313} \frac{\partial \chi _{1}^{11}}{\partial x_{3}} +a_{1331} \frac{\partial \chi _{3}^{11}}{\partial x_{1}}\right )=0. \end{aligned}$$

The remaining terms in the above expansion are zero either on account of $a_{{ijkh}}$’s being zero for appropriate indices, as is clear from (10), or because $a_{{ijkh}}(\mathbf{x})=a_{{ijkh}}(x_{2})$, which implies $\dfrac{\partial a_{{ijkh}}}{\partial x_{m}}=0$ for $m=1,3$. Using (10), we obtain

$$\begin{aligned} &\frac{\partial }{\partial x_{1}}\left \{ (\lambda +2\mu ) \frac{\partial \chi _{1}^{11}}{\partial x_{1}} +\lambda \frac{\partial \chi _{2}^{11}}{\partial x_{2}}+\lambda \frac{\partial \chi _{3}^{11}}{\partial x_{3}}\right \} + \frac{\partial }{\partial x_{2}}\left (\mu \frac{\partial \chi _{1}^{11}}{\partial x_{2}}+\mu \frac{\partial \chi _{2}^{11}}{\partial x_{1}}\right ) \\ &\quad {}+ \frac{\partial }{\partial x_{3}}\left (\mu \frac{\partial \chi _{1}^{11}}{\partial x_{3}} +\mu \frac{\partial \chi _{3}^{11}}{\partial x_{1}}\right )=0. \end{aligned}$$

(78)

Similarly, for $l=1$, $m=1$, $i=2$ and $l=1$, $m=1$, $i=3$, we have

$$\begin{aligned} &\frac{\partial }{\partial x_{1}}\left (\mu \frac{\partial \chi _{1}^{11}}{\partial x_{2}} +\mu \frac{\partial \chi _{2}^{11}}{\partial x_{1}}\right )+ \frac{\partial }{\partial x_{2}}\left \{ \lambda \frac{\partial \chi _{1}^{11}}{\partial x_{1}} +(\lambda +2\mu ) \frac{\partial \chi _{2}^{11}}{\partial x_{2}}+\lambda \frac{\partial \chi _{3}^{11}}{\partial x_{3}}\right \} \\ &\quad {} + \frac{\partial }{\partial x_{3}}\left (\mu \frac{\partial \chi _{2}^{11}}{\partial x_{3}} +\mu \frac{\partial \chi _{3}^{11}}{\partial x_{2}}\right )= \frac{\partial \lambda }{\partial x_{2}}, \end{aligned}$$

(79)

and

$$\begin{aligned} &\frac{\partial }{\partial x_{1}}\left (\mu \frac{\partial \chi _{1}^{11}}{\partial x_{3}} +\mu \frac{\partial \chi _{3}^{11}}{\partial x_{1}}\right )+ \frac{\partial }{\partial x_{2}}\left (\mu \frac{\partial \chi _{2}^{11}}{\partial x_{3}}+\mu \frac{\partial \chi _{3}^{11}}{\partial x_{2}}\right ) \\ &\quad {}+ \frac{\partial }{\partial x_{3}}\left \{ \lambda \frac{\partial \chi _{1}^{11}}{\partial x_{1}} +\lambda \frac{\partial \chi _{2}^{11}}{\partial x_{2}}+(\lambda +2\mu ) \frac{\partial \chi _{3}^{11}}{\partial x_{3}}\right \} =0, \end{aligned}$$

(80)

respectively. We solve (78)–(80) for $\boldsymbol{\chi }^{11}(\mathbf{x}):=(\chi ^{11}_{1},\chi ^{11}_{2}, \chi ^{11}_{3})$. To this end, we guess that $\chi ^{11}_{1}$, $\chi ^{11}_{2}$ and $\chi ^{11}_{3}$ are independent of $x_{1}$ and $x_{3}$, so that (78), (79) and (80) reduce, respectively, to the following:

$$\begin{aligned} \frac{\partial }{\partial x_{2}}\left (\mu \frac{\partial \chi _{1}^{11}}{\partial x_{2}}\right )=0,\quad \frac{\partial }{\partial x_{2}}\left \{ (\lambda +2\mu ) \frac{\partial \chi _{2}^{11}}{\partial x_{2}}\right \} = \frac{\partial \lambda }{\partial x_{2}}\quad \text{and}\quad \frac{\partial }{\partial x_{2}}\left (\mu \frac{\partial \chi _{3}^{11}}{\partial x_{2}}\right )=0. \end{aligned}$$

Solving the above set of equations, we obtain

$$\begin{aligned} \begin{aligned} &\chi _{1}^{11}=\chi _{3}^{11}=0 \\ &\quad \text{and}\quad \chi _{2}^{11}= \left \{ \begin{aligned} &\frac{(\lambda _{A}-\lambda _{B})(1-\alpha )}{(\lambda _{A}+2\mu _{A})(1-\alpha )+(\lambda _{B}+2\mu _{B})\alpha } \left (x_{2}-\frac{\alpha }{2}\right ), \quad \qquad 0< x_{2}< \alpha , \\ &\frac{(\lambda _{A}-\lambda _{B})\alpha }{(\lambda _{A}+2\mu _{A})(1-\alpha )+(\lambda _{B}+2\mu _{B})\alpha } \left (\frac{\alpha +1}{2} -x_{2}\right ), \quad \alpha < x_{2}< 1. \end{aligned} \right . \end{aligned} \end{aligned}$$

(81)

Similarly, with the assumption that $\boldsymbol{\chi }^{lm}(\mathbf{x})=\boldsymbol{\chi }^{lm}(x_{2})$ we solve for other $\boldsymbol{\chi }^{lm}$ as given below:

$$\begin{aligned} \chi _{2}^{12}&=\chi _{3}^{12}=0, \quad \chi _{1}^{12}= \left \{ \begin{aligned} &\frac{(\mu _{A}-\mu _{B})(1-\alpha )}{\mu _{A}(1-\alpha )+\mu _{B}\alpha } \left (x_{2}-\frac{\alpha }{2}\right ), \qquad \quad 0< x_{2}< \alpha , \\ &\frac{(\mu _{A}-\mu _{B})\alpha }{\mu _{A}(1-\alpha )+\mu _{B}\alpha } \left (\frac{\alpha +1}{2} -x_{2}\right ), \quad \alpha < x_{2}< 1, \end{aligned} \right . \\ \boldsymbol{\chi }^{13}&=\mathbf{0},\quad \boldsymbol{\chi }^{21}=\boldsymbol{\chi }^{12}, \\ \chi _{1}^{22}&=\chi _{3}^{22}=0, \\ \chi _{2}^{22}&= \left \{ \begin{aligned} &\frac{\left [(\lambda _{A}+2\mu _{A})-(\lambda _{B}+2\mu _{B})\right ](1-\alpha )}{(\lambda _{A}+2\mu _{A})(1-\alpha )+(\lambda _{B}+2\mu _{B})\alpha } \left (x_{2}-\frac{\alpha }{2}\right ), \qquad \quad 0< x_{2}< \alpha , \\ &\frac{\left [(\lambda _{A}+2\mu _{A})-(\lambda _{B}+2\mu _{B})\right ]\alpha }{(\lambda _{A}+2\mu _{A})(1-\alpha )+(\lambda _{B}+2\mu _{B})\alpha } \left (\frac{\alpha +1}{2} -x_{2}\right ), \quad \alpha < x_{2}< 1, \end{aligned} \right . \\ \chi _{1}^{23}&=\chi _{2}^{23}=0,\quad \chi _{3}^{23}=\chi _{1}^{12}, \\ \boldsymbol{\chi }^{31}&=\boldsymbol{\chi }^{13}=\mathbf{0},\quad \boldsymbol{\chi }^{32}= \boldsymbol{\chi }^{23}, \quad \text{and}\quad \boldsymbol{\chi }^{33}=\boldsymbol{\chi }^{11}. \end{aligned}$$

(82)

We note that $\boldsymbol{\chi }^{lm}=\boldsymbol{\chi }^{ml}$.

Appendix C: Components of the Effective Stiffness Tensor

Using (48), we compute the components of the effective stiffness tensor of the homogenized material. We start with $a_{1111}^{0}$:

$$\begin{aligned} a_{1111}^{0}&=\frac{1}{\lvert Y\rvert }\int _{Y}a_{1111}(x)\,dx -\frac{1}{\lvert Y\rvert }\int _{Y}\bigg(a_{1111} \frac{\partial \chi _{1}^{11}}{\partial x_{1}}+a_{1112} \frac{\partial \chi _{1}^{11}}{\partial x_{2}}+a_{1113} \frac{\partial \chi _{1}^{11}}{\partial x_{3}} \\ &\quad{} +a_{1121} \frac{\partial \chi _{2}^{11}}{\partial x_{1}}+ a_{1122} \frac{\partial \chi _{2}^{11}}{\partial x_{2}}+a_{1123} \frac{\partial \chi _{2}^{11}}{\partial x_{3}}+a_{1131} \frac{\partial \chi _{3}^{11}}{\partial x_{1}}+a_{1132} \frac{\partial \chi _{3}^{11}}{\partial x_{2}}+\!a_{1133} \frac{\partial \chi _{3}^{11}}{\partial x_{3}}\!\bigg)\,dx. \end{aligned}$$

In the second integrand on the right side above several terms vanish identically because, $a_{1112}=a_{1113}=a_{1121}=a_{1123}=a_{1131}=a_{1132}=0$ from (10). Also $\dfrac{\partial \chi _{1}^{11}}{\partial x_{1}}= \dfrac{\partial \chi _{3}^{11}}{\partial x_{3}}=0$ from (81). Thus, we compute

$$\begin{aligned} a_{1111}^{0}&=\frac{1}{\lvert Y\rvert }\int _{Y}a_{1111}(x)\,dx -\frac{1}{\lvert Y\rvert }\int _{Y}a_{1122}(x) \frac{\partial \chi _{2}^{11}}{\partial x_{2}}\,dx \\ &=\frac{l_{1}l_{3}}{\lvert Y \rvert }\left \{ \int _{0}^{ \alpha }(\lambda _{A}+2\mu _{A})\,dx_{2}+\int _{\alpha }^{1}( \lambda _{B}+2\mu _{B})\,dx_{2}\right \} \\ &\quad {} -\frac{l_{1}l_{3}}{\lvert Y \rvert }\Biggl\{ \int _{0}^{ \alpha } \frac{\lambda _{A}(\lambda _{A}-\lambda _{B})(1-\alpha )}{(\lambda _{A}+2\mu _{A})(1-\alpha )+(\lambda _{B}+2\mu _{B})\alpha } \,dx_{2} \\ &\quad {}+\int _{\alpha }^{1} \frac{-\lambda _{B}(\lambda _{A}-\lambda _{B})\alpha }{(\lambda _{A}+2\mu _{A})(1-\alpha )+(\lambda _{B}+2\mu _{B})\alpha } \,dx_{2}\Biggr\} \\ &=(\lambda _{A}+2\mu _{A})\alpha +(\lambda _{B}+2\mu _{B})(1-\alpha ) \\ &\quad {}- \frac{(\lambda _{A}-\lambda _{B})^{2}}{(\lambda _{A}+2\mu _{A})(1-\alpha )+(\lambda _{B}+2\mu _{B})\alpha } \alpha (1-\alpha ). \end{aligned}$$

Next, we calculate $a_{1112}^{0}$:

$$\begin{aligned} a_{1112}^{0}&=\frac{1}{\lvert Y\rvert }\int _{Y}a_{1112}(x)\,dx -\frac{1}{\lvert Y\rvert }\int _{Y}\bigg(a_{1111} \frac{\partial \chi _{1}^{12}}{\partial x_{1}}+a_{1112} \frac{\partial \chi _{1}^{12}}{\partial x_{2}}+a_{1113} \frac{\partial \chi _{1}^{12}}{\partial x_{3}} \\ &\quad{} +a_{1121} \frac{\partial \chi _{2}^{12}}{\partial x_{1}}+ a_{1122} \frac{\partial \chi _{2}^{12}}{\partial x_{2}}+a_{1123} \frac{\partial \chi _{2}^{12}}{\partial x_{3}}+a_{1131} \frac{\partial \chi _{3}^{12}}{\partial x_{1}}+a_{1132} \frac{\partial \chi _{3}^{12}}{\partial x_{2}}+a_{1133} \frac{\partial \chi _{3}^{12}}{\partial x_{3}}\bigg)\,dx \\ &=0 \end{aligned}$$

utilizing (10), along with $\dfrac{\partial \chi _{1}^{12}}{\partial x_{1}}=0$ and $\chi _{2}^{12}=\chi _{3}^{12}=0$ from (82). Similarly, we find the other coefficients that are provided in (50).