A mathematical model for determining and improving rollover stability of four-wheel earthmoving vehicles with arbitrary undercarriage system design

Abstract

Earthmoving vehicles, especially ones with articulated frame steering, are very vulnerable to rollover. Consequently many dangerous rollover accidents occur all around the world. This problem is not only caused by difficult operating conditions and high productivity requirements. The current standards in this area do not offer an acceptable method of assessing vehicle rollover stability. Furthermore, in the previous literature there have been no research on rollover stability of increasingly common unconventional undercarriage systems, equipped with inclined/virtual oscillation and steering axes. In response to the above-mentioned situation, an innovative test vehicle, whose undercarriage system can be optionally selected (including unconventional solutions), was designed and built. The experimental stand consisted of a rotary-tilting platform equipped in wheel weighting pads and a two-axis inclinometer. Completely new experimental results were presented, proving a strong influence of unconventional undercarriage system on vehicle rollover stability. Moreover, the extensive experimental investigation was used to derive and validate an accurate and universal mathematical model, enabling to calculate and improve the rollover stability of any four-wheeled vehicle. It was also shown that a geometrical optimisation of an unconventional undercarriage system permits an increase in rollover stability—even up to several dozen percentage relative to the conventional solutions.

1 Introduction

The productivity of a vehicle used in earthworks (e.g. construction works) depends on a number of characteristics that, such as manoeuvrability or mobility, and other parameters, such as maximum lifting capacity, speed or digging range. As a rule, the increase in any of these leads to a decrease in the vehicle’s rollover stability. Manufacturers are therefore forced to maintain a compromise between productivity and the safety of the vehicles offered. This situation is not facilitated by constantly growing market expectations and the lack of adequate standard requirements. On the one hand, there are provisions obliging manufacturers to ensure vehicle stability under dedicated operating conditions (e.g. the EN 474-1 + A5: 2018 standard). On the other hand, however, the effectiveness of this commitment is drastically reduced by the absence of a defined, normative (obligatory) method which would make it possible to unequivocally and comprehensively evaluate the tendency of the vehicle to roll over. As a consequence, it is not uncommon that the assessment of rollover stability in industrial practice is carried out in a simplified manner, disregarding the suspension arrangement, its type, kinematic characteristics and vulnerability to deformation. Good examples can be found in the method described in the ISO 14397-1: 2007 standard or the popular static stability factor [1], which is the ratio of wheel track to the centre of gravity of the vehicle. As a result, there are many incidents of rollover in this vehicle class worldwide every year. In the USA, according to [2], vehicle rollover caused 57 ($\approx$ 11%) of a total of 481 deaths in the excavation work industry from 1992 to 2002. Between January 2004 and July 2009, totally 42 ($\approx$ 7%) of all the 601 death cases recorded in Kastamonu (Turkey) were related to tractor overturn [3]. In addition, a tractor rollovers cause about 70% of fatal accidents in the Italian agricultural sector [4]. Numerous researches, however, suggest a strong need to consider the influence of the suspension arrangement on rollover stability. A good example is the well-known, old mathematical model for calculating vehicle rollover stability [5], which is taking into account a conventional oscillation axis (Fig. 1). In other experimental research [6], by locking an oscillation joint, a strong impact of the suspension system on the distribution of wheel loads on a sloping ground was demonstrated. In another research [7], the inaccuracies in rollover stability calculation by using a simplified methods (e.g. stability triangle) were indicated. Predictably, the experimental research on dynamic rollover stability of articulated frame steer vehicles [8] confirmed the necessity of considering the degree of freedom coming from the oscillation joint. The presence and location of the oscillation joint were also implemented in the previous mathematical model for rollover stability calculation, derived in the authors’ research centre [9]. The above-cited works relate to rollover stability of vehicles equipped only with conventional undercarriage systems.

Fig. 1

Conventional and unconventional design solutions connecting the front and rear body of an articulated frame steer vehicle

The suspension arrangement, on the one hand, compensates for the unevenness of the ground and reduces the amplitude of tilting of the body of the vehicle when driving on uneven ground (better dynamic rollover stability). On the other hand, however, the tendency of the vehicle body to tilt is increased in the case of a tangential force acting on it (e.g. weight component on inclined ground, centrifugal force). In practice, design solutions of suspension and steering systems which counteract excessive tilting in the conditions of tangential load applied on the vehicle body turn out to be very beneficial. A group of such unconventional solutions, dedicated to undercarriage systems having articulated frame and oscillation axis between rear and front body, was identified (Fig. 1). According to the assurances of manufacturers, these solution positively affect the stability of the vehicle. However, their real effectiveness has not been widely known until now. It should also be mentioned that in a vehicle where articulated frame steering is an alternative to wheel steering, the changeability of its key geometric and weight parameters must be expected. This leads to deterioration of both rollover and directional stability. On the other hand, the reason for the huge, ongoing popularity of articulated steering is the capability of achieving very high manoeuvrability while maintaining the simplicity and durability of the structure [10].

1.1 Inclined oscillation axis

The inclined oscillation joint axis is a solution which, according to the patent description [11], advertising materials, among others Volvo and Mecalac, and the results of preliminary simulation tests [12], can improve the machine’s rollover stability by reducing oscillations and providing a more even distribution of wheel loads on the ground. Currently, the popularity of this solution is growing. It is mainly used in small- and medium-sized loaders. Some manufacturers, for instance Volvo (Radlader L25F loader) or Mecalac (AX850 model) tilt the oscillation axes by a dozen or so degrees, others, such as Atlas, only by invisible several degrees. The main disadvantage of high inclination angle of the oscillation axis is noticeable change in the steering angle $\gamma$ of the articulated vehicle during movement on uneven terrain.

1.2 Inclined steering axis

This solution was first presented in 1964 [13]. Its advantage was justified by the increased directional and rollover stability of the vehicle. Currently, this solution also holds interest. In 2014, the Bomag Company patented [14] a method of manufacturing the inclined steering axis, implemented in their road rollers.

1.3 Virtual oscillation and steering axes

In this type of solution, one or two actuators connect the front body directly with the rear body of the vehicle via spherical joints. This spatial arrangement without separate physical oscillation and steering axes was probably first mentioned in a General Motors patent [15] and was related to the configuration I (Fig. 1). An example of an early patent presenting virtual oscillation and steering axes in the II variant is a patent [16]. Ongoing development and current value of this solution may be proved by the fact that, in 2013 Caterpillar has patented [17] a new method of its implementation used, among other machines, in the Caterpillar 906 M loader. Also in 2013, a Husqvarna patent was issued [18] showing a very similar way to the oldest solution [15].

The solution of the virtual oscillation axes is used very often in small- and medium-class loaders, dumpers and rollers. Examples of variant I are Liebherr L506 Compact, Caterpillar 906 M, Paus SMK163, Neumeier NK50, Weidemann WL48, Twaites 3.5 Tonne Powerswivel, Ammann ARX 26 K and many more. The virtual oscillation and steering axes variant II can be found, also in a large number of rollers manufactured by Hamm company [19]. Less popular III variant of the virtual oscillation and steering axes can be found in the Lännen 8600i multifunction loader.

2 Materials and methods

2.1 The rollover stability quantitative indicator

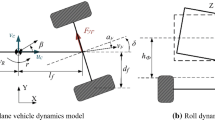
A popular indicator of the earthmoving vehicle rollover stability assessment is the critical ground slope angle $\alpha_{\text{cr}}$ (Fig. 2) at which, under quasi-static conditions, the stability is lost. In the literature [5, 6], two types of quasi-static rollover stability loss are distinguished: type I rollover stability loss occurs when the pressure of one of the four vehicle wheels on the ground equals zero. Similarly, a loss of contact with the ground by two vehicle wheels is called the type II rollover stability loss. The authors’ experience suggests that in case of earthmoving vehicles particularly exposed to the loss of rollover stability (such as mobile articulated loaders), often both types of rollover stability loss occur for the same $\alpha_{\text{cr}}$ ground slope angle. For this reason, numerous examples of pertinent research show [5, 6, 9], that only the ground slope angle $\alpha_{\text{cr}}^{{\left( {\text{I}} \right)}}$, at which stability is lost under quasi-static conditions, is taken as an indicator of the quantitative evaluation of type I of the vehicle rollover stability.

Fig. 2

The laboratory stand for testing rollover stability of vehicles with a universal test vehicle

Theoretically, for the complete assessment of the vehicle rollover stability, the critical ground slope angles $\alpha_{\text{cr}}$ should be measured at all the angular orientations $\varphi \in \left\langle {0^{^\circ } ;360^{^\circ } } \right\rangle$. Then, the global rollover stability indicator $A_{\text{cr}}^{{\left( {\text{I}} \right)}}$ [°], equal to $\hbox{min} \left[ {\alpha_{\text{cr}}^{{\left( {\text{I}} \right)}} \left( \varphi \right)} \right]$, could be determined. However, if the least favourable vehicle orientation $\varphi_{\text{cr}} \left[^\circ \right]$ to ground slope $\alpha \left[^\circ \right]$ is known, the global rollover stability indicator can be measured much easier—knowing that $A_{\text{cr}}^{{\left( {\text{I}} \right)}} \left[^\circ \right] = \alpha_{\text{cr}}^{{\left( {\text{I}} \right)}} \left( {\varphi_{cr} } \right)$.

2.2 The experimental test equipment

In off-road applications, it is usually necessary to have a suspension arrangement in the vehicle with a significant range of motion. In consequence, in most cases, the theoretical prediction of the $\varphi_{\text{cr}} \left[^\circ \right]$ angle turns out to be a very complex issue. This is why it is proposed to use a special stand for experimental tests of rollover stability (Fig. 2). Among other components, it consists of a rotary-tilting platform, measuring scales placed on its surface, and a double axis inclinometer giving the current inclination of the ground $\alpha \left[^\circ \right]$, and the angular orientation towards the incline $\varphi \left[^\circ \right]$. The digital format of any measured path (using HBM QuantumX measuring amplifiers) is sent wirelessly to a personal computer.

An approximate value of $\varphi_{\text{cr}} \left[^\circ \right]$ can be obtained by rotating the platform in the full range of $\varphi \in \left\langle {0^{ \circ } ;360^{ \circ } } \right\rangle$ while maintaining a constant inclination angle ($\alpha = {\text{const}}$). This is because the least favourable orientation $\varphi_{\text{cr}} \left[^\circ \right]$ to the slope turns out to be very close to $\varphi$ the orientation for which one of the vehicle’s wheels presses on the ground with the least force.

In order to enable comprehensive, experimental verification studies, primarily of the developed mathematical model, it was necessary to design and build a full-size, universal test vehicle with an adaptive undercarriage structure and variable geometric and weight parameters (Fig. 3).

Fig. 3

The universal test vehicle on the test stand

The solution includes two independent patented inventions [20, 21]. The first invention concerns the articulation and oscillation joint allowing any inclination of the axis of rotation (also in the active version) without affecting the other geometric and weight parameters of the vehicle (Fig. 4). The second invention is an adaptive structure of the undercarriage system with wide possibilities of changing the type of suspension of driving wheels, steering methods, geometric and weight parameters of the vehicle (Fig. 5). In other authors’ publications, a more extensive description of the universal test vehicle [22] as well as of all the experimental equipment [23] can be found.

Fig. 4

Articulation and oscillation joint with inclined axes of rotation: passive (a) and active (b) versions [20]

Fig. 5

Functionalities of adaptive chassis structure with variable geometric and weight parameters [21]

Fig. 6

Independent elastic-damping suspension mechanism used in the universal test vehicle; the diagrams show displacement and inclination characteristics as a function of the spring deflection

Fig. 7

The contact mechanism between the wheel and the ground

Fig. 8

Changes to the weight variant tested were introduced by attaching an additional 50 kg ballast to the load frame of the test vehicle; “0” means no additional weight

Fig. 9

Polar graph showing values of angles $\alpha_{\text{cr}}^{{\left( {\text{I}} \right)}}$ of loss of type I rollover stability against the function of tilt orientation $\varphi$ for three undercarriage systems and maintaining other parameters of the test vehicle unchanged

Fig. 10

Sample runs of normal and tangential reaction components in contact of contact wheels with rigid ground; “B” variant of the suspension arrangement, LP position of weights, $\varphi \approx 52.7^{ \circ }$

Fig. 11

Contour diagrams showing the values of rollover stability rating indices $A_{\text{cr}}^{{\left( {\text{II}} \right)}}$ depending on the height h [mm] and inclination $\chi$ [deg] of the oscillation axis (a) or one of the physical axes of rotation (b) in the solution with virtual oscillation and steering axes

3 The mathematical model

Very high requirements were imposed on the formulated simulation model for the quantitative evaluation of the rollover stability:

• universality covering any undercarriage systems of four-wheeled vehicles,

• unequivocal character of the assessment,

• efficiency in solving optimisation problems for many decision-making variables,

• accuracy of giving the physics of the phenomenon and, as a consequence, the obtained simulation results.

In order to meet the above requirements, the original mathematical model was formulated and verified experimentally for quasi-static calculations. Along with the computational algorithm, it has been implemented into a computer program written in MATLAB/Octave. The position of the vehicle balance is determined numerically using the principle of the lowest potential energy of gravity and elasticity (ground-tyre and suspension contacts) supplemented with dissipation of energy at skids and slight rolling of braked wheels on the ground. The generalised form of the developed simulation model is characterised by 11 variables:

$${\mathfrak{X}} = \left\{ {\kappa ,s_{1} ,s_{2} ,s_{3} ,s_{4} ,d_{x} ,d_{y} ,d_{z} ,\phi ,\theta ,\psi } \right\}$$

(1)

In order to ensure maximally unequivocal character of the assessment, it was decided to conduct a simulative evaluation of the vehicle’s rollover stability using two indicators for this purpose. They are the values of minimum inclination angles of the ground at which, under quasi-static conditions, there may be a zero normal reaction between one ($A_{\text{cr}}^{{\left( {\text{I}} \right)}}$) and two ($A_{\text{cr}}^{{\left( {\text{II}} \right)}}$) of the four wheels of the vehicle and the ground. These indicators can be recorded using the following Eqs. 2 and 3:

$$A_{\text{cr}}^{{\left( {\text{I}} \right)}} = \hbox{min} \left[ {\alpha_{\text{cr}}^{{\left( {\text{I}} \right)}} \left( \varphi \right)} \right]\;\;{\text{for}}\;\varphi \in \left\langle {0^\circ , 360^\circ } \right\rangle$$

(2)

$$A_{\text{cr}}^{{\left( {\text{II}} \right)}} = \hbox{min} \left[ {\alpha_{\text{cr}}^{{\left( {\text{II}} \right)}} \left( \varphi \right)} \right]\;\;{\text{for}}\;\varphi \in \left\langle {0^\circ , 360^\circ } \right\rangle$$

(3)

3.1 Potential energy of gravity

The coordinates of the centres of gravity of bodies of the vehicle, according to Fig. 12, can be determined from the following formulas:

$$S_{QR} = {\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}} + {\Re \mathfrak{o}\mathfrak{t}} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{R} \cdot \left[ {\begin{array}{*{20}c} { - l_{R} + q_{RX} } & {q_{RY} } & {q_{RZ} } \\ \end{array} } \right]^{\rm T}$$

(4)

$$S_{QF} = {\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}} + {\Re \mathfrak{o}\mathfrak{t}} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{F} \cdot \left[ {\begin{array}{*{20}c} { - q_{OX} } & {q_{OY} } & {q_{OZ} } \\ \end{array} } \right]^{\rm T}$$

(5)

$$S_{QO} = {\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}} + {\Re \mathfrak{o}\mathfrak{t}} \cdot \left[ {\begin{array}{*{20}c} {l_{F} - q_{FX} } & {q_{FY} } & {q_{FZ} } \\ \end{array} } \right]^{\rm T}$$

(6)

where

$${\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}} = \left[ {\begin{array}{*{20}c} {d_{x} } & {d_{y} } & {d_{z} } \\ \end{array} } \right]^{\rm T}$$

$${\Re \mathfrak{o}\mathfrak{t}} = \left[ {\begin{array}{*{20}c} {\cos \phi } & { - \sin \phi } & 0 \\ {\sin \phi } & {\cos \phi } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \theta } & { - \sin \theta } \\ 0 & {\sin \theta } & {\cos \theta } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \psi } & 0 & {\sin \psi } \\ 0 & 1 & 0 \\ { - \sin \psi } & 0 & {\cos \psi } \\ \end{array} } \right],$$

$${\Re \mathfrak{o}\mathfrak{t}}_{R} = \left[ {\begin{array}{*{20}c} {\cos \chi } & 0 & {\sin \chi } \\ 0 & 1 & 0 \\ { - \sin \chi } & 0 & {\cos \chi } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \kappa } & { - \sin \kappa } \\ 0 & {\sin \kappa } & {\cos \kappa } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \chi } & 0 & {\sin \chi } \\ 0 & 1 & 0 \\ { - \sin \chi } & 0 & {\cos \chi } \\ \end{array} } \right]^{ - 1}$$

$${\Re \mathfrak{o}\mathfrak{t}}_{F} = \left[ {\begin{array}{*{20}c} {\cos \beta } & 0 & {\sin \beta } \\ 0 & 1 & 0 \\ { - \sin \beta } & 0 & {\cos \beta } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \gamma } & { - \sin \gamma } & 0 \\ {\sin \gamma } & {\cos \gamma } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \beta } & 0 & {\sin \beta } \\ 0 & 1 & 0 \\ { - \sin \beta } & 0 & {\cos \beta } \\ \end{array} } \right]^{ - 1}$$

The value of potential energy of gravity of the vehicle is obtained from the following formula:

$$E_{\text{pot}}^{\left( G \right)} = g \cdot \left[ {\left( {\overrightarrow {{v_{g} }} \circ S_{QR} } \right)M_{R} + \left( {\overrightarrow {{v_{g} }} \circ S_{QO} } \right)M_{O} + \left( {\overrightarrow {{v_{g} }} \circ S_{QF} } \right)M_{F} } \right] \cdot 10^{ - 3}$$

(7)

where

$$\overrightarrow {{v_{g} }} = \vec{g}/g = \left[ {\begin{array}{*{20}c} { - { \cos }\left( {\alpha + \frac{\pi }{2}} \right){ \cos }\varphi } & { - { \cos }\left( {\alpha + \frac{\pi }{2}} \right){ \sin }\varphi } & { - { \sin }\left( {\alpha + \frac{\pi }{2}} \right)} \\ \end{array} } \right]^{\rm T}$$

Fig. 12

Designations of geometric dimensions of the vehicle, which were included in the developed mathematical model

3.2 Energy in the wheel-ground contact and in the suspension

It was assumed that the ground of the vehicle is situated in the XOY plane. The presence of the suspension arrangement with elastic elements and tyre vulnerability to deformation was temporarily ignored. Then, according to the indications from Fig. 12, the centres of the rear wheels $S_{0RL}$ and $S_{0RR}$ are located at a distance of $r_{OR}$ from the XOY plane, while analogous points $S_{0FL}$ and $S_{0FR}$ at the distance of $r_{OF}$. For such assumptions, the initial rotation matrices of are determined: (${\Re \mathfrak{o}\mathfrak{t}}_{0}$, ${\Re \mathfrak{o}\mathfrak{t}}_{0R}$ and $\cdot {\Re \mathfrak{o}\mathfrak{t}}_{0F}$) and translation (${\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}}_{0}$) of the bodys of the vehicle:

$$S_{0RL} = {\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}}_{0} + {\Re \mathfrak{o}\mathfrak{t}}_{0} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{0R} \cdot \left[ {\begin{array}{*{20}c} { - l_{R} } & {k_{R} } & { - h_{OR} } \\ \end{array} } \right]^{\rm T}$$

(8)

$$S_{0RL} = {\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}}_{0} + {\Re \mathfrak{o}\mathfrak{t}}_{0} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{0R} \cdot \left[ {\begin{array}{*{20}c} { - l_{R} } & {w_{R} - k_{R} } & { - h_{OR} } \\ \end{array} } \right]^{\rm T}$$

(9)

$$S_{0FL} = {\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}}_{0} + {\Re \mathfrak{o}\mathfrak{t}}_{0} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{0F} \cdot \left[ {\begin{array}{*{20}c} {l_{F} } & {k_{F} } & { - h_{OF} } \\ \end{array} } \right]^{\rm T}$$

(10)

$$S_{0FL} = {\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}}_{0} + {\Re \mathfrak{o}\mathfrak{t}}_{0} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{0F} \cdot \left[ {\begin{array}{*{20}c} {l_{F} } & {w_{F} - k_{F} } & { - h_{OF} } \\ \end{array} } \right]^{\rm T}$$

(11)

The contact point of the wheels with the ground was assumed. Initial coordinates of the points $S_{0RL}^{\left( C \right)}$, $S_{0RR}^{\left( C \right)}$, $S_{0FL}^{\left( C \right)}$ and $S_{0FR}^{\left( C \right)}$ (Fig. 12), in the ground coordinates system were obtained by zeroing the vertical coordinate value (z) of the points $S_{0RL}$, $S_{0RR}$, $S_{0FL}$ and $S_{0FR}$. For example, for the left rear wheel:

$$S_{0RL}^{\left( C \right)} = \left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 0 \\ 0 &\quad 1 &\quad 0 \\ 0 &\quad 0 &\quad 0 \\ \end{array} } \right] \cdot {\text{S}}_{0RL}$$

(12)

Figure 6 presents an example of the mechanism and suspension characteristics used in the built universal test vehicle (Fig. 3). It should be taken into account that there are also such suspension arrangements in which there are relationships present between deflections in individual wheels, and displacements may also go in direction x. For this reason, in order to preserve the universality of the mathematical model, it was proposed to add to each of the coordinates points associated with the wheels of the vehicle the polynomial functions $\varvec{f}\left( {s_{1} ,s_{2} ,s_{3} , s_{4} } \right)$ of the four variables (deformation of elastic elements of the vehicle suspension).

In order to precisely locate the metacentre of the tilt of the centre of the wheel with respect to the ground which would not falsely overestimate the theoretically determined rollover stability and increase the accuracy of the results, special contact mechanisms have been introduced (Fig. 7). It should be noted that due to the constraints imposed on the proposed mechanisms, apart from the main support point (index 1), there are also two additional ones (index 2) carrying small loads.

In order to model the introduced contact mechanisms, virtual points associated with the wheels of the vehicle were created. At the same time, the suspension arrangement with spring elements was not forgotten. For the left rear wheel:

$$S_{RL}^{\left( C \right)} = {\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}} + {\Re \mathfrak{o}\mathfrak{t}} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{R} \cdot \left[ {{\Re \mathfrak{o}\mathfrak{t}}_{0R}^{ - 1} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{0}^{ - 1} \cdot \left( {S_{0RL}^{\left( C \right)} - {\mathfrak{T}\mathfrak{r}\mathfrak{a}\mathfrak{n}}_{0} } \right)} \right] + \varvec{f}_{RL} \left( {s_{1} ,s_{2} ,s_{3} , s_{4} } \right)$$

(13)

Further, still operating on the rear left wheel, displacement ${\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL0}$ of the virtual point $S_{RL}^{\left( C \right)}$ relative to the contact point was obtained $S_{0RL}^{\left( C \right)}$ (Eq. 14) and the unit vector $\widehat{v}_{RL}$ (Eq. 15) which, in the initial position of the vehicle, will be perpendicular to the ground XOY:

$${\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL0} = B_{RL} \cdot \left( {S_{RL}^{\left( C \right)} - S_{RL0}^{\left( C \right)} } \right)$$

(14)

$$\widehat{v}_{RL} = B_{RL} \cdot {\Re \mathfrak{o}\mathfrak{t}} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{R} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{0R}^{ - 1} \cdot {\Re \mathfrak{o}\mathfrak{t}}_{0}^{ - 1} \frac{{\left( {S_{RL} - S_{RL}^{\left( C \right)} } \right)}}{{\left| {S_{RL} - S_{RL}^{\left( C \right)} } \right|}}$$

(15)

Using the above values (Eqs. 14 and 15), it is possible to determine longitudinal and lateral deformations (including skidding) and radial tyres (or tyres and the ground) for the developed model of contact.

$${\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL} = \left[ {\begin{array}{*{20}l} {\frac{1}{{\widehat{v}_{RL\left( 3 \right)} }}\left[ { - {\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL0\left( 3 \right)} \cdot \widehat{v}_{RL\left( 1 \right)} } \right] + {\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL0\left( 1 \right)} } \hfill \\ {\frac{1}{{\widehat{v}_{RL\left( 3 \right)} }}\left[ { - {\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL0\left( 3 \right)} \cdot \widehat{v}_{RL\left( 2 \right)} } \right] + {\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL0\left( 2 \right)} } \hfill \\ {\frac{1}{{\widehat{v}_{RL\left( 3 \right)} }}\widehat{v}\left[ {\widehat{v}_{RL\left( 1 \right)} \cdot {\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL0\left( 1 \right)} + \widehat{v}_{RL\left( 2 \right)} \cdot {\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL0\left( 2 \right)} + \widehat{v}_{RL\left( 3 \right)} \cdot {\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL0\left( 3 \right)} } \right]} \hfill \\ \end{array} } \right]$$

(16)

In the first step of calculating the reaction components occurring in the running wheel—ground contact pair, possible skids and the possibility of the wheel coming off from the ground were ignored:

$$\overrightarrow {{F^{\prime \prime}_{RL} }} = \left[ {\begin{array}{*{20}c} {K_{1} } & {K_{2} } & {K_{3} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {{\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{\left( 1 \right)} } & {{\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{\left( 2 \right)} } & {{\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{\left( 3 \right)}^{p} } \\ \end{array} } \right]^{\rm T}$$

(17)

In the additional points of support of the contact mechanism, there are marginal forces $F_{RL}^{ + }$ (Eq. 18), which, keeping in mind the correctness of results, should be added to the vector $F^{\prime \prime}_{RL}$ (Eq. 19):

$$\overrightarrow {{F_{RL}^{ + } }} = {\text{sign}}\left( {1 - {\text{sign}}{\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL\left( 3 \right)} } \right)\frac{1}{{\widehat{v}_{RL\left( 3 \right)} }}\left[ {\begin{array}{*{20}c} {\left( {F^{\prime \prime}_{RL\left( 3 \right)} \cdot \widehat{v}_{RL\left( 1 \right)} } \right)} \\ {\left( {F^{\prime \prime}_{RL\left( 3 \right)} \cdot \widehat{v}_{RL\left( 2 \right)} } \right)} \\ {\left( { - \widehat{v}_{RL\left( 1 \right)} \cdot F^{\prime \prime}_{RL\left( 1 \right)} - \widehat{v}_{RL\left( 2 \right)} \cdot F^{\prime \prime}_{RL\left( 2 \right)} } \right)} \\ \end{array} } \right]$$

(18)

$$\overrightarrow {{F^{\prime}_{RL} }} = \overrightarrow {{F^{\prime \prime}_{RL} }} + \overrightarrow {{F_{RL}^{ + } }}$$

(19)

Having taken into account the coefficient of adhesion $\mu$ (according to the Coulomb hypothesis) and the possibility of the wheel coming off from the ground, the final form of the reaction vector in the contact pair is obtained:

$$\overrightarrow {{F_{RL} }} = \left\{ {\begin{array}{*{20}l} {\overrightarrow {{F'_{RL} }} {\text{dla }}\sqrt {(F'_{RL\left( 1 \right)} )^{2} + (F'_{RL\left( 2 \right)} )^{2} } \le \mu F'_{RL\left( 3 \right)} } \hfill \\ {\left[ {\begin{array}{*{20}c} {\mu F'_{RL\left( 3 \right)} \frac{{F'_{RL\left( 1 \right)} }}{{\sqrt {(F'_{RL\left( 1 \right)} )^{2} + (F'_{RL\left( 2 \right)} )^{2} } }}} \\ {\mu F'_{RL\left( 3 \right)} \frac{{F'_{RL\left( 2 \right)} }}{{\sqrt {(F'_{RL\left( 1 \right)} )^{2} + (F'_{RL\left( 2 \right)} )^{2} } }}} \\ {{\text{sign}}\left( {1 - {\text{sign}}F'_{RL\left( 3 \right)} } \right)F'_{RL\left( 3 \right)} } \\ \end{array} } \right]{\text{dla}}\sqrt {(F'_{RL\left( 1 \right)} )^{2} + (F'_{RL\left( 2 \right)} )^{2} } > \mu F'_{RL\left( 3 \right)} } \hfill \\ \end{array} } \right.$$

(20)

The energy accumulated in contact springs, and consumed during the skid, is determined according to the laws of physics as the definite integral of the force after the displacement. According to this principle, and with a simplified, linear trajectory of the skid, a formula for energy in the contact pair was derived:

$$\begin{aligned} & E_{{}}^{{\left( {RL} \right)}} = {\text{sign}}\left[ {1 + {\text{sign}}\left( {{\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL\left( 3 \right)} } \right)} \right] \cdot K_{1} \cdot \frac{{|{\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL\left( 3 \right)} |^{1 + p} }}{1 + p} \\ & \quad + \mu \cdot F_{RL\left( 3 \right)}^{*} \cdot \sqrt {{\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL\left( 1 \right)}^{2} + {\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL\left( 2 \right)}^{2} } \\ & \quad - \frac{{(\mu \cdot F_{RL\left( 3 \right)}^{*} )^{2} }}{{2\sqrt {F_{RL\left( 1 \right)}^{2} + F_{RL\left( 2 \right)}^{2} } }} \cdot \sqrt {{\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL\left( 1 \right)}^{2} + {\mathfrak{D}\mathfrak{i}\mathfrak{s}}_{RL\left( 2 \right)}^{2} } \\ \end{aligned}$$

(21)

Energy caused by rolling of the road wheel on the ground (it is suggested to take it into account for very wide tyres) can be determined by the following formula:

$$E_{\text{roll}}^{{\left( {RL} \right)}} = \sqrt {\left( {{ \arctan }\left| {\frac{{v_{RL\left( 1 \right)} }}{{v_{RL\left( 3 \right)} }}} \right| \cdot f_{\text{lon}} } \right)^{2} + \left( {{ \arctan }\left| {\frac{{v_{RL\left( 2 \right)} }}{{v_{RL\left( 3 \right)} }}} \right| \cdot f_{\text{lat}} } \right)^{2} } \cdot r_{RL} \cdot F_{RL\left( 3 \right)}^{*}$$

(22)

The energy accumulated in the elements of suspension vulnerable to deformation is determined by the equation taking into account the characteristics of progressive/degressive stiffness:

$$E_{\text{pot}}^{{\left( {SUS} \right)}} = K_{s1} \cdot \frac{{s_{1}^{{p_{s1} + 1}} }}{{p_{s1} + 1}} + K_{s2} \cdot \frac{{s_{2}^{{p_{s2} + 1}} }}{{p_{s2} + 1}} + K_{s3} \cdot \frac{{s_{3}^{{p_{s3} + 1}} }}{{p_{s3} + 1}} + K_{s4} \cdot \frac{{s_{4}^{{p_{s4} + 1}} }}{{p_{s4} + 1}}$$

(23)

3.3 The lowest energy principle

Numerical calculations, performed by the created computer program, help arrive at a set ${\mathfrak{X}}$ of mathematical variables of the model (Eqs. 1, 24). On this basis, reaction values are then analytically calculated in the road wheels—ground contact pairs, applied to determine the adopted rating indicators $A_{\text{cr}}^{{\left( {\text{I}} \right)}}$ and $A_{\text{cr}}^{{\left( {\text{II}} \right)}}$ (Eqs. 2, 3).

$${\mathfrak{X}} = { \arg }\;{ \hbox{min} }\left( {E_{\text{pot}}^{\left( Q \right)} + E_{{}}^{{\left( {RL} \right)}} + E_{{}}^{{\left( {RR} \right)}} + E_{{}}^{{\left( {FL} \right)}} + E_{{}}^{{\left( {FR} \right)}} + E_{\text{pot}}^{{\left( {SUS} \right)}} + E_{\text{roll}}^{{\left( {RL} \right)}} + E_{\text{roll}}^{{\left( {RR} \right)}} + E_{\text{roll}}^{{\left( {FL} \right)}} + E_{\text{roll}}^{{\left( {FR} \right)}} } \right)\;{\text{dla}}\;{\mathfrak{X}}_{ \hbox{min} } \le {\mathfrak{X}} \le {\mathfrak{X}}_{ \hbox{max} }$$

(24)

The coordinates of the points presented in Eqs. 8–11$S_{0RL}^{\left( C \right)}$, $S_{0RR}^{\left( C \right)}$, $S_{0FL}^{\left( C \right)}$ and $S_{0FR}^{\left( C \right)}$ and the resulting contact points of the wheels with the ground $S_{0RL}$, $S_{0RR}$, $S_{0FL}$ i $S_{0FR}$ are initially determined with the omission of the force of gravity, using only the relationships resulting from the geometric dimensions of the vehicle frame. It is proposed to correct them by performing (one or more iterations) calculations of the static equilibrium of the vehicle positioned on horizontal surface and at zero friction coefficient $\mu = 0$. Consequently, excessive tangential stresses already present on the horizontal surface will be eliminated, and the test conditions will be closer to real conditions.

4 Experimental verification

Extensive experimental verification of the developed mathematical model has been carried out. Using the purpose built universal test vehicle, a total of six different wheel suspension arrangements were configured:

• A. a undercarriage system equipped with a suspension in the form of an oscillating rear body with a horizontal axis of rotation and a steering joint with a vertical axis of rotation,

• B. a undercarriage system equipped with a suspension in the form of an oscillating rear body with an axis of rotation inclined by 25° and a steering joint with a vertical axis of rotation,

• C. a undercarriage system equipped with a suspension in the form of an oscillating rear body with a horizontal axis of rotation and a steering joint with an axis of rotation inclined by 15°,

• D. a undercarriage system equipped with a suspension in the form of a swivel rear axle and a steering joint with a vertical axis of rotation,

• E. a undercarriage system equipped with a steering joint with a vertical axis of rotation and without any suspension,

• F. a undercarriage system equipped with an independent double wishbone suspension in each of the wheels and a steering joint with a vertical axis of rotation.

Moreover, each suspension arrangement was tested in 7 weight variants (Fig. 8)—which offered a total of 42 different variants of the vehicle. All the tests were carried out at the turning angle value $\gamma \approx 45^{ \circ }$.

In the first stage, the accuracy in the prediction of normal road wheel loads on the horizontal ground was tested (Table 1). In the second stage of experimental verification, a relatively constant inclination of the ground under the vehicle was introduced $\alpha \approx 16^{ \circ }$ and the orientation $\varphi$ of the vehicle was changed with respect to the inclination in the full range from $0^{ \circ }$ to $360^{ \circ }$ (Table 2). Both presented Tables 1 and 2 contain both average values of relative and absolute contact reactions errors for all four road wheels, as well as maximum recorded error values for the entire characteristic.

Table 1 Prediction errors in the developed mathematical model of normal reactions between vehicle wheels and the ground with reference to experimental results for $\alpha \approx 0^{ \circ }$

Table 2 Prediction errors in the developed mathematical model of normal reactions between vehicle wheels and the ground with reference to experimental results for $\alpha \approx 16^{ \circ }$

From the viewpoint of the intended mathematical model, the most important part of the experimental verification was the examination of the inclination angles of the ground $\alpha$ at which zero pressure occurs under one of the road wheels, i.e. the loss of type I rollover stability (Table 3). These tests were conducted at orientations to inclinations $\varphi$ closest to the least favourable.

Table 3 Critical angles of inclination of the ground at which there is a zero reaction in contact of the contact wheel with the ground obtained for the tested variants of the vehicle; comparison of experimental and theoretical results obtained for different vehicle orientations $\varphi$ to the ground inclination

On the polar graph, Fig. 8 shows the experimental results of critical angles of ground inclination $\alpha_{\text{cr}}^{{\left( {{\text{I}},{\text{E}}} \right)}}$ (Table 3) supplemented with courses obtained from the developed mathematical model. The presented results concern “A”, “B” and “C” undercarriage systems, each in “FL” weight variant. It was attempted to take measurements at the closest values. $\varphi$.

Using the linear trend estimation, the potentially worst values were estimated. $\varphi_{\text{cr}}$. Table 4 shows the values of relative errors pertinent to the indicators $A_{\text{cr}}^{{\left( {\text{I}} \right)}}$ of global assessment of rollover stability.

Table 4 Globally the lowest values of ground substrate inclination angles $A_{\text{cr}}^{{\left( {\text{I}} \right)}}$ leading to type I loss of rollover stability, determined on the basis of linear estimation of the experiment results, and calculated using the developed mathematical model

Figure 10 presents an example of the course of normal and tangential reactions as a function of ground inclination $\alpha$ illustrating the mechanism of skidding.

5 The method of improving rollover stability

Using the parameters of a typical articulated underground loader, a method was presented enabling the development of a new generation, optimal undercarriage systems in the aspect of maximising rollover stability. For this purpose, a mathematical model has been used, implemented into a computer program enabling efficient performance of calculations.

5.1 Specifying the scope

First of all, the scope of configuration of undercarriage systems should be determined, out of which the initial selection of one or several of the most favourable ones will be made. In this example, the range of conventional solutions was limited to the swivel rear and front axles and the oscillating rear and front body of the vehicle. Unconventional solutions have also been introduced in the form of an oscillating rear and front body with inclined axis of rotation as well as virtual oscillation and steering axes in the variant I and III (Fig. 1).

5.2 Initial selection

It is advisable to perform a preliminary assessment of the rollover stability using different undercarriage systems in the vehicle under consideration (with given dimensions and weight parameters), taking into account the following principles:

• 1. Indicator values are determined $A_{\text{cr}}^{{\left( {\text{I}} \right)}}$ i $A_{\text{cr}}^{{\left( {\text{II}} \right)}}$ for a fixed range of suspension solutions with a conventional, horizontal oscillation axis of the front or rear axle or the front or rear body of the articulated vehicle. The initial height of the axis of oscillation in individual locations should be determined by following the industrial practice and design of the vehicle under consideration.

• 2. The initial assessment of suspension arrangements in the form of a oscillating body is made with the exclusion of unconventional solutions. These solutions constitute, in a sense, an extension of conventional systems with a horizontal axis of oscillation and allow for increasing the rollover stability by individually adjusting geometrical parameters to a given vehicle.

The end of this stage is a selection of one or several of the most favourable locations of the oscillation joint. On the basis of the preliminary selection of undercarriage systems which might be used in the articulated underground loader under consideration, in the calculations carried out for rigid ground, the most and the least favourable locations of the oscillation joint were determined (Table 5). The tests were carried out at the maximum lifting capacity and the highest position of the machine tool and the maximum turn. A typical range of rotation around the axis of oscillation was assumed $\kappa = \pm 12^{ \circ }$.

Table 5 Values of rollover stability rating indices from the viewpoint of location of the horizontal axis of oscillation in percentage are given; an increase in the rating indices with reference to the typical solution of oscillating rear wheel axle

5.3 Optimisation of the most advantageous solutions

The last stage of the proposed method is to optimise the most advantageous solutions of undercarriage systems for the vehicle under consideration. By default, the function of the objective is the indicator $A_{\text{cr}}^{{\left( {\text{II}} \right)}}$ being a measure of vehicle inclination to full loss of rollover stability under quasi-static conditions:

$$\hbox{max} \left[ {A_{\text{cr}}^{{\left( {\text{II}} \right)}} \left( {\chi ,h, \ldots } \right)} \right]$$

(25)

The first of the decision making variables is the height [mm]. What should be determined in order to define the value of this variable, is the distance between the point of intersection of the oscillating axis and the steering axis from the plane routed through the axes of the wheels. If we are considering the solution of the virtual oscillation and steering axes, then the sought point will be the one at the intersection of physical axes of rotation. The second decision making variable is the angle $\chi$ [°] denoting the inclination of the oscillating axis, in the solution assuming the virtual oscillation and steering axes, the inclination of one of the physical axis of rotation. Importantly, in order to maintain the assumed level of mobility of the vehicle (typically assessed by the maximum vertical wheel travel), the range of the rotation angle $\kappa$ around the axis subjected to the inclination should be adjusted. The formula from Eq. 26 can be used here:

$$\kappa \in \left\langle { - \arcsin \left( {\frac{{\sin \kappa_{{0{ \hbox{min} } }} }}{\cos \chi }} \right) , \arcsin \left( {\frac{{\sin \kappa_{{0{ \hbox{max} } }} }}{\cos \chi }} \right)} \right\rangle$$

(26)

It is possible to adopt additional decision making variables, for example, the angle of inclination of the other physical axis in the virtual axes of the oscillating and steering joint design solution. It is important, however, that the limitations of individual decision-making variables are adopted in a rational manner, with the awareness of design and dimensions of the vehicle, realising the phenomenon of drift occurs as a result of using an oscillating articulated joint with an inclined axis of rotation.

In the case of articulated underground loader, undercarriage systems equipped with inclined and virtual oscillation axes in the rear body have been optimised (the most favourable location based on the initial assessment). For the system with an inclined axis of oscillation, the following limitations of decision making variables have been adopted:

$$h \in \left\langle {\begin{array}{*{20}c} {0 \,{\text{mm}}} & {800 \,{\text{mm }}} \\ \end{array} } \right\rangle ,\quad \chi \in \left\langle {\begin{array}{*{20}c} { - 25^{ \circ } } & {25^{ \circ } } \\ \end{array} } \right\rangle$$

(27)

In the case of virtual oscillation and steering axes, due to the reduction in the drift angle, it was possible to adopt a larger range of the angle of the physical axis of rotation $\chi$:

$$h \in \left\langle {\begin{array}{*{20}c} {0 \,{\text{mm}}} & {800\, {\text{mm }}} \\ \end{array} } \right\rangle ,\quad \chi \in \left\langle {\begin{array}{*{20}c} { - 75^{ \circ } } & {75^{ \circ } } \\ \end{array} } \right\rangle$$

(28)

The values of the rollover stability assessment indices for the obtained optimised undercarriage systems of the tested articulated underground loader are given in Table 6.

Table 6 Values of rollover stability assessment indicators of the optimised solutions; the increase in the rating indices for the typical solution of the oscillating rear axle of the road wheels is given in percentages

Two-dimensional contour diagrams of indicators $A_{\text{cr}}^{{\left( {\text{II}} \right)}}$ constitute an additional result of the exemplary optimisation performed as a function of adopted decision-making variables (Fig. 11a, b).

6 Summary and conclusions

• Thanks to a comprehensive analysis of the state of the art and technology in the area of undercarriage systems and the possibility of extensive and precise experimental verification, the developed mathematical model is characterised by unrivalled universality and accuracy of calculations in comparison with existing models intended for conducting efficient quasi-static calculations of rollover stability of four-wheel earthmoving vehicles [5,6,7, 9]. The developed solution is distinguished by a unique accurate wheel—ground model of contact, the possibility of describing virtually any independent and dependent systems of flexible suspension and taking into account unconventional (inclined and virtual) axes of rotation in oscillating and steering joints.

• The computer program developed to calculate the rollover stability of any four-wheeled vehicles is a universal engineering tool for verification and improvement in the rollover stability of vehicles still at the design stage. It is a reaction to the urgent need of the industry, and its potential reaches any vehicles and mobile machines on a wheeled chassis.

• Thanks to the innovative universal test vehicle, the influence of inclined oscillation joint axis (which is used, for example, by Volvo [10]) on vehicle rollover stability has been unequivocally proven by showing higher value at approx. $8.5\%$ of the indicator $A_{\text{cr}}^{{\left( {\text{I}} \right)}}$ (obtained by linear estimation of experimental results) for the oscillation joint axis inclined at the angle $\chi = 25^{ \circ }$ located in the rear body of the vehicle with respect to the horizontal rotation axis solution (Table 4). The difference in the level of rollover stability between the two solutions is also flawlessly illustrated by the polar graph (Fig. 9).

• High potential of unconventional undercarriage systems with inclined and virtual oscillating axes in effective improvement in rollover stability has been demonstrated.

• To the authors’ knowledge, there have been no research on inclined and virtual oscillation and steering axes (Fig. 1) and their impact on rollover stability presented in the previous literature.

• The research carried out may be the basis for discussing the current, overly simplified international standards, therefore not providing sufficient security, such as ISO 14397-1: 2007.

• Since the main role of the developed mathematical model is the quantitative comparative evaluation of rollover stability of any four-wheeled vehicles, both experimental verification and previously presented results were carried out on a rigid and flat surface. It is incorrect to compare the rollover stability of vehicles using rating indicators $A_{\text{cr}}^{{\left( {{\text{I}}, {\text{II}}} \right)}}$ obtained for differing bearing capacities and differing unevenness of the ground. The developed mathematical model, however, enables the introduction of substitute, joint parameters of vulnerability to deformation of the tyres and the ground. A known mathematical formula [24] can be used to determine substitute contact stiffness. The pressure-sinkage parameters of considered ground can be taken from [25].

• A big advantage of the method presented in Sect. 5 its negligible impact on suspension travel, manoeuvrability or weight parameters of the vehicle.

• The functionality of the constructed experimental vehicle (Figs. 3, 4, 5) goes well beyond the presented quasi-static studies on rollover stability. It was also designed for further research in dynamic conditions, and in the teleoperated mode.

• Further development of the computer program (written in MATLAB/Octave) is in progress to improve the calculation performance. For this purpose, an implementation of optimisation solutions such as surrogate model (e.g. Kriging) and genetic algorithm (e.g. NSGA-II) [26] is planned.

7 The most important designations

See Fig. 12.

• $d_{x} ,d_{y} ,d_{z}$—parameters of the vehicle translation matrix in space [mm],

• $\phi ,\theta ,\psi$—parameters of the vehicle’s rotation matrix in space [°],

• $\kappa \in \left\langle {\kappa_{ \hbox{min} } ,\kappa_{ \hbox{max} } } \right\rangle$—the rotation angle of the rear or front body of the vehicle with respect to the centre body, about one of the physical rotation axes (Fig. 1) [°]; for virtual oscillation axes there is the following correlation $\gamma = f\left( \kappa \right) ,$

• $s_{1} ,s_{2} ,s_{3} ,s_{4}$—linear (mm) or angular [°] deformations of flexible elements (springs) of wheel suspension,

• $\varphi$—vehicle orientation to the inclination of the ground $\alpha$ [°],

• $\alpha_{\text{cr}}^{{\left( {\text{I}} \right)}} \left( \varphi \right) , \alpha_{\text{cr}}^{{\left( {\text{II}} \right)}} \left( \varphi \right)$—ground inclination angles when rollover stability loss occurs—type I and II [°].

• $M_{R} ,M_{F} ,M_{O}$—weights of bodys of the vehicle [kg],

• $g \approx 9.80665\,{\text{m/s}}^{2}$—standard gravity,

• $E_{\text{pot}}^{\left( G \right)}$—potential energy of the vehicle’s gravity,

• $B_{RL} , B_{RR} , B_{FL} , B_{FR}$—transition matrices from the systems of ground coordinates to the system of coordinates associated with individual running wheels; it was assumed that the tyre stiffness directions do not change with respect to the ground,

• $K_{1}$, $K_{2}$, $K_{3}$—directorial stiffens of the tyre or replacement stiffness of the tyre and the ground [${\text{N}}/{\text{mm}}^{p}$];

• $p$—exponent of force taking into account the progressive/degressive characteristics of tyre stiffness,

• $F_{RL\left( 3 \right)}^{*}$, $F_{RR\left( 3 \right)}^{*}$, $F_{FL\left( 3 \right)}^{*}$, $F_{FR\left( 3 \right)}^{*}$—predicted (e.g. based on previous simplified calculations) normal pressure of the wheel on the ground [N],

• $f_{\text{lon}}$—wheel rolling resistance coefficient,

• $f_{\text{lat}}$—lateral direction wheel rolling resistance coefficient,

• $K_{\text{s}}$—stiffness of the suspension spring,

• $p_{\text{s}}$—force exponent accounting for the progressive/degressive stiffness characteristics.