Abstract
The equations of motion of a test particle are integrated for the field of a rotating Kerr black hole (BH) (in accordance with [1]). Due to the lack of analytical transformations for the Carter–Penrose diagrams (CPDs) for the Kerr metric, the topology of the Kerr BH is studied by analytical investigation of the equations of motion. Transformations for the CPDs for the Reisner–Nordström metric are analyzed. The problem of boundary conditions for the Reisner–Nordström topology is analyzed. A solution to this problem of boundary conditions is proposed. It is proved that, in the Reisner–Nordström topology, only one way to go to another universe is possible. For the Kerr topology, the possibility of the existence of an alternative transition to another universe that does not coincide with the universe for the ordinary transition is found. This alternative transition is performed through a surface with a zero radial coordinate (zero radius). Initial conditions for the falling particle are found that correspond to an alternative transition to another universe. The tidal forces acting on a falling body in the Kerr metric are estimated, and the possibility of the transition of the body to other universes without being destroyed by tidal forces is proved.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
We will write the word “universe” with a lowercase letter, meaning by this different parts of the big Universe, which combines different parts into the complex topology of the Universe.
The question is the convergence of the integral \(\int {\sqrt K } \)ds, where K is the Kretschmann scalar and s is the proper time of a freely falling particle [3].
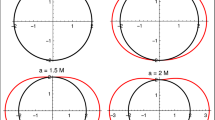
However, for any metric tensor (including the Kerr metric), it is possible to construct a graphical representation of a CPD (see, for example, Fig. 3). Such a graphical representation of a CPD is not always supported by the analytical transformations from this section, which are found only for centrally symmetric solutions.
The quantities u+ and u– are defined up to πn, where n is an integer, since the period of the functions tan and cotan is π.
Here {0 < c1 < c2 < π} and {π/2 < c3 < c4 < 3π/2}.
However, it is likely that any such connection will be destroyed by infinite gravitational forces inside the black–white hole.
This follows upon substituting dt, dr, dθ, and dφ from (17)–(20), expressed in terms of dλ, into (1).
REFERENCES
B. Carter, Comm. Math. Phys. 10, 280 (1968).
V. P. Frolov and I. D. Novikov, Black Hole Physics. Basic Concepts and New Developments (Kluwer Academic, Netherlands, 1998).
N. S. Kardashev, L. N. Lipatova, I. D. Novikov, and A. A. Shatskiy, Astron. Rep. 59, 89 (2015).
F. Tipler, Phys. Lett. A 64, 8 (1977).
N. S. Kardashev, L. N. Lipatova, I. D. Novikov, and A. A. Shatskiy, J. Exp. Theor. Phys. 119, 63 (2014).
K. S. Thorne, Astrophys. J. 191, 507 (1974).
R. C. Henry, Astrophys. J. 535, 350 (2000).
Ch. Misner, K. Thorne, and J. Wheeler, Gravitation, vol. 3 (Freeman, San Francisco, 1973; Mir, Moscow, 1977).
B. Carter, Phys. Lett. 21, 423 (1966).
K. S. Thorne, in Abstracts of Ginzburg Conference on Physics (Lebedev Inst., Moscow, 2012). http://www.gc.lpi.ru/proceedings/thorne_pl.pdf.
A. A. Shatskiy, I. D. Novikov, and N. S. Kardashev, Phys. Usp. 54, 381 (2011).
S. W. Hawking, Observatory 89, 38 (1969).
K. Martel and E. Poisson, arXiv:gr-qc/0107104 (2008).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by I. Nikitin
Rights and permissions
About this article
Cite this article
Shatskiy, A.A. Analysis of the Topology of the Kerr Metric. J. Exp. Theor. Phys. 130, 409–417 (2020). https://doi.org/10.1134/S1063776120010185
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1063776120010185