Anisotropic cosmological dynamics in Einstein–Gauss–Bonnet gravity: an example of dynamical compactification in $7+1$ dimensions

Abstract

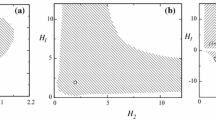
We consider a particular example of dynamical compactification of an anisotropic $7+1$ dimensional Universe in Einstein–Gauss–Bonnet gravity. Starting from rather general totally anisotropic initial conditions a Universe in question evolves towards a product of two isotropic subspaces. The first subspace expands isotropically, the second represents an “inner” isotropic subspace with stabilized size. The dynamical evolution does not require fine-tuning of initial conditions, though it is possible for a particular range of coupling constants. The corresponding condition have been found analytically and have been confirmed using numerical integration of equations of motion.

Appendix A: Geometric frustration for low-dimensional cases

In this section we prove that compactification and isotropization regimes do not coexist in ($5+1$) and ($6+1$)-dimensional EGB cosmological models. For ($5+1$)-dimensional model we also find all possible values of $\xi =\alpha \Lambda$ for which compactified solutions exist; it is much more complicated to find all such $\xi$ for ($6+1$)-dimensional model, so in the latter case we restrict ourselves by proving that compactification regime can not coexist with isotropic regime.

1.1 ($5+1$)-Dimensional model

Asymptotic equations in ($5+1$)-dimensional EGB cosmological model:

$$\begin{aligned} b_0^{2}(\xi -6H_0^{2}\alpha )+24H_0^{2}{\alpha }^{2}+2\alpha= & {} 0 \end{aligned}$$

(A1)

$$\begin{aligned} 24H_0^{4}\alpha ^{2}+12H_0^{2}\alpha -\xi= & {} 0 \end{aligned}$$

(A2)

Let $z=H_0^{2};\;y=b_0^{2}$. Then Eqs. (A9)–(A10) take the form:

$$\begin{aligned} y(\xi -6z\alpha )+24z{\alpha }^{2}+2\alpha= & {} 0\Longleftrightarrow y=\frac{2\alpha \left( 12\,z\alpha +1\right) }{6\,z\alpha -\xi } \end{aligned}$$

(A3)

$$\begin{aligned} 24z^2\alpha ^{2}+12z\alpha -\xi= & {} 0\Longleftrightarrow z_{\pm }=\frac{-1\pm \sqrt{1+\frac{2}{3}\xi }}{4\alpha } \end{aligned}$$

(A4)

Substituting $z_+$ and $z_-$ into expression for y (see (A11)) we obtain correspondingly

$$\begin{aligned} y_+=\frac{4\alpha \left( \sqrt{1+\frac{2}{3}\xi }-\frac{2}{3}\right) }{\sqrt{1+\frac{2}{3}\xi }-\left( 1+\frac{2}{3}\xi \right) }\quad \text{ and }\quad y_-=\frac{4\alpha \left( \sqrt{1+\frac{2}{3}\xi }+\frac{2}{3}\right) }{\sqrt{1+\frac{2}{3}\xi }+\left( 1+\frac{2}{3}\xi \right) } \end{aligned}$$

(A5)

One can see that real values of $z_{\pm }$ and $y_{\pm }$ exist only for $\xi >-\frac{3}{2}$. Also both z and y must be positive. Table 2 demonstrates values of $\xi$ for which positive z and y exist. This allows us to conclude that compactification in ($5+1$) model is possible iff $\xi \in \left( -\frac{3}{2};-1\right)$.

Table 2 Values of $\xi$ for which positive z and y exist

Isotropic solutions in ($5+1$)-dimensional EGB cosmological model are defined as

$$\begin{aligned} H^2=\frac{-1\pm \sqrt{1+\frac{6}{5}\xi }}{12\alpha } \end{aligned}$$

(A6)

For $\xi \in \Bigl [-\frac{5}{6};0\Bigr )$ we have 4 possible solutions:

$$\begin{aligned} H=\pm \sqrt{\frac{-1\pm \sqrt{1+\frac{6}{5}\xi }}{12\alpha }},\;\alpha <0 \end{aligned}$$

(A7)

For $\xi >0$ we have 2 possible solutions:

$$\begin{aligned} H=\pm \sqrt{\frac{-1+\sqrt{1+\frac{6}{5}\xi }}{12\alpha }},\;\alpha >0 \end{aligned}$$

(A8)

Taking into account that isotropic solutions exist for $\xi \geqslant -\frac{5}{6}$, but asymptotic equations (A1)–(A2) has no real solutions for $\xi \geqslant -\frac{5}{6}$, we conclude isotropization and compactification regimes do not coexist in ($5+1$)-dimensional EGB cosmological model.

Note that numerical attempts to find compactification solution in $(5+1)$ dimensions have been unsuccessful [33], and the reason for that is still unknown.

1.2 ($6+1$)-Dimensional model

Asymptotic equations in ($6+1$)-dimensional EGB cosmological model:

$$\begin{aligned} \left( 6\alpha b_0^4-72\alpha ^{2}b_0^{2}\right) H_0^{2}-\xi b_0^{4}-6\alpha b_0^{2}= & {} 0 \end{aligned}$$

(A9)

$$\begin{aligned} 24H_0^{4}\alpha ^{2}b_0^{4}+\left( 12\alpha b_0^{4}-48\alpha ^{2}b_0^{2}\right) H_0^{2}-\xi b_0^{4}-2\alpha b_0^{2}= & {} 0 \end{aligned}$$

(A10)

Let $z=H_0^{2};\;y=b_0^{2}$. Then equations (A9)–(A10) take the form:

$$\begin{aligned} \left( 6\alpha y^2-72\alpha ^{2}y\right) z-\xi y^2-6\alpha y= & {} 0 \end{aligned}$$

(A11)

$$\begin{aligned} 24\alpha ^{2}z^2y^2+\left( 12\alpha y^2-48\alpha ^{2}y\right) z-\xi y^2-2\alpha y= & {} 0 \end{aligned}$$

(A12)

Note that both z and y must be positive. Solving (A11) to z we get

$$\begin{aligned} z=\frac{y\xi +6\alpha }{6\alpha (y-12\alpha )} \end{aligned}$$

(A13)

Substitution (A13) into (A12) gives us equation for y:

$$\begin{aligned} \xi \left( \xi +\frac{3}{2}\right) {y}^{3}+15\,\alpha \,{y}^{2}-72\left( \xi +\frac{5}{2}\right) {\alpha }^{2}y+432{\alpha }^{3}=0 \end{aligned}$$

(A14)

First, we show that there are no real-valued solutions of the Eqs. (A9)–(A10) for $\xi >-\frac{3}{2}$. It is easy to check that

$$\begin{aligned} F'(y)= & {} 3\xi \left( \xi +\frac{3}{2}\right) y^2+30\alpha y-72\alpha ^2\left( \xi +\frac{5}{2}\right) \end{aligned}$$

(A15)

$$\begin{aligned} F'(y)= & {} 0\Longleftrightarrow y_{\pm }=\frac{-5\alpha \pm 5|\alpha |\sqrt{1+\frac{24}{25}\xi \left( \xi +\frac{3}{2}\right) \left( \xi +\frac{5}{2}\right) }}{\xi \left( \xi +\frac{3}{2}\right) } \end{aligned}$$

(A16)

I. $-\frac{3}{2}<\xi<0\Longrightarrow \alpha<0;\;\xi \left( \xi +\frac{3}{2}\right)<0;\;y_+<0,\,y_-<0$, therefore $F'(y)<0$ for all $y>0$, so function F(y) decrease monotonically for $y>0$. Taking into account that $F(0)=432{\alpha }^{3}<0$ and $F(y)\xrightarrow [y\rightarrow +\infty ]{}-\infty$ we conclude that function F(y) has no positive roots for $\xi \in \Bigl (-\frac{3}{2};0\Bigr )$ and, therefore, there does not exist real values of $b_0$ for $\xi \in \Bigl (-\frac{3}{2};0\Bigr )$.

II. $\xi>0\Longrightarrow \alpha>0;\;\xi \left( \xi +\frac{3}{2}\right)>0;\;y_-<0,\,y_+>0$. Function F(y) has minimum at $y_+>0$; $F(0)=432{\alpha }^{3}>0,\;F(y)\xrightarrow [y\rightarrow +\infty ]{}+\infty$, so if $F(y_+)<0$ then F(y) has 2 positive zeros. Substituting $y_+$ into function F we get

$$\begin{aligned}&F(y_+)=-\frac{2\alpha ^3\left( 125\left( Q^{3/2}-1\right) -18\xi \left( \xi +\frac{3}{2}\right) (12\,{\xi }^{2}+28\,\xi +25)\right) }{\xi ^2\left( \xi +\frac{3}{2}\right) ^2},\;\nonumber \\&\quad \quad Q=1+\frac{24}{25}\xi \left( \xi +\frac{3}{2}\right) \left( \xi +\frac{5}{2}\right) \end{aligned}$$

(A17)

and it is easy to see that it is negative for any $\xi >0$, $\alpha >0$.

Once we find y from (A14), we should substitute it to (A13) and find z; since z must be positive, solution of (A14) must obey inequality $y>12\alpha$.

Since $F(12\alpha )=1728\alpha ^3\left( \xi +\frac{1}{2}\right) ^2>0$ the point $y=12\alpha$ can not been located between two roots of the equation $F(y)=0$. Thus, if $y_+<12\alpha$ then both roots are smaller than $12\alpha$.

In order to compare $y_+$ and $12\alpha$ we introduce function $G(\xi )\equiv \frac{y_+(\xi ,\alpha )}{12\alpha }= \frac{5\left( \sqrt{1+\frac{24}{25}\xi \left( \xi +\frac{3}{2}\right) \left( \xi +\frac{5}{2}\right) }-1\right) }{12\xi \left( \xi +\frac{3}{2}\right) }$. It is easy to check that $G'(\xi )<0$ for $\xi >0$, so function $G(\xi )$ decrease monotonically for all positive values $\xi$. On the other hand $\lim \limits _{\xi \rightarrow 0}G(\xi )=\frac{1}{2}$. It means that $G(\xi )<\frac{1}{2}$ for $\xi >0$ and, therefore, $y_+<6\alpha$. So, all positive roots of function F(y) are smaller than $12\alpha$, values of z corresponding to these roots are negative and, therefore, there does not exist real values of $H_0$ for $\xi >0$.

Second, we turn to isotropic solutions in ($6+1$)-dimensional EGB cosmological model:

$$\begin{aligned} H^2=\frac{-1\pm \sqrt{1+\frac{8}{5}\xi }}{24\alpha } \end{aligned}$$

(A18)

For $\xi \in \Bigl [-\frac{5}{8};0\Bigr )$ we have 4 possible solutions:

$$\begin{aligned} H=\pm \sqrt{\frac{-1\pm \sqrt{1+\frac{8}{5}\xi }}{24\alpha }},\;\alpha <0 \end{aligned}$$

(A19)

For $\xi >0$ we have 2 possible solutions:

$$\begin{aligned} H=\pm \sqrt{\frac{-1+\sqrt{1+\frac{8}{5}\xi }}{24\alpha }},\;\alpha >0 \end{aligned}$$

(A20)

So, isotropic solutions exist for $\xi \geqslant -\frac{5}{8}$. Remember the asymptotic equations (A9)–(A10) has no real solutions for $\xi \geqslant -\frac{3}{2}$. Consequently, isotropization and compactification regimes do not coexist in ($6+1$)-dimensional EGB cosmological model.

Compactification regime in $(6+1)$ dimensions have been found numerically [33]. Note, however, that structure of equations prevents solution with zero effective cosmological constant in the bigger subspace since $H=0$ requires $b=0$.