1 Introduction

Current communication networks have difficulty satisfying the transmission requirements of the internet of things, such as communication capacity, transmission quality, data rate, and secrecy. As the newest generation of mobile communication systems, fifth-generation (5G) mobile communication technology is attracting increased attention. As an alternative modulation scheme for 5G communication, offset quadrature amplitude modulation–based orthogonal frequency division multiplexing (OQAM/OFDM) outperforms OFDM with respect to spectral efficiency, side lobes, and sensitivity to asynchronous transmission [1, 2]. As one of the important components of OQAM/OFDM systems, the prototype filter will affect the side lobes of the system and the power spectral density of the transmitted signal. Hence the prototype filter is a crucial component of OQAM/OFDM systems and plays a significant role in their overall performance.

Many effective prototype filter design methods have been discussed in the literature, and these can be classified as direct and indirect approaches [3]. Indirect approaches mainly include the windowing-based method and frequency sampling method. Direct approaches optimize all coefficients of the prototype filter. With many more degrees of design freedom, direct approaches have the potential to achieve better performance than indirect approaches [4].

However, direct approaches require the optimization of thousands of coefficients, and the complexity grows rapidly with the number of coefficients. To reduce the computational complexity, Androulakis et al. [5] utilized the α-based branch and bound (αBB) algorithm to design the prototype filter. However, the αBB algorithm can only marginally narrow the search scope of the optimal solution. Aiming to obtain superior spectrum features, Ricardo et al. [6] used convex optimization to design the prototype filter. Viholainen et al. [3] proposed an efficient iterative algorithm to design the prototype filter when the subcarrier number is large. The algorithm was obtained by deriving the gradient vector of the objective function [3]. The unknowns in these methods make it difficult to obtain the global optimum. The box-based branch and bound (Box-BB) method can solve this problem. Wu et al. proposed this method to decrease the number of iterations [7]. The method converged quickly and obtained the global optimum.

Accurate channel estimation (CE) at the receiver is indispensable for reliable signal detection. There have been some studies on CE for the OQAM/OFDM system.

Two modified CE methods were proposed by placing guard symbols at different sides of a reference preamble symbol [8]. Both proposed preambles improved the CE performance, but the existence of guard symbols reduced spectrum efficiency. To overcome this defect and increase spectrum efficiency, coded auxiliary pilot symbols that also carry information were designed [9]. At the same time, some pilot symbols were used to deal with imaginary interference. However, at least two pilot symbols were needed to achieve acceptable performance in practice. An efficient preamble structure was proposed to achieve a better CE with less preamble consumption [10]. Because compressed sensing has no pilot, CE methods based on it were proposed to further increase the spectral efficiency. When prior sparse knowledge was unknown, an adaptive, regularized, compressive sampling matching pursuit was chosen as the support set to achieve better CE accuracy [11]. The complexity of this method was high, which limited its application. Inspired by Wang et al. [11], two improved CE methods were derived, based respectively on the interference approximation method (IAM) and a pair of real pilots [12]. Both methods based on compressed sensing achieved remarkable results compared with the conventional CE method. However, whether the system, like the scattering channel, is sparse is debatable. No matter what CE method is utilized, the intrinsic interference must be eliminated to guarantee CE performance.

Few studies have taken CE into account the prototype filter design. The prototype filter is designed by utilizing the mean square error (MSE) of the CE [13]. However, zero symbols inserted in the preambles will reduce the system’s spectral efficiency. Inspired by Inching et al. [10], a preamble without guard symbols is considered in this paper to achieve higher transmission efficiency. The proposed structure would improve the accuracy of CE by increasing pseudo pilot power.

The influence of noise may also be ignored in prototype filter design. For example, the weight signal-to-interference ratio was treated as the utility function to design a prototype filter under a highly doubly dispersive channel without noise [14]. However, the noise power is generally equal to, or even larger than, the interference power in practical systems. Therefore, the noise influence should be given sufficient attention in prototype filter design. The signal-to-interference-plus-noise ratio (SINR) is usually adopted to measure the noise influence. A bigger SINR means better system performance. Therefore, it will be difficult to set the threshold when the SINR is added to the constraints. Under this condition, in this study, the reciprocal of the SINR (RSINR) is adopted to measure the influence of noise.

The contributions of this paper are two-fold.

  1. (1)

    A novel preamble structure is proposed to improve the channel spectral efficiency. Zero symbols are generally inserted between preambles and data symbols, but in this study, preambles without zero symbols are considered in order to acquire a higher transmission efficiency. This enables us to eliminate the influence of intrinsic interference on CE. Because of unknown items, a pre-decision method is adopted to estimate the channel impulse response (CIR) of the proposed preamble structure.

  2. (2)

    The influence of interference on CE and of noise is considered in the prototype filter design. The RSINR is utilized to measure these influences. In this study, the RSINR is expressed as functions of CIR and noise and is then added to the constraints. A lower out-of-band interference power means better system performance. Since the stop-band energy determines the total leaked out-of-band interference power, to minimize the stop-band energy is the optimization objective in this study.

The rest of the study is organized as follows. In section 2, the OQAM/OFDM model is described, the preamble is proposed, and the CE is obtained. In section 3, the prototype filter design is formulated by minimizing the stop-band energy with constraints on the RSINR, and a Box-BB algorithm is utilized to solve the optimization problem. The results of the simulations are discussed in section 4, and our conclusions are presented in section 5.

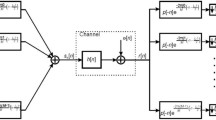
2 System model

Instead of transmitting complex symbols \( {c}_{m,n}={c}_{m,n}^{\mathfrak{R}}+j{c}_{m,n}^{\mathfrak{I}} \), OQAM/OFDM transmits the real-valued symbols am, n. am, n is from the constellation mapping of \( {C^{\mathfrak{R}}}_{m,n} \) and \( {C^{\mathfrak{I}}}_{m,n} \). According to Achaichia et al. [15], the continuous time baseband equivalent of the transmitting signal in OQAM/OFDM can be written as

(1)

where M is the number of subcarriers, V0 = 1/T0 = 1/2τ0 denotes the subcarrier spacing, T0 is the constellation interval, and τ0 is the offset between the real and imaginary parts of OQAM. g(t) is the prototype filter function. ϕm, n is an additional phase term,

$$ {\phi}_{m,n}={\phi}_0+\frac{\pi }{2}\left(m+n\right)\left(\mathit{\operatorname{mod}}\ \pi \right), $$
(2)

where ϕ0 can be chosen arbitrarily. For simplification, ϕ0 = 0 in this study.

Considering the multi-path channel with additive white Gaussian noise η(t), when the transmitted OQAM/OFDM signal is passed through, the baseband version of the received signal is described as.

$$ {\displaystyle \begin{array}{l}y(t)={\int}_0^{\Delta }h\left(\tau \right)s\left(t-\tau \right) d\tau +\eta (t)\\ {}\kern2.5em =\sum \limits_{n=-\infty}^{+\infty}\sum \limits_{m=0}^{M-1}{a}_{m,n}{\int}_0^{\Delta }h\left(\tau \right){e}^{-j2\pi m{\nu}_0\tau }{e}^{j\frac{\pi \left(m+n\right)}{2}}{e}^{j2\pi m{\nu}_0t},\\ {}\kern2.5em \times g\left(t-\tau -n{\tau}_0\right) d\tau +\eta (t)\end{array}} $$
(3)

where h(t) is the CIR and Δ is the maximum delay spread of the channel. We assume that g(t − τ − nτ0) ≈ g(t − nτ0) in the time interval τ ∈ [0, Δ]. In this case, we rewrite (3) as

$$ {\displaystyle \begin{array}{l}y(t)=\sum \limits_{n=-\infty}^{+\infty}\sum \limits_{m=0}^{M-1}{a}_{m,n}{e}^{j\frac{\pi \left(m+n\right)}{2}}{e}^{j2\pi m{\nu}_0t}g\left(t-n{\tau}_0\right)\\ {}\kern2em \times {\int}_0^{\triangle }h\left(\tau \right){e}^{-j2\pi m{\nu}_0\tau } d\tau +\eta (t)\\ {}\kern1.75em =\sum \limits_{n=-\infty}^{+\infty}\sum \limits_{m=0}^{M-1}{a}_{m,n}{g}_{m,n}(t){H}_m+\eta (t)\end{array}}, $$
(4)

where \( {H}_m={\int}_0^{\varDelta }h(t){e}^{-j2\pi m{v}_0t} dt \) is the channel impulse frequency response.

The demodulation signal at the (m0,n0) position can be written as

$$ {y}_{m_0,{n}_0}=\left\langle y(t),{g}_{m_0,{n}_0}\right\rangle =\sum \limits_{n=-\infty}^{+\infty}\sum \limits_{m=0}^{M-1}{a}_{m,n}{H}_m\left\langle {g}_{m,n}(t),{g}_{m_0,{n}_0}\right\rangle +{\eta}_{m_0,{n}_0}^1, $$
(5)

where 〈x, y〉 is the inner product of x and y, \( {\eta^1}_{m_0,{n}_0}=\left\langle \eta (t),{g}_{m_0,{n}_0}\right\rangle \).

The orthogonal condition in OQAM/OFDM is

$$ \mathfrak{R}\left\{\left\langle {g}_{m,n},{g}_{m_0,{n}_0}\right\rangle \right\}={\delta}_{m,{m}_0}{\delta}_{n,{n}_0}, $$
(6)

where \( \mathfrak{R}\left\{\cdotp \right\} \) is the real part of the argument, and \( {\hat{H}}_{m_0} \) is Dirac’s delta function.

Thus the OQAM/OFDM system model has been built. To improve the preamble, CE based on the preamble is needed to analyze the relationship between the preamble and CE.

2.1 CE based on the preamble

We define m = m0 + p, . n = n0 + q, . p, q ∈ Z, and the inner product of the pulse shaping filter in Eq. (5) can be rewritten as

$$ {\displaystyle \begin{array}{l}\begin{array}{l}\left\langle {g}_{m,n}(t),{g}_{m_{0,}{n}_0}\right\rangle ={\int}_{-\infty}^{+\infty }{g}_{m_0+p,{n}_0+q}(t){g^{\ast}}_{m_0+{n}_0}(t) dt\\ {}\kern8em ={\int}_{-\infty}^{+\infty }{e}^{j\frac{\pi }{2}\left({m}_0+{n}_0+p+q\right)}{e}^{j2\pi \left({m}_0+p\right){v}_0t}g\left(t-{n}_0{\pi}_0-q{\pi}_0\right)\end{array}\\ {}\kern8em x{e}^{-j\frac{\pi }{2}\left({m}_0+{n}_0\right)}{e}^{-j2\pi {m}_0{v}_0t}{g}^{\ast}\left(t-{n}_0{\tau}_0\right) dt\\ {}\kern8em ={j}^{\left(p+q\right)}{\int}_{-\infty}^{+\infty }g\left(t-{n}_0{\tau}_0-q{\tau}_0\right){g}^{\ast}\left(t-{n}_0{\tau}_0\right){e}^{j2\pi p{v}_0t} dt\end{array}}, $$
(7)

where ∗ denotes the conjugate operation. We make the notations \( t-{n}_0{\tau}_0-q{\tau}_0=l-\frac{q}{2}{\tau}_0 \), \( t-{n}_0{\tau}_0=l+\frac{q}{2}{\tau}_0 \). Then, since \( {\nu}_0{\tau}_0=\frac{1}{2} \), Eq. (7) can be rewritten as

$$ {\displaystyle \begin{array}{c}\left\langle {g}_{m,n}(t),{g}_{m_0,{n}_0}\right\rangle ={j}^{\left(p+q\right)}{\int}_{-\infty}^{+\infty }g\left(l+\frac{-q}{2}{\tau}_0\right){g}^{\ast}\left(l-\frac{-q}{2}{\tau}_0\right)\times \\ {}{e}^{j2\pi p{\nu}_0\left(l+{n}_0{\tau}_0+q{\tau}_0/2\right)} dl\\ {}\kern2.75em ={j}^{\left(p+q+ pq+2p{n}_0\right)}{A}_g\left(-q{\tau}_0,p{\nu}_0\right)\end{array}}, $$
(8)

where Ag(τ, v) is the ambiguity function of the filter,

$$ {A}_g\left(\tau, v\right)=\int g\Big(t+\frac{\tau }{2}{g}^{\ast}\left(t-\frac{\tau }{2}\right){e}^{j2\tau vt} dt $$
(9)

Since g(t) is an even function, its instantaneous autocorrelation function \( {\gamma}_g\left(\tau, t\right)=g\left(t+\frac{\tau }{2}\right){g}^{\ast}\left(t-\frac{\tau }{2}\right) \) is an even conjugate. Ag(τ, v) is the inverse Fourier transform of γg(τ, t), and therefore, Ag(τ, v) is a real-valued function [16].

From Eq. (5), we can obtain

$$ {\displaystyle \begin{array}{l}\begin{array}{l}{y}_{m_0,{n}_0}=\sum \limits_{\left(p,q\right)\in Z}{j}^{\left(p+q+ pq+2p{n}_0\right)}{A}_g\left(-q{\tau}_0,p{v}_0\right)\\ {}\kern3.25em \times {a}_{m_0+p,{n}_0+q}{H}_{m_0+p}+{\eta}_{m_0,{n}_0}^1\end{array}\\ {}\kern3em ={a}_{m_0{n}_0}{H}_{m_0}+\sum \limits_{\left(p,q\right)\ne \left(p,q\right)}{j}^{\left(p+q+ pq+2p{n}_0\right)}\\ {}\kern3em \times {A}_g\left(-q{\tau}_0,p{v}_0\right){a}_{m_0+p,{n}_0+q}{H}_{m_0+p}+{\eta^1}_{m_0,{n}_0}\end{array}} $$
(10)

According to the conventional OFDM CE method, the channel frequency response \( \hat{H}{m}_0 \) can be estimated by \( {\hat{H}}_{m_0,{n}_0}=\frac{y_{m_0,{n}_0}}{a_{m_0.{n}_0}} \) when the pilot symbol \( {a}_{m_0,{n}_0} \) is transmitted at time-frequency position (m0, n0).

We define \( {C}_{p,q}={j}^{\Big(p+q+ pq+2 pn{0}_{\Big)}}{A}_g\left(-q{\tau}_0,p{v}_0\right) \), and Δm0 and Δn0 are respectively the neighborhoods of m0 and n0. \( {\varOmega}_{\varDelta {m}_0,\varDelta {n}_0}=\left\{\left(p,q\right),\mid p\mid \le \varDelta {m}_0,\mid q\mid \le \varDelta {n}_0\mid {H}_{m_0+p,{n}_0+q}\approx {H}_{m_0,{n}_0}\right\} \) and \( {\varOmega_{\varDelta {m}_0,\varDelta {n}_0}}_{\ast }={\varOmega}_{\varDelta {m}_0,\varDelta {n}_0}-\left(0,0\right) \), where \( {\varOmega}_{\varDelta {m}_0,\varDelta {n}_0} \) is the neighborhood of position (m0, n0). With the increase in ∣p∣ and ∣q∣, Cp, q becomes very close to zero. For example, for an isotropic orthogonal transformation algorithm (IOTA) function, when (p, q) ∉ Ω1, 1, we have [17].

$$ \frac{\sum_{\left(p,q\right)\notin \varOmega 1,1}{\left|{C}_{p,q}\right|}^2}{\sum_{\left(p,q\right)\in {\varOmega}^{\ast }1,1}{\left|{C}_{p,q}\right|}^2}\approx 0.02, $$
(11)

from which, we can conclude that only one column of zero symbols is needed to prevent adjacent unknown data symbols from interfering with the preamble. However, the inserted zero symbols will affect the CE. According to LeLe et al. [17], when only one column of zero symbols is inserted in the preamble, the CE performance of the preamble is worse than that of the IAM.

The structure of the IAM is shown in Fig. 1, from which it is seen that there are two columns of zero symbols. Since \( {a}_{m_0-1,{n}_0} \) and \( {a}_{m_0+1,{n}_0} \) are opposite in sign, Eq. (10) can be rewritten as

Fig. 1
figure 1

Structure of IAM

Full size image
$$ {\displaystyle \begin{array}{l}\begin{array}{l}{y}_{m_0,{n}_0}={a}_{m_0,{n}_0}{H}_{m_0}+{C}_{-1,0}{a}_{m_0-1,{n}_0}{H}_{m_0-1}\\ {}\kern3.25em +{C}_{1,0}{a}_{m_0+1,{n}_0}{H}_{m_0+1}\end{array}\\ {}\kern3.25em +\sum \limits_{\left(p,q\right)\ne \left(0,0\right),\left(p,q\right)\ne \left(\pm 1,0\right),q\ne \pm 1}{C}_{p,q}{a}_{m_0+p,{n}_0+q}{H}_{m_0+p}\\ {}\kern3.25em +{\eta}_{m_0,{n}_0}^1\end{array}} $$
(12)

For the flat fading channel, we assume \( {H}_{m_0}={H}_{m_0+1}={H}_{m_0-1} \). The CE based on the IAM can be obtained by

$$ {\displaystyle \begin{array}{l}{\hat{H}}_{m_0}=\frac{y_{m_0}{,}_{n_0}}{b_{m_0,{n}_0}}\\ {}\kern2.25em ={H}_{m_0}+\sum \limits_{\left(p,q\right)\ne \left(0,0\right),\left(p,q\right)\ne \left(\pm 1,0\right),q\ne \pm 1}\frac{C_{p,q}{a}_{m_0+p,{n}_0+q}{H}_{m_0+p}}{b_{m_0,{n}_0}},\\ {}\kern2.25em +\frac{\eta_{m_0,{n}_0}^1}{b_{m_0,{n}_0}}\end{array}} $$
(13)

where \( {b}_{m_0,{n}_0}={a}_{m_0}{,}_{n_0}+{C}_{1,0}{a}_{m_0+1,{n}_0}+{C}_{-1,0}{a}_{m_0-1,{n}_0} \). \( {b}_{m_0}{,}_{n_0} \) can be treated as the pseudo pilot. Equation (13) implies that greater pseudo pilot power leads to a better CE. The power of pseudo pilot \( {b}_{m_0}{,}_{n_0} \) for the IAM is

$$ {\displaystyle \begin{array}{c}{E}_1\left\{{\left|{b}_{m_0,{n}_0}\right|}^2\right\}={a}_{m_0,{n}_0}^2+{\left|{C}_{-1,0}{a}_{m_0+1,{n}_0}+{C}_{1,0}{a}_{m_0+1,{n}_0}\right|}^2\\ {}\kern4.5em ={\sigma}_a^2\left(1+4{A}_g+4{A^2}_g\right)\end{array}}, $$
(14)

where σ2a is the variance of the transmitted OQAM/OFDM symbols am. n.

CE based on the IAM has two obvious drawbacks: (1) the preamble duration is 3τ0 , which leads to low spectrum efficiency, and (2) the second item in Eq. (13) cannot be ignored when both the signal-to-noise ratio (SNR) and constellation mapping order are high.

To overcome these drawbacks and increase the pseudo pilot power, a new preamble with duration τ0 is proposed in this paper. The structure of the preamble is shown in Fig. 2. For sufficient accuracy and concise description, only three-tap interference of neighborhood symbols is considered.

Fig. 2
figure 2

Proposed structure of OQAM/OFDM system

Full size image

The pseudo pilot power of the proposed structure is

$$ {E}_2\left\{{\left|{b}_{m_0,{n}_0}\right|}^2\right\}={a}_{m_0,{n}_0}^2+{\left|\sum \limits_{\left(p,q\right)\in {\varOmega}^{\ast }3,3}{C}_{p,q}{a}_{m_{0+}p,{n}_0+q}\right|}^2>{E}_1, $$
(15)

from which, we can conclude that the proposed structure can improve system performance for its larger pseudo pilot power. This means that the proposed structure can decrease the interference caused by the adjacent unknown data symbol, promote CE performance, and increase the frequency spectrum efficiency.

2.2 RSINR

According to the previous discussion, the noise and influence of the prototype filter on CE should be given sufficient attention in the prototype filter design. To take these into account while designing the prototype filter, the RSINR is chosen to measure their influences. The expression of RSINR based on the CIR is derived in this section.

First, we rewrite Eq. (10) as

$$ {\displaystyle \begin{array}{c}{y}_{m_0,{n}_0}={a}_{m_0,{n}_0}{H}_{m_0}+{a}_{m_0,{n}_0}^{(i1)}{H}_{m_0}\\ {}+{a}_{m_0,{n}_0}^{(i2)}{H}_{m_0}+{\eta}_{m_0,{n}_0}^1\end{array}}, $$
(16)

where

$$ {a}_{m_0,{n}_0}^{(i1)}=\sum \limits_{\left(p,q\right)\in {\varOmega}_{3,3}^{\ast },q=0}{C}_{p,q}{a}_{m_0+p,{n}_0+q}, $$
(17)
$$ {a}_{m_0,{n}_0}^{(i2)}=\sum \limits_{\left(p,q\right)\in {\varOmega}_{3,3}^{\ast },q\ne 0}{C}_{p,q}{a}_{m_0+p,{n}_0+q}, $$
(18)

and then the estimated channel frequency impulse response \( {\hat{H}}_{m_0} \) is obtained by

$$ {\hat{H}}_{m0}=\frac{y_{m_0,{n}_0}}{a_{m_0,{n}_0}+{a}_{m_0,{n}_0}^{(i1)}+{a}_{m_0,{n}_0}^{(i2)}} $$
(19)

Because the \( {{a_{m_0}}_{+}}_{p,{n}_0+q} \) in Eq. (18) belongs to a random signal, its value cannot be determined during transmission. As a result, the term \( {a^{(i2)}}_{m_0,{n}_0} \) is unknown, in which case Eq. (19) will be invalid. To solve this problem, the pre-decision method [18] is adopted.

First, the initial channel frequency response \( {\overline{H}}_{m_0} \) can be obtained from (16) as

$$ {\overline{H}}_{m_0}=\frac{y_{m_0,{n}_0}}{a_{m_0,{n}_0}+{a}_{m_0,{n}_0}^{(i1)}}={H}_{m_0}+\frac{a_{m_0,{n}_0}^{(i2)}{H}_{m_0}+{\eta}_{m_0,{n}_0}^1}{a_{m_0,{n}_0}+{a}_{m_0,{n}_0}^{(i1)}} $$
(20)

Next, \( {a}_{m_0+p,{n}_0+q} \) in the term \( {{a^{(i2)}}_{m_0}}_{,{n}_0} \) can be rebuilt based on zero-forcing equalization and the pre-decision method:

$$ {\hat{a}}_{m_0+p,{n}_0+q}=D\left[\frac{y_{m_0+p,{n}_0+q}}{{\overline{H}}_{m_0}}\right],\left(p,q\right)\in {\varOmega}_{3,3}^{\ast },q\ne 0, $$
(21)

where D[•] denotes the pre-decision operator.

Then \( {a^{(i2)}}_{m_0,{n}_0} \) can be estimated by

$$ {\hat{a}}_{m_0,{n}_0}^{(i2)}=\sum \limits_{\left(p,q\right)\in {\varOmega}_3^{\ast }{,}_3,q\ne 0}{C}_{p,q}{\hat{a}}_{m_0+p,{n}_0+q} $$
(22)

Finally, since \( {a^{(i2)}}_{m_0,{n}_0} \) has been obtained, the CE is obtained by substituting \( {a^{(i2)}}_{m_0,{n}_0} \) in Eq. (19). The final channel frequency response expression is

$$ {\hat{H}}_{m_0}=\frac{y_{m_0,{n}_0}}{a_{m_0,{n}_0}+{a}_{m_0,{n}_0}^{(i1)}+{\hat{a}}_{m_0,{n}_0}^{(i2)}} $$
(23)

By inverse Fourier transform, the CIR of the OQAM/OFDM system is obtained as

$$ \hat{h}(t)=\frac{1}{2\tau }{\int}_0^{\varDelta }{\hat{H}}_m{e}^{-j2\pi m{v}_0t} dt $$
(24)

We then discretize the CIR \( \hat{h}(t) \) into the form \( {\hat{h}}_1 \), as follows:

$$ \hat{h}(t)={\sum}_{i-0}^{p-1}{\hat{h}}_i\delta \left(\tau -{\tau}_i\right), $$
(25)
$$ {\hat{h}}_1=\Big\{{\displaystyle \begin{array}{c}{\hat{h}}_1,l=\left\lceil \frac{\tau_i}{T_s}\right\rceil \\ {}0,\mathrm{otherwise}\end{array}}, $$
(26)

where ⌈x⌉ denotes the smallest integer greater than or equal to x, and \( {T}_s=\frac{T_0}{2M} \) is the sampling period.

The desired power of the system is closely related to the transmitted symbol. The transmitted symbol at the position (m0, n0) can be estimated as

$$ {\hat{a}}_{m_0,{n}_0}=\mathfrak{R}\left(\frac{y_{m_0,{n}_0}}{{\hat{H}}_{m_0}}\right) $$
(27)

The QAM symbols are reconstructed by

$$ {\hat{C}}_{m_0,{n}_0}={\hat{a}}_{m_0,2{n}_0}+j{\hat{a}}_{m_0}{,}_{2{n}_0+1} $$
(28)

We then define

$$ {H}_{m_0}^{p,q}=\sum \limits_{l=0}^{L_h-1}{\hat{h}}_l{e}^{- j\pi \left(2{m}_0+p\right)l/M}{A}_g\left[-l-q\frac{M}{2},-p\right], $$
(29)

where \( {A}_g\left[k,l\right]={A}_g\left(k{T}_s,\frac{l}{M{T}_s}\right) \), and Lh is the number of channel taps at the sampling rate.

Then the desired power expression of the system is

$$ {P}_d\left({m}_0\right)={\sigma^2}_c{\left|\mathfrak{R}\left\{\frac{H_{m_0}^{p,q}}{{\hat{H}}_{m_0}}\right\}\right|}^2, $$
(30)

where \( {\sigma}_c^2 \) is the variance of the complex symbol c.

Similarly, the interference power and noise power are expressed as [19].

$$ {P}_{ISI+ ICI}\left({m}_0\right)=2{\sigma^2}_a\sum \limits_{\left(p,q\right)\ne \left(0,0\right)}{\left|\mathfrak{R}\left\{\frac{e^{j\frac{\pi }{2}\left(p+q+ pq\right)}{H}_{m_0}^{p,q}}{{\hat{H}}_{m_0}}\right\}\right|}^2, $$
(31)
$$ {P}_{\boldsymbol{noise}}\left({m}_0\right)=\mathit{\operatorname{var}}\left[{\eta^1}_{m_0,{n}_0}\right]=\frac{{\sigma^2}_n}{{\left|{\hat{H}}_{m_0}\right|}^2}, $$
(32)

where σ2n is the variance of the noise η.

Thus the expression of RSINR is obtained by Eqs. (30), (31), and (32) as

$$ {\displaystyle \begin{array}{c}\boldsymbol{RSINR}=\frac{P_{ICI+ ISI}+{P}_{\boldsymbol{noise}}}{P_d\left({m}_0\right)}\\ {}=\frac{2{\sigma^2}_n\sum \limits_{\left(p,q\right)\ne \left(0,0\right)}{\left|\mathfrak{R}\left\{\frac{e^{j\frac{\pi }{2}\left(p+q+ pq\right)}{H}_{m_0}^{p,q}}{{\hat{H}}_{m_0}}\right\}\right|}^2+\frac{{\sigma^2}_n}{{\left|{\hat{H}}_{m_0}\right|}^2}}{{\sigma^2}_n{\left|\mathfrak{R}\left\{\frac{H_{m_0}^{p,q}}{{\hat{H}}_{m_0}}\right\}\right|}^2}\end{array}} $$
(33)

3 Prototype filter design

3.1 Problem formulation

The prototype filter in the OQAM/OFDM system is assumed to be real-valued, symmetric, and of unit energy. According to the previous discussion, when there is intrinsic interference and noise in the system, the prototype filter will influence the CE. Therefore, the RSINR will be chosen as an important constraint in the problem formulation. At the same time, the prototype filter design should minimize the stop-band energy. Thus the prototype filter design problem can be formulated as

$$ {\displaystyle \begin{array}{c}P1{:}_{g(k)}^{\mathrm{min}}{\int}_{\frac{2\pi }{M}}^{\pi }{\left|G\left({e}^{j\omega}\right)\right|}^2 d\omega \\ {}s.t.\Big\{\begin{array}{c}g\left[k\right]=g\left[{L}_g-1-k\right],k=0,1\dots -1\\ {}\sum \limits_{K=0}^{L_g-1}{g}^2\left[k\right]=1\\ {}\mathrm{RSINR}\le TH\end{array}\end{array}} $$
(34)

where \( \mid G\left({e}^{j\omega}\right)\mid =\mid \sum \limits_{k=0}^{L_{g-1}}g\left[k\right]{e}^{- j\omega k}\mid \) is the magnitude response of the prototype filter, TH is a constant threshold, and Lg is the length of the prototype filter. According to Siohan et al. [20], \( g\left[k\right]=\sqrt{T_s}g\left(\left(k-\frac{L_g-1}{2}\right){T}_s\right) \).

There are many variables in P1. The objective and constraint functions have quadratic forms. It is difficult to directly solve the optimization problem P1. As everyone knows, orthogonal transformation does not change the nature of the original function. However, it can be utilized to change the form of (34).

The first constraint function in (34) implies that only half the filter coefficients are independent. To reduce the number of variables, we replace g[k] with a new variable,

$$ {\displaystyle \begin{array}{c}X={\left[{x}_1{x}_2\dots {x}_L\right]}^T\\ {}={\left[g\left[0\right]g\left[1\right]\dots g\left[\frac{L_g-1}{2}\right]\right]}^T\end{array}} $$
(35)

The objective function can be rewritten in vector form as f0(x) = xTCx, where C is a real symmetric positive-definite matrix. λ1, λ2, …λL denote positive eigenvalues in ascending order, and v1, v2, …, vL denote corresponding unit orthogonal eigenvectors.

Then the orthogonal transformation X = VZ is applied to the variable X, where Z = [z1z2…zL]T is the new orthogonal variable.

Finally, the optimization problem after variable substitution and orthogonal transformation is expressed as

$$ {\displaystyle \begin{array}{c}P2:\mathit{\min}\sum \limits_{j=1}^L{\lambda}_j{Z}_j^2\\ {}s.t.\Big\{\begin{array}{c}{C}_1(z)=-\left(\sum \limits_{k=0}^{L_g-1}{g}^2\left[k\right]-1\right)\le 0\\ {}{C}_2(z)=\mathrm{RSINR}\le TH\end{array}\end{array}} $$
(36)

3.2 Problem solution

Variable substitution reduces the number of variables by half. After orthogonal transformation, all functions in (36) take standard forms. According to Androulakis et al. [5], P2 can be directly solved by the αBB algorithm.

The αBB algorithm has disadvantages. If there is no intersection between the two constraint functions in (36) and a certain subset, then the αBB algorithm will be invalid. Furthermore, it never pays to determine the parameter ɑ and confirm the upper and lower bounds for the αBB algorithm because it is time consuming.

To avoid these disadvantages, the Box-BB algorithm [7] is proposed. The Box-BB algorithm to solve optimization problem P2 is as follows.

figure a

4 Simulation result

The validity of the proposed prototype filter design method is verified through a series of simulations. We set the number of subcarriers as M = 128, the subcarrier spacing as v0 = 10.94 kHz, the filter length as Lg = 4M + 1, and the power ratio threshold as TH = 10−4 in simulations. The ITU-VehB channel model without mobility is adopted for the highly frequency-selective channels [22].

4.1 Performance of the proposed preamble

The truncation of an IOTA filter of length 4T0 [23] is chosen as the prototype filter in this simulation. Figure 3 illustrates the CE performances of the proposed structure (A) and the IAM (B) for two kinds of constellation mapping. For 16-QAM modulation, when the SNR is low (SNR < 15 dB), the CE performances of A are slightly better than those of B. Along with the SNR increasing, the CE performances of A become better and better, and the performance advantages become increasingly obvious. This is because there are imaginary preamble symbols in the proposed structure to increase the pseudo pilot power. Additionally, the IAM performance curve tends to flatten due to the performance platform when SNR > 15 dB. Similarly, for 4-QAM modulation, the IAM performance curve tends to be gentle when SNR > 20 dB. From Fig. 3, we can conclude that the proposed structure in this study is better than the IAM structure when it comes to CE.

Fig. 3
figure 3

Normalized MSE performance of A proposed structure and B IAM structure for 4-QAM and 16-QAM in CE

Full size image

Therefore, the proposed structure is able to increase the CE performance. Moreover, because the proposed structure is without zero symbols, the frequency spectrum of the system is improved.

4.2 Performance of the designed prototype filter

Figure 4 shows the normalized amplitude responses of different filters, from which it can be seen that the prototype filter designed in this paper has a much higher amplitude than the other three filters, which means that it has a greater energy spectral density and lower stop-band energy. To further reveal the performance of the prototype filter proposed in this paper, Table 1 presents the stop-band energy of different filters. It shows that the stop-band energies of the IOTA filter, the filter designed by Yuan et al. [13], and that designed by Wu et al. [7] are − 32 dB, − 43 dB, and − 41 dB, respectively. The proposed prototype filter achieves the lowest stop-band energy (− 50 dB).

Fig. 4
figure 4

Normalized amplitude responses of different filters

Full size image
Table 1 Stop-band energy of different filters
Full size table

Since the proposed filter is designed with a constraint on the RSINR, not only the influence of noise is considered to guarantee the effectiveness of the method. The desired power is also increased as the interference power decreases. Wu et al. [7] did not consider the influence of noise, but it should not be ignored in practice. It caused worse performance of the method proposed by Wu et al. in the simulation when compared with the method proposed in this study. Similarly, Yuan et al. [13] did not consider the desired symbol power in the prototype filter design problem, which may have caused the solution to the optimization problem to not be the minimum.

5 Conclusion

In this study, a new prototype filter was designed based on the CE for the OQAM/OFDM system in frequency-selective channels. The proposed method is able to minimize the stop-band energy and increase the CE performance. RSINR, which is utilized to measure the influence of the prototype filter on the CE, is an important constraint for prototype filter design. A new preamble structure was proposed to save the frequency spectrum before the RSINR calculation. Then an optimization problem of the prototype filter design was formulated to minimize the stop-band energy with constraints on the RSINR. Finally, the Box-BB algorithm was employed to solve this optimization problem in order to obtain a low convergence time and the global optimal solution. Simulation results verified the superiority of the designed prototype filter over other filters.