Skip to main content
SpringerLink
Log in

Semi-classical Limit of Confined Fermionic Systems in Homogeneous Magnetic Fields

  • Published:
Annales Henri Poincaré Aims and scope Submit manuscript

Abstract

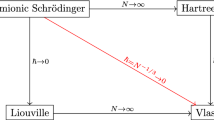
We consider a system of N interacting fermions in \( {\mathbb {R}}^3 \) confined by an external potential and in the presence of a homogeneous magnetic field. The intensity of the interaction has the mean-field scaling 1/N. With a semi-classical parameter \( \hbar \sim N^{-1/3} \), we prove convergence in the large N limit to the appropriate magnetic Thomas–Fermi-type model with various strength scalings of the magnetic field.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Braun, W., Hepp, K.: The Vlasov dynamics and its fluctuations in the \(1/N\) limit of interacting classical particles. Commun. Math. Phys. 56, 101–113 (1977)

    Article  ADS  MathSciNet  Google Scholar 

  2. Caglioti, E., Lions, P.-L., Marchioro, C., Pulvirenti, M.: A special class of stationary flows for two-dimensional Euler equations: a statistical mechanics description. Commun. Math. Phys. 143, 501–525 (1992)

    Article  ADS  MathSciNet  Google Scholar 

  3. de Finetti, B.: Funzione caratteristica di un fenomeno aleatorio. Atti della R. Accademia Nazionale dei Lincei, 1931. Ser. 6, Memorie, Classe di Scienze Fisiche, Matematiche e Naturali

  4. Diaconis, P., Freedman, D.: Finite exchangeable sequences. Ann. Probab. 8, 745–764 (1980)

    Article  MathSciNet  Google Scholar 

  5. Fournais, S., Lewin, M., Solovej, J.P.: The semi-classical limit of large fermionic systems. Calc. Var. Partial Differ. Equ. 57, 105 (2018)

    Article  MathSciNet  Google Scholar 

  6. Hainzl, C., Seiringer, R.: Bounds on one-dimensional exchange energies with application to lowest Landau band quantum mechanics. Lett. Math. Phys. 55, 133–142 (2001)

    Article  MathSciNet  Google Scholar 

  7. Hainzl, C., Seiringer, R.: A discrete density matrix theory for atoms in strong magnetic fields. Commun. Math. Phys. 217, 229–248 (2001)

    Article  ADS  MathSciNet  Google Scholar 

  8. Hauksson, B., Yngvason, J.: Asymptotic exactness of magnetic Thomas–Fermi theory at nonzero temperature. J. Stat. Phys. 116, 523–546 (2004)

    Article  ADS  MathSciNet  Google Scholar 

  9. Hewitt, E., Savage, L.J.: Symmetric measures on Cartesian products. Trans. Am. Math. Soc. 80, 470–501 (1955)

    Article  MathSciNet  Google Scholar 

  10. Hudson, R.L., Moody, G.R.: Locally normal symmetric states and an analogue of de Finetti’s theorem. Z. Wahrscheinlichkeitstheor. und Verw. Gebiete 33, 343–351 (1975/76)

  11. Ivrii, V.: Asymptotics of the ground state energy of heavy molecules in a strong magnetic field. I. Russ. J. Math. Phys. 4, 29–74 (1996)

    MathSciNet  MATH  Google Scholar 

  12. Ivrii, V.: Heavy molecules in the strong magnetic field. Russ. J. Math. Phys. 4, 449–455 (1996)

    MathSciNet  MATH  Google Scholar 

  13. Ivrii, V.: Asymptotics of the ground state energy of heavy molecules in a strong magnetic field. II. Russ. J. Math. Phys. 5, 321–354 (1997)

    MathSciNet  MATH  Google Scholar 

  14. Ivrii, V.: Heavy molecules in a strong magnetic field. III. Estimates for ionization energy and excessive charge. Russ. J. Math. Phys. 6, 56–85 (1999)

    MathSciNet  MATH  Google Scholar 

  15. Kiessling, M.K.-H.: Statistical mechanics of classical particles with logarithmic interactions. Commun. Pure. Appl. Math. 46, 27–56 (1993)

    Article  MathSciNet  Google Scholar 

  16. Lewin, M., Madsen, P.S., Triay, A.: Semi-classical limit of large fermionic systems at positive temperature. ArXiv e-prints (2019)

  17. Lewin, M., Nam, P.T., Rougerie, N.: Derivation of Hartree’s theory for generic mean-field Bose systems. Adv. Math. 254, 570–621 (2014)

    Article  MathSciNet  Google Scholar 

  18. Lewin, M., Nam, P.T., Rougerie, N.: Remarks on the quantum de Finetti theorem for bosonic systems. Appl. Math. Res. Express (AMRX) 2015, 48–63 (2015)

    MathSciNet  MATH  Google Scholar 

  19. Lewin, M., Nam, P.T., Rougerie, N.: The mean-field approximation and the non-linear Schrödinger functional for trapped Bose gases. Trans. Am. Math. Soc 368, 6131–6157 (2016)

    Article  Google Scholar 

  20. Lieb, E.H., Loss, M.: Analysis. Graduate Studies in Mathematics, vol. 14, 2nd edn. American Mathematical Society, Providence, RI (2001)

    MATH  Google Scholar 

  21. Lieb, E.H., Simon, B.: The Hartree–Fock theory for Coulomb systems. Commun. Math. Phys. 53, 185–194 (1977)

    Article  ADS  MathSciNet  Google Scholar 

  22. Lieb, E.H., Simon, B.: The Thomas–Fermi theory of atoms, molecules and solids. Adv. Math. 23, 22–116 (1977)

    Article  MathSciNet  Google Scholar 

  23. Lieb, E.H., Solovej, J.P., Yngvason, J.: Asymptotics of heavy atoms in high magnetic fields: I. Lowest Landau band regions. Commun. Pure Appl. Math. 47, 513–591 (1994)

    Article  MathSciNet  Google Scholar 

  24. Lieb, E.H., Solovej, J.P., Yngvason, J.: Asymptotics of heavy atoms in high magnetic fields: II. Semiclassical regions. Commun. Math. Phys. 161, 77–124 (1994)

    Article  ADS  MathSciNet  Google Scholar 

  25. Lieb, E.H., Solovej, J.P., Yngvason, J.: Ground states of large quantum dots in magnetic fields. Phys. Rev. B 51, 10646–10665 (1995)

    Article  ADS  Google Scholar 

  26. Lieb, E.H., Thirring, W.E.: Gravitational collapse in quantum mechanics with relativistic kinetic energy. Ann. Phys. 155, 494–512 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  27. Lieb, E.H., Yau, H.-T.: The Chandrasekhar theory of stellar collapse as the limit of quantum mechanics. Commun. Math. Phys. 112, 147–174 (1987)

    Article  ADS  MathSciNet  Google Scholar 

  28. Madsen, P.: In preparation, Ph.D. thesis, Aarhus University (2019)

  29. Messer, J., Spohn, H.: Statistical mechanics of the isothermal Lane–Emden equation. J. Stat. Phys. 29, 561–578 (1982)

    Article  ADS  MathSciNet  Google Scholar 

  30. Rougerie, N.: De Finetti theorems, mean-field limits and Bose–Einstein condensation. ArXiv e-prints (2015)

  31. Seiringer, R.: On the maximal ionization of atoms in strong magnetic fields. J. Phys. A Math. General 34, 1943–1948 (2001)

    Article  ADS  MathSciNet  Google Scholar 

  32. Sobolev, A.V.: The quasi-classical asymptotics of local Riesz means for the Schrödinger operator in a strong homogeneous magnetic field. Duke Math. J. 74, 319–429 (1994)

    Article  MathSciNet  Google Scholar 

  33. Spohn, H.: On the Vlasov hierarchy. Math. Methods Appl. Sci. 3, 445–455 (1981)

    Article  ADS  MathSciNet  Google Scholar 

  34. Størmer, E.: Symmetric states of infinite tensor products of \(C^{\ast } \)-algebras. J. Funct. Anal. 3, 48–68 (1969)

    Article  MathSciNet  Google Scholar 

  35. Thirring, W.: A lower bound with the best possible constant for Coulomb Hamiltonians. Commun. Math. Phys. 79, 1–7 (1981)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors were partially supported by the Sapere Aude Grant DFF–4181-00221 from the Independent Research Fund Denmark. Part of this work was carried out while both authors visited the Mittag-Leffler Institute in Stockholm, Sweden.

Author information

Authors and Affiliations

  1. Department of Mathematics, Aarhus University, Ny Munkegade 118, DK-8000, Aarhus C, Denmark

    Søren Fournais

  2. CNRS & CEREMADE, Paris-Dauphine University, PSL University, 75016, Paris, France

    Peter S. Madsen

Authors
  1. Søren Fournais
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Peter S. Madsen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Søren Fournais.

Additional information

Communicated by Jan Derezinski.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fournais, S., Madsen, P.S. Semi-classical Limit of Confined Fermionic Systems in Homogeneous Magnetic Fields. Ann. Henri Poincaré 21, 1401–1449 (2020). https://doi.org/10.1007/s00023-019-00880-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00023-019-00880-6

Mathematics Subject Classification

Search

Navigation