Abstract
Classical field theory is insensitive to the split of the field into a background configuration and a dynamical perturbation. In gauge theories, the situation is complicated by the fact that a covariant (w.r.t. the background field) gauge fixing breaks this split independence of the action. Nevertheless, background independence is preserved on the observables, as defined via the BRST formalism, since the violation term is BRST exact. In quantized gauge theories, however, BRST exactness of the violation term is not sufficient to guarantee background independence, due to potential anomalies. We define background-independent observables in a geometrical formulation as flat sections of the observable algebra bundle over the manifold of background configurations, with respect to a flat connection which implements background variations. A theory is then called background independent if such a flat (Fedosov) connection exists. We analyze the obstructions to preserve background independence at the quantum level for pure Yang–Mills theory and for perturbative gravity. We find that in the former case, all potential obstructions can be removed by finite renormalization. In the latter case, as a consequence of power-counting non-renormalizability, there are infinitely many non-trivial potential obstructions to background independence. We leave open the question whether these obstructions actually occur.
Similar content being viewed by others
1 Introduction
In quantum field theory (QFT), one frequently considers the quantum fluctuations around classical field configurations. Examples are:
Spontaneous symmetry breaking in the standard model, where one considers quantum fluctuations around a non-trivial classical configuration of the Higgs field;
The background field method, which is an efficient tool, for example, for the computation of the renormalization group flow (see, e.g., [1]);
Perturbative quantum gravity, where one has to use a non-trivial background metric, providing the necessary structure for the formulation of a QFT [2, 3].
Hence, the issue of background independence seems to be of high conceptual importance. Apart from the discussion in [2], on which we comment in detail below, there are basically two approaches to deal with it in the literature. One is the Riemannian path integral framework, which faces the problem that, in the presence of non-trivial background fields, the relation between correlation functions on Riemannian spaces, and the QFT on Lorentzian space-time in which one is ultimately interested, is unclear. In particular, in the absence of an Osterwalder–Schrader theorem, it is not clear whether such correlation functions define a QFT in the sense of observables represented by operators on some Hilbert space. The other approach, discussed in more detail at the end of this section, is to treat the background field as an infinitesimal perturbation around a fixed flat reference background. However, for a full proof of background independence, one should treat the background field non-perturbatively. Then, one faces the problem that on generic backgrounds, there is no unique vacuum state and that the usual renormalization techniques based on momentum space are not available. A further common shortcoming of these approaches is that they are not “operational” in the sense that they do not address the following question:
Given a background configuration and an observable defined w.r.t. this background, what is the same observable on a different background?
In view of the difficulties mentioned above, we follow the algebraic approach, i.e., we directly (perturbatively) construct the algebras of observables for the different background configurations, using locally covariant renormalization techniques developed in the context of QFT on curved space-times [4]. Background independence for us then means that we can unambiguously identify observables on different backgrounds (at least for infinitesimally close backgrounds). As suggested in [5, 6], this can be formulated in the spirit of Fedosov quantization [7]: One considers the bundle of observable algebras over the manifold of background configurations and constructs a flat connection on it. The sections that are flat, i.e., covariantly constant, w.r.t. this connection provide a consistent assignment of an observable to each background. The similarity of background independence and Fedosov’s approach has already been noted, in a quantum mechanical framework, in [8].Footnote 1
1.1 The Scalar Field as a Toy Model
To motivate our definition of background independence and to introduce some of the relevant concepts, let us first discuss a toy model, namely the self-interacting \(\Phi ^4\)-theory. Consider splitting the basic scalar field
into a background configuration\({{\bar{\phi }}}\), which is kept classical at the quantum level (i.e., it commutes with all quantum fields) and a dynamical field\(\phi \) which is viewed as fluctuations around \({{\bar{\phi }}}\) and is quantized in perturbation theory. The question of background independence is then the following: Is field theory independent of the splitting of \(\Phi \) into a background \({{\bar{\phi }}}\) and a perturbation \(\phi \)? Clearly, the action functional \(S[\Phi ]\) depends only on the combination \({{\bar{\phi }}}+ \phi \); hence, the classical field theory is independent of this split. We say that it exhibits split independence. Here, we ask whether and in which mathematically rigorous sense this split independence is preserved at the quantum level.
To analyze the issue, we find it convenient to adopt the framework of locally covariant quantum field theory [4, 11] which has proven to be powerful for QFT in curved space-time or in the presence of non-trivial background gauge connections [12]. In this framework, the covariance with respect to suitable transformations of background data (e.g., isometries of the background metric or gauge transformations of the background connection) is manifest by construction. The objects of primary interest are renormalized interacting time-ordered products, which include interacting fields. They are constructed in perturbation theory and generate the non-commutative local algebra of observables.
More concretely, for the example of scalar field theory expanded around a classical solution \({{\bar{\phi }}}\) of \(\Phi ^4\)-theory, one constructs for each such background \({{\bar{\phi }}}\), the local algebra \({{\mathbf {W}}}_{{{\bar{\phi }}}}\). To each classical local functional \(F[{{\bar{\phi }}}, \phi ]\), one associates the generating functional \(T^{\mathrm {int}}_{{\bar{\phi }}}(e^{i F})\) of interacting time-ordered products, which is an element of \({{\mathbf {W}}}_{{{\bar{\phi }}}}\). These elements generate the algebra \({{\mathbf {W}}}_{{\bar{\phi }}}^{\mathrm {int}}\) of interacting observables. Now consider a local functional \(F[\Phi ]\). Obviously, it induces local functionals \(F[{{\bar{\phi }}}, \phi ] = F[{{\bar{\phi }}}+ \phi ]\) for the different backgrounds \({{\bar{\phi }}}\). Their background independence can be stated via functional derivatives as
where \({{\bar{\varphi }}}\) is some variation of the background. The question is how to implement this on the quantum observables \(T^{\mathrm {int}}_{{\bar{\phi }}}(e^{i F})\). While the second derivative (w.r.t. the dynamical field \(\phi \)) is well defined on \({{\mathbf {W}}}_{{{\bar{\phi }}}}\), the first derivative (w.r.t. the background field \({{\bar{\phi }}}\)) has no obvious meaning on \({{\mathbf {W}}}_{{{\bar{\phi }}}}\), as one is comparing elements of different algebras.Footnote 2 The way out is to replace this derivative with the retarded variation\(\delta ^{\mathrm {r}}\) [13], which is the infinitesimal version of the Møller operator relating the algebras on the different backgrounds [14] (see below). The natural translation of (2) to an assignment
of interacting fields to different backgrounds is thus
It turns out [5], cf. [15] for details, that in the \(\Phi ^4\)-theory, this is equivalent to (2) in the sense that
precisely if perturbative agreementFootnote 3 [13] holds for changes in the (position dependent) mass of the scalar field.Footnote 4 As a consequence of the flatness of \({\mathcal {D}}\), also \({\mathfrak {D}}\) is then flat. For variations in the mass, perturbative agreement can be fulfilled [15, 16], so that (5) indeed holds.
It is natural to give this a geometric interpretation along the lines of Fedosov quantization, as suggested in [5, 6] (see [15] for details). Consider the manifold \({\mathcal {S}}_{\Phi ^4}\) of solutions to the interacting \(\Phi ^4\) field equations. The tangent space at each \({{\bar{\phi }}}\in {\mathcal {S}}_{\Phi ^4}\) is the space of solutions \({{\bar{\varphi }}}\) of the field equations linearized around \({{\bar{\phi }}}\). We patch all algebras \({{\mathbf {W}}}^{\mathrm {int}}_{{{\bar{\phi }}}}\) together to obtain the algebra bundle:
An assignment \({{\bar{\phi }}}\mapsto T^{\mathrm {int}}_{{\bar{\phi }}}(e^{i F[{{\bar{\phi }}}, -]})\) as above is then interpreted as a section of \({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4}\), and \({\mathfrak {D}}_{{{\bar{\varphi }}}}\) as a covariant derivative (connection) on this bundle in the direction of the vector field \({{\bar{\varphi }}}\). If this connection is flat, we call the QFT background independent. Flatness ensures that, at least formally, any interacting observable on one background can be uniquely parallel transported to any other background, providing an answer to the question posed at the beginning of this section. Or, in the spirit of Fedosov quantization: The space of sections of \({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4}\) is much larger than the space of functionals of \(\Phi \), i.e., the space of functions on \({\mathcal {S}}_{\Phi ^4}\). However, when restricting to sections that are flat w.r.t. \({\mathfrak {D}}\), i.e., fulfill (4), one obtains a one-to-one correspondence between functions on \({\mathcal {S}}_{\Phi ^4}\) and flat sections of \({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4}\). Again, flatness of \({\mathfrak {D}}_{{{\bar{\varphi }}}}\) is crucial.
1.2 Gauge Theories
The main aim of the present work is to analyze the issue of background independence for gauge theories where more complications arise due to gauge fixing. Let us for definiteness consider the pure Yang–Mills theory which is the theory of a G-connection \({{\mathcal {A}}}\) on a principal bundle, subject to the Yang–Mills field equations. We split
into a background connection \(\bar{{{\mathcal {A}}}}\) and a dynamical \({\mathfrak {g}}\)-valued 1-form \(A\) (a vector potential) which will be quantized in perturbation theory. \({\bar{{{\mathcal {A}}}}}\) is a solution to the Yang–Mills equation. Similar to the scalar case, the classical Yang–Mills action is independent of this split. However, for the purpose of perturbative quantization, one has to fix the gauge, which necessarily breaks this split independence if one requires a covariant gauge fixing. The gauge-fixed action exhibits a residual fermionic symmetry, the BV-BRST symmetry. It acts by a nilpotent operator s, and the physical (gauge invariant) observables are obtained as the cohomology of s. In fact, the violation of the split independence in the gauge-fixed action is s exact. It follows that, classically, split independence holds at the level of gauge-invariant observables, i.e., there is a flat connection \({\hat{{\mathcal {D}}}}_{{\bar{a}}}\) on classical local functionals that is well defined on s cohomology, i.e., \({\hat{{\mathcal {D}}}}_{{\bar{a}}}\circ s = s \circ {\hat{{\mathcal {D}}}}_{{\bar{a}}}\). Here \({{\bar{a}}}\) is an infinitesimal variation of the background.
To quantize, one constructs, for each background \({\bar{{{\mathcal {A}}}}}\), the (unphysical) algebra \({{\mathbf {W}}}^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}\). The subalgebra \({{\mathbf {F}}}_{{\bar{{{\mathcal {A}}}}}} \subset {{\mathbf {W}}}^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}\) of physical (gauge invariant) observables is given by the cohomology of \([Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}},-]_\star \), where \(Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}\) is the renormalized interacting BRST charge, and the commutator is taken w.r.t. the algebra \(\star \) product. Therefore, for background independence to hold, the desired connection \({\mathfrak {D}}_{{{\bar{a}}}}\) has to be well defined on the BRST cohomology, that is, it must satisfy
on-shell. Furthermore, on the kernel of \([Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, -]_\star \), the curvature of \({\mathfrak {D}}_{{{\bar{a}}}}\) has to vanish modulo an element in the image of \( [Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}},-]_\star \). If this is the case, background-independent observables can be defined as those sections of the observable algebra bundle which are flat w.r.t. \({\mathfrak {D}}_{{{\bar{a}}}}\) modulo \({{\,\mathrm{Im}\,}}[Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}},-]_\star \). We find that there are potential obstructions (anomalies) for the construction of such a connection. However, for pure Yang–Mills theory in \(D=4\) space-time dimensions, these turn out to be trivial. Power-counting renormalizability is a crucial ingredient of our proof. If the relevant anomaly is absent, then an identity analogous to (5) holds in \({{\mathbf {F}}}_{\mathrm {YM}}= \sqcup _{{\bar{{{\mathcal {A}}}}}} {{\mathbf {F}}}_{{\bar{{{\mathcal {A}}}}}}\), namely
where \({\hat{A}}\) incorporates quantum corrections. Hence, a classically gauge-invariant and background-independent local functional does not automatically give rise to a background- independent observable at the quantum level, but quantum corrections may be necessary.
We also sketch the application of our framework to perturbative quantum gravity. As in any diffeomorphism-invariant theory, the definition of local observables is a major issue, and we follow recent proposals [2, 17], based on [18], for the construction of such (relational) observables employing a set of configuration-dependent covariant coordinates. As opposed to the pure Yang–Mills case, our analysis of potential anomalies to background independence shows that for the case of perturbative gravity, one can indeed find infinitely many candidates for such anomalies using the dimensionful coupling of the theory. From this perspective, it seems difficult to prove the absence of anomalies, as they may appear at arbitrarily high order in perturbation theory.Footnote 5
We would like to point out that our work does not yet provide a full Fedosov quantization of Yang–Mills theories. First of all, one should then work on gauge equivalence classes of classical solutions as base space, not on the full space of classical solutions, as we do (but see [19] for a different point of view). Second, the set of solutions to the Yang–Mills equation is a manifold only up to singular points corresponding to solutions with symmetries [20]. We work locally in configuration space, i.e., in a neighborhood of a generic configuration, avoiding these singularities. We should also emphasize that the main focus of our work is algebraic, not (functional) analytic. In particular, we do not discuss the analytical aspects of the infinite-dimensional manifolds of solution spaces, and algebra bundles upon these. We refer to [15] for a thorough discussion.
1.3 Comparison with the Path Integral Approach
Let us compare our treatment of background independence with more formal approaches, in particular the path integral formalism. In the case of the scalar field, one defines the generating functional of connected graphs as
and the corresponding effective action as
with
Assuming that the path integral measure \(D \phi \) is shift invariant, one obtains, with the shift \(\phi \rightarrow \phi - {{\bar{\phi }}}\), that
with \(\Gamma \) the generating functional in the absence of the background field [1]. In particular,
In this sense, background independence holds, provided that shift invariance of the path integral measure is fulfilled. One can thus see perturbative agreement as the rigorous version of the shift invariance of the formal path integral.Footnote 6
Shift invariance of the path integral measure is also a crucial requirement in the treatment of background independence in gauge theory given in [21]. However, as described above, this is not sufficient, as the gauge-fixed action is not split independent. To deal with this, an extended BRST differential is introduced in [21], which also implements a shift between the background and the dynamical vector potential. It is then argued that the corresponding Slavnov identities can be fulfilled. As in our treatment, a crucial ingredient in that proof is power-counting renormalizability, which restricts the number of possible counterterms.
Let us summarize two major conceptual differences between our treatment and the path integral approach:
Typically, renormalization techniques are employed which require that the propagator is translation invariant. This means that the background is in fact treated perturbatively, i.e., it enters only the vertices, not the propagators. This entails that the background field is a vector potential, not a principal bundle connection and also that shift invariance of the path integral measure is trivially fulfilled. But the perturbative expansion with all the background fields in the vertices is ill-defined, unless the background field is treated as an infinitesimal perturbation, so that one may expand in powers of the background field. Hence, only an infinitesimal neighborhood of a fixed flat reference connection is actually treated. In contrast, in our approach, the background connection is treated non-perturbatively.
A formulation of background independence such as (8) does not refer to observables, i.e., it does not address the question posed at the beginning of the introduction. For this, one would need to couple generic observables through source terms to the action and study the background independence of the resulting effective action. To the best of our knowledge, this has not been done in the literature.
1.4 Outline
The article is structured as follows. To set the stage, we review, in the next section, the case of scalar field theory, in particular the construction of the algebras \({{\mathbf {W}}}_{{{\bar{\phi }}}}\). Following [5, 15], the relation of background independence and perturbative agreement is discussed. In the main part of this work, Sect. 3, we study the case of Yang–Mills theories. Perturbative quantum gravity is treated in Sect. 4. An “Appendix” contains technical lemmata. For the convenience of the reader, we provide a glossary of symbols used.
2 Background Independence for Scalar Field Theory
2.1 Perturbative QFT on a Background \({{\bar{\phi }}}\)
In this section, we review the discussion of background independence for a self-interacting scalar field \(\Phi \) [5, 15]. Throughout this work, we consider globally hyperbolic space-times (M, g) with signature \((-, +, \dots +)\) and compact Cauchy surfaces. \(J^\pm ({\mathcal {L}})\) denotes the causal future/past of a space-time region \({\mathcal {L}}\subset M\), cf., for example, [22] for a definition.
Due to the time-slice axiom [23], it is sufficient to define the interacting observables localized in a causally closed, compact space-time region \({\mathcal {R}}\)\(\subset M\) which contains a Cauchy surface. In particular, we may choose \({\mathcal {R}}= J^+(\Sigma _0) \cap J^-(\Sigma _1)\) for two non-intersecting Cauchy surfaces \(\Sigma _{0/1}\). We may thus replace the coupling constant \(\lambda _0\) with a smooth compactly supported cutoff function \(\lambda (x)\) which equals \(\lambda _0\) on a neighborhood of \({\mathcal {R}}\). For the perturbations \(\phi \), we consider the expansion of the action
around a background \({{\bar{\phi }}}\)
Note that the free Lagrangians for different backgrounds \({{\bar{\phi }}}\) coincide outside of the support of \(\lambda \). This is essential for identifying quantum theories around different backgrounds as discussed in the next section. Also note that there is no source term in (9), i.e., a term linear in \(\phi \), since the background configuration is required to fulfill the interacting equation of motion
The solutions to (10) form a manifold \(\mathcal {S}_{\Phi ^4}\), with tangent space \(T_{{\bar{\phi }}}{\mathcal {S}}_{\Phi ^4}\) at \({{\bar{\phi }}}\) given by the solution space to the linearized equation of motion
This means that given a smooth curve \(\{ {{\bar{\phi }}}_s \}_s\) in \({\mathcal {S}}_{\Phi ^4}\), i.e., of solutions to (10), with \({{\bar{\phi }}}_0 = {{\bar{\phi }}}\), its derivative
is a solution to (11). We refer to [15] for details, in particular on the notion of smoothness.
Background independence of the classical scalar field theory now means that it is independent of the arbitrary split (1) into background and dynamical fields. One manifestation of this is the split independence of the action in the sense that
where the interaction part \(S_{\mathrm {int}}\) of the action was defined in (9).
2.2 The Free Algebra \({{\mathbf {W}}}_{{{\bar{\phi }}}}\)
The algebra \({{\mathbf {W}}}_{{{\bar{\phi }}}}\) (also called the free algebra in contrast to the interacting one defined below) consists of evaluation functionals
where the singularities of the symmetric distributions \(f_n\) on \(M^n\) are constrained by a condition on their wave front set, cf. [4]. We define the support of a functional of the form (14) as
Given a Hadamard two-point function\(\omega _{{{\bar{\phi }}}}\) for \(P_{{\bar{\phi }}}\), cf. [4] for a definition, one defines a non-commutative \(\star \) product
where \({\mathfrak {m}}\) is the point-wise multiplication of functionals, \({\mathfrak {m}}( F \otimes G)(\phi ) = F(\phi ) G(\phi )\), and
Here, the functional derivative \(\frac{\delta }{\delta \phi (x)} F\) is interpreted as a \({{\mathbf {W}}}_{{\bar{\phi }}}\) valued density, whose evaluation on test functions \(\varphi \) is defined as
The definition of the \(\star \) product, and thus also that of \({{\mathbf {W}}}_{{\bar{\phi }}}\), depends on the two-point function \(\omega _{{\bar{\phi }}}\). However, it turns out that algebras equipped with \(\star \) products defined by different Hadamard two-point functions \(\omega _{{\bar{\phi }}}\), \(\omega '_{{\bar{\phi }}}\) are isomorphic [4], justifying the notation.Footnote 7 Note that, in particular, (15) implies that
where \(\Delta _{{{\bar{\phi }}}} = \Delta ^{\mathrm {a}}_{{\bar{\phi }}}- \Delta ^{\mathrm {r}}_{{\bar{\phi }}}\) is the causal propagator of \(P_{{\bar{\phi }}}\), with \(\Delta ^{{\mathrm {r}}/{\mathrm {a}}}_{{{\bar{\phi }}}}\) denoting the retarded/advanced propagator.
Elements of \({{\mathbf {W}}}_{{\bar{\phi }}}\) are considered in the sense of formal power series in \(\hbar \), i.e., \({{\mathbf {W}}}_{{\bar{\phi }}}\) is considered as a graded vector space with grading provided by \(\deg _\hbar \), which counts the number of \(\hbar \) factors. A further grading is given by
where \(\deg _\phi \) counts the number of fields. For example, for an F of the form (14), with \(f_n \ne 0\) and \(f_m = 0\) for all \(m \ne n\), one has \(\deg _\phi (F) = n\). It is obvious that the \(\star \) product respects the grading, i.e.,
This grading is in fact the natural grading in the context of Fedosov quantization [7].
Local covariance [4, 11] is a crucial ingredient of our approach.Footnote 8 It is implemented as follows: A morphism\(\psi : (M', g', {{\bar{\phi }}}') \rightarrow (M, g, {{\bar{\phi }}})\) is an isometric embedding \(\psi : M' \rightarrow M\), i.e., \(\psi ^*g =g'\), which preserves the causal structure, and such that \(\psi ^*{{\bar{\phi }}}={{\bar{\phi }}}'\). For each morphism \(\psi \), there exists an algebra homomorphism
defined by
To implement the equations of motion, one passes to the on-shell algebra. This proceeds by quotienting out the ideal
of functionals F that vanish on all solutions \(\phi \) of the linearized equations of motion \(P_{{\bar{\phi }}}\phi = 0\).
The subspace \({{\mathbf {W}}}^{\mathrm {loc}}_{{\bar{\phi }}}\)\(\subset {{\mathbf {W}}}_{{\bar{\phi }}}\) of local functionals consists of those F of the form (14) for which each \(f_n\) is supported on the total diagonal of \(M^n\). It is generated by smearing fields\({{\mathcal {O}}}(x)\) with appropriate test tensors. Fields depend locally and covariantly on \(g, {{\bar{\phi }}}, \phi \), or, abstractly,
for a morphism \(\psi \). They are of the form
where P is a polynomial, \(\alpha \) stands for multi-indices and \(R_{\mu \nu \rho \sigma }\) is the Riemannian curvature of g. It is sometimes useful to express a local functional in terms of its integral kernel.
2.3 Time-Ordered Products
To obtain the interacting renormalized quantum fields, one needs to define renormalized time-ordered products (or renormalization schemes) on the algebra \({{\mathbf {W}}}_{{{\bar{\phi }}}}\). These are a collection of symmetric multi-linear maps
which are subject to the axioms (or renormalization conditions) of [4, 24], cf. also the reviews [25,26,27]. In particular, they fulfill:
Grading Time-ordered products respect the \({{\,\mathrm{Deg}\,}}\) grading, i.e.,
$$\begin{aligned} {{\,\mathrm{Deg}\,}}(T_{{{\bar{\phi }}}, n}(F_1 \otimes \dots \otimes F_n)) = \sum _i {{\,\mathrm{Deg}\,}}(F_i). \end{aligned}$$Locality and covariance Let \(\psi : (M', g', {{\bar{\phi }}}') \rightarrow (M, g, {{\bar{\phi }}})\) be a morphism, and \(\alpha _\psi \) as in (16). Then,
$$\begin{aligned} \alpha _\psi \circ T_{{{\bar{\phi }}}', n} = T_{{{\bar{\phi }}}, n} \circ {\alpha _\psi }^{\otimes n}. \end{aligned}$$(19)Scaling Each \(T_{{{\bar{\phi }}}, n}\) scales almost homogeneously, cf. [4], under
$$\begin{aligned} (g_{ab}, \lambda , m, {{\bar{\phi }}}, \phi ) \mapsto (\mu ^{-2} g_{ab}, \lambda ,\mu m, \mu {{\bar{\phi }}}, \mu \phi ). \end{aligned}$$(20)Causal factorization For \(\cup _{m=1}^i {{\,\mathrm{supp}\,}}F_m \cap J^{-}( \cup _{l=i+1}^n {{\,\mathrm{supp}\,}}F_l) = \emptyset \), it holds
$$\begin{aligned} T_{{{\bar{\phi }}}, n}( F_1 \otimes \dots \otimes F_n) = T_{{{\bar{\phi }}}, i}( F_1 \otimes \dots \otimes F_i) \star T_{{{\bar{\phi }}}, n-i}( F_{i+1} \otimes \dots \otimes F_n). \end{aligned}$$(21)Field independence Each \(T_{{{\bar{\phi }}}, n}\) is independent of the dynamical field \(\phi \), in the sense that
$$\begin{aligned} \tfrac{\delta }{\delta \phi (x)}T_{{{\bar{\phi }}}, n}( F_1 \otimes \dots \otimes F_n) = \sum _{i=1}^n T_{{{\bar{\phi }}}, n}( F_1\otimes \dots \otimes \tfrac{\delta }{\delta \phi (x)} F_i \otimes \dots \otimes F_n). \end{aligned}$$(22)Single field factor A time-ordered product with a single field factor simplifies as
$$\begin{aligned}&T_{{{\bar{\phi }}}, n+1}( \phi (x) \otimes F_1 \otimes \dots \otimes F_n) = \phi (x) \star T_{{{\bar{\phi }}}, n}(F_1 \otimes \dots \otimes F_n) \nonumber \\&\quad +\, i\hbar \sum _{j = 1}^n \int \Delta _{{\bar{\phi }}}^{\mathrm {a}}(x,y) T_{{{\bar{\phi }}}, n}(F_1 \otimes \dots \tfrac{\delta }{\delta \phi (y)} F_j \otimes \dots \otimes F_n). \end{aligned}$$(23)Support Time-ordered products do not increase the support, i.e.,
$$\begin{aligned} {{\,\mathrm{supp}\,}}T_{{{\bar{\phi }}}, n}(F_1 \otimes \dots \otimes F_n) \subset \cup _{i} {{\,\mathrm{supp}\,}}F_i. \end{aligned}$$(24)
For fields, it is more convenient to use the mass dimension instead of the scaling dimension, defined by the power of \(\mu \) in the scaling law (20). It is defined as the scaling dimension plus the number of lower indices minus the number of upper indices. It has the advantage that it does not depend on the position of the indices.
As shown in [24, 28], time-ordered products exist and are unique up to a well-characterized, local and covariant renormalization ambiguity which is described by the main theorem of renormalization theory. These ambiguities are best expressed in terms of the generating functional for time-ordered products given by

where we have introduced the notation

In passing, we note that for F a proper interaction, i.e., \(\deg _\phi (F) \ge 3\), the expression is well defined w.r.t. the \({{\,\mathrm{Deg}\,}}\) grading, i.e., at any given grade only a finite number of terms contribute.
Now, let \(T_{{{\bar{\phi }}}}\) and \(T'_{{{\bar{\phi }}}}\) be two different time-ordered products (renormalization schemes) which satisfy the above axioms. The main theorem of renormalization theory then states that they are related via

with \(D(e_\otimes ^{F}) = \sum _{n \ge 1} \frac{1}{n!} D_n(F^{\otimes n})\), where
correspond to finite local counter terms, characterizing the renormalization ambiguity. They are of order \(O(\hbar )\), decrease the total \({{\,\mathrm{Deg}\,}}\) by \(2 (n-1)\), are supported on the total diagonal, i.e., they vanish unless the supports of all arguments overlap, and are locally covariant and field independent, i.e., fulfill (19) and (22) with \(T_n\) replaced by \(D_n\). Furthermore, they scale homogeneously under (20) and vanish if one of their arguments is a linear field.
The time-ordered products \(T_{{{\bar{\phi }}}, 1}({{\mathcal {O}}})\) are usually called Wick powers and are constructed by point splitting w.r.t. the Hadamard parametrixh, cf. [4, 29], which is constructed covariantly from the local geometric data and captures the singularities of Hadamard two-point functions \(\omega \), i.e., \(\omega - h\) is smooth. Concretely, one defines
where
and the subscript \(\omega \) on the l.h.s. denotes the two-point function w.r.t. which the \(\star \) product is defined. Time-ordered products \(T_{{{\bar{\phi }}}, n}\) for \(n > 1\) can be constructed recursively using in particular the causal factorization to define the distributions up to the diagonal in \(M^n\) and extending them to the diagonal as first proposed by Epstein and Glaser [30] (for details, see [4, 24, 28]).
2.4 The Interacting Algebra \({{\mathbf {W}}}_{{\bar{\phi }}}^{\mathrm {int}}\)
Interacting observables are represented in \({{\mathbf {W}}}_{{\bar{\phi }}}\) via retarded products, defined by Bogoliubov’s formula

By causal factorization (21), retarded products are trivial if the support of second argument does not intersect the past of the support of the first, i.e.,

The generating functional of interacting time-ordered products is then given by

Given a field \({{\mathcal {O}}}\), one thus defines the corresponding interacting field as
As for time-ordered products, interacting time-ordered products fulfill causal factorization, i.e.,

The interacting algebra\({{\mathbf {W}}}_{{\bar{\phi }}}^{\mathrm {int}}\) is the subalgebra of \({{\mathbf {W}}}_{{\bar{\phi }}}\) generated by the interacting time-ordered products for \({{\,\mathrm{supp}\,}}F \subset {\mathcal {R}}\). The subalgebras \({{\mathbf {W}}}^{\mathrm {int}}_{{\bar{\phi }}}({\mathcal {L}})\) of observables measurable in compact, causally closed space-time regions \({\mathcal {L}}\subset {\mathcal {R}}\) are generated by  with \({{\,\mathrm{supp}\,}}F \subset {\mathcal {L}}\). By (29), the algebras corresponding to causally disjoint space-time regions commute.
with \({{\,\mathrm{supp}\,}}F \subset {\mathcal {L}}\). By (29), the algebras corresponding to causally disjoint space-time regions commute.
Finally, we also introduce interacting retarded products by

We note that (the equality holds both for usual and interacting time-ordered/retarded products)

and that, as a consequence of (22), field independence of interacting time-ordered products holds in the sense that

2.5 Background Independence of Renormalized Scalar Field Theory
As discussed in the introduction, the naive derivative \({\bar{\delta }}_{{{\bar{\varphi }}}} \mathrel {:=}\langle \tfrac{\delta }{\delta {{\bar{\phi }}}} - , {{\bar{\varphi }}} \rangle \) in (2) w.r.t. the background field is not properly defined on the algebra bundle \({{\mathbf {W}}}_{\Phi ^4} = \sqcup _{{{\bar{\phi }}}}{{\mathbf {W}}}_{{{\bar{\phi }}}}\rightarrow {\mathcal {S}}_{\Phi ^4}\). The natural replacement is the retarded variation \(\delta ^{\mathrm {r}}_{{{\bar{\varphi }}}}\) defined as follows. Given two backgrounds \({{\bar{\phi }}}\) and \({{\bar{\phi }}}'\), one defines the retarded Møller operator [14], cf. also [4] for an on-shell version, as an algebra isomorphism [4, 31]
by its action on functionals as
Here, \(r_{{{\bar{\phi }}}', {{\bar{\phi }}}}\) is the retarded wave operator
mapping solutions of \(P_{{{\bar{\phi }}}} \phi = 0\) to solutions of \(P_{{{\bar{\phi }}}'} \phi = 0\) which coincide outside of \(J^+({{\,\mathrm{supp}\,}}({{\bar{\phi }}}-{{\bar{\phi }}}'))\).Footnote 9 In (32), the subscript \(\omega \) denotes a two-point function w.r.t. which the \(\star \) product on \({{\mathbf {W}}}_{{{\bar{\phi }}}}\) is defined, and \(\omega _{{{\bar{\phi }}}'}\) is obtained by acting with \(r_{{{\bar{\phi }}}', {{\bar{\phi }}}}\) on both variables of \(\omega _{{\bar{\phi }}}\). Given an infinitesimal background variation \({{\bar{\varphi }}}\), as in (12), and a family \(\{ F_s \}_{s \in {\mathbb {R}}}\) of functionals, \(F_s \in {{\mathbf {W}}}_{{{\bar{\phi }}}_s}\),Footnote 10 one defines the retarded variation
A key identity on which our discussion of background independence is based is the so-called perturbative agreement formulated in [13]. It is derived from the requirement that it should not matter whether one includes terms quadratic in the fields into the free or the interacting part of the action. The comparison between the two theories thus defined is performed by the retarded Møller operator or, infinitesimally, by the retarded variation. This implies a further renormalization condition, supplementing those mentioned in the previous section:
Background variation For an infinitesimal variation \({{\bar{\varphi }}}\) of the background \({{\bar{\phi }}}\), we have

As shown in [15, 16], this condition can indeed be implemented. In the following, we thus assume that (35) holds. In particular, we then have the following version of perturbative agreement on interacting time-ordered products.
Lemma 2.1
On interacting time-ordered products, perturbative agreement implies

Proof
We compute

The claim then follows from

which is a consequence of (30). \(\square \)
Corresponding to the subalgebras \({{\mathbf {W}}}^{\mathrm {int}}_{{\bar{\phi }}}({\mathcal {L}})\) for observables localized in the space-time region \({\mathcal {L}}\), we may introduce the subbundles \({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4}({\mathcal {L}})\). The space of sections \(\Gamma ({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4})\) of the algebra bundle \({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4}\) is an algebra in itself, with the product being fiber-wise given by \(\star \). With a slight abuse of notation, we denote the resulting product again by \(\star \). One may define the subalgebra \(\Gamma ^\infty ({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4})\) of smooth sections, cf. [15] for details. For our purposes, it is sufficient to think of it as generated by sections (3) for local functionals F with a smooth dependence on the background \({{\bar{\phi }}}\). Analogously to the usual definition of connections on vector bundles, we give a tentative definition of a connection on the interacting algebra bundle, with a supplementary space-time localization condition, which seems natural in a quantum field theoretical context.
Definition 2.2
A connection\({\mathfrak {D}}\) on \({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4}\) is a map
which is \(C^\infty ({\mathcal {S}}_{\Phi ^4})\) linear in the first and additive in the second argument, reduces to the ordinary derivative on c-number functionals, i.e.,
is a derivation, i.e., fulfilling
and respects space-time localization, in the sense that
By (36), due to the second term on the r.h.s., the background variation \(\delta ^{\mathrm {r}}_{{{\bar{\varphi }}}}\) violates the locality requirement (38).Footnote 11 But, as seen in the following proposition, subtracting the derivative w.r.t. \(\phi \) yields a connection. The following propositions, first proven in [5], cf. [15] for details, summarize background independence for scalar fields.
Proposition 2.3
The operator
defines a connection on \({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4}\), acting as

where \(\delta _{{{\bar{\varphi }}}}\) and \({\mathcal {D}}_{{{\bar{\varphi }}}}\) are defined in (2).
Proof
That \({\mathfrak {D}}_{{{\bar{\varphi }}}}\) is a derivation is a consequence of the retarded Møller operator being an algebra isomorphism and of \(\delta _{{{\bar{\varphi }}}}\) being a derivation. The localization requirement (38) is a consequence of (40). To prove the latter, we note that by (36) and (31), we have

The claim then follows from (13). \(\square \)
Proposition 2.4
The connection \({\mathfrak {D}}_{{{\bar{\varphi }}}} \), defined in (39), is flat.
Proof
It is straightforward to check that \({\mathcal {D}}_{{{\bar{\varphi }}}}\) satisfies
where
is the Lie bracket of vector fields \({{\bar{\varphi }}}\) and \({{\bar{\varphi }}}'\) on \({\mathcal {S}}_{\Phi ^4}\). Therefore, using (40), the curvature of \({\mathfrak {D}}_{{{\bar{\varphi }}}}\) vanishes:

\(\square \)
Hence, defining the background-independent observables as sections which are covariantly constant w.r.t. \({\mathfrak {D}}_{{{\bar{\varphi }}}}\), (40) implies that background-independent interacting fields \({{\mathcal {O}}}^{\mathrm {int}}_{{\bar{\phi }}}\) correspond to classically split independent fields \({{\mathcal {O}}}\), i.e., fulfilling \({\mathcal {D}}_{{{\bar{\varphi }}}} {{\mathcal {O}}}=0\). This means that there is a one-to-one correspondence between classical and quantum background-independent fields.
3 Pure Yang–Mills Theory
This main part of the article is structured as follows: We begin by setting up Yang–Mills theory on the classical level, culminating in the identification of \({\hat{{\mathcal {D}}}}_{{\bar{a}}}\) as the relevant connection on classical local functionals. In Sect. 3.2, we discuss, following [25, 32], quantization, in particular the occurrence of anomalies. As a crucial ingredient for background independence, we prove a theorem on the background dependence of the anomaly, assuming that perturbative agreement holds. In Sect. 3.3, we then prove our main result on background independence in Yang–Mills theories.
3.1 Classical Gauge Theory
3.1.1 The Basic Setting
Let \(P \rightarrow M\) be a G principal fiber bundle over space-time M, with G a semi-simple Lie group. We denote by \({{\,\mathrm{Ad}\,}}\) the adjoint action of a Lie group G on itself, \({{\,\mathrm{Ad}\,}}_g h \mathrel {:=}g h g^{-1}\), and the adjoint action on the corresponding Lie algebra \({\mathfrak {g}}\) by \({{\,\mathrm{ad}\,}}\). The Lie bracket on \({\mathfrak {g}}\) is denoted by \([-,-]_{\mathfrak {g}}\).
The Yang–Mills theory is the dynamical theory of a G connection \({{\mathcal {A}}}\) on P whose dynamics is governed by the Yang–Mills action
where F is the curvature of \({{\mathcal {A}}}\), interpreted as a section of \({\mathfrak {p}}\otimes \Omega ^2\), with \({\mathfrak {p}}\)\(\mathrel {:=}P \times _{{{\,\mathrm{ad}\,}}} {\mathfrak {g}}\) and \(\Omega ^k\) the bundle of k forms on M. Let \(\{T_I\}_I\) be a basis of \({\mathfrak {g}}\), normalized as \({{\,\mathrm{Tr}\,}}(T_I T_J) = - \frac{1}{2} \delta _{IJ}\). Then, we can write \(F = \frac{1}{2} F^I_{\mu \nu } T_I \mathrm {d}x^\mu \wedge \mathrm {d}x^\nu \).
Classical solutions will play the role of background configurations, and these will be typically denoted by a bar, i.e., we will consider connections \({\bar{{{\mathcal {A}}}}}\) which are solutions to the Yang–Mills equation
where \(\bar{F}\) is the curvature of \(\bar{{{\mathcal {A}}}}\) and \(\bar{\nabla }_\mu \) is the associated covariant derivative on sections of \({\mathfrak {p}}\otimes \Omega ^k\). The Yang–Mills equation is well-posed [33], guaranteeing the existence of global solutions. Furthermore, the set \(\mathcal {S}_{\mathrm {YM}}\) of such solutions is a manifold, i.e., its tangent space \(T_{{\bar{{{\mathcal {A}}}}}} {\mathcal {S}}_{{\mathrm {YM}}}\) at a solution \({\bar{{{\mathcal {A}}}}}\) is the space of solutions \({{\bar{a}}}\) to the Yang–Mills equation linearized around \({\bar{{{\mathcal {A}}}}}\),
except at certain symmetric background configurations \({\bar{{{\mathcal {A}}}}}\), cf. [20]. At these symmetric background configurations, there are solutions to (43) that are not tangent to \({\mathcal {S}}_{{\mathrm {YM}}}\), i.e., do not arise as the derivative of a curve in \({\mathcal {S}}_{{\mathrm {YM}}}\). The presence of such singular points in configuration space \({\mathcal {S}}_{{\mathrm {YM}}}\) does not impart our considerations, as these are local in \({\mathcal {S}}_{{\mathrm {YM}}}\), so that we can restrict to regions not containing such exceptional points. Thus, we will henceforth identify the space of solutions to (43) with the tangent space \(T_{{\bar{{{\mathcal {A}}}}}} {\mathcal {S}}_{\mathrm {YM}}\) of \({\mathcal {S}}_{\mathrm {YM}}\) at \({\bar{{{\mathcal {A}}}}}\).
3.2 Background and Dynamical Gauge Transformations
We consider the decomposition (6) of \({{\mathcal {A}}}\) into a background connection\(\bar{{{\mathcal {A}}}}\) and a dynamical\({\mathfrak {g}}\)-valued one-form A, i.e., a section of \({\mathfrak {p}}\otimes \Omega ^1\). In local coordinates, the corresponding covariant derivative operator D when acting on sections of \({\mathfrak {p}}\otimes \Omega ^k\) takes the form
Then, the curvature two-form F in local coordinates is given by
Gauge transformations are parametrized by smooth sections g of \(P \times _{{{\,\mathrm{Ad}\,}}} G\). On a connection \({{\mathcal {A}}}\), they act as
with \(\theta \) the Maurer–Cartan form. For \({{\mathcal {A}}}\) split as in (6), there are then two natural implementations of this gauge transformation. A background gauge transformation acts as
The covariance of the quantum theory under such a transformation will be part of the requirement of local (gauge) covariance. On the other hand, one may keep the background fixed and implement the change \({{\mathcal {A}}}\mapsto {{\mathcal {A}}}^g\) by solely changing A, i.e.,
This is called a dynamical gauge transformation which needs to be gauge fixed.
3.3 Localization of the Interaction and Split Independence
As for the scalar field, we need to localize the interaction in a compact space-time region. For the scalar field, we used a smooth compactly supported cutoff function \(\lambda (x)\) which was equal to \(\lambda _0\) in the space-time region \({\mathcal {R}}\) for which the algebra of interacting observables was constructed. This cutoff had the additional consequence that, for any two background solutions \({{\bar{\phi }}}\), \({{\bar{\phi }}}'\), the corresponding linearized wave operators \(P_{{\bar{\phi }}}\), \(P_{{{\bar{\phi }}}'}\), cf. (11), coincided outside of a compact space-time region (the support of \(\lambda \)). This made it possible to define the flat connection \({\mathfrak {D}}_{{{\bar{\varphi }}}}\), using the retarded variation \(\delta ^{\mathrm {r}}\).
Also for Yang–Mills theory, we use a smooth cutoff function \(\lambda (x)\) to localize the interaction (see below). This cutoff, however, does not affect the linearized wave operator \(P^{\mathrm {lin}}_{{\bar{{{\mathcal {A}}}}}}\), defined in (43).Footnote 12 Hence, the operators \(P^{\mathrm {lin}}_{{\bar{{{\mathcal {A}}}}}}\) in general do not coincide outside of a compact space-time region, which, however, is a prerequisite for the use of the retarded variation. Hence, we relax the condition that \({\bar{{{\mathcal {A}}}}}\) is on-shell, i.e., a solution to (42), on the whole space-time. We proceed as follows: We choose a neighborhood \({\mathcal {U}}\) of \({\mathcal {R}}\) on which we require the backgrounds \({\bar{{{\mathcal {A}}}}}\) to be on-shell, i.e.,
Furthermore, we require all backgrounds \({\bar{{{\mathcal {A}}}}}\) to coincide outside of a larger region \({\mathcal {V}}\supset {\mathcal {U}}\) with an arbitrary reference connection \({{\mathcal {A}}}_0\). Consequently, the variations \({{\bar{a}}}\) of the background are supported in \({\mathcal {V}}\) and fulfill the linearized Yang–Mills equation (43) in \({\mathcal {U}}\). In this way, one ensures that the retarded variation \(\delta ^{\mathrm {r}}_{{\bar{a}}}\) is well defined.
Furthermore, one localizes the interaction by introducing a cutoff function \(\lambda \), which is supposed to be supported in \({\mathcal {U}}\) and equal to 1 on a neighborhood of \({\mathcal {R}}\). The action is, then, defined as
where summation over repeated indices I is understood. In \({\mathcal {R}}\), where \(\lambda =1\) and the background \(\bar{{{\mathcal {A}}}}\) is on-shell, this is the Yang–Mills action (41) expanded around \(\bar{{{\mathcal {A}}}}\), with the constant term \(-\frac{1}{4} \int \bar{F}^I_{\mu \nu } {\bar{F}}^{I \mu \nu } \mathrm {vol}\) omitted. Note that the full Yang–Mills action (41) would have a source term, i.e., a term linear in A, which however vanishes in \({\mathcal {R}}\), as \({\bar{{{\mathcal {A}}}}}\) is on-shell there. The setup of our localization prescription is summarized in Fig. 1.
Since \(\bar{\nabla }\), \(\bar{F}\) and A transform covariantly under background gauge transformations, the action (46) is invariant under background gauge transformations. Analogously to (13), the action is split independent in the sense that
Here, \(S_{{\mathrm {YM}}, {\mathrm {int}}}\) is the part of \(S_{\mathrm {YM}}\) which is of degree higher than 2 in A. The restriction to \(x \in {\mathcal {R}}\) is due to the infrared cutoff \(\lambda \) of the interaction.
3.3.1 BV-BRST Formalism and Background Covariant Gauge Fixing
In this section, we outline the straightforward generalization of the BV-BRST formalism [25, 34,35,36], to the case with non-trivial backgrounds.
In order to perform gauge fixing in the BV-BRST formalism, we need to augment the field variables with a set of ghosts and anti-fields, some of which are fermions, i.e., have an odd Grassmann parity.Footnote 13 The resulting gauge-fixed theory enjoys the BV-BRST symmetry s as follows. Let us denote the set of all dynamical fields by \(\Phi =(A_\mu ^I, B^I, C^I, \bar{C}^I)\), where C (\({\bar{C}}\)) are called (anti-) ghosts and B is a Lagrange multiplier. One assigns mass dimensions \(d_\Phi =(1, 2, 0, 2)\) and a ghost number\(g_\Phi =(0, 0, 1, -1)\) to the fields. The latter defines the Grassmann parity. The BV-BRST operator \(s\), which increases the ghost number by 1, acts by
One also introduces anti-fields\(\Phi ^\ddag = (A^{\ddag I \mu }, B^{\ddag I} , C^{\ddag I}, \bar{C}^{\ddag I})\), with mass dimensions \(d_{\Phi ^\ddag } = (3, 2, 4, 2)\) and ghost numbers \(g_{\Phi ^\ddag } = (-1, -1, -2, 0)\). They are interpreted as densities and act as classical, non-dynamical sources of BRST transformations of the fields, appearing in the action via
To perform the gauge fixing, we add a manifestly BV-BRST-invariant term \(s \Psi \) to the action, where \(\Psi \) is a gauge-fixing fermion with ghost number \(-1\) which does not contain anti-fields and we choose here to be
This is the so-called background covariant gauge fixing. It breaks dynamical gauge invariance, while keeping the background gauge invariance. In this respect, (48) is a useful gauge in practical calculations and is commonly employed in the background field formalism [1, 21, 38,39,40,41].
The BV-BRST transformations of all fields and anti-fields can now be written as
where S is the extended and gauge-fixed action
and where \((-, -)\) is the so-called anti-bracket defined by
cf. [37] for a definition of left and right derivatives w.r.t. fields with Grassmann parity. In the following, field derivatives will be left derivatives, unless states otherwise. The anti-bracket satisfies the graded Jacobi identity
and has the following graded symmetry
We remark that only on functionals supported in \({\mathcal {R}}\), where \(\bar{{{\mathcal {A}}}}\) is on-shell and \(\lambda = 1\), the operator s coincides with the standard nilpotent BV-BRST differential and the gauge-fixed action fulfills the classical master equation:
which expresses the BRST invariance of S.
As usual, we split the action into a free and an interaction part:
where the free action \(S_0\) is quadratic in \(\Phi \) and \(\Phi ^\ddag \), and the compactly supported interaction \({S_{\mathrm {int}}}\) contains the terms of degree higher than 2 in \(\Phi \) and \(\Phi ^\ddag \). This, in turn, leads to the decomposition
of the BV-BRST differential. The action of \(s_{0}\) on all fields and anti-fields is given in Table 1. Note that the requirement of the background connection being on-shell is necessary for the nilpotency of \(s_0\). For instance, one can check by direct calculation that \({s}^2_0 A^{\ddag I}_\mu = [\bar{\nabla }^\nu \bar{F}_{\mu \nu }, C]_{\mathfrak {g}}^I\), which vanishes only if \(\bar{\nabla }^\nu \bar{F}_{\mu \nu }=0\). Hence, \(s_0\) is only nilpotent when restricted to functionals localized in \({\mathcal {U}}\), motivating our condition that \({{\,\mathrm{supp}\,}}\lambda \subset {\mathcal {U}}\).
The gauge-fixed action S is invariant under background gauge transformations since all the dynamical fields and anti-fields transform in the adjoint. However, it is no longer split independent, not even in \({\mathcal {R}}\), since \(\Psi \) destroys split independence as \({\bar{{{\mathcal {A}}}}}\) and A no longer appear in \(\Psi \) in the form \({\bar{{{\mathcal {A}}}}} + A\).
Proposition 3.1
The gauge-fixed action (50) satisfies
Proof
For \(x \in {\mathcal {R}}\), we calculate
where we have used that (47) also holds with \(S_{\mathrm {YM}}\) replaced by \(S_{\mathrm {sc}}\) and that \(\frac{\delta }{\delta A} \Psi \) is proportional to \({\bar{C}}\), on which \(s_{\mathrm {int}}\) vanishes. \(\square \)
It is advantageous to also compute the action of \({\mathcal {D}}_{{{\bar{a}}}}\) on S, the former being defined, analogously to (2), by
Corollary 3.2
In \({\mathcal {R}}\), i.e., when restricted to configurations supported in \({\mathcal {R}}\), we have
Proof
Using (52), we compute
The second term on the r.h.s. vanishes due to \({{\bar{a}}}\) being, in \({\mathcal {R}}\), a solution to the linearized equation of motion. The result then follows from \(\delta _{{{\bar{a}}}} s_0 \Psi = s \delta _{{{\bar{a}}}} \Psi \), which holds for any \(\Psi \) which is quadratic in fields and does not contain anti-fields. \(\square \)
3.4 Local Gauge Covariance
Our background data now consist of \((P \rightarrow M, g, \bar{{{\mathcal {A}}}})\), i.e., a principal fiber bundle \(P \rightarrow M\) with a fixed structure group G, the metric g and a background connection \(\bar{{{\mathcal {A}}}}\) on P. To make the notion of local covariance precise, we define, following [12], morphisms \(\chi : (P' \rightarrow M', g', {\bar{{{\mathcal {A}}}}}') \rightarrow (P \rightarrow M, g, {\bar{{{\mathcal {A}}}}})\) as G equivariant smooth maps \(\chi : P' \rightarrow P\), which cover a causality preserving isometric embedding \(\psi : M' \rightarrow M\), i.e., a morphism in the sense of the previous section, such that \(\chi ^* \bar{{{\mathcal {A}}}} =\bar{{{\mathcal {A}}}}'\). This covers the case of background gauge transformations where \(\chi _g : P \rightarrow P\) is the natural action of a section g of \(P \times _{{{\,\mathrm{Ad}\,}}} G\) on P. Locally covariant fields should then satisfy
By the Thomas replacement theorem [25, 42], such a field takes the form
where P is a polynomial, \(\alpha \) stands for multi-indices, \(R_{\mu \nu \rho \sigma }\) is the Riemannian curvature of g, and \(\bar{F}_{\mu \nu }\) is the curvature of \(\bar{{{\mathcal {A}}}}\).
3.5 Classical BV-BRST Cohomology
For the case of pure Yang–Mills theory, for semi-simple G, the cohomology ring H(s) is generated by elements of the form
where \(\alpha \) stands for multi-indices, \(p_r\) and \(\Theta _s\) are invariant polynomials of \({\mathfrak {g}}\), and \(r_t\) is a local functional of the metric g, the background field strength \(\bar{F}\), the Riemann tensor R and their derivatives. F is the full field strength, cf. (44). This result for the case of trivial backgrounds, i.e., with \(\bar{F}=0\), is proven in [25, 43]. The above expression is then obtained by the requirement of local covariance (54) in the presence of a non-trivial background connection. As there is no invariant polynomial of degree 1 on a semi-simple Lie algebra, the cohomology at ghost number 1, \(H_1(s)\), is trivial.
Now restricting to sections of vector bundles associated with P via the trivial representation of G, that is, those \({{\mathcal {O}}}\) without a Lie algebra index, the cohomology ring \(H(s| \mathrm {d})\) is generated by linear combination of elements of the form (55) and elements of the form
where
are the Chern–Simons forms in the presence of a background connection [44]. In this expression, \({\bar{\mathrm {d}}}\) denotes the covariant differential, induced on sections of \({\mathfrak {p}}\otimes \Omega \) by the Leibniz rule and \({\bar{\mathrm {d}}} b = {\bar{\nabla }}_\mu b \mathrm {d}x^\mu \) for b a section of \({\mathfrak {p}}\), and m(r) are the degrees of the independent Casimir elements of G. The trace is in some representation of \({\mathfrak {g}}\). Furthermore, \(f_s\) are strictly gauge-invariant monomials of F, and \(r_t\) are closed forms. Again, the result (56) is a generalization of the well-known results in [25, 43] to the case with non-trivial background connection.
Elements of the cohomology class \(H_0(s)\) at ghost number 0 are in one-to-one correspondence with the gauge-invariant observables of the original Yang–Mills theory, while those in the class \(H_1^4(s | \mathrm {d})\) of four forms at ghost number 1 turn out to contain the gauge anomalies of the Yang–Mills theory, see, e.g., [25].
3.6 The BRST Charge
Classically, the action of the BRST differential on fields is also generated by the Noether charge of the BRST symmetry via the graded Peierls bracket [45, 46] \(\{ -, -\}_{{\bar{{{\mathcal {A}}}}}}\), i.e.,
The charge Q is constructed as follows [25]: One chooses a one-form \(\gamma _\mu \), supported in \({\mathcal {R}}\), such that
for a Cauchy surface \(\Sigma \) contained in \({\mathcal {R}}\) and any closed three-form \(\alpha \). One then sets
where J is the Noether current of the BRST symmetry, which is a 3- form with ghost number 1, and is conserved on-shell in \({\mathcal {R}}\).
3.6.1 Background-Independent Local Functionals
In the case of scalar field theory, we defined the background- independent classical local functionals as those in the kernel of \( {\mathcal {D}}_{{{\bar{\varphi }}}} \), cf. (2). However, as discussed above, the gauge-invariant observables are defined to be equivalence classes of the BV-BRST cohomology. Therefore, the suitable operator whose kernel defines the background-independent classical local functionals must be well defined on BV-BRST cohomology (i.e., it must commute with s). However, in view of (53), this is not the case for \({\mathcal {D}}_{{{\bar{a}}}}\). We, therefore, define the following modified operator
which turns out to have the desired properties, as stated in the following theorem.
Theorem 3.3
The operator \(\hat{{\mathcal {D}}}_{{{\bar{a}}}}\) defined in (58) satisfies, for \(F_i\) with arbitrary support and F supported in \({\mathcal {R}}\),
Proof
To prove (59), we calculate
where we have used the identity
and the Jacobi identity (51) for the anti-bracket. To prove (60), we compute
where we have used (59) and (53). To prove (61), we calculate
Therefore, we find
where we have used
and the Jacobi identity (51). However, since \(\Psi \) does not contain anti-fields, \( ({\mathcal {D}}_{{{\bar{a}}}'} \Psi , {\mathcal {D}}_{{{\bar{a}}}} \Psi )=0\) and thus the curvature of \(\hat{{\mathcal {D}}}_{{{\bar{a}}}}\) vanishes. \(\square \)
Remark 3.4
The “correction term” \((-, {\mathcal {D}}_{{{\bar{a}}}} \Psi )\) in (58) can also be motivated as follows. Before introducing the gauge-fixing \(\Psi \) in the action (50), the BV-BRST differential is given by \((S_{{\mathrm {YM}}} + S_{{\mathrm {sc}}}, -)\) which is related to the gauge-fixed differential s by
where
is a “canonical transformation” generated by \(\Psi \) (in the cases of interest here, Yang–Mills theory and gravity, the series truncates, as \(\Psi \) does not contain anti-fields). Consequently, the cohomologies of \( (S_{{\mathrm {YM}}} + S_{{\mathrm {sc}}}, -) \) and s turn out to be isomorphic under the map \(F \mapsto e^{(-, \Psi )} F\). In the non-gauge-fixed theory, \({\mathcal {D}}_{{{\bar{a}}}}\) is the correct derivative operator, in the sense that it commutes with \((S_{{\mathrm {YM}}} + S_{{\mathrm {sc}}}, -)\). The operator \(\hat{{\mathcal {D}}}_{{{\bar{a}}}}\) is then obtained by the same canonical transformation, applied to \({\mathcal {D}}_{{{\bar{a}}}}\):
Thus, in view of (62), the correction term can be seen to naturally arise as a consequence of gauge fixing.
Remark 3.5
In view of (61), one may, similarly to Fedosov’s approach, add the tangent vector fields \({{\bar{a}}}\) to \({\mathcal {S}}_{\mathrm {YM}}\) as a new non-dynamical fermionic field and define a differential \({\hat{\delta }} = \langle \hat{{\mathcal {D}}} - , {{\bar{a}}} \rangle \) on \({{\bar{a}}}\) independent functionals and extend it naturally to \({{\bar{a}}}\) dependent ones. By (60), \({\hat{\delta }}\) and s then anticommute, so that one may define a new differential \({\hat{s}} = s + {\hat{\delta }}\), whose cohomology at grade 0 gives the gauge- invariant, background-independent, on-shell local functionals. Such an approach was pursued by several authors in the literature, cf. [21, 47,48,49,50] for example. We do not proceed in this way here, basically because in the quantized theory, the flatness of the analog of \(\hat{{\mathcal {D}}}\) will only hold on cohomology, see below.
3.7 Perturbative Quantum Yang–Mills Theory on a Background \(\bar{{{\mathcal {A}}}}\)
In this section, we outline the perturbative quantization of the gauge-fixed Yang–Mills theory, described in the previous section, i.e., we adapt [25] to the case of non-trivial background gauge fields.
The construction of the free algebra \({{\mathbf {W}}}_{\bar{{\mathcal {A}}}}\) is similar to the scalar case, discussed in Sect. 2.1, now with the differential operator
acting on \((A_\nu , B, C, {\bar{C}})\). Here, \({\bar{P}}^{\mathrm {lin}}\) was defined in (43). The corresponding Hadamard two-point function is of the form
where one assumes the vector and scalar two-point functions \(\omega _{\mathrm {v}}\), \(\omega _{\mathrm {s}}\) to be related by
in \({\mathcal {U}}\). The latter condition ensures that \(s_0\) defines a graded derivation on \({{\mathbf {W}}}_{\bar{{{\mathcal {A}}}}}\), i.e.,
for \(F_i\)’s supported in \({\mathcal {U}}\). That one can construct Hadamard two-point functions \(\omega _{\mathrm {v}}\), \(\omega _{\mathrm {s}}\) fulfilling these properties was shown in [51, 52].
As for scalar fields, the on-shell algebra is defined by dividing out the ideal \({{\mathbf {J}}}_{{\bar{{{\mathcal {A}}}}}}\) generated by the equations of motion \(s_0 \Phi ^\ddagger _i = 0\). It is important to note that these in general contain anti-fields, cf. Table 1. These are being treated as sources, cf. [13], for example.
Time-ordered products on the algebra \(\mathbf{W }_{\bar{{{\mathcal {A}}}}}\) are defined analogously to the scalar case to be a collection of maps graded symmetric linear maps
which satisfy the axioms mentioned below (18) with obvious modifications to adapt to the gauge fields, and with the difference that local covariance is now defined with respect to the morphisms \(\chi \). Time-ordered products with one factor, i.e., Wick powers, are defined analogously to the scalar case, cf. (27), with a Hadamard parametrix H of the same form of the two-point functions, cf. (65). In particular, the vector and scalar parametrices \({H_{\mathrm {v}}}^{\ \mu }_{\nu }\) and \(H_{\mathrm {s}}\) fulfill identities analogous to (66), up to smooth remainders, which in fact vanish in the coinciding point limit.Footnote 14
3.7.1 Ward Identities
A crucial aspect of quantized gauge theory is the interplay of gauge invariance and renormalization. It is encoded in the anomalous Ward identity [25]

valid for F supported in \({\mathcal {U}}\).Footnote 15 Here \(A(e_\otimes ^F)= \sum _{n \ge 1} \frac{1}{n!} A_n(F^{\otimes n})\) is the anomaly, where each \(A_n\) is a map
with properties similar to \(D_n\), cf. (26), that is, it is of order \(O(\hbar )\), decreases the total \({{\,\mathrm{Deg}\,}}\) by \(2 (n-1)\), is supported on the total diagonal, is local and covariant and graded symmetric and scales homogeneously under (20). As proven in Lemmata A.1 and A.2 , it is (anti-) field independent and vanishes if one of the arguments is a linear (anti-) field. In addition, each \(A_n\) increases the ghost number by 1. Furthermore, it is subject to the consistency condition [25]
Remark 3.6
In generating identities such as (67) or (68), we always assume F to be Grassmann even. To handle Grassmann odd F, one proceeds by multiplying with Grassmann odd parameters and differentiating w.r.t. them (taking care about the order).
As argued below, a crucial consistency requirement is the absence of gauge anomalies, i.e.,
The consistency condition (68) is crucial for the removal of anomalies, i.e., for achieving (69). Let us indicate how this proceeds. Consider the expansion of \(A(e_\otimes ^{{S_{\mathrm {int}}}})\) in powers of \(\hbar \):
for some integer \(m>0\). Now we write \(A^{(m)}(e_\otimes ^{{S_{\mathrm {int}}}}) = \int _M \alpha \) as an integral of a local four-form \(\alpha (x)\) with ghost number 1 and mass dimension 4 (this follows from the homogeneous scaling of the anomaly). The consistency condition (68) for \(F = S_{\mathrm {int}}\) implies that \(\alpha (x) \in H^{4}_1(s| \mathrm {d})\). If the cohomology ring \(H^{4}_1(s| \mathrm {d})\) is trivial, then
for some fields \(\beta \), \(\gamma \), of ghost number 0 and 1, respectively. Such an anomaly can be removed by passing to another renormalization scheme, as follows. Let us write the interaction (50) as \({S_{\mathrm {int}}} = \int _M L_{\mathrm {int}}\), and let \(L_1\) be the term of degree 3 in fields and anti-fields (so that  . We now choose a new scheme \({T}'\) by setting the following local finite counter terms \(D_n\):
. We now choose a new scheme \({T}'\) by setting the following local finite counter terms \(D_n\):
where \(D^{(m)}\) is the first non-trivial term in the \(\hbar \) expansion of \(D(e_\otimes ^{{S_{\mathrm {int}}}})\) and where \(n= 2 (m-1) + \deg _\phi \beta \). The anomalies \(A'\) and A in the schemes \(T'\) and T are related via [25]
and therefore, with the choice (70) the anomaly in the new scheme vanishes:
Repeating the argument for higher-order coefficients of A in \(\hbar \), we can fully remove the anomaly.
For the pure Yang–Mills case, as can be seen from (56), \(H^{4}_1(s| \mathrm {d})\) is actually non-trivial. However, one can argue [25] that the parity property of the possible gauge anomaly is indeed not compatible with that of \(A(e_\otimes ^{{S_{\mathrm {int}}}})\) and hence is absent, so that there exists a renormalization scheme in which (69) holds. In the following, we assume to work with such a scheme.
3.7.2 Quantum BRST Charge and the Algebra of Physical Observables
In analogy with the scalar field theory, we can now define the generating functional

of interacting time-ordered products. These generate the interacting algebra \({{\mathbf {W}}}^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}\). Due to the time-slice axiom [23], it suffices to consider F’s supported in \({\mathcal {R}}\). However, the algebra \({{\mathbf {W}}}^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}\) also contains gauge-variant and unphysical functionals. They can be represented only on a space with indefinite inner product. However, the algebra of physical and gauge-invariant renormalized observables is defined to be [25, 54]
in the interacting on-shell algebra \({{\mathbf {W}}}^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}} \mod {{\mathbf {J}}}_{{\bar{{{\mathcal {A}}}}}}\). Here, \(Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}\) is the renormalized interacting quantum BRST charge, obtained by applying definition (28) to the local functional Q defined in (57). Equality in \({{\mathbf {F}}}_{{\bar{{{\mathcal {A}}}}}}\) is thus equality modulo equations of motion and \({{\,\mathrm{Im}\,}}[Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, -]_\star \), i.e.,
for some H. Under certain conditions, \({{\mathbf {F}}}_{{\bar{{{\mathcal {A}}}}}}\) admits a Hilbert space representation [52, 55].
Whether such a construction of \({{\mathbf {F}}}_{\bar{{{\mathcal {A}}}}}\) can be implemented turns out to be closely related to the issue of local gauge-symmetry preservation at the quantum level, which has the following manifestations:
- (i)
conservation of the renormalized interacting Noether current \(J^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}\) of BRST symmetry,
- (ii)
nilpotency of \([Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, -]_\star \) generated by BRST charge \(Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}\) (obtained from \(J^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}\)),
- (iii)
invariance of renormalized operators \([Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, {{\mathcal {O}}}_{\bar{{{\mathcal {A}}}}}^{\mathrm {int}}]_\star =0\), for classically gauge-invariant \({{\mathcal {O}}}\).
As proven in [25, 32], for any theory with local gauge symmetry, the first two manifestations listed above hold in the absence of gauge anomalies, i.e., when (69) holds. Also, the last manifestation follows from the anomalous Ward identity (67) if, in addition to (69), we have [25, 32]:
which turns out to be a consequence of the triviality of \(H_1(s)\).
The key identity in the proof of the above statements is the following interacting anomalous Ward identity [32]:

which holds for all F supported in \({\mathcal {R}}\), under assumption (69).Footnote 16 Here, \(\mathrel {\approx }\) means equal modulo the ideal \({{\mathbf {J}}}_{{\bar{{{\mathcal {A}}}}}}\) of free equations of motion, defined analogously to (17), i.e.,
and \(A^{\mathrm {int}}(e_\otimes ^{F})= \sum _{n \ge 1} \frac{1}{n!} A^{\mathrm {int}}_{n}(F^{\otimes n})\) is the generating functional of interacting anomalies, defined by
These are subject to the interacting consistency conditions
At first order in F, this implies that the quantum BV-BRST operator [32] defined by
is nilpotent, i.e., \(q^2 = 0\). Using this notation, we may express (71) at first order in F as
We also note that by (71), the gauge-invariant generators of interacting time-ordered products are given by  , with F fulfilling
, with F fulfilling
In particular, an interacting field \(F^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}} = T^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}(F)\) is gauge invariant if \(q F = 0\). Furthermore, given F of ghost number 0 and fulfilling \(q F = 0\), one may supplement it with “contact terms” to \(F' = F + C(e_\otimes ^{F})\) such that \(F'\) fulfills (75) in the sense of power series in F [56].
3.7.3 Perturbative Agreement and the Background Dependence of the Anomaly
As for the scalar case, perturbative agreement is a crucial ingredient for background independence. For variations of the background connection, it means

In the following, we sketch the proof that this can indeed be fulfilled in pure Yang–Mills theories, on a proof in a simpler context given in [31].Footnote 17 We then explore the interplay of perturbative agreement and anomalies.
We first need to define the retarded variation, to make sense of the l.h.s. of (76). We recall the differential operator-valued matrix \({\bar{P}}_{i j}\) defined by
cf. (64), and denote the corresponding retarded/advanced propagator by \(\Delta ^{ij}_{{\mathrm {r}}/{\mathrm {a}}}\). It fulfills
Let us also introduce the (differential operator valued) matrix \(K^i_{\ j}\) defined by
so that \(K^i_{\ j} \Phi ^j = s_0 \Phi ^i\), and its formal adjoint \({\hat{K}}_i^{\ j}\) such that
Then,
with \(\varepsilon \) the Grassmann parity of \(\Phi ^i\).
Analogously to the definition of the retarded wave operator in the scalar case, cf. (33), we now defineFootnote 18
It maps solutions to the free equations of motion \(s_0 \Phi ^\ddag _i = 0\) on the background \({\bar{{{\mathcal {A}}}}}\) to solutions on the background \({\bar{{{\mathcal {A}}}}}'\). It follows that the retarded Møller operator \(\tau ^{\mathrm {r}}\), defined as in (32), is well defined on the on-shell algebra. One also defines its infinitesimal version, the retarded variation \(\delta ^{\mathrm {r}}_{a}\), as for the scalar case, cf. (34).
A crucial ingredient in the proof that perturbative agreement can be fulfilled is the free current, obtained as the variation of the free part of the action w.r.t. the background connection, i.e.,
Here, we naturally extend the action to off-shell backgrounds, i.e., a is an arbitrary section of \({\mathfrak {p}}\otimes \Omega ^1\), not subject to the linearized equations of motion. When no sources are present, this current is classically covariantly conserved on-shell. In the present case, this is spoiled by the presence of anti-fields. One finds the off-shell identity
with \(\varepsilon \) the Grassmann parity of \(\Phi ^i\).
We now have all the necessary ingredients to prove that (76) can be fulfilled.
Proposition 3.7
In space-time dimension \(D \le 4\), perturbative agreement (76) can be fulfilled.
Proof
As shown in [31], cf. also [13], perturbative agreement (76) can be fulfilled, by a redefinition of time-ordered products involving at least one factor of j(a), provided thatFootnote 19

This quantity is (anti-) field independent. It was also shown [31] that, for space-time dimension \(D \le 4\), (84) holds on-shell, provided that the divergence of the Wick-ordered current vanishes on-shell,
As we argue below, this is true when anti-fields are set to zero (i.e., when the ideal generated by \(\Phi ^\ddag _i\) is modded out). Thus, (84) holds when equations of motion \(s_0 \Phi ^\ddag _i\) and anti-fields \(\Phi ^\ddag _i\) are modded out. But as \(E(a_1, a_2)\) is independent of (anti-) fields, (84) then also holds off-shell, and so does perturbative agreement (76).
It remains to argue that (85) indeed holds when anti-fields are set to zero. The first term on the r.h.s. of (83) then yields equations of motion \([\Phi ^i, {\bar{P}}_{i j} \Phi ^j]^I_{\mathfrak {g}}\). To evaluate the corresponding Wick-ordered product, one has to apply \({\bar{P}}\) to the Hadamard parametrix H and evaluate the limit of coinciding points. This can be done, for example using the methods developed in [53]. However, one can directly see that the result must vanish, as it is a locally and covariantly constructed section of \({\mathfrak {p}}\) of mass dimension 4. No such quantity exists in parity non-violating models for semi-simple gauge groups. \(\square \)
Theorem 3.8
If perturbative agreement (76) holds, background variations of the anomaly satisfy
for all F supported in \({\mathcal {U}}\).
Proof
As the anomaly is local andFootnote 20
we may choose \({{\bar{a}}}\) to be supported in the region \({\mathcal {U}}' \supset {\mathcal {U}}\) in which the background \({\bar{{{\mathcal {A}}}}}\) is on-shell. As nilpotency of \(s_0\) and the anomalous Ward identity (67) also hold on functionals supported in \({\mathcal {U}}'\), we may thus use perturbative agreement (76) and (67) to obtain

where we have again used (86). Regarding the last term on the r.h.s., one computes
In particular, this is supported outside of \({\mathcal {U}}\). We may thus decompose as
with \({{\,\mathrm{supp}\,}}(s_0 {\bar{\delta }}_{{\bar{a}}}S_0)_\pm \subset J^\pm ({\mathcal {U}}) {\setminus } {\mathcal {U}}\). It follows that the last term in (87) may be rewritten as a commutator,

On the other hand, we have

We thus obtain

In particular, \([ {\delta }^{\mathrm {r}}_{{{\bar{a}}}}, s_0]\) acts on linear (anti-) fields as

for \(x \in {\mathcal {U}}\), since the anomaly of a linear (anti-) field vanishes, cf. Lemma A.2.Footnote 21 The action of both \(s_0\) and \(\delta ^{\mathrm {r}}_{{{\bar{a}}}}\), and thus also of \([ {\delta }^{\mathrm {r}}_{{{\bar{a}}}}, s_0]\), on nonlinear functionals is defined by their action on linear functionals, i.e.,Footnote 22

Comparing with (88) shows that we are finished if we can show that

The r.h.s. of this equation is of the form
with some smoothFootnote 23 kernel \(W^{ij}\) which vanishes unless \(\varepsilon _i + \varepsilon _j \mod 2 = 1\). It thus suffices to show that this vanishes when acting on \(\Phi ^i(x) \Phi ^j(y)\) with \(\varepsilon _i + \varepsilon _j \mod 2 = 1\). By this restriction, we have \(T_2( \Phi ^i(x) \otimes \Phi ^j(y) ) = \Phi ^i(x) \Phi ^j(y)\) and plugging \(F = \lambda _1 \Phi ^i(x) + \lambda _2 \Phi ^j(y)\) in (88) and considering the equation at \(O(\lambda _1 \lambda _2)\), we indeed find that \(W^{i j}\) must vanish, again by the absence of anomalies of linear fields, Lemma A.2. \(\square \)
For the following considerations, it turns out to be convenient to introduce the notation
even though outside of \({\mathcal {R}}\), \({{\underline{s}}}\) does not need to be well defined as an operator on local functionals. The important point is that in \({\mathcal {R}}\), i.e., when restricted to configurations supported in \({\mathcal {R}}\), \({{\underline{s}}}\) reduces to the BV-BRST differential s, cf. Proposition 3.1.
Corollary 3.9
If perturbative agreement (76) holds, then, for F supported in \({\mathcal {U}}\),
with \({{\underline{s}}}{\bar{\delta }}_{{{\bar{a}}}} \Psi \) defined by (89). In particular, for F supported in \({\mathcal {R}}\), and \(n \ge 1\),
Proof
By field independence of the anomaly, Lemma A.1, we have
With Theorem 3.8, we obtain
which proves the first claim. The locality of the anomaly and the fact that on \({\mathcal {R}}\), \({{\underline{s}}}{\bar{\delta }}_{{{\bar{a}}}} \Psi = s {\bar{\delta }}_{{{\bar{a}}}} \Psi \), then leads to (90). \(\square \)
3.8 Background Independence
Having introduced the setting for the quantum Yang–Mills theory perturbatively constructed around each background \(\bar{{{\mathcal {A}}}}\), we now turn to the formulation of background independence. In analogy with the case of scalar field theory (Sect. 2.2), we can identify the theories defined on different backgrounds via the retarded variation \( \delta ^{\mathrm {r}}_{{{\bar{a}}}}\). As shown in Sect. 3.2.3, we can assume that perturbative agreement (76) holds, and we will do so from now on. Using this variation, we want to define a flat connection \({\mathfrak {D}}_{{{\bar{a}}}}\) on the bundle
where \({\mathcal {S}}_{\mathrm {YM}}\) is the manifold of background field configurations which are solutions to the Yang–Mills equation, cf. also the discussion following (43). A connection is here defined in complete analogy to Definition 2.2. The local algebras \({{\mathbf {F}}}_{{\bar{{{\mathcal {A}}}}}}({\mathcal {L}})\) are then generated by  with F supported in \({\mathcal {L}}\) and fulfilling (75). We would also like to ensure that in the classical limit, it should reduce to the connection \(\hat{{\mathcal {D}}}_{{{\bar{a}}}}\) on classical local functionals, in the sense that
with F supported in \({\mathcal {L}}\) and fulfilling (75). We would also like to ensure that in the classical limit, it should reduce to the connection \(\hat{{\mathcal {D}}}_{{{\bar{a}}}}\) on classical local functionals, in the sense that

for all F fulfilling (75).
We proceed by defining \({\mathfrak {D}}_{{{\bar{a}}}}\) on the full bundle
and showing that it reduces to a connection on \({{\mathbf {F}}}_{\mathrm {YM}}\), fulfilling the required properties. In particular, we have to ensure that
- (i)
it is well defined on the on-shell algebra;
- (ii)
it is well defined on \([Q^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}, -]_\star \) cohomology, i.e., it fulfills (7) on-shell, ensuring that it maps kernel and image of \([Q^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}, -]_\star \) onto themselves;
- (iii)
it is a derivation, i.e., fulfills (37);
- (iv)
it respects space-time localization in the sense defined in (38).
A crucial requirement for the fulfillment of these properties will be the absence of a certain anomaly. We will later show that time-ordered products can indeed be defined accordingly.
Remark 3.10
There is a subtlety regarding the definition of the bundles \({{\mathbf {F}}}_{\mathrm {YM}}\) and \({{\mathbf {W}}}_{\mathrm {YM}}\). We recall that the backgrounds \({\bar{{{\mathcal {A}}}}}\) are only required to be on-shell in \({\mathcal {U}}\) (and to coincide with an arbitrary reference connection \({{\mathcal {A}}}_0\) outside of \({\mathcal {V}}\)). Hence, their behavior in \({\mathcal {V}}{\setminus } {\mathcal {U}}\) is arbitrary. A further requirement should thus be that the construction is independent of the choice of a representative, i.e., the connection \({\mathfrak {D}}_{{\bar{a}}}\) should vanish for \({{\bar{a}}}\) supported in \({\mathcal {V}}{\setminus } {\mathcal {U}}\), when applied to  for F supported in \({\mathcal {R}}\). That this is indeed the case is checked below, cf. Remark 3.14.
for F supported in \({\mathcal {R}}\). That this is indeed the case is checked below, cf. Remark 3.14.
To construct the desired connection \({\mathfrak {D}}\), it is useful to split the connection \(\hat{{\mathcal {D}}}\) on local functionals as
where the two terms on the r.h.s. are obtained by applying the canonical gauge-fixing transformation as in (63) separately to \({\bar{\delta }}_{{\bar{a}}}\) and \(\delta _{{\bar{a}}}\). Hence, it is natural to see the first term on the r.h.s. as the gauge-fixed background variation and replace it by the retarded variation. Our first tentative definition is thus
That this is a natural starting point is evidenced by the following Lemma:
Lemma 3.11
The operator \({\mathfrak {D}}^0_{{\bar{a}}}\) is well defined on the on-shell algebra.
Proof
As the retarded variation is well defined on the on-shell algebra, it remains to check for the last two terms. We have
so that the last two terms are derivatives w.r.t. (anti-) fields. Such a derivative is well defined on the on-shell algebra if it acts in the direction of a solution to the free equations of motion, i.e., those obtained by \(s_0 \Phi ^\ddag _i\), cf. Table 1. The perturbation given by
indeed fulfills that requirement, as \({{\bar{a}}}\) is, in \({\mathcal {U}}\), a solution to (43). \(\square \)
3.8.1 Well-Definedness of the Connection on the Quantum BRST Cohomology
Similarly to the case of scalar field theory (Proposition 2.3), \({\mathfrak {D}}_{{{\bar{a}}}}^0\) acts as

where
We note that, by \(({S_{\mathrm {int}}}, {\delta }_{{{\bar{a}}}} \Psi ) =0\), we have
With the notation (89), we thus obtain

Note the presence of the second term on the r.h.s. of (93) which is absent in the case of scalar field theory, cf. (40). It leads to a violation of the locality requirement (38). This term appears because the gauge-fixing fermion breaks the split independence of the action S, cf. (52).
We first state a lemma which is crucial for the proof of the following theorem.
Lemma 3.12
For all F supported in \({\mathcal {R}}\), it holds
Proof
As a consequence of (60), (59), the graded Jacobi identity (51) and (90), the l.h.s. equals
The first three terms cancel due to (49) and (51) and the last two terms due to Lemma A.1, taking into account (92) and the fact that \(S_{\mathrm {int}}\) is independent of \({\bar{C}}^\ddagger \). \(\square \)
Theorem 3.13
Assuming
with a not necessarily a solution to (43), the operator

where \( {{\underline{s}}}( {\bar{\delta }}_{\eta {{\bar{a}}}} \Psi )\) is defined in (89) and \(\eta \) is a smooth nonnegative function supported on \(J^-({\mathcal {R}})\) and equal to 1 on \(J^-({\mathcal {R}}) {\setminus } {\mathcal {R}}\), is well defined on the on-shell \([Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, -]_\star \) cohomology, in the sense that

for all F supported in \({\mathcal {R}}\). On this cohomology, it is independent of the choice of \(\eta \). Furthermore, for F fulfilling (75), we have

In particular, \({\mathfrak {D}}_{{{\bar{a}}}}\) is a connection on \({{\mathbf {F}}}_{{\mathrm {YM}}}\) fulfilling (91).
Remark 3.14
The last term in definition (96) can be motivated as follows: Assume that \({{\bar{a}}}\) is supported outside of \({\mathcal {U}}\). As discussed in Remark 3.10, the corresponding derivative \({\mathfrak {D}}_{{\bar{a}}}\) should vanish on  with F localized in \({\mathcal {R}}\). The first term on the r.h.s. of (93) does indeed vanish (as the supports of \({{\bar{a}}}\) and F are disjoint), but the second one does not. However, due to causal factorization (29) of interacting time-ordered products, it is canceled by the commutator which is added in (96). This is completely analogous to the unitary transformation (its generator in the present case) which compensates a change of the infrared cutoff of the interaction in the so-called algebraic adiabatic limit, cf. [24].
with F localized in \({\mathcal {R}}\). The first term on the r.h.s. of (93) does indeed vanish (as the supports of \({{\bar{a}}}\) and F are disjoint), but the second one does not. However, due to causal factorization (29) of interacting time-ordered products, it is canceled by the commutator which is added in (96). This is completely analogous to the unitary transformation (its generator in the present case) which compensates a change of the infrared cutoff of the interaction in the so-called algebraic adiabatic limit, cf. [24].
Proof
We begin by proving the independence of the choice of \(\eta \). The difference \(\xi = \eta _1 - \eta _2\) of two admissible \(\eta \)s is supported in \({\mathcal {R}}\), where \({{\underline{s}}}\) coincides with s. Hence, under the assumption (95) and using (74),

But \([ [Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, ( {\bar{\delta }}_{\xi {{\bar{a}}}} \Psi )^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}} ]_\star , -]_\star \) vanishes on \([Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, -]_\star \) cohomology, as
so that the action of \([ [Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, ( {\bar{\delta }}_{\xi {{\bar{a}}}} \Psi )^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}} ]_\star , -]_\star \) on a \([Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, -]_\star \) closed functional yields a \([Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, -]_\star \) exact functional, i.e., a zero element in the cohomology.
We continue with proving (97). From Eq. (93) and for all F, we have

By the above, we may, without loss of generality, assume that \({{\,\mathrm{supp}\,}}\eta \cap J^+( {{\,\mathrm{supp}\,}}F ) = \emptyset \). We split
in the second term on the r.h.s. of (99), where \(\eta \), \(\chi \) and \(\psi \) are smooth nonnegative functions, summing up to 1, with \(\chi \) being supported inside \({\mathcal {R}}\) and equal to 1 in a neighborhood of \({{\,\mathrm{supp}\,}}F\), \(\eta \) being supported in \(J^-({\mathcal {R}})\), and \(\psi \) supported in \(J^+({\mathcal {R}})\). By causal factorization (29) and (30), we have

We thus obtain

With (71), we compute, using the assumption (95),

and

It follows that

with \(C_{{{\bar{a}}}}(F)\) the expression on the l.h.s. of (94). Lemma 3.12 thus proves (97).
Finally, we note that using (71) and (95), we may rewrite (100) as

which proves (98).
As a direct consequence of (98), \({\mathfrak {D}}_{{{\bar{a}}}}\) fulfills (91) and respects space-time localization in the sense defined in (38), and so defines a connection on \({{\mathbf {F}}}_{\mathrm {YM}}\).
\(\square \)
3.8.2 Flatness of the Connection on the Quantum BRST Cohomology
Finally, we want to prove flatness of \({\mathfrak {D}}_{{{\bar{a}}}}\).
Theorem 3.15
For all F supported in \({\mathcal {R}}\), fulfilling (75), and under the assumption (95), we have

Proof
Using (98), it suffices to prove

with
By (90), we have
The last term on the r.h.s. vanishes by the flatness of \({\bar{\delta }}\) and Lemma A.2. Thus, with (61), we have
With the consistency condition (72), this simplifies to
where we used Lemma A.1, taking into account (92) and the fact that \(S_{\mathrm {int}}\) is independent of \({\bar{C}}^\ddagger \), and that \(\Psi \) does not contain anti-fields, so that \(( {\bar{\delta }}_{{{\bar{a}}}'} \Psi , {\bar{\delta }}_{{{\bar{a}}}} \Psi ) = 0\). With (71), we thus obtain

which proves the statement. \(\square \)
3.8.3 Absence of Obstructions to Background Independence
Above, we found that condition (95) is sufficient to ensure well-definedness and flatness of the connection \({\mathfrak {D}}_{{{\bar{a}}}}\) on \([Q^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}, -]_\star \) cohomology. We now show that this can indeed be satisfied in pure Yang–Mills theory.
Lemma 3.16
Let T and \(T'\) be two renormalization schemes related via (25), and let A and \(A'\) be the corresponding anomalies of the anomalous Ward identities (67) in these schemes. Assuming the anomalies of the interaction \(S_{\mathrm {int}}\) vanish in both schemes, i.e., \(A(e_\otimes ^{S_{\mathrm {int}}}) = A'(e_\otimes ^{S_{\mathrm {int}}})=0\), then for all G supported in \({\mathcal {R}}\), it holds
where \(D_{S_{\mathrm {int}}} := D( e_\otimes ^{S_{\mathrm {int}}})\) and \({Z}_{S_{\mathrm {int}}} G := G + D(G \otimes e_\otimes ^{S_{\mathrm {int}}})\).
Proof
From relation (25), it follows that

Using this identity, the anomalous Ward identity in the scheme \(T'\) takes the form

On the other hand using (25), we can write the anomalous Ward identity as

Comparing (102) and (103), we arrive at
Now (101) follows by replacing F with \(F + \tau G\), differentiating with respect to \(\tau \), and setting \(\tau =0\) and \(F={S_{\mathrm {int}}}\). \(\square \)
In the following, we show that the violation of condition (95) can be removed by a redefinition of time-ordered products. The strategy is as follows: Assume that the anomaly has been removed up to order \(O(\hbar ^{m-1})\), i.e.,
with \(A^{{\mathrm {int}}(n)}\) independent of \(\hbar \). We denote by \(A^{(m)}\) and \(D^{(m)}\) the anomaly and the redefinition of time-ordered product at order \(O(\hbar ^m)\). From (101), we conclude that
There are thus two possible strategies to remove the anomaly of \({\bar{\delta }}_a \Psi \) at order \(O(\hbar ^m)\): The first one would be to set
However, such a definition must not spoil the absence of gauge anomalies or perturbative agreement. As discussed in the proof of Proposition 3.7, achieving perturbative agreement proceeds by redefining time-ordered products involving at least one factor \(j(a) = {\bar{\delta }}_a S_0\), cf. (82). Hence, redefinitions of such time-ordered products should not be allowed. Furthermore, due to field independence, a redefinition of a time-ordered product of the form  , with the interaction \(S_{\mathrm {int}}= S_1 + S_2\) and
, with the interaction \(S_{\mathrm {int}}= S_1 + S_2\) and  , would spoil the absence of gauge anomalies. However, by (52), we have
, would spoil the absence of gauge anomalies. However, by (52), we have
Hence, the time-ordered products  must not be redefined. Thus, to implement (106), one would have to redefine time- ordered products of the form
must not be redefined. Thus, to implement (106), one would have to redefine time- ordered products of the form  . Concretely, one would set
. Concretely, one would set
for \(n \ge 1\), with
Note the different number of interaction terms on the two sides of (107), which is enforced by the fact that \(s_{\mathrm {int}}\bar{\delta }_a \Psi \) is cubic in the fields, while \(\bar{\delta }_a \Psi \) is only quadratic. This redefinition is still problematic. First, one has to show that the r.h.s. of (107) vanishes for \(n = 0\). Second, and more severe, are constraints from field independence. One can find \(a'\) such that \(\delta _{a'} s_{\mathrm {int}}\bar{\delta }_a \Psi \) vanishes. Hence, if such a derivative \(\delta _{a'}\) acts on the first variable of the functional on the l.h.s., one gets a functional that identically vanishes. Hence, all such derivatives only act on the \(S_i\) factors. But there are less such factors on the l.h.s. than on the r.h.s., so that the redefinition (107) might be inconsistent with field independence.
In order to circumvent these difficulties, we exploit the second (in fact related, cf. Remark 3.21) possibility to removing an anomaly based on (105). Namely, if \(A^{(m)}({\bar{\delta }}_a \Psi \otimes e_\otimes ^{S_{\mathrm {int}}})\) happens to be s exact, i.e., \(A^{(m)}({\bar{\delta }}_a \Psi \otimes e_\otimes ^{S_{\mathrm {int}}}) = s H_a\), then we may set
Unfortunately, \(A^{(m)}({\bar{\delta }}_a \Psi \otimes e_\otimes ^{S_{\mathrm {int}}})\) need not be s exact. However, it turns out to be \(s_0\) exact, which is sufficient to remove the anomaly order by order in the number of fields. To prove these statements, we collect a few lemmata.
Lemma 3.17
The cohomology \(H^k(s_0)\) is trivial at negative ghost number \(k < 0\).
Proof
The statement was shown in [43], Thm. 7.1, for the full differential s and the restricted algebra not containing B, \({\bar{C}}\) and their anti-fields. However, adding these does not change the statement, as they form trivial pairs and do not modify the cohomology. The proof given in [43] only uses the triviality of the homology of the Koszul–Tate differential at positive anti-field number, and this also holds for its free part. \(\square \)
Lemma 3.18
Let \(F = s G\) be of ghost number 0 and \(F_i \ne 0\) be the lowest-order term of F in an expansion in total (anti-) field number. Then, there exists \(G_i\) such that \(F_i = s_0 G_i\).
Proof
Let \(G_j \ne 0\) be the lowest-order term in the (anti-) field number expansion of G. If \(j = i\), we have found the sought for \(G_i\). For \(j < i\), we note that \(s_0 G_j = 0\). By Lemma 3.17, there is \(H_j\) such that \(G_j = s_0 H_j\). Define \(G^{(1)} = G - s H_j\). We still have \(s G^{(1)} = F\), but now the lowest-order term of \(G^{(1)}\) occurs at \(j^{(1)}> j\). We continue until \(j^{(k)} = i\). \(\square \)
Lemma 3.19
Let \({{\,\mathrm{supp}\,}}a \subset {\mathcal {R}}\), \(A_1^{{\mathrm {int}}(m)}({\bar{\delta }}_a \Psi ) \ne 0\) be the lowest term in the \(\hbar \) expansion of \(A_1^{\mathrm {int}}({\bar{\delta }}_a \Psi )\), cf. (104), and \(A^{{\mathrm {int}}(m)}_1({\bar{\delta }}_a \Psi )_i \ne 0\) be the lowest-order term of \(A^{{\mathrm {int}}(m)}_1({\bar{\delta }}_a \Psi )\) in an expansion in total (anti-) field number. Then, there exists \(G_{a i}\) such that \(A^{{\mathrm {int}}(m)}_1({\bar{\delta }}_a \Psi )_i = s_0 G_{a i}\).
Proof
Expanding the consistency condition (72) in \(\hbar \), one finds \(A^{{\mathrm {int}}(n)}_1(s {\bar{\delta }}_a \Psi ) = 0\) for all \(n < m\) and
By Corollary 3.9 and the absence of gauge anomalies, cf. (69), we have \(A^{\mathrm {int}}_1({{\underline{s}}}{\bar{\delta }}_{{\bar{a}}} \Psi ) = 0\) for all \({\bar{a}}\) fulfilling the linearized field Eq. (43). In particular, the local functional \(A^{\mathrm {int}}_1(s {\bar{\delta }}_a \Psi )\) vanishes when evaluated in configurations supported in a region \({\mathcal {R}}' \subset {\mathcal {R}}\) where a is on-shell, i.e., where \({\bar{P}}^{\mathrm {lin}}a = 0\) holds. It follows that, for a supported in \({\mathcal {R}}\),
with \(\Phi ^{(m)}\) a locally and covariantly constructed section of \({\mathfrak {p}}\otimes \Omega ^1(M)\) of ghost number 1 and mass dimension 1. Furthermore, again by expanding the consistency condition (72), one finds \(s \Phi ^{(m)} = 0\). From the triviality of \(H^1(s)\), it follows that \(\Phi ^{(m) I}_\mu = c^{(m)} s A^I_\mu \) with some coefficient \(c^{(m)}\). Hence,
with \(\Theta ^{(m)}\) a locally and covariantly constructed section of \({\mathfrak {p}}\otimes \Omega ^1(M)\) of ghost number 0, mass dimension 3, and in the kernel of s. By (55), it must thus be of the form \(\Theta ^{(m) I \mu } = s \Sigma ^{(m) I \mu } + \Xi ^{(m) I \mu }\), with \(\Xi ^{(m)}\) a c-number. However, the only such c-number would be \({\bar{\nabla }}_\nu {\bar{F}}^{I \nu \mu }\), which vanishes in \({\mathcal {R}}\), cf. (45). Noting that the first term on the r.h.s. of (109) can be rewritten as an element of the image of \(s_0\) using \(s_0 (A^{\ddag I}_\mu + {\bar{\nabla }}_\mu {\bar{C}}^I) = ({\bar{P}}^{\mathrm {lin}}A)^I_\mu \), and using Lemma 3.18 on the second term, we obtain the desired statement. \(\square \)
We are now ready to perform the necessary redefinitions.
Theorem 3.20
There are renormalization schemes in which the condition (95) holds.
Proof
Let \(A_1^{{\mathrm {int}}(m)}({\bar{\delta }}_a \Psi )\) be the lowest term in the \(\hbar \) expansion (104) and \(A^{{\mathrm {int}}(m)}_1({\bar{\delta }}_a \Psi )_i \ne 0\) be the lowest-order term of \(A^{{\mathrm {int}}(m)}_1({\bar{\delta }}_a \Psi )\) in an expansion in total (anti-) field number. By Lemma 3.19, there is a \(G_{a i}\) such that \(A^{{\mathrm {int}}(m)}_1({\bar{\delta }}_a \Psi )_i = s_0 G_{a i}\). Now we perform the redefinition
where we used notation (108). Both expressions are at the same order in the interaction, so there are no potential obstructions from field independence. Expanding (105) in the total (anti-) field number, we see that the anomaly now occurs at a higher order in the total (anti-) field number. By power counting, the anomaly has a bounded total (anti-) field number, so the process terminates at some point, so that the anomaly at order \(O(\hbar ^m)\) is removed. Continuing at higher orders, one removes the anomaly to all orders. \(\square \)
Remark 3.21
The two possibilities for removing the anomaly, i.e., by either redefining time-ordered products involving \(s_{\mathrm {int}}{\bar{\delta }}_a \Psi \) or \({\bar{\delta }}_a \Psi \), are in fact related. This follows from field independence and the fact that \(\frac{\delta }{\delta C} s_{\mathrm {int}}{\bar{\delta }}_a \Psi \) involves the same Wick power as \({\bar{\delta }}_a \Psi \), namely \({\bar{C}} A\). Hence, the redefinition (110) implies a redefinition of the form (107), with a modified right-hand side. One can thus see the approach chosen here as a means to rule out the potential clashes with field independence discussed below (108).
Remark 3.22
The above arguments invoked power counting and thus relied on power-counting renormalizablity. Our method is thus not sufficient to rule out violation of background independence, for example in Yang–Mills in higher dimensions.
Remark 3.23
Let us consider the situation when the gauge group is not semi-simple, but contains abelian factors and possibly also matter fields. The proof of anomaly freedom given in [25] does then not apply, but let us assume that there are no gauge anomalies. How are our considerations then affected? The dynamical fields corresponding to the abelian factors are free (apart from the possible coupling to matter), so the gauge- fixing fermion \(\Psi \) is independent of the abelian background connection. In particular, \({\bar{\delta }}_{a} \Psi = 0\) if the perturbation a is only in the abelian background connection. It follows that no further potential obstructions to achieving (95) arise by including abelian factors.
3.8.4 Summary of Assumptions
Even though we discussed Yang–Mills theory here, the treatment of other gauge theories should be completely analogous, provided that a few conditions are met. Obviously, the theory should have no gauge anomaly, i.e., (69) holds, and fulfill perturbative agreement w.r.t. changes in the background. Also, the triviality of \(H_1(s)\) was used. Apart from that, we used that
- (i)
\(S_{\mathrm {int}}\) does not contain \({\bar{C}}^\ddag \),
- (ii)
the gauge-fixing fermion is quadratic in fields,
- (iii)
and does not contain anti-fields.
If these conditions are met, then background independence holds, provided that the analog of (95) does.
Remark 3.24
Throughout, we also assumed compact Cauchy surfaces. This assumption is of technical nature only. It is relevant for the existence of the interacting BRST charge \(Q^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}\), but as long as one is not interested in singling out the physical subspace in a Hilbert space representation, this charge is not needed. We only use it in the form \([Q^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}, - ]_\star \) of the on-shell interacting BRST differential. One could equally well work with the off-shell interacting BRST differential \({\hat{s}}\) recently constructed in [56] (which does not require compact Cauchy surfaces). For non-compact Cauchy surfaces, the construction of the cutoff functions needed, for example in Theorem 3.13 or Theorem 3.8, becomes slightly more involved, but apart from the fact that the existence of Hadamard states for non-compact Cauchy surfaces has not been proven in full generality [51], our conclusions also hold for non-compact Cauchy surfaces (with the obvious replacements of \([Q^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}, - ]_\star \) by \({\hat{s}}\)).
3.8.5 Renormalized Background-Independent Interacting Fields
Lemma 3.12 can be seen as a master equation for the compatibility of \(\hat{{\mathcal {D}}}_{{\bar{a}}}= {\mathcal {D}}^0_{{\bar{a}}}- (-, {\bar{\delta }}_{{\bar{a}}}\Psi )\) and s in the renormalized setting. Let us explore some consequences.
We recall that for a local functional F to give rise to a gauge- invariant interacting field \(T^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}(F)\), it must fulfill \(q F = 0\), cf. (73) for the definition of q, corresponding to the linearization of (75). As shown in [56], for any field \({{\mathcal {O}}}\) of ghost number 0 which is classically gauge invariant, \(s {{\mathcal {O}}}= 0\), there is extension \({{\mathcal {O}}}' = {{\mathcal {O}}}+ O(\hbar )\) such that \(q {{\mathcal {O}}}' = 0\). A further structure that naturally occurs at second order in F is the quantum anti-bracket [32]:
We may now define
which is equal to \(\hat{{\mathcal {D}}}_{{{\bar{a}}}}\) up to quantum corrections. It follows from (98) that a functional F giving rise to a background-independent interacting field \(T^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}(F)\) must fulfill
A straightforward consequence of the consistency condition (72), Lemma 3.12 and Theorem 3.15 is the following:
Corollary 3.25
For all F supported in \({\mathcal {R}}\), we have, under the assumption (95),
If furthermore \(q F = 0 = q G\), then also
A natural question is now the following. Assume a field \({{\mathcal {O}}}\) is given which is classically gauge invariant and background independent, i.e.,
is there an extension \({{\mathcal {O}}}' = {{\mathcal {O}}}+ O(\hbar )\) such that
holds, so that \({{{\mathcal {O}}}'}^{\mathrm {int}}_{{\bar{{{\mathcal {A}}}}}}\) is a gauge-invariant, background-independent field? Given an extension \({{\mathcal {O}}}'\) such that \(q {{\mathcal {O}}}' = 0\), one may evaluate it on one background \({\bar{{{\mathcal {A}}}}}'\) and then obtain local functionals on general backgrounds by parallel transport w.r.t. \({\mathcal {D}}^\hbar \), at least locally on \({\mathcal {S}}_{\mathrm {YM}}\) (using that \({\mathcal {D}}^\hbar \) is flat on q cohomology). However, it is not obvious whether one may choose the extension \({{\mathcal {O}}}'\) such that this procedure results in a proper field in the sense defined in Sect. 2.1, i.e., is independent of \({\bar{{{\mathcal {A}}}}}'\). We leave this as an interesting open problem.
4 Perturbative Quantum Gravity
Having treated background independence for Yang–Mills theory in full detail, we now turn to perturbative quantum gravity, with an emphasis on the differences to the Yang–Mills case. Quantum gravity in the sense of perturbation theory around generic backgrounds was recently formulated in [2]. Our setup differs in an important point, so this difference will also be highlighted.
The principal dynamical variable is the metric perturbation \(h_{\mu \nu }\), i.e., the full metric is given by
with \({\bar{g}}_{\mu \nu }\) the background metric. It is supplemented by ghosts \(c^\mu \), anti-ghosts \({\bar{c}}_\mu \) and Lagrange multipliers \(b_\mu \), which are (co-) vector fields and transform under the BRST transformation as
with \(\nabla \) the Levi-Civita derivative w.r.t. \(g_{\mu \nu }\). Correspondingly, the Einstein–Hilbert action is extended to
where the anti-fields \(\Phi ^\ddagger \) are interpreted as tensor-valued densities. The action is invariant under background gauge transformations, i.e., diffeomorphisms \(\psi : M' \rightarrow M\) acting via pullback on \({\bar{g}}\) and the dynamical fields.
As for Yang–Mills fields, the interaction terms are adiabatically cutoff. There is a slight complication w.r.t. the Yang–Mills case in that the cutoff function should be a function of covariant coordinates, cf. below. That, however, does not change anything substantial, so this cutoff can be treated as for Yang-Mills fields. Hence, we ignore this subtlety in the following. In the region where the cutoff function is equal to one, the extended action has the shift symmetry
To implement the harmonic (or de Donder) gauge, we employ the gauge- fixing fermion [59]
which is a covariant functional of the dynamical fields and the background metric \({\bar{g}}\). Here, \({\bar{\nabla }}\) is the Levi-Civita derivative w.r.t. \({\bar{g}}_{\mu \nu }\). The gauge-fixed action then becomes
with \(h \mathrel {:=}{\bar{g}}^{\mu \nu } h_{\mu \nu }\). It leads to hyperbolic equations of motion at the linearized level for \(c^\mu \), \({\bar{c}}_\nu \) and \(\gamma _{\mu \nu } \mathrel {:=}h_{\mu \nu } - \frac{1}{2} {\bar{g}}_{\mu \nu } h\) (after eliminating \(b_\nu \)).
Local observables can be constructed as proposed in [2, 17], by what one might call covariant coordinates. One chooses backgrounds \({\bar{g}}\) that are sufficiently genericFootnote 24 to allow, in a neighborhood of \({\bar{g}}\), for four curvature scalars to provide a coordinate system \(X[g] : M \rightarrow U \subset {\mathbb {R}}^4\). By definition, these fulfill
for a diffeomorphism \(\psi \). It follows that
Given a test tensor t on M, and T[g] a tensor covariantly constructed out of the metric, i.e., obtained by contractions of \(g_{\mu \nu }\), \(g^{\mu \nu }\), \(\nabla _{(\lambda _1} \dots \nabla _{\lambda _r)} R_{\mu \nu \rho \sigma }\), one defines
From (111), it follows that the observable (112) transforms covariantly,
and is in the kernel of the BRST operator. We refer to [2, 17] for the interpretation of these observables.
An adiabatic cutoff of the interaction terms, respecting covariance, can be implemented similarly. Let \(L_{\mathrm {int}}\) be the interaction Lagrangian density, obtained by Taylor expansion of the Lagrangian density in \((h, c, {\bar{c}}, b, h^\ddagger , c^\ddagger , {\bar{c}}^\ddagger )\) and keeping only the terms of order higher than two. Then, a covariant cutoff can be implemented as
with \(\lambda \) a test function on the background, assumed to be equal to one in a neighborhood of the region \({\mathcal {R}}\), cf. the setup for the Yang–Mills case.
As for the case of pure Yang–Mills theory, there are no gauge anomalies and \(H_1(s)\) is trivial [62], and there is also no obstruction to the fulfillment of perturbative agreement [13] for variations in the background metric. Also, the conditions (i)–(iii) stated in Sect. 3.3.4 are met. It follows that it suffices to check the fulfillment of the analog of condition (95), which is
where
Due to power-counting non-renormalizability, the arguments invoked in Sect. 3.3.3 to prove the fulfillment of (95) cannot be adapted to the present setting, cf. also Remark 3.22. For example, even if \(A_1^{\mathrm {int}}(s {\bar{\delta }}_k \Psi ) = 0\) holds, one can, using the covariant coordinates, still find non-trivial analogs of \(\Theta \) in the proof of Lemma 3.19, such as
with
for any covariant symmetric tensor T. We leave open the question whether such obstructions to background independence occur in perturbative quantum gravity.
Remark 4.1
In one respect, our setup severely deviates from the one employed in [2]. There, the gauge condition is that the four curvature scalars X that are used as coordinates are harmonic. The corresponding Lagrange multipliers b are then a collection of four scalars, and accordingly for the anti-ghosts \({\bar{c}}\). It follows that the gauge-fixed action is no longer covariant, but explicitly depends on the choice of the coordinates X. It is in fact not even invariant under changing the coordinates to \(Y = \psi \circ X\) using a diffeomorphism \(\psi \) of \({\mathbb {R}}^4\), i.e., under relabeling the points in the chart. The advantage of this approach is that the gauge-fixing fermion does not break the split independence. The downside is of course that in the end, one has to show that covariance is still intact in the observable algebra. Furthermore, having given up covariance, renormalization schemes and thus also potential anomalies are much less constrained than in our approach.
4.1 Background Independence as Triviality of the Relative Cauchy Evolution
Finally, let us comment on a different criterion for background independence, which is used in [2] in the context of perturbative quantum gravity. Based on ideas formulated in [63], background independence is there defined as triviality of the interacting relative Cauchy evolution\(\beta \). We first discuss it in the example of the scalar field. One defines

Here, \(\tau ^{\mathrm {a}}\) is the advanced Møller operator, defined in complete analogy to the retarded one, cf. (32), and A is the advanced productFootnote 25 defined as

The inverses of retarded and advanced products appearing here are purely formal. However, the requirement that \(\beta \) is trivial on-shell can be properly formulated as

The infinitesimal version of this is, using perturbative agreement,

Formally, i.e., putting aside cutoff issues, we have \(\delta _{{{\bar{\varphi }}}} S_0 = 0\), so that, with (13), we may replace \({\bar{\delta }}_{{{\bar{\varphi }}}} S\) by \(\delta _{{{\bar{\varphi }}}} S\) and conclude that the equation is indeed fulfilled, by the field equation, which follows from (23).
In the case of Yang–Mills theory, the split independence of the action is broken by gauge fixing, cf. (52), so that one then obtains, again ignoring cutoff issues,

For F fulfilling (75) and assuming (95) and  , the r.h.s. can be written as an element of \({{\,\mathrm{Im}\,}}[Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, -]_\star \), i.e., as a trivial element. Hence, assuming the absence of the anomaly (95), one finds that the interacting relative Cauchy evolution is indeed trivial on the cohomology.
, the r.h.s. can be written as an element of \({{\,\mathrm{Im}\,}}[Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}, -]_\star \), i.e., as a trivial element. Hence, assuming the absence of the anomaly (95), one finds that the interacting relative Cauchy evolution is indeed trivial on the cohomology.
Two comments are in order:
As discussed in Remark 4.1, in [2] the breaking of the split independence of the action is avoided by the use of a non-covariant gauge fixing. In particular, the relevance of the absence of the anomaly (95) was not noted there. The problems with such a non-covariant gauge fixing were discussed in Remark 4.1.
The significance of the criterion proposed in [2], i.e., triviality of the interacting relative Cauchy evolution, seems unclear. Following the derivation above, one finds that, in the case of gravity, it is implied by the on-shell vanishing of the stress-energy tensor \({\bar{\delta }}_{{\bar{k}}} S\), or, equivalently, by the on-shell fulfillment of the equations of motion. However, it gives no information about how to relate observables defined on different backgrounds, i.e., does not answer our initial question, as evidenced by the fact that all derivatives of F w.r.t. the background fields drop out in the above calculations. We therefore think that triviality of the interacting relative Cauchy evolution is not a sufficient criterion for background independence.
Notes
Even if one interprets \(T^{\mathrm {int}}_{{\bar{\phi }}}(e^{i F[{{\bar{\phi }}}, -]})\) as an evaluation functional, which one can differentiate w.r.t. \({{\bar{\phi }}}\), this operation is not well defined on the on-shell algebra. Furthermore, we would like a differentiation that respects the algebraic structure, i.e., fulfills the Leibniz rule w.r.t. the algebra product. This will not be the case for such a naive derivative.
Perturbative agreement asserts that it should, on the infinitesimal level, not matter whether one puts terms quadratic in \(\phi \) into the free part or the interacting part of the action.
The free theories linearized around different backgrounds \({{\bar{\phi }}}\) differ in the mass term, see below.
This interpretation was already suggested in [13].
Despite the explicit dependence of the star product on the background, we drop the subscript \({{\bar{\phi }}}\) and simply write \(\star \).
To get the full strength of requirement of local covariance, one should not restrict to space-times with compact Cauchy surfaces from the outset. We thus assume that we have implemented local covariance without this restriction, i.e., constructed algebras \({{\mathbf {W}}}_{{\bar{\phi }}}\) and time-ordered products \(T_{{{\bar{\phi }}}, n}\), cf. below, and then restricted to space-times with compact Cauchy surfaces.
It is well defined as \(P_{{{\bar{\phi }}}} - P_{{{\bar{\phi }}}'}= - \tfrac{1}{2} \lambda ({{\bar{\phi }}}^2 - \bar{\phi '}^2 )\) is compactly supported.
A typical family of such functionals would be given by the assignment \({{\bar{\phi }}}\mapsto {{\mathcal {O}}}^{\mathrm {int}}_{{\bar{\phi }}}\) of an interacting observable to each background, given a field \({{\mathcal {O}}}\).
It is not even obvious that it is well defined on \({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4}\), i.e., that \({\mathfrak {D}}_{{{\bar{\varphi }}}} F \in \Gamma ^\infty ({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4})\), as \({\bar{\delta }}_{{\bar{\varphi }}}S\) is not supported in \({\mathcal {R}}\).
Introducing a cutoff there would spoil gauge covariance.
This can be shown, for example using the methods developed in [53].
In [25], this was proven for a flat background connection without restrictions on the support of F. This proof can be straightforwardly generalized to general background connections. However, a crucial ingredient is that \(s_0\) is a derivation and nilpotent, which is only true on functionals supported in \({\mathcal {U}}\). This motivates the localization \({{\,\mathrm{supp}\,}}S_{\mathrm {int}}\subset {\mathcal {U}}\), which by (24) ensures that
 for \({{\,\mathrm{supp}\,}}F \subset {\mathcal {R}}\) (those are the generators that we will be concerned with).
for \({{\,\mathrm{supp}\,}}F \subset {\mathcal {R}}\) (those are the generators that we will be concerned with).Perturbative agreement will in general not hold when the gauge fields couple to chiral fermions, due to the usual chiral anomalies cf. [53].
We refer to [31] for a treatment of fermionic fields.
This requirement can be seen as a stronger version of the Wess–Zumino consistency condition, cf. [57].
This can also be shown directly, using the definition of \(s_0\) and \(\delta ^{\mathrm {r}}_{{\bar{a}}}\) on \(\Phi ^i\).
To be precise, \(\delta ^{\mathrm {r}}_{{\bar{a}}}\) also acts non-trivially on background fields, by \(\delta ^{\mathrm {r}}_{{\bar{a}}}{\bar{{{\mathcal {A}}}}} = {{\bar{a}}}\). However, as \(s_0\) acts trivially on background fields, so does \([\delta ^{\mathrm {r}}_{{\bar{a}}}, s_0]\).
Smoothness follows from the Hadamard property of the two-point function and [58], Thm. 8.2.14.
In this section, A denotes the advanced product, not the anomaly.
References
Abbott, L.F.: Introduction to the background field method. Acta Phys. Pol. B 13, 33 (1982)
Brunetti, R., Fredenhagen, K., Rejzner, K.: Quantum gravity from the point of view of locally covariant quantum field theory. Commun. Math. Phys. 345, 741 (2016). arXiv:1306.1058
Becker, D., Reuter, M.: En route to background independence: broken split-symmetry, and how to restore it with bi-metric average actions. Ann. Phys. 350, 225 (2014). arXiv:1404.4537
Hollands, S., Wald, R.M.: Local Wick polynomials and time ordered products of quantum fields in curved space-time. Commun. Math. Phys. 223, 289 (2001). arXiv:gr-qc/0103074
Hollands, S.: Background independence in quantum field theory. Unpublished notes (2011)
Hollands, S.: Constructing quantum field theories with fedosov quantization, 2012, Talk given at workshop Mathematical Aspects of Quantum Field Theory and Quantum Statistical Mechanics, Hamburg (2012). https://www.lqp2.org/node/1492. Accessed 3 Jan 2018
Fedosov, B.V.: A simple geometrical construction of deformation quantization. J. Differ. Geom. 40, 213 (1994)
Reuter, M.: Quantum mechanics as a gauge theory of metaplectic spinor fields. Int. J. Mod. Phys. A 13, 3835 (1998). arXiv:hep-th/9804036
Witten, E.: Conference on highlights of particle and condensed matter physics (SALAMFEST) Trieste, Italy, 8–12 March 1993, pp. 257–275 (1993). arXiv:hep-th/9306122
Sen, A., Zwiebach, B.: Quantum background independence of closed string field theory. Nucl. Phys. B 423, 580 (1994). arXiv:hep-th/9311009
Brunetti, R., Fredenhagen, K., Verch, R.: The generally covariant locality principle: a new paradigm for local quantum field theory. Commun. Math. Phys. 237, 31 (2003). arXiv:math-ph/0112041
Zahn, J.: The renormalized locally covariant Dirac field. Rev. Math. Phys. 26, 1330012 (2014). arXiv:1210.4031
Hollands, S., Wald, R.M.: Conservation of the stress tensor in perturbative interacting quantum field theory in curved spacetimes. Rev. Math. Phys. 17, 227 (2005)
Brennecke, F., Dütsch, M.: Removal of violations of the master ward identity in perturbative QFT. Rev. Math. Phys. 20, 119 (2008). arXiv:0705.3160
Collini, G.: Fedosov quantization and perturbative quantum field theory. Ph.D. dissertation, Universität Leipzig (2016). arXiv:1503.03754
Drago, N., Hack, T.P., Pinamonti, N.: The generalised principle of perturbative agreement and the thermal mass. Ann. Henri Poincaré 18, 807 (2017)
Khavkine, I.: Local and gauge invariant observables in gravity. Class. Quantum Grav. 32, 185019 (2015). arXiv:1503.03754
Bergmann, P.G., Komar, A.B.: Poisson brackets between locally defined observables in general relativity. Phys. Rev. Lett. 4, 432 (1960)
Benini, M., Schenkel, A., Schreiber, U.: The stack of Yang–Mills fields on Lorentzian manifolds. Commun. Math. Phys. 359, 765 (2018). arXiv:1704.01378
Arms, J.M.: The structure of the solution set for the Yang–Mills equations. Math. Proc. Camb. Philos. Soc. 90, 361 (1981)
Kluberg-Stern, H., Zuber, J.B.: Renormalization of nonabelian gauge theories in a background field gauge. 1. Green functions. Phys. Rev. D 12, 482 (1975)
Wald, R.M.: General Relativity. University of Chicago Press, Chicago (1984)
Chilian, B., Fredenhagen, K.: The time slice axiom in perturbative quantum field theory on globally hyperbolic spacetimes. Commun. Math. Phys. 287, 513 (2009). arXiv:0802.1642
Brunetti, R., Fredenhagen, K.: Microlocal analysis and interacting quantum field theories: renormalization on physical backgrounds. Commun. Math. Phys. 208, 623 (2000). arXiv:math-ph/9903028
Hollands, S.: Renormalized quantum Yang–Mills fields in curved spacetime. Rev. Math. Phys. 20, 1033 (2008). arXiv:0705.3340
Hollands, S., Wald, R.M.: Quantum fields in curved spacetime. Phys. Rep. 574, 1 (2015). arXiv:1401.2026
Rejzner, K.: Perturbative Algebraic Quantum Field Theory. Springer, Berlin (2016)
Hollands, S., Wald, R.M.: Existence of local covariant time ordered products of quantum fields in curved space-time. Commun. Math. Phys. 231, 309 (2002). arXiv:gr-qc/0111108
DeWitt, B.S., Brehme, R.W.: Radiation damping in a gravitational field. Ann. Phys. 9, 220 (1960)
Epstein, H., Glaser, V.: The role of locality in perturbation theory. Annales de l’IHP Physique théorique A 19, 211 (1973)
Zahn, J.: Locally covariant charged fields and background independence. Rev. Math. Phys. 27, 1550017 (2015). arXiv:1311.7661
Taslimi Tehrani, M.: Quantum BRST charge in gauge theories in curved space-time. J. Math. Phys. 60, 012304 (2019). arXiv:1703.04148
Chrusciel, P.T., Shatah, J.: Global existence of solutions of the Yang–Mills equations on globally hyperbolic four dimensional Lorentzian manifolds. Asian J. Math. 1, 530 (1997)
Becchi, C., Rouet, A., Stora, R.: Renormalization of gauge theories. Ann. Phys. 98, 287 (1976)
Batalin, I., Vilkovisky, G.: Gauge algebra and quantization. Phys. Lett. B 102, 27 (1981)
Fredenhagen, K., Rejzner, K.: Batalin–Vilkovisky formalism in perturbative algebraic quantum field theory. Commun. Math. Phys. 317, 697 (2013). arXiv:1110.5232
Rejzner, K.: Fermionic fields in the functional approach to classical field theory. Rev. Math. Phys. 23, 1009 (2011). arXiv:1101.5126
DeWitt, B.S.: Quantum theory of gravity. 2. The manifestly covariant theory. Phys. Rev. 162, 1195 (1967)
’t Hooft, G.: An algorithm for the poles at dimension four in the dimensional regularization procedure. Nucl. Phys. B 62, 444 (1973)
Honerkamp, J.: The question of invariant renormalizability of the massless Yang–Mills theory in a manifest covariant approach. Nucl. Phys. B 48, 269 (1972)
Boulware, D.G.: Gauge dependence of the effective action. Phys. Rev. D 23, 389 (1981)
Iyer, V., Wald, R.M.: Some properties of Noether charge and a proposal for dynamical black hole entropy. Phys. Rev. D 50, 846 (1994). arXiv:gr-qc/9403028
Barnich, G., Brandt, F., Henneaux, M.: Local BRST cohomology in gauge theories. Phys. Rep. 338, 439 (2000). arXiv:hep-th/0002245
Mañes, J., Stora, R., Zumino, B.: Algebraic study of chiral anomalies. Commun. Math. Phys. 102, 157 (1985)
Peierls, R.E.: The commutation laws of relativistic field theory. Proc. R. Soc. Lond. A214, 143 (1952)
DeWitt, B., DeWitt-Morette, C.: From the Peierls bracket to the Feynman functional integral. Ann. Phys. 314, 448 (2004)
Grassi, P.A.: Stability and renormalization of Yang–Mills theory with background field method: a regularization independent proof. Nucl. Phys. B 462, 524 (1996). arXiv:hep-th/9505101
Ferrari, R., Picariello, M., Quadri, A.: Algebraic aspects of the background field method. Ann. Phys. 294, 165 (2001). arXiv:hep-th/0012090
Anselmi, D.: Background field method, Batalin–Vilkovisky formalism and parametric completeness of renormalization. Phys. Rev. D 89, 045004 (2014). arXiv:1311.2704
Becchi, C., Collina, R.: Further comments on the background field method and gauge invariant effective actions. Nucl. Phys. B 562, 412 (1999). arXiv:hep-th/9907092
Gérard, C., Wrochna, M.: Hadamard states for the linearized Yang–Mills equation on curved spacetime. Commun. Math. Phys. 337, 253 (2015). arXiv:1403.7153
Wrochna, M., Zahn, J.: Classical phase space and Hadamard states in the BRST formalism for gauge field theories on curved spacetime. Rev. Math. Phys. 29, 1750014 (2017). arXiv:1407.8079
Zahn, J.: Locally covariant chiral fermions and anomalies. Nucl. Phys. B 890, 1 (2014). arXiv:1407.1994
Kugo, T., Ojima, I.: Local covariant operator formalism of nonabelian gauge theories and quark confinement problem. Prog. Theor. Phys. Suppl. 66, 1 (1979)
Dütsch, M., Fredenhagen, K.: A local (perturbative) construction of observables in gauge theories: the example of QED. Commun. Math. Phys. 203, 71 (1999)
Fröb, M.B.: Anomalies in time-ordered products and applications to the BV-BRST formulation of quantum gauge theories. Commun. Math. Phys. 372, 281 (2019). arXiv:1803.10235
Schenkel, A., Zahn, J.: Global anomalies on Lorentzian space-times. Ann. Henri Poincaré 18, 2693 (2017). arXiv:1609.06562
Hörmander, L.: The Analysis of Linear Partial Differential Operators. I. Springer, Berlin (2003)
Ichinose, S.: BRS symmetry on background field, Kallosh theorem and renormalization. Nucl. Phys. B 395, 433 (1993)
Brunetti, R., et al.: Cosmological perturbation theory and quantum gravity. JHEP 08, 032 (2016). arXiv:1605.02573
Fröb, M.B., Hack, T.P., Higuchi, A.: Compactly supported linearised observables in single-field inflation. JCAP 1707, 043 (2017). arXiv:1703.01158
Barnich, G., Brandt, F., Henneaux, M.: General solution of the Wess–Zumino consistency condition for Einstein gravity. Phys. Rev. D 51, 1435 (1995). arXiv:hep-th/9409104
Brunetti, R., Fredenhagen, K.: Quantum gravity. In: Fauser, B., Tolksdorf, J., Zeidler, E. (eds.) Towards a Background Independent Formulation of Perturbative Quantum Gravity, pp. 151–159. Springer, Basel (2006)
Rejzner, K.: Remarks on local symmetry invariance in perturbative algebraic quantum field theory. Ann. Henri Poincaré 16, 205 (2015). arXiv:1301.7037
Acknowledgements
Open Access funding provided by Projekt DEAL. We thank Klaus Fredenhagen, Markus Fröb, Thomas-Paul Hack, Kasia Rejzner, Martin Reuter, Pedro Ribeiro, Gerd Rudolph, Michał Wrochna and Stefan Hollands for helpful discussions and/or valuable hints to the literature (the latter also for several suggestions for improving the manuscript). Some of these discussion took place at the workshop “Foundational and structural aspects of gauge theories” at the Mainz Institute for Theoretical Physics (MITP). M.T.T. is grateful to the MITP for support and hospitality during this workshop. This work is part of M.T.T.’s PhD dissertation. He gratefully acknowledges financial support by the Max Planck Institute for Mathematics in the Sciences and its International Max Planck Research School (IMPRS).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Karl-Henning Rehren.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Lemmata on the Anomaly
Lemma A.1
The anomaly \(A(e_\otimes ^F)\) is (anti-) field independent, in the sense that
where \(\Phi ^i = (A_\mu ^I, B^I, C^I, \bar{C}^I)\) and \(\varepsilon \) is the Grassmann parity of \(\Phi ^i\), and analogously for \(\Phi ^\ddagger _i\).
Proof
From the anomalous Ward identity (67) and field independence (22) of time-ordered products, we have

On the other hand, we have

We thus obtain

where
It thus remains to show that

which together with (114) implies the claim. To prove this, we note that \(\frac{\delta S_0}{\delta \Phi ^i}\) is a linear expression in fields and anti-fields and, hence, can be written \(\frac{\delta S_0}{\delta \Phi ^i}= a_{i j} \Phi ^j + {b_i}^j \Phi ^{\ddag }_j\) for some (differential operator valued) coefficients \(a_{i j}, {b^i}_j\). Thus,
Therefore, (115) follows from (anti-) field independence of time-ordered products. For anti-field independence, the proof proceeds analogously. \(\square \)
Lemma A.2
Let \(\Phi ^i = (A_\mu ^I, B^I, C^I, \bar{C}^I)\). Then, \(A(\Phi ^i(x) \otimes e_\otimes ^{F})=0\), for all F, and analogously for anti-fields.
Proof
To prove the claim, we use the single field axiom, i.e., (23), which in the present situation reads

where \(\Delta ^{ij}_{\mathrm {a}}(x, y)\) is the advanced propagator of the differential operator \({\bar{P}}_{i j}\) defined in (77). We also recall definitions (79) and (80) of the (differential operator valued) matrices \(K^i_{\ j}\) and \({\hat{K}}_i^{\ j}\). From (81) and \(s_0^2 \Phi ^\ddag _i = 0\), it follows that
with \(\varepsilon \) the Grassmann parity of \(\Phi ^i\). This implies, cf. [64],
From (117) it follows that for the linear fields \( s_0 \Phi ^i\), we have

where for simplicity we omitted the variable x and \(\Delta ^{jk}_{\mathrm {a}}\tfrac{\delta }{\delta \Phi ^k}\) should be read as \(\int \Delta ^{jk}_{\mathrm {a}}(x,y) \tfrac{\delta }{\delta \Phi ^k(y)}\). To prove the claim, we first apply \(s_0\) on the left-hand side of (117) and find

with \(\varepsilon \) the Grassmann parity of \(\Phi ^i\). In the first step, we have used the anomalous Ward identity (67) and the sign factor appears by commuting \(\Phi ^i\) and \(s_0 F + \frac{1}{2}(F, F) + A(e_\otimes ^{F})\), which is fermionic. In the second step, we used (117) to pull \(\Phi ^i\) out of the time-ordered product, and in the last step, we have again used (67) and the field independence of \( A(e_\otimes ^{F})\), i.e., (113). Now applying \(s_0\) on the r.h.s. of (117), we find

Equating (120) and (121), we arrive at

where we have used (116). Using (78) and noting that \(S_0 = {S_0}|_{\Phi ^\ddag =0} - \int \Phi ^j {\hat{K}}_j^{\ k} \Phi ^\ddag _k\), we find
Inserting this back into (122) and using (118), we obtain

which vanishes by (119). This proves the claim.
For an anti-field \(\Phi ^\ddag _i\), the second term on the r.h.s. of (117) is absent, and so are the last two terms on the r.h.s. of (120) and (121). The claim then follows from (81), which entails

with \(\varepsilon \) the Grassmann parity of \(\Phi ^i\). \(\square \)
Glossary
- \({{\bar{a}}}\) :
-
Background variation satisfying \(\bar{P}^{\mathrm {lin}}{{\bar{a}}}=0\) (tangent vector fields on \(\mathcal {S}_{\mathrm {YM}}\))
- \(\bar{{{\mathcal {A}}}}\) :
-
Background G-connection
- \(A\) :
-
Dynamical \({\mathfrak {g}}\)-valued 1-form
- \(A^{\mathrm {int}}_n\) :
-
Interacting anomaly with n local insertions
- \(\Delta ^{{\mathrm {r}}/{\mathrm {a}}}_{{{\bar{\phi }}}}\) :
-
Retarded/advanced propagator of \(P_{{{\bar{\phi }}}}\)
- \(\bar{\delta }_{{{\bar{\varphi }}}}\) :
-
Variation w.r.t. background field \(\bar{\delta }_{{{\bar{\varphi }}}} = \langle \frac{\delta }{\delta {{\bar{\phi }}}} - , {{\bar{\varphi }}} \rangle \)
- \(\delta _{{{\bar{\varphi }}}}\) :
-
Variation w.r.t. dynamical field \(\delta _{{{\bar{\varphi }}}} = \langle \frac{\delta }{\delta {\phi }}- , {{\bar{\varphi }}} \rangle \)
- \(\delta ^{\mathrm {r}}_{{{\bar{\varphi }}}}\) :
-
Retarded variation
- \({\mathcal {D}}_{{{\bar{\varphi }}}}\) :
-
Connection on local functionals \(F[{{\bar{\phi }}}, \phi ]\), \({\mathcal {D}}_{{{\bar{\varphi }}}} = \bar{\delta }_{{{\bar{\varphi }}}}- \delta _{{{\bar{\varphi }}}}\)
- \({\mathfrak {D}}_{{{\bar{\varphi }}}}\) :
-
Connection on sections
 , \({\mathfrak {D}}_{{{\bar{\varphi }}}} =\delta ^{\mathrm {r}}_{{{\bar{\varphi }}}}- \delta _{{{\bar{\varphi }}}}\)
, \({\mathfrak {D}}_{{{\bar{\varphi }}}} =\delta ^{\mathrm {r}}_{{{\bar{\varphi }}}}- \delta _{{{\bar{\varphi }}}}\) - \({\mathcal {D}}_{{{\bar{a}}}}\) :
-
Connection on local functionals \(F[\bar{{{\mathcal {A}}}}, A]\), \({\mathcal {D}}_{{{\bar{a}}}} = \bar{\delta }_{{{\bar{a}}}}- \delta _{{{\bar{a}}}}\)
- \(\hat{{\mathcal {D}}}_{{{\bar{a}}}}\) :
-
Connection on local functionals \(F[\bar{{{\mathcal {A}}}}, A]\), \(\hat{\mathcal {D}}_{{{\bar{a}}}} = {{\mathcal {D}}}_{{{\bar{a}}}} - (-, {\mathcal {D}}_{{{\bar{a}}}} \Psi )\)
- \({\mathfrak {D}}_{{{\bar{a}}}}\) :
-
Connection on sections
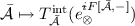
- \(\check{{\mathcal {D}}}_{{{\bar{a}}}}\) :
-
Connection on local functionals \(F[\bar{{{\mathcal {A}}}}, A]\), \(\check{{\mathcal {D}}}_{{{\bar{a}}}} = {{\mathcal {D}}}_{{{\bar{a}}}} + (-, \delta _{{{\bar{a}}}} \Psi )\)
- \({{\,\mathrm{Deg}\,}}\) :
-
Grading on functionals, \({{\,\mathrm{Deg}\,}}= \deg _\phi + 2 \deg _{\hbar }\)
- \(\mathrel {\approx }\) :
-
Equal modulo free field equations
- \(\mathrel {\approx _{{\mathbf {F}}}}\) :
-
Equality in \({{\mathbf {F}}}_{\bar{{\mathcal {A}}}}\)
- \({{\bar{\varphi }}}\) :
-
Background variation satisfying \(P_{{{\bar{\phi }}}} {{\bar{\varphi }}}=0\) (tangent vector fields on \(\mathcal {S}_{\Phi ^4}\))
- \({{\bar{\phi }}}\) :
-
Background scalar field
- \(\phi \) :
-
Dynamical scalar field
- \(\bar{F}\) :
-
Curvature of \(\bar{{\mathcal {A}}}\)
- \({{\mathbf {F}}}_{\bar{{{\mathcal {A}}}}}\) :
-
Local algebra of physical, gauge-invariant interacting quantum fields on \(\bar{{{\mathcal {A}}}}\)
- \({{\mathbf {F}}}_{{\mathrm {YM}}}\) :
-
Bundle of physical, gauge-invariant interacting quantum fields for Yang–Mills theory
-
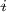 :
: -
\(\frac{i}{\hbar }\)
- \({{\mathbf {J}}}_{{\bar{\phi }}}\) :
-
Ideal of free equations of motion in background \({{\bar{\phi }}}\)
- \(J^\pm ({\mathcal {L}})\) :
-
Causal future/past of \({\mathcal {L}}\)
- \(\bar{\nabla }_\mu \) :
-
Background covariant derivative
- \({{\mathcal {O}}}\) :
-
Field
- \({{\mathcal {O}}}_{{{\bar{\phi }}}}^{\mathrm {int}}(x)\) :
-
Renormalized interacting fields at \({{\bar{\phi }}}\) (sections of \(\mathbf{W} _{\Phi ^4}\))
- \(\Omega ^k\) :
-
Bundle of k forms on M
- \(\Psi \) :
-
Gauge-fixing fermion
- \({\mathfrak {p}}\) :
-
Associated bundle \({\mathfrak {p}}= P \times _{{{\,\mathrm{ad}\,}}} {\mathfrak {g}}\)
- \(\bar{P}^{\mathrm {lin}}\) :
-
Linearized Yang–Mills operator around \(\bar{{{\mathcal {A}}}}\)
- \(P_{{{\bar{\phi }}}}\) :
-
Linearized \(\Phi ^4\) differential operator around \({{\bar{\phi }}}\)
- \(q\) :
-
Quantum BV-BRST differential, \(q= s + O(\hbar )\)
- \(Q^{\mathrm {int}}_{\bar{{{\mathcal {A}}}}}\) :
-
Quantum BRST charge
- \({\mathcal {R}}\) :
-
Localization region of observables
- \(R_{{{\bar{\phi }}}}\) :
-
Retarded products valued in \(\mathbf{W} _{{{\bar{\phi }}}}\)
- \(\mathcal {S}_{\Phi ^4}\) :
-
Manifold of on-shell background \(\Phi ^4\) configurations
- \(\mathcal {S}_{\mathrm {YM}}\) :
-
Manifold of on-shell background Yang–Mills connections
- \(s\) :
-
BV-BRST differential
- \(S\) :
-
Gauge-fixed action, \(s = {(S, - )} \)
- \(T_{{{\bar{\phi }}},n}\) :
-
Time-ordered products valued in \({{\mathbf {W}}}_{{{\bar{\phi }}}}\)
- \(T_{\bar{{\mathcal {A}}},n}\) :
-
Time-ordered products valued in \({{\mathbf {W}}}_{\bar{{{\mathcal {A}}}}}\)
- \(T^{\mathrm {int}}_{{{\bar{\phi }}}}\) :
-
Interacting time-ordered products valued in \({{\mathbf {W}}}_{{{\bar{\phi }}}}\)
- \({{\mathbf {W}}}_{{{\bar{\phi }}}}\) :
-
Algebra of quantum fields for the background \({{\bar{\phi }}}\)
- \({{\mathbf {W}}}^{\mathrm {loc}}_{{\bar{\phi }}}\) :
-
Local functionals on the background \({{\bar{\phi }}}\)
- \({{\mathbf {W}}}_{\bar{{\mathcal {A}}}}\) :
-
Algebra of quantum fields for the background \(\bar{{\mathcal {A}}}\)
- \({{\mathbf {W}}}^{\mathrm {int}}_{\Phi ^4}\) :
-
Algebra bundle of \(\Phi ^4\)-theory
- \({{\mathbf {W}}}_{{\mathrm {YM}}}\) :
-
Algebra bundle of Yang–Mills theory
- \({(F_1, F_2)}\) :
-
Anti-bracket
- \({(\mathcal {O}_1,\mathcal {O}_2)}_\hbar \) :
-
Quantum anti-bracket, \({(-,-)}_\hbar = {(-, - )} + O(\hbar )\)
- \({[\phi (x), \phi (y)]}_{\star }\) :
-
Graded commutator of quantum fields
- \(\lfloor {{\bar{\varphi }}} , {{\bar{\varphi }}}' \rfloor \) :
-
Lie bracket of vector fields on \(\mathcal {S}_{\Phi ^4}/ \mathcal {S}_{\mathrm {YM}}\)
- \([-,-]_{\mathfrak {g}}\) :
-
Lie bracket on the Lie algebra \({\mathfrak {g}}\)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Taslimi Tehrani, M., Zahn, J. Background Independence in Gauge Theories. Ann. Henri Poincaré 21, 1135–1190 (2020). https://doi.org/10.1007/s00023-020-00887-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-020-00887-4





 for
for  ,
, 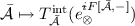
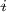 :
: