Water wave scattering and energy dissipation by interface-piercing porous plates

Abstract

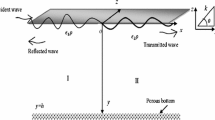
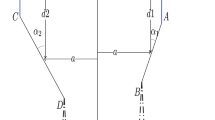
An integral equation method is developed to study the wave interaction with two symmetric permeable plates submerged in a two-layer fluid. The plates are inclined and penetrate the common interface between the layers. The existence of two different wave modes for the incident wave gives rise to two problems. Both of these are tackled by reducing them to a set of coupled hypersingular integral equations of the second kind. Unknown functions of the integral equations are the discontinuities in the potential functions across portions of the plates. These are computed numerically by employing an expansion collocation method. New results for the reflection coefficients and the amount of energy loss are presented by varying several parameters such as porosity, angle of inclination, plate-length, separation between the plates, interface position and density ratio. Known results for two symmetric vertical permeable and impermeable plates, single vertical impermeable and horizontal permeable plates are recovered from the present analysis.

Appendices

Appendix 1

The expressions of the Green’s functions ${\mathcal {G}}^{(i)}_j(x_i,z_i;\xi _j,\eta _j)$ are given in this Appendix as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {G}}^{(i)}_j(x_i,z_i;\xi _j,\eta _j)&={\mathcal {P}}^{(i)}_j\log r-{\mathcal {Q}}^{(i)}_j\log {r_1}\\&\quad -{\mathcal {R}}^{(i)}_j\log {r_2}-2\int ^{\infty }_0\\&\quad \times \frac{g^{(i)}_j(u;z_i,\eta _j)\cos u(x_i-\xi _j)}{u\Delta (u)}\text {d}u, \end{aligned} \end{aligned}$$

(40)

where ${\mathcal {P}}^{(1)}_1={\mathcal {P}}^{(1)}_2={\mathcal {P}}^{(2)}_2=1$, ${\mathcal {P}}^{(2)}_1=\rho$, ${\mathcal {Q}}^{(1)}_1={\mathcal {Q}}^{(1)}_2=1$, ${\mathcal {Q}}^{(2)}_1={\mathcal {Q}}^{(2)}_2=\rho$, ${\mathcal {R}}^{(1)}_1={\mathcal {R}}^{(2)}_1={\mathcal {R}}^{(2)}_1=0$, ${\mathcal {R}}^{(2)}_2=1-\rho$, $r,r_2=\sqrt{(x_i-\xi _j)^2+(z_i\mp \eta _j)}, r_1=\sqrt{(x_i-\xi _j)^2+(2h+z_i+\eta _j)^2}$,

$$\begin{aligned} g^{(1)}_{1}(u;z_1,\eta _1)&=\Big [-\{(u\sinh uH-K\cosh uH)\\&\quad -\rho (u-K)\sinh uH\}{\text {e}}^{-uh}\\&\quad \times \sinh u(\eta _1+h)\{u\cosh u(z_1+h)\\&\quad -K\sinh u(z_1+h)\}+{\text {e}}^{-u(\eta _1+h)}\{(1-\rho )u^2\\&\quad \times \sinh uH\cosh uz_1+\rho uK\cosh u(z_1-H)\\&\quad -uK\cosh uH\cos uz_1\}\Big ],\\ g^{(2)}_{1}(u;z_2,\eta _1)&=\rho \Big [(u^2-K^2){\text {e}}^{-uh}\sinh uh\sinh u(\eta _1+h)\\&\quad \times (1-\rho +\rho {\text {e}}^{-uH}\cosh uH)+(u\sinh uh-K\cosh uh)\\&\quad \times (K\sinh uH-u\cosh uH)\sinh u(\eta _1+h){\text {e}}^{-u(h+H)}\\&\quad +uK{\text {e}}^{-u(\eta _1+h)}\Big ]\cosh u(H-z_2)-\rho {\text {e}}^{-u(h+H)}\\&\quad \times \sinh u(\eta _1+h)\Delta (u)\sinh u(H-z_2),\\ g^{(1)}_{2}(u;z_1,\eta _2)&=\{\rho (u^2-K^2)\sinh uh \sinh uH\\&\quad +K^2\sinh uh \\&\quad \times \cosh uH-u^2\sinh uh\sinh uH-uK\cosh uh {\text {e}}^{-uH}\}\\&\quad \times {\text {e}}^{-u(h+\eta _2)}\sinh u(z_1+h)-uK\cosh uH{\text {e}}^{-u(h+\eta _2)}\\&\quad \times (\cosh uz_1-\sinh uz_1)+K{\text {e}}^{-uH}\sinh u\eta _2\\&\quad \times \{K\sinh u(z_1+h)-u\cosh u(z_1+h)\},\\g^{(2)}_{2}(u;z_2,\eta _2)& =\Big [\{\rho ^2\\&\quad \times \sinh uh(u^2-K^2)\sinh uh \sinh uH\\&\quad -\rho \sinh uh(K\cosh uh-u\sinh uh)\times (u\cosh uH-K\\&\quad \times \sinh uH)\}{\text {e}}^{-u(h+H+\eta _2)}+\rho \{(K^2-u^2)\sinh ^2uh-uK\}{\text {e}}^{-u(h+\eta _2)}\\&\quad +(\rho -1)u{\text {e}}^{-u\eta _2}\\&\quad \times (K\cosh uh-u\sinh uh)+\rho {\text {e}}^{-uH}\\&\quad \times \sinh u\eta _2 \sinh uh \\&\quad \times \cosh uH(K^2-u^2)-{\text {e}}^{-uH}\sinh u\eta _2\\&\quad \times (u\cosh uH-K\sinh uH)(K\cosh uh-u\sinh uh)\Big ] \\&\quad \times \cosh u(H-z_2)-\{{\text {e}}^{-uH}\sinh u\eta _2\\&\quad +\rho {\text {e}}^{-u(h+H+\eta _2)}\sinh uh\}\Delta (u)\sinh u(H-z_2). \end{aligned}$$

Our analysis may be restricted to the region $x\ge 0$ only due to the geometrical symmetry of the two plates about the z-axis. When the source point is in the upper layer, we first apply Green’s integral theorem to the functions ${\mathcal {G}}^{(1)S,A}_1(x_1,z_1;\xi _1,\eta _1)={\mathcal {G}}^{(1)}_1(x_1,z_1;\xi _1,\eta _1)\pm {\mathcal {G}}^{(1)}_1(-x_1,z_1;\xi _1,\eta _1)$ and the scattered velocity potentials ${\widehat{\varphi }}^{(1)S,A}_n=\varphi ^{(1)S,A}(x_1,z_1)-f^{(1)}_n(z_1){\text {e}}^{-\text {i}M_n(x_1-a)}$ in the region bounded by the lines $z_1=-h,0 (0\le x_1\le X); x_1=0,X (-h\le z_1\le 0);$ a small circle of radius $\varepsilon$ with center at $(\xi _1,\eta _1)$ and a contour enclosing the arc $L_1$, and ultimately we make $X\rightarrow \infty , \varepsilon \rightarrow 0$ and shrink the contour enclosing $L_1$ in the two sides of $L_1$. Using conditions 2 and 10, we obtain

$$\begin{aligned}&\int ^{0}_{-h}\Big ({\widehat{\varphi }}^{(1)S,A}_n\frac{\partial {\mathcal {G}}^{(1)S,A}_1}{\partial x_1}\nonumber \\&\quad -{\mathcal {G}}^{(1)S,A}_1\frac{\partial {\widehat{\varphi }}^{(1)S,A}_n}{\partial x_1}\Big )_{x_1=\infty }\text {d}z_1+\int ^{\infty }_0\Big ({\widehat{\varphi }}^{(1)S,A}_n\nonumber \\&\quad \times \frac{\partial {\mathcal {G}}^{(1)S,A}_1}{\partial z_1}-{\mathcal {G}}^{(1)S,A}_1\frac{\partial {\widehat{\varphi }}^{(1)S,A}_n}{\partial z_1}\Big )_{z_1=0}\text {d}x_1\nonumber \\&\quad +{\text {e}}^{\text {i}M_na}\int _{-h}^0\Big (\text {i}M_n {\mathcal {G}}^{(1)S}_1(0,z_1;\xi _1,\eta _1),\nonumber \\&\quad \times \frac{\partial {\mathcal {G}}^{(1)A}_1}{\partial x_1}(0,z_1;\xi _1,\eta _1)\Big ) f^{(1)}_n(z_1)\text {d}z_1\nonumber \\&\quad -\int _{L_1}[\varphi ^{(1)S,A}_n](q_1)\nonumber \\&\quad \times \frac{\partial {\mathcal {G}}^{(1)S,A}_1(q_1:\xi _1,\eta _1)}{\partial N_{q_1}}~\text {d}s_{q_1}\nonumber \\&\quad -2\pi {\widehat{\varphi }}^{(1)S,A}_n(\xi _1,\eta _1)=0. \end{aligned}$$

(41)

Again we apply Green’s integral theorem to the functions ${\mathcal {G}}^{(2)S,A}_1(x_2,z_2;\xi _1,\eta _1)={\mathcal {G}}^{(2)}_1(x_2,z_2;\xi _1,\eta _1)\pm {\mathcal {G}}^{(2)}_1(-x_2,z_2;\xi _1,\eta _1)$ and the scattered velocity potentials ${\widehat{\varphi }}^{(2)S,A}_n=\varphi ^{(2)S,A}(x_2,z_2)-f^{(2)}_n(z_2){\text {e}}^{-\text {i}M_n(x_2-a)}$ in the region bounded by the lines $z_2=0,H (0\le x_2\le X); x_2=0,X (0\le z_2\le H);$ and a contour enclosing the arc $L_2$, and ultimately we make $X\rightarrow \infty ,$ and shrink the contour enclosing $L_2$ in the two sides of $L_2$. Using conditions 5 and 10, we obtain

$$\begin{aligned}&\int ^{H}_0\Bigg ({\widehat{\varphi }}^{(2)S,A}_n\frac{\partial {\mathcal {G}}^{(2)S,A}_1}{\partial x_2}\nonumber \\&\quad -{\mathcal {G}}^{(2)S,A}_1\frac{\partial {\widehat{\varphi }}^{(2)S,A}_n}{\partial x_2}\Bigg )_{x_2=\infty }\text {d}z_2\nonumber \\&\quad -\int ^{\infty }_0\Big ({\widehat{\varphi }}^{(2)S,A}_n\nonumber \\&\quad \times \frac{\partial {\mathcal {G}}^{(2)S,A}_1}{\partial z_2}-{\mathcal {G}}^{(2)S,A}_1\nonumber \\&\quad \times \frac{\partial {\widehat{\varphi }}^{(2)S,A}_n}{\partial z_2}\Big )_{z_2=0}\text {d}x_2\nonumber \\&\quad +{\text {e}}^{\text {i}M_na}\int _{0}^H\Big (\text {i}M_n {\mathcal {G}}^{(2)S}_1(0,z_2;\xi _2,\eta _1),\nonumber \\&\quad \times \frac{\partial {\mathcal {G}}^{(2)A}_1}{\partial x_2}(0,z_2;\xi _1,\eta _1)\Big ) f^{(2)}_n(z_2)\text {d}z_2\nonumber \\&\quad -\int _{L_2}[\varphi ^{(2)S,A}_n](q_2)\nonumber \\&\quad \times \frac{\partial {\mathcal {G}}^{(2)S,A}_1(q_2:\xi _1,\eta _1)}{\partial N_{q_2}}~\text {d}s_{q_2}=0. \end{aligned}$$

(42)

Multiplying Eq. 41 by $\rho$ and adding to Eq. 42 and using the interface conditions we find

$$\begin{aligned}&-\int _{L_1} \rho [\varphi ^{(1)S,A}_n](q_1)\frac{\partial {\mathcal {G}}^{(1)S,A}_1(q_1:\xi _1,\eta _1)}{\partial N_{q_1}}~\text {d}s_{q_1}\nonumber \\&\quad -\int _{L_2} [\varphi ^{(2)S,A}_n](q_2)\frac{\partial {\mathcal {G}}^{(2)S,A}_1(q_2:\xi _1,\eta _1)}{\partial N_{q_2}}~\text {d}s_{q_2}\nonumber \\&\quad -2\pi \rho {\widehat{\varphi }}^{(1)S,A}_n(\xi _1,\eta _1)\\&\quad \pm 2\pi \rho f^{(1)}_n(\eta _1){\text {e}}^{\text {i}M_n(\xi _1+a)}=0. \end{aligned}$$

Thus, the above equation simplifies to

$$\begin{aligned}&\int _{L_1} \rho [\varphi ^{(1)S,A}_n](q_1)\nonumber \\&\qquad \times \frac{\partial {\mathcal {G}}^{(1)S,A}_1(q_1:\xi _1,\eta _1)}{\partial N_{q_1}}~\text {d}s_{q_1}+\int _{L_2} [\varphi ^{(2)S,A}_n](q_2)\nonumber \\&\qquad \times \frac{\partial {\mathcal {G}}^{(2)S,A}_1(q_2:\xi _1,\eta _1)}{\partial N_{q_2}}~\text {d}s_{q_2}\nonumber \\&\qquad +2\pi \rho \varphi ^{(1)S,A}(\xi _1,\eta _1)\nonumber \\&\quad =4\pi \rho {\text {e}}^{\text {i}M_na}f^{(1)}_n(\eta _1)(\cos (M_n\xi _1),\nonumber \\&\qquad -\text {i}\sin (M_n\xi _1)). \end{aligned}$$

(43)

Next, we consider the case when the source point is in the lower layer. Following a similar procedure as described above, we obtain

$$\begin{aligned}&\int _{L_1} \rho [\varphi ^{(1)S,A}_n](q_1)\frac{\partial {\mathcal {G}}^{(1)S,A}_2(q_1:\xi _2,\eta _2)}{\partial N_{q_1}}~\text {d}s_{q_1}\nonumber \\&\quad +\int _{L_2} [\varphi ^{(2)S,A}_n](q_2)\nonumber \\&\qquad \times \frac{\partial {\mathcal {G}}^{(2)S,A}_2(q_2:\xi _2,\eta _2)}{\partial N_{q_2}}~\text {d}s_{q_2}\nonumber \\&\qquad +2\pi \varphi ^{(2)S,A}(\xi _2,\eta _2)\nonumber \\&\quad =4\pi {\text {e}}^{\text {i}M_na}f^{(2)}_n(\eta _2)(\cos (M_n\xi _2),-\text {i}\sin (M_n\xi _2)). \end{aligned}$$

(44)

Appendix 2

The functions ${\mathcal {H}}^{(i)S,A}_j(t,s)$ given in 23 are computed by taking repeated normal derivatives of ${\mathcal {G}}^{(i)S,A}_{j}(q_i:p_j)$. The final explicit expression of ${\mathcal {H}}^{(i)S,A}_j(t,s)$ are

$$\begin{aligned} {\mathcal {H}}^{(i)S,A}_j(t,s)&=-\lambda ^{(i)}_{j}\frac{1}{(tb_i+sb_j)^2}+A^{(i)}_{j}\nonumber \\&\quad \times \Bigg [\frac{(Z^{(i)}_j+2h)^2-(X^{(i)}_j)^2}{\{(Z^{(i)}_j+2h)^2+(X^{(i)}_j)^2\}^2}\nonumber \\&\quad \pm \frac{(Z^{(i)}_{1j})^2-(X^{(i)}_{1j})^2}{\{(Z^{(i)}_{1j})^2+(X^{(i)}_{1j})^2\}^2}\mp \nonumber \\&\quad \times \cos 2\theta \frac{(Z^{(i)}_j+2h)^2-(X^{(i)}_{1j})^2}{\{(Z^{(i)}_j+2h)^2+(X^{(i)}_{1j})^2\}^2}\nonumber \\&\quad \pm 2\sin 2\theta \frac{(Z^{(i)}_j+2h)(X^{(i)}_{1j})}{\{(Z^{(i)}_j+2h)^2+(X^{(i)}_{1j})^2\}^2}\Bigg ]\nonumber \\&\quad +B^{(i)}_{j}\Bigg [\frac{(Z^{(i)}_{j})^2-(X^{(i)}_{j})^2}{\{(Z^{(i)}_{j})^2+(X^{(i)}_{j})^2\}^2}\nonumber \\&\quad \pm \frac{(Z^{(i)}_{1j})^2-(X^{(i)}_{1j})^2}{\{(Z^{(i)}_{1j})^2+(X^{(i)}_{1j})^2\}^2}\nonumber \\&\quad \mp \cos 2\theta \frac{(Z^{(i)}_j)^2-(X^{(i)}_{1j})^2}{\{(Z^{(i)}_j)^2+(X^{(i)}_{1j})^2\}^2}\nonumber \\&\quad \pm \sin 2\theta \frac{(Z^{(i)}_j)(X^{(i)}_{1j})}{\{(Z^{(i)}_j)^2+(X^{(i)}_{1j})^2\}^2}\Bigg ]\nonumber \\&\quad -\Bigg [2\pi \text {i}\sum \limits _{n=I}^{II}M_n\{C^{(i)}_{j}(M_n;z_i,\eta _j)\nonumber \\&\quad +\frac{1}{\text {i}}D^{(i)}_{j}(M_n;z_i,\eta _j)\}\frac{{\text {e}}^{iM_n\mid X^{(i)}_j\mid }}{\Delta ^{'}(M_n)}\nonumber \\&\quad \pm 2\pi \text {i}\sum \limits _{n=I}^{II}M_n\{E^{(i)}_{j}(M_n;z_i,\eta _j)\nonumber \\&\quad +\frac{1}{\text {i}}F^{(i)}_{j}(M_n;z_i,\eta _j)\}\frac{{\text {e}}^{iM_n\mid X^{(i)}_{1j}\mid }}{\Delta ^{'}(M_n)}\Bigg ]\nonumber \\&\quad -\Bigg [\text {i}\int ^{\infty }_0r\{C^{(i)}_{j}(r{\text {e}}^{\text {i}\frac{\pi }{4}};z_i,\eta _j)+\frac{1}{\text {i}}D^{(i)}_{j}(r{\text {e}}^{\text {i}\frac{\pi }{4}};z_i,\eta _j)\}\nonumber \\&\quad \times \frac{{\text {e}}^{ir{\text {e}}^{\text {i}\frac{\pi }{4}}\mid X^{(i)}_j\mid }}{\Delta ^(r{\text {e}}^{\text {i}\frac{\pi }{4}})}\text {d}r\nonumber \\&\quad +\text {i}\int ^{\infty }_0r\{-C^{(i)}_{j}(r{\text {e}}^{-\text {i}\frac{\pi }{4}};z_i,\eta _j)\nonumber \\&\quad +\frac{1}{\text {i}}D^{(i)}_{j}(r{\text {e}}^{-\text {i}\frac{\pi }{4}};z_i,\eta _j)\}\frac{{\text {e}}^{-ir{\text {e}}^{\text {i}\frac{\pi }{4}}\mid X^{(i)}_j\mid }}{\Delta ^(r{\text {e}}^{-\text {i}\frac{\pi }{4}})}\text {d}r\nonumber \\&\quad \pm \text {i}\int ^{\infty }_0r\{E^{(i)}_{j}(r{\text {e}}^{\text {i}\frac{\pi }{4}};z_i,\eta _j)\nonumber \\&\quad +\frac{1}{\text {i}}F^{(i)}_{j}(r{\text {e}}^{\text {i}\frac{\pi }{4}};z_i,\eta _j)\}\frac{{\text {e}}^{ir{\text {e}}^{\text {i}\frac{\pi }{4}}\mid X^{(i)}_{1j}\mid }}{\Delta ^(r{\text {e}}^{\text {i}\frac{\pi }{4}})}\text {d}r\nonumber \\&\quad \pm \text {i}\int ^{\infty }_0r\{-E^{(i)}_{j}(r{\text {e}}^{-\text {i}\frac{\pi }{4}};z_i,\eta _j)\nonumber \\&\quad +\frac{1}{\text {i}}F^{(i)}_{j}(r{\text {e}}^{-\text {i}\frac{\pi }{4}};z_i,\eta _j)\}\frac{{\text {e}}^{-ir{\text {e}}^{\text {i}\frac{\pi }{4}}\mid X^{(i)}_{1j}\mid }}{\Delta ^(r{\text {e}}^{-\text {i}\frac{\pi }{4}})}\text {d}r\Bigg ]. \end{aligned}$$

(45)

The various quantities appearing in 45 are given by $\lambda ^{(1)}_{1}=\lambda ^{(2)}_{2}=0$,$\lambda ^{(2)}_{1}=\lambda ^{(1)}_{2}=1$,$A^{(1)}_{1}=A^{(1)}_{2}=1,A^{(2)}_{1}=A^{(2)}_{2}=\rho$,$B^{(1)}_{1}=B^{(1)}_{2}=B^{(2)}_{1}=0,B^{(2)}_{2}=1-\rho$, $X^{(i)}_j=x_i-\xi _j$, $Z^{(i)}_j=z_i+\eta _j$, $X^{(i)}_{1j}=x_i+\xi _j$, $Z^{(i)}_{1j}=z_i-\eta _j$, $C^{(i)}_{j}(u;z_i,\eta _j)=\cos ^2\theta g^{(i)}_{j}(u;z_i,\eta _j)+\sin ^2\theta \frac{1}{u^2}\frac{\partial ^{2}g^{(i)}_{j}}{\partial z_i\partial \eta _j}(u;z_i,\eta _j)$, $D^{(i)}_{j}(u;z_i,\eta _j)=\cos \theta \sin \theta \{ -\frac{1}{u}\frac{\partial g^{(i)}_{j}}{\partial \eta _j}(u;z_i,\eta _j)+\frac{1}{u}\frac{\partial g^{(i)}_{j}}{\partial z_i}(u;z_i,\eta _j)\}$, $E^{(i)}_{j}(u;z_i,\eta _j)=-\cos ^2\theta g^{(i)}_{j}(u;z_i,\eta _j)+\sin ^2\theta \frac{1}{u^2}\frac{\partial ^{2}g^{(i)}_{j}}{\partial z_i\partial \eta _j}(u;z_i,\eta _j)$, $F^{(i)}_{j}(u;z_i,\eta _j)=\cos \theta \sin \theta \{ -\frac{1}{u}\frac{\partial g^{(i)}_{j}}{\partial \eta _j}(u;z_i,\eta _j)-\frac{1}{u}\frac{\partial g^{(i)}_{j}}{\partial z_i}(u;z_i,\eta _j)\}$.