Abstract
Scalar wave propagation across a semi-infinite step or step-like discontinuity on any one boundary of the square lattice waveguides is considered within nearest-neighbour interaction approximation. An application of the Wiener–Hopf method does yield an exact solution of the discrete scattering problem, using which, as the main result of the paper, the transmission coefficients for energy flux are obtained. It is assumed that a wave mode is incident from either side of the step and the question addressed is what fraction of incident energy is transmitted across the atomic step discontinuity. A total of ten configurations are presented that arise due to various placements of discrete Dirichlet and Neumann boundary conditions on the waveguide. Numerical illustrations of a measure of ‘conductance’ are provided.








Similar content being viewed by others
Notes
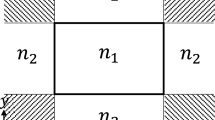
except for site(s) located at the step discontinuity in four cases (e), (f), (i), and (j), as shown in Fig. 1, on the interface of two types of boundary, pointed out individually as well; at \({{\mathtt {x}}}=0, {{\mathtt {y}}}=1\) in (e) and (f), in place of (1.2b), \(\mathrm {b}^2\ddot{\mathtt {u}}_{{{\mathtt {x}}}, {{\mathtt {y}}}}={\mathtt {u}}_{{{\mathtt {x}}}+1, {{\mathtt {y}}}}+{\mathtt {u}}_{{{\mathtt {x}}}, {{\mathtt {y}}}+ 1}-2{\mathtt {u}}_{{{\mathtt {x}}}, {{\mathtt {y}}}}\) while in (i) and (j), \(\mathrm {b}^2\ddot{\mathtt {u}}_{{{\mathtt {x}}}, {{\mathtt {y}}}}={\mathtt {u}}_{{{\mathtt {x}}}+1, {{\mathtt {y}}}}+{\mathtt {u}}_{{{\mathtt {x}}}, {{\mathtt {y}}}+ 1}-3{\mathtt {u}}_{{{\mathtt {x}}}, {{\mathtt {y}}}}\).
Evidently,
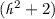 in Table 1 can be also written as \({{F}}({{z}}; {{z}}_{{F}}({\frac{1}{2}}\pi ))\); also
in Table 1 can be also written as \({{F}}({{z}}; {{z}}_{{F}}({\frac{1}{2}}\pi ))\); also 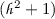 can be written as \({{F}}({{z}}; {{z}}_{{F}}(\frac{1}{3}\pi ))\).
can be written as \({{F}}({{z}}; {{z}}_{{F}}(\frac{1}{3}\pi ))\).
References
Papadopoulos, V.M.: The scattering effect of a junction between two circular waveguides. Q. J. Mech. Appl. Math. 10(2), 191–209 (1957). https://doi.org/10.1093/qjmam/10.2.191
Cahill, D.G., Ford, W.K., Goodson, K.E., Mahan, G.D., Majumdar, A., Maris, H.J., Merlin, R., Phillpot, S.R.: Nanoscale thermal transport. J. Appl. Phys. 93(2), 793–818 (2003). https://doi.org/10.1063/1.1524305
Cahill, D.G., Braun, P.V., Chen, G., Clarke, D.R., Fan, S., Goodson, K.E., Keblinski, P., King, W.P., Mahan, G.D., Majumdar, A., Maris, H.J., Phillpot, S.R., Pop, E., Li, S.: Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 1(1), 100305 (2014). https://doi.org/10.1063/1.4832615
Fellay, A., Gagel, F., Maschke, K., Virlouvet, A., Khater, A.: Scattering of vibrational waves in perturbed quasi-one-dimensional multichannel waveguides. Phys. Rev. B 55, 1707–1717 (1997). https://doi.org/10.1103/PhysRevB.55.1707
Ladik, J.: Ab-initio self-consistent field theory for the treatment of interface between two different quasi-one-dimensional chains. Prog. Surf. Sci. 26(1), 135–143 (1987). https://doi.org/10.1016/0079-6816(87)90054-2
Kosevich, Y.A., Feher, A., Syrkin, E.S.: Resonance absorption, reflection, transmission of phonons and heat transfer through interface between two solids. Low Temp. Phys. 34(7), 575–582 (2008). https://doi.org/10.1063/1.2957011
Kosevich, Y.A.: Multichannel propagation and scattering of phonons and photons in low-dimension nanostructures. Phys. Uspekhi 51(8), 848 (2008)
Santamore, D.H., Cross, M.C.: Effect of phonon scattering by surface roughness on the universal thermal conductance. Phys. Rev. Lett. 87(11), 115502 (2001)
Sánchez-Gil, J.A., Freilikher, V., Yurkevich, I., Maradudin, A.A.: Coexistence of ballistic transport, diffusion, and localization in surface disordered waveguides. Phys. Rev. Lett. 80(5), 948 (1998)
Sánchez-Gil, J.A., Freilikher, V., Maradudin, A.A., Yurkevich, I.V.: Reflection and transmission of waves in surface-disordered waveguides. Phys. Rev. B 59(8), 5915 (1999)
Mujica, V., Kemp, M., Ratner, M.A.: Electron conduction in molecular wires. I. A scattering formalism. J. Chem. Phys. 101(8), 6849–6855 (1994). https://doi.org/10.1063/1.468314
Virlouvet, A., Khater, A., Aouchiche, H., Rafil, O., Maschke, K.: Scattering of vibrational waves in perturbed two-dimensional multichannel asymmetric waveguides as on an isolated step. Phys. Rev. B 59, 4933–4942 (1999). https://doi.org/10.1103/PhysRevB.59.4933
Wiener, N., Hopf, E.: Über eine klasse singulärer integralgleichungen. Sitzungsber. Preuss. Akad. Wiss. Berlin Phys. Math. 32, 696–706 (1931)
Noble, B.: Methods Based on the Wiener–Hopf Technique. Pergamon Press, London (1958)
Mittra, R., Lee, S.W.: Analytical Techniques in the Theory of Guided Waves, Macmillan Series in Electrical Science. Macmillan, New York (1971)
Kosevich, Arnold M.: The Crystal Lattice: Phonons, Solitons, Dislocations, Superlattices. Wiley, Weinheim (2005). 2nd rev. and updated ed
Ohring, M.: Mechanical properties of thin films. In: Ohring, M. (ed.) Materials Science of Thin Films, 2nd edn, pp. 711–781. Academic Press, San Diego (2002). https://doi.org/10.1016/B978-012524975-1/50015-X
Gong, H., Rao, M., Laughlin, D.E., Lambeth, D.N.: Highly oriented perpendicular Co-alloy media on Si(111) substrates. J. Appl. Phys. 85, 4699–4701 (1999). https://doi.org/10.1063/1.370452
Ohtake, M., Yabuhara, O., Nukaga, Y., Futamoto, M.: Preparation of Co(0001)\(_{hcp}\) and (111)\(_{fcc}\) films on single-crystal oxide substrates. J. Phys. Conf. Ser. 303(1), 012016 (2011). https://doi.org/10.1088/1742-6596/303/1/012016
Sharma, B.L.: Diffraction of waves on square lattice by semi-infinite crack. SIAM J. Appl. Math. 75(3), 1171–1192 (2015). https://doi.org/10.1137/140985093
Sharma, B.L.: Diffraction of waves on square lattice by semi-infinite rigid constraint. Wave Motion 59, 52–68 (2015). https://doi.org/10.1016/j.wavemoti.2015.07.008
Sharma, B.L., Maurya, G.: Discrete scattering by a pair of parallel defects. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 378, 1–20 (2019). https://doi.org/10.1098/rsta.2019.0102
Sharma, B.L., Eremeyev, V.A.: Wave transmission across surface interfaces in lattice structures. Int. J. Eng. Sc. 145, 103173 (2019). https://doi.org/10.1016/j.ijengsci.2019.103173
Eremeyev, V.A., Sharma, B.L.: Anti-plane surface waves in media with surface structure: discrete vs. continuum model. Int. J. Eng. Sci. 143, 33–38 (2019). https://doi.org/10.1016/j.ijengsci.2019.06.007
Gurtin, M.E., Murdoch, A.I.: A continuum theory of elastic material surfaces. Arch. Ration. Mech. An. 57(4), 291–323 (1975)
Gurtin, M.E., Murdoch, A.I.: Surface stress in solids. Int. J. Solids Struct. 14(6), 431–440 (1978)
Steigmann, D.J., Ogden, R.W.: Plane deformations of elastic solids with intrinsic boundary elasticity. Proc. R. Soc. A 453(1959), 853–877 (1997)
Steigmann, D.J., Ogden, R.W.: Elastic surface-substrate interactions. Proc. R. Soc. A 455(1982), 437–474 (1999)
Rego, L.G.C., Kirczenow, G.: Quantized thermal conductance of dielectric quantum wires. Phys. Rev. Lett. 81, 232–235 (1998). https://doi.org/10.1103/PhysRevLett.81.232
Schwab, K., Henriksen, E.A., Worlock, J.M., Roukes, M.L.: Measurement of the quantum of thermal conductance. Nature 404(6781), 974–977 (2000)
Marcuvitz, N.: Waveguide Handbook. IEE Electromagnetic Waves Series, Institution of Electrical Engineers. P. Peregrinus, ISBN 9780863410581, (1951)
Collin, R.E.: Field Theory of Guided Waves. IEEE/OUP Series on Electromagnetic Wave Theory. IEEE Press (1991)
Linton, C.M., McIver, P.: Handbook of Mathematical Techniques for Wave/Structure Interactions. CRC Press, Boca Raton (2001)
Burns, W.K., Milton, A.: Mode conversion in planar-dielectric separating waveguides. Quantum Electron. IEEE J. 11(1), 32–39 (1975). https://doi.org/10.1109/JQE.1975.1068511
Kokubo, Y.: Waveguide Mode Converters. INTECH Open Access Publisher, London (2011)
Sharma, B.L.: Wave propagation in bifurcated waveguides of square lattice strips. SIAM J. Appl. Math. 76(4), 1355–1381 (2016). https://doi.org/10.1137/15M1051464
Mason, J.C., Handscomb, D.C.: Chebyshev polynomials. Chapman & Hall/CRC, Boca Raton (2003)
Sharma, B.L.: On linear waveguides of square and triangular lattice strips: an application of chebyshev polynomials. SIAM J. Appl. Math. 42(6), 901–927 (2017). https://doi.org/10.1007/s12046-017-0646-4
Jury, E.I.: Theory and Application of the z-transform Method. John Wiley, New York (1964)
Slepyan, L.I.: Models and Phenomena in Fracture Mechanics. Springer, New York (2002)
Chebyshev, P.L.: Théorie des mécanismes connus sous le nom de parallélogrammes. Mém. Acad. Sci. Pétersb. 7, 539–568 (1854). The theory of mechanisms that are known under the name of parallelograms
Sharma, B.L.: On prototypical wave transmission across a junction of waveguides with honeycomb structure. Zeitschrift für angewandte Mathematik und Physik 69(1), 16 (2018). https://doi.org/10.1007/s00033-018-0909-x
Brillouin, L.: Wave Propagation in Periodic Structures; Electric Filters and Crystal Lattices. Dover Publications, New York (1953)
Sharma, B. L.: Kinematically restricted phonon transmission in partly-unzipped tubes of square and triangular lattices (2018). arXiv:1808.01873
Sharma, B.L.: Electronic transport across a junction between armchair graphene nanotube and zigzag nanoribbon. Eur. Phys. J. B 91(5), 84 (2018). https://doi.org/10.1140/epjb/e2018-80647-2
Sharma, B.L.: On electronic conductance of partially unzipped armchair nanotubes: further analysis. Eur. Phys. J. B 92(1), 1 (2019). https://doi.org/10.1140/epjb/e2018-90391-2
Maurya, G., Sharma, B.L.: Wave scattering on lattice structures involving array of cracks. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. (2019). https://doi.org/10.1098/rspa.2019.0866
Sharma, B.L.: On scattering of waves on square lattice half-plane with mixed boundary condition. Zeitschrift für angewandte Mathematik und Physik 68(5), 120 (2017). https://doi.org/10.1007/s00033-017-0854-0
ScienceDaily. Unzipping graphene nanotubes into nanoribbons: elegant mathematical solution explains how flow of electrons changes when carbon nanotubes turn into zigzag nanoribbons. (2018). https://www.sciencedaily.com/releases/2018/06/180605103416.htm
Callaway, J.: Energy Band Theory Pure and Applied Physics. Academic Press, New York (1964)
Acknowledgements
The partial support of SERB MATRICS grant MTR/2017/000013 is gratefully acknowledged. This work has been available free of peer review on the arXiv since 12/2019. The author thanks both anonymous reviewers for their constructive comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
A Auxiliary expressions
1.1 A.1
It is easily conceivable that there are four combinatorial variants of the square lattice waveguides (also the same are studied in detail by [38]) which are denoted by self-explanatory notation  where the superscript on \({{\mathfrak {S}}}\) represents the upper boundary and the subscript represents the lower boundary. Indeed, in terms of the Chebyshev polynomials, using the definition (2.7), the dispersion relations for square lattice waveguides of width \({\mathtt {N}}\) [36, 38] are:
where the superscript on \({{\mathfrak {S}}}\) represents the upper boundary and the subscript represents the lower boundary. Indeed, in terms of the Chebyshev polynomials, using the definition (2.7), the dispersion relations for square lattice waveguides of width \({\mathtt {N}}\) [36, 38] are:



Also (A.1c), using the Chebyshev polynomials \({\mathtt {V}}_n\) of the third kind, can be expressed as \({\mathtt {V}}_{{\mathtt {N}}}({\vartheta })=0\). Moreover, the expressions of the numerator and denominator of the kernel can be further expanded as stated in Table 1; in particular, (2.10) transforms to  (2.13) to
(2.13) to  (2.17) to
(2.17) to  (2.18) to
(2.18) to  (2.27) to
(2.27) to  (2.30) to
(2.30) to  (2.35) to
(2.35) to  (2.36) to
(2.36) to  (2.45) to
(2.45) to  and (2.48) to
and (2.48) to  .
.
1.2 A.2
By application of the discrete Fourier transform (1.5), the discrete Helmholtz equation (1.4), for all \({\mathtt {y}}\in {\mathbb {Z}}\) with \({\mathtt {y}}\) away from the boundary of the given lattice waveguide, is expressed as




The complex functions  ,
,  , and \({\lambda }\) are defined on \({\mathbb {C}}\setminus {{\mathcal {B}}}\) where \({{\mathcal {B}}}\) denotes the union of branch cuts for \({{\lambda }}\), borne out of the chosen branch
, and \({\lambda }\) are defined on \({\mathbb {C}}\setminus {{\mathcal {B}}}\) where \({{\mathcal {B}}}\) denotes the union of branch cuts for \({{\lambda }}\), borne out of the chosen branch  for
for  and
and  such that \(|{{\lambda }}({{z}})|\le 1, {{z}}\in {\mathbb {C}}\setminus {{\mathcal {B}}},\) as \({\upomega }_2\) in (A.2c) is positive. Note that
such that \(|{{\lambda }}({{z}})|\le 1, {{z}}\in {\mathbb {C}}\setminus {{\mathcal {B}}},\) as \({\upomega }_2\) in (A.2c) is positive. Note that  . The general solution of (A.2a) is given by the expression
. The general solution of (A.2a) is given by the expression
where \({ c }_{1, 2}\) are arbitrary analytic functions of z in \({{{\mathcal {A}}}}\) (to be specified in the Wiener–Hopf formulation for each case).
B Reflectance and transmittance using the numerical solution
The reflectance \({{{\mathscr {R}}}}\) (resp. transmittance \({{\mathscr {T}}}\)) is the ratio of the energy flux in the outgoing wave ahead (resp. behind) of the cracks to the energy flux carried by the incident wave [43]. The energy flux is calculated across two vertical segments \({\mathscr {S}}_{{A},{B}}\) between \(\mathtt {x}=\pm X\) and \(\mathtt {x}=\pm X\pm 1\) (X is taken much larger than \({\mathtt {N}}\) so that \({\mathscr {S}}_{A,B}\) are far away from the location of step). The segment \({\mathscr {S}}_{A}\) intersects \({\mathtt {N}}\) horizontal bonds as it is located on the portion ahead of the step, while the segment \({\mathscr {S}}_{B}\) intersects \({\mathtt {N}}-{\mathtt {N}}_{step}\) horizontal bonds as it is located on the portion behind the step. Assume that the wave mode is incident from the portion ahead of the step (i.e., \({s}={A}\)). Then, following [43], the energy flux carried by the incident wave across \({\mathscr {S}}_{A}\) is
and the energy flux in the outgoing wave reflected back across \({\mathscr {S}}_{A}\) can be written as
Similarly, the energy flux in the outgoing wave behind the step, that is, the energy flux carried by the transmitted waves across \({\mathscr {S}}_{B}\) is determined as
Using (B.1), (B.2), and (B.3), the reflectance and transmittance can be written as
respectively. Analogous expressions holds for the incident from the portion behind the step (i.e., \({s}={B}\)).
Rights and permissions
About this article
Cite this article
Sharma, B.L. Transmission of waves across atomic step discontinuities in discrete nanoribbon structures. Z. Angew. Math. Phys. 71, 73 (2020). https://doi.org/10.1007/s00033-020-01294-9
Received:
Revised:
Published:
DOI: https://doi.org/10.1007/s00033-020-01294-9



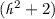 in Table
in Table 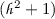 can be written as
can be written as