Two-Body Orbital Boundary Value Problems in Regularized Coordinates

Abstract

Lambert’s two-body orbital boundary value problem (BVP) is the determination of the terminal velocity vectors of a trajectory connecting two fixed positions in a specified transfer time. The solution to Lambert’s problem is often the basis for preliminary trajectory design and optimization. In this work, several related two-body orbital BVPs, with constraints involving terminal velocities, flight-path angle, Δv, final radius, transfer angle, etc., are studied. Exact solutions to these BVPs are derived in a universal form via the Kustaanheimo-Stiefel transformation. The solutions are regular and completely analytic if the energy of the transfer orbit is known a priori. Otherwise, they require root-finding of either a polynomial or a transcendental equation with well-defined bounds on its roots. The algorithms developed are validated on several orbit transfer problems and can enable complex mission analysis and parametric studies or serve as initial guesses for high-fidelity numerical optimization schemes.

Appendices

Appendix A: Bounds on the Iteration Variable

For the BVPs with fixed transfer times, e.g., the Lambert and reentry BVPs, the transfer-time equation must be solved iteratively using numerical root-finding methods. The iteration variable is the argument (z) of the Stumpff functions. It is essential to know the bounds on the values of z for each type of conic trajectory. For parabolic transfers, the value of z is trivially 0. For the other two cases, a relation between z and the eccentric anomaly or hyperbolic anomaly is sought, which can be used to compute the appropriate bounds on z. [27] (Chapter III) have shown that the parametric trajectory in $\mathcal {U}^{4}$ space is an ellipse for an elliptic trajectory in Cartesian space. Similarly, it can also be shown that the parametric trajectory in $\mathcal {U}^{4}$ is a hyperbola for a hyperbolic trajectory in Cartesian space. Therefore, the orbital plane of the two-body trajectories in $\mathcal {U}^{4}$ parametric space remains fixed. Without loss of generality, it is assumed here that the u₁-axis is aligned with the apse line of the conic trajectory in $\mathcal {U}^{4}$ and the initial point of the trajectory corresponding to s = 0 has only the u₁ component. As a result, the initial conditions take the form

$$ \begin{array}{@{}rcl@{}} \boldsymbol{U}_{0} &=& \left[\begin{array}{llll} \alpha & 0 & 0 & 0 \end{array}\right]^{T}, \\ \boldsymbol{U}^{\prime}_{0} &=& \left[\begin{array}{llll} 0 &\sqrt{\rho}\upbeta & 0 & 0 \end{array}\right]^{T}. \end{array} $$

Substitution of the preceding equations in Eq. 15 results in

$$ \begin{array}{@{}rcl@{}} \boldsymbol{U} &= \left[\begin{array}{llll} \alpha c_{0}(z) & \upbeta \sqrt{z} c_{1}(z) & 0 & 0 \end{array}\right]^{T}. \end{array} $$

(153)

Therefore, the radius of the orbit is given by

$$ \begin{array}{@{}rcl@{}} R_{f} &=& (\boldsymbol{U},\boldsymbol{U}), \end{array} $$

(154)

$$ \begin{array}{@{}rcl@{}} &=& \alpha^{2} {c_{0}^{2}}(z) + {\upbeta}^{2} z {c_{1}^{2}}(z). \end{array} $$

(155)

Using the definition of the Stumpff functions, the preceding equation for an elliptic trajectory may be written as

$$ R_{f} = \frac{{\upbeta}^{2}+\alpha^{2}}{2} - \frac{{\upbeta}^{2}-\alpha^{2}}{2}\cos 2\sqrt{z} $$

(156)

and for a hyperbolic trajectory as

$$ R_{f} = \frac{{\upbeta}^{2}+\alpha^{2}}{2} - \frac{{\upbeta}^{2}-\alpha^{2}}{2}\cosh 2\sqrt{-z}. $$

(157)

It can be shown by comparison with the standard orbit equations that $E=2\sqrt {z}$ (elliptic) and $H=2\sqrt {-z}$ (hyperbolic), where E is the eccentric anomaly and H is given by the relation

$$ \tanh H/2 = \sqrt{\frac{e-1}{e+1}} \tan f/2, $$

(158)

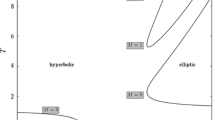
where f is the true anomaly. Therefore, for an elliptic transfer, z is bounded by (0,π²), whereas for an hyperbolic transfer, z is bounded by $(-\infty ,0)$. The latter result is due to the fact that the R.H.S. of Eq. 158 approaches unity when R_f approaches infinity. It is noted that for multiple-revolution elliptic transfers, the bounds on z may be chosen as z ∈ (m²π², (m + 1)²π²), where m is the desired number of complete revolutions.

Appendix B: A Few Stumpff Function Identities

$$ \begin{array}{@{}rcl@{}} \int s^{n} c_{n}(z) \mathrm{d}s &=& s^{n+1} c_{n+1}(z) . \end{array} $$

(159)

$$ \begin{array}{@{}rcl@{}} {c_{0}^{2}}(z)+z {c_{1}^{2}}(z) &=& 1 . \end{array} $$

(160)

$$ \begin{array}{@{}rcl@{}} c_{3} (4 z) &=& \frac{1 - c_{1} (4 z)}{4 z}. \end{array} $$

(161)

$$ \begin{array}{@{}rcl@{}} c_{2} (4 z) &=& \frac{1 - c_{0} (4 z)}{4 z}, \\ &=& \frac{{c_{1}^{2}}(z)}{2}. \end{array} $$

(162)

$$ \begin{array}{@{}rcl@{}} \frac{c_{1}(z) - c_{0}(z)}{z} &=& c_{2}(z) - c_{3}(z). \end{array} $$

(163)

Appendix C: Orbit-Injection BVP Equations

The complete derivation of Eq. 99 for the orbit-injection BVP is given here. First, V₀ is expressed in terms of U₀ and U_f using Eqs. 20 and 6:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{V}_{0} &=& \frac{2}{R_{0}} L(\boldsymbol{U}_{0}) \boldsymbol{U}^{\prime}_{0}, \\ &=& \frac{2}{s c_{1}(z)R_{0}} \left( L\left( \boldsymbol{U}_{f}\right)\boldsymbol{U}_{0} -c_{0}(z)L\left( \boldsymbol{U}_{0}\right)\boldsymbol{U}_{0} \right), \\ &=& \frac{2}{s c_{1}(z)R_{0}} \left( L\left( \boldsymbol{U}_{f}\right)\boldsymbol{U}_{0} -\frac{2c_{0}(z)}{R_{f}}(\boldsymbol{U}_{f},\boldsymbol{U}_{0})L\left( \boldsymbol{U}_{f}\right)\boldsymbol{U}_{0} \right. \\ && \left. +\frac{c_{0}(z)R_{0}}{R_{f}}L\left( \boldsymbol{U}_{f}\right)\boldsymbol{U}_{f} \right). \end{array} $$

(164)

Next, the inner product of R_f and V₀ is

$$ \begin{array}{@{}rcl@{}} \left( \boldsymbol{R}_{f}, \boldsymbol{V}_{0} \right) &=& \left( L\left( \boldsymbol{U}_{f}\right)\boldsymbol{U}_{f},\boldsymbol{V}_{0}\right), \\ &=& \frac{2}{s c_{1}(z)R_{0}} \left( R_{f}(\boldsymbol{U}_{f},\boldsymbol{U}_{0}) -2c_{0}(z)(\boldsymbol{U}_{f},\boldsymbol{U}_{0})^{2} +c_{0}(z)R_{0} R_{f} \right), \end{array} $$

(165)

where (U_f, U₀) is computed by using Eq. 15 and is given by

$$ (\boldsymbol{U}_{f},{\boldsymbol{U}}_{0}) = c_{0}(z) R_{0} + s c_{1}((z)(\boldsymbol{U}_{0},{\boldsymbol{U}}^{\prime}_{0}). $$

(166)

Further, $(\boldsymbol {U}_{0},{\boldsymbol {U}}^{\prime }_{0})$ can be eliminated from the preceding equation by using

$$ \begin{array}{@{}rcl@{}} R_{f} &=& (\boldsymbol{U}_{f},\boldsymbol{U}_{f}), \\ &=& {c_{0}^{2}}(z) R_{0} + s^{2} {c_{1}^{2}}(z) (\boldsymbol{U}^{\prime}_{0},{\boldsymbol{U}}^{\prime}_{0}) + 2 s c_{0}(z) c_{1}(z) (\boldsymbol{U}_{0},{\boldsymbol{U}}^{\prime}_{0}), \end{array} $$

(167)

where Eq. 15 is used. Substituting the preceding equation in Eq. 166 and then substituting the result in Eq. 165, the following equation involving a single unknown s is obtained:

$$ \begin{array}{@{}rcl@{}} &&s c_{0}(\rho s^{2})c_{1}(\rho s^{2})R_{0}\left( \boldsymbol{R}_{f}, \boldsymbol{V}_{0} \right) \end{array} $$

(168)

$$ \begin{array}{@{}rcl@{}} &=& \left[\left( \frac{R_{f}}{\rho}(\boldsymbol{U}^{\prime}_{0},\boldsymbol{U}^{\prime}_{0})-\frac{(\boldsymbol{U}^{\prime}_{0},\boldsymbol{U}^{\prime}_{0})^{2}}{\rho^{2}} \right) \right. \\ &&+ \left. {c_{0}^{2}}(\rho s^{2})\left( R_{0} R_{f} + \frac{(\boldsymbol{U}^{\prime}_{0},\boldsymbol{U}^{\prime}_{0})}{\rho}(2R_{0}-R_{f}) + \frac{2}{\rho^{2}}(\boldsymbol{U}^{\prime}_{0},\boldsymbol{U}^{\prime}_{0})^{2}\right) \right. \\ &&+ \left. {c_{0}^{4}}(\rho s^{2})\left( -{R_{0}^{2}} - \frac{2R_{0}(\boldsymbol{U}^{\prime}_{0},\boldsymbol{U}^{\prime}_{0})}{\rho} - \frac{(\boldsymbol{U}^{\prime}_{0},\boldsymbol{U}^{\prime}_{0})^{2}}{\rho^{2}} \right) \right],\\ \end{array} $$

(169)

where Eq. 160 is also used. This equation is valid for elliptic and hyperbolic transfers, but not for parabolic transfers (for which ρ = 0). The preceding equation can be rewritten as

$$ s c_{0}(\rho s^{2})c_{1}(\rho s^{2})A = B + {c_{0}^{2}}(\rho s^{2})C + {c_{0}^{4}}(\rho s^{2})D, $$

(170)

where

$$ \begin{array}{@{}rcl@{}} A &=& 16\rho^{2}\left( \boldsymbol{R}_{f}, \boldsymbol{V}_{0} \right), \end{array} $$

(171)

$$ \begin{array}{@{}rcl@{}} B &=& {V_{0}^{2}}(4\rho R_{f} - R_{0} {V_{0}^{2}}), \end{array} $$

(172)

$$ \begin{array}{@{}rcl@{}} C &=& 2\left( R_{0} {V_{0}^{4}} + 2\rho {V_{0}^{2}} (2R_{0}-R_{f}) + 8\rho^{2} R_{f}\right), \end{array} $$

(173)

$$ \begin{array}{@{}rcl@{}} D &=& -R_{0}\left( 8 \rho {V_{0}^{2}} + {V_{0}^{4}} + 16 \rho^{2} \right). \end{array} $$

(174)

Appendix D: Reentry BVP Equations

First, the reentry transcendental equation given in Eq. 123 is derived by relating the energy of the transfer trajectory and the specified quantities. Using Eqs. 15-16, the inner product of U_e and $\boldsymbol {U}^{\prime }_{e}$ maybe written as

$$ (\boldsymbol{U}_{e},\boldsymbol{U}^{\prime}_{e}) = -\rho s c_{0} c_{1} R_{0} + s c_{0} c_{1} (\boldsymbol{U}^{\prime}_{0},\boldsymbol{U}^{\prime}_{0}) + (2 {c_{0}^{2}} - 1) (\boldsymbol{U}_{0},\boldsymbol{U}^{\prime}_{0}), $$

(175)

wherein the argument z of the Stumpff functions is omitted for brevity. Similarly, $(\boldsymbol {U}_{0},\boldsymbol {U}^{\prime }_{0})$ can be computed in terms of $(\boldsymbol {U}_{e},\boldsymbol {U}^{\prime }_{e})$ from Eqs. 18-19, as shown below:

$$ (\boldsymbol{U}_{0},\boldsymbol{U}^{\prime}_{0}) = \rho s c_{0} c_{1} R_{e} - s c_{0} c_{1} (\boldsymbol{U}^{\prime}_{e},\boldsymbol{U}^{\prime}_{e}) + (2 {c_{0}^{2}} - 1) (\boldsymbol{U}_{e},\boldsymbol{U}^{\prime}_{e}). $$

(176)

Substituting the above result in Eq. 175 and eliminating $(\boldsymbol {U}^{\prime }_{e},\boldsymbol {U}^{\prime }_{e})$ and $(\boldsymbol {U}^{\prime }_{0},\boldsymbol {U}^{\prime }_{0})$ by using the vis-viva equation results in

$$ (\boldsymbol{U}_{e},\boldsymbol{U}^{\prime}_{e})4 {c_{0}^{2}} (1-{c_{0}^{2}}) = s c_{0} c_{1} ({c_{0}^{2}}(4 R_{e} \rho - \mu) + \mu - 2\rho(R_{0}+R_{e})). $$

(177)

Using Eq. 29, the preceding equation can be written in terms of the fixed parameters, the energy of the transfer orbit, and s to obtain the final transcendental equation:

$$ 2 c_{0} (1-{c_{0}^{2}}) \cos {\upbeta}_{e} \sqrt{2 \mu R_{e} - 4 \rho {R_{e}^{2}}}= s c_{1} ({c_{0}^{2}}(4 R_{e} \rho - \mu) + \mu - 2\rho(R_{0}+R_{e})). $$

(178)

In order to solve the reentry problem using the Lambert transfer-time given in Eq. 45, the quantity (U₀, U_f) needs to be expressed in terms of z. The inner products $(\boldsymbol {U}^{\prime }_{e},\boldsymbol {U}^{\prime }_{e})$ and $(\boldsymbol {U}_{e},\boldsymbol {U}^{\prime }_{e})$ can be computed using Eq. 21 to obtain

$$ \begin{array}{@{}rcl@{}} (\boldsymbol{U}_{e},\boldsymbol{U}^{\prime}_{e}) &=& \frac{R_{e} V_{e} \cos {\upbeta}_{e}}{2} = \frac{c_{0}(z) R_{e} - (\boldsymbol{U}_{0},\boldsymbol{U}_{e})}{s c_{1}(z)}, \end{array} $$

(179)

$$ \begin{array}{@{}rcl@{}} (\boldsymbol{U}^{\prime}_{e},\boldsymbol{U}^{\prime}_{e}) &=& \frac{R_{e} {V_{e}^{2}}}{4} \qquad= \frac{R_{0} + {c_{0}^{2}}(z) R_{e} - 2c_{0}(z)(\boldsymbol{U}_{0},\boldsymbol{U}_{e})}{s^{2} {c_{1}^{2}}(z)}. \end{array} $$

(180)

Elimination of $s^{2} {c_{1}^{2}}(z){V_{e}^{2}}$ from the preceding equation by using Eq. 179 gives

$$ (\boldsymbol{U}_{0},\boldsymbol{U}_{e})^{2} - 2R_{e}\sin^{2} {\upbeta}_{e} c_{0}(z) (\boldsymbol{U}_{0},\boldsymbol{U}_{e}) + {R_{e}^{2}} {c_{0}^{2}}(z) \sin^{2} {\upbeta}_{e} - R_{0} R_{e} \cos^{2} {\upbeta}_{e} = 0. $$

(181)

For real roots, the following condition must be satisfied:

$$ R_{0} \ge R_{e} {c_{0}^{2}}(z) \sin^{2} {\upbeta}_{e}. $$

(182)

It is noted that the preceding condition for the existence of the reentry solution is the same as that given by Eq. 129. There can be at most two real roots of Eq. 181. For a given root, ρ can be computed from Eq. 44 and 160. Then, the correct root for (U₀, U_e) is found by back substituting its value in Eq. 179 with the corresponding value of V_e determined from the vis-viva equation. It is noted that compared to Eq. 128, Eq. 181 has no singularity for ρ = 0.

Computation of R_e

If a feasible declination of R_e is selected, then the corresponding right ascension values for the prograde and retrograde solutions can be computed. For this purpose, the reentry cone is determined first by computing its aperture as well as the declination and right ascension of its axis. The aperture angle, 2ϕ, is obtained from the transfer angle (𝜃) by using

$$ \phi = \left\{\begin{array}{ll} \theta & \text{if}\ 0^{\circ} \le \theta \le 90^{\circ}, \\ |\pi - \theta| & \text{if}\ 90^{\circ} < \theta \le 270^{\circ}, \\ 2\pi-\theta & \text{otherwise.} \end{array}\right. $$

(183)

If 𝜃 lies in the first or fourth quadrant, then the reentry cone axis is in the direction of R₀, otherwise it is in the opposite direction. Considering Fig. 7, the declination of R_e lies within δ_min = δ_a − ϕ and δ_max = δ_a + ϕ, where δ_a is the declination of the reentry cone axis. If δ_min < − 90^∘, then δ_min is replaced by − δ_min − 180^∘ and if δ_max > 90^∘, then δ_max is replaced by − δ_max + 180^∘. For a fixed reentry declination, δ_e ∈ (δ_min, δ_max), the feasible right ascension values are computed by constructing a spherical triangle as shown in Fig. 7. The cosine rule gives

$$ \begin{array}{@{}rcl@{}} \cos \phi &=& \cos (90^{\circ}-\delta_{a})\cos (90^{\circ}-\delta_{e})+\sin (90^{\circ}-\delta_{a})\sin (90^{\circ}-\delta_{e}) \cos \alpha, \\ &=& \cos (\delta_{a}-\delta_{e}) - \cos \delta_{a}\cos \delta_{e} (1-\cos \alpha), \end{array} $$

(184)

where α is the right ascension of R_e with respect to the cone axis. The preceding equation is ill-conditioned for small ϕ and a more useful form can be obtained by using the haversine function as shown below:

$$ \text{hav} (\phi) = \text{hav} (\delta_{e}-\delta_{a}) + \cos \delta_{e} \cos \delta_{a} \text{hav} (\alpha), $$

(185)

where $\text {hav}(x)=\sin \limits ^{2}(x/2)$. There are two right ascension values corresponding to the posigrade and retrograde solutions. These values are α_a + α and α_a − α, where α_a is the right ascension of the reentry cone axis. It is noted that if |δ_e − δ_a| = ϕ, i.e., the fixed declination is either the maximum or minimum value possible, then α = 0 and the reentry right ascension is equal to that of the reentry cone axis.