Abstract
We construct orthogonal trigonometric polynomials satisfying a new spectral condition and such that their  -norms are bounded below and the uniform norm of their partial sums has extremely small order of growth. We obtain new results that relate the uniform norm and
-norms are bounded below and the uniform norm of their partial sums has extremely small order of growth. We obtain new results that relate the uniform norm and 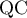 -norm on subspaces of the vector space of trigonometric polynomials.
-norm on subspaces of the vector space of trigonometric polynomials.
Export citation and abstract BibTeX RIS
§ 1. Introduction
We begin with some necessary definitions. The sets of positive integers, integers and real numbers are denoted by  ,
,  and
and  , respectively. Given
, respectively. Given  , put
, put

Given  , we consider the Fourier coefficients
, we consider the Fourier coefficients
Given a real number  , we denote by
, we denote by ![$[x]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn9.gif) its integer part and by
its integer part and by  the least integer
the least integer  such that
such that  . We write
. We write  for the cardinality of a finite set
for the cardinality of a finite set  . We denote the exact order of a non-zero trigonometric polynomial
. We denote the exact order of a non-zero trigonometric polynomial  by
by  . The Lebesgue measure of
. The Lebesgue measure of  is denoted by
is denoted by  .
.
If ![$x, y\in (0, 2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn19.gif) , then
, then  stands for the distance around the circle, that is,
stands for the distance around the circle, that is,

Let  be a real number and
be a real number and  a subset of
a subset of ![$(0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn23.gif) . We define
. We define  as follows. Put
as follows. Put

when ![$\varnothing \neq X\subset (0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn25.gif) and
and 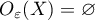 when
when  . We also define
. We also define  for
for ![$X\subset (0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn29.gif) : put
: put  when
when  is a non-empty subset of
is a non-empty subset of ![$(0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn23.gif) having
having  components with respect to the topology of the circle and
components with respect to the topology of the circle and  when
when  .
.
Let  . For a positive integer
. For a positive integer  put
put

The function  is called the Fejér kernel of order
is called the Fejér kernel of order  . We mention some properties of the Fejér kernel. If
. We mention some properties of the Fejér kernel. If  is a positive integer, then
is a positive integer, then  is a non-zero real positive even trigonometric polynomial,
is a non-zero real positive even trigonometric polynomial,  ,
,  ,
,  ,
,  , and the following inequality holds:
, and the following inequality holds:

Let  be a positive integer. Given
be a positive integer. Given  , put
, put
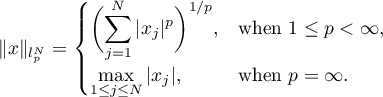
We denote by  ,
,  , the
, the  th coordinate of
th coordinate of  . We write
. We write  for the dimension of a finite-dimensional vector space
for the dimension of a finite-dimensional vector space  over
over  .
.
Put

Let  be a positive integer. We denote by
be a positive integer. We denote by  the vector space of real trigonometric polynomials of the form
the vector space of real trigonometric polynomials of the form

and by  the vector space of real trigonometric polynomials of the form
the vector space of real trigonometric polynomials of the form

It easy to see that  and
and  are finite dimensional and that
are finite dimensional and that  and
and  . It is also evident that
. It is also evident that

§ 2. Some trigonometric polynomials with extremely small uniform norm
We first note the following fact. Let  be a real number and
be a real number and  a sequence of orthogonal trigonometric polynomials such that
a sequence of orthogonal trigonometric polynomials such that  ,
,  . Then
. Then

Thus, under the assumptions above, the uniform norm of  cannot have order of growth smaller than
cannot have order of growth smaller than  . We have the following result.
. We have the following result.
Theorem 1. Let  be a real number,
be a real number,  a positive non-increasing function, and
a positive non-increasing function, and  a sequence of positive integers such that
a sequence of positive integers such that

Also, let a sequence  of positive integers satisfy the condition
of positive integers satisfy the condition  ,
,  . Then there is a sequence
. Then there is a sequence 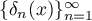 of complex trigonometric polynomials such that
of complex trigonometric polynomials such that

where  is an absolute constant.
is an absolute constant.
Remark 1. Theorem 1 is a generalization of a result in [1], where the corresponding assertion is obtained in the case when  . The proof of Theorem 1 is based on ideas in [1]–[3].
. The proof of Theorem 1 is based on ideas in [1]–[3].
Proof of Theorem 1. A celebrated result of Carleson and Hunt (see [4]) implies that if  , and
, and

then

where  is an absolute constant. It is easy to see that
is an absolute constant. It is easy to see that  . Note that if
. Note that if  are positive integers, then
are positive integers, then
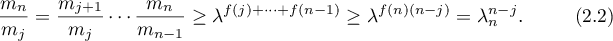
Put  . We will construct trigonometric polynomials
. We will construct trigonometric polynomials  ,
,  , such that
, such that

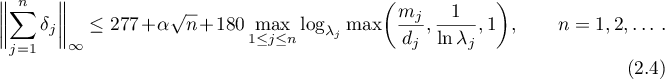
It is obvious that this will prove the theorem. There is no loss of generality in assuming that  ,
,  . Put
. Put

Note that  is a positive integer and
is a positive integer and

We proceed to construct by induction trigonometric polynomials  ,
,  , satisfying (2.3) and then show that (2.4) also holds. Put
, satisfying (2.3) and then show that (2.4) also holds. Put  . It is clear that it satisfies (2.3). Assume that
. It is clear that it satisfies (2.3). Assume that  is a positive integer and
is a positive integer and  have been constructed. We introduce the notation
have been constructed. We introduce the notation

Put


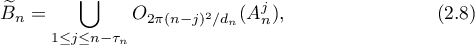

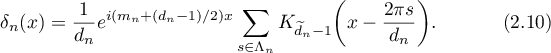
When  , the union in (2.8) is defined as the empty set.
, the union in (2.8) is defined as the empty set.
We claim that

Indeed, if  , then
, then  and so (2.11) holds. Suppose that
and so (2.11) holds. Suppose that  . Then
. Then
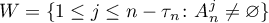
is not empty and

We will first find an upper bound for  . Define
. Define
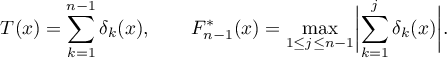
It is evident that

Then we have (see (2.6), (2.7))
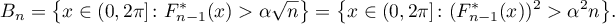
Applying Chebyshev's inequality and (2.1), and then using the orthogonality of the polynomials  and the bound
and the bound  ,
,  , we obtain
, we obtain
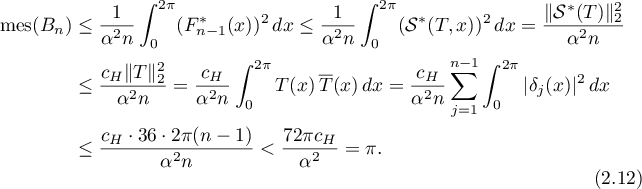
Let  . Then
. Then
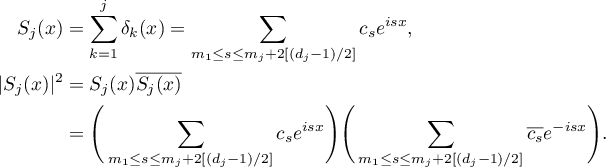
The trigonometric polynomial 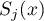 is non-zero since the spectra of
is non-zero since the spectra of  ,
,  , are pairwise disjoint and
, are pairwise disjoint and  . Thus there is an
. Thus there is an ![$x_0 \in (0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn91.gif) such that
such that  . Therefore
. Therefore  and so
and so  . Hence
. Hence  is a non-zero real trigonometric polynomial. It is easy to see that
is a non-zero real trigonometric polynomial. It is easy to see that ![$\deg (|S_j|^2)\leq m_j +2[(d_j-1)/2]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn96.gif) . Put
. Put 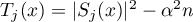 . It is obvious that
. It is obvious that
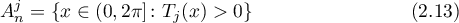
and  since
since  . Therefore there is an
. Therefore there is an ![$x_1\in (0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn99.gif) such that
such that 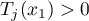 . Hence
. Hence  is a non-zero real trigonometric polynomial and
is a non-zero real trigonometric polynomial and

It follows from well-known facts about trigonometric polynomial (see, for example, [5], V. 2, Ch. X, Theorem 1.7) that the number of zeros of  in
in ![$(0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn23.gif) (counted with multiplicities) is equal to
(counted with multiplicities) is equal to ![$R_j\leq 2(m_j +2[(d_j-1)/2])$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn102.gif) . Note that
. Note that

Therefore we can find an ![$x_2\in(0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn103.gif) such that
such that  . Since there is an
. Since there is an ![$x_1\in (0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn99.gif) such that
such that 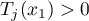 , there is an
, there is an ![$x_3\in(0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn105.gif) such that
such that  . Hence
. Hence  . Applying (2.13), we obtain that
. Applying (2.13), we obtain that  is the union of finitely many pairwise-disjoint open intervals on the circle
is the union of finitely many pairwise-disjoint open intervals on the circle ![$(0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn23.gif) and
and

Since
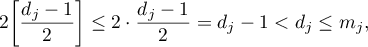
we have

Combining (2.7), (2.8), (2.12), (2.14) and (2.2), we obtain

To continue estimating  we need the inequality
we need the inequality
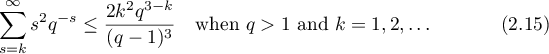
(with 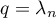 and
and  ). This bound follows easily from the equality
). This bound follows easily from the equality
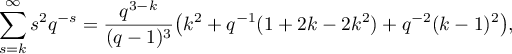
for all  and
and  , as is easily checked. Also, using the fact that
, as is easily checked. Also, using the fact that

we have

We now claim that

Two cases may occur.
1) Let 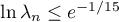 . Then
. Then  . Hence,
. Hence,

Therefore,
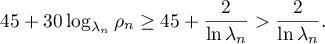
2) Let  . Then
. Then 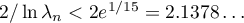 . Therefore,
. Therefore,

Thus (2.17) is proved.
It is not hard to see that 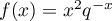 is decreasing when
is decreasing when 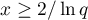 , where
, where  is a real number. It follows from the inequality
is a real number. It follows from the inequality
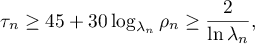
that

Because
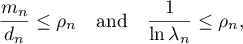
and also 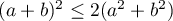 ,
, 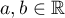 , it follows that
, it follows that

Since  when
when  , we have
, we have

Thus,

We claim further that

Two cases may occur.
1) Let  . Then
. Then  . It follows from
. It follows from  that
that

2) Let  . Then
. Then  . Therefore,
. Therefore,

Thus (2.18) is proved.
Consequently,

This bound implies, in particular, that ![$\widetilde{B}_{n}\neq (0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn129.gif) . Thus
. Thus  is the union of finitely many pairwise-disjoint open intervals on the circle
is the union of finitely many pairwise-disjoint open intervals on the circle ![$(0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn23.gif) .
.
We claim, in addition, that

We have (see (2.14), (2.2), (2.16)) that

It follows from

that

Two cases may occur.
1) Let  . Then
. Then  . It follows from
. It follows from  that
that

2) Let  . Then
. Then  and so
and so
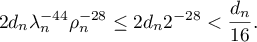
Thus (2.20) is proved.
Put

It is obvious that the length of  is
is  and the intervals are pairwise disjoint. Consider
and the intervals are pairwise disjoint. Consider

the complement of the subset  (see (2.9)). We will find an upper bound for
(see (2.9)). We will find an upper bound for  . It is not hard to see that
. It is not hard to see that  is at most the number of intervals
is at most the number of intervals  ,
,  , intersecting
, intersecting  non-trivially. Such intervals are of two types: those contained in
non-trivially. Such intervals are of two types: those contained in  and those containing a boundary point of
and those containing a boundary point of  . Denote by
. Denote by  and
and  the numbers of intervals of the first and second types, respectively. Then (see (2.19))
the numbers of intervals of the first and second types, respectively. Then (see (2.19))
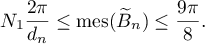
Therefore,

It is clear (see (2.20)) that
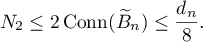
Hence,

Thus,
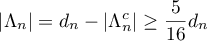
and (2.11) is proved.
We have (see (2.10))

Let ![$x\in (0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn142.gif) . Then (see (2.10), (1.1), (2.5))
. Then (see (2.10), (1.1), (2.5))
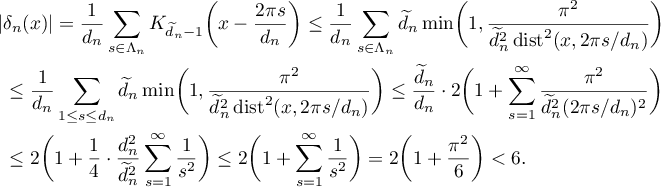
Hence  . It is clear that
. It is clear that 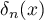 has the form (see (2.10))
has the form (see (2.10))
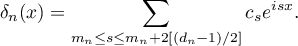
Thus we have constructed trigonometric polynomials  ,
,  , satisfying the conditions in (2.3).
, satisfying the conditions in (2.3).
We now claim that these trigonometric polynomials satisfy (2.4). Let  be a positive integer. If
be a positive integer. If 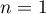 , then (2.4) holds. Suppose that
, then (2.4) holds. Suppose that  . Put
. Put

Since

the function  is well defined. Let
is well defined. Let ![$x\in (0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn142.gif) . Two cases may occur.
. Two cases may occur.
1) Let  . Then
. Then

2) Let  . Then
. Then

We will estimate the last summand. Suppose that  . It follows from
. It follows from  that
that  . We claim that
. We claim that

Indeed, since
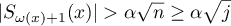
and  , the inclusion (2.21) holds (see (2.6), (2.8)). Therefore (see (2.8), (2.9))
, the inclusion (2.21) holds (see (2.6), (2.8)). Therefore (see (2.8), (2.9))

for any  . We have (see (2.10) and also (1.1), (2.5))
. We have (see (2.10) and also (1.1), (2.5))

Hence,

Therefore,

and inequality (2.4) is proved. This completes the proof of Theorem 1. 
Corollary 1. Let  ,
, 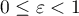 ,
,  be real numbers and
be real numbers and
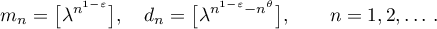
Then there are complex trigonometric polynomials  ,
,  , such that
, such that
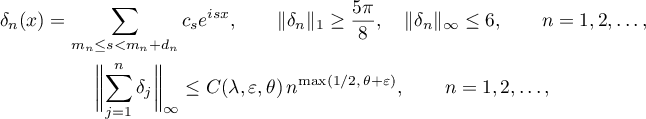
where  depends only on
depends only on  ,
,  and
and 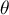 .
.
§ 3. Some properties of the space of quasi-continuous functions
Let  have the Fourier series
have the Fourier series 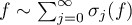 , where
, where 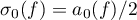 , and
, and

We put

where 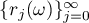 is the Rademacher system (see, for example, [6]). The norm in (3.1) is called the
is the Rademacher system (see, for example, [6]). The norm in (3.1) is called the 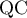 -norm. The closure of the set of trigonometric polynomials with respect to the
-norm. The closure of the set of trigonometric polynomials with respect to the 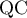 -norm is called the space of quasi-continuous functions. This norm and space were introduced by Kashin and Temlyakov in [7], [8], where they obtained many interesting results on the properties of this norm. In particular, the following theorem was proved in [8] (see [8], Theorem 2.1). If
-norm is called the space of quasi-continuous functions. This norm and space were introduced by Kashin and Temlyakov in [7], [8], where they obtained many interesting results on the properties of this norm. In particular, the following theorem was proved in [8] (see [8], Theorem 2.1). If  is a positive integer and
is a positive integer and  , where
, where  ,
,  , then
, then

In connection with the problems of approximation theory (see the details in [8]), it is interesting to relate the  - and
- and 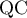 -norms. It follows from the inequality (3.2) and a result of Grigor'ev [2] that
-norms. It follows from the inequality (3.2) and a result of Grigor'ev [2] that

where 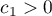 is an absolute constant. Oskolkov proved (see [8]) that
is an absolute constant. Oskolkov proved (see [8]) that

where  is an absolute constant. Oskolkov's example was generalized in [9]. The following question was open for a long time: do there exist subspaces
is an absolute constant. Oskolkov's example was generalized in [9]. The following question was open for a long time: do there exist subspaces  ,
,  , such that
, such that  ,
,  , and
, and

for any  and
and 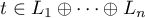 , where
, where 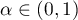 ,
, 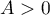 ,
,  are absolute constants? It was shown in [10] that the answer is negative. In the present paper, we strengthen Theorem 2 in [10] (see Corollary 2 below). Our result is obtained by specifying functions of the variable
are absolute constants? It was shown in [10] that the answer is negative. In the present paper, we strengthen Theorem 2 in [10] (see Corollary 2 below). Our result is obtained by specifying functions of the variable  considered in Theorems 1 and 2 in [10]. This is accomplished by a significant improvement of the argument in several places; in particular, Lemmas 1, 2 and 4 of [10] are refined. Note also that our Corollary 2 is stronger than results in [11]. The following theorem is central in this section.
considered in Theorems 1 and 2 in [10]. This is accomplished by a significant improvement of the argument in several places; in particular, Lemmas 1, 2 and 4 of [10] are refined. Note also that our Corollary 2 is stronger than results in [11]. The following theorem is central in this section.
Theorem 2. Let  be a real number,
be a real number, 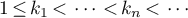 a sequence of positive integers, and
a sequence of positive integers, and 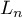 a subspace of
a subspace of  such that
such that  ,
,  . Then there are trigonometric polynomials
. Then there are trigonometric polynomials  ,
,  , such that
, such that
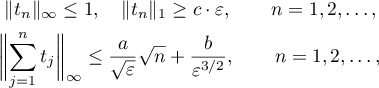
where  ,
,  ,
, 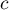 are positive absolute constants.
are positive absolute constants.
Proof. We need the following lemmas, of which Lemma 2 is well known. Lemma 1 can also be considered as well known, but we include a proof for completeness.
Lemma 1. Let 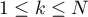 be positive integers and
be positive integers and  a subspace of
a subspace of  ,
,  . Then there is a non-zero
. Then there is a non-zero  such that
such that

Proof. The case when  is trivial. Suppose that
is trivial. Suppose that  and put
and put

Since  is compact, we can replace
is compact, we can replace  by
by  in (3.3). Let
in (3.3). Let  be an element of
be an element of  such that
such that  . Denote by
. Denote by  the number of coordinates of
the number of coordinates of  having absolute value
having absolute value  .
.
We claim that  . Assume the opposite, that is,
. Assume the opposite, that is,  . Let
. Let  and
and  be tuples of positive integers such that
be tuples of positive integers such that  ,
,  ,
,  ,
,
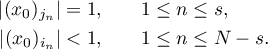
If  , then
, then  is empty. Put
is empty. Put

It is clear that  is a subspace of
is a subspace of  with
with  . We have
. We have
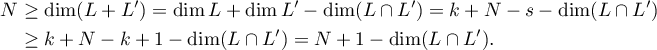
Therefore,

Put  . If
. If  is a real number and
is a real number and  , define
, define

Put
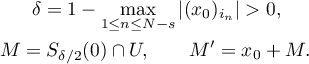
We claim further that

Indeed, let 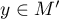 . Then
. Then  , where
, where  . Hence
. Hence  and so
and so

We have
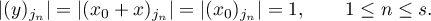
Note that
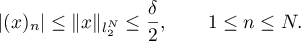
Therefore,

Thus,

and (3.4) is proved.
Since  and
and  , we have
, we have  . Hence
. Hence  . Note that
. Note that

Consider the ball  with centre
with centre  and radius
and radius 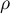 . Then
. Then  lies on the boundary of the ball. Also,
lies on the boundary of the ball. Also,  is either tangent to the boundary of
is either tangent to the boundary of  at
at  or intersects it transversally at
or intersects it transversally at  . In both cases, there is a
. In both cases, there is a  such that
such that  . Hence
. Hence  and
and  . But this is not the case because of (3.3). This contradiction implies that
. But this is not the case because of (3.3). This contradiction implies that 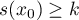 , as is claimed above.
, as is claimed above.
Thus  , whence
, whence  . Since
. Since 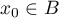 , we have
, we have  and
and 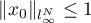 . Therefore,
. Therefore,
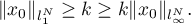
So we can take  as the desired vector
as the desired vector  . The proof of Lemma 1 is complete.
. The proof of Lemma 1 is complete. 
Lemma 2 (see [12], p. 40, Theorem 2.5). Let  be a positive integer,
be a positive integer,  ,
, 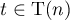 , and
, and

Then
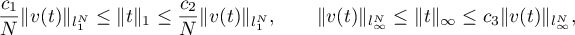
where  ,
,  ,
,  are positive absolute constants.
are positive absolute constants.
The proof of Lemma 3 given below is based on Lemmas 1 and 2. It was communicated to the author by Y. V. Malykhin. We notice that, when one does not specify  , the conclusion of the lemma follows from results in [13].
, the conclusion of the lemma follows from results in [13].
Lemma 3. Let  be a real number,
be a real number,  a positive integer, and
a positive integer, and  a subspace of
a subspace of  such that
such that  . Then there is a trigonometric polynomial
. Then there is a trigonometric polynomial  such that
such that

where  is an absolute constant.
is an absolute constant.
Proof. Put  . Since
. Since  , the subspace
, the subspace  is not trivial,
is not trivial,  ,
, 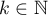 and
and  . Consider the map
. Consider the map
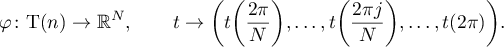
It is not hard to show that 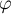 is linear and injective. Therefore
is linear and injective. Therefore  is a subspace of
is a subspace of  and
and  . By Lemma 1, there is a non-zero
. By Lemma 1, there is a non-zero  such that
such that  . Then
. Then  ,
,  and
and 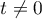 (because otherwise
(because otherwise  ). Applying Lemma 2, we have
). Applying Lemma 2, we have

Since

we obtain

Therefore,
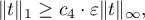
where  is an absolute constant. Since
is an absolute constant. Since 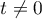 , we have
, we have  . Put
. Put 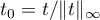 . Then
. Then  ,
,  and
and 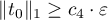 . We can take
. We can take  as the desired trigonometric polynomial
as the desired trigonometric polynomial 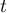 . Lemma 3 is proved.
. Lemma 3 is proved. 
Lemma 4. Let  a real number,
a real number,  a positive integer, and
a positive integer, and  a subspace of
a subspace of  such that
such that  . Then there is a trigonometric polynomial
. Then there is a trigonometric polynomial  such that
such that

where 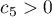 is an absolute constant.
is an absolute constant.
Proof. Put  . Then
. Then  is a positive integer,
is a positive integer,  is a subspace of
is a subspace of  and
and

Since  , it follows from Lemma 3 that there is a trigonometric polynomial
, it follows from Lemma 3 that there is a trigonometric polynomial  such that
such that  and
and
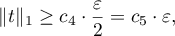
where  is an absolute constant. Lemma 4 is proved.
is an absolute constant. Lemma 4 is proved. 
Lemma 5. Let  be a real number,
be a real number,  ,
, 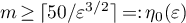 a positive integer, and
a positive integer, and 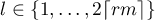 . Then
. Then
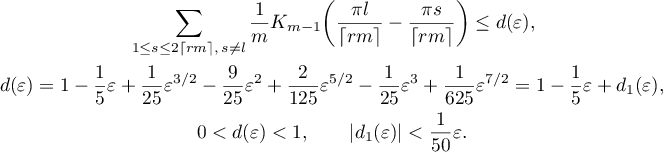
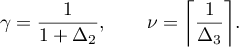
Then  . Note that
. Note that

because  . We introduce the sets
. We introduce the sets  ,
,

It is clear that 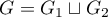 .
.
Note that

We claim that

Since  , we have
, we have
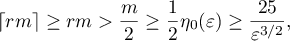
and it suffices to show that
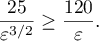
But this inequality holds because  . Thus (3.7) is proved.
. Thus (3.7) is proved.
Consider the sum
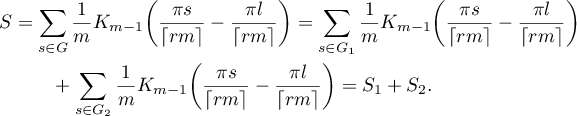
We have
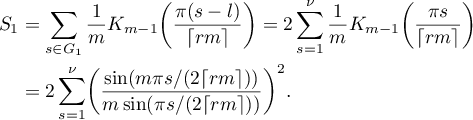
We claim that if  is a real number, then
is a real number, then
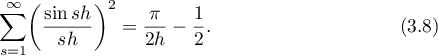
Indeed, it suffices to apply Parseval's identity to the function

We claim further that if  , then
, then

Indeed, if  , then (3.9) is trivial. Suppose that
, then (3.9) is trivial. Suppose that  . In view of the well-known inequality
. In view of the well-known inequality  when
when  , it suffices to prove that
, it suffices to prove that  . The last is equivalent to
. The last is equivalent to

Since

it is enough to show that  . But this inequality holds because
. But this inequality holds because  . Thus (3.9) is proved.
. Thus (3.9) is proved.
We now claim that

It suffices to prove that 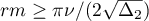 . Since
. Since  , it is enough to show that
, it is enough to show that 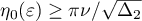 . It is enough to show, in turn, that
. It is enough to show, in turn, that

Applying (3.6), we obtain
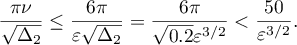
Thus the inequality (3.10) is proved.
Therefore,
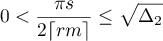
when  and hence (see (3.9))
and hence (see (3.9))
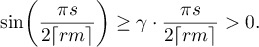
Then

Applying (3.8) with  (it is clear that
(it is clear that  ) and using the fact that
) and using the fact that  , we have
, we have

Next, we will find a bound for  . Applying (1.1), (3.5) and
. Applying (1.1), (3.5) and  , we deduce (see also the definition of
, we deduce (see also the definition of  ) that
) that
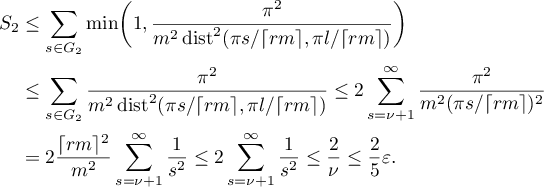
We finally have

Since  , we obtain
, we obtain

Therefore,

Lemma 5 is proved. 
Lemma 6. Let  ,
,  , be a real number,
, be a real number,  ,
,  a positive integer,
a positive integer,  ,
,  , and
, and

Then
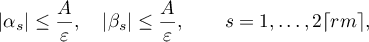
where 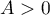 is an absolute constant.
is an absolute constant.
Proof. We first claim that if the real trigonometric polynomial
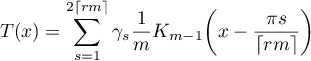
satisfies  , then
, then

where  is as in Lemma 5. Let the absolute value of
is as in Lemma 5. Let the absolute value of  be the largest for the
be the largest for the  ,
,  . If
. If 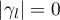 , then (3.11) is trivial. Suppose that
, then (3.11) is trivial. Suppose that 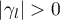 . Put
. Put
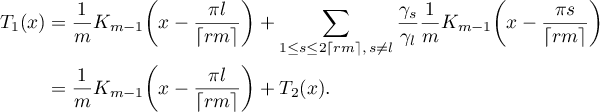
Then 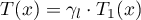 . Hence,
. Hence,

We have
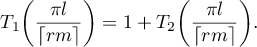
Applying Lemma 5, we obtain

Therefore,

Thus (see (3.12))

and (3.11) is proved.
We continue with the proof of the lemma. Put

By hypothesis,  . Consider the points
. Consider the points
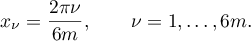
Then  ,
,  ,
,  , and so
, and so
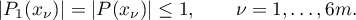
Since  , it follows from the celebrated theorem of Marcinkiewicz (see [5], V. II, Russian p. 54, Theorem 7.28) that
, it follows from the celebrated theorem of Marcinkiewicz (see [5], V. II, Russian p. 54, Theorem 7.28) that
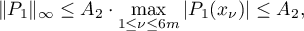
where 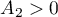 is an absolute constant. Therefore,
is an absolute constant. Therefore,

It follows from the argument above that  ,
,  ,
,  , that is,
, that is,

Put

Then 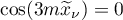 ,
,  ,
,  , and so
, and so

Again applying Marcinkiewicz' theorem, we obtain
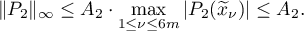
Therefore,  and so
and so  ,
,  , that is,
, that is,

By Lemma 5, we have

where  is an absolute constant. Lemma 6 is proved.
is an absolute constant. Lemma 6 is proved. 
Lemma 7. Let  be a real number,
be a real number,  ,
,  a positive integer,
a positive integer,  ,
,  , and
, and

Then 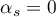 ,
,  ,
,  .
.
Proof. If 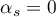 ,
,  ,
,  , then (3.13) holds. Suppose that
, then (3.13) holds. Suppose that  is a non-zero tuple of real numbers such that (3.13) holds. Suppose for definiteness that
is a non-zero tuple of real numbers such that (3.13) holds. Suppose for definiteness that  . Put
. Put

Let  be a real number. Then
be a real number. Then  . By Lemma 6, we have
. By Lemma 6, we have  . But this is not the case when
. But this is not the case when  is sufficiently large (for example, when
is sufficiently large (for example, when  ). We have a contradiction. Thus (3.13) holds only when
). We have a contradiction. Thus (3.13) holds only when  ,
,  ,
,  . Lemma 7 is proved.
. Lemma 7 is proved. 
We continue with the proof of the theorem. Suppose that  . Put
. Put

where  is the absolute constant in Lemma 6 and
is the absolute constant in Lemma 6 and 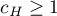 is the absolute constant in (2.1). Then
is the absolute constant in (2.1). Then

We have
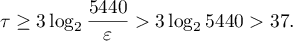
Hence  is a positive integer.
is a positive integer.
We claim that

It is not hard to see that  when
when  . Hence,
. Hence,

Therefore,

The last inequality is equivalent to  , which obviously holds. Thus (3.16) is proved.
, which obviously holds. Thus (3.16) is proved.
Note that if  are positive integers, then
are positive integers, then

We define

It is clear that  ,
,  .
.
We write
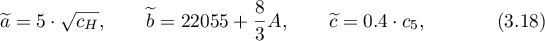
where 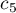 is the absolute constant in Lemma 4. Thus
is the absolute constant in Lemma 4. Thus  ,
,  are
are  are positive absolute constants. We put
are positive absolute constants. We put

Hence  ,
,  are
are 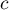 are positive absolute constants.
are positive absolute constants.
We will construct trigonometric polynomials  ,
,  , such that
, such that


We use induction to construct trigonometric polynomials  ,
,  , satisfying the conditions in (3.20) and then show that (3.21) also holds. Suppose that
, satisfying the conditions in (3.20) and then show that (3.21) also holds. Suppose that  . By Lemma 4, there is a trigonometric polynomial
. By Lemma 4, there is a trigonometric polynomial  such that
such that  ,
, 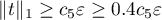 . We define
. We define 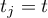 . Thus
. Thus  ,
, 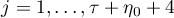 have been constructed. We now proceed by induction. Suppose that
have been constructed. We now proceed by induction. Suppose that  is a positive integer and
is a positive integer and  are given. We shall now construct
are given. We shall now construct  . Write
. Write
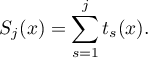
Put




We claim that

Indeed, if  , then
, then
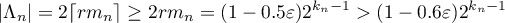
and (3.26) is proved.
Let  . Then the set
. Then the set

is not empty and
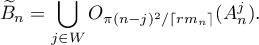
We will first find an upper bound for  . Put
. Put
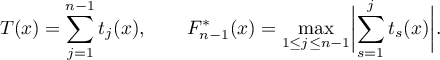
It is obvious that
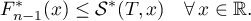
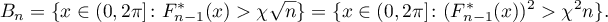
Applying Chebyshev's inequality and (2.1), and then using the orthogonality of the polynomials  and the bound
and the bound  ,
,  , we obtain
, we obtain

Let  . As in the proof of Theorem 1, one can show that
. As in the proof of Theorem 1, one can show that  is the union of finitely many pairwise-disjoint open intervals on the circle
is the union of finitely many pairwise-disjoint open intervals on the circle ![$(0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn23.gif) and
and

Taking (3.23), (3.24), (3.27) and (3.28) into account, we obtain

Applying (3.17) and (2.15) with  and
and  , we have
, we have
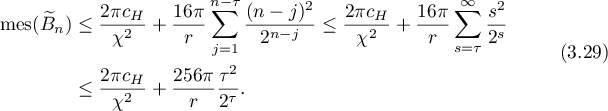
This bound implies, in particular, that  and so
and so ![$\widetilde{B}_{n} \neq (0, 2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn374.gif) . Indeed (see (3.15), (3.16)),
. Indeed (see (3.15), (3.16)),
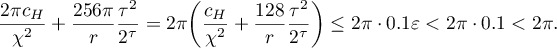
Thus  is the union of finitely many pairwise-disjoint open intervals on the circle
is the union of finitely many pairwise-disjoint open intervals on the circle ![$(0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn23.gif) . We have (see (3.28), (3.17))
. We have (see (3.28), (3.17))

Put

It is obvious that the length of  is
is 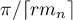 and the intervals are pairwise disjoint. Consider
and the intervals are pairwise disjoint. Consider

the complement of the subset  (see (3.25)). We will find an upper bound for
(see (3.25)). We will find an upper bound for  . It is not hard to see that
. It is not hard to see that  is at most the number of
is at most the number of  ,
,  , intersecting
, intersecting  non-trivially. Such intervals are of two types: those contained in
non-trivially. Such intervals are of two types: those contained in  and those containing a boundary point of
and those containing a boundary point of  . Denote by
. Denote by  and
and  the numbers of intervals of the first and second types, respectively. Then (see (3.29))
the numbers of intervals of the first and second types, respectively. Then (see (3.29))
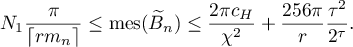
Since  , we obtain
, we obtain
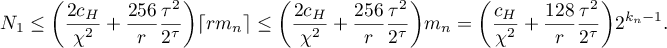
It is clear (see (3.30)) that
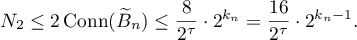
Therefore,

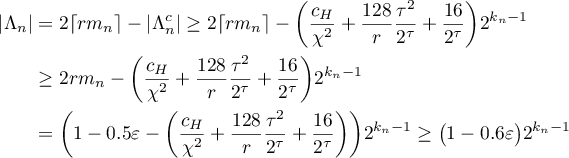
and (3.26) is proved.
We define  as the linear hull (over
as the linear hull (over  ) of
) of
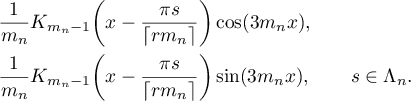
It is obvious that  is a subspace of
is a subspace of  . Since
. Since 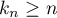 , we have
, we have

It follows from Lemma 7 that  . Hence,
. Hence,
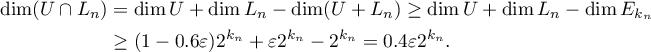
By Lemma 4, there is a  such that
such that  ,
, 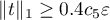 . Put
. Put  . Since
. Since  , we have
, we have
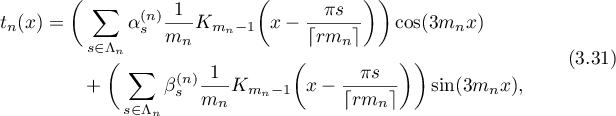
where  ,
,  ,
,  , are real numbers. Since
, are real numbers. Since  and
and  , it follows from Lemma 6 that
, it follows from Lemma 6 that

Thus we have constructed trigonometric polynomials  ,
,  , satisfying the conditions in (3.20).
, satisfying the conditions in (3.20).
We now claim that these trigonometric polynomials satisfy (3.21). Let  be a positive integer. If
be a positive integer. If  , then
, then
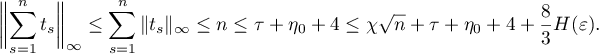
Suppose that 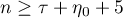 . Put
. Put
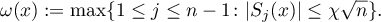
Since
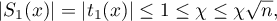
the function  is well defined. Let
is well defined. Let ![$x\in (0,2\pi]$](https://content.cld.iop.org/journals/1064-5632/84/2/361/revision1/IZV_84_2_361ieqn142.gif) . Two cases may occur.
. Two cases may occur.
1)  . Then
. Then

2) 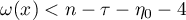 . Then
. Then
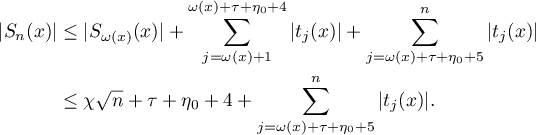
We will estimate the last summand. Suppose that  . We claim that
. We claim that

Indeed, since

and  , the inclusion (3.33) is proved (see (3.22), (3.24)). Therefore (see (3.24), (3.25)), we obtain
, the inclusion (3.33) is proved (see (3.22), (3.24)). Therefore (see (3.24), (3.25)), we obtain

for any  . We have (see (3.31), (3.32), (1.1), (3.34)) that
. We have (see (3.31), (3.32), (1.1), (3.34)) that

Hence,
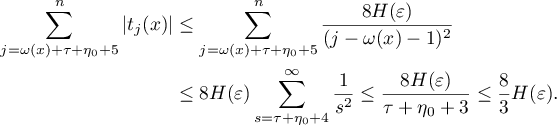
We finally have that in the second case

and (3.21) is proved. Thus we have constructed trigonometric polynomials  ,
,  , satisfying (3.20) and (3.21).
, satisfying (3.20) and (3.21).
It is easy to see that  when
when 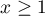 . Since
. Since  , we have
, we have  . Hence (see (3.14)),
. Hence (see (3.14)),
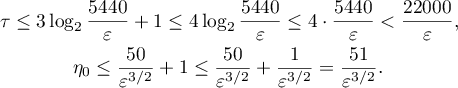
Let  . We obtain (see (3.18))
. We obtain (see (3.18))
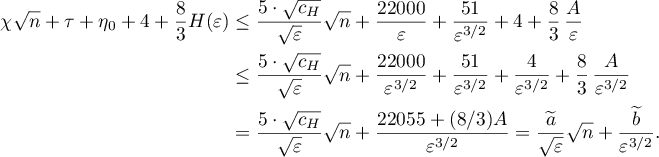
Thus we have constructed a sequence  of trigonometric polynomials such that
of trigonometric polynomials such that

It is evident that the constants  ,
,  and
and  can be replaced by
can be replaced by  ,
,  and
and 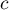 , respectively (see (3.19)).
, respectively (see (3.19)).
Now suppose that  . Then
. Then
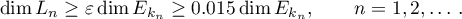
It follows from the argument above that there is a sequence  of trigonometric polynomials such that
of trigonometric polynomials such that

for any positive integer  . Theorem 2 is proved.
. Theorem 2 is proved. 
Theorem 3. Let  be a real number,
be a real number, 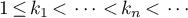 a sequence of positive integers, and
a sequence of positive integers, and 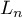 a subspace of
a subspace of  such that
such that  ,
,  . Then
. Then

where  ,
,  ,
,  and
and  are positive absolute constants and, moreover,
are positive absolute constants and, moreover,  and
and  are the constants in Theorem 2.
are the constants in Theorem 2.
Proof. By Theorem 2, there is a sequence 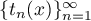 of trigonometric polynomials such that
of trigonometric polynomials such that
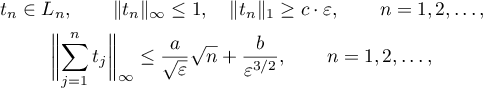
where  ,
,  and
and 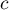 are positive absolute constants. Let
are positive absolute constants. Let  be a positive integer. Put
be a positive integer. Put  . Then
. Then  and
and

Since the spectra of the trigonometric polynomials  ,
,  , are pairwise disjoint and
, are pairwise disjoint and  , we obtain that
, we obtain that  is a non-zero real trigonometric polynomial. By the inequality (3.2),
is a non-zero real trigonometric polynomial. By the inequality (3.2),

where  is a positive absolute constant. Thus
is a positive absolute constant. Thus
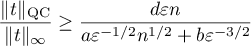
and the first inequality in (3.35) is proved. Further,

where  is a positive absolute constant. Thus the second inequality in (3.35) is also proved. The proof of Theorem 3 is complete.
is a positive absolute constant. Thus the second inequality in (3.35) is also proved. The proof of Theorem 3 is complete. 
Corollary 2. Suppose that sequences  and
and  of real numbers sasisfy the conditions
of real numbers sasisfy the conditions
i)  ,
,  (
( ) and
) and  when
when  ;
;
ii)  ,
,  (
( ) and, starting at some
) and, starting at some  ,
,
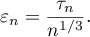
Let 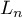 be a subspace of
be a subspace of  such that
such that

Then

where 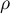 is a positive absolute constant. In particular,
is a positive absolute constant. In particular,
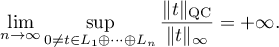
Proof. Let  be a positive integer. Write
be a positive integer. Write  . Then
. Then  is a real number and, by condition ii), the inequality
is a real number and, by condition ii), the inequality  holds for any positive integer
holds for any positive integer  ,
,  . Put
. Put  when
when  and
and  when
when  .
.
We claim that  is a subspace of
is a subspace of  and
and

Indeed, if  , then
, then  is a subspace of
is a subspace of  and
and

If  , then
, then  is a subspace of
is a subspace of  and
and
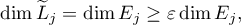
and so (3.36) is proved.
Putting  ,
,  , in Theorem 3 we have
, in Theorem 3 we have
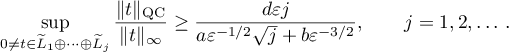
In particular,

when  . Since
. Since  ,
,

Thus,
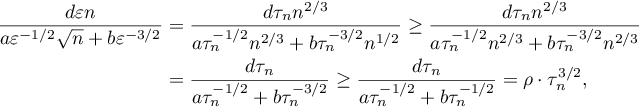
where  is a positive absolute constant. Corollary 2 is proved.
is a positive absolute constant. Corollary 2 is proved. 
The author grateful to the referee for his careful reading of the paper.






