Ticket queues with regular and strategic customers

Abstract

We study a Markovian single-server ticket queue where, upon arrival, each customer can draw a number from a take-a-number machine, while the number of the customer currently being served is displayed on a panel. The difference between the above two numbers is called the “virtual queue length.” We consider a nonhomogeneous population of customers comprised of two types: “regular” and “strategic.” Upon arrival, a regular customer, regardless of the value of the virtual queue length, draws a number from the machine, joins the queue and waits in the system until being served. A strategic customer, depending on the virtual queue length, may either join, leave, or go to “orbit” for a random duration. If, upon return from orbit, a strategic customer realizes that s/he missed her/his turn, s/he balks. Otherwise, s/he joins the queue and waits to be served. We analyze this intricate stochastic system, calculate its steady-state probabilities, derive the sojourn time’s Laplace–Stieltjes transform of a regular and of a strategic customer and calculate the system’s performance measures. Finally, an economic analysis is performed to determine the optimal mean orbiting time of strategic customers for two types of objective functions. Numerical examples are presented.

Appendix: How to construct diagram (m, n + 1) given diagram (m, n)?

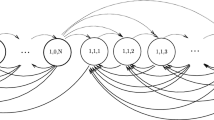
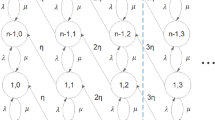
Each node in the diagram is represented by a string. A node having a string of length j represents a state with $j - 1$ strategic customers. Thus, in a state represented by a node of the form (i), i ≥ 0, there are no strategic customers. Observe from the form of Fig. 1 that all the nodes in any row i ≥ 0 of diagram (m, n), have i regular customers that have arrived after the arrival of the last strategic customer.

It is quite easy to transform a given diagram (m, n), m ≥ 1, n ≥ 3 and m < n – 1, to a diagram (m + 1, n) as the number of nodes is independent of m; see Proposition 1. The only changes required are to redirect some of the arcs of the diagram. We skip the details of the changes needed in the diagram for increasing m, as they are straightforward.

In what follows, we provide a forward recursion that builds diagram (m, n + 1) from any given diagram (m, n), where m < n – 1, m ≥ 1, n ≥ 3 and m + n > 4. The nodes of diagram (m, n) in row $i \ge 0$ that need to be augmented when increasing n by 1 are the nodes for which a new incoming strategic customer has to quit the system upon arrival as $D = n$, even if the last i regular customers that joined the system are totally removed. Alternatively, in a node that can be augmented, the last strategic customer of its string is preceded by $n - 1$ customers of any type. We call such a node an augmentable node. As will be shown below, the augmentation process does not alter the length of the strings that are generated from the augmentable nodes.

In addition to the augmentation process, we need add some new nodes to the diagram $\left( {m,n + 1} \right)$ that are not generated by the augmentable nodes of diagram (m, n). These new nodes are represented by strings of length n + 2.

Next, we describe in detail the two steps for generating the diagram for (m, n + 1) from diagram (m, n):

• 1. New nodes obtained by augmentation: consider the augmentable nodes of row i ≥ 0 in diagram (m, n) whose string is of length j, 1 < j ≤ n + 1: augment each of these nodes by adding $j - 1$ new nodes of the same length j, where the string that is associated with each augmented node is the same as the string of the node it is augmented from, except that the number in one of the first $j - 1$ locations is increased by 1, without affecting the “in/out” status of the strategic customers. For example, the node $(10^{\text{in}} 1^{\text{out}} )$ is augmented by two nodes, namely $(20^{\text{in}} 1^{\text{out}} )$ and $(11^{\text{in}} 1^{\text{out}} )$. Thus, from each augmentable node in diagram (m, n) that is represented by a string of length 1 < j ≤ n + 1, we get $j - 1$ augmented nodes. For example, in row $i$ of the diagram for $n = 3,$ and for $j = 2$, only nodes ($2i^{\text{in}}$) and ($2i^{\text{out}}$) are augmentable. Node ($2i^{\text{in}}$) is augmented by node $(3i^{\text{in}} )$, and node ($2i^{\text{out}}$) is augmented by node ($3i^{\text{out}}$).

  Note that, in any row $i \ge 1$, there are $i$ regular customers after the last strategic customer. If the first element of a string in row $i$ of diagram (m, n) is 0, then the second element must be “in”, as otherwise the next existing customer (regular or “in”) will get served immediately, while throwing away all the “out” strategic customers that were bypassed. Thus, in such a case, we complete the described augmentation of a node by generating one additional augmented string that its first element is 1, the second element is changed to “out”, and the remaining elements of the string are unchanged with respect to the augmentable node of diagram (m, n).

We should pay attention that the augmentation process may generate a duplication of augmented nodes as shown in the sequel: first, augment in diagram (m, n) = (1, 3) the augmentable node $(01^{\text{in}} 0^{\text{out}} )$, which results in the augmented nodes $(11^{\text{in}} 0^{\text{out}} )$ and $(02^{\text{in}} 0^{\text{out}} )$. Second, augment the augmentable node $(10^{\text{in}} 0^{\text{out}} )$, which results in the augmented nodes $(20^{\text{in}} 0^{\text{out}} )$ and $(11^{\text{in}} 0^{\text{out}} )$. Thus, the augmented node $( 1 1^{\text{in}} 0^{\text{out}} )$ is generated twice. More specifically, with respect to diagram (1,3), each of the augmentable nodes $( 1 0^{\text{in}} i^{\text{out}} )$, $(10^{\text{in}} i^{\text{in}} )$, $( 1 0^{\text{out}} i^{\text{out}} )$ and $( 1 0^{\text{out}} i^{\text{in}} )$ for i ≥ 0, is augmented by two nodes, where, for example, node $( 1 0^{\text{in}} i^{\text{out}} )$ is augmented by $( 2 0^{\text{in}} i^{\text{out}} )$ and by $( 1 1^{\text{in}} i^{\text{out}} )$. At the end, eight nodes are augmented by the above four nodes of diagram (1, 3). Consequently, at the end of the process, duplicated nodes should be removed.

By applying the same process to the augmentable nodes $( 0 1^{\text{in}} i^{\text{out}} )$, $(01^{\text{in}} i^{\text{in}} )$ in diagram (1, 3), we get an additional two new augmentation nodes $( 0 2^{\text{in}} i^{\text{out}} )$ and $( 0 2^{\text{in}} i^{\text{in}} )$ in addition to two more nodes that are duplicates, namely nodes $( 1 1^{\text{in}} i^{\text{out}} )$ and $( 1 1^{\text{in}} i^{\text{in}} )$ that have already been generated. In addition, the strings of the augmentable nodes $( 0 1^{\text{in}} i^{\text{out}} )$, $( 0 1^{\text{in}} i^{\text{in}} )$ have 0 at the beginning of the string, and therefore they can be also augmented by $( 1 1^{\text{out}} i^{\text{out}} )$ and $( 1 1^{\text{out}} i^{\text{in}} )$, but these nodes have already been augmented by $\left( { 1 0^{\text{out}} i^{\text{out}} } \right)$ and $\left( { 1 0^{\text{out}} i^{\text{in}} } \right)$, respectively. Thus, the augmentation of the nodes $( 0 1^{\text{in}} i^{\text{out}} )$ and $( 0 1^{\text{in}} i^{\text{in}} )$ results in just two new augmentation nodes.

Finally, the augmentable nodes $( 0 0^{\text{in}} 0^{\text{in}} 0^{\text{in}} )$, $( 0 0^{\text{in}} 0^{\text{in}} 0^{\text{out}} )$, $(00^{in} 0^{out} 0^{in} )$ and $( 0 0^{\text{in}} 0^{\text{out}} 0^{\text{out}} )$ generate four augmentation nodes for each of them. Three are obtained by increasing by 1 the value of one of the first three locations. The last is obtained by increasing the first 0 to 1, and changing the second 0 to an “out”. For example, $( 0 0^{\text{in}} 0^{\text{in}} 0^{\text{in}} )$ is augmented by $( 1 0^{\text{in}} 0^{\text{in}} 0^{\text{in}} )$, $( 0 1^{\text{in}} 0^{\text{in}} 0^{\text{in}} )$, $( 0 0^{\text{in}} 1^{\text{in}} 0^{\text{in}} )$ and $( 1 0^{\text{out}} 0^{\text{in}} 0^{\text{in}} )$. Thus, we get 16 such augmented nodes.

In total, we have 28 augmentation nodes added to diagram (1, 3).

• 2. New nodes. In any diagram (m, n), m < n – 1, m ≥ 1, n ≥ 3, the longest string of nodes is of size n + 1. Such strings consist of n + 1 zeros, where the second zero is “in”, and the following n – 1 zeros can be in any combination of “in” or “out”. In diagram (m, n + 1), the longest string is of length n + 2. Thus, the total number of new nodes is $2^{n}$.

In conclusion of the presentation of the rows’ construction in diagram (1, 4) from that of diagram (1, 3): (i) all nodes in diagram (1, 3) appear in diagram (1, 4), (ii) in each row i ≥ 0, of diagram (1, 3), 28 augmentation nodes will be added. (iii) 8 new nodes, each having a string 5 zeros, are added to the set of nodes. Thus, each row of diagram (1, 4) consists of 54 nodes, namely $18 + 28 + 8 = 54 = 2 \cdot 3^{4 - 1}$ nodes.

Construction of the matrices in Q

The matrices $A_{0}$ and $A_{2}$ in the new diagram (m, n + 1) will be similar to those corresponding to diagram (m, n). Namely, $A_{0}$ and $A_{2}$ are each of order $f = 2 \cdot 3^{n}$: $A_{0} = \lambda I_{f \times f}$ and $A_{2} = \left[ {a_{2}^{i,j} } \right]_{f \times f}$, where $a_{2}^{i,j} = \left\{ {\begin{array}{*{20}l} \mu \hfill & {i = j = 1.} \hfill \\ 0 \hfill & {{\text{otherwise}} .} \hfill \\ \end{array} } \right.$. The matrix $A_{1}$ is also of order $f \times f$, where $a_{1}^{i,j} = \left\{ {\begin{array}{*{20}l} { - (\lambda + \mu )} \hfill & {i = j = 1,2.} \hfill \\ {b_{1,1}^{i,j} } \hfill & {{\text{otherwise}} .} \hfill \\ \end{array} } \right.$. The entries $\left[ {b_{1,1}^{i,j} } \right]_{f \times f}$ are constructed by adding a column for each augmented node as described above.