Admission control in a two-class loss system with periodically varying parameters and abandonments

Abstract

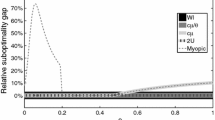
Motivated by service systems, such as telephone call centers and emergency departments, we consider admission control for a two-class multi-server loss system with periodically varying parameters and customers who may abandon from service. Assuming mild conditions for the parameters, a dynamic programming formulation is developed. We show that under the infinite horizon discounted problem, there exists an optimal threshold policy and provide conditions for a customer class to be preferred for each fixed time, extending stationary results to the non-stationary setting. We approximate the non-stationary problem by discretizing the time horizon into equally spaced intervals and examine how policies for this approximation change as a function of time and parameters numerically. We compare the performance of these approximations with several admission policies used in practice in a discrete-event simulation study. We show that simpler admission policies that ignore non-stationarity or abandonments lead to significant losses in rewards.

A Appendix

This section is dedicated to showing that the discounted reward optimality equations have a solution and that these solutions can be computed via successive approximations. The result is an application of Theorems 4.1 and 4.2 in Wakuta [36]. There are minor adjustments to the proofs since the distribution of the state change and the time between decision points is not separable. The following notation and definitions are used throughout this Appendix.

• Let $\mathbb {X}$ and $\mathbb {A}$, respectively, denote the state and action space for a generic semi-Markov decision process (SMDP).

• Let the Euclidean distance between $\ell = \left( \left( i,j,k,z\right) ,a\right)$, $\ell ' = \left( \left( i',j',k',z'\right) ,a'\right) \in \text {Gr}(\mathbb {A})$ be given by

  $$\begin{aligned} \Vert \ell -\ell '\Vert&:= \sqrt{(i-i')^2 + (j-j')^2 + (k-k')^2 + (z-z')^2 + (a-a')^2}. \end{aligned}$$

Definition A1

The transition kernel $Q(\cdot |x,a)$ is called strongly continuous provided the mapping $(x,a) \rightarrow \int _{x' \in \mathbb {X}} \! f(x') \, Q(\mathrm {d}x'|x,a)$ is continuous and bounded whenever f is measurable and bounded on $\mathbb {X}$.

1.1 A.1 Discounted reward optimality equations (DROE)

In this section, we show that the DROE have a solution and that the solution can be computed via the (contraction) mappings defined in Sect. 4. Before doing so we note that because the rewards are bounded below, it suffices (and is in fact equivalent) to consider the case with nonnegative rewards. That is to say that adding the lower bound on rewards to all rewards does not change the optimal control. Let this lower bound be denoted L and, throughout this section, assume $r(x,a) \ge 0$.

Lemma 2

The following hold:

• 1. There exist a Borel measurable function w on $\mathbb {X}$ with $w(x) \ge 1, x \in \mathbb {X}$, a number $\xi$ ($0< \xi < 1$), and a number $M > 0$ such that

  • (a) for any $(x,a) \in Gr(\mathbb {A})$

    $$\begin{aligned} \Vert r(x,a)\Vert \le M w(x). \end{aligned}$$

  • (b) for any policy, the sequence of decision times $\{t_n, n \ge 0\}$ are such that $\limsup _{n \rightarrow \infty } t_n = \infty$ almost surely.

• 2. $\mathbb {X}$ and $\mathbb {A}$ are non-empty Borel subsets of a complete separable metric space.

• 3. A(x) is a Borel measurable compact-valued multi-function from $\mathbb {X}$ into $\mathbb {A}$.

• 4. The one-stage reward function r(x, a) is upper-semicontinuous on $\mathbb {A}$ for each fixed $x \in \mathbb {X}$.

• 5. The transition kernel Q is strongly continuous.

We remark that it is usual that Statement 1(b) (see Proposition 3.1 of [36]) is proved under the assumption of the existence of a Lyapunov function (see inequality (3.2) in [36]).

Proof

Statement 1(a) holds with $w(x) \equiv 1$ and for any M that maximizes the one-stage reward functions r(x, a) (below and above). For Statement 1(b), notice that if the initial state is (i, j, k, 0), the expected number of transitions before the dummy transition at time T is ${{\,\mathrm{\mathbb {E}}\,}}N(T) < \infty$ (in fact $\varPsi T$), where N(T) is a Poisson process of rate $\varPsi$. This implies that $N(T) < \infty$ almost surely. At time T, there is a renewal. Since there are deterministic renewals at times $(T, 2T, \ldots )$, we have that it requires an infinite time to see an infinite number of transitions (almost surely).

Statements 2, 3 and 4 hold by construction and by the finiteness of A(x) for each x. For Statement 5, it is enough to show that

$$\begin{aligned}&\int _z^T \Big [ \lambda _{1}(t) f(i,j,1,t) + \lambda _{2}(t) f(i,j,2,t) \nonumber \\&\quad + \left( \mu _{i}^{1}(t) + \beta _{i}^{1}(t) \right) f(i,j,-1,t) + \left( \mu _{j}^{2}(t) + \beta _{j}^{2}(t) \right) f(i,j,-2,t) \nonumber \\&\quad + \big ( 1 - \lambda (t) - \mu _{i}^{1}(t) - \beta _{i}^{1}(t) -\mu _{j}^{2}(t) - \beta _{j}^{2}(t) \big ) f(i,j,0,t) \Big ] e^{-(1+\alpha )(t-z)}\,{\text {d}}t \end{aligned}$$

(8.1)

is continuous for any bounded, real-valued measurable function f. To this end, fix $\epsilon > 0$ and let $x = (i,j,k,z), x' = (i',j',k',z') \in \mathbb {X}$ with $z < z'$. Next, choose $\delta < 1$ so that $\Vert (x,a) - (x',a')\Vert < \delta$ implies that $i = i', j = j', k = k'$ and $a = a'$. It follows that

$$\begin{aligned}&\Big | \Big [\int _{z}^{T} \Big [ \lambda _{1}(t) f(i,j,1,t) + \lambda _{2}(t) f(i,j,2,t) \\&\quad + \left( \mu _{i}^{1}(t) + \beta _{i}^{1}(t) \right) f(i,j,-1,t) + \left( \mu _{j}^{2}(t) + \beta _{j}^{2}(t) \right) f(i,j,-2,t) \\&\quad + \big ( 1 - \lambda (t) - \mu _{i}^{1}(t) - \beta _{i}^{1}(t) -\mu _{j}^{2}(t) - \beta _{j}^{2}(t) \big ) f(i,j,0,t) \Big ] e^{-(1+\alpha )(t-z)}\,{\text {d}}t \Big ] \\&\quad - \Big [\int _{z'}^{T} \Big [ \lambda _{1}(t) f(i',j',1,t) + \lambda _{2}(t) f(i',j',2,t) \\&\quad + \left( \mu _{i'}^{1}(t) + \beta _{i'}^{1}(t) \right) f(i',j',-1,t) + \left( \mu _{j'}^{2}(t) + \beta _{j'}^{2}(t) \right) f(i',j',-2,t) \\&\quad + \big ( 1 - \lambda (t) - \mu _{i'}^{1}(t) - \beta _{i'}^{1}(t) -\mu _{j'}^{2}(t) - \beta _{j'}^{2}(t) \big ) f(i',j',0,t) \Big ] e^{-(1+\alpha )(t-z')}\,{\text {d}}t \Big ] \Big | \\&= \Big | \Big [\int _z^T \Big [ \lambda _{1}(t) f(i,j,1,t) + \lambda _{2}(t) f(i,j,2,t) \\&\quad + \left( \mu _{i}^{1}(t) + \beta _{i}^{1}(t) \right) f(i,j,-1,t) + \left( \mu _{j}^{2}(t) + \beta _{j}^{2}(t) \right) f(i,j,-2,t) \\&\quad + \big ( 1 - \lambda (t) - \mu _{i}^{1}(t) - \beta _{i}^{1}(t) -\mu _{j}^{2}(t) - \beta _{j}^{2}(t) \big ) f(i,j,0,t) \Big ] e^{-(1+\alpha )(t-z)}\,{\text {d}}t \Big ] \\&\quad - \Big [\int _{z'}^T \Big [ \lambda _{1}(t) f(i,j,1,t) + \lambda _{2}(t) f(i,j,2,t) \\&\quad + \left( \mu _{i}^{1}(t) + \beta _{i}^{1}(t) \right) f(i,j,-1,t) + \left( \mu _{j}^{2}(t) + \beta _{j}^{2}(t) \right) f(i,j,-2,t) \\&\quad + \big ( 1 - \lambda (t) - \beta _{i}^{1}(t) - \beta _{j}^{2}(t) - \mu _{i}^{1}(t) -\mu _{j}^{2}(t) \big ) f(i,j,0,t) \Big ] e^{-(1+\alpha )(t-z')}\,{\text {d}}t \Big ] \Big |, \end{aligned}$$

which simplifies to

$$\begin{aligned}&\Big | \Big [\int _{z}^{z'} \Big [ \lambda _{1}(t) f(i,j,1,t) + \lambda _{2}(t) f(i,j,2,t) \\&\quad + \left( \mu _{i}^{1}(t) + \beta _{i}^{1}(t) \right) f(i,j,-1,t) + \left( \mu _{j}^{2}(t) + \beta _{j}^{2}(t) \right) f(i,j,-2,t) \\&\quad + \big ( 1 - \lambda (t) - \mu _{i}^{1}(t) - \beta _{i}^{1}(t) -\mu _{j}^{2}(t) - \beta _{j}^{2}(t) \big ) f(i,j,0,t) \Big ] e^{-(1+\alpha )(t-z)}\,{\text {d}}t \Big ] \\&\quad + \Big (e^{-(z'-z)} - 1\Big )\Big [\int _{z'}^T \Big [ \lambda _{1}(t) f(i,j,1,t) + \lambda _{2}(t) f(i,j,2,t) \\&\quad + \left( \mu _{i}^{1}(t) + \beta _{i}^{1}(t) \right) f(i,j,-1,t) + \left( \mu _{j}^{2}(t) + \beta _{j}^{2}(t) \right) f(i,j,-2,t) \\&\quad + \big ( 1 - \lambda (t) - \mu _{i}^{1}(t) - \beta _{i}^{1}(t) -\mu _{j}^{2}(t) - \beta _{j}^{2}(t) \big ) f(i,j,0,t) \Big ] e^{-(1+\alpha )(t-z')}\,{\text {d}}t \Big ] \Big |. \end{aligned}$$

Let $M < \infty$ be such that $\sup _{x \in \mathbb {X}} |f(x)| \le M < \infty$. The convexity of the function $x^2$ for $0< x < \infty$ implies that $\Big ( \frac{f+g}{2} \Big )^2 \le \frac{1}{2} \big (f^2 + g^2 \big )$, and hence, that $(f+g)^2 \le 2f^2 + 2g^2$ for any two functions f, g. It follows that the previous expression is bounded above by

$$\begin{aligned}&\left[ 2 \left[ \int _{z}^{z'} \big ( \lambda _{1}(t) f(i,j,1,t) + \lambda _{2}(t) f(i,j,2,t) \right. \right. \\&\quad + \left( \mu _{i}^{1}(t) + \beta _{i}^{1}(t) \right) f(i,j,-1,t) + \left( \mu _{j}^{2}(t) + \beta _{j}^{2}(t) \right) f(i,j,-2,t) \\&\quad \left. \left. + \big ( 1 - \lambda (t) - \mu _{i}^{1}(t) - \beta _{i}^{1}(t) -\mu _{j}^{2}(t) - \beta _{j}^{2}(t) \big ) f(i,j,0,t) \right] e^{-(1+\alpha )(t-z)}\big ),{\text {d}}t \right] ^2 \\&\quad + 2 \left[ (e^{-(z'-z)} - 1) \left( \int _{z'}^T \Big [ \lambda _{1}(t) f(i,j,1,t) + \lambda _{2}(t) f(i,j,2,t)\right. \right. \\&\quad + \left( \mu _{i}^{1}(t) + \beta _{i}^{1}(t) \right) f(i,j,-1,t) + \left( \mu _{j}^{2}(t) + \beta _{j}^{2}(t) \right) f(i,j,-2,t) \\&\quad \left. \left. + \big ( 1 - \lambda (t) - \mu _{i}^{1}(t) - \beta _{i}^{1}(t) -\mu _{j}^{2}(t) - \beta _{j}^{2}(t) \big ) f(i,j,0,t) \right) e^{-(1+\alpha )(t-z')}\,{\text {d}}t \Big ]^2 \right] ^{\frac{1}{2}}. \end{aligned}$$

This last expression is bounded above by $\sqrt{2} M (1 - e^{-(1+\alpha )(z'-z)})$. The continuity of $e^{-x}$ on $-\infty< x < \infty$ implies that we can choose $\delta$ so that $z'-z < \delta$ implies $\sqrt{2} M (1 - e^{-(1+\alpha )(z'-z)}) < \epsilon$. This proves the last statement. $\square$

The previous lemma implies that Theorem 4.1 in [36] holds with some minor adjustments. We include the statement and proof of necessity (for the current model) for completeness. Sufficiency holds with almost no changes to that in [36] since A(x) is finite for each $x \in \mathbb {X}$.

Theorem 3

A policy $\pi$ is optimal if and only if its reward $v^{\pi }_{\alpha }(x)$ satisfies the discounted reward optimality equations (see (4.1)).

Proof

Suppose $v^{\pi '}_{\alpha }(x)$ satisfies the DROE. Fix $n \ge 1$. Denote the history under a generic policy $\pi = \{d_0, d_1, \ldots \}$ by

$$\begin{aligned} h_k = \{t_0,x,a_0,\ldots ,t_{k},x_{k},a_{k}\}, \end{aligned}$$

and note that

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{\pi ,x}\Big [ \sum _{k=0}^{n-1} \big [ e^{-\alpha t_{k+1}} v_{\alpha }^{\pi '}(x_{k+1}) - {{\,\mathrm{\mathbb {E}}\,}}_{\pi ,h_k} e^{-\alpha t_{k+1}} v_{\alpha }^{\pi '}(x_{k+1}) \big ] \Big ] = 0, \end{aligned}$$

(8.2)

for any $n \ge 2$. For ease of notation, for any fixed $s \in \mathbb {X}$, let p(y|s, a) denote the probability of next entering state y given that the current state is s and action a is chosen. Let $\{\tau _n, n \ge 1\}$ be the inter-event times so that $\tau _n = t_n - t_{n-1}$. Consider the second term above,

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{\pi ,h_k} e^{-\alpha t_{k+1}} v_{\alpha }^{\pi '}(x_{k+1})&= e^{-\alpha t_{k}} {{\,\mathrm{\mathbb {E}}\,}}_{\pi ,h_k} e^{-\alpha \tau _{k+1}} v_{\alpha }^{\pi '}(x_{k+1})\\&= e^{-\alpha t_{k}} \Big [ \int _{y \in \mathbb {X}} e^{-\alpha t(y)} v_{\alpha }^{\pi '}(y) p({\text {d}}y|x_k,a_k)\Big ] \\&= e^{-\alpha t_{k}} \Big [ r(x_k,a_k) + \int _{y \in \mathbb {X}} e^{-\alpha t(y)} v_{\alpha }^{\pi '}(y) p({\text {d}}y|x_k,a_k)\Big ] \\&\quad - e^{-\alpha t_{k}} r(x_k,a_k) \\&\le e^{-\alpha t_{k}} \Big [ v_{\alpha }^{\pi '}(x_k)\Big ] - e^{-\alpha t_{k}} r(x_k,a_k), \end{aligned}$$

where we have denoted by t(y) the discount time associated with next transition and the last inequality holds by taking the maximum in the DROE and the assumption that $v_{\alpha }^{\pi '}$ satisfies it. Thus, using (8.2) yields

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{\pi ,x}\Big [ \sum _{k=0}^{n-1} e^{-\alpha t_{k+1}} v_{\alpha }^{\pi '}(x_{k+1}) - e^{-\alpha t_{k}} \Big [ v_{\alpha }^{\pi '}(x_{k})\Big ] + e^{-\alpha t_{k}} r(x_k,a_k)\Big ] \le 0. \end{aligned}$$

The first two terms in the sum telescope, yielding the following inequality:

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}_{\pi ,x}\Big [e^{-\alpha t_{n}} v_{\alpha }^{\pi '}(x_{n}) - v_{\alpha }^{\pi '}(x) + \sum _{k=0}^{n-1} e^{-\alpha t_{k}} r(x_k,a_k)\Big ] \le 0. \end{aligned}$$

Statement 1(a) of Lemma 2 implies that $v_{\alpha }^{\pi '}$ is bounded. The Dominated Convergence Theorem and Statement 1(b) of Lemma 2 yield that ${{\,\mathrm{\mathbb {E}}\,}}_{\pi ,x}e^{-\alpha t_{n}} v_{\alpha }^{\pi '}(x_{n}) \rightarrow 0$ as $n \rightarrow \infty$. The last term converges to the total discounted reward of $\pi$ so that we have $v_{\alpha }^{\pi '} \ge v_{\alpha }^{\pi }$, which yields the result. $\square$

We conclude this section by stating Lemma 5.7 and Theorem 5.8 of [36], which follow in the same manner.

Theorem 4

The following hold for the discounted reward model:

• 1. The mapping $U_{n, \alpha }$ maps the set of bounded functions on $\mathbb {X}$ back into the same set and is a contraction mapping. This implies that $v_{\alpha }$ is the unique solution to the DROE.

• 2. There exists a Borel measurable function f that achieves the maximum in the DROE.

• 3. There exists an optimal stationary policy.