Abstract
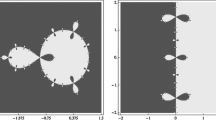
In this work we provide analytic and graphic arguments to explain the behaviour of Chebyshev’s method applied to cubic polynomials in the complex plane. In particular, we study the parameter plane related to this method and we compare it with other previously known, such as Newton’s or Halley’s methods. Our specific interest is to characterize “bad” polynomials for which Chebyshev’s method presents convergence to points distinct from the roots (i.e. the root-finding algorithm fails). In particular, we prove the existence of polynomials for which Chebyshev’s method has superattracting n-cycles and the existence of polynomials for which Chebyshev’s method has superattracting extraneous fixed points. The first fact is shared with other root-finding methods, such as Newton’s or Halley’s, but the second one is an established dynamic feature of Chebyshev’s method. Here we go depth on the study of the dynamics related to the superattracting n-cycles of Chebyshev’s method and its relationships with the superattracting extraneous fixed points, providing some analytical and geometric arguments to explain the related parameter plane. In particular, we prove the existence of a sequence of parameters for which the corresponding Chebyshev’s iterative method has a superattracting n-cycle.











Similar content being viewed by others
References
Amat, S., Busquier, S., Plaza, S.: Review of some iterative root-finding methods from a dynamical point of view. SCIENTIA Ser. A Math. Sci. 10, 3–35 (2004)
Argyros, I.K., Hilout, S.: Computational Methods in Nonlinear Analysis: Efficient Algorithms. Fixed Point Theory and Applications. World Scientific, Singapore (2013)
Beardon, A.F.: Iteration of Rational Functions. Springer, New York (1991)
Blanchard, P., Cuzzocreo, D., Devaney, R.L., Fitzgibbon, E.: Accessible Mandelbrot sets in the family \(z^n+\lambda /z^n\). Qual. Theory Dyn. Syst. 15(1), 49–66 (2016)
Cordero, A., Torregrosa, J.R., Vindel, P.: Bulbs of period two in the family of Chebyshev-Halley iterative methods on quadratic polynomials. Abstr. Appl. Anal. 2013, 536910 (2013)
Cordero, A., Torregrosa, J.R., Vindel, P.: Dynamics of a family of Chebyshev–Halley type methods. Appl. Math. Comput. 219(16), 8568–8583 (2013)
Curry, J.H., Garnett, L., Sullivan, D.: On the iteration of a rational function: computer experiments with Newton’s method. Commun. Math. Phys. 91(2), 267–277 (1983)
Diloné, M.A., García-Olivo, M., Gutiérrez, J.M.: A note on the semilocal convergence of Chebyshev’s method. Bull. Aust. Math. Soc. 88(1), 98–105 (2013)
García-Olivo, M., Gutiérrez, J.M., Magreñán, Á.A.: A complex dynamical approach of Chebyshev’s method. SeMA J. 71(1), 57–68 (2015)
Gutiérrez, J.M.: The Cayley problem and the Chebyshev method. Gac. R. Soc. Math. Espanola 19(3), 542 (2016). (Spanish)
Kneisl, K.: Julia sets for the super-Newton method, Cauchy’s method and Halley’s method. Chaos 11(2), 359–370 (2001)
Lyubich, MYu.: The dynamics of rational transforms: the topological picture. Rus. Math. Surv. 41(4), 43–117 (1986)
McMullen, C.: Families of rational maps and iterative root-finding algorithms. Ann. Math. (2) 125(3), 467–493 (1987)
McMullen, C.: The Mandelbrot set is universal. In: The Mandelbrot Set, Theme and Variations. London Mathematical Society Lecture Note Series 274, pp. 1–17. Cambridge University Press, Cambridge (2000)
Milnor, J.: Dynamics in One Complex Variable, 3rd edn. Annals of Mathematics Studies, vol. 160. Princeton University Press, Princeton (2006)
Roberts, G.E., Horgan-Kobelski, J.: Newton’s versus Halley’s methods: a dynamical systems approach. Int. J. Bifurc. Chaos Appl. Sci. Engrg. 14(10), 3459–3475 (2004)
Smale, S.: On the efficiency of algorithms of analysis. Bull. Am. Math. Soc. (N.S.) 13(2), 87–121 (1985)
Varona, J.L.: Graphic and numerical comparison between iterative methods. Math. Intell. 24(1), 37–46 (2002)
Vrscay, E.R.: Julia sets and Mandelbrot-like sets associated with higher order Schröder rational iteration functions: a computer assisted study. Math. Comput. 46(173), 151–169 (1986)
Vrscay, E.R., Gilbert, W.J.: Extraneous fixed points, basin boundaries and chaotic dynamics for Schröder and König rational iteration functions. Numer. Math. 52(1), 1–16 (1988)
Walsh, J.: The dynamics of Newton’s method for cubic polynomials. Coll. Math. J. 26(1), 22–28 (1995)
Acknowledgements
This research was partially supported by Ministerio de Ciencia, Innovación y Universidades under Grants PGC2018-095896-B-C21 and PGC2018-096504-B-C32. The authors want to acknowledge the helpful, constructive and detailed revision of the manuscript by the referees, that has allowed us to improve the final version of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Gutiérrez, J.M., Varona, J.L. Superattracting Extraneous Fixed Points and n-cycles for Chebyshev’s Method on Cubic Polynomials. Qual. Theory Dyn. Syst. 19, 54 (2020). https://doi.org/10.1007/s12346-020-00390-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12346-020-00390-5