Fractional Gallai–Edmonds decomposition and maximal graphs on fractional matching number

Abstract

A fractional matching of a graph G is a function f that assigns to each edge a number in [0, 1] such that for each vertex v, $\sum \nolimits _{e\in \Gamma (v)}f(e) \le 1$, where $\Gamma (v)$ is the set of all edges incident with v. The fractional matching number $\mu _{f}(G)$ of G is the supremum of $\sum \nolimits _{e\in E(G)}f(e)$ over all fractional matchings f of G. Let $D_f(G)$ be the set of vertices which are unsaturated by some maximum fractional matching of G, $A_f(G)$ the set of vertices in $V(G)-D_f(G)$ adjacent to a vertex in $D_f(G)$ and $C_f(G)=V(G)-A_f(G)-D_f(G)$. In this paper, the partition $(C_f(G), A_f(G), D_f(G))$, named fractional Gallai–Edmonds decomposition, is obtained by an algorithm in polynomial time via the Gallai–Edmonds decomposition. A graph G is maximal on $\mu _{f}(G)$ if any addition of edge increases the fractional matching number $\mu _{f}(G)$. The Turán number is the maximum of edge numbers of maximal graphs and the saturation number is the minimum of edge numbers of maximal graphs. In this paper, the maximal graphs are characterized by using the fractional Gallai–Edmonds decomposition. Thus the Turán number, saturation number and extremal graphs are obtained.

1 Introduction and notation

Graphs considered in this paper are finite, undirected and simple. Let G be a graph. The size of G is the number of edges, denoted by m(G). The complement of G is denoted by ${\overline{G}}$. A matching of G is a set of pairwise disjoint edges. The matching number$\mu (G)$ of G is the number of edges in a maximum matching. Let M be a matching of G. A vertex of G is M-saturated if it is incident with an edge in M, otherwise, is M-unsaturated.

Let G be a graph and p(G) a parameter of G. Then G is said to be maximal on p(G) if for any edge $e\in E({\overline{G}})$, $p(G+e)\ne p(G)$. The maximum size of maximal n-vertex graphs on p(G) is said to be the Turán number on p(G), denoted by ex(n, p(G)). There exists a “dual” problem to the above one: to determine the minimum size of maximal n-vertex graphs, named the saturation number on p(G), denoted by sat(n, p(G)). The maximal n-vertex graphs on p(G) whose size are ex(n, p(G)) and sat(n, p(G)) are said to be Turán graph on p(G) and saturated extremal graph on p(G), respectively. Moreover, we can investigate the set of all possible sizes of maximal n-vertex graphs, named edge spectrum on p(G), denoted by ES(n, p(G)). When p(G) is the matching number $\mu (G)$, MaderMader (1973) characterized the maximal graph on $\mu (G)$ which implies that if $\mu (G)=k$ and $|V(G)|\ge 4k$, then the Turán graph on $\mu (G)$ is $K_{k}+\overline{K_{n-k}}$. In 1986, $sat(n,\mu (G))$ and the saturated extremal graph on $\mu (G)$ are provided by L. Kászonyi and Zs. Tuza in  Kászonyi and Tuza (2010).

A fractional matching of a graph G is a function f that assigns to each edge a number in [0, 1] such that for each vertex v, $\sum \nolimits _{e \epsilon \Gamma _{G} (v)}f(e)\le 1$, where $\Gamma _{G} (v)$ is the set of all edges incident with v (in short, $\Gamma (v)$). A vertex v is said to be f-saturated if $\sum \nolimits _{e \epsilon \Gamma (v)}f(e)=1$, otherwise, v is f-unsaturated. The fractional matching number of G, denoted by $\mu _{f}(G)$, is the supremum of $\sum \nolimits _{e\in E(G)}f(e)$ over all fractional matchings f of G. A fractional matching f of G is said to be perfect if every vertex is f-saturated, that is, $\mu _{f}(G)=\frac{n}{2}$. For details about fractional matchings, see  Liu and Liu (2017). A graph G is said to be maximal on $\mu _{f}(G)$ if for any edge $e\in E({\overline{G}})$, $\mu _{f}(G+e)>\mu _{f}(G)$. In this paper, we investigate $ex(n,\mu _{f}(G))$, $sat(n,\mu _{f}(G))$, $ES(n,\mu _{f}(G))$ and the extremal graphs. Note that if $\mu _{f}(G)=\frac{n}{2}$, the maximal graphs on $\mu _{f}(G)$ are unique, which is $K_{n}$. Then the Turán graph and the saturated extremal graph are both $K_{n}$. Therefore, we only consider the graphs with no perfect fractional matching in the following. For characterizing the maximal graphs on $\mu _{f}(G)$, we need to introduce the Gallai–Edmonds structure theorem in the following. And then we give a decomposition of a graph with respect to maximum fractional matching, named fractional Gallai–Edmonds decomposition in Sect. 2.

Let D(G) be the set of all vertices in V(G) which are missed by at least one maximum matching of G and A(G) the set of vertices in $V(G)-D(G)$ adjacent to a vertex in D(G). Finally, Let $C(G)=V(G)-A(G)-D(G)$. Then the partition (C(G), A(G), D(G)) of V(G) is said to be Gallai–Edmonds decomposition. Clearly, if there exists an algorithm in polynomial time finding D(G), then there exists an algorithm in polynomial time determining (C(G), A(G), D(G)).

Lemma 1.1

 Lovász and Plummer (1985) Let G be a graph. Then there exists an algorithm in polynomial time finding D(G).

A connected graph G is factor-critical if $G-v$ has a perfect matching for any $v\in V(G)$. A bipartite graph $H=(U, W)$ is said to have positive surplus (as viewed from U) if $|N_H (X)|>|X|$ for any nonempty subset X of U. Let M be a maximum matching of G. The number of M-unsaturated vertices is the deficiency of G, denoted by def(G); that is, $def(G)=|V(G)|-2\mu (G)$. It is easy to check the following. If G has a perfect matching, then $def(G)=0$ and $C(G)=V(G)$. If G is factor-critical, then $def(G)=1$ and $D(G)=V(G)$. If a bipartite graph $G=(U,W)$ has positive surplus (as viewed from U), then $D(G)=W$, $A(G)=U$ and $def(G)=|W|-|U|$. Let $T\subseteq V(G)$. The subgraph of G induced by T is denoted by $\langle T\rangle$. Let X, Y be two disjoint subsets of V(G), $E(X)=\{xy\in E(G)|x, y\in X \}$ and $E(X, Y)=\{xy\in E(G)|x\in X, y\in Y \}$. If $E(X)=\emptyset$, then X is said to be independent. The bipartite subgraph of G with vertex set $X\bigcup Y$ and edge set E(X, Y) is denoted by $\langle X, Y\rangle$. In the following, the Gallai–Edmonds decompositions of bipartite graphs and general graphs are characterized, respectively.

Lemma 1.2

 Lovász and Plummer (1985) (Gallai–Edmonds structure theorem for bipartite graph) Let $H=(U_{1},U_{2})$ be a bipartite graph. Let $A_{i}=A(H)\bigcap U_{i}$, $C_{i}=C(H)\bigcap U_{i}$ and $D_{i}=D(H)\bigcap U_{i}$, where $i=1,2$ and (A(H), C(H), D(H)) is the Gallai–Edmonds decomposition of H. Then

• (1) $D(H)=D_{1}\bigcup D_{2}$ is an independent set,

• (2) the subgraph $\langle C_{1}, C_{2}\rangle$ has a perfect matching and hence $|C_{1}|=|C_{2}|$,

• (3) $N_{H}(D_{1})=A_{2}$ and $N_{H}(D_{2})=A_{1}$,

• (4) every maximum matching of H consists of a perfect matching of $\langle C_{1}, C_{2}\rangle$, a maximum matching of $\langle A_{1}, D_{2}\rangle$ and a maximum matching of $\langle A_{2}, D_{1}\rangle$,

• (5) the subgraphs induced by $A_{1}\bigcup D_{2}$ and $A_{2}\bigcup D_{1}$ have positive surplus as viewed from $A_{1}$ and $A_{2}$, respectively. Thus, $|A_{1}|<|D_{2}|$ and $|A_{2}|<|D_{1}|$.

Lemma 1.3

 Lovász and Plummer (1985) (Gallai–Edmonds structure theorem) Let G be a graph and $G_{1}$, ..., $G_{k}$ all components of $\langle D(G)\rangle$. Then

• (1) every $G_{i}$ is factor-critical and $\langle C(G)\rangle$ has a perfect matching;

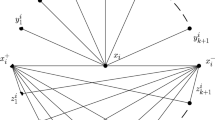
• (2) a matching M of G is a maximum matching if and only if $M\bigcap E(C(G))$ is a perfect matching of $\langle C(G)\rangle$, $M\bigcap E(G_{i})$ is a maximum matching of $G_{i}$ for each $1\le i \le k$ and M matches every vertex in A(G) with a vertex in distinct components $G_{i}$(see Fig. 1);

• (3) $def(G)=k-|A(G)|$

Fig. 1

Gallai–Edmonds decomposition of G

For a component $G_{i}$ of $\langle D(G)\rangle$, $G_{i}$ is nontrivial if $|V(G_{i})|\ge 3$, otherwise, $G_{i}$ is trivial, that is, $G_{i}$ is a single vertex. Let $D_{0}$ be the set of vertices in D(G) which forms trivial components of $\langle D(G)\rangle$. Let M be a maximum matching of G. For a nontrivial component $G_{i}$ of $\langle D(G)\rangle$, $G_{i}$ is M-full if some vertex of $G_{i}$ is matched by M with a vertex in A(G), that is, every vertex of $G_{i}$ is M-saturated, otherwise, $G_{i}$ is M-near full. The number of M-near full components is denoted by nc(M). Let $nc(G)=max\{nc(M)|M$ is a maximum matching $\}$. Then we have the following.

Lemma 1.4

(Liu and Liu (2018), Pulleyblank (1987)) Let G be a graph, M a maximum matching of G and $D_{0}$ defined as above. Then $nc(M)=nc(G)$ if and only if M induces a maximum matching of $\langle N_{G}(D_{0}), D_{0} \rangle$.

Let $H=\langle N_G(D_{0}), D_{0}\rangle$, $D_{1}=N_G(D_{0})\bigcap D(H)$, $D_{2}=D_{0}\bigcap D(H)$, $A_{1}=N_{H}(D_{2})$, $A_{2}=N_{H}(D_{1})$, $C_{1}=N_G(D_{0})-D_{1}-A_{1}$, and $C_{2}=D_{0}-D_{2}-A_{2}$(see Fig. 2). Let M be a maximum matching of G such that $nc(M)=nc(G)$. By Lemma 1.3, every vertex in $D_1$ is M-saturated since $D_1\subseteq N_G(D_{0})\subseteq A(G)$ and the number of M-unsaturated vertices in $D(G)-D_0$ is nc(M). In fact, there is exactly one M-unsaturated vertex in every M-near full component of $\langle D(G)\rangle$. Furthermore, by Lemmas 1.4 and 1.2, the number of M-unsaturated vertices in $D_0$ is $|D_2|-|A_1|$. It follows that $def(G)=nc(G)+|D_2|-|A_1|$.

Fig. 2

Decomposition of H and G

Lemma 1.5

(Edmonds, Fulkerson Lovász and Plummer (1985)) Let G be a graph and $X\subseteq V(G)$. If X is covered by some matching of G, then X is also covered by a maximum matching of G.

Lemma 1.6

Let G be a graph, $D_0$ and $D_2$ defined as above. Then $D_{2}=\{v\in D_{0}|$ there exists a maximum matching M of G such that $nc(M)=nc(G)$ and v is M-unsaturated $\}$.

Proof

Let $v\in D_{0}$ and M a maximum matching of G such that $nc(M)=nc(G)$ and v is M-unsaturated. By Lemma 1.4, $M\bigcap E(H)$ is a maximum matching of H, where $H=\langle N(D_{0}), D_{0}\rangle$. Then $v\in D(H)$. Hence $v\in D_{2}$.

Conversely, let $v\in D_{2}$. Then there exists a maximum matching $M_{0}$ of H missing v. Let $S=\{u\in V(H)|$u is $M_{0}$-saturated $\}$. By Lemma 1.5, there exists a maximum matching M of G covering S. By Lemma 1.3, $M\bigcap E(N(D_{0})) =$ Ø since $N(D_{0})\subseteq A(G)$. Note that $D_0$ is independent. It follows that $M\bigcap E(H)$ is a matching covering S. Hence $M\bigcap E(H)$ is a maximum matching of H missing v. By Lemma 1.4, we have that $nc(M)=nc(G)$. $\square$

2 Fractional Gallai–Edmonds decomposition

Similar with the Gallai–Edmonds decomposition, let

$D_{f}(G)=\{v\in V(G)|$G has a maximum fractional matching f such that v is f-unsaturated $\}$, $A_{f}(G)=\{v\in V(G)-D_{f}(G)|$$\exists$$u\in D_{f}(G)$ such that $uv\in E(G) \}$ and $C_{f}(G)=V(G)-D_{f}(G)-A_{f}(G)$. We say that $(C_f(G), A_f(G), D_f(G))$ is the fractional Gallai–Edmonds decomposition. First, we show that $D_2\subseteq D_{f}(G)$. The following lemma is useful.

Lemma 2.1

 Liu and Liu (2002) For any graph G,

$$\begin{aligned} \mu _{f}(G)=\mu (G)+\frac{nc(G)}{2}. \end{aligned}$$

Then by Lemma 2.1, $\mu _{f}(K_{n})=\frac{n}{2}$ for $n\ge 2$. A subgraph H of a graph G is said to be nice if $G-V(H)$ has a perfect matching.

Lemma 2.2

 Liu and Liu (2002) Let G be a factor-critical graph with at least three vertices. Then G has a nice odd cycle.

Let $v\in D_2$. Then we can assume that M is a maximum matching of G such that $nc(M)=nc(G)$ and v is M-unsaturated by Lemma 1.6. Construct a fractional matching f from M in the following way. Let $G_{1},G_{2},\ldots ,G_{nc(G)}$ be all M-near full components of $\langle D(G)\rangle$. By Lemma 1.3, every $G_{j}$ is factor-critical. Then $G_{j}$ has a nice odd cycle, say $C_{j}$ by Lemma 2.2. Let $M_{j}$ be a perfect matching of $G_{j}-V(C_{j})$ and $M'=M-\bigcup \limits _{1\le j \le nc(G)} E(G_{j})$. Let

$$\begin{aligned} f(e) =\left\{ \begin{array}{lll} \quad 1 ,&{} \quad if \; e\in M'\bigcup M_{1}\bigcup M_{2}\bigcup \cdot \cdot \cdot \bigcup M_{nc(G)}, \\ \quad \frac{1}{2},&{} \quad if \; e\in E(C_{1}) \bigcup E(C_{2})\bigcup \cdot \cdot \cdot \bigcup E(C_{nc(G)}), \\ \quad 0 ,&{} \quad otherwise. \end{array} \right. \end{aligned}$$

(2.1)

Then $\sum \nolimits _{e\in \Gamma (v)}f(e)=0$ and the number of f-saturated vertices is nc(G) more than the number of M-saturated vertices. Hence $\sum \nolimits _{e\in E(G)}f(e)=\frac{1}{2}(|V(G)|-def(G)+nc(G))=\frac{1}{2}(|V(G)|-(|D_{2}|-|A_{1}|))$. The fractional matching f constructed as above is said to be an ${\mathcal {M}}$-fractional matching of G.

Lemma 2.3

 Liu and Liu (2018) Let G be a graph and f an ${\mathcal {M}}$-fractional matching of G. Then f is a maximum fractional matching with the maximum number of 0-edges.

By Lemma 2.3, $v\in D_{f}(G)$. Thus $D_2\subseteq D_{f}(G)$. Moreover, we have the following.

Lemma 2.4

For any graph G, $\mu _{f}(G)=\frac{1}{2}(|V(G)|-(|D_{2}|-|A_{1}|))$.

Secondly, we give the following fractional Gallai–Edmonds structure theorem.

Theorem 2.1

Let G be a graph and $D_{f}(G)$, $A_{f}(G)$, $C_{f}(G)$, $C_{1}$, $A_{1}$, $D_{1}$, $C_{2}$, $A_{2}$, and $D_{2}$ defined as above. Then

(1) $D_{f}(G)=D_{2}$ and $A_{f}(G)=A_{1}$;

(2) every maximum fractional matching g of G consists of a maximum fractional matching $g_{1}$ of $\langle A_{1},D_{2}\rangle$ that saturates every vertex in $A_{1}$, a perfect fractional matching $g_{2}$ of $\langle C_{1},C_{2}\rangle$ and a perfect fractional matching $g_{3}$ of $\langle V(G)-C_{1}-C_{2}-A_{1}-D_{2}\rangle$; Moreover, $g_{3}$ induces a maximum fractional matching of $\langle D_{1},A_{2}\rangle$ that saturates every vertex in $A_{2}$.

Proof

Let g be a maximum fractional matching of G.

(1) It suffices to prove that $D_{f}(G)\subseteq D_{2}$. Note that $D_{2}$ is independent and $N_{G}(D_{2})=A_{1}$. Then we have that

$$\begin{aligned} \sum \nolimits _{v\in D_{2}}\sum \limits _{e\in \Gamma (v)}g(e)=\sum \limits _{e\in E(A_{1},D_{2})}g(e)\le \sum \limits _{v\in A_{1}}\sum \limits _{e\in \Gamma (v)}g(e)\le |A_{1}|. \end{aligned}$$

(2.2)

Hence

$$\begin{aligned} \sum \limits _{v\in V(G)}\sum \limits _{e\in \Gamma (v)}g(e)= & {} \sum \limits _{v\in V(G)-D_{2}}\sum \limits _{e\in \Gamma (v)}g(e)+\sum \limits _{v\in D_{2}}\sum \limits _{e\in \Gamma (v)}g(e)\nonumber \\\le & {} |V(G)|-|D_{2}|+|A_{1}|. \end{aligned}$$

(2.3)

By Lemma 2.4,

$$\begin{aligned} \sum \limits _{v\in V(G)}\sum \limits _{e\in \Gamma (v)}g(e)=2\mu _{f}(G)=|V(G)|-(|D_{2}|-|A_{1}|). \end{aligned}$$

(2.4)

It follows that $\sum \nolimits _{e\in \Gamma (v)}g(e)=1$ for any $v\in V(G)-D_{2}$. Then $D_{f}(G)\subseteq D_{2}$. Hence $D_{f}(G)=D_{2}$. Thus $A_{f}(G)=A_{1}$.

(2) According to (2.2)–(2.4), we know that

$$\begin{aligned} \sum \limits _{v\in D_{2}}\sum \limits _{e\in \Gamma (v)}g(e)=\sum \limits _{e\in E(A_{1},D_{2})}g(e)= \sum \limits _{v\in A_{1}}\sum \limits _{e\in \Gamma (v)}g(e)=|A_{1}|. \end{aligned}$$

(2.5)

That is, g induces a maximum fractional matching of $\langle A_{1},D_{2}\rangle$ that saturates every vertex in $A_{1}$, say $g_1$.

According to the statements in (1), $C_{2}\bigcup C_{1}\subseteq C_f(G)$. Then

$$\begin{aligned} |C_{1}|=\sum \limits _{v\in C_{1}}\sum \limits _{e\in \Gamma (v)}g(e), |C_{2}|=\sum \limits _{v\in C_{2}}\sum \limits _{e\in \Gamma (v)}g(e). \end{aligned}$$

(2.6)

Since $N_{G}(C_{2})\subseteq C_{1}\bigcup A_{1}$ and $C_{2}$ is independent,

$$\begin{aligned} |C_{2}|=\sum \limits _{e\in E(C_{1},C_{2})}g(e)+\sum \limits _{e\in E(A_{1},C_{2})}g(e). \end{aligned}$$

(2.7)

By Eq. (2.5), $\sum \limits _{e\in E(A_{1},C_{2})}g(e)=0$. By Lemma 1.2 (2), $|C_{2}|=|C_{1}|$. Then we have that

$$\begin{aligned} |C_{2}|=\sum \limits _{e\in E(C_{1},C_{2})}g(e)=|C_{1}|=\sum \limits _{v\in C_{1}}\sum \limits _{e\in \Gamma (v)}g(e). \end{aligned}$$

(2.8)

This implies that g induces a perfect fractional matching of $\langle C_{1},C_{2}\rangle$, say $g_2$. It follows that g induces a perfect fractional matching of $\langle V(G)-D_{2}-A_{1}-C_{1}-C_{2}\rangle$, say $g_3$.

Since $A_{2}$ is independent and $A_{2}\subseteq C_f(G)$, we have that

$$\begin{aligned} |A_{2}|=\sum \limits _{v\in A_{2}}\sum \limits _{e\in \Gamma (v)}g(e)=\sum \limits _{e\in E(C_{1},A_{2})}g(e)+\sum \limits _{e\in E(A_{1},A_{2})}g(e)+\sum \limits _{e\in E(D_{1},A_{2})}g(e).\nonumber \\ \end{aligned}$$

(2.9)

By Eq. (2.5), $\sum \nolimits _{e\in E(A_{1},A_{2})}g(e)=0$. By Eq. (2.8), we know that $\sum \nolimits _{e\in E(C_{1},A_{2})}g(e)=0$. This implies that $\sum \nolimits _{e\in E(D_{1},A_{2})}g(e)=|A_{2}|$. Thus g induces a maximum fractional matching of $\langle D_{1},A_{2}\rangle$ that saturates every vertex in $A_{2}$. $\square$

By Lemma 1.1, there exists an algorithm in polynomial time determining (C(G), A(G), D(G)). Then it is easy to know that there exists an algorithm in polynomial time finding the bipartite subgraph $\langle N_G(D_{0}), D_{0}\rangle$ since $D_0$ consists of trivial components of $\langle D(G)\rangle$. Thus there exists an algorithm in polynomial time finding $D_2$. So by Theorem 2.1, we have the following.

Corollary 2.1

Let G be a graph. Then there exists an algorithm in polynomial time determining $(C_f(G), A_f(G), D_f(G))$.

Remark 2.1

By Lemma 2.4 and Theorem 2.1, $\mu _{f}(G+xy)=\mu _{f}(G)$ for any $xy\in E({\overline{G}})$ such that $x\in A_{1}$, $y\in D_{2}$ or $x,y\in V(G)-D_2$.

3 Structure of maximal graphs on $\mu _{f}(G)$

Let G and H be disjoint graphs. The union of G and H is denoted by $G\bigcup H$. The disjoint union of k copies of G is denoted by kG. The graph obtained from $G\bigcup H$ by adding all possible edges joining a vertex of G and a vertex of H is denoted by $G+H$. By Lemma 2.1, $2\mu _{f}(G)$ is non-negative integer for any graph G.

Lemma 3.1

Let G be a maximal graph on $\mu _{f}(G)$ with that $|V(G)|\ge 2\mu _{f}(G)+1$. Then $G=(K_{2\mu _{f}(G)-2s}\bigcup \overline{K_{|V(G)|-2\mu _{f}(G)+s}})+K_{s}$, where s is an integer such that $0\le s\le \mu _{f}(G)$.

Proof

Let $H=\langle D_{0}, N_G(D_{0})\rangle$, $D_{1},D_{2},A_{1},A_{2},C_{1}$ and $C_{2}$ defined as above. Then by Theorem 2.1, $\langle V(G)-D_{2}\rangle$ is a complete graph since G is a maximal graph on $\mu _{f}(G)$. Let $s=|A_{1}|$. Then $0\le s\le \mu _{f}(G)$ and $\langle A_{1}\rangle =K_{s}$. By Remark 1, $\langle A_{1}, D_{2}\rangle$ is a complete bipartite graph since G is maximal on $\mu _{f}(G)$. By Lemma 2.4, $|D_{2}|=|V(G)|-2\mu _{f}(G)+s$. Then $\langle D_{2}\rangle =\overline{K_{|V(G)|-2\mu _{f}(G)+s}}$. Hence $\langle V(G)-D_{2}-A_{1}\rangle =K_{2\mu _{f}(G)-2s}$. So G is isomorphic to $(K_{2\mu _{f}(G)-2s}\bigcup \overline{K_{|V(G)|-2\mu _{f}(G)+s}})+K_{s}$.

$\square$

Theorem 3.1

Let k be a positive integer and G a graph on n vertices.

• (1) If $\mu _{f}(G)=k$, then G is a maximal graph on $\mu _{f}(G)$ if and only if $G= H(n, k, s)=(K_{2k-2s}\bigcup \overline{K_{n-2k+s}})+K_{s}$, where s is an integer such that $0 \le s \le k$ and $s\ne k-1$.

• (2) If $\mu _{f}(G)=k+\frac{1}{2}$, then G is a maximal graph on $\mu _{f}(G)$ if and only if $G=H'(n, k, s)=(K_{2k-2s+1}\bigcup \overline{K_{n-2k+s-1}})+K_{s}$, where s is an integer such that $0 \le s \le k-1$.

Proof

(1) Let k be an integer and $\mu _{f}(G)=k$.

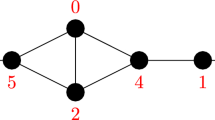
“$\Leftarrow$” First, let $s=k$. Then $G=H(n, k, k)=K_{k}+\overline{K_{n-k}}$. Clearly, G is maximal on $\mu _{f}(G)$. Secondly, let $0\le s\le k-2$. By the definition of H(n, k, s), we have that $D(H(n, k, s))=V(\overline{K_{n-2k+s}})$. Then $\mu (H(n, k, s))=k$ by Lemma 1.3. Let $A=V(K_{s})$, $C=V(K_{2k-2s})$, $D=V(\overline{K_{n-2k+s}})$. By Lemma 2.1, $\mu _{f}(H(n, k, s))=k$ since $nc(H(n, k, s))=0$. Let $e_{0}=uv \in E(\overline{H(n, k, s)})$. If $u, v\in D$, then $\mu _{f}(H(n, k, s)+e_{0})\ge k+\frac{1}{2}$ since we can find a fractional matching f such that $\sum _{e \epsilon E(H(n, k, s)+e_{0})}f(e)=k+\frac{1}{2}$(see Fig. 3). Suppose that $u\in C$ and $v \in D$.

Fig. 3

a fractional matching of $H(n, k, s)+e_{0}$

Let $M_{1}$ be a maximum matching of $H(n, k,s)-C$ missing v. Then $|M_{1}|=s$ by Lemma 1.3. Let g be a maximum fractional matching of $\langle C\rangle -\{u\}$. Then $\sum _{e \epsilon E(\langle C\rangle -\{u\})}g(e)=k-s-\frac{1}{2}$ since $\langle C\rangle -\{u\}=K_{2k-2s-1}$. Let

$$\begin{aligned} f(e) =\left\{ \begin{array}{lll} \quad 1,&{}\quad if \; e\in M_{1}\bigcup \{uv\}, \\ \quad g(e),&{}\quad if \; e\in E(\langle C\rangle -\{u\}),\\ \quad 0&{}\quad otherwize. \end{array} \right. \end{aligned}$$

(3.1)

Then $\mu _{f}(H(n, k, s)+e_{0})\ge \sum _{e \epsilon E(H(n, k, s)+e_{0})}f(e)=k+\frac{1}{2}>\mu _{f}(H(n, k, s))$. Hence H(n, k, s) is maximal on $\mu _{f}(G)$.

“$\Rightarrow$” Suppose that G is a maximal graph on $\mu _{f}(G)$. By Lemma 3.1, we can assume that $G=H(n, k, s)$. It suffices to prove that if $s=k-1$, then G is not maximal on $\mu _{f}(G)$. Let $G=H(n, k, k-1)=(K_{2}\bigcup \overline{K_{n-k-1}})+K_{k-1}$, $u\in V(K_{2})$ and $x\in V(\overline{K_{n-k-1}})$. Then $G+ux$ is a spanning subgraph of $K_{k}+\overline{K_{n-k}}$. Hence $\mu _{f}(G)\le \mu _{f}(G+ux)\le \mu _{f}(K_{k}+\overline{K_{n-k}})$. It follows that $\mu _{f}(G)=\mu _{f}(G+ux)$ since $\mu _{f}(G)=k=\mu _{f}(K_{k}+\overline{K_{n-k}})$.

(2)Let k be an integer and $\mu _{f}(G)=k+\frac{1}{2}$.

“$\Leftarrow$” Let s be an integer such that $0\le s\le k-1$. By Lemma 1.3, we know that $D(H'(n, k, s))=V(\overline{K_{n-2k+s-1}}\bigcup K_{2k-2s+1})$ and $\mu (H'(n, k, s))=k$. By Lemma 2.1, $\mu _{f}(H'(n, k, s))=k+\frac{1}{2}$ since $nc(H'(n, k, s))=1$. It is easy to check that $H'(n, k, s)$ is maximal on $\mu _{f}(G)$.

“$\Rightarrow$” Suppose that G is a maximal graph on $\mu _{f}(G)$. By Lemma 3.1, $G=H'(n, k, s)$, where $0\le s\le k+\frac{1}{2}$. Then $0\le s\le k$. It suffices to prove that $s\ne k$. In fact, if $s=k$, then $H'(n, k, k)=K_{k}+\overline{K_{n-k}}$. So $\mu _{f}(G)=\mu _{f}(H'(n, k, k))=k$ since $nc(H'(n, k, k))=0$, a contradiction. $\square$

4 Extremal graphs with Turán number and saturation number

Let G be a maximal graph on $\mu (G)$, $n=|V(G)|$ and $k=\mu (G)$. Mader  Mader (1973) characterized the structure of the maximal graph and obtained that if n is large enough, then the Turán graph on $\mu (G)$ is $K_{k}+\overline{K_{n-k}}=H(n,k,k)$. Thus $ex(n,\mu (G))=nk-\frac{k(k+1)}{2}$. Later in 1986, L. Kászonyi and Z. Tuza in  Kászonyi and Tuza (2010) obtained that $sat(n,\mu (G))=3k$ and the saturated extremal graph on $\mu (G)$ is $kK_{3}\bigcup \overline{K_{n-3k}}$.

Let G be a maximal graph on $\mu _{f}(G)$. By Theorem 3.1, in the case that $\mu _{f}(G)=k$, $G=H(n, k,s)$. Then

$$\begin{aligned} ES(n,\mu _{f}(G))= & {} \{m(H(n, k,s))| 0\le s\le k, s\ne k-1\}\\= & {} \left\{ \frac{3s^{2}}{2}+\left( n-4k+\frac{1}{2}\right) s+2k^{2}-k| 0\le s\le k, s\ne k-1\right\} . \end{aligned}$$

Let $g_{1}(s)=m(H(n,k,s))$, where $0\le s\le k$, $s\ne k-1$.

In the case that $\mu _{f}(G)=k+\frac{1}{2}$, $G=H'(n, k,s)$. Then

$$\begin{aligned} ES(n,\mu _{f}(G))= & {} \left\{ m(H'(n, k,s))| 0\le s\le k-1\right\} \\= & {} \left\{ \frac{3s^{2}}{2}+\left( n-4k-\frac{3}{2}\right) s+2k^{2}+k| 0\le s\le k-1\right\} . \end{aligned}$$

Let $g_{2}(s)=m(H'(n,k,s))$, where $0\le s\le k-1$.

Clearly, $g_{1}(s)$ is a quadratic function whose axis of symmetry is $s_{0}=-\frac{n-4k}{3}-\frac{1}{6}$. If $n\ge 4k$, then $s_{0}<0$. Hence $g_{1}(s)$ is a monotone increasing function. Thus in the case that $\mu _{f}(G)=k$, $sat(n,\mu _{f}(G))=g_{1}(0)$ and $ex(n, \mu _{f}(G))=g_{1}(k)$. Then we have the following theorem according to the discussion as above.

Theorem 4.1

Let G be a graph on n vertices, k a positive integer such that $n\ge 4k$ and $\mu _{f}(G)=k$. Then $ex(n, \mu _{f}(G))=nk-\frac{k(k+1)}{2}$, the Turán graphs are unique which is $H(n,k,k)=K_{k}+\overline{K_{n-k}}$, $sat(n, \mu _{f}(G))=k(2k-1)$ and the saturated extremal graphs are unique which is $H(n,k,0)=K_{2k}\bigcup \overline{K_{n-2k}}$.

Similarly, $g_{2}(s)$ is a quadratic function whose axis of symmetry is $s_{1}=-\frac{n-4k}{3}+\frac{1}{2}$. In a similar way, we obtain the following.

Theorem 4.2

Let G be a graph on n vertices, k a positive integer such that $n>4k+1$ and $\mu _{f}(G)=k+\frac{1}{2}$. Then $ex(n, \mu _{f}(G))=g_{2}(k-1)=(k-1)n-\frac{k(k-1)}{2}+3$, the Turán graphs are unique which is $H'(n,k,k-1)=(K_3\bigcup \overline{K_{n-k-2}})+K_{k-1}$, $sat(n, \mu _{f}(G)) =g_{2}(0)=2k^2+k$ and the saturated extremal graphs are unique which is $H'(n,k,0)=K_{2k+1}\bigcup \overline{K_{n-2k-1}}$.

Note that for any positive integer k and $n> 4k$, $m(H(n, k+1, k+1))\ge m(H(n, k, k))$, $m(H'(n, k+1, k))\ge m(H'(n, k, k-1))$ and $m(H(n, k, k))>m(H'(n, k, k-1))$. Then we have the following corollary.

Corollary 4.1

Let h be a number such that $0<h<\frac{n}{4}$ and G a n-vertex graph such that $\mu _{f}(G)\le h$, then $m(G)\le m(K_{\lfloor h\rfloor }+\overline{K_{n-\lfloor h\rfloor }})$ and the equality holds if and only if $G=K_{\lfloor h\rfloor }+\overline{K_{n-\lfloor h\rfloor }}$.