A classification of tetravalent non-normal Cayley graphs of order twice a prime square

Abstract

A Cayley graph $\mathrm{Cay}(G, S)$ on a group G is said to be normal if the right regular representation R(G) of G is normal in the full automorphism group of $\mathrm{Cay}(G, S)$. In this paper, a complete classification is given of tetravalent non-normal Cayley graphs of order $2p^2$ for each prime p.

1 Introduction

For a finite, simple, undirected and connected graph $\Gamma$, we use $V(\Gamma )$, $E(\Gamma )$, $A(\Gamma )$ and $\mathrm{Aut}(\Gamma )$ to denote its vertex set, edge set, arc set and full automorphism group, respectively. For $u,v\in V(\Gamma )$, denote by $\{u, v\}$ the edge incident to u and v in $\Gamma$. A graph $\Gamma$ is said to be vertex-transitive, edge-transitive and arc-transitive (or symmetric) if $\mathrm{Aut}(\Gamma )$ acts transitively on $V(\Gamma )$, $E(\Gamma )$ and $A(\Gamma )$, respectively. In particular, if $\mathrm{Aut}(\Gamma )$ acts regularly on $A(\Gamma )$, then $\Gamma$ is said to be 1-regular.

Let G be a permutation group on a set $\Omega$ and $\alpha \in \Omega$. Denote by $G_\alpha$ the stabilizer of $\alpha$ in G, that is, the subgroup of G fixing the point $\alpha$. We say that G is semiregular on $\Omega$ if $G_\alpha =1$ for every $\alpha \in \Omega$ and regular if G is transitive and semiregular. Given a finite group G and an inverse closed subset $S\subseteq G\setminus \{1\}$, the Cayley graph $\mathrm{Cay}(G,S)$ on G with respect to S is defined to have vertex set G and edge set $\{\{g,sg\}\mid g\in G,s\in S\}$. A Cayley graph $\mathrm{Cay}(G,S)$ is connected if and only if S generates G. Given a $g\in G$, define the permutation R(g) on G by $x\mapsto xg, x\in G$. Then, $R(G)=\{R(g)\ |\ g\in G\}$, called the right regular representation of G, is a regular permutation group isomorphic to G. It is well known that $R(G)\le \mathrm{Aut}(\mathrm{Cay}(G,S))$. So, $\mathrm{Cay}(G,S)$ is vertex-transitive. In general, a vertex-transitive graph $\Gamma$ is isomorphic to a Cayley graph on a group G if and only if its automorphism group has a subgroup isomorphic to G, acting regularly on the vertex set of $\Gamma$ (see [1, Lemma 16.3]). A Cayley graph $\mathrm{Cay}(G, S)$ is said to be normal if R(G) is normal in $\mathrm{Aut}(\mathrm{Cay}(G, S))$ (see Xu [2]).

For two inverse closed subsets S and T of a group G not containing the identity 1, if there is an $\alpha \in \mathrm{Aut}(G)$ such that $S^\alpha =T$ then S and T are said to be equivalent, denoted by $S\equiv T$. One may easily show that if S and T are equivalent then $\mathrm{Cay}(G, S)\cong \mathrm{Cay}(G, T)$, and then $\mathrm{Cay}(G,S)$ is normal if and only if $\mathrm{Cay}(G,T)$ is normal.

Normal Cayley graphs were first introduced by Xu [2], and following this article, the normality of Cayley graphs has been extensively studied in the literature. Much of the work has been focused on the classification of non-normal Cayley graphs with a certain order. Let p, q be two primes. Every Cayley graph of order p is normal if it is neither empty nor complete. This can be easily obtained by Burnside’s theorem which states that every transitive permutation group of degree p is either 2-transitive or has a regular normal subgroup (see, for example, [3, Corollary 3.5B]). Another nice work is the classification of non-normal Cayley graphs of order pq which were done by Dobson et al. in three papers [4,5,6]. However, in general, it is quite difficult to determine the normality of Cayley graphs. Actually, the groups of order p or pq are the only groups for which the complete information about the normality of Cayley graphs is available.

In view of this fact, it is natural to consider the normality of Cayley graphs with prescribed valency. It is easy to see that every 2-valent Cayley graph of order n is normal since it is a cycle whose automorphism group has order 2n. So the first interesting case is the cubic graph. As mentioned above, all non-normal Cayley graphs of order p or pq are already known. The next natural candidates are Cayley graphs of order 2pq. A complete classification of cubic non-normal Cayley graphs of order 2pq is given by Zhou et al. [7,8,9]. For the tetravalent case, the only work is the classification of tetravalent non-normal Cayley graphs of order 4p which was done by Zhou [10]. Motivated by this, in this paper, we shall give a classification of tetravalent non-normal Cayley graphs of order $2p^2$. This work was also partially motivated by the following work. Combining [11] with [12, 13], we see that every tetravalent edge-transitive graph of order $2p^2$ is arc-transitive, and a complete classification of tetravalent arc-transitive graphs of order $2p^2$ was given by Zhou and Feng [14]. Recently, Cheng et al. [15] gave a complete classification of tetravalent vertex-transitive non-Cayley graphs of order $2p^2$. So once all tetravalent non-normal Cayley graphs of order $2p^2$ are classified, in some sense the highly symmetric tetravalent graphs of order $2p^2$ are all known. For more work about the normality of Cayley graphs, we refer the reader to [2, 16].

Before stating the main result of this paper, we introduce some definitions and notations. Let $\Gamma _1$ and $\Gamma _2$ be two graphs. The lexicographic product $\Gamma _1\circ \Gamma _2$ is defined as the graph with vertex set $V(\Gamma _1\circ \Gamma _2)=V(\Gamma _1)\times V(\Gamma _2)$ such that for any vertices $u=(x_1, y_1)$ and $v=(x_2, y_2)$ in $V(\Gamma _1\circ \Gamma _2)$, u is adjacent to v in $\Gamma _1\circ \Gamma _2$ whenever $x_1=x_2$ and $\{y_1, y_2\} \in E(\Gamma _2)$ or $\{x_1, x_2\}\in E(\Gamma _1)$.

From elementary group theory, for each odd prime p, every non-abelian group of order $2p^2$ is isomorphic to one of the following three groups:

$$\begin{aligned} G_1(p)= & {} \langle a,b\mid a^{p^2}=b^2=1, bab=a^{-1}\rangle ; \\ G_2(p)= & {} \langle a,b,c\mid a^p=b^p=c^2=1, ab=ba, cac=a^{-1},cbc=b^{-1}\rangle ; \\ G_3(p)= & {} \langle a,b,c\mid a^p=b^p=c^2, ab=ba, ac=ca, cbc=b^{-1}\rangle . \end{aligned}$$

For an integer $m\ge 2$, the triple cross ladder graph, denoted by $\mathrm{TL}_{6m}$, is a tetravalent graph of order 6m with vertex set $V_0\cup V_1\cup \ldots \cup V_{2m-2}\cup V_{2m-1}$, where $V_i=\{x_i^0, x_i^1, x_i^2\}$, and edge set $\{\{x_{2i}^r, x_{2i+1}^r\}, \{x^r_{2i+1}, x^s_{2i+2}\}\mid i\in {\mathbb Z}_m, r,s\in {\mathbb Z}_3\}$.

Throughout this paper, for a positive integer n, denote by ${\mathbb Z}_n$ the cyclic group of order n as well as the ring of integers modulo n, by ${\mathbb Z}_n^*$ the multiplicative group of ${\mathbb Z}_n$ consisting of numbers coprimes to n, by $D_{2n}$ the dihedral group of order 2n, by $\mathrm{C}_n$, and $K_{n}$ the cycle and the complete graph of order n, respectively, and by $K_{n,n}$ the complete bipartite graph with two parts of size n. For two groups M and N, $M\rtimes N$ denotes the semidirect product of M by N.

Note that all disconnected normal Cayley graphs are known by [17] and all tetravalent non-normal Cayley graphs of order 4p are known by Zhou [10]. The following theorem is the main result of this paper which gives a complete classification of tetravalent connected non-normal Cayley graphs of order $2p^2$ for each odd prime p.

Theorem 1.1

Let $\Gamma =\mathrm{Cay}(G, S)$ be a connected tetravalent Cayley graph of order $2p^2$ with p an odd prime. Then, either $\Gamma$ is a normal Cayley graph for G, or one of the following holds:

• (1) $G=G_1(3)$, $S\equiv \{b, ba^3, ba^6, ba\}$ and $\Gamma \cong \mathrm{TL}_{18}$;

• (2) $G=G_2(3)$, $S\equiv \{c,ca,ca^2,cb\}$, and $\Gamma \cong \mathrm{TL}_{18}$;

• (3) $G=G_2(3)$, $S\equiv \{c, ca, cb, ca^2b^2\}$, and $\Gamma \cong \mathrm{TL}_{18}$;

• (4) $G=G_3(3)$, $S\equiv \{c,ca,ca^2,cb\}$ and $\Gamma \cong \mathrm{TL}_{18}$;

• (5) $G=\langle a \rangle \times \langle b \rangle \cong \mathbb {Z}_{p^2}\times \mathbb {Z}_2$, $S\equiv \{a, ab, a^{-1}, a^{-1}b\}$ and $\Gamma \cong \mathrm{C}_{p^2}\circ (2K_1)$;

• (6) $G=G_1(p)$, $S\equiv \{a, a^{-1}, ba, ba^{-1}\}$ and $\Gamma \cong \mathrm{C}_{p^2}\circ (2K_1)$;

• (7) $G=G_3(p)$, $S\equiv \{ca, ca^{-1}, cb, cb^{-1}\}$, and $\mathrm{Aut}(\Gamma )\cong ({\mathbb Z}_2\times {\mathbb Z}_p^2)\rtimes D_8$;

• (8) $G=G_3(p) (p>3)$, $S\equiv \{c, cab, (cab)^{-1}, cb^\ell \}$ with $3\ell \equiv 2\ (\mathrm{mod}\,p)$, and $\mathrm{Aut}(\Gamma )\cong G_2(p)\rtimes \mathrm{Sym}(3)$.

2 Preliminaries

In this section, we introduce some notations and definitions as well as some preliminary results which will be used later in the paper. Throughout this paper, groups are assumed to be finite, and graphs assumed to be finite, connected, simple and undirected.

Given a group G, denoted by $\mathrm{Aut}(G)$ the full automorphism group of G. For a subgroup H of G, denote by $C_G(H)$, $N_G(H)$ the centralizer and normalizer of H in G, respectively. Of course, $C_G(H)$ is normal in $N_G(H)$, and the well-known $\mathrm{N/C}$ theorem asserts that the quotient group $N_G(H)/C_G(H)$ is isomorphic to a subgroup of $\mathrm{Aut}(H)$.

A block of imprimitivity of a permutation group G on a set $\Omega$ is a subset $\Delta$ of $\Omega$ with $1<|\Delta |<|\Omega |$ such that for any $g\in G$, either $\Delta ^g=\Delta$ or $\Delta ^g\cap \Delta =\emptyset$. In this case, the blocks $\Delta ^g$, $g\in G$ form a G-invariant partition of $\Omega$.

Given a graph $\Gamma$ and $v\in V(\Gamma )$, denote by $\Gamma (v)$ the neighborhood of $\Gamma$. For any subset B of $V(\Gamma )$, the subgraph of $\Gamma$ induced by B will be denoted by $\Gamma [B]$. Let $\Gamma$ be a connected vertex-transitive graph, and let $G\le \mathrm{Aut}(\Gamma )$ be vertex-transitive on $\Gamma$. For a G-invariant partition $\Omega$ of $V(\Gamma )$, the quotient graph $\Gamma _\Omega$ is defined as the graph with vertex set $\Omega$ such that, for any two vertices $B, C \in \Omega$, B is adjacent to C if and only if there exist $u \in B$ and $v \in C$ which are adjacent in $\Gamma$. Let N be a normal subgroup of G. Then, the set $\Omega$ of orbits of N in $V(\Gamma )$ is a G-invariant partition of $V(\Gamma )$. In this case, the symbol $\Gamma _\Omega$ will be replaced by $\Gamma _N$.

Let $\Gamma =\mathrm{Cay}(G, S)$ be a Cayley graph on G relative to S, and $A=\mathrm{Aut}(\Gamma )$. Recall that we say that $\Gamma$ is a normal Cayley graph of G if R(G) is normal in A. The following proposition gives a sufficient and necessary condition for a Cayley graph being normal.

Proposition 2.1

[2, Proposition 1.5] Let $A_1$ be the stabilizer of the identity 1 in A and $\mathrm{Aut}(G,S)=\{\alpha \in \mathrm{Aut}(G,S)\mid S^\alpha =S\}$. Then, $\Gamma$ is normal if and only if $A_1=\mathrm{Aut}(G,S)$.

A graph $\Gamma$ is called a bi-Cayley graph over a group H if $\mathrm{Aut}(\Gamma )$ admits a semiregular subgroup which is isomorphic to H with two orbits. Note that every bi-Cayley graph admits the following concrete realization. Given a group H, let R, L and S be subsets of H such that $R^{-1}=R$, $L^{-1}=L$, and $R\cup L$ does not contain the identity element of H. The bi-Cayley graph over H relative to the triple (R, L, S), denoted by $\mathrm{BiCay}(H,R,L,S)$, is the graph having vertex set the union of the right part $H_0=\{h_0\mid h\in H\}$ and the left part $H_1=\{h_1\mid H\in H\}$, and the edge set the union of the right edges $\{\{h_0,g_0\}\mid gh^{-1}\in R\}$, the left edges $\{\{h_1,g_1\}\mid gh^{-1}\in L\}$ and the spokes $\{\{h_0,g_1\}\mid gh^{-1}\in S\}$. Let $\Gamma =\mathrm{BiCay}(H,R,L,S)$. For $g\in H$, define a permutation R(g) on the vertices of $\Gamma$ by the rule

$$\begin{aligned} h_i^{R(g)}=(hg)_i,\ \ \forall i\in {\mathbb Z}_2,\ h\in H. \end{aligned}$$

Then, $R(H)=\{R(g)\mid g\in H\}$ is a semiregular subgroup of $\mathrm{Aut}(\Gamma )$ which is isomorphic to H and has $H_0$ and $H_1$ as its two orbits. When R(H) is normal in $\mathrm{Aut}(\Gamma )$, the bi-Cayley graph $\Gamma =\mathrm{BiCay}(H,R,L,S)$ will be called a normal bi-Cayley graph over H.

Let $\Gamma =\mathrm{BiCay}(H,R,L,S)$. For an automorphism $\alpha$ of H and $x,y,g\in H$, define two permutations on $V(\Gamma )=H_0\cup H_1$ as following:

$$\begin{aligned} \delta _{\alpha ,x,y}: h_0\mapsto (xh^\alpha )_1, h_1\mapsto (yh^\alpha )_0, \forall h\in H,\\ \sigma _{\alpha ,g}: h_0\mapsto (h^\alpha )_0, h_1\mapsto (gh^\alpha )_1, \forall h\in H. \end{aligned}$$

Set

$$\begin{aligned} I = \{\delta _{\alpha ,x,y}\mid \alpha \in \mathrm{Aut}(H)\ \mathrm{s.t.}\ R^{\alpha }=x^{-1}Lx, L^\alpha =y^{-1}Ry, S^\alpha =y^{-1}S^{-1}x\}, \end{aligned}$$

(1)

$$\begin{aligned} F = \{\sigma _{\alpha ,g}\mid \alpha \in \mathrm{Aut}(H)\ \mathrm{s.t.}\ R^{\alpha }=R, L^\alpha =g^{-1}Lg, S^\alpha =g^{-1}S\}. \end{aligned}$$

(2)

The following obvious facts are basic for bi-Cayley graphs.

Proposition 2.2

[18, Lemma 3.1] Let $\Gamma =\mathrm{BiCay}(H,R,L,S)$ be a connected bi-Cayley graph over a group H. Then, the following hold.

• (1) H is generated by $R\cup L\cup S$;

• (2) Up to graph isomorphism, S can be chosen to contain the identity element of H;

• (3) For any automorphism $\alpha$ of H, $\mathrm{BiCay}(H,R,L,S)\cong \mathrm{BiCay}(H,R^\alpha ,L^\alpha ,S^\alpha )$;

• (4) $\mathrm{BiCay}(H,R,L,S)\cong \mathrm{BiCay}(H,R,L, S^{-1})$.

Proposition 2.3

[19, Theorem 1.1] Let $\Gamma =\mathrm{BiCay}(H,R,L,S)$ be a connected bi-Cayley graph over the group H. If I is empty, then $N_{\mathrm{Aut}(\Gamma )}(R(H))=R(H)\rtimes F$, and if $I\ne \emptyset$, then $N_{\mathrm{Aut}(\Gamma )}(R(H))=R(H)\langle F,\delta _{\alpha ,x,y}\rangle$ for some $\delta _{\alpha ,x,y}\in I$. Furthermore, for any $\delta _{\alpha ,x,y}\in I$, we have the following:

• (1) $\langle R(H),\delta _{\alpha ,x,y}\rangle$ acts transitively on $V(\Gamma )$;

• (2) if $\alpha$ has order 2 and $x=y=1$, then $\Gamma$ is isomorphic to the Cayley graph $\mathrm{Cay}(\bar{H}, R\cup \alpha S)$, where $\bar{H}=H\rtimes \langle \alpha \rangle$.

3 Proof of Theorem 1.1

The goal of this section is to prove Theorem 1.1. We shall finish the proof by a series of lemmas. Before proceeding, we set some notation. Throughout this section, we shall always make the following assumption.

Assumption 1

• p: an odd prime,

• G: a group of order $2p^2$,

• $\Gamma =\mathrm{Cay}(G, S)$: a connected tetravalent Cayley graph of order $2p^2$,

• $A:=\mathrm{Aut}(\Gamma )$,

• $A_1:$ the stabilizer of the identity 1 of G in A.

We first consider the case where $\Gamma$ is symmetric.

Lemma 3.1

Assume that $\Gamma$ is symmetric. Then, $\Gamma$ is non-normal if and only if one of (5)–(7) of Theorem 1.1 happens.

Proof

By checking [14, Theorem 3.3], $\Gamma$ is isomorphic to one of the graphs in Table 1.

Table 1 Tetravalent symmetric graphs of order $2p^2$

If $\Gamma \cong X_{2p^2}^0$ or $X_{2p^2}^2$, then A has a normal Sylow p-subgroup, say P such that $A/P\cong {\mathbb Z}_2\times {\mathbb Z}_4$. Clearly, $P\le R(G)$, so $R(G)/P\unlhd A/P$. It follows that $R(G)\unlhd A$, and hence, $\Gamma$ is a normal Cayley graph of G.

Suppose that $\Gamma \cong \mathrm{C}_{p^2}\circ (2K_1)$. Then, $A\cong {\mathbb Z}_2^{p^2}\rtimes D_{2p^2}$. We first claim that $\Gamma$ must be a non-normal Cayley graph for all possible regular subgroup G of A. Otherwise, if $\Gamma$ is normal, then by Proposition 2.1, $A_1=\mathrm{Aut}(G, S)$ would have order dividing 24, and so $|A|\mid 2p^2\cdot 24$. This is clearly impossible because A has order $2p^2\cdot 2^{p^2}$.

Next we consider the possibility of the regular subgroup G and the corresponding Cayley subset S. If G is abelian, then by checking [20, Theorem 1.2], we see that the item (5) of Theorem 1.1 happens. Assume now that G is non-abelian. Clearly, every Sylow p-subgroup of R(G) is also a Sylow p-subgroup of A. Since $A\cong {\mathbb Z}_2^{p^2}\rtimes D_{2p^2}$, every Sylow p-subgroup of G is cyclic, and as G has order $2p^2$, one has $G\cong D_{2p^2}=G_1(p)$. Let $G=G_1(p)=\langle a,b\mid a^{p^2}=b^2=1, bab=a^{-1}\rangle .$ Since $\Gamma \cong \mathrm{C}_{p^2}\circ (2K_1)$, we may decompose the vertex set of $\Gamma$ into $p^2$ subsets, say $B_0, B_1, \ldots , B_{p^2-1}$ such that $|B_i|=2$, $\Gamma [B_i]\cong 2K_1$ and $\Gamma [B_i\cup B_{i+1}]\cong K_{2,2}$ with $i\in {\mathbb Z}_{p^2}$. Then each $B_i$ is a block of imprimitivity of A on $V(\Gamma )$. Let $1\in B_0$. Since R(G) acts regularly on $V(\Gamma )$ by right multiplication, $B_0$ is a subgroup of G of order 2. We may assume that $B_0=\{1, b\}$. Then, $\langle R(a)\rangle$ acts regularly on $\{B_0, B_1, \ldots , B_{p^2-1}\}$. Without loss of generality, we may assume that $B_1=B_0^{R(a)}=\{a, ba\}$. Then, $B_i=\{a^i, ba^i\}$ with $i\in {\mathbb Z}_{2p^2}$. This implies that $\Gamma =\mathrm{Cay}(G_1(p), \{a, a^{-1}, ba, ba^{-1}\}).$ Consequently, we obtain the item (6) of Theorem 1.1.

Finally, suppose that $\Gamma \cong X_{2p^2}^1$. By [14, Example 2.4], we see that $\Gamma =\mathrm{Cay}(H, T)$, where

$$\begin{aligned} H=\langle a\rangle \times \langle b\rangle \times \langle c\rangle \cong {\mathbb Z}_p\times {\mathbb Z}_p\times {\mathbb Z}_2, T=\{ca, ca^{-1}, cb, cb^{-1}\}. \end{aligned}$$

By [14, Proposition 2.5], $\Gamma$ is a normal Cayley graph of H, and the stabilizer $A_1=\mathrm{Aut}(H, T)=\langle \alpha ,\beta \rangle \cong D_8$, where $\alpha ,\beta$ are automorphisms of H induced by the following maps, respectively,

$$\begin{aligned} \alpha : a\mapsto b, b\mapsto a^{-1}, c\mapsto c; \beta : a\mapsto a, b\mapsto b^{-1}, c\mapsto c. \end{aligned}$$

Now we shall find all possible non-normal regular subgroups G of A and the corresponding Cayley subset S. Let $P=\langle R(a), R(b)\rangle$. Then, P is the normal Sylow p-subgroup of A. So $P\le R(G)$. Then, R(G)/P is a non-normal subgroup of A/P of order 2. Note that $A/P=\langle R(c)P\rangle \times \langle \alpha P, \beta P\rangle \cong {\mathbb Z}_2\times D_8$. Since R(G) is regular, we have $R(G)/P=\langle xP\rangle$ with

$$\begin{aligned} x\in \{R(c)\alpha ^i\beta \ |\ i\in {\mathbb Z}_4\}. \end{aligned}$$

For each $i\in {\mathbb Z}_4$, it is easy to see that the map $R(a)\mapsto R(a), R(b)\mapsto R(b), R(c)\mapsto R(c), \alpha \mapsto \alpha , \alpha ^i\beta \mapsto \beta$ induces an automorphism of A. So we may let $x=R(c)\beta$, and then

$$\begin{aligned} R(G)=\langle R(a), R(b)\rangle \rtimes \langle R(c)\beta \rangle . \end{aligned}$$

Recall that $\Gamma =\mathrm{Cay}(H, T)$ with $T=\{ca, ca^{-1}, cb, cb^{-1}\}$. It is easy to see that

$$\begin{aligned} ca=1^{R(c)\beta R(a)}, ca^{-1}=1^{R(c)\beta R(a^{-1})}, cb=1^{R(c)\beta R(b)}, cb^{-1}=1^{R(c)\beta R(b^{-1})}. \end{aligned}$$

For convenience, let $y=R(a), z=R(b)$. Then, we have

$$\begin{aligned} G=\langle y,z,x\mid y^p=z^p=x^2=1, yz=zy, xyx=y, xzx=z^{-1}\rangle \cong G_3(p). \end{aligned}$$

Furthermore, $\Gamma \cong \mathrm{Cay}(G, S)$ with $S=\{xy, xy^{-1}, xz, xz^{-1}\}$. We obtain the item (7) of Theorem 1.1. $\square$

Next, we shall consider the case where $\Gamma =\mathrm{Cay}(G, S)$ is non-symmetric. We will finish this case by four lemmas.

Lemma 3.2

Suppose that $\Gamma$ is non-symmetric and that either $p>3$ or $A_1$ is a 2-group. Then, the following hold.

• (1) Every Sylow p-subgroup of A has order $p^2$.

• (2) If N is a normal $\{2,3\}$-subgroup of A, then $N\cong {\mathbb Z}_2$ is semiregular on $V(\Gamma )$.

Proof

• (1) Let P be a Sylow p-subgroup of A. Since $\Gamma$ is of valency 4, one has $|A_1|=2^\ell \cdot 3^t$ for some integers $\ell , t$, and so $|A|=2^{\ell +1}\cdot 3^t\cdot p^2$. It then follows that $|P|={p^2}$ whenever either $p>3$ or $A_1$ is a 2-group.

• (2) Consider the quotient graph $\Gamma _N$ of $\Gamma$ relative to N. Then, $\Gamma _N$ has valency no more than 4. Keep in mind we assume that either $p>3$ or $A_1$ is a 2-group. Since $|V(\Gamma )|=2p^2$ and N is a normal $\{2,3\}$-subgroup of A, each orbit of N has length 2. It follows that $|V(\Gamma _N)|=p^2$, and so the valency of $\Gamma _N$ is 2 or 4. If $\Gamma _N$ has valency 2, then since $\Gamma _N$ has odd order, the two vertices of each orbit of N are non-adjacent, and then, we have $\Gamma \cong \mathrm{C}_{p^2}\circ (2K_1)$, contrary to the assumption that $\Gamma$ is non-symmetric. Thus, $\Gamma _N$ has valency 4. Let K be the kernel of A acting on $V(\Gamma _N)$. Then, $N\le K$, and for any $v\in V(\Gamma )$, no two neighbors are in the same orbit of N. It follows that the stabilizer $K_v$ will fix every neighbor of v. By the connectedness of $\Gamma$, $K_v$ will fix every vertex of $\Gamma$, and so $K_v=1$. As a result, we obtain that $K=N$ is semiregular on $V(\Gamma )$, and so $K=N\cong {\mathbb Z}_2$. $\square$

Lemma 3.3

Suppose that $\Gamma$ is non-symmetric. If $A_1$ is a 2-group and A has a normal cyclic Sylow p-subgroup, then $\Gamma$ is normal.

Proof

Let P be a normal cyclic Sylow p-subgroup of A. By Lemma 3.2 (1), we have $P\cong {\mathbb Z}_{p^2}$. Since G has order $2p^2$, one has $P\le R(G)$. Clearly, $P\le C_{A}(P)$, and by N/C-theorem, $A/C_A(P)\le \mathrm{Aut}(P)\cong {\mathbb Z}_{p(p-1)}$. It follows that if $C_A(P)=P$, then $R(G)/P\unlhd A/C_A(P)$, and then $R(G)\unlhd A$, as required. Suppose that $C_A(P)>P$. Let H be a $p'$-Hall subgroup of $C_A(P)$. Then, $C_A(P)=P\times H$. Clearly, H is characteristic in $C_A(P)$ and so normal in A because $C_{A}(P)\unlhd A$. By Lemma 3.2 (2), $H\cong {\mathbb Z}_2$ is semiregular on $V(\Gamma )$. Consequently, $C_A(P)=P\times H\cong {\mathbb Z}_{2p^2}$. Again, by N/C-theorem, we have $(A/P)/(C_A(P)/P)\cong A/C_A(P)\le \mathrm{Aut}(P)\cong {\mathbb Z}_{p(p-1)}$. Clearly, $C_A(P)/P\cong {\mathbb Z}_2$ is contained in the center of A/P, so A/P is abelian. Then, $R(G)/P\unlhd A/P$, and then $R(G)\unlhd A$, completing the proof. $\square$

Lemma 3.4

Suppose that $\Gamma$ is non-symmetric. If $A_1$ is a 2-group and A has a normal Sylow p-subgroup, then $\Gamma$ is normal.

Proof

Assume that $A_1$ is a 2-group and let P be a normal Sylow p-subgroup of A. If P is cyclic, then by Lemma 3.3, $\Gamma$ is normal. In what follows, we may assume that $P=\langle a\rangle \times \langle b\rangle \cong {\mathbb Z}_p\times {\mathbb Z}_p$. Since $p>3$, P is semiregular on $V(\Gamma )$ with two orbits. It follows that $\Gamma$ is a normal bi-Cayley graph over P. For convenience of the statement, we shall abuse the notation by letting $\Gamma =\mathrm{BiCay}(P, R, L, T)$ in the proof of this lemma.

Recall that R(G) acts regularly on $V(\Gamma )$. Since $P\unlhd A$, one has $P\le R(G)$, and so $R(G)\cong P\rtimes {\mathbb Z}_2$. By Proposition 2.3, there exists an involution $\delta _{\alpha , x, y}\in \mathrm{Aut}(\Gamma )$ for some $\alpha \in \mathrm{Aut}(P)$ and $x,y\in P$ such that $\delta _{\alpha , x, y}$ swaps $1_0$ and $1_1$. By the definition of $\delta _{\alpha ,x,y}$, we obtain that $x=y=1$. Since $\delta _{\alpha , 1, 1}\in \mathrm{Aut}(\Gamma )$, the following equalities hold:

$$\begin{aligned} R^\alpha =L, L^\alpha =R, T^\alpha =T^{-1}. \end{aligned}$$

By Proposition 2.2, we may assume that T contains the identity of P. If $\langle T, R\rangle \ne P$, then we must have $\langle T\rangle =\langle R\rangle$ since $P\cong {\mathbb Z}_p\times {\mathbb Z}_p$. Then, $R\ne \emptyset$, and so $|R|\ge 2$ since $R=R^{-1}$. Since $\Gamma$ has valency 4, one has $R=\{x, x^{-1}\}$ and $T=\{1, x^i\}$ for some $1\ne x\in P$ and $i\in {\mathbb Z}_p^*$. Then from the above third equality, we obtain that $\alpha$ fixes $\langle T\rangle$ and so fixes $\langle R\rangle$. Since $L=R^\alpha$, one has $\langle L\rangle =\langle R\rangle$ and so $\langle R,L,S\rangle =\langle R\rangle \cong {\mathbb Z}_p$. However, since $\Gamma$ is connected, by Proposition 2.2, we have $P=\langle R,L,S\rangle$, a contradiction. Thus, $\langle T, R\rangle =P$.

Let $v=1_0$. By Proposition 2.3, we have $A_v=\{\sigma _{\alpha ,g}\mid \alpha \in \mathrm{Aut}(P), g\in P\ \mathrm{s.t.}\ R^{\alpha }=R, L^\alpha =g^{-1}Lg, S^\alpha =g^{-1}S\}.$ Note that the neighborhood of v in $\Gamma$ is $\Gamma (v)=\{t_1\mid t\in T\}\cup \{r_0\mid r\in R\}.$ Let $A_v^*$ be the subgroup of $A_v$ fixing $\Gamma (v)$ pointwise. Take $\sigma _{\alpha , g}\in A_v^*$. Then $\sigma _{\alpha , g}$ fixes $t_1$ and $r_0$ for any $t\in T$ and $r\in R$. Since $1\in T$, one has $1_1=(1_1)^{\sigma _{\alpha , g}}=g_1$, implying that $g=1$. Then for any $t\in T$, we have $t_1=t_1^{\sigma _{\alpha , g}}=(t^\alpha )_1$, and so $t^\alpha =t$. Similarly, for any $r\in R$, we have $r_0=r_0^{\sigma _{\alpha , g}}=(r^\alpha )_0$, and so $r^\alpha =r$. Consequently, $\alpha$ fixes every element in $T\cup R$. Since $\langle T, R\rangle =P$, one has $\alpha =1$, and hence $\sigma _{\alpha ,g}$ is an identity automorphism of $\Gamma$. Thus, $A_v^*=1$, and hence $A_v\lesssim \mathrm{Sym}(4)$. Since $\Gamma$ is assume to be non-symmetric and $A_v$ is a 2-group, one has either $A_v\cong {\mathbb Z}_2$, or $A_v\cong {\mathbb Z}_2\times {\mathbb Z}_2$ and $A_{v1_1}\cong {\mathbb Z}_2$. To complete the proof, it suffices to show that $A_v\cong {\mathbb Z}_2$. By way of contradiction, suppose that $A_v\cong {\mathbb Z}_2\times {\mathbb Z}_2$ and $A_{v1_1}\cong {\mathbb Z}_2$.

First let $R\ne \emptyset$. By Proposition 2.2, we may assume that $T=\{1,a\}$ and $R=\{b, b^{-1}\}$. Recall that there exists $\delta _{\alpha _1, 1, 1}\in R(G)$ with $\alpha _1\in \mathrm{Aut}(P)$ satisfying the following equalities:

$$\begin{aligned} R^{\alpha _1}=L, L^{\alpha _1}=R, T^{\alpha _1}=T^{-1}. \end{aligned}$$

Then, $a^{\alpha _1}=a^{-1}$, and $b^{\alpha _1}=a^ib (i\in {\mathbb Z}_p)$ or $b^{-1}$. By Proposition 2.3 (2), $\Gamma =\mathrm{Cay}(G, S)$ with $G=P\rtimes \langle \alpha _1\rangle$ and $S=\{b, b^{-1}\}\cup \{\alpha _1, \alpha _1a\}$. It is easy to check that the following two maps

$$\begin{aligned} \gamma _1: a\mapsto a^{-1}, b\mapsto b, \alpha _1\mapsto \alpha _1a; \gamma _2: a\mapsto a, b\mapsto b^{-1}, \alpha _1\mapsto \alpha _1 \end{aligned}$$

induce two automorphisms of G. Furthermore, $A_1=\mathrm{Aut}(G, S)=\langle \gamma _1\rangle \times \langle \gamma _2\rangle$. Thus, $\Gamma$ is a normal Cayley graph on G, as required.

Now let $R=\emptyset$. By Proposition 2.2 (2), we may assume that $T=\{1, a, b, a^ib^j\}$ for some $i,j\in {\mathbb Z}_p$. Then, $\Gamma (v)=\{1_1, a_1, b_1, (a^ib^j)_1\}$. Without loss of generality, we may assume that $A_v^{\Gamma (v)}=\langle (1_1\ a_1)\rangle \times \langle (b_1\ (a^ib^j)_1)\rangle$.

Then, there exists $\sigma _{\alpha ,g}\in A_v$ such that $\sigma _{\alpha ,g}$ swaps $1_1$ and $a_1$, and fixes both $b_1$ and $(a^ib^j)_1$. By the definition of $\sigma _{\alpha ,g}$, we have $a_1=(1_1)^{\sigma _{\alpha ,g}}=g_1$ and $1_1=(a_1)^{\sigma _{\alpha ,g}}=(ga^\alpha )_1$. It follows that $g=a$ and $a^\alpha =a^{-1}$. Furthermore, from $b_1=(b_1)^{\sigma _{\alpha ,g}}=(gb^\alpha )_1$ we get that $b^\alpha =g^{-1}b=a^{-1}b$, and from $(a^ib^j)_1=((a^ib^j)_1)^{\sigma _{\alpha ,g}}=(g(a^ib^j)^\alpha )_1$ we obtain that $(a^ib^j)^\alpha =g^{-1}a^ib^j=a^{i-1}b^j$. On the other hand, since $a^\alpha =a^{-1}$ and $b^\alpha =a^{-1}b$, one has $(a^ib^j)^\alpha =a^{-i-j}b^j$. It follows that $a^{i-1}=a^{-i-j}$ and so $2i+j-1\equiv 0~(\mathrm{mod }~p)$.

Also, there exists $\sigma _{\beta ,h}\in A_v$ such that $\sigma _{\beta ,h}$ swaps $b_1$ and $(a^ib^j)_1$, and fixes both $1_1$ and $a_1$. With a similar argument as in the above paragraph, we have $h=1$, and $\beta$ fixes a and swaps b and $a^ib^j$. It follows that $b=a^{i+ij}b^{j^2}$, and hence

$$\begin{aligned} i(j+1)\equiv 0\ ({\mathrm{mod}}\,p)\ \mathrm{and}\ j^2\equiv 1\ ({\mathrm{mod}}\,p). \end{aligned}$$

Combining these two equalities with $2i+j-1\equiv 0~(\mathrm{mod }~p)$, we have $(i,j)=(1,-1)$ or (0, 1), and then $T=\{1, a, b, ab^{-1}\}$.

Let $\gamma$ be the automorphism of P induced by the map $a\mapsto a^{-1}b^2$ and $b\mapsto b$. It is easy to check that $\sigma _{\gamma , ab^{-1}}\in A_v$ and $\sigma _{\gamma , ab^{-1}}$ swaps $1_1$ and $(ab^{-1})_1$. It follows that $A_v$ is transitive on $\Gamma (v)$, and hence, $\Gamma$ is symmetric, a contradiction. $\square$

Lemma 3.5

Assume that $\Gamma =\mathrm{Cay}(G, S)$ is non-symmetric. Then, $\Gamma$ is non-normal if and only if one of (1)–(4) or (8) of Theorem 1.1 happens.

Proof

Since $\Gamma$ has valency 4, the vertex-stabilizer $A_1$ has order $2^\ell 3^t$ for some nonnegative integers $\ell$ and t. We first prove the following claim.

Claim 1

If $t=0$, then $\Gamma$ is normal.

In this case, $A_1$ is a 2-group and $|A|=|V(\Gamma )||A_1|=2^{\ell +1}\cdot p^2$. Let P be a Sylow p-subgroup of A. By Lemma 3.2 (1),P has order $p^2$. Since $A_1$ is a 2-group and $p>2$, P acts semiregularly on $V(\Gamma )$. It follows that $\Gamma$ is a bi-Cayley graph over P. By Lemmas 3.3 and 3.4, to prove our claim, it suffices to prove that $P\unlhd A$.

By Burnside $p^aq^b$-theorem, A is solvable, and so every minimal normal subgroup of A is an elementary abelian r-subgroup, where $r=2$ or p. Assume first that A has a minimal normal 2-subgroup, say N. From the proof of Lemma 3.2 (2), we see that $N\cong {\mathbb Z}_2$ is semiregular on $V(\Gamma )$, and the quotient graph $\Gamma _N$ of $\Gamma$ relative to N has valency 4. Since $p>2$, PN/N is regular on $V(\Gamma _N)$, and so $\Gamma _N$ is a tetravalent Cayley graph on PN/N. Note that P is abelian due to $|P|=p^2$. By [20, Corollary 1.3], $\Gamma _N$ is a normal Cayley graph on PN/N. It follows that $PN/N\unlhd A/N$, and so $PN\unlhd A$. Note that $PN=N\times P$. Then, P is characteristic in PN and so normal in A, as required.

Assume now that A has no normal 2-subgroups. Still let N be a minimal normal subgroup of A. Then, $N\cong {\mathbb Z}_p\times {\mathbb Z}_p$ or ${\mathbb Z}_p$. If $N\cong {\mathbb Z}_p\times {\mathbb Z}_p$, then $P=N\unlhd A$, as required. Suppose $N\cong {\mathbb Z}_p$. Clearly, $N<P$ and $P\le C_A(N)$, so $N<C_A(N)$. Note that $C_A(N)/N\unlhd N_A(N)/N=A/N$. Let M/N be a minimal normal subgroup of A/N such that $M/N\le C_A(N)/N$. Then, either $M/N\cong {\mathbb Z}_p$ or M/N is a 2-group. For the latter case, since $M\le C_A(N)$, one has $M=N\times Q$, where Q is a 2-group of M. So Q is characteristic in M and so normal in A because $M\unlhd A$, a contradiction. Consequently, we have $M/N\cong {\mathbb Z}_p$, and then M is a normal Sylow p-subgroup of A. Therefore, we have $P=M\unlhd A$. This completes the proof of Claim 1.

By Claim 1, in what follows, we shall assume $t\ne 0$. Let $A_v^{*}$ be the kernel of $A_v$ acting on the neighborhood $\Gamma (v)$ of v. Let T be a Sylow 3-subgroup of $A_v$. If $T\le A_v^{*}$, then the connectedness and vertex-transitivity of $\Gamma$ implies that $T=1$, a contradiction. Thus, $T\nleq A_v^{*}$ and so $\mathbb {Z}_3\cong TA_v^{*}/A_v^{*}\le A_v/A_v^{*}$. Since $\Gamma$ is non-symmetric, one has $A_v/A_v^{*}\cong \mathbb {Z}_3$ or $S_3$. It follows that for any $v \in V(\Gamma )$, there is a unique vertex $u \in \Gamma (v)$ such that $A_u=A_v$. Set

$$\begin{aligned} E_0=\{\{u,v\} \in E(\Gamma )\mid A_v=A_u \}\ \mathrm{and}\ \Sigma =\Gamma -E_0. \end{aligned}$$

Then $\Sigma$ is a cubic graph. For any $g \in A$ and $\{u,v\} \in E_0$, one has $\{u,v\}^g=\{u^g,v^g\}$. Furthermore, $A_{u^g}=A_u^g=A_v^g=A_{v^g}$. It follows that $\{u,v\}^g=\{u^g,v^g\} \in E_0$ and hence $E_0^g=E_0$. Consequently, A is a vertex-transitive group of automorphisms of $\Sigma$. Since $3\mid |A_v|$, A acts transitively on the arcs of $\Sigma$. Furthermore, $\Sigma =\mathrm{Cay}(G, T)$, where $T=S\setminus \{x\}$ with x an involution of G contained in S.

Claim 2

If $\Sigma$ is disconnected, then $\Gamma$ is non-normal if and only if one of (1), (2) or (4) of Theorem 1.1 happens.

As $\Sigma$ is a cubic symmetric graph, all components of $\Sigma$ are isomorphic, and each component of $\Sigma$ is also a connected cubic symmetric Cayley graph of order 2p. It follows that $\langle T\rangle$ is a subgroup of G of order 2p, and $\mathrm{Cay}(\langle T\rangle , T)$ is a component of $\Sigma$.

Let $\Sigma _i$ $(0 \le i <p)$ be the components of $\Sigma$, and let $\Sigma _0=\mathrm{Cay}(\langle T\rangle , T)$. For each $0\le i < p$, let $B_i=V(\Sigma _i)$ and set $\Omega =\{B_i \mid 0\le i < p \}$. Then, $\Omega$ is an A-invariant partition of $V(\Sigma )=V(\Gamma )$. Consider the quotient graph $\Gamma _\Omega$ of $\Gamma$ relative to $\Omega$, and let K be the kernel of A acting on $\Omega$. Then, $A/K\le \mathrm{Aut}(\Gamma _\Omega )\lesssim \mathrm{Sym}(p)$. This implies that $p\mid |K|$, and so K has at most two orbits on each $B_i$. Since $\Sigma _i$ is of valency 3, if K is transitive on $B_i$, then the subgraph induced by any two adjacent components would have valency 4, and then $\Gamma$ would be disconnected, a contradiction. Thus, K has two orbits, say $B_{i,0}$, $B_{i,1}$ on each $B_i$. Now it is easy to see that the quotient graph $\Gamma _K$ of $\Gamma$ relative to K is a cycle of length 2p, and so $\Gamma _{\Omega }\cong \mathrm{C}_p$. Then, $A/K\le \mathrm{Aut}(\Gamma _\Omega )\cong D_{2p}$, and then, A/K is regular on the set of orbits of K. Without loss of generality, assume that $B_{(i-1)1}$ is adjacent to $B_{i,0}$ and $B_{i,1}$ is adjacent to $B_{(i-1)0}$ for $i\in {\mathbb Z}_p$. Furthermore, since $\Sigma _i$ is cubic, the edges between $B_{(i-1)1}$ and $B_{i0}$ form a perfect matching, the edges between $B_{i1}$ and $B_{(i+1)0}$ also form a perfect matching. This implies that K acts faithfully on each $B_i$, and so $K\le \mathrm{Aut}(\Sigma _i)$. Since A/K is regular on the set of orbits of K, one has $A_v=K_v$ for any $v\in V(\Gamma )$. Consequently, $3\mid |K_v|$ and hence K is an edge-transitive group of automorphisms of each component of $\Gamma$.

Fig. 1

The graph $\mathrm{TL}_{18}$

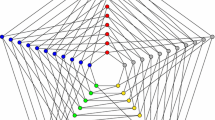
If $p=3$, then it is easy to see that $\Gamma$ is just the triple ladder graph $\mathrm{TL}_{18}$ (see Fig. 1). By Magma [21], we have $\mathrm{Aut}(\mathrm{TL}_{18})\cong \mathrm{Sym}(3)\wr \mathrm{Sym}(3)$, and so $\mathrm{TL}_{18}$ is must be a non-normal Cayley graph of G. By [20, Corollary 1.3], G is non-abelian. Recall that $\Sigma _0=\mathrm{Cay}(\langle T\rangle , T)$ is a component of $\Gamma$. So if $G=G_1(3)$ or $G_2(3)$, then $\langle T\rangle \cong D_6$, and then T consists of three involutions. Without loss of generality, let

$$\begin{aligned} \langle T\rangle =\langle a,c\mid a^3=c^2=1, cac=a^{-1}\rangle . \end{aligned}$$

Then, $T=\{c, ca, ca^2\}$. Note that $\Gamma =\mathrm{Cay}(G, T\cup \{x\})$ with x an involution. Then, we may let $x=cb$, where $\langle a, b\rangle$ is a Sylow 3-subgroup of G. So we get the graphs in (1) and (2) of Theorem 1.1. If $G=G_3(3)$, then since $\Gamma =\mathrm{Cay}(G, T\cup \{x\})$ with x an involution, $\langle T\rangle$ is abelian. Since $\Sigma \cong K_{3,3}$ which has no triangles, one has $T=\{c, ca, ca^2\}$, and then $x=cb$, where

$$\begin{aligned} G_3(3)=\langle a,b,c\mid a^3=b^3=c^2=1, ab=ba, ca=ac, cbc=b^{-1}\rangle . \end{aligned}$$

We obtain the graph in (4) of Theorem 1.1.

Now we assume that $p>3$. Since $\Sigma _i$ is a Cayley graph, by [22, Proposition 2.8], either $\Sigma _i$ is isomorphic to $K_{3,3}$ or to the Heawood graph, or $\Sigma _i$ is one-regular and $\mathrm{Aut}(\Sigma _i)\cong D_{2p}\rtimes {\mathbb Z}_3$ with $3\mid p-1$. It follows that $\langle T\rangle \cong D_{2p}$. Assume that $\langle T\rangle =\langle a, c\mid a^p=c^2=1, cac=a^{-1}\rangle$. By [23, Theorem 1.1], we may assume that $T=\{c, ca, ca^{-\lambda }\}$ with $\lambda ^2+\lambda +1\equiv 0\ ({\mathrm{mod}}\,p)$. Since $T\le G$, one has $G\cong G_1(p)$ or $G_2(p)$. Recall that $S=T\cup \{x\}$ with x an involution of G outside $\langle T\rangle$. Then, $x=ca^ib$, where $i\in {\mathbb Z}_p$, and $\langle a, b\rangle$ is a Sylow p-subgroup of G. If $\Sigma _i$ is isomorphic to the Heawood graph, then $p=7$, and then by Magma [21], $\Gamma =\mathrm{Cay}(G, S)$ is a normal Cayley graph of G.

Now assume that $\Sigma _i$ is one-regular and $\mathrm{Aut}(\Sigma _i)\cong D_{2p}\rtimes {\mathbb Z}_3$ with $3\mid p-1$. Then, $p>7$. Since $\Sigma _i$ is one-regular and $\mathrm{Aut}(\Sigma _i)\cong D_{2p}\rtimes {\mathbb Z}_3$, one has $K\cong {\mathbb Z}_p\rtimes {\mathbb Z}_3$. Let N and P be the Sylow p-subgroups of K and A, respectively, such that $N\le P$. Then, N is characteristic in K and so normal in A since $K\unlhd A$. By N/C-theorem, we obtain that $A/C_A(N)\le \mathrm{Aut}(N)\cong {\mathbb Z}_{p-1}$. Clearly, $P\le C_A(N)$ since P is an abelian group of order $p^2$. As $A/K\cong D_{2p}$ and $K\cong {\mathbb Z}_p\rtimes {\mathbb Z}_3$, one has $P\unlhd A$ and $3\not \mid |C_A(N)|$. It follows that $|A|=6p^2$ and $|C_A(N)|=2p^2$ or $p^2$. If $|C_A(N)|=2p^2$, then $R(G)=C_A(N)$ is a normal Hall $3'$-subgroup of A, and so $\Gamma$ is a normal Cayley graph of G. If $|C_A(N)|=p^2$, then $P=C_A(N)\le R(G)$, and since $A/C_A(N)\le {\mathbb Z}_{p-1}$, we have $R(G)/P\unlhd A/P$, and so $R(G)\unlhd A$. Again, $\Gamma$ is a normal Cayley graph of G, as claimed.

Finally, we shall finish the proof by the following claim.

Claim 3

If $\Sigma$ is connected, then $\Gamma$ is non-normal if and only if either (3) or (8) of Theorem 1.1 happens.

Suppose that $\Gamma$ is non-normal. Since $p>2$, by [7, Theorem 2.4], we have $\Sigma =\mathrm{Cay}(G, T)$, and all the possibilities for G and T are listed as follows:

$$\begin{aligned} \begin{array}{ll} G=G_2(3)=\langle a,b,c\mid a^3=b^3=c^2=1, ab=ba, cac=a^{-1}, cbc=b^{-1}\rangle ,\\ T=\{c,ca,cb\}, G=G_3(p)=\langle a,b,c\mid a^p=b^p=c^2=1, ab=ba,\\ ac=ca, cbc=b^{-1}\rangle , T=\{c,cab,(cab)^{-1}\}.\end{array} \end{aligned}$$

If $p=3$, then by Magma [21], we can obtain the graph in (3) of Theorem 1.1. In what follows, we assume that $p>3$. Then, $G=G_3(p)$ and $T=\{c, cab, (cab)^{-1}\}$. Recall that $\Gamma =\mathrm{Cay}(G, S)$, where $S=T\cup \{x\}$ with x an involution. Then, $x=cb^\ell$ with $\ell \in {\mathbb Z}_p$. Define a map from $G=G_3(p)$ to $G_2(p)$ by the following rule:

$$\begin{aligned} \delta : a^ib^j\mapsto a^{\frac{p+1}{2}(i+j)}b^{\frac{p-1}{2}i+\frac{p+1}{2}j}, ca^ib^j\mapsto ca^{\frac{p+1}{2}(i+j)}b^{\frac{p-1}{2}i+\frac{p+1}{2}j}, i, j\in {\mathbb Z}_p. \end{aligned}$$

It is easy to check that $\delta$ is a bijection. Set $\Gamma '=\mathrm{Cay}(G_2(p), \{c,ca,cb, ca^{\frac{p+1}{2}\ell }b^{\frac{p+1}{2}\ell }\})$. A direct computation shows that

$$\begin{aligned} \Gamma '((a^ib^j)^\delta )= & {} (\Gamma (a^ib^j))^\delta \\= & {} \left\{ ca^{\frac{p+1}{2}(i+j)}b^{\frac{p-1}{2}i+\frac{p+1}{2}j}, ca^{\frac{p+1}{2}(i+j)+1}b^{\frac{p+1}{2}i+\frac{p+1}{2}j}, \right. \nonumber \\&\left. ca^{\frac{p+1}{2}(i+j)}b^{\frac{p-1}{2}i+\frac{p+1}{2}j+1},ca^{\frac{p+1}{2}(i+j+\ell )}b^{\frac{p-1}{2}i+\frac{p+1}{2}(j+\ell )}\right\} ,\\ \Gamma '((ca^ib^j)^\delta )= & {} (\Gamma (ca^ib^j))^\delta \\= & {} \left\{ a^{\frac{p+1}{2}(i+j)}b^{\frac{p-1}{2}i+\frac{p+1}{2}j}, a^{\frac{P+1}{(}i+j)-1}b^{\frac{p+1}{2}i+\frac{p+1}{2}j}, a^{\frac{p+1}{2}(i+j)}\right. \nonumber \\&\left. b^{\frac{p-1}{2}i+\frac{p+1}{2}j-1}, a^{\frac{p+1}{2}(i+j-\ell )}b^{\frac{p-1}{2}i+\frac{p+1}{2}(j-\ell )}\right\} . \end{aligned}$$

Thus, $\delta$ is an isomorphism from $\Gamma$ to $\Gamma '$. Also, $\delta$ maps the subgraph $\Sigma =\mathrm{Cay}(G, T)$ of $\Gamma$ to the subgraph $\Sigma '=\mathrm{Cay}(G_2(p), \{c, ca, cb\})$ of $\Gamma '$. So $A_1\le \mathrm{Aut}(\Sigma ')_1$. Again, by [7, Theorem 2.4], $\Sigma '$ is a normal Cayley graph of $G_2(p)$. It follows that $A_1\lesssim \mathrm{Aut}(G_2(p), \{c, ca, cb\})$. Note the automorphism $\alpha$ of $G_2(p)$ induced by the following map:

$$\begin{aligned} \alpha : c\mapsto ca, a\mapsto a^{-1}b, b\mapsto a^{-1} \end{aligned}$$

cyclically permutates the three elements in $\{c, ca, cb\}$. Since $3\mid |A_1|$, one has $\alpha \in \mathrm{Aut}(\Sigma ')_1$. Then,

$$\begin{aligned} ca^{\frac{p+1}{2}\ell }b^{\frac{p+1}{2}\ell }=(ca^{\frac{p+1}{2}\ell }b^{\frac{p+1}{2}\ell })^\alpha =ca(a^{-1}b)^{\frac{p+1}{2}\ell } (a^{-1})^{\frac{p+1}{2}\ell }. \end{aligned}$$

It follows that $\frac{p+1}{2}\ell \equiv 1-(p+1)\ell \ ({\mathrm{mod}}\,p),$ and so $3\ell \equiv 2\ ({\mathrm{mod}}\,p)$. Therefore, $\Gamma =\mathrm{Cay}(G, S)$, where $G=G_3(p)$, $S=\{c, cab, (cab)^{-1}, cb^\ell \}$ and $3\ell \equiv 2\ ({\mathrm{mod}}\,p)$.

We already know that $\mathrm{Aut}(\Sigma )_1$ contains an element of order 3. Since $\Gamma \cong \Sigma$, $\mathrm{Aut}(\Gamma )_1$ also has an element of order 3, which cannot be an automorphism of G because S consists of two involutions and two elements of order 2p. By Proposition 2.1, $\Gamma$ is non-normal, completing the proof of Claim 3. $\square$

Proof of Theorem 1.1

If $\Gamma$ is symmetric, then by Lemma 3.1, we have (5)–(7) of Theorem 1.1. If $\Gamma$ is not symmetric, then by Lemma 3.5, we have (1)–(4) and (8) of Theorem 1.1. $\square$