Magnetic Relaxation in a Viscoelastic Ferrocolloid

Abstract

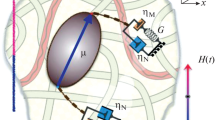
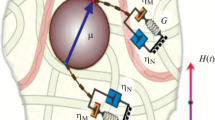
A method has been proposed for calculating linear dynamic magnetization of a viscoelastic ferrocolloid in a constant magnetic field (displacement field). The magnetic phase of the colloid consists of Brownian ferromagnetic nanoparticles placed into a Jeffry’s fluid. Therefore, each particle, upon its rotation induced by an alternating (probe) field, dissipates energy via two friction “channels” operating in parallel. The usual (Newtonian) viscosity prevails at short times, while the retarded (Maxwellian) dissipative interaction plays the main role at long times. It has been shown that the retarded friction on the Jeffry’s medium gives rise to a slow magnetization relaxation mode, which must be most pronounced in ferrocolloids having substantial elasticity. As the displacement field is enhanced, this mode weakens and the friction relevant to the Newtonian viscosity becomes prevailing, because it causes small-angle orientational fluctuations of particle magnetic moments. The proposed method yields an exact solution of the model, and the results obtained using method prove that previous approximate calculations are substantially limited.

Orthogonalization of Basis Polynomials

We consider the even K-subbasis. Its orthogonality is determined by the standard condition

$${{\left\langle {{{K}_{i}}(2n){{K}_{j}}(2m)} \right\rangle }_{0}} = {{{\delta }}_{{nm}}}{{\left\langle {{{{\left( {\Psi _{n}^{{{\text{(0)}}}}} \right)}}^{2}}} \right\rangle }_{0}}{{\left\langle {{{e}_{i}}{{e}_{j}}} \right\rangle }_{0}}$$

and realized step-by-step according to the Gram–Schmidt procedure (see, e.g., [27]). Let us describe the operation of this algorithm. By definition, the first basis function is specified by first-order polynomial $\Psi _{1}^{{(0)}}({{{\mathbf{Q}}}^{{\text{2}}}}) = {{{\mathbf{Q}}}^{{\text{2}}}} + A.$ According to the normalizing condition, we have ${{\left\langle {\Psi _{1}^{{(0)}}({{{\mathbf{Q}}}^{2}})} \right\rangle }_{0}} = 0,$ which yields $\Psi _{1}^{{(0)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{{\text{2}}}} - {{\left\langle {{{{\mathbf{Q}}}^{{\text{2}}}}} \right\rangle }_{0}} = {{{\mathbf{Q}}}^{2}} - 3\tilde {T}.$

Furthermore, we take $\tilde {T} = 1$ to simplify the notation. The restoration of the explicit temperature dependence of any orthogonal polynomial is trivial. For this purpose, it is sufficient to take into account that its terms must have the same dimensionality and that ${{\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}n}}}} \right\rangle }_{0}} \sim {{\tilde {T}}^{n}}.$ The second polynomial of this subbasis has the form of $\Psi _{2}^{{(0)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{4}} + A{{{\mathbf{Q}}}^{2}} + B.$ It must meet the normalizing condition and be orthogonal to the first polynomial, with these circumstances, after averaging over the equilibrium distribution, leading to two equations for determining the coefficients: $5 \times 3 + 3A + B = 0,$$7 \times 5 + 5A + B = 0.$ Finding them, we obtain desired function $\Psi _{2}^{{(0)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{4}} - 10{{{\mathbf{Q}}}^{2}} + 15.$ (With the temperature dependence explicitly taken into account, we have $\Psi _{2}^{{(0)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{4}} - 10\tilde {T}{{{\mathbf{Q}}}^{2}} + 15{{\tilde {T}}^{2}}.$) The sequential continuation of this process yields the orthogonal polynomials of higher orders. For information, let us write out a few first functions from this set:

$$\begin{gathered} \Psi _{1}^{{(0)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{2}} - 1 \times 3, \\ \Psi _{2}^{{(0)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{4}} - 2 \times 5{{{\mathbf{Q}}}^{2}} + 3 \times 5, \\ \Psi _{3}^{{(0)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{6}} - 3 \times 7{{{\mathbf{Q}}}^{4}} \\ + \,\,3 \times 5 \times 7{{{\mathbf{Q}}}^{2}} - 3 \times 5 \times 7. \\ \end{gathered} $$

(A.1)

Let us consider the second even L-subbasis, which is determined by Eq. (7). The normalizing condition for all its functions is fulfilled automatically. Requiring the orthogonality of the first basis function of this set, ${{L}_{i}} \equiv {{L}_{i}}(2) = ({{Q}_{i}}{{Q}_{j}}){\kern 1pt} '{{e}_{j}}$, to the second one, ${{L}_{i}}(4) = ({{{\mathbf{Q}}}^{2}} + A){{L}_{i}},$ we arrive at the equation ${{\left\langle {{{L}_{i}}(4){{L}_{i}}(2)} \right\rangle }_{0}}$ = ${{\left\langle {({{{\mathbf{Q}}}^{2}} + A){{L}_{i}}{{L}_{j}}} \right\rangle }_{0}}$ ~ ${{\left\langle {({{{\mathbf{Q}}}^{2}} + A){{{\mathbf{Q}}}^{4}}} \right\rangle }_{0}} = 0,$ from which it follows that $\Psi _{1}^{{(4)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{{\text{2}}}} - 7.$ Here, the superscript of the orthogonal polynomial indicates the power of an complementary weight function. In the case of the K-polynomials, this complementary weight function is absent $({{Q}^{0}} = 1).$ Continuing this process, we derive successively the orthogonal polynomials until any order. The several first few of them are

$$\begin{gathered} \Psi _{1}^{{(4)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{2}} - 1 \times 7, \\ \Psi _{2}^{{(4)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{{\text{4}}}} - 2 \times 9{{{\mathbf{Q}}}^{2}} + 7 \times 9, \\ \Psi _{3}^{{(4)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{6}} - 3 \times 11{{{\mathbf{Q}}}^{4}} \\ + \,\,3 \times 9 \times 11{{{\mathbf{Q}}}^{2}} - 7 \times 9 \times 11. \\ \end{gathered} $$

(A.2)

Performing the procedure of orthogonalization for the odd M-subbasis, we derive one more series of polynomials. The first few of them are

$$\begin{gathered} \Psi _{1}^{{(2)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{2}} - 1 \times 5, \\ \Psi _{2}^{{(2)}}({{{\mathbf{Q}}}^{{\text{2}}}}) = {{{\mathbf{Q}}}^{4}} - 2 \times 7{{{\mathbf{Q}}}^{2}} + 5 \times 7, \\ \Psi _{3}^{{(2)}}({{{\mathbf{Q}}}^{2}}) = {{{\mathbf{Q}}}^{{\text{6}}}} - 3 \times 9{{{\mathbf{Q}}}^{4}} \\ + \,\,3 \times 7 \times 9{{{\mathbf{Q}}}^{2}} - 5 \times 7 \times 9. \\ \end{gathered} $$

(A.3)

Using the direct substitution, we easily ascertain that orthogonal polynomials (A.1)–(A.3) satisfy the following simple equation, which will be needed below:

$$\frac{d}{{dx}}\Psi _{n}^{{{\text{(}}p{\text{)}}}}(x) = n\Psi _{{n\, - \,{\text{1}}}}^{{{\text{(}}p + {\text{2)}}}}(x),\,\,\,\,x = {{{\mathbf{Q}}}^{2}},\,\,\,\,n \geqslant 2.$$

(A.4)

In concluding this section, it should be emphasized that the algorithm used above for deriving the orthogonal polynomials is based on the fulfillment of condition

$${{\left\langle {\left( {\Psi _{m}^{{{\text{(}}p{\text{)}}}}({{{\mathbf{Q}}}^{2}}){{{\mathbf{Q}}}^{{2n}}}} \right){{{\mathbf{Q}}}^{p}}} \right\rangle }_{0}} = 0{\text{ }},\,\,\,\,m{\text{ > }}n.$$

(A.5)

Note that the above-derived orthogonal polynomials are related by a simple equation to the known and well-studied Laguerre polynomials [27]:

$$\Psi _{n}^{{{\text{(}}p{\text{)}}}}(2x) \sim L_{n}^{{\alpha }}(x),\,\,\,\,{\alpha } = {{(1 + p)} \mathord{\left/ {\vphantom {{(1 + p)} 2}} \right. \kern-0em} 2},\,\,\,\,x = {{{{{\mathbf{Q}}}^{2}}} \mathord{\left/ {\vphantom {{{{{\mathbf{Q}}}^{2}}} 2}} \right. \kern-0em} 2}.$$

1.1 Calculation of the Isotropic Part of Moment Equations

The operators introduced into the initial set of stochastic equations (4) affect the phase variables as follows:

$$\begin{gathered} {\mathbf{\hat {H}}}{{e}_{i}} = {{({\mathbf{e}} \times {\mathbf{h}} \times {\mathbf{e}}{\text{)}}}_{i}},\,\,\,\,{\mathbf{\hat {H}}}{{Q}_{i}} = - {{{\text{(}}{\mathbf{e}} \times {\mathbf{h}}{\text{)}}}_{i}}, \\ {\mathbf{\hat {Q}}}{{e}_{i}} = {{{\text{(}}{\mathbf{Q}} \times {\mathbf{e}}{\text{)}}}_{i}},\,\,\,\,{\mathbf{\hat {Q}}}{{Q}_{i}} = 0, \\ {\mathbf{\hat {U}}}{{e}_{i}} = {{\left( {{\mathbf{u}}{\text{(t)}} \times {\mathbf{e}}} \right)}_{i}},\,\,\,\,{\mathbf{\hat {U}}}{{Q}_{i}} = {{{\tilde {u}}}_{i}}{\text{(}}t{\text{) }}. \\ \end{gathered} $$

(A.6)

The first equation in the chain of the moment equations was derived above (see Eq. (14)). Let us show how all other links of this chain are found. We begin the calculation with the isotropic part of the moment equations.

Let us average the equation for an odd moment of the general form $\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{M}_{i}}} \right\rangle .$ We consider the isotropic part of the moment equation, with this component being determined by diffusion operator

$$\begin{gathered} {\mathbf{\hat {U}}}\left( {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{M}_{i}}} \right) = 2m{{{\mathbf{Q}}}^{{{\text{2}}m - {\text{2}}}}}{\text{(}}{{{\tilde {u}}}_{j}}{{Q}_{j}}{\text{)}}{{M}_{i}} + {{{\mathbf{Q}}}^{{{\text{2}}m}}}{\mathbf{\hat {U}}}{{M}_{i}}, \\ {\mathbf{\hat {U}}}{{M}_{i}} = {{({\mathbf{\tilde {u}}} \times {\mathbf{e}}{\text{)}}}_{i}} + {{({\mathbf{Q}} \times {\mathbf{u}} \times {\mathbf{e}}{\text{)}}}_{i}}. \\ \end{gathered} $$

This expression is averaged using procedure (11) for calculating the singular part of phase variable ${\mathbf{e}}$ and an analogous procedure that is employed to determine the singular part of phase variable ${\mathbf{Q}}{\text{:}}$${\mathbf{\tilde {Q}}}{\text{(}}t{\text{)}} = {\mathbf{\hat {I}}}{\text{(}}{\mathbf{\hat {U}Q}}{\text{)}} = {\mathbf{\hat {I}}}({\mathbf{\tilde {u}}}{\kern 1pt} ').$ As a result, we have the following:

$$\begin{gathered} \left\langle {{\mathbf{\hat {U}}}({{{\mathbf{Q}}}^{{{\text{2}}m}}}{{M}_{i}})} \right\rangle = {\mathbf{\hat {I}}}\left\langle {{\mathbf{\hat {U}}}{\kern 1pt} '\left( {{\mathbf{\hat {U}}}{\text{(}}{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{M}_{i}}{\text{)}}} \right)} \right\rangle \\ = {\mathbf{\hat {I}}}\left\langle {{\mathbf{\hat {U}}}{\kern 1pt} '\left( {2m{{{\mathbf{Q}}}^{{{\text{2}}m - {\text{2}}}}}({{{\tilde {u}}}_{j}}{{Q}_{j}}{\text{)}}{{M}_{i}} + {{{\mathbf{Q}}}^{{{\text{2}}m}}}{\mathbf{\hat {U}}}{{M}_{i}}} \right)} \right\rangle \\ = {\mathbf{\hat {I}}}\left\langle {4m{\text{(}}m - 1)\left( {\tilde {u}_{j}^{'}Q_{j}^{'}} \right){\text{(}}{{{\tilde {u}}}_{k}}{{Q}_{k}}{\text{)}}{{{\text{Q}}}^{{{\text{2}}m - {\text{4}}}}}{{M}_{i}}} \right. \\ 2m{{{\mathbf{Q}}}^{{{\text{2}}m - {\text{2}}}}}{\text{(}}\tilde {u}_{j}^{'}{{{\tilde {u}}}_{j}}{\text{)}}{{M}_{i}} + 4m{{{\mathbf{Q}}}^{{{\text{2}}m - {\text{2}}}}}{\text{(}}{{{\tilde {u}}}_{j}}{{Q}_{j}}{\text{)(}}{\mathbf{\hat {U}}}{\kern 1pt} '{{M}_{i}}{\text{)}} \\ + \left. {{{{\mathbf{Q}}}^{{{\text{2}}m}}}\left( {{\mathbf{\hat {U}}}{\kern 1pt} '\left( {{\mathbf{\hat {U}}}{{M}_{i}}} \right)} \right)} \right\rangle . \\ \end{gathered} $$

When writing this equation, the symmetry of correlation relations (2) for the random functions was taken into account. Let us calculate the integral using these relations. Taking into account the contribution from the effect of operator ${\mathbf{\hat {Q}}}$ on the desired moment, we derive the following equation:

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{{2m + 1}}}} \right)\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{M}_{i}}} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}\left( {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{M}_{i}}} \right)} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{N}}}}\left\langle {\left( {{{{\mathbf{Q}}}^{{{\text{2}}m}}} - 4m\tilde {T}{{{\mathbf{Q}}}^{{{\text{2}}m - {\text{2}}}}}} \right){{N}_{i}}} \right\rangle \\ + \,\,m{\text{(2}}m + 3){{{{\tilde {\gamma }}}}_{{\text{D}}}}\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m - {\text{2}}}}}{{M}_{i}}} \right\rangle + 2{{{\gamma }}_{{\text{D}}}}\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{e}_{i}}} \right\rangle , \\ {{N}_{i}}{\text{ = }}{{\left( {{\mathbf{Q}}\,\,{ \times }\,\,{\mathbf{M}}} \right)}_{i}} = {{L}_{i}} - \frac{2}{3}{{{\mathbf{Q}}}^{{\text{2}}}}{{e}_{i}}, \\ {{\Gamma }_{n}} \equiv {{{\gamma }}_{{\text{D}}}} + n{\tilde {\gamma }},\,\,\,\,{{{{\tilde {\gamma }}}}_{{\text{D}}}} = {{{\gamma }}_{{\text{D}}}}(1 + 1{\text{/}}q){\text{ }}{\text{.}} \\ \end{gathered} $$

From this general relation, we, assuming that $m = 0,$ find an equation for the moment of retarded friction forces. After some transformations, this equation is reduced to form (15).

Let us find the isotropic part of the equation for the next $(m = 1)$ odd orthogonal moment $\left\langle {{\mathbf{M}}(3)} \right\rangle = \left\langle {({{{\mathbf{Q}}}^{2}} - 5\tilde {T}){\mathbf{M}}} \right\rangle {\text{:}}$

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{3}}} \right)\left\langle {\left( {{{{\mathbf{Q}}}^{2}} - 5\tilde {T}} \right){{M}_{i}}} \right\rangle - {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}\left( {{{{\mathbf{Q}}}^{2}} - 5\tilde {T}} \right){{M}_{i}}} \right\rangle \\ = {{{\gamma }}_{{\text{N}}}}\left\langle {\left( {{{{\mathbf{Q}}}^{2}} - 4\tilde {T} - 5\tilde {T}} \right)\left( {{{L}_{i}} - \frac{2}{3}{{{\mathbf{Q}}}^{2}}{{e}_{i}}} \right)} \right\rangle \\ + \,\,(5{{{{\tilde {\gamma }}}}_{{\text{D}}}} - 5\tilde {T}2{\tilde {\gamma }})\left\langle {{{M}_{i}}} \right\rangle + 2{{{\gamma }}_{{\text{D}}}}\left\langle {\left( {{{{\text{Q}}}^{2}} - 5\tilde {T}} \right){{e}_{i}}} \right\rangle \\ = {{{\gamma }}_{{\text{N}}}}\left\langle {\left( {{{{\mathbf{Q}}}^{2}} - 7\tilde {T}} \right){{L}_{i}}} \right\rangle - 2\tilde {T}{{{\gamma }}_{{\text{N}}}}\left\langle {{{L}_{i}}} \right\rangle \\ - \,\,\,\,\frac{2}{3}{{{\gamma }}_{{\text{N}}}}\left\langle {\left( {{{{\mathbf{Q}}}^{4}} - 9\tilde {T}{{{\mathbf{Q}}}^{2}}} \right){{e}_{i}}} \right\rangle + 2{{{\gamma }}_{{\text{D}}}}\left\langle {\left( {{{{\mathbf{Q}}}^{2}} - 5\tilde {T}} \right){{e}_{i}}} \right\rangle . \\ \end{gathered} $$

Here, basis function ${\mathbf{L}}(4)$ has been isolated and it has been taken into account that ${{\Gamma }_{1}} = {{\Gamma }_{3}} - 2{\tilde {\gamma }}$ and ${{{\tilde {\gamma }}}_{{\text{D}}}} = 2\tilde {T}{\tilde {\gamma }}{\text{.}}$ Grouping the rest of the terms in accordance with the definition of the basis K-functions, we obtain the desired equation for the orthogonal moment:

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{3}}} \right)\left\langle {{{M}_{i}}(3)} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}{{M}_{i}}(3)} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{N}}}}\left\langle {{{L}_{i}}(4) - \frac{2}{3}{{K}_{i}}(4)} \right\rangle - {{{\gamma }}_{{\text{D}}}}\left\langle {{{L}_{i}}{\text{(2)}}} \right\rangle + \frac{5}{3}{{{\gamma }}_{{\text{D}}}}\left\langle {{{K}_{i}}{\text{(2)}}} \right\rangle . \\ \end{gathered} $$

Acting in a similar way, we find the isotropic part of equation for the next $(m = 2)$ orthogonal moment $\left\langle {{\mathbf{M}}(5)} \right\rangle {\text{:}}$

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{5}}} \right)\left\langle {{{M}_{i}}(5)} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}{{M}_{i}}(5)} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{N}}}}\left\langle {{{L}_{i}}(6) - \frac{2}{3}{{K}_{i}}(6)} \right\rangle - 2{{{\gamma }}_{{\text{D}}}}\left\langle {{{L}_{i}}{\text{(4)}}} \right\rangle + \frac{7}{3}{{{\gamma }}_{{\text{D}}}}\left\langle {{{K}_{i}}{\text{(4)}}} \right\rangle . \\ \end{gathered} $$

The form of these equations evidently shows the algorithm of deriving the isotropic part of the odd orthogonal moments of any order:

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{{{\text{2}}m{\text{ + 1}}}}}} \right)\left\langle {{{M}_{i}}(2m + 1)} \right\rangle \\ = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}{{M}_{i}}(2m + 1)} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{N}}}}\left\langle {{{L}_{i}}(2m + 2) - \frac{2}{3}{{K}_{i}}(2m + 2)} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{D}}}}\left( {\frac{{2m + 3}}{3}\left\langle {{{K}_{i}}(2m)} \right\rangle - m\left\langle {{{L}_{i}}(2m)} \right\rangle } \right){\text{ }}. \\ \end{gathered} $$

(A.7)

Let us derive an expression for the isotropic part of the even moments of the K-subbasis. Acting in the aforementioned way, we obtain the following equation for an even moment of the general form $\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{\mathbf{e}}} \right\rangle {\text{:}}$

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{{{\text{2}}m}}}} \right)\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{e}_{i}}} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}({{{\mathbf{Q}}}^{{{\text{2}}m}}}{{e}_{i}})} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{N}}}}\left\langle {\left( {{{{\mathbf{Q}}}^{{{\text{2}}m}}} - 4m\tilde {T}{{{\mathbf{Q}}}^{{{\text{2}}m - {\text{2}}}}}} \right){{M}_{i}}} \right\rangle \\ + \,\,m{\text{(2}}m + 1){{{{\tilde {\gamma }}}}_{{\text{D}}}}\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m - {\text{2}}}}}{{e}_{i}}} \right\rangle . \\ \end{gathered} $$

(A.8)

Using the definition of the K-functions, we find the isotropic parts of the equations for several orthogonal moments of this subbasis:

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{2}}} \right)\left\langle {{{K}_{i}}(2)} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}\left( {{{K}_{i}}{\text{(2)}}} \right)} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{N}}}}\left\langle {{{M}_{i}}(3)} \right\rangle - {{{\gamma }}_{{\text{D}}}}\left\langle {{{M}_{i}}} \right\rangle , \\ \left( {{{\partial }_{t}} + {{\Gamma }_{4}}} \right)\left\langle {{{K}_{i}}(4)} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}\left( {{{K}_{i}}(4)} \right)} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{N}}}}\left\langle {{{M}_{i}}(5)} \right\rangle - 2{{{\gamma }}_{{\text{D}}}}\left\langle {{{M}_{i}}(3)} \right\rangle , \\ \left( {{{\partial }_{t}} + {{\Gamma }_{6}}} \right)\left\langle {{{K}_{i}}(6)} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}\left( {{{K}_{i}}(6)} \right)} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{N}}}}\left\langle {{{M}_{i}}(7)} \right\rangle - 3{{{\gamma }}_{{\text{D}}}}\left\langle {{{M}_{i}}(5)} \right\rangle {\text{ }}. \\ \end{gathered} $$

These equations clearly show the general algorithm for the derivation of the isotropic parts of the equation for the orthogonal K-moments:

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{{{\text{2}}m}}}} \right)\left\langle {{{K}_{i}}(2m)} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}\left( {{{K}_{i}}(2m)} \right)} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{N}}}}\left\langle {{{M}_{i}}(2m + 1)} \right\rangle - m{{{\gamma }}_{{\text{D}}}}\left\langle {{{M}_{i}}(2m - 1)} \right\rangle . \\ \end{gathered} $$

(A.9)

To obtain the isotropic part of the equation for the L-moments, we, acting in the above-described way, find the following equation for moment $\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{\mathbf{N}}} \right\rangle {\text{:}}$

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{{{\text{2}}m{\text{ + 2}}}}}} \right)\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{N}_{i}}} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}\left( {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{N}_{i}}} \right)} \right\rangle \\ + \,\,{{{\gamma }}_{{\text{N}}}}\left\langle {\left( { - {{{\mathbf{Q}}}^{{{\text{2}}m{\text{ + 2}}}}} + 2(2m + 3)\tilde {T}{{{\mathbf{Q}}}^{{{\text{2}}m}}}} \right){{M}_{i}}} \right\rangle \\ + m{\text{(2}}m + 5){{{{\tilde {\gamma }}}}_{{\text{D}}}}\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m{\text{ - 2}}}}}{{N}_{i}}} \right\rangle - 2{{{{\tilde {\gamma }}}}_{{\text{D}}}}\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{e}_{i}}} \right\rangle {\text{ }}. \\ \end{gathered} $$

Equation for moment $\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{L}_{i}}} \right\rangle$ is derived taking into account the fact that ${{L}_{i}} = {{N}_{i}} + ({2 \mathord{\left/ {\vphantom {2 {3){{{\mathbf{Q}}}^{{\text{2}}}}{{e}_{i}}}}} \right. \kern-0em} {3){{{\mathbf{Q}}}^{{\text{2}}}}{{e}_{i}}}}.$ After simple transformations, we find

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{{{\text{2}}m{\text{ + 2}}}}}} \right)\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{L}_{i}}} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}\left( {{{{\mathbf{Q}}}^{{{\text{2}}m}}}{{L}_{i}}} \right)} \right\rangle \\ - \,\,\frac{1}{3}{{{\gamma }}_{{\text{N}}}}\left\langle {\left( {{{{\mathbf{Q}}}^{{{\text{2}}m{\text{ + 2}}}}} + 2(2m + 3)\tilde {T}{{{\mathbf{Q}}}^{{{\text{2}}m}}}} \right){{M}_{i}}} \right\rangle \\ + \,\,m{\text{(2}}m + 5){{{{\tilde {\gamma }}}}_{{\text{D}}}}\left\langle {{{{\mathbf{Q}}}^{{{\text{2}}m - {\text{2}}}}}{{L}_{i}}} \right\rangle {\text{ }}. \\ \end{gathered} $$

This relation yields the isotropic parts of the equations for the orthogonal L-moments. Let us begin from the first moment $(m = 0)$ of this subbasis:

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{2}}} \right)\left\langle {{{L}_{i}}} \right\rangle - {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}\left( {{{L}_{i}}} \right)} \right\rangle \\ = - \frac{1}{3}{{{\gamma }}_{{\text{N}}}}\left\langle {\left( {{{{\mathbf{Q}}}^{{\text{2}}}} - 10\tilde {T}} \right){{M}_{i}}} \right\rangle \\ = - \frac{1}{3}{{{\gamma }}_{{\text{N}}}}\left\langle {\left( {{{{\mathbf{Q}}}^{2}} - 5\tilde {T}} \right){{M}_{i}}} \right\rangle + \frac{5}{3}{{{\gamma }}_{{\text{N}}}}\tilde {T}\left\langle {{{M}_{i}}} \right\rangle \\ = - \frac{1}{3}{{{\gamma }}_{{\text{N}}}}\left\langle {{{M}_{i}}{\text{(3)}}} \right\rangle + \frac{5}{6}{{{\gamma }}_{{\text{D}}}}\left\langle {{{M}_{i}}} \right\rangle . \\ \end{gathered} $$

For the next moment $\left\langle {{\mathbf{L}}{\text{(4)}}} \right\rangle = \left\langle {({{{\mathbf{Q}}}^{2}} - 7\tilde {T}){\mathbf{L}}} \right\rangle$, we, from the general equation at $m = 1$, obtain the following:

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{4}}} \right)\left\langle {{{L}_{i}}(4)} \right\rangle - {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}\left( {{{L}_{i}}(4)} \right)} \right\rangle \\ = \,\, - \frac{1}{3}{{{\gamma }}_{{\text{N}}}}\left\langle {{{M}_{i}}(5)} \right\rangle + \frac{7}{6}{{{\gamma }}_{{\text{D}}}}\left\langle {{{M}_{i}}{\text{(3)}}} \right\rangle . \\ \end{gathered} $$

It is evident that the algorithm for finding the isotropic parts of the equations for the orthogonal L-moments is determined by the following equation:

$$\begin{gathered} \left( {{{\partial }_{t}} + {{\Gamma }_{{{\text{2}}m}}}} \right)\left\langle {{{L}_{i}}(2m{\text{)}}} \right\rangle = {{{\gamma }}_{{\text{H}}}}\left\langle {{\mathbf{\hat {H}}}{{L}_{i}}(2m)} \right\rangle \\ - \,\,\frac{1}{3}{{{\gamma }}_{{\text{N}}}}\left\langle {{{M}_{i}}(2m + 1)} \right\rangle + \frac{{2m + 3}}{6}{{{\gamma }}_{{\text{D}}}}\left\langle {{{M}_{i}}(2m - 1)} \right\rangle . \\ \end{gathered} $$

(A.10)

Thus, all equations (A.7), (A.9), and (A.10) derived above for the orthogonal moments differ from those found previously [22] only in the existence of the field-related parts, which vanish in the absence of a constant field.

1.2 Calculation of Field-Related Parts. Complete Set of Moment Equations

In the previous section, the isotropic parts of the moment equations were calculated in a new way and in a more general form as compared with [22]. In this section, we show the effect of the constant magnetic field on the structure of the moment equations. It should be noted that, under the considered approximation, all nonequilibrium moments are proportional to the weak probe field; therefore, when calculating the field-related parts, we should take into account only the constant field; i.e., ${\mathbf{h}} = {\mathbf{k}}$ should be taken in Eqs. (A.6).

Let us begin with the calculation of the field-related parts of the odd orthogonal moments. Using definition (7) of the M-subbasis functions and taking into account the effect of operator ${\mathbf{\hat {H}}}$ on the phase variables, we obtain

$$\begin{gathered} \left\langle {{\mathbf{\hat {H}}}{{M}_{i}}(2m + 1)} \right\rangle = \left\langle {{\mathbf{\hat {H}}}({\Psi }_{m}^{{{\text{(2)}}}}{\text{(}}{{{\mathbf{Q}}}^{{\text{2}}}}{\text{)}}{{M}_{i}})} \right\rangle \\ = \left\langle {{\Psi }_{m}^{{{\text{(2)}}}}{\text{(}}{{{\mathbf{Q}}}^{{\text{2}}}}{\text{)(}}{\mathbf{Q}}{ \times }{\mathbf{v}}{{{\text{)}}}_{i}}} \right\rangle + \left\langle {{\Psi }_{m}^{{{\text{(2)}}}}{{{v}}_{i}}{\text{ + 2}}{{M}_{z}}{{M}_{i}}\frac{{\partial \Psi _{m}^{{{\text{(2)}}}}}}{{\partial {{{\mathbf{Q}}}^{2}}}}} \right\rangle , \\ {{{v}}_{i}} \equiv {{{\text{(}}{\mathbf{e}} \times {\mathbf{k}} \times {\mathbf{e}}{\text{)}}}_{i}}\,\,{\text{ = }}\,\,{{k}_{i}} - {{e}_{i}}{{e}_{z}}{\text{,}}\,\,\,\,{\mathbf{k}} = (0,0,1). \\ \end{gathered} $$

(A.11)

The first term in this relation is odd with respect to phase variable ${\mathbf{Q}},$ while the others are even. Upon the averaging with distribution (8), the odd component of this relation will be proportional to the odd moments, while the even component will, accordingly, be expressed via the even moments. Let us initially calculate the first term of relation (A.11)

$$\begin{gathered} \left\langle {{\Psi }_{m}^{{{\text{(2)}}}}{\text{(}}{{{\mathbf{Q}}}^{{\text{2}}}}{\text{)(}}{\mathbf{Q}} \times {\mathbf{v}}{{{\text{)}}}_{i}}} \right\rangle \\ = \sum\limits_{n{\text{ = 0}}{\text{,12}},...} {{{b}_{j}}(n,t)} {{\left\langle {{\Psi }_{n}^{{{\text{(2)}}}}{\Psi }_{m}^{{{\text{(2)}}}}{{{{\text{(}}{\mathbf{Q}}{ \times }{\mathbf{v}}{\text{)}}}}_{i}}{{M}_{j}}} \right\rangle }_{0}} \\ = {{{\varepsilon }}_{{ikl}}}{{{\varepsilon }}_{{jpq}}}\sum\limits_{n{\text{ = 0}}{\text{,12}},...} {{{b}_{j}}(n,t)} {{\left\langle {{\Psi }_{n}^{{{\text{(2)}}}}{\Psi }_{m}^{{{\text{(2)}}}}{{Q}_{k}}{{Q}_{p}}{{e}_{q}}{{{v}}_{l}}} \right\rangle }_{0}} \\ = ({{{\delta }}_{{lq}}}{{{\delta }}_{{ij}}}{\text{ - }}{{{\delta }}_{{lj}}}{{{\delta }}_{{iq}}}{\text{)}}{{\left\langle {{{e}_{q}}{{{v}}_{l}}} \right\rangle }_{{\text{0}}}}{{b}_{j}}(m,t){{\left\langle {{{{{{\left( {{\Psi }_{m}^{{{\text{(2)}}}}} \right)}}^{{\text{2}}}}{{{\mathbf{Q}}}^{{\mathbf{2}}}}} \mathord{\left/ {\vphantom {{{{{\left( {{\Psi }_{m}^{{{\text{(2)}}}}} \right)}}^{{\text{2}}}}{{{\mathbf{Q}}}^{{\mathbf{2}}}}} 3}} \right. \kern-0em} 3}} \right\rangle }_{0}} \\ = - {{b}_{j}}(m,t){{\left\langle {{{{{{\left( {{\Psi }_{m}^{{{\text{(2)}}}}} \right)}}^{{\text{2}}}}{{{\mathbf{Q}}}^{{\mathbf{2}}}}} \mathord{\left/ {\vphantom {{{{{\left( {{\Psi }_{m}^{{{\text{(2)}}}}} \right)}}^{{\text{2}}}}{{{\mathbf{Q}}}^{{\mathbf{2}}}}} 3}} \right. \kern-0em} 3}} \right\rangle }_{0}}{{A}_{{ij}}}, \\ {{A}_{{ij}}} \equiv {{\left\langle {{{e}_{i}}{{{v}}_{j}}} \right\rangle }_{0}} = ({{c}_{1}} - {{c}_{3}})\left( {P_{{ij}}^{\parallel } - \frac{1}{2}P_{{ij}}^{ \bot }} \right). \\ \end{gathered} $$

Here, the vector products have been written using the antisymmetric Levy–Civita tensor [27] and taking into account that ${{\left\langle {{{Q}_{j}}{{Q}_{k}}} \right\rangle }_{0}} = {{{{{\delta }}_{{jk}}}\left\langle {{{{\mathbf{Q}}}^{{\text{2}}}}} \right\rangle } \mathord{\left/ {\vphantom {{{{{\delta }}_{{jk}}}\left\langle {{{{\mathbf{Q}}}^{{\text{2}}}}} \right\rangle } 3}} \right. \kern-0em} 3}{\text{.}}$

Using relation (10) between the nonequilibrium amplitude and the moment, we derive the desired expression in the following form:

$$\begin{gathered} \left\langle {{\Psi }_{m}^{{{\text{(2)}}}}{\text{(}}{{{\mathbf{Q}}}^{{\text{2}}}}{\text{)(}}{\mathbf{Q}}\,\,{ \times }\,\,{\mathbf{v}}{{{\text{)}}}_{i}}} \right\rangle \\ = - \frac{{\text{1}}}{{\xi }}{{A}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{)}}\left\langle {{{M}_{j}}(2m + 1)} \right\rangle , \\ {{A}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{)}} = (3{{c}_{2}} - 1)\left( {\frac{{P_{{ij}}^{\parallel }}}{{1 - {{c}_{2}}}} - \frac{{P_{{ij}}^{ \bot }}}{{1 + {{c}_{2}}}}} \right). \\ \end{gathered} $$

(A.12)

Let us substitute this expression into the left-hand side of the equation for the odd moment and combine it with the diffusion part of the relaxation rate of this moment. As a result, taking into account that ${{{{{\gamma }}_{{\text{H}}}}} \mathord{\left/ {\vphantom {{{{{\gamma }}_{{\text{H}}}}} {\xi }}} \right. \kern-0em} {\xi }} = {T \mathord{\left/ {\vphantom {T {{{{\zeta }}_{{\text{N}}}}}}} \right. \kern-0em} {{{{\zeta }}_{{\text{N}}}}}} = {{{{{\gamma }}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{{\gamma }}_{{\text{D}}}}} 2}} \right. \kern-0em} 2}{\text{,}}$ we have

$${{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{)}} = {{{\gamma }}_{{\text{D}}}}\left( {{{{\delta }}_{{ij}}}{\text{ + }}\frac{{\text{1}}}{{\text{2}}}{{A}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{)}}} \right){\text{.}}$$

(A.13)

This expression comprises no number of a moment; therefore, the temperature-dependent diagonal part of the relaxation matrix is the same for all odd moments.

The terms even with respect to variable ${\mathbf{Q}}$ in Eq. (A.11) are expressed via the orthogonal even moments. Let us initially find the K-component, which is determined by the following equation:

$$\begin{gathered} {{\left\langle {{\mathbf{\hat {H}}}{{M}_{i}}(2m + 1)} \right\rangle }^{{{\text{(}}K{\text{)}}}}} = ( - 1)\sum\limits_{n{\text{ = 0}}{\text{,1}}{\text{,2}},..} {{{a}_{j}}(n,t)} \\ \times \,\,{{\left\langle {{\Psi }_{n}^{{{\text{(0)}}}}{{e}_{j}}\left( {{\Psi }_{m}^{{{\text{(2)}}}}{{{v}}_{i}}{\text{ + 2}}{{M}_{z}}{{M}_{i}}\frac{{\partial {\Psi }_{m}^{{{\text{(2)}}}}}}{{\partial {{{\mathbf{Q}}}^{{\text{2}}}}}}} \right)} \right\rangle }_{0}}. \\ \end{gathered} $$

The first term in this equation is easily calculated with allowance for the properties (Eq. A.5) of orthogonal polynomials ${\text{ }}{{\left\langle {{\Psi }_{n}^{{{\text{(0)}}}}{\Psi }_{m}^{{{\text{(2)}}}}} \right\rangle }_{0}} = {{{\delta }}_{{nm}}}{{\left\langle {{{{\left( {{\Psi }_{n}^{{{\text{(0)}}}}} \right)}}^{{\text{2}}}}} \right\rangle }_{{\text{0}}}}{\text{.}}$ It is easy to transform the second term with the use of relation (A.4); as a result, the matrix element under the sign of sum acquires the form of

$$\begin{gathered} {{\left\langle {{\Psi }_{n}^{{{\text{(0)}}}}{{e}_{j}}\left( {{\Psi }_{m}^{{{\text{(2)}}}}{{{v}}_{i}} + {\text{2}}{{M}_{z}}{{M}_{i}}\frac{{\partial \Psi _{m}^{{{\text{(2)}}}}}}{{\partial {{{\mathbf{Q}}}^{{\text{2}}}}}}} \right)} \right\rangle }_{0}} \\ {{\left\langle {{\Psi }_{n}^{{{\text{(0)}}}}{{e}_{j}}\left( {{\Psi }_{m}^{{{\text{(2)}}}}{{{v}}_{i}} + 2m{\Psi }_{{m - {\text{1}}}}^{{{\text{(4)}}}}{{M}_{z}}{{M}_{i}}} \right)} \right\rangle }_{0}} \\ = {{\left\langle {{\Psi }_{n}^{{{\text{(0)}}}}\left( {\Psi _{m}^{{{\text{(2)}}}} + \frac{{2m}}{3}{\Psi }_{{m - {\text{1}}}}^{{{\text{(4)}}}}{{{\mathbf{Q}}}^{{\text{2}}}}} \right)} \right\rangle }_{0}}{{A}_{{ij}}} \\ = {{{\delta }}_{{nm}}}\left( {1 + \frac{{2m}}{3}} \right){{\left\langle {{{{\left( {{\Psi }_{n}^{{{\text{(0)}}}}} \right)}}^{{\text{2}}}}} \right\rangle }_{0}}{{A}_{{ij}}}. \\ \end{gathered} $$

When deriving this equation, the averaging was performed over variable ${\mathbf{e}}$ and property (A.5) of the orthogonal polynomials was used. Using this expression and taking into account Eq. (10), we, for amplitude $a(n,t)$, find the K-component of the field-related part of the equation for the odd moment:

$$\begin{gathered} {{\left\langle {{\mathbf{\hat {H}}}{{M}_{i}}(2m + 1)} \right\rangle }^{{(K)}}} \\ = - \frac{{\text{1}}}{{\xi }}\left( {1 + \frac{{2m}}{3}} \right){{A}_{{ij}}}(K)\left\langle {K(2m)} \right\rangle , \\ {{A}_{{ij}}}(K) = (3{{c}_{2}} - 1)\left( {\frac{{P_{{ij}}^{\parallel }}}{{2{{c}_{2}}}} - \frac{{P_{{ij}}^{ \bot }}}{{1 - {{c}_{2}}}}} \right). \\ \end{gathered} $$

(A.14)

To calculate the L-component, it is necessary to find the following matrix element:

$$\begin{gathered} {{\left\langle {{{L}_{j}}(2n + 2){\mathbf{\hat {H}}}{{M}_{i}}(2m + 1)} \right\rangle }_{0}} \\ = {{\left\langle {{\Psi }_{n}^{{{\text{(4)}}}}{{L}_{j}}\left( {{\Psi }_{m}^{{{\text{(2)}}}}{{{v}}_{i}} + 2m{\Psi }_{{m - {\text{1}}}}^{{{\text{(4)}}}}{{M}_{z}}{{M}_{i}}} \right)} \right\rangle }_{0}} \\ = 2m{{\left\langle {{\Psi }_{n}^{{{\text{(4)}}}}{\Psi }_{{m - {\text{1}}}}^{{{\text{(4)}}}}{{L}_{j}}{{M}_{z}}{{M}_{i}}} \right\rangle }_{0}}. \\ \end{gathered} $$

The anisotropic part of this expression is found using the tensor representation of the vector product and taking into account the isotropy of the basic state with respect to variable ${\mathbf{Q}}$:

$$\begin{gathered} {{\left\langle {{{L}_{j}}{{M}_{z}}{{M}_{i}}} \right\rangle }_{{\text{0}}}} \\ = {{{\varepsilon }}_{{zpq}}}{{{\varepsilon }}_{{ikl}}}{{\left\langle {\left( {{{Q}_{j}}{{Q}_{r}}} \right){\kern 1pt} '{{Q}_{p}}{{Q}_{k}}{{e}_{r}}{{e}_{q}}{{e}_{l}}} \right\rangle }_{0}} \\ = - \frac{2}{3}{{\left\langle {\frac{{{{{\mathbf{Q}}}^{{\text{4}}}}}}{{{\text{15}}}}} \right\rangle }_{{\text{0}}}}{{A}_{{ij}}}{\text{.}} \\ \end{gathered} $$

Now, we can easily calculate the explicit form of the L-component of the field-related part of the equation for the odd moment. As a result, we obtain

$$\begin{gathered} {{\left\langle {{\mathbf{\hat {H}}}{{M}_{i}}(2m + 1)} \right\rangle }^{{{\text{(}}L{\text{)}}}}} \\ {\text{ = }}( - 1)\sum\limits_{n{\text{ = 0}}{\text{,1}},..} {{{c}_{j}}(n,t){{{\left\langle {{\Psi }_{n}^{{{\text{(4)}}}}{{L}_{j}}{\text{2}}{{M}_{z}}{{M}_{i}}\frac{{\partial {\Psi }_{m}^{{{\text{(2)}}}}}}{{\partial {{{\mathbf{Q}}}^{2}}}}} \right\rangle }}_{0}}} \\ {\text{ = }} - \,\,4m\frac{{{{A}_{{ij}}}{\text{(}}L{\text{)}}}}{{\xi }}\left\langle {{{L}_{j}}(2m + 2)} \right\rangle , \\ {\text{ }}{{A}_{{ij}}}{\text{(}}{\mathbf{L}}{\text{)}} = (3{{c}_{2}} - 1)\left( {\frac{{P_{{ij}}^{\parallel }}}{{3 + {{c}_{2}}}} - \frac{{P_{{ij}}^{ \bot }}}{{7 - {{c}_{2}}}}} \right). \\ \end{gathered} $$

Taking into account all the above-derived components of the field-related and isotropic parts, the equation for the orthogonal odd moments acquires the following form:

$$\begin{gathered} \left( {\left( {{{\partial }_{t}} + (2m + 1){\tilde {\gamma }}} \right){{{\delta }}_{{ij}}} + {{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{)}}} \right)\left\langle {{{M}_{j}}(2m + 1)} \right\rangle \\ = {{{\gamma }}_{{\text{N}}}}\left( {\left\langle {{{L}_{i}}(2m + 2)} \right\rangle - \frac{2}{3}\left\langle {{{K}_{i}}(2m + 2)} \right\rangle } \right) \\ + \,\,\frac{{2m + 3}}{3}{{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{,}}{\mathbf{K}}{\text{)}}\left\langle {{{K}_{j}}(2m)} \right\rangle \\ - \,\,m{{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{,}}{\mathbf{L}}{\text{)}}\left\langle {{{L}_{j}}(2m)} \right\rangle ,\,\,\,\,m \geqslant 0, \\ {{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{,}}{\mathbf{K}}{\text{)}} = {{{\gamma }}_{{\text{D}}}}\left( {{{{\delta }}_{{ij}}} - \frac{{\text{1}}}{{\text{2}}}{{A}_{{ij}}}{\text{(}}{\mathbf{K}}{\text{)}}} \right), \\ {{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{,}}{\mathbf{L}}{\text{)}} = {{{\gamma }}_{{\text{D}}}}\left( {{{{\delta }}_{{ij}}} - 2{{A}_{{ij}}}{\text{(}}{\mathbf{L}}{\text{)}}} \right). \\ {\text{ }} \\ \end{gathered} $$

(A.15)

Let us turn to the calculation of the field-related part of the even K-moment. Initially, we find the diagonal matrix element:

$$\begin{gathered} {{\left\langle {{{K}_{j}}(2n){\mathbf{\hat {H}}}{{K}_{i}}(2m)} \right\rangle }_{0}} \\ = {{\left\langle {{\Psi }_{n}^{{{\text{(0)}}}}{{e}_{j}}\left( {{\Psi }_{m}^{{{\text{(0)}}}}{{{{\text{(}}{\mathbf{e}}\,\,{ \times }\,\,{\mathbf{k}}\,\,{ \times }\,\,{\mathbf{e}}{\text{)}}}}_{i}}} \right)} \right\rangle }_{0}} \\ = {{{\delta }}_{{nm}}}{{\left\langle {{{{\left( {{\Psi }_{n}^{{{\text{(0)}}}}} \right)}}^{{\text{2}}}}} \right\rangle }_{0}}{{A}_{{ij}}}{\text{.}} \\ \end{gathered} $$

In view of the orthogonality of the subbases, the L-component of the field-related part of the equation for the K-moment is equal to zero. To find the M-component of the equation, let us calculate the corresponding matrix element:

$$\begin{gathered} {{\left\langle {{{M}_{j}}{\text{(}}2n + 1){\mathbf{\hat {H}}}{{K}_{i}}(2m)} \right\rangle }_{0}} \\ = - 2{{\left\langle {{\Psi }_{n}^{{{\text{(2)}}}}{{M}_{j}}{{M}_{z}}{{e}_{i}}\frac{{\partial {\Psi }_{m}^{{{\text{(0)}}}}}}{{\partial {{{\mathbf{Q}}}^{{\text{2}}}}}}} \right\rangle }_{0}} \\ = - 2m{{{\delta }}_{{n,m - {\text{1}}}}}{{\left\langle {{{{\left( {{\Psi }_{n}^{{{\text{(2)}}}}} \right)}}^{{\text{2}}}}\frac{{{{{\mathbf{Q}}}^{{\text{2}}}}}}{{\text{3}}}} \right\rangle }_{0}}{{A}_{{ij}}}{\text{.}} \\ \end{gathered} $$

Let us, using the above-derived matrix elements, average the field-related part of Eq. (A.9) over nonequilibrium distribution (8). As a result, we obtain the complete equation for the orthogonal K-moment:

$$\begin{gathered} \left( {\left( {{{\partial }_{t}} + 2m{\tilde {\gamma }}} \right){{{\delta }}_{{ij}}} + {{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{K}}{\text{)}}} \right)\left\langle {{{K}_{j}}(2m)} \right\rangle \\ = {{{\gamma }}_{{\text{N}}}}\left\langle {{{M}_{i}}(2m + 1)} \right\rangle - m{{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{K}}{\text{,}}{\mathbf{M}}{\text{)}}\left\langle {{{M}_{i}}(2m - 1)} \right\rangle , \\ {{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{K}}{\text{)}} = {{{\gamma }}_{{\text{D}}}}\left( {{{{\delta }}_{{ij}}} - \frac{{\text{1}}}{{\text{2}}}{{A}_{{ij}}}{\text{(}}{\mathbf{K}}{\text{)}}} \right){\text{,}} \\ {{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{K}}{\text{,}}{\mathbf{M}}{\text{)}} = {{{\gamma }}_{{\text{D}}}}\left( {{{{\delta }}_{{ij}}} + {{A}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{)}}} \right){\text{,}}\,\,\,\,m \geqslant 1{\text{ }}.{\text{ }} \\ \end{gathered} $$

(A.16)

Now, we have only to find the field-related part of the equation of the even L-moment. To begin with, let us obtain the diagonal matrix element:

$$\begin{gathered} {{\left\langle {{{L}_{j}}(2n + 2){\mathbf{\hat {H}}}{{L}_{i}}(2m + 2)} \right\rangle }_{0}} \\ = {{\left\langle {{\Psi }_{n}^{{{\text{(4)}}}}{\Psi }_{m}^{{{\text{(4)}}}}({{Q}_{j}}{{Q}_{p}}){\kern 1pt} '{{Q}_{i}}{{Q}_{q}}{{e}_{p}}\left( {{{{{\text{(}}{\mathbf{e}}\,\,{ \times }\,\,{\mathbf{k}}\,\,{ \times }\,\,{\mathbf{e}}{\text{)}}}}_{q}}} \right)} \right\rangle }_{0}} \\ = \frac{1}{3}{{{\delta }}_{{nm}}}{{\left\langle {{{{\left( {{\Psi }_{n}^{{{\text{(4)}}}}} \right)}}^{{\text{2}}}}\frac{{{{{\mathbf{Q}}}^{{\text{4}}}}}}{{{\text{15}}}}} \right\rangle }_{{\text{0}}}}{{A}_{{ij}}}{\text{.}} \\ \end{gathered} $$

The mutual orthogonality of the subbases leads to the fact that the K-component of the field-related part of the equation for the L-moment is equal to zero. The last matrix element necessary for our calculation is

$$\begin{gathered} {{\left\langle {{{M}_{j}}(2n + 1){\mathbf{\hat {H}}}{{L}_{i}}(2m + 2)} \right\rangle }_{0}} \\ = {{\left\langle {{\Psi }_{n}^{{{\text{(2)}}}}{{M}_{j}}\left( { - 2{{L}_{i}}{{M}_{z}}\frac{{\partial {\Psi }_{m}^{{{\text{(4)}}}}}}{{\partial {{{\mathbf{Q}}}^{{\text{2}}}}}} + \frac{2}{3}{{M}_{z}}{{e}_{i}}{\Psi }_{m}^{{{\text{(4)}}}}} \right)} \right\rangle }_{0}}. \\ {\text{ }} \\ \end{gathered} $$

Averaging the anisotropic part of this expression and taking into account properties (A.4) and (A.5) of the orthogonal basis polynomials, we have

$$\begin{gathered} {{\left\langle {{{M}_{j}}(2n + 1){\mathbf{\hat {H}}}{{L}_{i}}(2m + 2)} \right\rangle }_{0}} \\ = \frac{2}{3}{{A}_{{ij}}}{{\left\langle {2m{\Psi }_{n}^{{{\text{(2)}}}}{\Psi }_{{m - {\text{1}}}}^{{{\text{(6)}}}}\frac{{{{{\mathbf{Q}}}^{{\text{4}}}}}}{{{\text{15}}}} + \Psi _{n}^{{(2)}}\Psi _{m}^{{(4)}}\frac{{{{{\mathbf{Q}}}^{{\text{2}}}}}}{{\text{3}}}} \right\rangle }_{0}} \\ = {{{\delta }}_{{nm}}}\frac{{\text{2}}}{{\text{3}}}{{A}_{{ij}}}\frac{{2m + 5}}{5}{{\left\langle {{{{\left( {{\Psi }_{n}^{{{\text{(2)}}}}} \right)}}^{{\text{2}}}}\frac{{{{{\mathbf{Q}}}^{{\text{2}}}}}}{{\text{3}}}} \right\rangle }_{0}}. \\ \end{gathered} $$

Using the expressions obtained for the matrix elements, we average the field-related part of Eq. (A.10) to derive the following equation for the even orthogonal L-moments:

$$\begin{gathered} \left( {\left( {{{\partial }_{t}} + 2m{\tilde {\gamma }}} \right){{{\delta }}_{{ij}}} + {{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{L}}{\text{)}}} \right)\left\langle {{{L}_{j}}(2m)} \right\rangle \\ = - \frac{{{{{\gamma }}_{{\text{N}}}}}}{{\text{3}}}\left\langle {{{M}_{i}}(2m + 1)} \right\rangle \\ + \,\,\frac{{2m + 3}}{6}{{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{L}}{\text{,}}{\mathbf{M}}{\text{)}}\left\langle {{{M}_{i}}{\text{(2}}m - {\text{1)}}} \right\rangle , \\ m \geqslant 1,\,\,\,\,\,{\text{ }}{{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{L}}{\text{)}} = {{{\gamma }}_{{\text{D}}}}\left( {{{{\delta }}_{{ij}}} - \frac{{\text{1}}}{{\text{2}}}{{A}_{{ij}}}{\text{(}}{\mathbf{L}}{\text{)}}} \right){\text{,}} \\ {{{\gamma }}_{{ij}}}{\text{(}}{\mathbf{L}}{\text{,}}{\mathbf{M}}{\text{)}} = {{{\gamma }}_{{\text{D}}}}\left( {{{{\delta }}_{{ij}}} + \frac{{\text{2}}}{{\text{5}}}{{A}_{{ij}}}{\text{(}}{\mathbf{M}}{\text{)}}} \right){\text{.}} \\ \end{gathered} $$

(A.17)

Now, let us summarize the results. The complete set of moment equations (A.15)–(A.17) has been derived for describing the influence of a weak probe field on the magnetization of a viscoelastic magnetic colloid in a constant magnetic field. It should be noted that the field-induced anisotropy of the system has no effect on the structure of the engagement between the moment equations; it remains the same as that in the isotropic case [22]. It has appeared that an equation for any moment contains only “neighboring” moments that are higher or lower than a given one by one order of $Q$ magnitude. Ander the action of a constant magnetic field, some coefficients in the moment equations have been transformed in matrices. All “diagonal” parts of the equations have been subjected to such renormalization. Therewith, it has appeared that this “diagonal” renormalization does not depend on the order of a moment and is completely determined by its belonging to one or another subbasis. Moreover, the field-induced anisotropy of the system has resulted in the renormalization of those parts of the moment equations that depend on the moments, the values of which are lower by unity. The calculation has shown that the anisotropy of all moment equations is completely determined by a set of four symmetric matrices $({{A}_{{ij}}}({\mathbf{B}}),{\mathbf{B}} = {\mathbf{e}}{\text{,}}{\mathbf{M}}{\text{,}}{\mathbf{K}}{\text{,}}{\mathbf{L}}),$ which satisfy the following simple relations:

$$\begin{gathered} {{{\gamma }}_{{ik}}}{\text{(}}{\mathbf{K}}{\text{,}}{\mathbf{M}}{\text{)}}{{{\gamma }}_{{kj}}}{\text{(}}{\mathbf{M}}{\text{,}}{\mathbf{K}}{\text{)}} \\ = {{{\gamma }}_{{ik}}}{\text{(}}{\mathbf{M}}{\text{,}}{\mathbf{K}}{\text{)}}{{{\gamma }}_{{kj}}}{\text{(}}{\mathbf{K}}{\text{,}}{\mathbf{M}}{\text{)}} = {\gamma }_{{\text{D}}}^{{\text{2}}}{{{\delta }}_{{ij}}}{\text{,}} \\ {{{\gamma }}_{{ik}}}{\text{(}}{\mathbf{L}}{\text{,}}{\mathbf{M}}{\text{)}}{{{\gamma }}_{{kj}}}{\text{(}}{\mathbf{M}}{\text{,}}{\mathbf{L}}{\text{)}} \\ = {{{\gamma }}_{{ik}}}{\text{(}}{\mathbf{M}}{\text{,}}{\mathbf{L}}{\text{)}}{{{\gamma }}_{{kj}}}{\text{(}}{\mathbf{L}}{\text{,}}{\mathbf{M}}{\text{)}} = {\gamma }_{{\text{D}}}^{{\text{2}}}{{{\delta }}_{{ij}}}{\text{.}} \\ \end{gathered} $$

(A.18)

The direct calculation confirms the validity of these equations.

One more important property of the obtained set of equations should be noted: a probe field is present only in the two first equations of the infinite chain of the moment equations, as well as in the case of an isotropic system [22]. In addition to symmetry condition (A.18) and engagement of equations only with the moments “neighboring” with respect to their parity, this property proves the validity of the chosen functional basis.