Existence and uniqueness of dynamic evolutions for a one-dimensional debonding model with damping

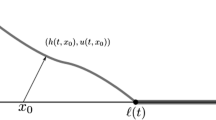
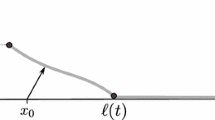
Abstract

In this paper we analyse a one-dimensional debonding model when viscosity is taken into account. It is described by the weakly damped wave equation whose domain, the debonded region, grows according to a Griffith’s criterion. Firstly we prove that the equation admits a unique solution when the evolution of the debonding front is assigned. Finally we provide an existence and uniqueness result for the coupled problem given by the wave equation together with Griffith’s criterion.

Appendix A: Chain rule and Leibniz differentiation rule

In this “Appendix” we gather some results about the Chain rule and the Leibniz differentiation rule under low regularity assumptions. These results have been used throughout the paper, and they are of some interest on their own.

For the sake of brevity we assume that in all the statements the function $\varphi$ is nondecreasing (or strictly increasing), although they are still valid if $\varphi$ is nonincreasing (or strictly decreasing), with little changes in the proofs.

Lemma A.1

(Change of variables formula) Let $\varphi \in C^{0,1}([a,b])$ be nondecreasing. Then for every nonnegative and measurable function g on $[\varphi (a),\varphi (b)]$ (and hence for every $g\in L^1(\varphi (a),\varphi (b)$), it holds

$$\begin{aligned} \int _{\varphi (a)}^{\varphi (b)}g(y)\,\mathrm {d}y=\int _{a}^{b}g(\varphi (s))\dot{\varphi }(s)\,\mathrm {d}s. \end{aligned}$$

(A.1)

Remark A.2

In general the expression $g(\varphi (s))\dot{\varphi }(s)$ in (A.1) has to be meant replacing g by a Borel function $\tilde{g}$ equal to g a.e. in $[\varphi (a),\varphi (b)]$ and finite everywhere (if g is finite a.e.); in the particular case in which $\dot{\varphi }(t)>0$ for a.e. $t\in [a,b]$ that expression is meaningful without modifications on sets of measure zero (see Corollary A.4).

Proof of Lemma A.1

If $\varphi$ is strictly increasing, hence injective, the result is well known. If not, by the area formula for Lipschitz maps (see [14], Corollary 5.1.13) we have

$$\begin{aligned} \int _{\varphi (a)}^{\varphi (b)}g(y)\#\varphi ^{-1}(\{y\})\,\mathrm {d}y=\int _{a}^{b}g(\varphi (s))\dot{\varphi }(s)\,\mathrm {d}s. \end{aligned}$$

(A.2)

We conclude if we prove that $\#\varphi ^{-1}(\{y\})=1$ for a.e. $y\in [\varphi (a),\varphi (b)]$.

Since $\varphi$ is nondecreasing and continuous, for every $y\in [\varphi (a),\varphi (b)]$ the set $\varphi ^{-1}(\{y\})$ can be either a singleton either a closed interval, so $\#\varphi ^{-1}(\{y\})\in \{1,+\infty \}$. Taking $g\equiv 1$ in (A.2) we deduce

$$\begin{aligned} +\infty >\varphi (b)-\varphi (a)=\int _{a}^{b}\dot{\varphi }(s)\,\mathrm {d}s= \int _{\varphi (a)}^{\varphi (b)}\#\varphi ^{-1}(\{y\})\,\mathrm {d}y. \end{aligned}$$

This yields $\#\varphi ^{-1}(\{y\})<+\infty$ for a.e. $y\in [\varphi (a),\varphi (b)]$ and so necessarily $\#\varphi ^{-1}(\{y\}) =1$ a.e..

As an alternative proof we notice that the set $\{y\in [\varphi (a),\varphi (b)]\mid \#\varphi ^{-1}(\{y\})=+\infty \}$ is in bijection with a subset of rational numbers, so it is countable and hence of measure zero. $\square$

Remark A.3

Formula (A.1) still holds true only assuming that $\varphi$ is absolutely continuous on [a, b] (and nondecreasing), see Theorem 7.26 in [26]. This ensures that every result in this “Appendix” is valid replacing the assumption $\varphi \in C^{0,1}([a,b])$ by $\varphi \in AC([a,b])$; indeed the reader can easily check that the only ingredient needed to carry out all the proofs is (A.1).

Corollary A.4

Let $\varphi \in C^{0,1}([a,b])$ be nondecreasing, and let $N\subset [\varphi (a),\varphi (b)]$ be a set of measure zero. Then the set $M=\{t\in \varphi ^{-1}(N)\mid \dot{\varphi }(t)\text { exists and }\dot{\varphi }(t)>0\}$ has measure zero as well. In particular, if $\dot{\varphi }(t)>0$ for a.e. $t\in [a,b]$, then $\varphi ^{-1}$ maps sets of measure zero in sets of measure zero.

Proof

Let $N\subset [\varphi (a),\varphi (b)]$ be a set of measure zero; then by Lemma A.1

$$\begin{aligned} 0=\int _{\varphi (a)}^{\varphi (b)}\chi _N(y)\,\mathrm {d}y=\int _{a}^{b}\chi _N(\varphi (s))\dot{\varphi }(s)\,\mathrm {d}s=\int _{\varphi ^{-1}(N)}^{}\dot{\varphi }(s)\,\mathrm {d}s=\int _{M}^{}\dot{\varphi }(s)\,\mathrm {d}s. \end{aligned}$$

Since by construction $\dot{\varphi }(t)>0$ for every $t\in M$, we deduce that the set M has measure zero. $\square$

Corollary A.5

Let $\varphi \in C^{0,1}([a,b])$ be a strictly increasing function such that $\dot{\varphi }(t)>0$ for a.e. $t\in [a,b]$. Then $\varphi ^{-1}$ belongs to $AC([\varphi (a),\varphi (b)])$ and $\displaystyle \frac{\,\mathrm {d}}{\,\mathrm {d}x}(\varphi ^{-1})(x)=\frac{1}{\dot{\varphi }(\varphi ^{-1}(x))}$ for a.e. $x\in [\varphi (a),\varphi (b)]$.

Proof

Firstly we notice that Lemma A.1 ensures that $\displaystyle \frac{1}{\dot{\varphi }\circ \varphi ^{-1}}$ belongs to $L^1(\varphi (a), \varphi (b)$:

$$\begin{aligned} \int _{\varphi (a)}^{\varphi (b)}\frac{1}{\dot{\varphi }(\varphi ^{-1}(y))}\,\mathrm {d}y=\int _{a}^{b}\frac{1}{\dot{\varphi }(s)}\dot{\varphi }(s)\,\mathrm {d}s=b-a<+\infty . \end{aligned}$$

Moreover for every $x\in [\varphi (a),\varphi (b)]$

$$\begin{aligned} \varphi ^{-1}(x)-\varphi ^{-1}(\varphi (a))=\int _{a}^{\varphi ^{-1}(x)}\,\mathrm {d}s=\int _{a}^{\varphi ^{-1}(x)}\frac{\dot{\varphi }(s)}{\dot{\varphi }(s)}\,\mathrm {d}s=\int _{\varphi (a)}^{x}\frac{1}{\dot{\varphi }(\varphi ^{-1}(y))}\,\mathrm {d}y, \end{aligned}$$

so we conclude. $\square$

Lemma A.6

(Chain rule) Let $\varphi \in C^{0,1}([a,b])$ be nondecreasing, and let $\phi \in AC([\varphi (a),\varphi (b)])$. Then $\phi \circ \varphi$ belongs to AC([a, b]) and $\frac{\,\mathrm {d}}{\,\mathrm {d}t}(\phi \circ \varphi )(t)=\dot{\phi }(\varphi (t))\dot{\varphi }(t)$ for a.e. $t\in [a,b]$, where the right-hand side is meant as in Remark A.2.

Proof

Since $\phi \in AC([\varphi (a),\varphi (b)])$, Lemma A.1 ensures that $\dot{\phi }(\varphi (\cdot ))\dot{\varphi }(\cdot )$ belongs to $L^1(a,b)$. Moreover for every $t\in [a,b]$

$$\begin{aligned} \phi (\varphi (t))-\phi (\varphi (a))=\int _{\varphi (a)}^{\varphi (t)}\dot{\phi }(y)\,\mathrm {d}y=\int _{a}^{t}\dot{\phi }(\varphi (s))\dot{\varphi }(s)\,\mathrm {d}s, \end{aligned}$$

so we conclude. $\square$

Remark A.7

With a similar proof one can show that if $\phi \in W^{1,p}(\varphi (a),\varphi (b))$ for $p\in [1,+\infty ]$, then $\phi \circ \varphi \in W^{1,p}(a,b)$ and the same formula for the derivative holds. In contrast with Remark A.3, for the validity of this fact we cannot replace $\varphi \in C^{0,1}([a,b])$ by $\varphi \in AC([a,b])$.

Theorem A.8

(Leibniz differentiation rule) Let $\varphi \in C^{0,1}([0,T])$ be nondecreasing and let $a\le \varphi (0)$. Consider the set $\Omega _T^\varphi :=\{(t,y)\mid 0\le t\le T,\,a\le y\le \varphi (t)\}$ and let $f:\Omega _T^\varphi \rightarrow \mathbb {R}$ be a measurable function such that:

• ((a) for every $t\in [0,T]$ it holds $f(t,\cdot )\in L^1(a,\varphi (t))$,

• (b) for a.e. $y\in [a,\varphi (T)]$ it holds $f(\cdot ,y)\in AC(I_y)$, where $I_y=\{t\in [0,T]\mid y\le \varphi (t) \}$,

• (c) the partial derivative $\displaystyle \frac{\partial f}{\partial t}(t,y):=\lim \limits _{h\rightarrow 0}\frac{f(t+h,y)-f(t,y)}{h}$ (which for a.e. $y\in [a,\varphi (T)]$ is well defined for a.e. $t\in I_y$) is summable in $\Omega _T^\varphi$.

Then the function $F(t):=\displaystyle \int _{a}^{\varphi (t)}f(t,y)\,\mathrm {d}y$ belongs to AC([0, T]) and moreover for a.e. $t\in [0,T]$

$$\begin{aligned} \dot{F}(t)=f(t,\varphi (t))\dot{\varphi }(t)+\int _{a}^{\varphi (t)}\frac{\partial f}{\partial t}(t,y)\,\mathrm {d}y. \end{aligned}$$

(A.3)

Proof

To conclude we need to prove two things :

• (1) The right-hand side in (A.3) belongs to $L^1(0,T)$.

• (2) $\displaystyle F(t)=\int _{a}^{\varphi (T)}f(T,y)\,\mathrm {d}y-\int _{t}^{T}f(s,\varphi (s))\dot{\varphi }(s)\,\mathrm {d}s-\int _{t}^{T}\int _{a}^{\varphi (s)}\frac{\partial f}{\partial t}(s,y)\,\mathrm {d}y\,\mathrm {d}s$, for every $t\in [0,T]$.

To prove (1) notice that the integral part in the formula belongs to $L^1(0,T)$ by (c) and Fubini’s theorem. To ensure that also $f(\cdot ,\varphi (\cdot ))\dot{\varphi }(\cdot )\in L^1(0,T)$ we argue as follows:

• By (b) we know that for a.e. $y\in [a,\varphi (T)]$ it holds $\displaystyle f(t,y)=f(T,y)-\int _{t}^{T}\frac{\partial f}{\partial t}(s,y)\,\mathrm {d}s$ for every $t\in I_y$,

• since $\varphi$ is continuous and nondecreasing we know that for a.e. $y\in [\varphi (0),\varphi (T)]$ there exists a unique element of [0, T], denoted by $\varphi ^{-1}(y)$, such that $\varphi (\varphi ^{-1}(y))=y$ (see the proof of Lemma A.1).

Hence $f(\varphi ^{-1}(y),y)=f(T,y)-\displaystyle \int _{\varphi ^{-1}(y)}^{T}\frac{\partial f}{\partial t}(s,y)\,\mathrm {d}s$ for a.e $y\in [\varphi (0),\varphi (T)]$, and so

$$\begin{aligned} \int _{\varphi (0)}^{\varphi (T)}|f(\varphi ^{-1}(y),y)|\,\mathrm {d}y&\le \int _{\varphi (0)}^{\varphi (T)}|f(T,y)|\,\mathrm {d}y+\int _{\varphi (0)}^{\varphi (T)}\int _{\varphi ^{-1}(y)}^{T}\left| \frac{\partial f}{\partial t}\right| (s,y)\,\mathrm {d}s\,\mathrm {d}y\\&\le \Vert f(T,\cdot )\Vert _{L^1(a,\varphi (T))}+\left\| \frac{\partial f}{\partial t}\right\| _{L^1(\Omega _T^\varphi )}<+\infty . \end{aligned}$$

Using Lemma A.1 and recalling Corollary A.4, we deduce:

$$\begin{aligned} +\infty >\int _{\varphi (0)}^{\varphi (T)}|f(\varphi ^{-1}(y),y)|\,\mathrm {d}y=\int _{0}^{T}|f(s,\varphi (s))|\dot{\varphi }(s)\,\mathrm {d}s. \end{aligned}$$

Now we prove (2). Fix $t\in [0,T]$, then

$$\begin{aligned} F(t)&=\int _{a}^{\varphi (t)}f(t,y)\,\mathrm {d}y=\int _{a}^{\varphi (t)}f(T,y)\,\mathrm {d}y-\int _{a}^{\varphi (t)}\int _{t}^{T} \frac{\partial f}{\partial t}(s,y)\,\mathrm {d}s\,\mathrm {d}y\\&=\int _{a}^{\varphi (T)}f(T,y)\,\mathrm {d}y-\int _{\varphi (t)}^{\varphi (T)}f(T,y)\,\mathrm {d}y-\int _{t}^{T}\int _{a}^{\varphi (t)} \frac{\partial f}{\partial t}(s,y)\,\mathrm {d}y\,\mathrm {d}s\\&=\int _{a}^{\varphi (T)}f(T,y)\,\mathrm {d}y-\int _{t}^{T}\int _{a}^{\varphi (s)}\frac{\partial f}{\partial t}(s,y)\,\mathrm {d}y\,\mathrm {d}s-\int _{\varphi (t)}^{\varphi (T)}f(T,y)\,\mathrm {d}y\\&\quad +\,\int _{t}^{T}\int _{\varphi (t)}^{\varphi (s)}\frac{\partial f}{\partial t}(s,y)\,\mathrm {d}y\,\mathrm {d}s. \end{aligned}$$

So we conclude if we prove $\displaystyle -\int _{\varphi (t)}^{\varphi (T)}f(T,y)\,\mathrm {d}y+\int _{t}^{T}\int _{\varphi (t)}^{\varphi (s)}\frac{\partial f}{\partial t}(s,y)\,\mathrm {d}y\,\mathrm {d}s=-\int _{t}^{T}f(s,\varphi (s))\dot{\varphi }(s)\,\mathrm {d}s$. This is true by the following computation:

$$\begin{aligned} \int _{t}^{T}\int _{\varphi (t)}^{\varphi (s)}\frac{\partial f}{\partial t}(s,y)\,\mathrm{d}y\,\mathrm{d}s&=\int _{\varphi (t)}^{\varphi (T)}\int _{\varphi ^{-1}(y)}^{T}\frac{\partial f}{\partial t}(s,y)\,\mathrm{d}s\,\mathrm {d}y\\&=\int _{\varphi (t)}^{\varphi (T)}f(T,y)\,\mathrm{d}y-\int _{\varphi (t)}^{\varphi (T)}f(\varphi ^{-1}(y),y)\,\mathrm{d}y\\&=\int _{\varphi (t)}^{\varphi (T)}f(T,y)\,\mathrm{d}y-\int _{t}^{T}f(s,\varphi (s))\dot{\varphi }(s)\,\mathrm{d}s. \end{aligned}$$

All the equalities are justified by part (1), Lemma A.1 and Corollary A.4. $\square$

Remark A.9

We can replace assumption (a) in Theorem A.8 by the weaker

a’:

$f(T,\cdot )\in L^1(a,\varphi (T))$.

Indeed exploiting (b) and (c) one can recover (a) from (a$'$).

Remark A.10

If for some $p\in [1,+\infty ]$ the function f in Theorem A.8 satisfies

$\alpha$:

$f(t,\cdot )\in L^p(a,\varphi (t))$ for every $t\in [0,T]$,

$\beta$:

$f(\cdot ,y)\in W^{1,p}(I_y)$ for a.e. $y\in [a,\varphi (T)]$,

$\gamma$:

$\displaystyle \frac{\partial f}{\partial t}\in L^p(\Omega _T^\varphi )$,

then the function F belongs to $W^{1,p}(0,T)$ and the same formula for the derivative holds. As in Remark A.7, for the validity of this fact we cannot replace $\varphi \in C^{0,1}([a,b])$ by $\varphi \in AC([a,b])$.