Abstract
We consider an infinite horizon control problem for dynamics constrained to remain on a multidimensional junction with entry costs. We derive the associated system of Hamilton–Jacobi equations (HJ), prove the comparison principle and that the value function of the optimal control problem is the unique viscosity solution of the HJ system. This is done under the usual strong controllability assumption and also under a weaker condition, coined ‘moderate controllability assumption’.
Similar content being viewed by others
1 Introduction
In this paper, we consider an infinite horizon control problem for the dynamics of an agent constrained to remain on a multidimensional junction on \({\mathbb {R}}^3\), i.e. a union of \(N\ge 2\) half-planes \({\mathcal {P}}_i\) which share a straight line \(\Gamma \), see Fig. 2. The controlled dynamics are given by a system of ordinary differential equations, where in each \( {\mathcal {P}}_i \) it is given by a drift \(f_i(\cdot ,\cdot )\) and to which is associated a running cost \(\ell _i(\cdot ,\cdot )\). Moreover, the agent pays a cost \(c_i(\cdot )\) each time it enters the half-plane \({\mathcal {P}}_i\) from \(\Gamma \). The goal of this work is to study the properties of the value function of this control problem and derive the associated Hamilton–Jacobi equation (HJ) under some regularity conditions on the involved dynamics, running and entry cost functions. Although we will not discuss it in this paper, the optimal control problem with exit costs, i.e. instead of paying an entry cost each time the agent enters the half-plane, it pays a cost each time it exits it, can be solved similarly. Oudet [25] considers a similar optimal control problem but without entry or exit costs from the interface to the half-planes.
When the interface \(\Gamma \) is reduced to a point, the junction becomes a simple network with one vertex, i.e. a 1-dimensional junction. Optimal control problems (without entry costs) in which the set of admissible states are networks attracted a lot of interest in recent years. Being among the first papers discussing this topic, Achdou et al. [2], derived an HJ equation associated to an infinite horizon optimal control on networks and proposed a suitable notion of viscosity solutions, where the admissible test-functions whose restriction to each edge are \( C^1 \) are applied. Independently and at the same time, Imbert et al. [18] proposed an equivalent notion of viscosity solution for studying an HJ approach to junction problems and traffic flows. Both [2] and [18] contain first results on the comparison principle. In the particular case of eikonal equations on networks, Schieborn and Camilli [26] considered a less general notion of viscosity solution. For that later case, Camilli and Marchi [12] showed the equivalence between the definitions notion of viscosity solution given in [2, 18] and [26]. Optimal control on networks with entry costs (and exit costs) has recently been considered by the first author [14].
An important feature of the effect of the entry costs is a possible discontinuity of the value function. Discontinuous solutions of HJ equations have been studied by various authors, see for example Barles [5] for general open domains in \( {\mathbb {R}}^d \), Frankowska and Mazzola [15] for state constraint problems, and in particular Graber et al. [16] for a class of HJ equations on networks.
In the case considered in the present work, the effect of entry costs induces a discontinuity of the value function \( {\mathcal {V}}\) at the interface \(\Gamma \), while it is still continuous on each \( {\mathcal {P}}_i \backslash \Gamma \). This allows us to adopt the techniques which apply to the continuous solution case in the works of Barles et al. [7] and Oudet [25], where we split the value function \({\mathcal {V}}\) into the collection \(\{v_1,\ldots ,v_N\}\) of functions, where each \( v_i \) is continuous function defined on \( {\mathcal {P}}_i \) and satisfies
We note that the existence of the limit in the above formula comes from the fact that the value functions is Lipschitz continuous on the neighborhood of \( \Gamma \) (see Lemma 3.3), thanks to the ’strong controllability assumption’, which is introduced below. The first main result of the present work is to show that \((v_1,\ldots ,v_N,{\mathcal {V}}|_\Gamma )\) is a viscosity solution of the following system
where \( H_i \) is the Hamiltonian corresponding to the half-plane \( {\mathcal {P}}_i \), \( {\mathcal {V}}|_\Gamma \) is the restriction of our value function on the interface and \( H_{\Gamma } \) is the Hamiltonian defined on \(\Gamma \). At \(x \in \Gamma \), the definition of the Hamiltonian has to be particular, in order to consider all the possibilities when x is in the neighborhood of \( \Gamma \). More specifically,
the term \( H_i^+ \left( x, \partial u_i (x) \right) \) accounts for the situation in which the trajectory does not leave \( {\mathcal {P}}_i \),
the term \( \min _{i=1,\ldots ,N} \{v_i (x) + c_i(x) \} \) accounts for situations in which the trajectory enters \({\mathcal {P}}_k\) where \( v_k(x) + c_k(x) = \min _{i=1,\ldots ,N} \{v_i (x) + c_i(x) \} \),
the term \( H_\Gamma (x,\frac{\partial {\mathcal {V}}|_\Gamma }{\partial e_0} (x)) \) accounts for situations in which the trajectory remains on \( \Gamma \).
This feature is quite different from the one induced by the effect of entry costs in a network (i.e. when \(\Gamma \) is reduced to a point) considered in [14], where the value function at the junction point is a constant which is the minimum of the cost when the trajectory stays at the junction point forever and the cost when the trajectory enters immediately the edge that has the lowest possible cost.
The paper is organized as follows. In Sect. 2, we formulate the optimal control problem on a multidimensional junction on \({\mathbb {R}}^3\) with entry cost. In Sect. 3, we study the control problem under the strong controllability condition, where we derive the system of HJ equations associated with the optimal control problem, propose a comparison principle, which leads to the well-posedness of (1.1)–(1.3), and prove that the value function of the optimal control problem is the unique discontinuous solution of the HJ system. We suggest two different proofs of the comparison principle. The first one is inspired from the work by Lions and Souganidis [21] and uses arguments from the theory of PDEs, and the second one uses a blend of arguments from optimal control theory and PDE techniques suggested in [3, 7, 8] and [25]. Finally, in Sect. 4, the same program is carried out when the strong controllability is replaced by the weaker one that we coin ’moderate controllability near the interface’. The proof of the comparison principle under the moderate controllability condition is carried on by only using the PDE techniques provided in Lions and Souganidis [21].
The results obtained in the present work extend easily to multidimensional junction on \({\mathbb {R}}^d\), i.e. a union of \(N\ge 2\) half-hyperplanes \({\mathcal {P}}_i\) which share an affine space \(\Gamma \) of dimension \( d-2 \), and to the more general class of ramified sets, i.e. closed and connected subsets of \({\mathbb {R}}^d\) obtained as the union of embedded manifolds with dimension strictly less than d, for which the interfaces are non-intersecting manifolds of dimension \(d-2\), see Fig. 1a for example. We do not know whether these results apply to the ramified sets for which interfaces of dimension \( d-2 \) cross each other (see Fig. 1b). Recent results on optimal control and HJ equations on ramified sets include Bressan and Hong [11], Camilli et al. [13], Nakayasu [24] and Hermosilla and Zidani [17] and the book of Barles and Chasseigne [9].
2 Formulation of the control problem on a junction
2.1 The geometry of the state of the system
Let \(\left\{ e_{i}\right\} _{0\le i\le N}\) be distinct unit vectors in \(\mathbb {R}^{3}\) such that \(\ e_i \cdot e_0 =0\) for all \(i\in \left\{ 1,\ldots ,N\right\} \). The state of the system is given by the junction \(\mathcal {S}\) which is the union of N closed half-planes \(\mathcal {P}_{i}=\mathbb {R}e_{0}\times \mathbb {R}^{+}e_{i}\). The half-planes \(\mathcal {P}_{i}\) are glued at the straight line \(\Gamma :=\mathbb {R}e_{0}\) (see Fig. 2).
If \(x\in {\mathcal {S}}\backslash \Gamma \), there exist unique \(i\in \left\{ 1,\ldots ,N\right\} \), \(x_i>0\) and \(x_0\in {\mathbb {R}}\) such that
Let \(x=(x^i,x^0)\in {\mathcal {P}}_i\) and \(y=(y^j,y^0)\in {\mathcal {P}}_j\), the geodesic distance d(x, y) between two points \(x,y\in {\mathcal {S}}\) is
2.2 The optimal control problem
We consider an infinite horizon optimal control problem which has different dynamics and running costs for each half-plane. For \(i=1,\ldots ,N\),
the set of controls (action set) on \({\mathcal {P}}_i\) is denoted by \(A_i\),
on \({\mathcal {P}}_i\) the dynamics of the system is deterministic with associated dynamic \(f_i\),
the agent has to pay the running cost \(\ell _i\) while (s)he is on \({\mathcal {P}}_i\).
The following conditions, referred to as [A] hereafter, are our standing assumptions throughout the paper.
- [A0]:
Control sets. Let A be a metric space (for example \(A=\mathbb {R}^d\)). For \(i=1,\ldots , N\), \( A_i \) is a nonempty compact subset of A and the sets \(A_{i}\) are disjoint.
- [A1]:
Dynamics and running costs. For \(i=1,\ldots ,N\), the functions \(\ell _i:{\mathcal {P}}_i\times A_{i}\rightarrow \mathbb {R}\) and \( f_{i}: {\mathcal {P}}_i\times A_{i} \rightarrow {\mathbb {R}}^3 \) are continuous and bounded by M. Moreover, there exists \(L>0\) such that
$$\begin{aligned} \left| f_{i}\left( x,a\right) -f_{i}\left( y,a\right) \right| ,~ \left| \ell _{i}\left( x,a\right) -\ell _{i}\left( y,a\right) \right| \le L\left| x-y\right| ,\quad \hbox { for all } x,y\in {\mathcal {P}}_i, a\in A_{i}. \end{aligned}$$Hereafter, we will use the notation
$$\begin{aligned} F_{i}\left( x\right) :=\left\{ f_{i}\left( x,a\right) :a\in A_{i}\right\} . \end{aligned}$$Entry costs.\(\left\{ c_1,\ldots ,c_N\right\} \) is a set of entry cost functions, where \(c_i: \Gamma \rightarrow {\mathbb {R}}^+\) is Lipschitz continuous and bounded from below by some positive constant C.
- [A2]:
Convexity of dynamics and costs. For \(x\in {\mathcal {P}}_i\), the following set
$$\begin{aligned} \textsc {FL}_{i}\left( x\right) :=\left\{ \left( f_{i}\left( x,a\right) ,\ell _{i}\left( x,a\right) \right) :a\in A_{i}\right\} \end{aligned}$$is non empty, closed and convex.
Remark 2.1
In [A0], the assumption that the set \(A_i\) are disjoint is not restrictive since we can always replace \(A_i\) by \({\tilde{A}}_i=A_i\times \left\{ i\right\} \). Assumption [A2] is made to avoid the use of relaxed control (see the definition for relaxed control in [4]). Many of these conditions can be weakened at the cost of keeping the presentation of the results easy to follow.
2.2.1 Controlled dynamics
Let \({\mathcal {M}}\) be the closed set given by
and define the function f on \({\mathcal {M}}\) by
The function f is continuous on \({\mathcal {M}}\) since the sets \(A_{i}\) are disjoint. Consider the set \({\tilde{F}}\left( x\right) \) which contains all the ’possible speeds’ at x defined by
For \(x\in {\mathcal {S}}\), the set of admissible trajectories starting from x is
Thanks to the Filippov implicit function lemma (see [23]), it is shown in [25, Theorems 3.2.2 and 3.3.1] that under the respective assumptions [A3] and \([{\tilde{A}}3]\) below, the set \(Y_x\) is not empty. We introduce the set of admissible controlled trajectories starting from x
where \( \left( y_{x},\alpha \right) \in L_{loc}^{\infty }\left( \mathbb {R}^{+};\mathcal {M}\right) \) means \( t\mapsto \left( y_{x} (t),\alpha (t)\right) \in L_{loc}^{\infty }\left( \mathbb {R}^{+};\mathcal {M}\right) \). We note that if \((y_x,\alpha )\in {\mathcal {T}}_x\) then \(y_x\in Y_x\). Thus, from now on, we will denote \(y_x\) by \(y_{x,\alpha }\) if \((y_x,\alpha )\in {\mathcal {T}}_x\). By continuity of the trajectory \(y_{x,\alpha }\), the set \(T^{\Gamma }_{x,\alpha }:=\left\{ t\in {\mathbb {R}}^+: y_{x,\alpha }(t)\in \Gamma \right\} \) containing all the times at which the trajectory stays on \(\Gamma \) is closed and therefore, the set \(T^{i}_{x,\alpha }:=\left\{ t\in {\mathbb {R}}^+: y_{x,\alpha }(t)\in {\mathcal {P}}_i \backslash \Gamma \right\} \) is open. Consequently, \(T^{i}_{x,\alpha }\) is a countable union of disjoint open intervals
where \(K_{i}=\left\{ 1,\ldots ,n\right\} \) if the trajectory \(y_{x,\alpha }\) enters \({\mathcal {P}}_i\)n times, \(K_{i}=\mathbb {N}\) if the trajectory \(y_{x,\alpha }\) enters \({\mathcal {P}}_i\) infinite times and \( K_i = \emptyset \) if the trajectory never enters \( {\mathcal {P}}_i \).
Remark 2.2
From the previous definition, we see that \(t_{ik}\) is an entry time in \({\mathcal {P}}_i \backslash \Gamma \) and \(\eta _{ik}\) is an exit time from \({\mathcal {P}}_i \backslash \Gamma \). Hence
We now define a cost functional and a value function corresponding to the optimal problem.
2.2.2 Cost functional and value function
Definition 2.3
The cost functional associated to the trajectory \((y_x,\alpha )\in {\mathcal {T}}_x\) is defined by
where \( \lambda >0 \) and the running cost \(\ell : {\mathcal {M}}\rightarrow {\mathbb {R}}\) is
The value function of the infinite horizon optimal control problem is defined by
Remark 2.4
By the definition of the value function, we are mainly interested in admissible control laws \(\alpha \) for which \(J(x,\alpha )<+\infty \). In such a case, even if the set \(K_i\) may be infinite, it is possible to reorder \(\left\{ t_{ik},\eta _{ik}:k\in {\mathbb {N}}\right\} \) such that
and
Indeed, because of the positivity of the entry cost functions, if there exists a cluster point, \(J(x,\alpha )\) has to be infinite which leads to a contradiction, since we assumed that \(J(x,\alpha )<+\infty \). This means that the state cannot switch half-planes infinitely many times in finite time, otherwise the cost functional becomes obviously infinite.
The following example shows that the value function with entry costs can possibly be discontinuous at the interface \(\Gamma \).
Example 2.5
Consider a simple junction \( {\mathcal {S}}\) with two half-planes \( {\mathcal {P}}_1\) and \( {\mathcal {P}}_2 \). To simplify, we may identify \( {\mathcal {S}}\equiv {\mathbb {R}}^2 \) and \({\mathcal {P}}_1= {\mathbb {R}}^+ e_1 \times {\mathbb {R}}e_0 \equiv (-\infty , 0] \times {\mathbb {R}}\), \({\mathcal {P}}_2 = {\mathbb {R}}^+ e_2 \times {\mathbb {R}}e_0 \equiv [0, +\infty ) \times {\mathbb {R}}\) and \(\Gamma = {\mathbb {R}}e_0 \equiv \{0\} \times {\mathbb {R}}\). The control sets are \(A_i=\left\{ (a_i,a_0)\in {\mathbb {R}}^2 : a_0^2+a_i^2\le 1\right\} \) with \(i\in \left\{ 1,2\right\} \). Set
and entry costs functions \(c_1\equiv C_1\), where \(C_1\) is a positive constant and
For \(x\in {\mathcal {P}}_2\backslash \Gamma \), then \({\mathcal {V}}(x)=v_2(x)=0\) with optimal strategy which consists of choosing \(\alpha \equiv (a_2 = 1, a_0 = 0)\). For \(x\in {\mathcal {P}}_1\), we can check that
If \( 2\ge 1/\lambda \), then \( {\mathcal {V}}(x) = 1/\lambda \) with optimal control law \( \alpha \equiv (a_1 = 0, a_0 = 1) \).
If \( 2<1/\lambda \), we consider \( x= (x_1,x_0) \in {\mathcal {P}}_i \) in two cases:
- Case 1::
If \( |x_1| \ge 1 \), then the optimal control law \( \alpha (t) = (a_1= -1, a_0 =0)\) if \( t\le |x_1| \) and \( \alpha (t) = (a_2 = 1, a_0 = 0) \) if \( t\ge |x_1| \) and
$$\begin{aligned} {\mathcal {V}}(x) = \int ^{|x_1|}_0 1 dt + c_2 ((0,x_1)) e^{-\lambda |x_1|}+0 = \dfrac{1-e^{-\lambda |x_1|} }{\lambda } +2e^{-\lambda |x_1|}. \end{aligned}$$The optimal trajectory starting from \( x = (x_1,x_0) \in {\mathcal {P}}_1 \) in case \( |x_1|\ge 1 \) is plotted in red in Fig. 3.
- Case 2::
If \( |x_1| \le 1 \), let \( \tau (x) = \left( |x_1|^2 +|x_0 - 1|^2\right) ^{1/2} \) and \( s: [-1,1] \rightarrow {\mathbb {R}}\) where \( s(\zeta ) =1 \) if \( \zeta \ge 0 \) and \( s(\zeta ) =-1 \) if \( \zeta < 0 \). We have the optimal control law
$$\begin{aligned} \alpha (t) = {\left\{ \begin{array}{ll} \left( a_1 = -\dfrac{x_1}{\tau (x)}, a_0 = \dfrac{1 - x_0}{\tau (x)}\right) , &{} t\le \tau (x),\\ (a_2 = 1, a_0 = 0), &{} t\ge \tau (x). \end{array}\right. } \end{aligned}$$and the value function
$$\begin{aligned} {\mathcal {V}}(x)= \int ^{\tau (x)}_0 1 dt + c_2 ( (0,s(x_1)) ) e^{-\lambda }+0= \frac{1-e^{-\lambda \tau (x)}}{\lambda }+ 2 e^{-\lambda \tau (x)}. \end{aligned}$$The optimal trajectory starting from \( x = (x_1,x_0) \in {\mathcal {P}}_1 \) in case \( |x_1|< 1 \) is plotted in blue in Fig. 3.
To sum up, there are two cases
- 1.
If \(\displaystyle \inf _{x\in \Gamma }c_2(x) = 2 \ge 1/\lambda \), then
$$\begin{aligned} {\mathcal {V}}(x)= {\left\{ \begin{array}{ll} 0 &{} \text {if } x\in {\mathcal {P}}_2 \backslash \Gamma ,\\ \dfrac{1}{\lambda } &{} \text {if } x\in {\mathcal {P}}_1. \end{array}\right. } \end{aligned}$$The graph of the value function with entry costs satisfying \( \inf _{x\in \Gamma } c_2(x) \ge 1/\lambda \) is plotted in Fig. 4a.
- 2.
If \(\displaystyle \inf _{x\in \Gamma }c_2(x) = 2 <1/\lambda \), then
$$\begin{aligned} {\mathcal {V}}(x)= {\left\{ \begin{array}{ll} 0 &{} \text {if } x\in {\mathcal {P}}_2 \backslash \Gamma ,\\ \dfrac{1-e^{-\lambda |x_1| }}{\lambda }+ 2 e^{-\lambda |x_1| } &{} \text {if } x\in {\mathcal {P}}_1\text { and } |x_1| \ge 1,\\ \dfrac{1-e^{-\lambda \left( |x_1|^2 +|x_0 - 1|^2\right) ^{1/2} }}{\lambda }+ 2 e^{-\lambda \left( |x_1|^2 +|x_0 - 1|^2\right) ^{1/2} } &{} \text {if } x\in {\mathcal {P}}_1 \text { and } |x_1| \le 1. \end{array}\right. } \end{aligned}$$The graph of the value function in the case \(\inf c_2 <1/\lambda \) is plotted in Fig. 4b.
3 Hamilton–Jacobi system under strong controllability condition near the interface
In this section we derive the Hamilton–Jacobi system (HJ) associated with the above optimal control problem and prove that the value function given by (2.2) is the unique viscosity solution of that (HJ) system, under the following condition:
- \(\left[ A3\right] \):
(Strong controllability) There exists a real number \(\delta >0\) such that for any \(i=1,\ldots ,N\) and for all \(x\in \Gamma \),
$$\begin{aligned} B(0,\delta )\cap ({\mathbb {R}}e_0 \times {\mathbb {R}}e_i)\subset F_{i}\left( x\right) . \end{aligned}$$
Remark 3.1
If x is close to \(\Gamma \), we can use [A3] to obtain the coercivity of the Hamiltonian which will be needed in Lemma 3.17 below to prove the Lipschitz continuity of the viscosity subsolution of the HJ system.
Hereafter we will denote by \(B(\Gamma ,\rho ),\,\rho >0,\) the set
Lemma 3.2
Under Assumptions [A1] and [A3], there exist two positive numbers \(r_0\) and C such that for all \(x_1,x_2\in B(\Gamma ,r_0)\), there exist \((y_{x_1}, \alpha _{x_1,x_2})\in {\mathcal {T}}_{x_1}\) and \(\tau _{x_1,x_2}<C d(x_1,x_2)\) such that \(y_{x_1}(\tau _{x_1,x_2})=x_2\).
Proof
The proof is classical and similar to the one in [14], so we skip it. \(\square \)
3.1 Value function on the interface
Lemma 3.3
Under Assumptions [A] and [A3], for all \(i\in \{1,\ldots ,N\}\), \({\mathcal {V}}|_{{\mathcal {P}}_i \backslash \Gamma }\) is continuous. Moreover, there exists \(\varepsilon >0\) such that \({\mathcal {V}}|_{{\mathcal {P}}_i \backslash \Gamma }\) is Lipschitz continuous in \(B(\Gamma ,\varepsilon )\cap {\mathcal {P}}_i \backslash \Gamma \). Therefore, it is possible to extend \({\mathcal {V}}|_{{\mathcal {P}}_i \backslash \Gamma }\) to the interface \(\Gamma \) and from now on, we use the following notation
Proof
This lemma is a consequence of Lemma 3.2, see [1] and [14] for more details. \(\square \)
For \(x\in \Gamma \), we set
and
where \( \textsc {FL}_i(x) \) is defined in Assumption [A2] . Let us define a viscosity solution of the switching Hamilton–Jacobi equation on the interface \(\Gamma \):
where \(H_\Gamma \) is the Hamiltonian on \(\Gamma \) defined by
Definition 3.4
An upper (resp. lower) semi-continuous \(u_\Gamma : \Gamma \rightarrow {\mathbb {R}}\) is a viscosity subsolution (resp. supersolution) of (3.4) if for any \(x\in \Gamma \), any \(\varphi \in C^1 ( \Gamma )\) such that \(u_\Gamma - \varphi \) has a local maximum (resp. minimum) point at x, then
The continuous function \(u_\Gamma : \Gamma \rightarrow {\mathbb {R}}\) is called viscosity solution of (3.4) if it is both viscosity sub and supersolution of (3.4).
We have the following characterization of the value function \({\mathcal {V}}\) on the interface.
Theorem 3.5
Under Assumptions [A] and [A3], the restriction of value function \({\mathcal {V}}\) on the interface \(\Gamma \), \({\mathcal {V}}|_{\Gamma }\), is a viscosity solution of (3.4).
The proof of Theorem 3.5 is made in several steps. The first step is to prove that \({\mathcal {V}}|_\Gamma \) is a viscosity solution of an HJ equation with an extended definition of the Hamiltonian on \(\Gamma \). For that, we consider the following larger relaxed vector field: for \(x\in \Gamma \),
We have
Lemma 3.6
For any function \(\varphi \in C^1 (\Gamma )\) and \(x\in \Gamma \),
Proof
See Appendix. \(\square \)
The second step consists of proving the following lemma.
Lemma 3.7
The restriction of the value function \({\mathcal {V}}\) on the interface \(\Gamma \), \({\mathcal {V}}|_{\Gamma }\) satisfies
in the viscosity sense.
Proof
Let \(x \in \Gamma \) and \(\varphi \in C^1 (\Gamma )\) such that \({\mathcal {V}}|_\Gamma -\varphi \) has a maximum at x, i.e.
From Lemma 3.6, it suffices to prove that
Let \((\zeta ,\xi ) \in f\ell _\Gamma (x) \), there exist \((y_{x,n},\alpha _n)\in {\mathcal {T}}_x\) and \(t_n \rightarrow 0^+\) such that \(y_{x,n} (t) \in \Gamma \) for all \(t\le t_n\) and
According to (3.7) and the dynamic programming principle, for all \(n\in {\mathbb {N}}\),
Dividing both sides by \(t_n\), the goal is to take the limit as n tends to \(\infty \). On the one hand, we have
On the other hand, since \(y_{x,n} (t_n) = x + t_n (\zeta + o(1)e_0 )\), we obtain
Hence, in view of (3.9) and (3.10), we have
Thus (3.11) holds for any \((\zeta ,\xi ) \in f\ell _\Gamma (x) \) and therefore (3.8) holds. \(\square \)
Lemma 3.8
Under Assumptions [A] and [A3], for all \(x\in \Gamma \),
Proof
Let \(i\in \{1,\ldots ,N\}\), \(x\in \Gamma \) and \(z\in {\mathcal {P}}_i \backslash \Gamma \) such that \(|x-z|\) is small. It suffices to prove (a) \( v_i (x) \le {\mathcal {V}}|_\Gamma (x) \) and (b) \( {\mathcal {V}}|_\Gamma (x)\le v_i(x)+c_i (x) \).
- (a)
Consider any control law \(\alpha \) such that \((y_{x}, \alpha ) \in {\mathcal {T}}_x\). Let \(\alpha _{z,x}\) be a control law which connects z to x (which exists thanks to Lemma 3.2) and consider the control law
$$\begin{aligned} {\hat{\alpha }}(x) = {\left\{ \begin{array}{ll} \alpha _{z,x} (s) &{} \text {if } s\le \tau _{z,x},\\ \alpha (s-\tau _{z,x}) &{} \text {if } s>\tau _{z,x}. \end{array}\right. } \end{aligned}$$This means that the trajectory goes from z to x with the control law \(\alpha _{z,x}\) and then proceeds with the control law \(\alpha \). Therefore,
$$\begin{aligned} {\mathcal {V}}(z) = v_i (z) \le J(z,{\hat{\alpha }}) = \int _0^{\tau _{z,x}} \ell _i \left( y_{z,{\hat{\alpha }}} (s), {\hat{\alpha }}(s) \right) e^{-\lambda s} ds + e^{-\lambda \tau _{z,x}} J(x,\alpha ). \end{aligned}$$Since \(\alpha \) is chosen arbitrarily and \(\ell _i\) is bounded by M, we obtain
$$\begin{aligned} v_i(z) \le M \tau _{z,x} + e^{-\lambda \tau _{z,x}} {\mathcal {V}}(x). \end{aligned}$$Let z tend to x (then \(\tau _{z,x}\) tends to 0 by Lemma 3.2), we conclude \(v_i(x)\le {\mathcal {V}}(x)\).
- (b)
Consider any control law \(\alpha _z\) such that \((y_{z}, \alpha _z)\in {\mathcal {T}}_z\) and use Lemma 3.2 to pick a control law \(\alpha _{x,z}\) connecting x to z. Consider the control law
$$\begin{aligned} {\hat{\alpha }}(x)= {\left\{ \begin{array}{ll} \alpha _{x,z}(s) &{} \text {if } s\le \tau _{x,z},\\ \alpha _z (s-\tau _{x,z}) &{} \text {if } s > \tau _{x,z}, \end{array}\right. } \end{aligned}$$for which the trajectory \(y_{x,{\hat{\alpha }}}\) goes from x to z using the control law \(\alpha _{x,z}\) and then proceeds with the control law \(\alpha _z\). Therefore,
$$\begin{aligned} {\mathcal {V}}(x) \le J(x,{\hat{\alpha }}) = c_i (x) + \int ^{\tau _{x,z}}_0 \ell _i \left( y_{x,{\hat{\alpha }}} (s), {\hat{\alpha }}(s) \right) e^{-\lambda s }ds + e^{-\lambda \tau _{x,z}} J(z,\alpha _z). \end{aligned}$$Since \(\alpha _z\) is chosen arbitrarily and \(\ell _i\) is bounded by M, we obtain
$$\begin{aligned} {\mathcal {V}}(x) \le c_i(x) + M\tau _{x,z}+ e^{-\lambda \tau _{x,z}} v_i(z). \end{aligned}$$Let z tend x (then \(\tau _{x,z}\) tends to 0, by Lemma 3.2), we conclude \({\mathcal {V}}(x)\le c_i(x) + v_i (x)\). \(\square \)
From Lemmas 3.7 and 3.8, we conclude that \({\mathcal {V}}|_{\Gamma }\) is a viscosity subsolution of (3.4). The last step of of the proof of Theorem 3.5 is to prove that \({\mathcal {V}}|_{\Gamma }\) is a viscosity supersolution of (3.4).
Lemma 3.9
The restriction of the value function \({\mathcal {V}}\) on the interface \(\Gamma \), \({\mathcal {V}}|_{\Gamma }\) satisfies
in the viscosity sense.
Proof
Let \( x\in \Gamma \) and assume that
it suffices to prove that \({\mathcal {V}}(x)\) satisfies
in the viscosity sense. Let \( \{\varepsilon _n\} \) be a sequence which tends to 0. For any n, let \(\alpha _n\) be an \(\varepsilon _n\)-optimal control, i.e. \({\mathcal {V}}(x) + \varepsilon _n > J(x,\alpha _n)\), and \( \tau _n \) be the first time the trajectory \(y_{x,\alpha _n}\) leaves \(\Gamma \), i.e.
We note that \(\tau _n\) is possibly \(+\infty \), in which case the trajectory \(y_{x,\alpha _n}\) stays on \(\Gamma \) for all \(s\in [0,+\infty )\). We consider the two following cases:
- Case 1::
There exists a subsequence of \(\{\tau _n\}\) (which is still denoted \(\{\tau _n\}\)) such that \(\tau _n \rightarrow 0\) as \(n\rightarrow +\infty \) and at time \(\tau _n\) the trajectory enters \({\mathcal {P}}_{i_0}\), for some \(i_0 \in \{1,\ldots ,N \}\). This implies
$$\begin{aligned} {\mathcal {V}}(x) + \varepsilon _n&> J(x,\alpha _n) \\&= \int _0^{\tau _n} \ell \left( y_{x,\alpha _n} (s), \alpha _n (s) \right) e^{-\lambda s} ds + c_{i_0}(y_{x,\alpha _n} (\tau _n)) e^{-\lambda \tau _n} \\&\quad + v_{i_0} (y_{x,\alpha _n} (\tau _n)) e^{-\lambda \tau _n}. \end{aligned}$$Since \( \ell \) is bounded by M, sending n to \(+\infty \), yields
$$\begin{aligned} {\mathcal {V}}(x) \ge c_{i_0}(x) +v_{i_0} (x), \end{aligned}$$which leads to a contradiction to (3.12).
- Case 2::
There exist a subsequence of \(\{\tau _n\}\) (which is still denoted \(\{\tau _n\}\)) and a positive constant C such that \(\tau _n >C\). This means that from 0 to C, the trajectory \(y_{x,\alpha _n}\) still remains in \(\Gamma \). Thus, for all \(\tau \in [0,C],\)
$$\begin{aligned} {\mathcal {V}}|_\Gamma (x) + \varepsilon _n&\ge \int _{0}^{\tau }\ell \left( y_{x,n}\left( t\right) , \alpha _n(t) \right) e^{-\lambda t}dt+\mathcal {V}|_{\Gamma }\left( y_{x,n}\left( \tau \right) \right) e^{-\lambda \tau }\nonumber \\&\ge \int _{0}^{\tau }\ell \left( y_{x,n}\left( t\right) , \alpha _n(t) \right) dt+\mathcal {V}|_{\Gamma }\left( y_{x,n}\left( \tau \right) \right) e^{-\lambda \tau }+ o(\tau ), \end{aligned}$$(3.13)where \(o(\tau )/\tau \rightarrow 0\) as \(\tau \rightarrow 0\) and the last inequality is obtained by using the boundedness of \(\ell \). Let \(\varphi \in C^1 (\Gamma )\) such that \({\mathcal {V}}|_\Gamma -\varphi \) has a minimum on \( \Gamma \) at x, i.e.
$$\begin{aligned} \varphi (x) - \varphi (z) \ge {\mathcal {V}}|_\Gamma (x) - {\mathcal {V}}|_\Gamma (z), \quad \text {for all }z\in \Gamma . \end{aligned}$$(3.14)From Lemma 3.6, it suffices to prove that
$$\begin{aligned} \lambda {\mathcal {V}}|_\Gamma (x) + \max _{(\zeta ,\xi )\in f\ell _\Gamma (x) } \left\{ - (\zeta \cdot e_0) \dfrac{\partial \varphi }{\partial e_0} (x) -\xi \right\} \ge 0. \end{aligned}$$(3.15)Since \( \lim _{n\rightarrow \infty } \varepsilon _n =0 \), it is possible to choose a sequence \( \{t_n\} \) such that \(0<t_n <C \) and \( \varepsilon _n / t_n \rightarrow 0 \) as \( n \rightarrow \infty \). Thus from (3.13) and (3.14), we obtain
$$\begin{aligned}&\dfrac{\varphi (x) - \varphi (y_{x,n}(t_n))}{t_n} -\dfrac{1}{t_n} \int _0^{t_n} \ell (y_{x,n} (t), \alpha _n (t) ) dt + \dfrac{1-e^{-\lambda t_n} }{t_n}{\mathcal {V}}|_\Gamma (y_{x,n} (t_n) )\nonumber \\&\quad \ge -\dfrac{\varepsilon _n}{t_n} + o(1). \end{aligned}$$(3.16)Since f and \(\ell \) are bounded, then the sequence \(\big \{ \frac{y_{x,n} (t_n) - x }{t_n}, \frac{1}{t_n} \int _0^{t_n} \ell (y_{x,n} (t), \alpha _n (t) ) dt \big \}\) is bounded in \(\Gamma \times {\mathbb {R}}\). Therefore, we can extract a subsequence of this sequence which converges to \(({\bar{\zeta }},{\bar{\xi }})\) as \(n\rightarrow +\infty \). Obviously, we have \(\left( {\bar{\zeta }},{\bar{\xi }} \right) \in f\ell _\Gamma (x)\). Hence, sending n to \(\infty \) in (3.16), we obtain
$$\begin{aligned} \lambda {\mathcal {V}}|_\Gamma (x) - ({\bar{\zeta }}\cdot e_0) \dfrac{\partial \varphi }{\partial e_0} (x) -{\bar{\xi }} \ge 0, \end{aligned}$$and thus (3.15) holds. \(\square \)
3.2 The Hamilton–Jacobi system and viscosity solutions
3.2.1 Admissible test-functions
Definition 3.10
A function \(\varphi :{\mathcal {P}}_1 \times \ldots \times {\mathcal {P}}_N \times \Gamma \rightarrow {\mathbb {R}}^N\) is an admissible test-function if there exist \((\varphi _1,\ldots ,\varphi _N, \varphi _\Gamma )\), \(\varphi _i\in C^1({\mathcal {P}}_i)\) and \( \varphi _\Gamma \in C^1(\Gamma ) \), such that \(\varphi (x_1,\ldots ,x_N,x_\Gamma )=(\varphi _1 (x_1), \ldots , \varphi _N (x_N), \varphi _\Gamma (x_\Gamma ) )\). The set of admissible test-function is denoted by \(\mathcal {R}({\mathcal {S}})\).
3.2.2 Hamilton–Jacobi system
Define the Hamiltonian \(H_i : {\mathcal {P}}_i \times ({\mathbb {R}}e_0 \times {\mathbb {R}}e_i) \rightarrow {\mathbb {R}}\) by
and the Hamiltonian \(H_i^+ : \Gamma \times ({\mathbb {R}}e_0 \times {\mathbb {R}}e_i) \rightarrow {\mathbb {R}}\) by
where \(A_i^+ (x) = \{a\in A_i : f_i(x,a)\cdot e_i \ge 0 \}\) and consider the following Hamilton–Jacobi system
and its viscosity solution \(U:=\left( u_{1},\ldots ,u_{N}, u_\Gamma \right) \).
Definition 3.11
(Viscosity solution with entry costs)
A function \(U:=\left( u_{1},\ldots ,u_{N},u_\Gamma \right) \) where \(u_{i}\in USC\left( {\mathcal {P}}_{i};\mathbb {R}\right) \) for all \(i\in \{1,\ldots , N \}\) and \( u_\Gamma \in C(\Gamma ,{\mathbb {R}}) \), is called a viscosity subsolution of (3.17) if for any \(\left( \varphi _{1},\ldots ,\varphi _{N}, \varphi _\Gamma \right) \in \mathcal {R}({\mathcal {S}})\), any \(i\in \{1,\ldots , N \}\) and any \(x_{i}\in {\mathcal {P}}_{i}\), \( x\in \Gamma \) such that \(u_{i}-\varphi _{i}\) has a local maximum point on \({\mathcal {P}}_{i}\) at \(x_{i}\) and \( u_\Gamma - \varphi _\Gamma \) has a local maximum point on \(\Gamma \) at x, then
$$\begin{aligned} \lambda u_{i}\left( x_i\right) +H_{i}\left( x_i, \partial \varphi _i (x_i) \right) \le 0,&\quad \text {if } x_i\in {\mathcal {P}}_{i}\backslash \Gamma ,\\ \lambda u_{i} (x_i)+\max \left\{ H_{i}^{+}\left( x_i,\partial \varphi _i (x_i) \right) , -\lambda u_\Gamma (x_i) \right\} \le 0,&\quad \text {if } x_i\in \Gamma ,\\ \displaystyle \lambda u_{\Gamma }(x) + \max \left\{ -\lambda \min _{i=1,\ldots ,N} \{u_i (x) + c_i(x) \} , H_\Gamma \left( x,\dfrac{\partial \varphi _\Gamma }{\partial e_0} (x) \right) \right\} \le 0, \end{aligned}$$A function \( U:=\left( u_{1},\ldots ,u_{N}, u_\Gamma \right) \) where \(u_{i}\in LSC\left( {\mathcal {P}}_{i};\mathbb {R}\right) \) for all \(i\in \{1,\ldots , N \}\) and \( u_\Gamma \in C(\Gamma ;{\mathbb {R}}) \), is called a viscosity supersolution of (3.17) if for any \(\left( \varphi _{1},\ldots ,\varphi _{N}, \varphi _\Gamma \right) \in \mathcal {R}({\mathcal {S}})\), any \(i\in \{1,\ldots , N \}\) and any \(x_{i}\in {\mathcal {P}}_{i}\) and \( x\in \Gamma \) such that \(u_{i}-\varphi _{i}\) has a local minimum point on \({\mathcal {P}}_{i}\) at \(x_{i}\) and \( u_\Gamma - \varphi _\Gamma \) has a local minimum point on \(\Gamma \) at x, then
$$\begin{aligned} \lambda u_{i}\left( x_i\right) +H_{i}\left( x_i, \partial \varphi _i (x_i) \right) \ge 0&\quad \text {if } x_i\in {\mathcal {P}}_{i}\backslash \Gamma ,\\ \lambda u_{i} (x_i)+\max \left\{ H_{i}^{+}\left( x_i,\partial \varphi _i (x_i) \right) , -\lambda u_\Gamma (x_i) \right\} \ge 0&\quad \text {if } x_i\in \Gamma ,\\ \displaystyle \lambda u_{\Gamma }(x) + \max \left\{ -\lambda \min _{i=1,\ldots ,N} \{u_i (x) + c_i(x) \} , H_\Gamma \left( x,\dfrac{\partial \varphi _\Gamma }{\partial e_0} (x) \right) \right\} \ge 0, \end{aligned}$$A functions \( U:=\left( u_{1},\ldots ,u_{N}, u_\Gamma \right) \) where \(u_{i}\in C\left( {\mathcal {P}}_{i};\mathbb {R}\right) \) for all \(i\in \{1,\ldots ,N\}\) and \( u_\Gamma \in C(\Gamma ;{\mathbb {R}}) \), is called a viscosity solution of (3.17) if it is both a viscosity subsolution and a viscosity supersolution of (3.17).
3.3 Relations between the value function and the HJ system
In this section, we wish to prove that
Theorem 3.12
Under Assumptions [A] and [A3], \( V:=(v_1,\ldots ,v_N, {\mathcal {V}}|_\Gamma )\) is a viscosity solution of (3.17), where the functions \(v_i\) are defined in (3.1).
Proof
By Theorem 3.5, \( {\mathcal {V}}|_\Gamma \) is a viscosity solution of (3.4). Furthermore, if \( x \in {\mathcal {P}}_i \backslash \Gamma \) , for any \( i \in \{1,\ldots ,N \} \) and \( (y_x,\alpha ) \in {\mathcal {T}}_{x} \), there exists a time \( \tau \) small enough so that \( y_{x,\alpha } (t) \in {\mathcal {P}}_i \backslash \Gamma \) for \( 0\le t \le \tau \). Thus, the proof in this case is classical by using dynamic programming principle (see [4, 6]) and we do not detail it. Now assume \( x\in \Gamma \), we shall prove that for all \(i\in \{1,\ldots ,N\}\), the function \(v_i\) satisfies
in the viscosity sense. The proof of this case is a consequence of Lemma 3.13 and Lemma 3.15 below. \(\square \)
Lemma 3.13
For \(i\in \{1,\ldots N\}\), the function \(v_i\) satisfies
in the viscosity sense.
Proof
Let \(x\in \Gamma \). From Lemma 3.8 we have \(v_i(x)\le {\mathcal {V}}|_\Gamma (x)\). Hence, it suffices to prove that
in the viscosity sense. Let \(a_{i} \in A_i\) be such that \(f_{i}\left( x,a_i\right) \cdot e_i >0\). By the Lipschitz continuity of \( f_i(\cdot ,a_i) \), there exist \( r >0 \) such that \(f_{i}\left( z,a_i\right) \cdot e_i >0\) for all \( z\in B(x,r) \cap ({\mathcal {P}}_i \backslash \Gamma ) \). Thus, there exists \( \tau >0\) such that for all \( z\in B(x,r) \cap ({\mathcal {P}}_i \backslash \Gamma ) \), there exists \( (y_z, \alpha _z) \in {\mathcal {T}}_z\) for which
where \( {\hat{\alpha }} \) is chosen arbitrarily. It follows that \(y_{z}\left( t\right) \in {\mathcal {P}}_{i}\backslash \Gamma \) for all \( t\le \tau \). In other words, the trajectory \( y_z \) cannot approach \(\Gamma \) since the speed pushes it away from \(\Gamma \), for \(y_{z} (t)\in {\mathcal {P}}_{i}\cap B\left( \Gamma ,r\right) \). Note that it is not sufficient to choose \(a_{i}\in A_{i}\) such that \(f_i\left( x,a_{i}\right) \cdot e_i=0\) since it may lead to \(f\left( z,a_{i}\right) \cdot e_i <0\) for all \(z\in {\mathcal {P}}_{i}\backslash \Gamma \). Next, since \(y_{z}\left( t\right) \in {\mathcal {P}}_{i}\backslash \Gamma \) for all \( t\le \tau \), we have
This inequality holds for any \({\hat{\alpha }}\), thus
Furthermore, since \(f_{i}\left( \cdot ,a\right) \) is Lipschitz continuous by \(\left[ A1\right] \), for all \(t\in \left[ 0,\tau \right] \),
and by Grönwall’s inequality,
yielding that \(y_{z}(s)\) tends to \(y_{x}(s)\) and \(\int _0^\tau \ell _i(y_{z}(s),\alpha _z (s) ) ds\) tends to \(\int _0^\tau \ell _i(y_{x}(s),\alpha _x (s) ) ds\) when z tends to x. Hence, from (3.19), by letting \(z \rightarrow x\), we obtain
Let \(\varphi \) be a function in \(C^{1}\left( {\mathcal {P}}_{i}\right) \) such that \(0=v_{i}\left( x\right) -\varphi \left( x\right) =\max _{{\mathcal {P}}_{i}}\left( v_{i}-\varphi \right) \). This yields
By letting \(\tau \) tend to 0, we obtain that \( - f_{i}\left( x,a_{i}\right) \cdot \partial \varphi (x) \le \ell _{i}\left( x,a_{i}\right) - \lambda v_{i}\left( x\right) \). Hence,
Finally, by [A] , it is easy to check that
The proof is complete. \(\square \)
Before we give a proof of the fact that \(v_i\) is a viscosity supersolution of (3.18), we prove the following useful lemma.
Lemma 3.14
Let \(x\in \Gamma \) and assume that
Then, there exist \({\bar{\tau }}>0\) and \(r>0\) such that for any \(z\in ({\mathcal {P}}_i \backslash \Gamma ) \cap B(x,r) \), any \(\varepsilon \) sufficiently small and any \(\varepsilon \)-optimal control law \(\alpha ^{\varepsilon }_z\) for z,
This lemma means that if (3.20) holds, then any trajectories starting from \(z\in ({\mathcal {P}}_i \backslash \Gamma ) \cap B(x,\varepsilon )\) still remains on \({\mathcal {P}}_i \backslash \Gamma \) for a fixed amount of time. Hence, this lemma takes into account the situation that the trajectory does not leave \({\mathcal {P}}_i \backslash \Gamma \).
Proof of Lemma 3.14
We proceed by contradiction. Suppose that there exist sequences of positive numbers \(\{\varepsilon _n\}, \{\tau _n\}\) and \(\{x_n\}\subset {\mathcal {P}}_i \backslash \Gamma \) such that \(\varepsilon \rightarrow 0^+\), \(x_n\rightarrow x\), \(\tau _n \rightarrow 0^+ \) and \((y_{x_n}, \alpha _n) \in {\mathcal {T}}_{x_n} \) where \(\alpha _n\), \(\varepsilon _n\)-optimal control law, satisfies \(y_{x_n} (\tau _n) \in \Gamma \). This implies that
Since \(\ell \) is bounded by M by [A1], then \(v_i(x_n)+\varepsilon _n \ge -\tau _n M + e^{- \lambda \tau _n}{\mathcal {V}}|_\Gamma (y_{x_n}(\tau _n))\). Take a limit at infinity as \(n\rightarrow \infty \), we get \(v_i(x) \ge {\mathcal {V}}|_\Gamma (x)\) which contradicts (3.20). \(\square \)
Lemma 3.15
The function \(v_i\) is a viscosity supersolution of (3.18).
Proof
Let \(x\in \Gamma \). From Lemma 3.8, we have \( v_j (x) \le {\mathcal {V}}|_\Gamma (x) \) for all j. This yields that if the inequality (3.20) does not hold then \( v_i (x) = {\mathcal {V}}|_\Gamma (x) \) and therefore \( v_i \) satisfies
Hence, in the rest of the proof, we assume that the inequality (3.20) holds and we aim to prove that
in the viscosity sense. Let \(\varphi \in C^{1}\left( {\mathcal {P}}_{i}\right) \) be such that
and \(\left\{ x_{\varepsilon }\right\} \subset {\mathcal {P}}_{i}\backslash \Gamma \) be any sequence such that \(x_{\varepsilon }\) tends to x when \(\varepsilon \) tends to 0. From the dynamic programming principle and Lemma 3.14, there exists \({\bar{\tau }}\) such that for any \(\varepsilon >0\), there exists \(\left( y_{\varepsilon },\alpha _{\varepsilon }\right) :=\left( y_{x_{\varepsilon }},\alpha _{\varepsilon }\right) \in \mathcal {T}_{x_{\varepsilon }}\) such that \(y_{\varepsilon }\left( \tau \right) \in {\mathcal {P}}_{i}\backslash \Gamma \) for all \(\tau \in \left[ 0,{\bar{\tau }}\right] \) and
Then, according to (3.21),
Next, one has
and
where the notation \(o_{\varepsilon }\left( 1\right) \) is used for a quantity which is independent on \(\tau \) and tends to 0 as \(\varepsilon \) tends to 0. For a positive integer k, the notation \(o(\tau ^{k})\) is used for a quantity that is independent on \(\varepsilon \) and such that \(o(\tau ^{k})/\tau ^{k}\rightarrow 0\) as \(\tau \rightarrow 0\). Finally, \(\mathcal {O}(\tau ^k)\) stands for a quantity independent on \(\varepsilon \) such that \(\mathcal {O}(\tau ^{k})/\tau ^{k}\) remains bounded as \(\tau \rightarrow 0\). From (3.22), we obtain that
Since \(y_{\varepsilon }\left( \tau \right) \in {\mathcal {P}}_{i}\) for all \(\varepsilon \), we have
Hence, from (3.23)
Moreover, \(\varphi \left( x_{\varepsilon }\right) -\varphi \left( x\right) =o_{\varepsilon }\left( 1\right) \) and that \(\partial \varphi \left( y_{\varepsilon }\left( s\right) \right) =\partial \varphi \left( x\right) +o_{\varepsilon }\left( 1\right) +\mathcal {O}\left( s\right) \). Thus
Let \(\varepsilon _{n}\rightarrow 0\) as \(n\rightarrow \infty \) and \(\tau _{m}\rightarrow 0\) as \(m\rightarrow \infty \) such that
as \(n,m\rightarrow \infty \). In view of \(\left[ A1\right] \) and \(\left[ A2\right] \), we have
Therefore,
Hence,
since \(\text {FL}_{i}\left( x\right) \) is closed and convex. Let \(n,m\rightarrow \infty \), then \(\left( a,b\right) \in \text {FL}_{i}\left( x\right) \) and therefore there exists \({\overline{a}}\in A_{i}\) such that
On the other hand, by Lemma 3.14, \(y_{\varepsilon _{n}}\left( s\right) \in {\mathcal {P}}_{i}\backslash \Gamma \) for all \(s\in \left[ 0,\tau _{m}\right] \). This yields
Since \(y_{\varepsilon _{n}}\left( \tau _{m}\right) \cdot e_i >0\), then
Let \(\varepsilon _{n} \rightarrow 0\) then let \(\tau _{m} \rightarrow 0\), to obtain \(f_{i}\left( x,{\overline{a}}\right) \cdot e_i \ge 0\), thus \({\overline{a}}\in A_{i}^{+}(x)\). Hence, from (3.25) and (3.26), replacing \(\varepsilon \) by \(\varepsilon _{n}\) and \(\tau \) by \(\tau _{m}\), let \(\varepsilon _{n} \rightarrow 0 \), then let \(\tau _{m} \rightarrow 0\), we finally obtain
\(\square \)
3.4 A comparison principle and uniqueness
In this section we establish a comparison principle for the Hamilton–Jacobi system (3.17). From the comparison principle, it easily follows that \(V:=(v_1,\ldots ,v_N,{\mathcal {V}}|_\Gamma )\) is the unique viscosity solution of (3.17).
Theorem 3.16
(Comparison Principle) Under Assumptions [A] and [A3], let U and W be respectively bounded continuous viscosity sub and supersolution of (3.17). Then \(U\le W\) componentwise.
We are going to give two proofs of Theorem 3.16. The first one, given below, is inspired by Lions and Souganidis [21, 22] by using arguments from the theory of PDE. The second one (displayed in the appendix) is inspired by the works of Achdou et al. [3] and Barles et al. [7, 8] by using arguments from the theory of optimal control and PDE techniques. Both proofs make use of the following important properties of viscosity subsolutions displayed in the next lemma.
Lemma 3.17
Under Assumptions [A] and [A3], let \( U = (u_1,\ldots ,u_N,u_\Gamma )\) be a bounded continuous viscosity subsolution of (3.17), for any \(i\in \{1,\ldots ,N\}\) and \(x\in \Gamma \), the function \(u_i\) is Lipschitz continuous in \(B(\Gamma ,r) \cap {\mathcal {P}}_i\). Therefore, there exists a test-function \(\varphi _i \in C^1 ({\mathcal {P}}_i)\) touching \(u_i\) from above at x.
Proof
The proof of Lemma 3.17 is based on the fact that if \( U = (u_1,\ldots ,u_N,u_\Gamma ) \) is a viscosity subsolution of (3.17), then for any \( i\in \{1,\ldots ,N\} \), \( u_i \) is a viscosity subsolution of
Therefore, the proof is complete by applying the result in [25, Section 3.2.3] (which is based on the proof of Ishii [19]). \(\square \)
A first proof of Theorem 3.16
First of all, we claim that there exists a positive constant \( {\bar{M}} \) such that \( (\phi _1,\ldots \phi _N, \phi _\Gamma ) \), where \(\phi _j: {\mathcal {P}}_j \rightarrow {\mathbb {R}}\), \(\phi _j(x)= -|x|^2 - {\bar{M}}\) and \(\phi _\Gamma : \Gamma \rightarrow {\mathbb {R}}\), \(\phi _\Gamma (z)= -|z|^2 - {\bar{M}}\), is a viscosity subsolution of (3.17). Indeed, for any \( j \in \{1,\ldots ,N\} \), since \( f_j \) and \( \ell _j \) are bounded by M, one has
Thus, using Cauchy-Schwarz inequality, there exists \( {\bar{M}} >0 \) such that
The claim for \( \phi _j \) is proved and we can prove similarly the one for \( \phi _\Gamma \). Next, for \( 0<\mu <1 \), \( \mu \) close to 1, setting \( u_j^\mu = \mu u_j + (1-\mu ) \phi _j \) and \( u_\Gamma ^\mu = \mu u_\Gamma + (1-\mu ) \phi _\Gamma \), then \( (u_1^\mu , \ldots , u_N^\mu , u_\Gamma ^\mu ) \) is a viscosity subsolution of (3.17). Moreover, since \( u^\mu _j \) and \( u^\mu _\Gamma \) tend to \( -\infty \) as |x| and |z| tend to \( +\infty \) respectively, the functions \( u_j^\mu - w_j \) and \( u_\Gamma ^\mu - w_\Gamma \) have maximum values \( M_j^\mu \) and \( M_\Gamma ^\mu \) which are reached at some points \( {\bar{x}}_j \) and \( {\bar{x}}_\Gamma \) respectively. We argue by contradiction, through considering the two following cases:
- Case A:
Assume that \( M_i^\mu > M^\mu _\Gamma \) and \( M_i^\mu >0 \). Since \( (u_1^\mu , \ldots , u_N^\mu , u_\Gamma ^\mu ) \) is a viscosity subsolution of (3.17), by Lemma 3.17, there exists a positive number L such that \(u^\mu _i\) is Lipschitz continuous with Lipschitz constant L in \({\mathcal {P}}_{i}\cap B({\bar{x}}_i,r)\). We consider the function \( \Psi _{i,\varepsilon }:{\mathcal {P}}_{i}\times {\mathcal {P}}_{i} \rightarrow {\mathbb {R}}\) which is defined by
$$\begin{aligned}&\Psi _{i,\varepsilon }(x,y) := u_i^\mu \left( x\right) -w_{i}\left( y\right) -\dfrac{1}{2\varepsilon } \left( ( -x^0+y^0+\delta \left( \varepsilon \right) )^{2}\right. \nonumber \\&\quad \left. + ( -x^i + y^i + \delta \left( \varepsilon \right) )^{2} \right) -|x-{\bar{x}}_i|^2, \end{aligned}$$(3.28)where \( \varepsilon >0 \), \(\delta (\varepsilon ) :=\left( L+1\right) \varepsilon \) and \(x=(x^i,x^0),y=(y^i,y^0)\in {\mathbb {R}}e_i \times {\mathbb {R}}e_0\). It is clear that \(\Psi _{i,\varepsilon }\) attains its maximum \(M_{\varepsilon ,\gamma }\) at \(\left( x_{\varepsilon },y_{\varepsilon }\right) \in {\mathcal {P}}_{i}\times {\mathcal {P}}_{i}\). We claim that
$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle M_{\varepsilon } \rightarrow \max _{{\mathcal {P}}_i} \{u^\mu _i - w_i\} = u^\mu _i ({\bar{x}}_i) - w_i ({\bar{x}}_i) ,\\ x_\varepsilon , y_\varepsilon \rightarrow {\bar{x}}_i \text { and } \dfrac{\left( x_{\varepsilon }-y_{\varepsilon }\right) ^2}{\varepsilon } \rightarrow 0, \end{array}\right. } \text {as } \varepsilon \rightarrow 0. \end{aligned}$$(3.29)Indeed, we have
$$\begin{aligned} M_{\varepsilon }= & {} u_{i}^\mu \left( x_{\varepsilon }\right) -w_{i}\left( y_{\varepsilon }\right) -\dfrac{\left( -x_{\varepsilon }^0 + y_{\varepsilon }^0 + \delta \left( \varepsilon \right) \right) ^2 + \left( - x_{\varepsilon }^i + y_{\varepsilon }^i + \delta \left( \varepsilon \right) \right) ^2}{2\varepsilon } \nonumber \\&- |x_\varepsilon - {\bar{x}}_i|^2\ge u_{i}^\mu \left( {\bar{x}}_i\right) -w_{i}\left( {\bar{x}}_i\right) -\dfrac{\left( L+1\right) ^{2}}{2}\varepsilon . \end{aligned}$$(3.30)Since \(M_i^\mu = u_{i}^\mu ({\bar{x}}_i)-v_{i} ({\bar{x}}_i )>0\), \( M_\varepsilon \) is positive when \(\varepsilon \) is small enough. Furthermore, since \( w_i \) is bounded and \( u_i^\mu \) is bounded from above, we have \( |x_\varepsilon - {\bar{x}}_i|^2\) is bounded and \( x_\varepsilon - y_\varepsilon \rightarrow 0 \) as \( \varepsilon \rightarrow 0 \). Hence, after extraction of a subsequence, \(x_{\varepsilon },y_{\varepsilon }\rightarrow {\bar{x}} \in {\mathcal {P}}_i\) as \(\varepsilon \rightarrow 0\), for some \({\bar{x}} \in {\mathcal {P}}_{i}\).
Thus, from (3.30) we obtain
$$\begin{aligned} M_i^\mu \ge u_i ({\bar{x}}) - w_i ({\bar{x}}) - |{\bar{x}} - {\bar{x}}_i|^2 \ge \limsup _{\varepsilon \rightarrow 0} M_{\varepsilon } \ge \liminf _{\varepsilon \rightarrow 0} M_{\varepsilon } \ge M_i^\mu . \end{aligned}$$This implies that \( M_\varepsilon \rightarrow M_i^\mu \), \( (x_\varepsilon - y_\varepsilon )^2 / \varepsilon \rightarrow 0 \) as \( \varepsilon \rightarrow 0 \) and \( {\bar{x}} = {\bar{x}}_i \). The claim is proved.
From now on in this proof we only consider the case when \({\bar{x}}_i \in \Gamma \), since otherwise, the proof follows by applying the classical theory (see [4, 6]). We claim that \(x_{\varepsilon } \notin \Gamma \) for \( \varepsilon \) small enough. Indeed, assume by contradiction that \(x_{\varepsilon } \in \Gamma \), i.e. \( x_{\varepsilon }^i = 0 \), we have
- (a):
If \(y_{\varepsilon } \notin \Gamma \), then let \( z_{\varepsilon } = (y^i_{\varepsilon },x^0_{\varepsilon }) \), we have
$$\begin{aligned} M_{\varepsilon }&= u_{i}^\mu (x_{\varepsilon } )-w_{i} (y_{\varepsilon } )-\dfrac{\left( -|x_{\varepsilon }^0|+|y_{\varepsilon }^0|+\delta \left( \varepsilon \right) \right) ^2 + \left( |y_{\varepsilon }^i|+\delta \left( \varepsilon \right) \right) ^2 }{2\varepsilon } -|x_{\varepsilon } - {\bar{x}}_i|^2\\&\ge u_{i}^\mu (z_{\varepsilon } )-w_{i} (y_{\varepsilon })-\dfrac{\left( -|x_{\varepsilon }^0|+|y_{\varepsilon }^0|+\delta \left( \varepsilon \right) \right) ^2 + \left( -|y_{\varepsilon }^i|+|y_{\varepsilon }^i|+\delta \left( \varepsilon \right) \right) ^2 }{2\varepsilon }\\&\quad - |z_\varepsilon - {\bar{x}}_i|^2. \end{aligned}$$Since \(u_i^\mu \) is Lipschitz continuous in \(B\left( {\bar{x}}_i,r\right) \cap {\mathcal {P}}_{i}\), we see that for \(\varepsilon \) small enough
$$\begin{aligned} L|y^i_{\varepsilon }|\ge u_{i}\left( x_{\varepsilon }\right) -u_{i}\left( z_{\varepsilon }\right)&\ge \dfrac{|y^i_{\varepsilon }|^{2}}{2\varepsilon }+\dfrac{|y^i_{\varepsilon }|\delta \left( \varepsilon \right) }{\varepsilon } + |x_{\varepsilon } - {\bar{x}}_i|^2 - |z_\varepsilon - {\bar{x}}_i|^2\\&\ge \dfrac{|y_{\varepsilon }^i|\delta \left( \varepsilon \right) }{\varepsilon } - |y^i_{\varepsilon }| | x_\varepsilon + z_\varepsilon - 2{\bar{x}}_i|. \end{aligned}$$Therefore, if \(y^i_{\varepsilon ,\gamma }\not =0\), then \(L\ge L + 1 - | x_\varepsilon + z_\varepsilon - 2{\bar{x}}_i| \), which leads to a contradiction, since \( x_\varepsilon \), \( z_\varepsilon \) tend to \( {\bar{x}}_i \) as \( \varepsilon \rightarrow 0 \).
- (b):
If \(y_{\varepsilon }\in \Gamma \), i.e. \(y_{\varepsilon }^i = 0\), then let \( z_{\varepsilon } = (\varepsilon ,x_{\varepsilon }^0) \), we have
$$\begin{aligned} M_{\varepsilon }&= u_{i}\left( x_{\varepsilon }\right) -w_{i}\left( y_{\varepsilon }\right) -\dfrac{\left( -|x_{\varepsilon }^0|+|y_{\varepsilon }^0|+\delta \left( \varepsilon \right) \right) ^2 + \delta \left( \varepsilon \right) ^2 }{2\varepsilon } - |x_\varepsilon - {\bar{x}}_i|^2 \\&\ge u_{i}\left( z_{\varepsilon }\right) - w_{i}\left( y_{\varepsilon }\right) - \dfrac{\left( -|x_{\varepsilon }^0|+|y_{\varepsilon }^0|+\delta \left( \varepsilon \right) \right) ^2+\left( -|\varepsilon |+\delta \left( \varepsilon \right) \right) ^2 }{2\varepsilon } - |z_\varepsilon - {\bar{x}}_i|^2 . \end{aligned}$$Since \(u^\mu _i\) is Lipschitz continuous in \(B\left( {\bar{x}}_i,r\right) \cap {\mathcal {P}}_{i}\), we obtain
$$\begin{aligned} L\varepsilon \ge u_i^\mu (x_{\varepsilon })- u^\mu _{i} (z_{\varepsilon }) \ge - \dfrac{\varepsilon }{2} + \delta (\varepsilon )- \varepsilon | x_\varepsilon + z_\varepsilon - 2{\bar{x}}_i|. \end{aligned}$$This implies that \(L\ge L + 1/2 - | x_\varepsilon + z_\varepsilon - 2{\bar{x}}_i|\), which yields a contradiction since \( x_\varepsilon \), \( z_\varepsilon \) tend to \( {\bar{x}}_i \) as \( \varepsilon \rightarrow 0 \).
The second claim is proved. We consider the following three possible cases
- Case A.1:
There exists a subsequence of \( \{y_{\varepsilon } \} \) (still denoted by \( \{y_{\varepsilon } \} \)) such that \( y_{\varepsilon } \in \Gamma \) and \( w_i (y_{\varepsilon }) \ge w_\Gamma (y_{\varepsilon })\). Since \( x_\varepsilon ,y_\varepsilon \rightarrow {\bar{x}}_i \) as \( \varepsilon \rightarrow 0 \) and \( u_i^\mu \) is continuous, for \( \varepsilon \) small enough, we have
$$\begin{aligned} w_\Gamma (y_\varepsilon ) \le w_i (y_\varepsilon ) < u_i^\mu (y_\varepsilon ) = u_i^\mu (x_\varepsilon ) +o_\varepsilon (1) \le u_\Gamma ^\mu (y_\varepsilon ). \end{aligned}$$(3.31)Recall that the second inequality of (3.31) holds since \( M_i^\mu >0 \) and the last inequality of (3.31) holds since \( u^\mu _i \) and \( u^\mu _\Gamma \) satisfy
$$\begin{aligned} \lambda u^\mu _{i} (x)+\max \left\{ H_{i}^{+}\left( x,\partial u^\mu _i (x) \right) , -\lambda u^\mu _\Gamma (x) \right\} \le 0, \end{aligned}$$(3.32)in the viscosity sense. From (3.31),
$$\begin{aligned} u_i^\mu (x_\varepsilon ) - w_i (y_\varepsilon ) + o_\varepsilon (1) \le u_\Gamma ^\mu (y_\varepsilon ) - w_\Gamma (y_\varepsilon ) \le M_\Gamma ^\mu . \end{aligned}$$Let \( \varepsilon \rightarrow 0 \), thanks to (3.29), \( \sup \{u_i^\mu -w_i\} = M_i^\mu \le M_\Gamma ^\mu \), which leads us to a contradiction since we assume that \( M_i^\mu > M_\Gamma ^\mu \) in Case A.
- Case A.2:
There exists a subsequence of \( \{y_{\varepsilon } \} \) such that \( y_{\varepsilon } \in \Gamma \) and
$$\begin{aligned} \lambda w_{i}\left( y_{\varepsilon }\right) +H^+_{i}\left( y_{\varepsilon },\dfrac{-x_{\varepsilon }+y_{\varepsilon }+\delta (\varepsilon )}{\varepsilon } \right) \ge 0. \end{aligned}$$On the one hand, since \( H_i^+(x,p)\le H_i (x,p) \) for all \( x\in \Gamma \) and \( p\in {\mathbb {R}}e_i \times {\mathbb {R}}e_0 \), we have
$$\begin{aligned} \lambda w_{i}\left( y_{\varepsilon }\right) +H_{i}\left( y_{\varepsilon },\dfrac{-x_{\varepsilon }+y_{\varepsilon }+\delta \left( \varepsilon \right) }{\varepsilon } \right) \ge 0. \end{aligned}$$(3.33)On the other hand, we have a viscosity inequality for \( u^\mu _i \) at \( x_{\varepsilon } \in {\mathcal {P}}_i \backslash \Gamma \):
$$\begin{aligned} \lambda u_{i}^\mu \left( x_{\varepsilon }\right) +H_{i}\left( x_{\varepsilon },\dfrac{-x_{\varepsilon }+y_{\varepsilon } + \delta \left( \varepsilon \right) }{\varepsilon } + 2 (x_{\varepsilon } - {\bar{x}}_i)\right) \le 0. \end{aligned}$$(3.34)Subtracting (3.33) from (3.34), we obtain
$$\begin{aligned}&\lambda (u^\mu _{i}\left( x_{\varepsilon }\right) -w_{i}\left( y_{\varepsilon }\right) ) \\&\quad \le H_{i}\left( y_{\varepsilon },\dfrac{-x_{\varepsilon }+y_{\varepsilon }+\delta \left( \varepsilon \right) }{\varepsilon } \right) -H_{i}\left( x_{\varepsilon },\dfrac{-x_{\varepsilon }+y_{\varepsilon }+\delta \left( \varepsilon \right) }{\varepsilon } + 2 (x_\varepsilon - {\bar{x}}_i) \right) . \end{aligned}$$In view of [A1] and [A2], there exists \(C_{i}>0\) such that for any \(x,y\in {\mathcal {P}}_{i}\) and \(p,q\in \mathbb {R}\)
$$\begin{aligned} \left| H_{i}\left( x,p\right) -H_{i}\left( y,q\right) \right|&\le \left| H_{i}\left( x,p\right) -H_{i}\left( y,p\right) \right| +\left| H_{i}\left( y,p\right) -H_{i}\left( y,q\right) \right| \\&\le C_i \left| x-y\right| \left( 1+\left| p\right| \right) + C_i \left| p-q\right| . \end{aligned}$$This, in turn, yields
$$\begin{aligned}&\lambda (u^\mu _{i}\left( x_{\varepsilon }\right) -w_{i}\left( y_{\varepsilon }\right) ) \\&\quad \le C_i \left[ \left| x_{\varepsilon }-y_{\varepsilon }\right| (1 + \dfrac{\left| -x_{\varepsilon } + y_{\varepsilon }+\delta (\varepsilon ) \right| }{\varepsilon } + 2 |x_\varepsilon - {\bar{x}}_i| ) + 2 |x_\varepsilon - {\bar{x}}_i |\right] . \end{aligned}$$Letting \(\varepsilon \) to \(\infty \) and applying (3.29), we obtain that \(\max _{{\mathcal {P}}_i} \{u^\mu _{i}-w_{i}\} = M_i^\mu \le 0\), which leads to a contradiction.
- Case A.3:
There exists a subsequence of \( \{y_\varepsilon \} \) such that \( y_{\varepsilon } \in {\mathcal {P}}_i \backslash \Gamma \). Since the inequalities (3.33) and (3.34) still hold, a contradiction is obtained by using the similar arguments as in the previous case.
- Case B:
Assume that
$$\begin{aligned} M_\Gamma ^\mu \ge \max _j \{ M_j^\mu \} \text { and } M_\Gamma ^\mu >0 . \end{aligned}$$(3.35)We consider the function
$$\begin{aligned} \Phi _{\varepsilon }:\Gamma \times \Gamma&\longrightarrow {\mathbb {R}}\\ \left( \zeta ,\xi \right)&\longrightarrow u_\Gamma ^\mu (\zeta ) - w_\Gamma (\xi ) - \dfrac{|\zeta - \xi |^2}{2\varepsilon } - |\zeta - {\bar{x}}_\Gamma |^2. \end{aligned}$$By classical arguments, \(\Phi _{\varepsilon }\) attains its maximum \(K_{\varepsilon }\) at \(\left( \zeta _{\varepsilon }, \xi _{\varepsilon }\right) \in \Gamma \times \Gamma \) and
$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle K_{\varepsilon } \rightarrow M_\Gamma ^\mu = \max _\Gamma \{u^\mu _\Gamma - w_\Gamma \} = u^\mu _\Gamma ({\bar{x}}_\Gamma ) - w_\Gamma ({\bar{x}}_\Gamma ) ,\\ \zeta _\varepsilon , \xi _\varepsilon \rightarrow {\bar{x}}_\Gamma \text { and } \dfrac{\left( \zeta _{\varepsilon } - \xi _{\varepsilon }\right) ^2}{\varepsilon } \rightarrow 0, \end{array}\right. } \text {as } \varepsilon \rightarrow 0. \end{aligned}$$(3.36)We consider the following two cases:
- Case B.1:
There exists a subsequence \( \{\xi _\varepsilon \} \) (still denoted by \( \{\xi _\varepsilon \} \)) such that
$$\begin{aligned} \lambda w_\Gamma (\xi _\varepsilon ) + H_\Gamma \left( \xi _\varepsilon , \dfrac{\zeta _\varepsilon - \xi _\varepsilon }{2 \varepsilon } \right) \ge 0. \end{aligned}$$We also have a viscosity inequality for \( u_\Gamma ^\mu \) at \( \zeta _\varepsilon \)
$$\begin{aligned} \lambda u_\Gamma ^\mu (\zeta _\varepsilon ) + H_\Gamma \left( \zeta _\varepsilon , \dfrac{\zeta _\varepsilon - \xi _\varepsilon }{2 \varepsilon } + 2(\zeta _\varepsilon - {\bar{x}}_\Gamma ) \right) \le 0. \end{aligned}$$By applying the classical arguments, one has \( (\zeta _\varepsilon - \xi _\varepsilon )^2 / \varepsilon \rightarrow 0 \) and \( \zeta _\varepsilon , \xi _\varepsilon \rightarrow {\bar{x}}_\Gamma \) as \( \varepsilon \rightarrow 0 \). Subtracting the two above inequalities and sending \( \varepsilon \) to 0, we obtain that \( u_\Gamma ^\mu ({\bar{x}}_\Gamma ) - w_\Gamma ({\bar{x}}_\Gamma ) = M_\Gamma ^\mu \le 0\), which contradicts (3.35).
- Case B.2:
There exist a subsequence \( \{\xi _\varepsilon \} \) and \( k\in \{1,\ldots ,N\} \) such that
$$\begin{aligned} w_\Gamma (\xi _\varepsilon ) \ge \min _j \{ w_j(\xi _\varepsilon ) + c_j (\xi _\varepsilon ) \} = w_k(\xi _\varepsilon ) + c_k (\xi _\varepsilon ). \end{aligned}$$(3.37)Since \( \zeta _\varepsilon ,\xi _\varepsilon \rightarrow {\bar{x}}_\Gamma \) as \( \varepsilon \rightarrow 0 \) (by (3.36)) and \( u_\Gamma ^\mu \) is continuous, for \( \varepsilon \) small enough, we have
$$\begin{aligned} w_k (\xi _\varepsilon ) + c_k (\xi _\varepsilon ) \le w_\Gamma (\xi _\varepsilon ) < u_\Gamma ^\mu (\xi _\varepsilon ) = u_\Gamma ^\mu (\zeta _\varepsilon ) + o_\varepsilon (1) \le u_k^\mu (\xi _\varepsilon ) + c_k (\xi _\varepsilon ). \end{aligned}$$Recall that the second inequality holds since \( M_\Gamma ^\mu >0 \) and the last one comes from the fact that \( u_\Gamma ^\mu \) satisfies
$$\begin{aligned} \lambda u_{\Gamma }^\mu (x) + \max \left\{ -\lambda \min _{i=1,\ldots ,N} \{u^\mu _i (x) + c_i(x) \} , H_\Gamma \left( x,\dfrac{\partial u_\Gamma ^\mu }{\partial e_0} (x) \right) \right\} \ge 0, \end{aligned}$$in the viscosity sense. This implies that
$$\begin{aligned} u_\Gamma ^\mu (\zeta _\varepsilon ) - w_\Gamma (\xi _\varepsilon ) + o_\varepsilon (1) \le u_k^\mu (\xi _\varepsilon ) - w_k (\xi _\varepsilon ) \le M_k^\mu . \end{aligned}$$(3.38)Letting \( \varepsilon \rightarrow 0 \) and applying (3.36), we get \( M_\Gamma ^\mu \le u_k^\mu ({\bar{x}}_\Gamma ) - w_k ({\bar{x}}_\Gamma ) \le M_k^\mu \). This implies from (3.35) that
$$\begin{aligned} M_\Gamma ^\mu = M_k^\mu =u_k^\mu ({\bar{x}}_\Gamma ) -w_k ({\bar{x}}_\Gamma )>0. \end{aligned}$$(3.39)Now we apply similar arguments as in the proof of Case A by considering the function \( \Psi _{k,\varepsilon }:{\mathcal {P}}_{k}\times {\mathcal {P}}_{k} \rightarrow {\mathbb {R}}\) which is defined in (3.28) with the index i replacing the index k. Remark that we may assume \( {\bar{x}}_k = {\bar{x}}_\Gamma \) since \( {\bar{x}}_\Gamma \) is a maximum point of \( u_k^\mu - w_k \) by (3.39). It follows that the three cases B.2.1, B.2.2 and B.2.3 which are similar to A.1, A.2 and A.3, respectively. If Case B.2.1 occurs, i.e. there exists a subsequence of \( \{y_\varepsilon \} \) (still denoted by \( \{y_\varepsilon \} \)) such that \( w_k(y_\varepsilon ) \ge w_\Gamma (y_\varepsilon )\). Letting \( \varepsilon \rightarrow 0 \), one gets \( w_k ({\bar{x}}_\Gamma ) \ge w_\Gamma ({\bar{x}}_\Gamma )\). In the other hands, letting \( \varepsilon \rightarrow 0 \) in (3.37), one also gets \( w_\Gamma ({\bar{x}}_\Gamma ) \ge w_k({\bar{x}}_\Gamma ) + c_k ({\bar{x}}_\Gamma ) > w_k({\bar{x}}_\Gamma )\) which leads to a contradiction. Finally, the two last cases are proved by using the same arguments as in the proofs of Case A.2 and Case A.3.
Finally, we get \( M_\Gamma ^\mu \le 0 \) and \( M_i^\mu \le 0\) for all \( i\in \{1,\ldots ,N\} \) and \( \mu \in (0,1) \), \( \mu \) close to 1. We conclude by letting \( \mu \) tend to 1. \(\square \)
Corollary 3.18
The value function \({\mathcal {V}}\) has the property that the vector \(V=(v_1,\ldots ,v_N, {\mathcal {V}}|_\Gamma ) \) is the unique viscosity solution of (3.17).
4 Hamilton–Jacobi system under a moderate controllability condition near the interface
In this section we derive the Hamilton–Jacobi system (HJ) associated with the above optimal control problem and prove that the value function given by (2.2) is the unique viscosity solution of that (HJ) system, under the condition \([{\tilde{A}}3]\) below, which is weaker that the strong controllability condition [A3] used above.
\( [{\tilde{A}}3]\) (Moderate controllability) There exist positive numbers \(\delta \) and R such that
for any \( i=1,\ldots ,N \) and for \( x\in \Gamma \)
$$\begin{aligned}{}[-\delta , \delta ] \subset \{ f_i(x,a) \cdot e_i : a\in A_i \}. \end{aligned}$$(4.1)for any \( x\in \Gamma \), there exists \( j\in \{1,\ldots ,N\} \) such that
$$\begin{aligned} {[}-\delta , \delta ] \subset \{ f_j(x,a) \cdot e_0 : a\in A_j^{\Gamma } \}. \end{aligned}$$(4.2)
Remark 4.1
-
1.
\([{\tilde{A}}3] \) allows us to construct an admissible control law and a corresponding trajectory that goes from one point on \( B(\Gamma ,R)\cap {\mathcal {P}}_i \) to another one on \( \Gamma \), see Lemma 4.4 below.
-
2.
Assumption \( [{\tilde{A}}3] \) is rather stronger than the assumption (4.1) called normal “controllability” (and denoted \( [{\tilde{H}}3] \)) which is used in [25] related to the case without entry costs. With only \( [{\tilde{H}}3] \) and the effect of the entry costs, we could not prove that our value function is continuous on \( \Gamma \) and establish a corresponding Hamilton–Jacobi system. The moderate assumption \([{\tilde{A}}3]\) allows us to overcome the difficulties induced by the entry costs.
Remark 4.2
Since for any \( i \in \{1,\ldots ,N\} \), \(f_i\) is Lipschitz continuous with respect to the state variable (from Assumption [A1] ), it is easy to check that there exists a positive number R such that for all \( i\in \{1,\ldots ,N\} \) and \( x\in B(\Gamma ,R) \cap {\mathcal {P}}_i \)
Under Assumptions [A] and \( [{\tilde{A}}3] \), following the arguments used in [25, Theorem 3.3.1], it holds that for any \( x\in {\mathcal {S}}\), the set \( Y_x \) is not empty. Hence, we can define the set of admissible controlled trajectories starting from the initial datum x to be
The cost functional \( {\mathcal {J}}\) associated to the trajectory \( (y_{x} , \alpha ) \in {\mathcal {T}}_x\) is defined by
and
Compared to the proof of Lemma 3.3, we cannot use the classical control theory arguments to prove that the value function \( {\mathscr {V}}\) is continuous on \( {\mathcal {P}}_i \backslash \Gamma \) for all \( i\in \{1,\ldots ,N\} \). The main problem is that, unlike under Assumption [A3], with the new assumption \( [{\tilde{A}}3]\), for x, z close to \( \Gamma \), there is possibly no admissible trajectory \( y_{x} \in {\mathcal {T}}_x \) from x to z. We will later prove that \( {\mathscr {V}}\) is continuous on \({\mathcal {P}}_i \backslash \Gamma \) for any i by using the comparison principle, but for the moment, \( {\mathscr {V}}|_{{\mathcal {P}}_i \backslash \Gamma } \) is a priori a discontinuous function. In order to deal with such a discontinuity, we use the following notions
Definition 4.3
Let \( i\in \{1,\ldots ,N\} \) and \( u_i: {\mathcal {P}}_i \backslash \Gamma \rightarrow {\mathbb {R}}\) be a bounded function.
The upper semi-continuous envelope of u is defined by
$$\begin{aligned} u^{\star }_i (x) = \limsup _{z\rightarrow x} u_i(z). \end{aligned}$$The lower semi-continuous envelope of \( u_i \) is defined by
$$\begin{aligned} u_{i\star } (x) = \liminf _{z\rightarrow x} u(z). \end{aligned}$$
Notice that both functions \( u_i^\star \) and \( u_{i \star } \) are defined on \( {\mathcal {P}}_i \) instead of \( {\mathcal {P}}_i \backslash \Gamma \).
Lemma 4.4
Under Assumptions [A] and \([{\tilde{A}}3]\),
- (a):
there exists a positive constant C such that for all \( z\in \Gamma \) and \( x \in {\mathcal {S}}\cap B(\Gamma ,R)\), there exist \( (y_x,\alpha _{x,z}) \in {\mathcal {T}}_{x}\) and \( \tau _{x,z} \) such that \( z= y_x (\tau _{x,z}) \) and \( \tau _{x,z} \le C |x-z| \),
- (b):
\( {\mathscr {V}}|_\Gamma \) is Lipschitz continuous on \( \Gamma \).
Proof
We first note that by applying the classical arguments, (b) is a direct consequence of (a) (see [4]). To prove (a), we consider the two following cases.
- Case 1:
\( x, z\in \Gamma \). From (4.2), we can find \( (y_x,\alpha _{x,z}) \in {\mathcal {T}}_{x}\) for which \(\alpha _{x,z}\) satisfies
$$\begin{aligned} f\left( x+\dfrac{z-x}{|z-x|} \delta t, \alpha _{x,z} (t) \right) = \delta \dfrac{z-x}{|z-x|},\quad \text {for all } t\le \dfrac{|z-x|}{\delta }. \end{aligned}$$It is easy to check that \( y_x (|z-x|/\delta ) =z \), i.e. \( \tau _{x,z} = |z-x|/\delta \).
- Case 2:
\( x = (x^i,x^0) \in {\mathcal {P}}_i \backslash \Gamma \) and \( z = (0,z^0)\in \Gamma \). One the one hand, from (4.1) and (4.2), we can pick \( (y_x,\alpha _{x,z}) \in {\mathcal {T}}_{x}\) for which \(\alpha _{x,z}\) satisfies
$$\begin{aligned} {\left\{ \begin{array}{ll} f\left( y_x(t) , \alpha _{x,z} (t) \right) \cdot e_i = - \dfrac{\delta }{2}, &{} t\le \dfrac{2 x^i}{\delta },\\ f\left( y_x(t) , \alpha _{x,z} (t) \right) = \delta \dfrac{z- y_x(2 x^i / \delta ) }{|z- y_x(2 x^i / \delta )|}, &{} \dfrac{2 x^i}{\delta } \le t\le \dfrac{2 x^i}{\delta } + \dfrac{|z- y_x(2 x^i / \delta ) |}{ \delta }. \end{array}\right. } \end{aligned}$$This simply means that \( 2x^i / \delta \) is the exit time of \( y_x \) from \( {\mathcal {P}}_i \backslash \Gamma \) and \( \tau _{x,z} = \frac{2 x^i}{\delta } + \frac{|z- y_x(2 x^i / \delta ) |}{ \delta } \). On the other hand, let \( {\bar{x}}= (0,x^0) \in \Gamma \), since f is bounded by M, it holds that
$$\begin{aligned} | z - y_x ( 2 x^i /\delta ) | \le |z- {\bar{x}}| + |{\bar{x}} - y_x ( 2 x^i /\delta ) | \le |z-x|+ \dfrac{ x^i(4M^2 \delta ^2 -1)^{1/2}}{\delta } . \end{aligned}$$Since \( x^i \le |z-x| \), we finally obtain
$$\begin{aligned} \tau _{x,z} = \dfrac{2 x^i}{\delta } + \dfrac{|z- y_x(2 x^i / \delta ) |}{ \delta } \le \dfrac{|z-x|}{\delta } \left( 3+ \dfrac{(4M^2 \delta ^2 -1)^{1/2}}{\delta } \right) . \end{aligned}$$
\(\square \)
4.1 Value function on the interface
Theorem 4.5
Under Assumptions [A] and \([{\tilde{A}}3]\), the restriction of the value function \( {\mathscr {V}}\) to \(\Gamma \), \({\mathscr {V}}|_\Gamma \), is a unique viscosity solution of the equation
Here a function \( u_\Gamma : \Gamma \rightarrow {\mathbb {R}}\) is called a viscosity solution of (4.3) if it satisfies
The proof of Theorem 4.5 is a consequence of the next three lemmas which are similar to Lemma 3.7, Lemma 3.8 and Lemma 3.9, respectively.
Lemma 4.6
The restriction of the value function \({\mathscr {V}}\) on the interface \(\Gamma \), \({\mathscr {V}}|_{\Gamma }\) satisfies
in the viscosity sense.
Proof
The proof of this lemma is similar to the proof of Lemma 3.7. \(\square \)
Lemma 4.7
For all \(x\in \Gamma \)
Proof
Let \( i\in \{1,\ldots ,N\} \), it suffices to prove (a) \(v_i^\star (x) \le {\mathscr {V}}|_\Gamma (x)\) and (b) \({\mathscr {V}}|_\Gamma (x) \le v_{i}^{\star } (x) + c_i (x) \) below.
- (a)
There exists a sequence \( \{x_n\}_{n\in {\mathbb {N}}} \subset ({\mathcal {P}}_i \backslash \Gamma ) \cap B(\Gamma ,R) \) such that \( x_n \rightarrow x \) and \( v_i (x_n) \rightarrow v_i^\star (x) \) as \( n \rightarrow \infty \). From Lemma 4.4, there exists a positive constant C such that there exist \( (y_{x_n}, \alpha _n) \in {\mathcal {T}}_{x_n}\) and \( \tau _n \) such that \( y_{x_n} (\tau _n) = x \) and \( \tau _n \le |x_n - x| \) for all n. This implies
$$\begin{aligned} v_i (x_n)= & {} {\mathscr {V}}(x_n) \le \int _0^{\tau _n} \ell (y_{x_n} (s), \alpha _n (s) ) e^{-\lambda s} ds + {\mathscr {V}}(x) e^{-\lambda \tau _n}\\\le & {} MC |x_n - x| + {\mathscr {V}}(x) e^{-\lambda \tau _n}. \end{aligned}$$Letting \( n\rightarrow \infty \), one gets \( v_i^\star (x) \le {\mathscr {V}}(x) \).
- (b)
From Assumption \([{\tilde{A}}3]\), it allows to pick \( (y_{n},\alpha _n) \in {\mathcal {T}}_{x}\) and \( \tau _n \rightarrow 0 \) where \(\alpha _n\) satisfies
$$\begin{aligned} f(y_n(t), \alpha _n (t)) \cdot e_i = \dfrac{\delta }{2} >0, \quad \text {for all } t\le \tau _n. \end{aligned}$$Let \( x_n := y_n(\tau _n) \) then \( x_n\in {\mathcal {P}}_i \backslash \Gamma \) and \( x_n \rightarrow x \) as \( n \rightarrow \infty \). This implies
$$\begin{aligned} {\mathscr {V}}(x)\le & {} \int _0^{\tau _n} \ell (y_{n} (s), \alpha _n (s) ) e^{-\lambda s} ds + c_i(x) + {\mathscr {V}}(x_n) e^{-\lambda \tau _n} \nonumber \\\le & {} MC \tau _n + c_i (x) + v_i (x_n) e^{-\lambda \tau _n}. \end{aligned}$$Taking limsup of both sides as \( n\rightarrow \infty \), one gets \( {\mathscr {V}}(x) \le c_i (x) + v_i^\star (x) \).
\(\square \)
Lemma 4.8
Let \( x\in \Gamma \) and assume that \({\mathscr {V}}|_\Gamma (x) < \min \{v_{i \star } (x) +c_i(x) \}\), then \( {\mathscr {V}}|_\Gamma \) satisfies
in the viscosity sense.
Proof
The proof of this lemma is similar to the proof of Lemma 3.9. \(\square \)
4.2 Hamilton–Jacobi system and viscosity solution
Definition 4.9
A function \( {\mathcal {U}}:= ( u_1,\ldots ,u_N, u_\Gamma ) \), where each \( u_i: {\mathcal {P}}_i \rightarrow {\mathbb {R}}\) is a bounded function and \( u_\Gamma : \Gamma \rightarrow {\mathbb {R}}\) is a bounded continuous function, is called a discontinuous viscosity solution of (3.17) if \( {\mathcal {U}}^\star = (u_1^\star , \ldots u_N^\star , u_\Gamma ) \) is a viscosity subsolution of (3.17) and \( {\mathcal {U}}_\star = (u_{1\star }, \ldots u_{N\star }, u_\Gamma ) \) is a viscosity supersolution of (3.17).
Theorem 4.10
Under Assumptions [A] and \([{\tilde{A}}3]\), \( V:=(v_1,\ldots ,v_N, {\mathscr {V}}|_\Gamma ) \) is a viscosity solution of (3.17).
The proof of viscosity subsolution follows from that of Lemma 3.13 where instead of using an arbitrary sequence which tends to \( x \in \Gamma \) as \( n\rightarrow \infty \), we work with a sequence \( \{x_n\}_{n\in {\mathbb {N}}} \subset {\mathcal {P}}_i \backslash \Gamma \) which satisfies
The first difference between the proof of viscosity supersolution with the one of Lemma 3.15 is the following lemma, which has a similar proof as Lemma 3.14.
Lemma 4.11
Let \(x\in \Gamma \) and assume that
Then, for any sequence \( \{z_n\}_{n\in {\mathbb {N}}}\subset {\mathcal {P}}_i \backslash \Gamma \) such that
there exist \({\bar{\tau }}>0\) and \(r>0\) such that, for any \(\varepsilon \) sufficiently small and any \(\varepsilon \)-optimal control law \(\alpha ^{\varepsilon }_{z_n}\) for \(z_n\),
The last difference between the proof of viscosity supersolution with the one of Lemma 3.15 is that instead of using an arbitrary sequence which tends to \( x \in \Gamma \) as \( n\rightarrow \infty \), we work with a sequence \( \{z_n\}_{n\in {\mathbb {N}}} \subset {\mathcal {P}}_i \backslash \Gamma \) satisfying (4.7).
4.3 Comparison principle and uniqueness
In the proof of the Comparison Principle under the strong controllability assumption [A3], the key argument is that the restrictions of the viscosity subsolutions of (3.17) to \({\mathcal {P}}_i \backslash \Gamma \) are Lipschitz continuous in a neighborhood of \( \Gamma \). This property is not obtained directly in the current framework, under the moderate controllability assumption \([{\tilde{A}}3]\). We rather proceed as follows. First, we regularize a restriction of viscosity subsolution to \( {\mathcal {P}}_i \backslash \Gamma \) using sup-convolution to obtain a family of Lipschitz continuous functions. Then we use this family of regularized functions to prove a local comparison principle which we finally extend to a global comparison principle by applying similar arguments as the ones in the proof of [25, Theorem 3.3.4].
We begin the first step with sup-convolution definition.
Definition 4.12
Let \( u_i : {\mathcal {P}}_i \rightarrow {\mathbb {R}}\) be a bounded, USC function and \( \alpha ,p \) be positive numbers. Then sup-convolution of \( u_i \) with respect to the \( x^0 \)-variable is defined by
We borrow the following useful lemmas from [25, Lemma 3.3.7 to 3.3.10].
Lemma 4.13
Let \( u_i : {\mathcal {P}}_i \rightarrow {\mathbb {R}}\) be a bounded function and \( \alpha ,p \) be positive numbers. Then, for any \( x\in {\mathcal {P}}_i \), the supremum which defines \( u_i^\alpha \) is achieved at a point \( z^0\in {\mathbb {R}}\) such that
Lemma 4.14
Let \( u_i : {\mathcal {P}}_i \rightarrow {\mathbb {R}}\) be a bounded function. Then for any \( \alpha ,p>0 \), the sup-convolution \( u_\alpha \) is locally Lipschitz continuous with respect to \( x^0 \), i.e. for any compact subset K in \( {\mathbb {R}}^3 \), there exists \( C_K>0 \) such that for all \( x= x^0 e_0 + x^i e_i \), \( y= y^0 e_0 + x^i e_i \in K \cap {\mathcal {P}}_i\)
Lemma 4.15
Under Assumptions [A] and \([{\tilde{A}}3]\), let \( R>0 \) be a positive number as in Remark 4.2. Let \( u : {\mathcal {P}}_i \rightarrow {\mathbb {R}}\) be a bounded, USC subsolution of (3.17) and \( \alpha ,p \) be some positive numbers. Then for all \( M>0 \), \( u_i^\alpha \) is Lipschitz continuous in \( B_M (\Gamma , R) \cap {\mathcal {P}}_i\), where \( B_M (\Gamma ,R):=\{x\in B(\Gamma ,R) : |x^0|\le M \} \).
Lemma 4.16
Under Assumptions [A] and \([{\tilde{A}}3]\), let \( {\bar{y}} \in \Gamma \) and \( R>0 \) be as in Remark 4.2. We denote by \( Q_i \) the set \( {\mathcal {P}}_i \cap B({\bar{y}}, R) \). Let \( u_i : {\mathcal {P}}_i \rightarrow {\mathbb {R}}\) be a bounded, USC viscosity subsolution of (3.17) in \( Q_i \). Then for all \( \alpha , p>0 \) sufficient small, if we set
the function \( u_i^\alpha \) defined in Definition 4.12 is Lipschitz continuous in \( Q_i^\alpha \). Moreover, there exists \( m: (0,\infty ) \rightarrow (0,\infty ) \) such that \( \lim _{\alpha \rightarrow 0} m(\alpha ) =0 \) and \( (u_1^\alpha - m(\alpha ), \ldots , u_N^\alpha - m(\alpha ) , u_\Gamma )\) is a viscosity subsolution of (3.17) in \( Q^\alpha := \cup _i Q_i^\alpha \).
Lemmas 4.13 and 4.14 on sup-convolution are well known result, but we give a short proof for completeness. First of all, it is easy to see that the supremum in Definition 4.12 is achieved at some point \( z^0 \in {\mathbb {R}}\). We have
and because of the boundedness of u, we get (4.8). Next, let K be a compact subset of \( {\mathcal {P}}_i \), for \( x,y\in K \), from the definition of sup-convolution, we have
By the mean-value theorem and the fact that \( |z^0 - x^0|/\alpha ^2 \), \( |z^0 - y^0|/\alpha ^2\) are bounded, there exists a constant \( C_K>0 \) such that \( |u^\alpha _i (x) - u^\alpha _i (y)| \le C_K |x^0 - y^0| \). The proof of Lemma 4.14 is complete.
Finally, if \( u_i \) is a viscosity subsolution of (3.17), then it is also a viscosity subsolution of the following equation
We may now apply the proofs of [25, Lemmas 3.3.9 and 3.3.10] to conclude Lemmas 4.15 and 4.16.
We are ready to prove a local comparison principle.
Theorem 4.17
Under Assumptions [A] and \([{\tilde{A}}3]\), let \( {\mathcal {U}}=(u_1,\ldots ,u_N, u_\Gamma )\) be a bounded, USC viscosity subsolution of (3.17) and \( {\mathcal {W}}= (w_1,\ldots ,w_N,w_\Gamma )\) be a bounded, LSC viscosity supersolution of (3.17). Let \( R>0 \) as in Remark 4.2, \( i\in \{1, \ldots ,N \} \) and \( {\bar{y}} \in \Gamma \) be fixed. Then, if we set \( Q_i = B({\bar{y}}, R) \cap {\mathcal {P}}_i\), we have
Proof
Take \( \alpha ,p>0 \) sufficient small so that Lemma 4.16 can be applied. From Lemma 4.16, we know the fact that \( u_i^\alpha \) is Lipschitz continuous in \( Q_\alpha \) with a Lipschitz constant \( L_\alpha \) and that there exists \( m : (0,\infty ) \rightarrow (0,\infty ) \) such that \( \lim _{\alpha \rightarrow 0} m (\alpha )=0 \) and \((u_1^\alpha - m,\ldots ,u_N^\alpha - m, u_\Gamma ) \) is a viscosity subsolution of (3.17). Set \( {\mathfrak {u}}_j:= u_j^\alpha - m \) for all \( j\in \{1,\ldots ,N\} \). Let us prove that
We argue by contradiction by considering the two following cases
- Case A:
If there exist \( i\in \{1,\ldots ,N\} \) and \( {\bar{x}}_i \in Q_i^\alpha \backslash \partial Q_i^\alpha \) such that
$$\begin{aligned} M_i:= \max _{Q_i^\alpha } \{{\mathfrak {u}}_i - w_i\} = {\mathfrak {u}}_i ({\bar{x}}_i)- w_i({\bar{x}}_i) > \max \{M_\Gamma , 0\}, \end{aligned}$$where \( M_\Gamma := \max _{Q_i^\alpha \cap \Gamma } \{u_\Gamma - w_\Gamma \} \). Now we can apply the similar arguments as in Case A in the proof of Theorem 3.16 to obtain that either \( M_i \le 0 \) or \( M_i \le M_\Gamma \), which leads us to a contradiction.
- Case B:
If there exists \( {\bar{x}}_\Gamma \in (Q_i^\alpha \backslash \partial Q_i^\alpha ) \cap \Gamma \) such that
$$\begin{aligned} M_\Gamma = \max _{Q_i^\alpha \cap \Gamma } \{u_\Gamma - w_\Gamma \} = u_\Gamma ({\bar{x}}_\Gamma )- w_i({\bar{x}}_\Gamma ) \ge \max _{j\in \{1,\ldots ,N\}} M_j \text { and } M_\Gamma > 0. \end{aligned}$$Apply the similar arguments as in Case B in the proof of Theorem 3.16 to obtain that either \( M_\Gamma \le 0 \) (which leads to a contradiction) or there exists \( k\in \{1,\ldots ,N\} \) such that
$$\begin{aligned} w_\Gamma ({\bar{x}}_\Gamma ) \ge \min _{j} \{w_j({\bar{x}}_\Gamma ) +c_j ({\bar{x}}_\Gamma )\} = w_k({\bar{x}}_\Gamma ) +c_k ({\bar{x}}_\Gamma ), \end{aligned}$$(4.15)which leads to \( M_k = {\mathfrak {u}}_k ({\bar{x}}_\Gamma ) - w_k ({\bar{x}}_\Gamma ) = M_\Gamma >0 \). We now repeat Case A and note that thanks to (4.15), the case \( w_k ({\bar{x}}_\Gamma ) \ge {\mathfrak {u}}_k ({\bar{x}}_\Gamma ) \) does not occur, we finally obtain that \( M_k \le 0 \) which contradicts (4.15).
We finish the proof of (4.13) and (4.14).
In order to prove (4.11) and (4.12), we have to pass to the limit as \( \alpha \) tends to 0 in (4.13) and (4.14), respectively. Let \( \alpha _0>0 \) and \( y \in Q_{\alpha _0} \) be fixed. For all \( 0<\alpha \le \alpha _0 \), one has
We claim that \( \limsup _{\alpha \rightarrow 0} || (u_i^\alpha - m(\alpha ) - w_i)_+||_{L^\infty (\partial Q_\alpha )} \le || (u_i^\alpha - m(\alpha ) - w_i)_+||_{L^\infty (\partial Q)}\). Indeed, there exists \( x_\alpha \in \partial Q_\alpha \) such that
Thus, for any subsequence such that \( || (u_i^\alpha - m(\alpha ) - w_i)_+||_{L^\infty (\partial Q_\alpha )} \) converges to a limit \( \ell \) as \( \alpha \rightarrow 0 \), we can assume that \( x_\alpha \rightarrow {\tilde{x}} \) as \( \alpha \rightarrow 0 \). Hence, from the properties of the sup-convolution, the fact that \( u_i \) is USC and \( w_i \) is LSC, we can check that \( \ell \le ( u_i ({\tilde{x}}) - w_i ({\tilde{x}}) )_+ \le || (u_i- w_i)_+||_{L^\infty (\partial Q_i)}. \) The claim is proved and therefore, by the pointwise convergence of \( u_i^\alpha \) to \( u_i \), passing to the \(\limsup \) as \( \alpha \rightarrow 0 \) in (4.16), we have
The above inequality holds for any \( y\in Q_{\alpha _0} \) with \( \alpha _0 \) arbitrarily chosen, then we obtain (4.11). Finally, (4.12) is obtained by using the similarly arguments, the proof is complete. \(\square \)
Thanks to the local comparison principle, apply the similar arguments in [25, Theorem 3.3.4], we now have the global comparison principle which leads us to the uniqueness of (3.17).
Theorem 4.18
Under Assumptions [A] and \( [{\tilde{A}}3] \), let \( {\mathcal {U}}=(u_1,\ldots ,u_N,u_\Gamma )\ \) be a bounded,USC viscosity subsolution of (3.17) and \({\mathcal {W}}= (w_1,\ldots ,w_N, w_\Gamma ) \) be a bounded,USC viscosity supersolution of (3.17). Then \( u_i \le w_i \) on \( {\mathcal {P}}_i \) for all \( i\in \{1,\ldots ,N\} \) and \( u_\Gamma \le w_\Gamma \) on \( \Gamma \).
Corollary 4.19
The value function \( {\mathscr {V}}\) satisfies \( (v_1,\ldots ,v_N,{\mathscr {V}}|_\Gamma ) \) is a unique viscosity solution of (3.17) and \( v_i \) is continuous on \( {\mathcal {P}}_i \) for all \( i\in \{1,\ldots ,N\} \).
5 A more general optimal control problem
In this section, we generalize the control problem studied in Sect. 3 by allowing some of the entry costs functions to be zero. The situation can be seen as intermediary between the one studied in [25] when all the entry costs are zero, and that studied previously under the strong controllability condition [A3], in this work when all the entry costs function are positive. This generalization holds under the moderate controllability condition \([{\tilde{A}}3]\), but we omit the details. Accordingly, every results presented below will mainly be obtained by combining the arguments proposed above with those used in [25]. Hence, we will present the results without the proofs.
Specifically, we consider the optimal control problems with non-negative entry cost  , where
, where  if \( i\le m \) and for all \( x\in \Gamma \) if \( i>m \), keeping all the assumptions and definitions of Sect. 2 unchanged. The value function associated to
if \( i\le m \) and for all \( x\in \Gamma \) if \( i>m \), keeping all the assumptions and definitions of Sect. 2 unchanged. The value function associated to  is denoted by
is denoted by  . Similarly to Lemma 3.3,
. Similarly to Lemma 3.3,  is continuous and Lipschitz continuous in the neighborhood of \( \Gamma \). Hence, we can define
is continuous and Lipschitz continuous in the neighborhood of \( \Gamma \). Hence, we can define  as follows
as follows

Additionally, it is clear that for all \( i,j\le m \),  for all \( x\in \Gamma \), i.e.
for all \( x\in \Gamma \), i.e.  is a continuous function which will be noted
is a continuous function which will be noted  from now on.
from now on.
Combining the arguments in [25] and in Sect. 3.1 leads us to the following lemma.
Lemma 5.1
The value function  satisfies
satisfies

We now define a set of admissible test-function and the Hamilton–Jacobi system that will characterize  .
.
Definition 5.2
A function \(\varphi :\left( \cup _{i=1}^{m}{\mathcal {P}}_{i}\right) \times {\mathcal {P}}_{m+1}\times \ldots \times {\mathcal {P}}_{N}\rightarrow \mathbb {R}^{N-m+1}\) of the form
is an admissible test-function if
\(\varphi _{c}\) is continuous and for \(i\le m\), \(\varphi _{c}|_{{\mathcal {P}}_{i}}\) belongs to \(C^{1}\left( {\mathcal {P}}_{i}\right) \),
the space of admissible test-function is denoted by \(R\left( {\mathcal {S}}\right) \).
We ready to define a viscosity sub and supersolution of the Hamilton–Jacobi system related to  .
.
Definition 5.3
A function  , where
, where  and
and  , is called a viscosity subsolution of the Hamilton–Jacobi system if for any test-function \(\varphi \in R\left( {\mathcal {S}}\right) \):
, is called a viscosity subsolution of the Hamilton–Jacobi system if for any test-function \(\varphi \in R\left( {\mathcal {S}}\right) \):
- 1.
if
 has a local maximum at \(x_{c}\in \cup _{j=1}^{m}{\mathcal {P}}_{j}\) and if
has a local maximum at \(x_{c}\in \cup _{j=1}^{m}{\mathcal {P}}_{j}\) and if\(x_{c}\in {\mathcal {P}}_{j}\backslash \Gamma \) for some \(j\le m\), then
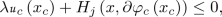
\(x_{c} \in \Gamma \), then
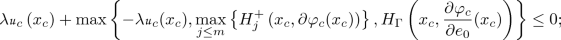
- 2.
if
 has a local maximum point at \(x_{i}\in {\mathcal {P}}_{i}\) for \(i>m\), and if
has a local maximum point at \(x_{i}\in {\mathcal {P}}_{i}\) for \(i>m\), and if\(x_{i}\in {\mathcal {P}}_{i}\backslash \Gamma \), then
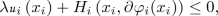
\(x_{i} \in \Gamma \), then
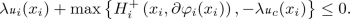
A function  where
where  is called a viscosity supersolution of the Hamilton–Jacobi system if for any test-function \(\varphi \in R\left( {\mathcal {S}}\right) \):
is called a viscosity supersolution of the Hamilton–Jacobi system if for any test-function \(\varphi \in R\left( {\mathcal {S}}\right) \):
- 1.
if
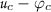 has a local minimum at \(x_{c}\in \cup _{j=1}^{m}{\mathcal {P}}_{j}\) and if
has a local minimum at \(x_{c}\in \cup _{j=1}^{m}{\mathcal {P}}_{j}\) and if\(x_{c}\in {\mathcal {P}}_{j}\backslash \Gamma \) for some \(j\le m\), then

\(x_{c} \in \Gamma \), then
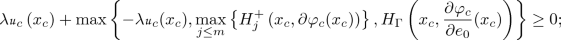
- 2.
if
 has a local minimum point at \(x_{i}\in {\mathcal {P}}_{i}\) for \(i>m\), and if
has a local minimum point at \(x_{i}\in {\mathcal {P}}_{i}\) for \(i>m\), and if\(x_{i}\in {\mathcal {P}}_{i}\backslash \Gamma \), then

\(x_{i} \in \Gamma \), then
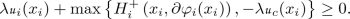
A function  where
where  and
and  for all \(i>m\) is called a viscosity solution of the Hamilton–Jacobi system if it is both a viscosity subsolution and a viscosity supersolution of the Hamilton–Jacobi system.
for all \(i>m\) is called a viscosity solution of the Hamilton–Jacobi system if it is both a viscosity subsolution and a viscosity supersolution of the Hamilton–Jacobi system.
Similarly to the previous sections, we have the relation between the value function  and the Hamilton–Jacobi system.
and the Hamilton–Jacobi system.
Theorem 5.4
Let  be the value function corresponding to
be the value function corresponding to  , then
, then  is a viscosity solution of the Hamilton–Jacobi system.
is a viscosity solution of the Hamilton–Jacobi system.
We now state and prove the comparison principle for the Hamilton–Jacobi system which is the main result of this section
Theorem 5.5
Let  and
and  be respectively a bounded viscosity sub and supersolution of the Hamilton–Jacobi system. Then
be respectively a bounded viscosity sub and supersolution of the Hamilton–Jacobi system. Then  , i.e.
, i.e.  on \( \cup _{j\le m} {\mathcal {P}}_j \) and
on \( \cup _{j\le m} {\mathcal {P}}_j \) and  on \( {\mathcal {P}}_i \) for all \( i>m \).
on \( {\mathcal {P}}_i \) for all \( i>m \).
Proof
First of all, similarly to the first step of the proof of Theorem 3.16 (Sect. 3.4) we can check that there exists \( (\phi _c, \phi _{m+1}, \ldots , \phi _N) \) such that for all \( 0<\mu <1 \) and \( \mu \) close to 1,  and
and  for all \( i\in \{m+1, \ldots ,N\} \) then
for all \( i\in \{m+1, \ldots ,N\} \) then  is a viscosity subsolution of HJ system related to
is a viscosity subsolution of HJ system related to  . We also have the function
. We also have the function  and
and  have maximum value \( M_c^\mu \) and \( M^\mu _j \) which are reached at some points \( {\bar{x}}_c \) and \( {\bar{x}}_j \). We argue by contradiction, through considering the two following cases:
have maximum value \( M_c^\mu \) and \( M^\mu _j \) which are reached at some points \( {\bar{x}}_c \) and \( {\bar{x}}_j \). We argue by contradiction, through considering the two following cases:
- Case A:
Assume that \( M_i^\mu > M_c^\mu \) and \( M_i^\mu >0 \). Repeat Case A as in the proof of Theorem 3.16, implies that either
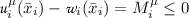 or \( M_i^\mu \le M_c^\mu \), the desired contradiction.
or \( M_i^\mu \le M_c^\mu \), the desired contradiction.- Case B:
Assume that \( M_c^\mu \ge \max _{j>m} \{M_j^\mu \} \) and \( M_c^\mu >0 \). If
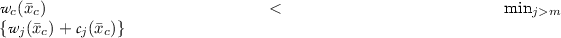 , we can check that
, we can check that 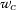 satisfies the super-optimality [25, Theorem 3.2.4] at \( {\bar{x}}_c \). Furthermore, since
satisfies the super-optimality [25, Theorem 3.2.4] at \( {\bar{x}}_c \). Furthermore, since  is a viscosity subsolution of
is a viscosity subsolution of 
Thanks to the comparison principle for HJ when all of entry costs are zero, see [25, Theorem 3.2.5], we obtain that
 which leads to a contradiction. Otherwise, if there exists \( k>m \) such that
which leads to a contradiction. Otherwise, if there exists \( k>m \) such that  (5.1)
(5.1)repeat Case B.3 as in in the proof of Theorem 3.16, implies that there exists \( k> m \) such that
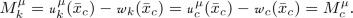
Repeat Case A and note that thanks to (5.1), the case
 does not occur, we finally obtain that \( M_k^\mu \le 0 \), the desired contradiction.
does not occur, we finally obtain that \( M_k^\mu \le 0 \), the desired contradiction.
Finally, we get \( M_c^\mu \le 0 \) and \( M_i^\mu \le 0 \) for all \( i\in \{1,\ldots ,N\} \) and \( 0< \mu <1 \), \( \mu \) close to 1. We conclude by letting \( \mu \) to 1. \(\square \)
References
Achdou, Y., Camilli, F., Cutrì, A., Tchou, N.: Hamilton–Jacobi equations on networks. IFAC Proc. Vol. 44(1), 2577–2582 (2011)
Achdou, Y., Camilli, F., Cutrì, A., Tchou, N.: Hamilton–Jacobi equations constrained on networks. NoDEA Nonlinear Differ. Equ. Appl. 20(3), 413–445 (2013)
Achdou, Y., Oudet, S., Tchou, N.: Hamilton–Jacobi equations for optimal control on junctions and networks. ESAIM Control Optim. Calc. Var. 21(3), 876–899 (2015)
Bardi, M., Capuzzo-Dolcetta, I.: Optimal Control and Viscosity Solutions of Hamilton–Jacobi–Bellman Equations. Systems and Control: Foundations and Applications. Birkhäuser Boston Inc., Boston (1997)
Barles, G.: Discontinuous viscosity solutions of first-order Hamilton–Jacobi equations: a guided visit. Nonlinear Anal. 20(9), 1123–1134 (1993)
Barles, G.: Solutions de viscosité des équations de Hamilton–Jacobi. Mathematics and Applications, vol. 17. Springer, Paris (1994)
Barles, G., Briani, A., Chasseigne, E.: A Bellman approach for two-domains optimal control problems in \({\mathbb{R}}^N\). ESAIM Control Optim. Calc. Var. 19(3), 710–739 (2013)
Barles, G., Briani, A., Chasseigne, E.: A Bellman approach for regional optimal control problems in \(\mathbb{R}^N\). SIAM J. Control Optim. 52(3), 1712–1744 (2014)
Barles, G., Chasseigne, E.: An illustrated guide of the modern approaches of Hamilton–Jacobi equations and control problems with discontinuities. Preprint. https://arxiv.org/abs/1812.09197
Barles, G., Jakobsen, E.R.: On the convergence rate of approximation schemes for Hamilton–Jacobi–Bellman equations. M2AN Math. Model. Numer. Anal. 36(1), 33–54 (2002)
Bressan, A., Hong, Y.: Optimal control problems on stratified domains. Netw. Heterog. Media 2(2), 313–331 (2007)
Camilli, F., Marchi, C.: A comparison among various notions of viscosity solution for Hamilton–Jacobi equations on networks. J. Math. Anal. Appl. 407(1), 112–118 (2013)
Camilli, F., Schieborn, D., Marchi, C.: Eikonal equations on ramified spaces. Interfaces Free Bound. 15(1), 121–140 (2013)
Dao, M.-K.: Hamilton–Jacobi equations for optimal control on networks with entry or exit costs. ESAIM Control Optim. Calc. Var. 25, 15 (2019)
Frankowska, H., Mazzola, M.: Discontinuous solutions of Hamilton–Jacobi–Bellman equation under state constraints. Calc. Var. Part. Differ. Equ. 46(3–4), 725–747 (2013)
Graber, P.J., Hermosilla, C., Zidani, H.: Discontinuous solutions of Hamilton–Jacobi equations on networks. J. Differ. Equ. 263(12), 8418–8466 (2017)
Hermosilla, C., Zidani, H.: Infinite horizon problems on stratifiable state-constraints sets. J. Differ. Equ. 258(4), 1430–1460 (2015)
Imbert, C., Monneau, R., Zidani, H.: A Hamilton–Jacobi approach to junction problems and application to traffic flows. ESAIM Control Optim. Calc. Var. 19(1), 129–166 (2013)
Ishii, H.: A short introduction to viscosity solutions and the large time behavior of solutions of Hamilton–Jacobi equations. In: Hamilton–Jacobi Equations: Approximations, Numerical Analysis and Applications, Volume 2074 of Lecture Notes in Mathematics, pp. 111–249. Springer, Heidelberg (2013)
Lions, P.-L.: Generalized Solutions of Hamilton–Jacobi Equations, Volume 69 of Research Notes in Mathematics. Pitman (Advanced Publishing Program), Boston (1982)
Lions, P.-L., Souganidis, P.: Viscosity solutions for junctions: well posedness and stability. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 27(4), 535–545 (2016)
Lions, P.-L., Souganidis, P.: Well-posedness for multi-dimensional junction problems with Kirchoff-type conditions. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 28(4), 807–816 (2017)
McShane, E.J., Warfield Jr., R.B.: On Filippov’s implicit functions lemma. Proc. Am. Math. Soc. 18, 41–47 (1967)
Nakayasu, A.: Metric viscosity solutions for Hamilton–Jacobi equations of evolution type. Adv. Math. Sci. Appl. 24(2), 333–351 (2014)
Oudet, S.: Hamilton–Jacobi equations on networks or heterogeneous structures. PhD thesis, Université de Rennes 1 (2016). http://theses.fr/2015REN1S051
Schieborn, D., Camilli, F.: Viscosity solutions of Eikonal equations on topological networks. Calc. Var. Part. Differ. Equ. 46(3–4), 671–686 (2013)
Acknowledgements
Open access funding provided by Royal Institute of Technology. This research was supported by the Swedish Research Council grant (2016-04086). This article is a continuation of the works in first author’s dissertation and he appreciate his advisors Yves Achdou, Olivier Ley and Nicoletta Tchou who suggested the topic to him. The authors would like to thank Olivier Ley for his insightful remarks. The authors are also grateful to the referees for careful reading and valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of Lemma 3.6
By the piecewise linearity of the function \((\zeta ,\xi ) \mapsto -(\zeta \cdot e_0) \frac{\partial \varphi }{\partial e_0} (x) - \xi \), we can obviously see that Lemma 3.6 is a directly consequence of the following lemma.
Lemma 6.1
Under Assumption [A], for \(x\in \Gamma \), then
where \(\textsc {FL}_\Gamma (x)\) is defined in (3.2).
Proof
In this case the proof is standard (see [4]), but we prove it for completeness.
The inclusion \(\textsc {FL}_\Gamma (x) \subset f\ell _\Gamma (x) \) is obtained by explicitly constructing trajectories which still remain on the interface \(\Gamma \) for a short time. More specifically, let \(i\in \{1,\ldots ,N\}\) and \(a\in A_i\) such that \((f_i(x,a),\ell _i(x,a)) \in \textsc {FL}_i \cap ({\mathbb {R}}e_0 \times {\mathbb {R}})\). Then from the strong controllability condition [A3] or the moderate controllability \( [{\tilde{A3}}] \), there exists \( (y_\alpha , \alpha )\in {\mathcal {T}}_x \) such that \(y_{x}\) remains on \(\Gamma \) at least for a while and satisfies
Thus, there exists a sequence of times \(t_n\rightarrow 0^+\) such that \(y_{x} (t) \in \Gamma \) for all \(t\in [0,t_n]\) and
Similarly, we get
Hence \((f_i(x,a), \ell _i(x,a)) \in f\ell _\Gamma (x)\) and the first inclusion is proved.
We now consider \((\zeta ,\xi )\in f\ell _\Gamma (x)\), there exists a sequence of admissible trajectories \((y_n,\alpha _n)\in {\mathcal {T}}_x\) which remain on \(\Gamma \) at least for a while and a sequence of times \(t_n\rightarrow 0^+\) such that
On the other hand
where o(1) is a vector tending to 0 as \(n\rightarrow \infty \). Therefore, the distance of
to the set \({\overline{co}} \left( \cup _{i=1}^N \textsc {FL}_i (x) \right) \) tends to 0 as \(n\rightarrow \infty \). Additionally, since \(f(y_n(t),\alpha _n (t))\in \Gamma \) for a.e. \(t\in [0,t_n]\), we get the distance of \((\zeta _n,\xi _n)\) to the set \({\overline{co}}\left( \textsc {FL}_\Gamma (x) \right) \) tends to 0 as \(n\rightarrow \infty \). Hence, we obtain the second inclusion \( f\ell _\Gamma (x) \subset \overline{\text {co}} \left( \textsc {FL}_\Gamma (x) \right) \).
\(\square \)
1.2 A second proof of Theorem 3.16
First of all, from Definition 3.11, we see that if \(U = \{u_1 , \ldots , u_N , u_\Gamma \}\) is a viscosity subsolution of (3.17), then for any \(i\in \{1,\ldots ,N\}\), \(u_i\) is a viscosity subsolution of (3.27) and \(u_i(x) \le u_\Gamma (x)\) for any \(x\in \Gamma \). Therefore, we have the following properties for U (see [25] for detailed proofs)
Lemma 6.2
Under Assumptions [A] and [A3], let \(i\in \{1,\ldots ,N\}\) and \(x\in \left( B(\Gamma ,r) \cap {\mathcal {P}}_i \right) \backslash \Gamma \) and \(\alpha _i \in L^{\infty } (0,\infty ; A_i)\). Let \(\eta >0\) be such that \(y_x(t)= x + \int _0^t f_i (y_x(s),\alpha _i(s) ds \) belongs to \( B(\Gamma ,r) \cap {\mathcal {P}}_i\) for any \(t\in [0,\eta ]\). Assume that \(u_i\) is a \(C^1\) function on \(\Gamma \). Then we have
Lemma 6.3
Assume [A] and [A3] and that \( u_i \in C ({\mathcal {P}}_i) \) is bounded for all \( i\in \{1,\ldots ,N\} \). Let \( \{\rho _\varepsilon \}_{\varepsilon } \) be a sequence of mollifiers defined on \( {\mathbb {R}}\) as follows
where
We consider the function \( u_i^\varepsilon \) defined on \( {\mathcal {P}}_i \) by
Then \( u_\varepsilon \) converges uniformly to u in \( L^\infty ({\mathcal {P}}_i, {\mathbb {R}}) \) and there exists a function \( m:(0,+\infty ) \rightarrow (0,+\infty ) \) such that \( \lim _{\varepsilon \rightarrow 0 } m(\varepsilon ) = 0 \) and the function \( u_\varepsilon - m(\varepsilon ) \) is a viscosity subsolution of (3.27) on a neighborhood of \( \Gamma \).
Remark 6.4
For a proof of Lemmas 6.2 and 6.3 see [25, Section 3.2.3 and Section 3.2.4]. The proof in Achdou et al. [3] is adopted to prove Lemma 6.2 and finally, the existence of a function \( m: (0,+\infty ) \rightarrow (0,+\infty ) \) with \( m(0^+) =0 \) such that \( u_i^\varepsilon - m (\varepsilon ) \) is a subsolution of (3.27) on a neighborhood of \( \Gamma \) was proved by Lions [20] or Barles and Jakobsen [10].
Next, we have the important property of viscosity supersolution.
Lemma 6.5
Let assumptions [A] and [A3] hold and let \(i\in \{1,\ldots ,N\}\) and \({\bar{x}}\in \Gamma \). Let \( \varphi \in C^1({\mathcal {P}}_i) \) be such that \( w_i-\varphi \) has a local maximum point at x. If the function \( w_i \) satisfies
then either (H1) or (H2) below is true:
- (H1):
There exists a sequence \( \{\eta _k\} \) of positive real numbers such that \( \lim _{k\rightarrow + \infty } \eta _k = \eta >0\) and a sequence \( \{x_k\} \subset {\mathcal {P}}_i \backslash \Gamma \) such that \( \lim _{k\rightarrow \infty } x_k = {\bar{x}} \) and for each k, there exists a control law \( \alpha _i^k \) such that the corresponding trajectory \( y_{x_k} (s) \in {\mathcal {P}}_i \) for all \( s\in [0,\eta _k] \) and
$$\begin{aligned} w_i(x_k) \ge \int _0^{\eta _k} \ell _i \left( y_{x_k}(s), \alpha _i^k (s)\right) e^{-\lambda s} ds + w_i (y_{x_k} (\eta _k)) e^{-\lambda \eta _k}. \end{aligned}$$- (H2):
- $$\begin{aligned} \lambda w_i({\bar{x}}) + \max _{a \in A^\Gamma _i} \{- f_i({\bar{x}},a) \cdot \partial \varphi ({\bar{x}}) - \ell _{i} ({\bar{x}},a) \} \ge 0. \end{aligned}$$
Proof
Since \( w_i \) and \( w_\Gamma \) are continuous on \( \Gamma \), from (6.2), there exists \( \varepsilon >0 \) such that \( \lambda w_i (x) < u_\Gamma (x) \) for all \( x\in \Gamma \) and \( | x - {\bar{x}} | < \varepsilon \). From the definition of supersolution, we get
in the viscosity sense. Hence, from [25, Theorem 3.2.4], the proof is complete.
\(\square \)
We are ready to give the second proof of Theorem 3.16.
A second proof of Theorem 3.16
Let \( u_i^\varepsilon \) be the approximation of \( u_i \) given by Lemma 6.3. Similarly to the first step of the proof of Theorem 3.16 (Sect. 3.4), we set \( u^{\varepsilon ,\mu }_{i} := \mu (u^\varepsilon _i - m(\varepsilon )) + (1-\mu ) \psi _i \) for all \( i\in \{1,\ldots ,N\} \) and \( u^\mu _\Gamma := \mu u_\Gamma + (1-\mu )\psi _\Gamma \), \( \mu \rightarrow 1^- \) then \( (u^{\varepsilon ,\mu }_{1}, \ldots , u^{\varepsilon ,\mu }_{N}, u^\mu _\Gamma ) \) is a viscosity subsolution of (3.17). Let \( M^{\varepsilon ,\mu }_i \) and \( M^{\mu }_\Gamma \) be respectively the maximal value of \( u^{\varepsilon ,\mu }_{i} - w_i\) and \( u^\mu _\Gamma - w_\Gamma \) which are reached at some point \( {\bar{x}}^{\varepsilon ,\mu }_i \in {\mathcal {P}}_i\) and \( {\bar{x}}^\mu _\Gamma \in \Gamma \). We argue by contradiction, through considering the two following cases:
- Case A:
Assume that \( M_i^{\varepsilon ,\mu } > M_\Gamma ^\mu \) and \( M_i^{\varepsilon ,\mu } > 0 \). If \( {\bar{x}}^{\varepsilon ,\mu }_i \), the proof is done by using the classical techniques. Therefore, we only focus on the case when \( {\bar{x}}^{\varepsilon ,\mu }_i \in \Gamma \). From Lemma 3.17, \( u^{\varepsilon ,\mu }_{i} \) is Lipschitz in a neighborhood of \( \Gamma \). Moreover, from Lemma 6.3, \( u^{\varepsilon ,\mu }_{i}|_\Gamma \in C^1(\Gamma ) \). Then, we can construct two test-function \(\psi , \varphi \in C^1({\mathcal {P}}_i) \) such that
$$\begin{aligned} \psi (x) = u^{\varepsilon ,\mu }_{i} (0,x^0) + Cx^i, \quad \varphi (x) = u^{\varepsilon ,\mu }_{i} (0,x^0) - Cx^i, \end{aligned}$$where \( x=(x^i,x^0) \) and C is a positive constant which is large enough. This implies that \(\psi |_\Gamma = \varphi |_\Gamma = u^{\varepsilon ,\mu }_{i}|_\Gamma \), \( \psi \) remains above and \( \varphi \) remains below \( u^{\varepsilon ,\mu }_{i} \) on a neighborhood of \( \Gamma \). Since \( M^{\varepsilon ,\mu }_i>0 \), it is easy to see that \( w_i - \varphi \) has a local minimum at \( {\bar{x}}^{\varepsilon ,\mu }_i \). Next, we claim that \( w_i( {\bar{x}}^{\varepsilon ,\mu }_i ) < w_\Gamma ( {\bar{x}}^{\varepsilon ,\mu }_i )\). Indeed, if it does not hold, then we have
$$\begin{aligned} w_\Gamma ( {\bar{x}}^{\varepsilon ,\mu }_i) \le w_i ( {\bar{x}}^{\varepsilon ,\mu }_i) < u_i^{\varepsilon ,\mu } ( {\bar{x}}^{\varepsilon ,\mu }_i) \le u_\Gamma ^\mu ( {\bar{x}}^{\varepsilon ,\mu }_i), \end{aligned}$$and this implies \( M_i^{\varepsilon ,\mu } \le M_\Gamma ^\mu \), the desired contradiction. Hence, from Lemma 6.5, we have the two following cases:
- (H1):
\( \lambda w_i ({\bar{x}}^{\varepsilon ,\mu }_i) + \max _{a \in A^\Gamma _i} \{- f_i({\bar{x}}^{\varepsilon ,\mu }_i,a) \cdot \partial \varphi ({\bar{x}}^{\varepsilon ,\mu }_i) - \ell _{i} ({\bar{x}}^{\varepsilon ,\mu }_i,a) \} \ge 0\). Moreover, since \( u^{\varepsilon ,\mu }_{i} \) is a subsolution of (4.10), \( u^{\varepsilon ,\mu }_{i}- \psi \) has a local maximum point at \( {\bar{x}}^{\varepsilon ,\mu }_i \), \(\psi |_\Gamma = u^{\varepsilon ,\mu }_{i}|_\Gamma \) and \( H_i({\bar{x}}^{\varepsilon ,\mu }_i, p) \ge \max _{a\in A_i^\Gamma }\{-f_i ({\bar{x}}^{\varepsilon ,\mu }_i, a) \cdot p - \ell _i ({\bar{x}}^{\varepsilon ,\mu }_i, a) \}\), we get
$$\begin{aligned} \lambda u^{\varepsilon ,\mu }_{i} ({\bar{x}}^{\varepsilon ,\mu }_i) + \max _{a \in A^\Gamma _i} \{- f_i({\bar{x}}^{\varepsilon ,\mu }_i,a) \cdot \partial \varphi ({\bar{x}}^{\varepsilon ,\mu }_i) - \ell _{i} ({\bar{x}}^{\varepsilon ,\mu }_i,a) \} \le 0. \end{aligned}$$Hence, \( u^{\varepsilon ,\mu }_{i} ({\bar{x}}^{\varepsilon ,\mu }_i) \le w_i ({\bar{x}}^{\varepsilon ,\mu }_i)\) and thus \( M^{\varepsilon ,\mu }_i \le 0 \), which leads to a contradiction.
- (H2):
With the notation in Lemma 6.5, we have
$$\begin{aligned} w_i(x_k) \ge \int _0^{\eta _k} \ell _i \left( y_{x_k}(s), \alpha _i^k (s)\right) e^{-\lambda s} ds + w_i (y_{x_k} (\eta _k)) e^{-\lambda \eta _k}. \end{aligned}$$On the other hand, from Lemma 6.2
$$\begin{aligned} u^{\varepsilon ,\mu }_{i} (x_k) \le \int _0^{\eta _k} \ell _i \left( y_{x_k}(s), \alpha _i^k (s)\right) e^{-\lambda s} ds + u^{\varepsilon ,\mu }_{i} (y_{x_k} (\eta _k)) e^{-\lambda \eta _k}. \end{aligned}$$This implies
$$\begin{aligned} u^{\varepsilon ,\mu }_{i} (x_k) - w_i (x_k) \le ( u^{\varepsilon ,\mu }_{i}(\eta _k) - w_i (\eta _k) ) e^{-\lambda \eta _k}. \end{aligned}$$Letting \( k\rightarrow \infty \), one gets \( M^{\varepsilon ,\mu }_i \le M^{\varepsilon ,\mu }_i e^{-\lambda \eta } \) and thus \( M^{\varepsilon ,\mu }_i<0 \), which is a contradiction.
- Case B:
Assume that \( M_\Gamma ^{\mu } \ge \max _j \{M^{\varepsilon ,\mu }_j\} \) and \( M_\Gamma ^{\mu }>0 \). If the case \( w_\Gamma ({\bar{x}}_\Gamma ^\mu ) < \min _j \{w_j({\bar{x}}_\Gamma ^\mu ) + c_j({\bar{x}}_\Gamma ^\mu )\} \) occurs, we can apply the similar arguments as in Case B.1 of the first proof of Theorem 3.16 to obtain \( M_\Gamma ^\mu \le 0 \), the desired contradiction. Otherwise, if the following case holds:
$$\begin{aligned} w_\Gamma ({\bar{x}}_\Gamma ^\mu ) \ge \min _j \{w_j({\bar{x}}_\Gamma ^\mu ) + c_j({\bar{x}}_\Gamma ^\mu )\} = w_k({\bar{x}}_\Gamma ^\mu ) + c_k({\bar{x}}_\Gamma ^\mu ), \end{aligned}$$(6.3)for some \( k\in \{1,\ldots ,N\} \) and by the fact that
$$\begin{aligned} \min _j \{u_j^{\varepsilon ,\mu }({\bar{x}}_\Gamma ^\mu ) + c_j({\bar{x}}_\Gamma ^\mu )\} \ge u_\Gamma ^\mu ({\bar{x}}_\Gamma ^\mu ) > w_\Gamma ({\bar{x}}_\Gamma ^\mu ), \end{aligned}$$we obtain \( M_\Gamma ^\mu = M_k^{\varepsilon ,\mu } = w_k({\bar{x}}_\Gamma ^\mu ) - u_k^{\varepsilon ,\mu }({\bar{x}}_\Gamma ^\mu )\). Now we repeat Case A with the index i replacing k, \( {\bar{x}}_i^{\varepsilon ,\mu } \) replacing \( {\bar{x}}_\Gamma ^{\mu } \) and note that \( w_k( {\bar{x}}_\Gamma ^{\mu }) < w_\Gamma ( {\bar{x}}_\Gamma ^{\mu }) \) because of (6.3). This implies \( M_k^{\varepsilon ,\mu } = M_\Gamma ^\mu \le 0\), which leads to a contradiction.
Finally, we conclude by letting \( \varepsilon \rightarrow 0 \) and \( \mu \rightarrow 1 \). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dao, MK., Djehiche, B. Hamilton–Jacobi equations for optimal control on multidimensional junctions with entry costs. Nonlinear Differ. Equ. Appl. 27, 23 (2020). https://doi.org/10.1007/s00030-020-0625-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00030-020-0625-z


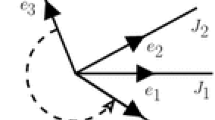





 has a local maximum at
has a local maximum at 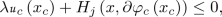
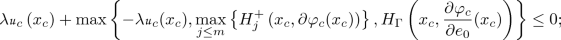
 has a local maximum point at
has a local maximum point at 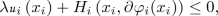
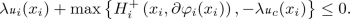
 has a local minimum at
has a local minimum at 
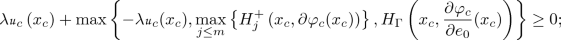
 has a local minimum point at
has a local minimum point at 
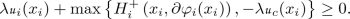
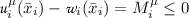 or
or 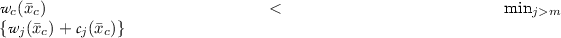 , we can check that
, we can check that  satisfies the super-optimality [
satisfies the super-optimality [ is a viscosity subsolution of
is a viscosity subsolution of 
 which leads to a contradiction. Otherwise, if there exists
which leads to a contradiction. Otherwise, if there exists 
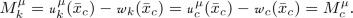
 does not occur, we finally obtain that
does not occur, we finally obtain that