Causal inference for left-truncated and right-censored data with covariate measurement error

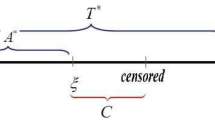
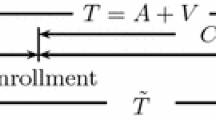Abstract

Causal inference is an important tool in observational studies. Many estimation procedures have been developed under complete data and precise measurements. However, when the datasets contain the incomplete responses induced by right-censoring and the covariate subject to measurement error, little work has been available to simultaneously address these features. Moreover, prevalent sampling is also a frequent phenomenon in survival analysis, and it makes analysis challenging since prevalent sampling causes a biased sample. In this paper, we are interested in exploring the causal estimation with those complex features incorporated. We propose the valid estimation procedure to estimate the average causal effect and the survivor functions based on different treatment assignments. Theoretical results of the proposed method are also established. Numerical studies are reported to assess the performance of the proposed method.

Appendices

Appendix A: Regularity conditions

Conditions for causal inference:

• • (A1) Stable Unit Treatment Value Assumption (SUTVA): Response of the ith subject is not to be affected by responses of other subjects (noninterference). Treatment $A^*$ could be assigned by different ways, but they all lead to the same outcome (consistency).

  • (A2) Strong Ignorable Treatment Assumption (SITA): Potential outcomes $\left( T^{*(0)}, T^{*(1)} \right)$ do not depend on the assigned treatment $A^*$ given the covariates $X^*$. Besides, $0< P\left( A^*= a | X^*\right) < 1$.

  Conditions for survival data and measurement error model:

  • (C1) $\Theta$ is a compact set, and the true parameter value $\theta _0$ is an interior point of $\Theta$.

  • (C2) Let $\mathbf{T}$ be the finite maximum support of the failure time.

  • (C3) The $\left\{ L_i, Y_i,X_i \right\}$ are independent and identically distributed for $i=1,\ldots ,n$.

  • (C4) The covariate $X_i$ is bounded.

  • (C5) Conditional on $X_i^*$, $\left( T_i^*, X_i^*\right)$ are independent of $L_i^*$.

  • (C6) Censoring time $C'_i$ is non-informative. That is, the failure time $T_i$ and the censoring time $C'_i$ are independent, given the covariates $X_i$.

  • (C7) The regression function $\varphi (\cdot )$ is true, and its first order derivative exists.

  • (C8) $\Lambda _\epsilon (\cdot )$ is second order differentiable. Besides, $\lambda _\epsilon (t) = \frac{{\text {d}}}{{\text {d}}t} \Lambda _\epsilon (t)$, also denoted by ${\text {d}}\Lambda _\epsilon (t)$, is a strictly increasing hazard function.

Conditions (A1) and (A2) are standard assumptions in causal inference, including Andersen et al. (2017, p. 2670) and Cheng and Wang (2012, p. 710). Condition (C1) is a basic condition that is used to derive the maximizer of the target function. (C2) to (C6) are standard conditions for survival analysis, which allow us to obtain the sum of i.i.d. random variables and hence to derive the asymptotic properties of the estimators. Condition (C7) is usually implemented in the developments of the asymptotic distribution of the SIMEX estimators (e.g., Chen 2019b, 2020). Finally, Condition (C8) is required in the development and also holds in applications. For example, when $\epsilon$ in (1) has an extreme value distribution, then according to the discussions in p. 3, $\lambda _\epsilon (t) = \exp (t)$ is a strictly increasing function.

Appendix B: Discussions of the unique solutions

In this appendix, we discuss the existence of the unique solutions of the system of estimating Eqs. (17) and (18).

We first discuss the unique solution of $H(\cdot )$ determined by (17). Since $\lambda _\epsilon (\cdot ) = {\text {d}}\Lambda _\epsilon (\cdot )$ is assumed to be a strictly increasing function, then for $t \in (0,\infty )$ and large n, we have

$$\begin{aligned} \sum \limits _{i=1}^n \left[ {\text {d}}N_i(t) - R_i(t) {\widehat{r}}(t,Y_i,\delta _i) {\text {d}}\Lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta + A_i + \left( H(t) - c_n \right) \right\} \right] > 0 \end{aligned}$$

and

$$\begin{aligned} \sum \limits _{i=1}^n \left[ {\text {d}}N_i(t) - R_i(t) {\widehat{r}}(t,Y_i,\delta _i) {\text {d}}\Lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta + A_i + \left( H(t) + c_n \right) \right\} \right] < 0 \end{aligned}$$

as $c_n$ is sufficiently large. Therefore, there exists a solution of H(t), denoted by ${\widehat{H}}(t;\beta )$, such that

$$\begin{aligned} \sum \limits _{i=1}^n \left[ {\text {d}}N_i(t) - R_i(t) {\widehat{r}}(t,Y_i,\delta _i) {\text {d}}\Lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta + A_i + {\widehat{H}}(t;\beta ) \right\} \right] = 0. \end{aligned}$$

(B.1)

On the other hand, according to discussions in Chen et al. (2002, p. 661) and the definition of $N_i(t)$ given in Sect. 2.1, functions $H(\cdot )$ and ${\widehat{H}}(t;\beta )$ only jump at the observed failure time $t=t_1,\ldots ,t_K$, i.e., (17) and (B.1) hold for $t = t_1,\ldots ,t_K$. We now discuss the uniqueness of ${\widehat{H}}(t;\beta )$ with $t=t_1,\ldots ,t_K$. For $k=1,\ldots ,K$, define

$$\begin{aligned} U_k = \sum \limits _{i=1}^n \left[ {\text {d}}N_i(t_k) - R_i(t_k) {\widehat{r}}(t_k,Y_i,\delta _i) \lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta +A_i + H(t_k) \right\} \right] , \end{aligned}$$

where $H(t_k)$ is a unknown scalar due to the unknown function H(t) with a fixed time point $t=t_k$. By taking the derivative on $U_k$ with respect to $H(t_k)$, we have

$$\begin{aligned} \frac{{\text {d}}U_k}{{\text {d}} H(t_k)} = -\sum \limits _{i=1}^n R_i(t_k) {\widehat{r}}(t_k,Y_i,\delta _i) {\text {d}}\lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta + A_i + H(t_k) \right\} < 0 \end{aligned}$$

since ${\text {d}}\lambda _\epsilon (t) = \frac{{\text {d}}}{{\text {d}}t} \lambda _\epsilon (t) > 0$ for every t due to that $\lambda _\epsilon (t)$ is a strictly increasing function. As a result, $U_k$ is a strictly decreasing function, and thus, the solution of $H(t_k)$, denoted by ${\widehat{H}}(t_k;\beta )$, is unique. Since this result holds for every $t=t_1,\ldots ,t_K$, then we conclude that the solution ${\widehat{H}}(t;\beta )$ is the unique solution of H(t).

We now discuss the unique solution determined by (18). By the derivation similar to the discussions above, we can show that the solution determined by (18) exists. On the other hand, taking the derivative on (18) with respect to $\beta$ gives

$$\begin{aligned} - \frac{1}{n} \sum \limits _{i=1}^n \int _0^\infty W_i(b,\zeta ) W_i^\top (b,\zeta ) \left[ R_i(t) {\widehat{r}}(t,Y_i,\delta _i) {\text {d}}\lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta + A_i + {\widehat{H}}(t;b,\zeta ,\beta )\right\} \right] , \end{aligned}$$

which is a negative definite matrix due to that ${\text {d}}\lambda _\epsilon (t) >0$, since $\lambda _\epsilon (t)$ is assumed to be a strictly increasing function. Therefore, solving (18) also yields the unique solution. $\square$

Appendix C: Proofs of main theorems

1.1 C.1 Proof of Theorem 3.1

Before presenting the proof, we first define some notation. Let ${\mathbf {T}}$ be the maximum value of the failure time. For any $s,t \in [0, {\mathbf {T}}]$, $b = 1,\ldots ,B$, and $\zeta \in {\mathcal {Z}}$, let

$$\begin{aligned} B_1(t;b,\zeta )= & {} E \left[ R_i(t) r(t,Y_i,\delta _i) \lambda _\epsilon '\left\{ W_i^\top (b,\zeta ) \beta (b,\zeta ) + A_i + H_0(t) \right\} \right] , \\ B_2(t;b,\zeta )= & {} E \left[ R_i(t) r(t,Y_i,\delta _i) \lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta (b,\zeta ) + A_i + H_0(t) \right\} \right] , \\ B_1^W(t;b,\zeta )= & {} E \left[ W_i(b,\zeta ) R_i(t) r(t,Y_i,\delta _i) \lambda _\epsilon '\left\{ W_i^\top (b,\zeta ) \beta (b,\zeta ) + A_i + H_0(t) \right\} \right] , \\ B_2^W(t;b,\zeta )= & {} E \left[ W_i(b,\zeta ) R_i(t) r(t,Y_i,\delta _i) \lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta (b,\zeta ) + A_i + H_0(t) \right\} \right] , \\ B(t,s;b,\zeta )= & {} \exp \left\{ \int _s^t B_2^{-1}(u;b,\zeta ) B_1(u;b,\zeta ) {\text {d}}H_0(u) \right\} , \end{aligned}$$

where $\lambda _\epsilon '(\cdot )$ is the derivative of $\lambda _\epsilon (\cdot )$. We further define

$$\begin{aligned} {\mathbf {w}}(t)= & {} B_2^{-1}(t;b,\zeta ) \left[ B_2^W(t;b,\zeta ) \right. \\&\left. + \int _t^{\mathbf {T}} \left\{ B_1^W(s;b,\zeta ) - B_2^{-1}(s;b,\zeta ) B_2^W(s;b,\zeta ) B_1(s;b,\zeta ) \right\} B(t,s;b,\zeta ) {\text {d}}H_0(s) \right] , \\ \mathbf{a}(t)= & {} \frac{1}{\pi (t)} \int _0^{\mathbf {T}} E \left[ \frac{W_i(b,\zeta ) \delta _i R_i(s)}{w(Y_i)} \left( I(t \le s) \int _t^s S_C(u) {\text {d}}u \right. \right. \\&\left. \left. - \frac{w(s)}{w(Y_i)} I(t \le Y_i ) \int _t^{Y_i} S_C(u) {\text {d}}u\right) {\text {d}}\Lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta (b,\zeta ) + A_i + H_0(s) \right\} \right] , \end{aligned}$$

where $\pi (t) = P\left( Y_i - L_i \ge t \right)$.

Proof of Theorem 3.1 (1)

The Kaplan–Meier estimator ${\widehat{S}}_C(t)$ over $[0, \mathbf{T }]$ is uniformly consistent to $S_C(t)$ in the sense that $\sup \nolimits _{t \in [0, \mathbf{T }]} \left| {\widehat{S}}_C(t) - S_C(t) \right| {\mathop {\longrightarrow }\limits ^{p}} 0$ as $n \rightarrow \infty$ (Pollard 1990, Sect. 8; van der Vaart 1998, Ch19). It implies that as $n \rightarrow \infty$,

$$\begin{aligned} \sup \limits _{t \in [0, \mathbf{T }]} \left| {\widehat{w}}(t) - w(t) \right| {\mathop {\longrightarrow }\limits ^{p}} 0 \ \ \text {and} \ \ \sup \limits _{t \in [0, \mathbf{T }]} \left| {\widehat{r}}(t,Y_i,\delta _i) - r(t,Y_i,\delta _i) \right| {\mathop {\longrightarrow }\limits ^{p}} 0, \end{aligned}$$

(C.1)

since $\sup \nolimits _{t \in [0, \mathbf{T }]} \left| \int _0^t {\widehat{S}}_C(u){\text {d}}u - \int _0^t S_C(u){\text {d}}u \right| \le \sup \nolimits \limits _{t \in [0, \mathbf{T }]} \int _0^t\left| {\widehat{S}}_C(u)- S_C(u)\right| {\text {d}}u {\mathop {\longrightarrow }\limits ^{p}} 0$ as $n \rightarrow \infty$. Furthermore, by the derivations similar to Step 2 in Kim et al. (2013), we have

$$\begin{aligned} \left. \frac{\partial {\widehat{H}}(t;b,\zeta ,\beta )}{\partial \beta } \right| _{\beta = \beta _0}= & {} - \int _0^t \frac{B(s,t;b,\zeta )}{B_2(s;b,\zeta )} B_1^W (s;b,\zeta ) {\text {d}}H_0(s) + o_p(1) \nonumber \\\triangleq & {} A(t) + o_p(1). \end{aligned}$$

(C.2)

Let $\theta (b,\zeta )$ be the solution of $E\left\{ U_{{\text {SIMEX}}}(\theta )\right\} = 0$. Since ${\widehat{\theta }}(b,\zeta )$ is the solution of $U_{{\text {SIMEX}}}(\theta ) = 0$. By (C.1), (C.2), and the Uniformly Law of Large Numbers (van der Vaart 1998), we have that $\frac{1}{n} U_{{\text {SIMEX}}}(\theta )$ converges uniformly to $E\left\{ U_{{\text {SIMEX}}}(\theta )\right\}$ as $n \rightarrow \infty$. Then we have that as $n \rightarrow \infty$,

$$\begin{aligned} {\widehat{\theta }}(b,\zeta ) {\mathop {\longrightarrow }\limits ^{p}} \theta (b,\zeta ). \end{aligned}$$

(C.3)

By definition (24), taking averaging with respect to b on both sides of (C.3) gives that ${\widehat{\theta }}(\zeta ) {\mathop {\longrightarrow }\limits ^{p}} \theta (\zeta )$ as $n \rightarrow \infty$ for every $\zeta \in {\mathcal {Z}}$. We can further show that ${\widehat{\Gamma }} {\mathop {\longrightarrow }\limits ^{p}} \Gamma$ as $n \rightarrow \infty$. Since ${\widehat{\theta }}_{{\text {SIMEX}}} = \varphi \left( -1,{\widehat{\Gamma }} \right)$, therefore, by the continuous mapping theorem, we have that as $n \rightarrow \infty$,

$$\begin{aligned} {\widehat{\theta }}_{{\text {SIMEX}}} {\mathop {\longrightarrow }\limits ^{p}} \theta _0. \end{aligned}$$

(C.4)

$\square$

Proof of Theorem 3.1 (2):

By (C.4), we have ${\widehat{H}}(t;b,\zeta ,{\widehat{\beta }}_{{\text {SIMEX}}}) - {\widehat{H}}(t;b,\zeta ,\beta _0) = o_p(1)$ for every $t \in [0, {\mathbf {T}}]$, b, and $\zeta$. Taking average with respect to b gives ${\widehat{H}}(t;\zeta ,{\widehat{\beta }}_{{\text {SIMEX}}}) - {\widehat{H}}(t;\zeta ,\beta _0) = o_p(1)$. On the other hand, by the Uniformly Law of Large Numbers and similar derivations to that of Step 1 in Kim et al. (2013) with $\zeta \rightarrow -1$, we have that as $n \rightarrow \infty$, ${\widehat{H}}(t;\beta _0) - H_0(t) {\mathop {\longrightarrow }\limits ^{p}} 0$ for all $t \in [0, {\mathbf {T}}]$. Therefore, we conclude that as $n \rightarrow \infty$ and $\zeta \rightarrow -1$, ${\widehat{H}}_{{\text {SIMEX}}}(t) - H_0(t) {\mathop {\longrightarrow }\limits ^{p}} 0$ by the fact that ${\widehat{H}}(t;-1,{\widehat{\beta }}_{{\text {SIMEX}}}) - H_0(t) = {\widehat{H}}(t;-1,{\widehat{\beta }}_{{\text {SIMEX}}}) - {\widehat{H}}(t;-1,\beta _0) + {\widehat{H}}(t;-1,\beta _0) - H_0(t)$. $\square$

Proof of Theorem 3.1 (3):

For $b = 1,\ldots ,B$ and $\zeta \in {\mathcal {Z}}$, applying the Taylor series expansion on (16) around ${\theta }(b,\zeta )$ gives

$$\begin{aligned} \sqrt{n} \left\{ {\widehat{\theta }}(b,\zeta ) - {\theta }(b,\zeta ) \right\}= & {} \left( -\frac{\partial U_{{\text {SIMEX}}}\left( {\theta }(b,\zeta ) \right) }{\partial \theta } \right) ^{-1} \sqrt{n} U_{{\text {SIMEX}}}\left( {\theta }(b,\zeta ) \right) \nonumber \\&+ o_p\left( 1 \right) . \end{aligned}$$

(C.5)

By (C.1), (C.2), and the Uniformly Law of Large Numbers, we have that as $n \rightarrow \infty$,

$$\begin{aligned} \left( -\frac{\partial U_{{\text {SIMEX}}}\left( {\theta }(b,\zeta ) \right) }{\partial \theta } \right) {\mathop {\longrightarrow }\limits ^{p}} {\mathcal {A}}\left( b,\zeta \right) , \end{aligned}$$

(C.6)

where

$$\begin{aligned}&{\mathcal {A}}\left( b,\zeta \right) \\&\quad = \text {diag} \left( - E\left[ \int _0^{\mathbf{T }} \left\{ W_i(b,\zeta ) \right. \right. \right. \\&\qquad \left. \left. \left. - {\mathbf {w}}(t) \right\} W_i^\top (b,\zeta ) R_i(t) r(t,Y_i,\delta _i) \lambda _\epsilon ' \left\{ W_i^\top (b,\zeta ) \beta (b,\zeta ) + A_i + H_0(t) \right\} {\text {d}}H_0(t) \right] , \right. \\&\quad \left. E\left\{ A_i \frac{p''p-(p')^{\otimes 2}}{p^2} + (1-A_i) \frac{p''(1-p) + (p')^{\otimes 2}}{(1-p)^2} \right\} \right) , \end{aligned}$$

$p''(x) = \frac{\partial ^2 p(x)}{\partial \gamma \partial ^\top \gamma }$, $a^{\otimes 2} = aa^\top$ for any vector a, and p, $p'$, and $p''$ represent $p(W_i(b,\zeta ))$, $p'(W_i(b,\zeta ))$, and $p''(W_i(b,\zeta ))$ for ease of notation.

On the other hand, $U_{{\text {SIMEX}}}({\theta }(b,\zeta ))$ can be expressed as a sum of i.i.d. random functions, which is given by

$$\begin{aligned} \sqrt{n} U_{{\text {SIMEX}}}({\theta }(b,\zeta )) = \frac{1}{\sqrt{n}} \sum \limits _{i=1}^n \Psi _i(b,\zeta ) + o_p(1), \end{aligned}$$

(C.7)

where

$$\begin{aligned} \Psi _i(b,\zeta )= & {} \left( \int _0^\mathbf{T } \left[ \left\{ W_i(b,\zeta ) - {\mathbf {w}}(t)\right\} {\text {d}}M_i(t) \mathbf{a}(t) {\text {d}}M_{C}(t) \right] , \right. \\&\left. \left\{ A_i \frac{p'(W_i(b,\zeta ))}{p(W_i(b,\zeta ))} - (1-A_i) \frac{p'(W_i(b,\zeta ))}{1-p(W_i(b,\zeta ))} \right\} \right) ^\top , \end{aligned}$$

$M_{C}(t) = I\left( Y_i \le t, \delta _i = 0 \right) - \int _0^t I\left( Y_i \ge u \right) {\text {d}}\Lambda _C(u)$, and $\Lambda _C(\cdot )$ is the cumulative hazard function of C.

Combining (C.7) and (C.6) with (C.5) yields

$$\begin{aligned} \sqrt{n} \left\{ {\widehat{\theta }}(b,\zeta ) - {\theta }(b,\zeta ) \right\} = \frac{1}{\sqrt{n}} \sum \limits _{i=1}^n {\mathcal {A}}^{-1}\left( b,\zeta \right) \Psi _i(b,\zeta ) + o_p\left( 1 \right) . \end{aligned}$$

(C.8)

By (24), taking average with respect to b on both sides of (C.8) gives

$$\begin{aligned} \sqrt{n} \left\{ {\widehat{\theta }}(\zeta ) - {\theta }(\zeta ) \right\} = \frac{1}{\sqrt{n}} \sum \limits _{i=1}^n \Phi _i(\zeta ) + o_p\left( 1 \right) \end{aligned}$$

(C.9)

for $\zeta \in {\mathcal {Z}}$, where $\Phi _i(\zeta ) = \frac{1}{B} \sum \nolimits _{b=1}^B {\mathcal {A}}^{-1}\left( b,\zeta \right) \Psi _i(b,\zeta )$.

Let ${\widehat{\theta }}({\mathcal {Z}}) = \text {vec}\left\{ {\widehat{\theta }}(\zeta ) : \zeta \in {\mathcal {Z}}\right\}$ denote the vectorization of estimator ${\widehat{\theta }}(\zeta )$ with every $\zeta \in {\mathcal {Z}}$. By the Central Limit Theorem on (C.9), we have that as $n \rightarrow \infty$,

$$\begin{aligned} \sqrt{n} \left\{ {\widehat{\theta }}({\mathcal {Z}}) - {\theta }({\mathcal {Z}}) \right\} {\mathop {\longrightarrow }\limits ^{d}} N\left( 0, \Omega \left( {\mathcal {Z}} \right) \right) , \end{aligned}$$

(C.10)

where $\Omega \left( {\mathcal {Z}} \right) = \text {cov}\left\{ \Phi _i({\mathcal {Z}}) \right\}$. By the Taylor series expansion on $\varphi \left( {\mathcal {Z}}, \Gamma \right)$ with respect to $\Gamma$, we have

$$\begin{aligned} \varphi \left( {\mathcal {Z}}, {\widehat{\Gamma }} \right) - \varphi \left( {\mathcal {Z}}, \Gamma \right) \approx \frac{\partial \varphi \left( {\mathcal {Z}}, \Gamma \right) }{\partial \Gamma } \left( {\widehat{\Gamma }} - \Gamma \right) . \end{aligned}$$

(C.11)

Let ${\mathcal {C}} = \frac{\partial \varphi \left( {\mathcal {Z}}, \Gamma \right) }{\partial \Gamma }$ and ${\mathcal {D}} = \left\{ \frac{\partial \varphi \left( {\mathcal {Z}}, \Gamma \right) }{\partial \Gamma }\right\} ^\top \frac{\partial \varphi \left( {\mathcal {Z}}, \Gamma \right) }{\partial \Gamma }$. Combining (C.10) and (C.11) gives that as $n \rightarrow \infty$,

$$\begin{aligned} \sqrt{n} \left( {\widehat{\Gamma }} - \Gamma \right) {\mathop {\longrightarrow }\limits ^{d}} N\left( 0, {\mathcal {D}}^{-1} {\mathcal {C}} \Omega ({\mathcal {Z}}) {\mathcal {C}}^\top {\mathcal {D}}^{-1} \right) . \end{aligned}$$

(C.12)

Finally, let ${\mathcal {Q}} = {\mathcal {D}}^{-1} {\mathcal {C}} \Omega ({\mathcal {Z}}) {\mathcal {C}}^\top {\mathcal {D}}^{-1}$. Since the SIMEX estimator is defined by ${\widehat{\theta }}_{{\text {SIMEX}}} = \varphi \left( -1, {\widehat{\Gamma }} \right)$, then combining (C.11) and (C.12) with $\zeta \rightarrow -1$ and ${\widehat{\Gamma }} \rightarrow \Gamma$, and then applying the delta method give that as $n \rightarrow \infty$,

$$\begin{aligned} \sqrt{n} \left( {\widehat{\theta }}_{{\text {SIMEX}}} - \theta _0 \right) {\mathop {\longrightarrow }\limits ^{d}} N\left( 0, \left\{ \frac{\partial \varphi }{\partial \Gamma }\left( -1, \Gamma \right) \right\} {\mathcal {Q}} \left\{ \frac{\partial \varphi }{\partial \Gamma } \left( -1, \Gamma \right) \right\} ^\top \right) . \end{aligned}$$

$\square$

Proof of Theorem 3.1 (4):

We first consider the expression of $\sqrt{n} \left\{ {\widehat{H}}(t;b,\zeta ,{\widehat{\beta }}_{{\text {SIMEX}}}) - {\widehat{H}}(t;b,\zeta ,\beta _0) \right\}$. Since $\Gamma$, ${\mathcal {D}}$, ${\mathcal {C}}$, and $\Phi _i(\cdot )$ are based on $\theta$, and $\theta$ contains the paramter $\beta$. So we take decomposition of $\Gamma$, ${\mathcal {D}}$, ${\mathcal {C}}$, and $\Phi _i(\cdot )$ and only take terms related to $\beta$. Let those term denote $\Gamma _\beta$, ${\mathcal {D}}_\beta$, ${\mathcal {C}}_\beta$, and $\Phi _{i,\beta }(\cdot )$, respectively. By the Taylor series expansion with respect to $\beta$, we have

$$\begin{aligned}&\sqrt{n} \left\{ {\widehat{H}}(t;b,\zeta ,{\widehat{\beta }}_{{\text {SIMEX}}}) - {\widehat{H}}(t;b,\zeta ,\beta _0) \right\} \nonumber \\&\quad = \frac{\partial {\widehat{H}}(t;b,\zeta ,\beta _0)}{\partial \beta } \sqrt{n} \left( {\widehat{\beta }}_{{\text {SIMEX}}} - \beta _0 \right) \nonumber \\&\quad = A(t) \sqrt{n} \left( {\widehat{\beta }}_{{\text {SIMEX}}} - \beta _0 \right) + o_p(1) \nonumber \\&\quad = A(t) \frac{1}{\sqrt{n}} \sum \limits _{i=1}^n \left\{ \frac{\partial \varphi }{\partial \Gamma _\beta }\left( -1, {\widehat{\Gamma }}_\beta \right) \right\} {\mathcal {D}}_\beta ^{-1} {\mathcal {C}}_\beta \Phi _{i,\beta }({\mathcal {Z}}) + o_p(1), \end{aligned}$$

(C.13)

where the second equality is due to (C.2) and the third equality is due to (C.12).

On the other hand, note that

$$\begin{aligned} \sum \limits _{i=1}^n {\text {d}}M_i(t)= & {} \sum \limits _{i=1}^n {\text {d}}N_i(t) - \sum \limits _{i=1}^n \left[ R_i(t) r(t,Y_i,\delta _i) {\text {d}}\Lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta _0 + A_i + H_0(t)\right\} \right] \\= & {} \sum \limits _{i=1}^n \left[ R_i(t) {\widehat{r}}(t,Y_i,\delta _i) {\text {d}}\Lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta _0 + A_i + {\widehat{H}}(t;b,\zeta ,\beta _0)\right\} \right] \\&- \sum \limits _{i=1}^n \left[ R_i(t) r(t,Y_i,\delta _i) {\text {d}}\Lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta _0 + A_i + H_0(t)\right\} \right] \\= & {} \sum \limits _{i=1}^n \left\{ 1 + o_p(1) \right\} \left( R_i(t) r(t,Y_i,\delta _i) d \left[ \lambda _\epsilon \left\{ W_i^\top (b,\zeta ) \beta _0 \right. \right. \right. \\&\quad \left. \left. \left. + A_i + H_0(t) \right\} \left\{ {\widehat{H}}(t;b,\zeta ,\beta _0) - H_0(t) \right\} \right] \right) . \end{aligned}$$

It also indicates that

$$\begin{aligned} \sqrt{n} \left\{ {\widehat{H}}(t;b,\zeta ,\beta _0) - H_0(t) \right\} = \frac{1}{\sqrt{n}} \sum \limits _{i=1}^n \int _0^t \frac{B(s,t;b,\zeta )}{B_2(s;b,\zeta )} {\text {d}}M_i(s) + o_p(1). \end{aligned}$$

(C.14)

Then combining (C.13) and (C.14) gives

$$\begin{aligned} \sqrt{n} \left\{ {\widehat{H}}(t;b,\zeta ,{\widehat{\beta }}_{{\text {SIMEX}}}) - H_0(t) \right\} = \frac{1}{\sqrt{n}} \sum \limits _{i=1}^n {\mathcal {T}}_i(t;b,\zeta ) + o_p(1), \end{aligned}$$

(C.15)

where ${\mathcal {T}}_i(t;b,\zeta ) = A(t) \left\{ \frac{\partial \varphi }{\partial \Gamma _\beta }\left( -1, {\widehat{\Gamma }}_\beta \right) \right\} {\mathcal {D}}_\beta ^{-1} {\mathcal {C}}_\beta \Phi _{i,\beta }({\mathcal {Z}}) + \int _0^t \frac{B(s,t;b,\zeta )}{B_2(s;b,\zeta )} {\text {d}}M_i(s)$. Taking average on both sides of (C.15) with respect to b yields

$$\begin{aligned} \sqrt{n} \left\{ {\widehat{H}}(t;\zeta ,{\widehat{\beta }}_{{\text {SIMEX}}}) - H_0(t) \right\} = \frac{1}{\sqrt{n}} \sum \limits _{i=1}^n {\mathcal {T}}_i(t;\zeta ) + o_p(1), \end{aligned}$$

(C.16)

where ${\mathcal {T}}_i(t;\zeta ) = \frac{1}{B} \sum \nolimits _{b=1}^B {\mathcal {T}}_i(t;b,\zeta )$.

Suppose that $\varphi _H(\zeta ,\Gamma _H(t))$ is a function with the same conditions in (C7), and $\Gamma _H(t)$ is the associated parameter depending on time t. For $t \in [0, {\mathbf {T}}]$ and $\zeta \in {\mathcal {Z}}$, we fit a regression model on ${\widehat{H}}(t;\zeta ,{\widehat{\beta }}_{{\text {SIMEX}}})$ and $\varphi _H(\zeta ,\Gamma _H(t))$, and derive the estimator of $\Gamma _H(t)$ which is denoted by ${\widehat{\Gamma }}_H(t)$. Furthermore, similar to the derivations in (C.11), we have

$$\begin{aligned} \varphi _H\left( {\mathcal {Z}}, {\widehat{\Gamma }}_H(t) \right) - \varphi _H\left( {\mathcal {Z}}, \Gamma _H(t) \right) \approx \frac{\partial \varphi _H\left( {\mathcal {Z}}, \Gamma _H(t) \right) }{\partial \Gamma _H(t)} \left\{ {\widehat{\Gamma }}_H(t) - \Gamma _H(t) \right\} . \end{aligned}$$

(C.17)

Let ${\mathcal {U}}(t) = \frac{\partial \varphi _H\left( {\mathcal {Z}}, \Gamma _H(t) \right) }{\partial \Gamma _H(t)}$ and ${\mathcal {V}}(t) = \left\{ \frac{\partial \varphi _H\left( {\mathcal {Z}}, \Gamma _H(t) \right) }{\partial \Gamma _H(t)}\right\} ^\top \frac{\partial \varphi _H\left( {\mathcal {Z}}, \Gamma _H(t) \right) }{\partial \Gamma _H(t)}$. Combining (C.16) and (C.17) yields

$$\begin{aligned} \sqrt{n} \left\{ {\widehat{\Gamma }}_H(t) - \Gamma _H(t) \right\} = \frac{1}{\sqrt{n}} \sum \limits _{i=1}^n {\mathcal {V}}^{-1}(t) {\mathcal {U}}(t) {\mathcal {T}}_i(t;{\mathcal {Z}}) + o_p(1), \end{aligned}$$

(C.18)

and since the estimator ${\widehat{H}}_{{\text {SIMEX}}}(t)$ is a predicted value of $\varphi _H(\zeta ,{\widehat{\Gamma }}_H(t))$ by taking $\zeta \rightarrow -1$, then by (C.18) and the delta method with $\zeta \rightarrow -1$, we obtain

$$\begin{aligned}&\sqrt{n} \left\{ {\widehat{H}}_{{\text {SIMEX}}}(t) - H_0(t) \right\} \nonumber \\&\quad = \frac{1}{\sqrt{n}} \sum \limits _{i=1}^n \left\{ \frac{\partial \varphi _H(-1,{\widehat{\Gamma }}_H(t))}{\partial \Gamma _H(t)} \right\} {\mathcal {V}}^{-1}(t) {\mathcal {U}}(t) {\mathcal {T}}_i(t;{\mathcal {Z}}) + o_p(1) \nonumber \\&\quad \triangleq \frac{1}{\sqrt{n}} \sum \limits _{i=1}^n {\mathcal {H}}_i(t) + o_p(1). \end{aligned}$$

(C.19)

where ${\mathcal {H}}_i(t) = \left\{ \frac{\partial \varphi _H(-1,{\widehat{\Gamma }}_H(t))}{\partial \Gamma _H(t)} \right\} {\mathcal {V}}^{-1}(t) {\mathcal {U}}(t) {\mathcal {T}}_i(t;{\mathcal {Z}})$. Finally, by the Central Limit Theorem, we conclude that $\sqrt{n} \left\{ {\widehat{H}}_{{\text {SIMEX}}}(t) - H_0(t) \right\}$ converges to the Gaussian process with mean zero and covariance function $E\left\{ {\mathcal {H}}_i(t) {\mathcal {H}}_i(s) \right\}$. $\square$

1.2 C.2 Proof of Theorem 3.2

The consistent estimators ${\widehat{\beta }}_{{\text {SIMEX}}}$ and ${\widehat{H}}_{{\text {SIMEX}}}(t)$ in Theorem 3.1 (a) and (b) suggests that (26) converges in probability to $q_a$ for $a=0,1$ as $n \rightarrow \infty$ and $\zeta \rightarrow -1$. In addition, Theorem 3.1 (a) indicates ${\widehat{\gamma }}_{{\text {SIMEX}}} = \gamma _0 + o_p(1)$. Therefore, we have that ${\widehat{p}}(\cdot ) {\mathop {\longrightarrow }\limits ^{p}} p(\cdot )$ as $n \rightarrow \infty$.

On the other hand, the Kaplan–Meier estimator ${\widehat{S}}_C(t)$ over $[0, \mathbf{T }]$ is uniformly consistent to $S_C(t)$ in the sense that $\sup \nolimits _{t \in [0, \mathbf{T }]} \left| {\widehat{S}}_C(t) - S_C(t) \right| {\mathop {\longrightarrow }\limits ^{p}} 0$ as $n \rightarrow \infty$ (Pollard 1990; van der Vaart 1998). As a result, for every b and $\zeta$, applying the Law of Large Numbers gives

$$\begin{aligned} \frac{1}{n} \sum \limits _{i=1}^n \frac{\delta _i A_i Y_i}{{\widehat{p}}(W_i(b,\zeta )) {\widehat{S}}_C(Y_i)} {\mathop {\longrightarrow }\limits ^{p}} E\left\{ \frac{\delta _i A_i Y_i}{p(W_i(b,\zeta )) S_C(Y_i)} \right\} \end{aligned}$$

(C.20)

and

$$\begin{aligned} \frac{1}{n} \sum \limits _{i=1}^n \frac{\delta _i (1-A_i) Y_i}{\left\{ 1-{\widehat{p}}(W_i(b,\zeta ))\right\} {\widehat{S}}_C(Y_i)} {\mathop {\longrightarrow }\limits ^{p}} E \left\{ \frac{\delta _i (1-A_i) Y_i}{\left\{ 1-p(W_i(b,\zeta ))\right\} S_C(Y_i)} \right\} . \end{aligned}$$

(C.21)

Based on the relationship of generation in Stage 1, we have $W_i(b,\zeta ) \rightarrow X_i$ as $\zeta \rightarrow -1$. Therefore, combining the result in Theorem 2.1 with (C.20) and (C.21) yields ${\widehat{\tau }}_{{\text {SIMEX}}} {\mathop {\longrightarrow }\limits ^{p}} \tau _0$ as $n \rightarrow \infty$. $\square$