Hilbert geometries with Riemannian points

Abstract

If a Hilbert geometry of twice differentiable boundary has two quadratic infinitesimal spheres, then the Hilbert geometry is a Cayley–Klein model of the hyperbolic geometry.

1 Introduction

Let $\overline{CD}$ denote the open segment of the points $C,D\in \mathbb {R}^n$ ($n=1,2,\ldots$), and if it is on the straight line AB of points $A,B\in \mathbb {R}^n$, then let (A, B; C, D) denote the cross-ratio of these points. If $\mathcal {M}$ is an open, strictly convex, and bounded subset of $\mathbb {R}^n$ ($n=2,3,\ldots$), then the function $d:\mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} d(A,B) ={\left\{ \begin{array}{ll} 0,&{}\text {if }A=B,\\ \frac{1}{2}\big |\ln (A,B;C,D)\big |, &{}\text {if }A\ne B,\hbox { where }\overline{CD}=\mathcal {M}\cap AB, \end{array}\right. } \end{aligned}$$

is a metric on $\mathcal {M}$ [4, p. 297] which satisfies the strict triangle inequality, i.e., $d(A,B)+d(B,C)=d(A,C)$ if and only if $B\in \overline{AC}\cup \{A,C\}$. This function d is called the Hilbert metric on$\mathcal {M}$, and $\mathcal {M}$ is its domain. Such pairs $(\mathcal {M},d)$ are called Hilbert geometries.

Hilbert geometries are Finslerian manifolds [4, (29.6)]. We call a point P of a Hilbert geometry $(\mathcal {M},d)$Riemannian if the Finsler norm on $T_P\mathcal {M}$ is quadratic. By Beltrami’s theorem [1, 2] (see also [4, (29.3)]), a Hilbert geometry is Riemannian if and only if it is a Cayley–Klein model of the hyperbolic geometry.

In this paper, we prove in Theorem 4.4 that

a Hilbert geometry in the plane has two Riemannian points if and only if it is a Cayley–Klein model of the hyperbolic geometry.

For the proof, we need the assumption that the boundary is twice differentiable at the points, where the line joining the two Riemannian points intersects the boundary. Theorem 5.2 shows that this assumption is also necessary.

Theorem 4.4 is also formulated in the language of geometric tomography [7] by Theorem 5.3:

the twice differentiable boundary of a strictly convex bounded domain in the plane is an ellipse if and only if its$(-1)$-chord functions are quadratic at two inner points.

2 Notations and preliminaries

Points of $\mathbb {R}^n$ are denoted by capital letters $A,B,\ldots$, vectors are $\overrightarrow{AB}$ or ${\varvec{a}} , {\varvec{b}} , \ldots$, but we use these latter notations also for points if the origin is fixed. We denote the interior of the convex hull of a point set $\mathcal {P}$ by $\overline{\mathcal {P}}$.

For $C\in AB$, the affine ratio (A, B; C) is defined by $(A,B;C)\overrightarrow{BC}=\overrightarrow{AC}$, and it satisfies $(A,B;C,D)=(A,B;C)/(A,B;D)$ [4, p. 243].

If a Euclidean metric $d_e$ is given, then the length of a segment $\overline{AB}$, or of a vector $\overrightarrow{AB}={\varvec{x}}$ is denoted by $|AB|=|{\varvec{x}}|=d_e(A,B)$.

We use the usual big-O and little-o notation. To indicate derivatives of a function or a map, we use prime, dot or $\mathsf D$ appropriately.

If the domain $\mathcal {M}$ of the Hilbert geometry $(\mathcal {M},d)$ is in $\mathbb {R}^n$, then we identify the tangent spaces $T_P\mathcal {M}$ with $\mathbb {R}^n$ by the map $\imath _P:{\varvec{v}}\mapsto P+{\varvec{v}}$. This way, the Finsler function $F_{\mathcal {M}}:\mathcal {M}\times \mathbb {R}^n\rightarrow \mathbb {R}$ associated with the Hilbert metric d can be given at a point $P\in \mathcal {M}$ by

$$\begin{aligned} F_{\mathcal {M}}(P,{\varvec{v}})=\frac{1}{2}\Big (\frac{1}{\lambda _{{\varvec{v}}}^-}+\frac{1}{\lambda _{{\varvec{v}}}^+}\Big ), \end{aligned}$$

(2.1)

where ${\varvec{v}}\in T_P\mathcal {M}$, and $\lambda _{{\varvec{v}}}^\pm \in (0,\infty ]$ is such that $P_{{\varvec{v}}}^\pm :=P\pm \lambda _{{\varvec{v}}}^\pm {\varvec{v}}\in \partial \mathcal {M}$ [4, (50.4)].¹ Equation (2.1) implies that $\imath _P$ maps the indicatrix of norm $F_{\mathcal {M}}(P,\cdot )$ into the strictly convex set $\mathcal {B}^{\mathcal {M}}_P\subset \mathbb {R}^n$, the infinitesimal ball, with boundary

$$\begin{aligned} \mathcal {S}^{\mathcal {M}}_P :=\partial \mathcal {B}^{\mathcal {M}}_P =\{ 2(P_{{\varvec{v}}}^+-P)(P,P_{{\varvec{v}}}^+;P_{{\varvec{v}}}^-) :{\varvec{v}}\in T_P\mathcal {M}\}, \end{aligned}$$

the infinitesimal sphere. Observe here that

(2.2)

So, infinitesimal spheres are called infinitesimal circles and denoted by $\mathcal {C}^{\mathcal {M}}_P$.

If a Euclidean metric is provided, then we frequently use the notation ${\varvec{u}}_\varphi =(\cos \varphi ,\sin \varphi )$. Further, if a bounded open domain $\mathcal {D}\subset \mathbb {R}^2$ is starlike with respect to a point $P\in \mathcal {D}$, then we usually polar parameterize the boundary$\partial \mathcal {D}$ with a function ${\varvec{r}}:[-\pi ,\pi )\rightarrow \mathbb {R}^2$ defined by ${\varvec{r}}(\varphi )= r(\varphi ){\varvec{u}}_\varphi \in \partial \mathcal {D},$ where $r>0$ is the radial function of $\mathcal {D}$ with respect to the base point P. For any ellipse $\mathcal {E}$ with center P there exists unique $\omega \in (-\pi /2,\pi /2]$ and $a\ge b>0$ such that

$$\begin{aligned} \frac{1}{r^2(\varphi )} =\frac{\cos ^2(\varphi -\omega )}{a^2}+\frac{\sin ^2(\varphi -\omega )}{b^2} \end{aligned}$$

(2.3)

is the polar equation with respect to origin P.

We also use the notation $\ell _{{\varvec{d}}}:=\{\lambda {\varvec{d}}:\lambda \in \mathbb {R}\}$ for the line through the origin with nonvanishing directional vector ${\varvec{d}}$, and $\ell _\xi =\ell _{{\varvec{u}}_\xi }$ as a short hand in the plane.

The following result is a rephrase of [5, Stable Manifold Theorem, p. 114]. See also [6, Theorem 4.1]!

Theorem 2.1

Let $\mathcal {N}_0\subset \mathbb {R}^2$ be a neighborhood of the origin ${\varvec{0}}$, and let the mapping $\Phi :\mathcal {N}_0\rightarrow \mathbb {R}^2$ be of class $C^l$$(l\in [1,\infty ])$.

If there are linearly independent vectors ${\varvec{u}}$ and ${\varvec{v}}$ such that $\Phi ({\varvec{w}})={\varvec{w}}$ for every ${\varvec{w}}\in \ell _{{\varvec{u}}}\cap \mathcal {N}_0$, and for some $k\in (0,1)$, then in some neighborhood $\mathcal {N}\subseteq \mathcal {N}_0$ of ${\varvec{0}}$ the set $\{{\varvec{w}}\in \mathcal {N}:\Phi ^{(r)}({\varvec{w}})\rightarrow {\varvec{0}}\text { as }r\rightarrow \infty \}$ is the graph of a $C^l$ function from $\ell _{{\varvec{v}}}\cap \mathcal {N}$ to $\ell _{{\varvec{u}}}\cap \mathcal {N}$.

Notice that $\Phi ^{(r)}$ refers to the r-th iterate, rather than, e.g., the r-th derivative.

Finally, we need the following easy consequence of [4, (28.11)]:

(2.4)

3 Utilities

Although it is known that the hyperbolic geometry is a Riemannian manifold, so its infinitesimal spheres are quadratic, the following result gives some more details.

Lemma 3.1

Let $\mathcal {E}_e$ be the ellipse $x^2+\frac{y^2}{e^2}=1$, and let $P=(p,0)$, where $p\in (-1,1)$. Then $\mathcal {C}^{\overline{\mathcal {E}}_e}_P$ is the ellipse $\frac{(x-p)^2}{a^2}+\frac{y^2}{b^2}=1$, where $a=1-p^2$ and $b=e\sqrt{1-p^2}$.

Proof

According to (2.2), we can assume that $e=1$ without loss of generality.

Let line $P+\ell _\xi$ intersect $\mathcal {E}_e$ in the points $P\pm \lambda _\pm {\varvec{u}}_\xi$. Then $1=\lambda _\pm ^2+p^2\mp 2p\lambda _\pm \cos \xi$, hence $\lambda _\pm =\pm p\cos \xi +\sqrt{1-p^2\sin ^2\xi }$. Thus (2.1) gives

$$\begin{aligned} \frac{1}{r^2(\xi )} =\Big (\frac{1}{\lambda _+}+\frac{1}{\lambda _-}\Big )^2 =\frac{1-p^2\sin ^2\xi }{(1-p^2)^2} =\frac{\cos ^2\xi }{{(1-p^2)^2}}+\frac{\sin ^2\xi }{1-p^2}. \end{aligned}$$

$\square$

Notice that $\mathcal {C}^{\bar{\mathcal {E}}_e}_P$ is a circle if and only if $1-p^2=e\sqrt{1-p^2}$, i.e., $p=\pm \sqrt{1-e^2}$ which can only happen if $e<1$. In this case, P is a focus of $\mathcal {E}_e$.

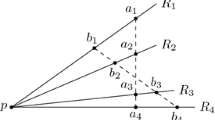
From now on, we always use the following general configuration: P is a point of a 2-dimensional Hilbert geometry $(\mathcal {M},d)$; $\ell$ is a straight line through P; I and J are the points where $\ell$ intersects $\partial \mathcal {M}$; a coordinate system is chosen² such that $I=(-1,0)$, $J=(1,0)$, and $P=(p,0)$, where $-1<p<1$; X and Y are the points where $P+\ell _\xi$ intersects $\partial \mathcal {M}$. Figure 1 shows qualitative depictions of what we have in general.

Fig. 1

Qualitative depiction of infinitesimal circles in Hilbert planes

Observe that for $X\in \partial \mathcal {M}$ we have $2F_{\mathcal {M}}(P,X-P)-1=1/\lambda _{X-P}^->0$ by (2.1), so, as a continuous function takes its minimal value, there is a suitably small $\varepsilon >0$ such that the map

$$\begin{aligned} \Phi _P:Z\mapsto \Phi _P(Z)=P+(P-Z)\frac{1}{2F_{\mathcal {M}}(P,Z-P)-1} \end{aligned}$$

(3.1)

is well defined on the Minkowski sum $\mathcal {M}^\varepsilon :=\partial \mathcal {M}+\varepsilon \mathcal {B}^2$, where $\mathcal {B}^2$ is the unit ball at (0, 0).

Choose the Euclidean metric $d_e$ such that $\{(1,0),(0,1)\}$ is an orthonormal basis, and polar parameterize $\mathcal {C}^{\mathcal {M}}_P$ with respect to P by ${\varvec{r}}:[-\pi ,\pi )\ni \xi \mapsto r(\xi ){\varvec{u}}_\xi \in \mathbb {R}^2$. Then (2.1) gives

$$\begin{aligned} \frac{1}{|XP|}+\frac{1}{|PY|}=\frac{2}{r(\xi )}. \end{aligned}$$

(3.2)

Thus r is twice differentiable if $\partial \mathcal {M}$ is twice differentiable, and

$$\begin{aligned} r(0)=\frac{2|IP||PJ|}{|IJ|}=1-p^2, \ \text { hence }\ 2|IP|-r(0)=(1+p)^2. \end{aligned}$$

(3.3)

Lemma 3.2

Let $X\in I+\varepsilon \mathcal {B}^2$, and set $Y=\Phi _P(X)$. Let $(x,y)=X-I$ and $(u,v)=J-Y$.

Then

$$\begin{aligned} v\Big (1+\frac{u}{1-p} +O(u^2)\Big ) =y\Big (\frac{1-p}{1+p}+x\frac{1-p}{(1+p)^2} +O(x^2)\Big ), \end{aligned}$$

(3.4)

and

$$\begin{aligned} \begin{aligned} -u&= x\frac{(1-p)^2}{(1+p)^2} -y\frac{2r'(0)}{(1+p)^3} +x^2\frac{2(1-p)^2}{(1+p)^4} - xy\frac{r'(0)2(3-p)}{(1+p)^5}+\\&\quad + y^2\frac{1}{(1+p)^3}\Big ( -(1-p)+\frac{2(r'(0))^2}{(1+p)^3} +\frac{r''(0)}{1+p} \Big ) +\\&\quad + O(x^3)+O(x^2y)+o(y^2). \end{aligned} \end{aligned}$$

(3.5)

Proof

Let ${\varvec{u}}_\xi =(X-P)/|X-P|$. Then we clearly have $\frac{y}{1+p-x}=-\tan \xi =\frac{v}{1-p-u}$, so the expansions of $\frac{1}{1-p-u}$ and $\frac{1}{1+p-x}$ give (3.4).

To prove (3.5), we are estimating $-u$ for the second order of x and y. We start with (3.2) and use (3.3) as

$$\begin{aligned} -u&=|PY|\cos \xi -|PJ| =\frac{\cos \xi }{\frac{2}{r(\xi )}-\frac{1}{|XP|}}-(1-p) =\frac{r(\xi )|XP|\cos \xi }{2|XP|-r(\xi )}-(1-p)\\&=\frac{r(\xi )(1+p-x)-(1-p)(2|XP|-r(\xi ))}{2|XP|-r(\xi )} =\frac{r(\xi )(2-x)-2(1-p)|XP|}{2|XP|-r(\xi )}\\&=\frac{(r(\xi )-r(0))(2-x)+r(0)(2-x)-2(1-p)|IP|+2(1-p)(|IP|-|XP|)}{2|XP|-r(\xi )}\\&=\frac{(r(\xi )-r(0))(2-x)-xr(0)+2(1-p)(|IP|-|XP|)}{2|XP|-r(\xi )} \end{aligned}$$

shows. Next we estimate |XP| by the binomial series so that

$$\begin{aligned} |XP|&=((|IP|-x)^2+y^2)^{1/2} =|IP|-x+\frac{y^2/2}{|IP|-x}+O(y^4) \nonumber \\&=|IP|-x+\frac{y^2}{2}\Big (\frac{1}{|IP|}+O(x)\Big )+O(y^4) =|IP|-x+\frac{y^2/2}{1+p}+O(xy^2)+O(y^4) . \end{aligned}$$

(3.6)

Substitution of this into the previous formula and some rearrangements result in

$$\begin{aligned} -u&=\frac{(1-p)\big (2x-\frac{y^2}{1+p}\big )+(2-x)(r(\xi )-r(0))-x(1-p^2)}{2|XP|-r(\xi )} +O(xy^2)+O(y^4) \nonumber \\&=\frac{x(1-p)(1-p^2)-(1-p)y^2+(2-x)(1+p)(r(\xi )-r(0))}{(2|XP|-r(\xi ))(1+p)}+\nonumber \\&\qquad +O(xy^2)+O(y^4). \end{aligned}$$

(3.7)

To estimate this, we need to consider $r(\xi )-r(0)$ and ${1}/({2|XP|-r(\xi )})$. We use the binomial series and (3.6) to get

$$\begin{aligned} \frac{1}{|XP|}&=\frac{1}{|IP|-(|IP|-|XP|)} =\Big (1+p-\Big (x-\frac{y^2/2}{1+p}+O(y^2x)+O(y^4)\Big )\Big )^{-1}\\&=\frac{1}{1+p}+\frac{x}{(1+p)^2}-\frac{y^2/2}{(1+p)^3} +\frac{x^2}{(1+p)^3} +O(xy^2)+O(y^4)+O(x^3). \end{aligned}$$

This, as $\sin \xi =-y/|XP|$, leads to

$$\begin{aligned} \xi =\sin \xi +O(\xi ^3)=\frac{-y}{|XP|}+O(y^3) =\frac{-y}{1+p}-\frac{yx}{(1+p)^2}+O(y^3)+O(yx^2). \end{aligned}$$

(3.8)

Substitution of this into the Taylor expansion of r gives

$$\begin{aligned} \begin{aligned} (1&+p)(r(\xi )-r(0))\\&=(1+p)\Big (\xi r'(0)+\frac{\xi ^2}{2}r''(0)+o(\xi ^2)\Big )\\&=\Big (-y-\frac{yx}{1+p}\Big )r'(0) +\frac{y^2}{1+p}\frac{r''(0)}{2} +o(y^2)+O(yx^2)+O(y^2x). \end{aligned} \end{aligned}$$

(3.9)

Again the binomial series, and then (3.3), (3.6), and (3.9) result in

$$\begin{aligned} \frac{1}{2|XP|-r(\xi )}&=\frac{1}{(2|IP|-r(0))-(2(|IP|-|XP|)+(r(\xi )-r(0)))}\nonumber \\&=\big ((1+p)^2-(2(|IP|-|XP|)+(r(\xi )-r(0)))\big )^{-1} \nonumber \\&=\frac{1}{(1+p)^2} +\frac{2x-y\frac{r'(0)}{1+p}}{(1+p)^4} +O(x^2)+O(xy)+O(y^2) . \end{aligned}$$

(3.10)

Putting estimates (3.9), (3.10), and (3.8) into (3.7) and confining ourselves to summands of degree less than three, we obtain

$$\begin{aligned}&-u+O(x^3)+O(x^2y)+o(y^2)\\&\quad =\Big (\frac{1}{(1+p)^3}+\frac{2x-y\frac{r'(0)}{1+p}}{(1+p)^5}\Big ) \big ((x(1-p^2)-y^2)(1-p)+(2-x)(1+p)(r(\xi )-r(0))\big )\\&\quad =\Big (\frac{1}{(1+p)^3}+\frac{2x-y\frac{r'(0)}{1+p}}{(1+p)^5}\Big ) (x(1-p^2)-y^2)(1-p)+\\&\qquad + \Big (\frac{1}{(1+p)^3}+\frac{2x-y\frac{r'(0)}{1+p}}{(1+p)^5}\Big )(2-x) \Big (\Big (-y-\frac{yx}{1+p}\Big )r'(0)+\frac{y^2}{1+p}\frac{r''(0)}{2}\Big )\\&\quad =\frac{(x(1-p^2)-y^2)(1-p)}{(1+p)^3} +\frac{(2x^2(1+p)-xyr'(0))(1-p)^2}{(1+p)^5} -\\&\qquad - \Big (\frac{2y-xy}{(1+p)^3}+\frac{2xy}{(1+p)^4} +\frac{4xy-2y^2\frac{r'(0)}{1+p}}{(1+p)^5}\Big ) r'(0) + \frac{y^2}{(1+p)^4}r''(0), \end{aligned}$$

where the summands that are estimated by $O(x^3)+O(x^2y)+o(y^2)$ was left out. Collecting the terms by their powers gives

$$\begin{aligned} -u&= x\frac{(1-p)^2}{(1+p)^2} -y\frac{2r'(0)}{(1+p)^3} +x^2\frac{2(1-p)^2}{(1+p)^4} -\\&\quad - xy\frac{r'(0)}{(1+p)^3} \Big (\frac{(1-p)^2}{(1+p)^2}-1 +\frac{2}{1+p}+\frac{4}{(1+p)^2} \Big ) +\\&\quad + y^2\frac{1}{(1+p)^3}\Big ( -(1-p)+\frac{2(r'(0))^2}{(1+p)^3} +\frac{r''(0)}{1+p} \Big ) + O(x^3)+O(x^2y)+o(y^2) . \end{aligned}$$

This implies (3.5) after reordering the summands. $\square$

4 Hilbert geometries with two Riemannian points

In what follows, we always assume that P and Q are Riemannian points of the Hilbert plane $(\mathcal {M},d)$, $\ell =PQ$ is the x-axis of the chosen coordinate system, I and J are the intersection points of $\ell$ and $\partial \mathcal {M}$, $I=(-1,0)$, $J=(1,0)$, $P=(p,0)$ and $Q=(q,0)$, where $-1<q<p<1$. Further, $\mathfrak {t}_I$ and $\mathfrak {t}_J$ are the respective tangents of $\mathcal {M}$ at I and J, and the tangents of $\mathcal {C}^{\mathcal {M}}_Q$ and $\mathcal {C}^{\mathcal {M}}_P$ at their respective intersections with $\ell$ are $\mathfrak {t}_I^Q$, $\mathfrak {t}_J^Q$ and $\mathfrak {t}_I^P$, $\mathfrak {t}_J^P$, respectively.

Notice that the infinitesimal circle $\mathcal {C}^{\mathcal {M}}_P$ is now an ellipse, so it is of form (2.3) in any Euclidean metric. Observe that differentiation of (2.3) yields

$$\begin{aligned} r'(\varphi )&=\Big (\frac{1}{a^2}-\frac{1}{b^2}\Big ) \frac{\sin (2\varphi -2\omega )}{2}r^3(\varphi ),\\ r''(\varphi )&=\Big (\frac{1}{a^2}-\frac{1}{b^2}\Big )r^2(\varphi ) \Big (\cos (2\varphi -2\omega )r(\varphi )+\frac{3\sin (2\varphi -2\omega )}{2}r'(\varphi )\Big ). \end{aligned}$$

Further, using

$$\begin{aligned} \frac{1}{r^2(0)}-\frac{1}{r^2(\pi /2)} = \frac{\cos ^2\omega }{a^2}+\frac{\sin ^2\omega }{b^2} -\frac{\sin ^2\omega }{a^2}-\frac{\cos ^2\omega }{b^2} =\Big (\frac{1}{a^2}-\frac{1}{b^2}\Big )\cos (2\omega ) , \end{aligned}$$

we obtain

$$\begin{aligned} r'(0)&=-r^3(0)\Big (\frac{1}{r^2(0)}-\frac{1}{r^2(\pi /2)}\Big )\frac{\tan (2\omega )}{2},\nonumber \\ r''(0)&=\Big (\frac{1}{r^2(0)}-\frac{1}{r^2(\pi /2)}\Big )r^3(0) +3\frac{(r'(0))^2}{r(0)}. \end{aligned}$$

(4.1)

Lemma 4.1

If $\partial \mathcal {M}$ is twice differentiable at I and J, then there is a unique ellipse $\mathcal {E}$ touching $\mathcal {M}$ at I, J such that $\mathcal {C}^{\overline{\mathcal {E}}}_Q \equiv C_Q^{\mathcal {M}}$ and $\mathcal {C}^{\overline{\mathcal {E}}}_P \equiv \mathcal {C}^{\mathcal {M}}_P$.

Proof

If $\mathfrak {t}_I^Q$ intersects $\mathfrak {t}_J^P$, then $\mathfrak {t}_I^{}$ also intersects $\mathfrak {t}_J^{}$ in a point, say L, by (2.4). Choose a straight line l through L that avoids $\mathcal {M}$, and let $\varpi$ be a perspectivity that takes l into the ideal line of $\mathbb {R}^2$. Then, by (2.2), $\dot{\varpi }(\mathcal {C}^{\mathcal {M}}_{Q})\equiv \mathcal {C}^{\varpi (\mathcal {M})}_{\varpi (Q)}$, and $\dot{\varpi }(\mathcal {C}^{\mathcal {M}}_{P})\equiv \mathcal {C}^{\varpi (\mathcal {M})}_{\varpi (P)}$, hold, where the derivative $\dot{\varpi }$ of $\varpi$ is an affine transform. As affinities keep quadraticity, $\varpi (Q)$ and $\varpi (P)$ are Riemannian points in the Hilbert geometry $(\varpi (\mathcal {M}),d_{\varpi (\mathcal {M})})$, so we can assume without loss of generality that $\mathfrak {t}_I^Q\parallel \mathfrak {t}_J^P$.

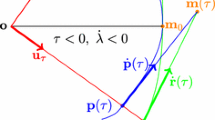
Fix the Euclidean metric d in which $\mathcal {C}^{\mathcal {M}}_Q$ is a circle and $d(I,J)=2$. Since $\mathcal {C}^{\mathcal {M}}_Q$ is a circle, $\mathfrak {t}_I^Q$ and $\mathfrak {t}_J^P$, and, by (2.4), also $\mathfrak {t}_I$ and $\mathfrak {t}_J$ are perpendicular to line QP. Figure 2 shows what we have.

Fig. 2

Riemannian points Q, P in a Hilbert plane $\mathcal {M}$

Thus we have $r'(0)=0$ and also $r''(0)=r^3(0)\big (\frac{1}{r^2(0)}-\frac{1}{r^2(\pi /2)}\big )$ by (4.1). So equation (3.5) reduces to

$$\begin{aligned} \begin{aligned} -u =&\,x\frac{(1-p)^2}{(1+p)^2} +\frac{x^2}{r(0)}\frac{2(1-p)^3}{(1+p)^3} -\frac{y^2}{r(0)}\frac{(1-p)^2}{(1+p)^2} +\\&+y^2r(0)\frac{(1-p)^2}{(1+p)^2}\Big (\frac{1}{r^2(0)}-\frac{1}{r^2(\pi /2)}\Big ) +O(x^3)+O(x^2y)+o(y^2). \end{aligned} \end{aligned}$$

(4.2)

Assume from now on that $X\in \partial \mathcal {M}$, hence also $Y=\Phi _P(X)\in \partial \mathcal {M}$.

Since $\mathfrak {t}_I$ and $\mathfrak {t}_J$ are perpendicular to line QP, basic differential geometry gives that the respective curvatures of $\partial \mathcal {M}$ at I and J are

$$\begin{aligned} \kappa _I:=\lim _{x\rightarrow 0}\frac{2x}{y^2} \quad \text { and }\quad \kappa _J:=\lim _{u\rightarrow 0}\frac{2u}{v^2} . \end{aligned}$$

(4.3)

So, dividing (4.2) by the square of (3.4) leads to

$$\begin{aligned} \kappa _J =\lim _{u\rightarrow 0}\frac{2u}{v^2} =\lim _{u\rightarrow 0}\frac{-2x}{y^2}+\frac{2}{r(0)}-2r(0)\Big (\frac{1}{r^2(0)}-\frac{1}{r^2(\pi /2)}\Big ) =-\kappa _I+\frac{2r(0)}{r^2(\pi /2)}. \end{aligned}$$

(4.4)

Repeating the same procedure for the circle $\mathcal {C}^{\mathcal {M}}_Q$ gives $\kappa _J=-\kappa _I+\frac{2}{1-q^2}$. This and (4.4) imply

$$\begin{aligned} r\Big (\frac{\pi }{2}\Big )=\sqrt{1-q^2}\sqrt{1-p^2}, \end{aligned}$$

(4.5)

hence Lemma 3.1 proves the statement with the ellipse $x^2+\frac{y^2}{1-q^2}=1$. $\square$

Lemma 4.2

If $\partial \mathcal {M}$ is twice differentiable at I and J, then $\mathcal {E}$ coincides $\partial \mathcal {M}$ in a neighborhood of I, J, respectively.

Proof

According to the last formula in the proof of Lemma 4.1, the infinitesimal circles $\mathcal {C}^{\overline{\mathcal {E}}}_P \equiv \mathcal {C}^{\mathcal {M}}_P$ and $\mathcal {C}^{\overline{\mathcal {E}}}_Q \equiv C_Q^{\mathcal {M}}$ can be represented by polar equations of form

$$\begin{aligned} \frac{1}{r^2(\varphi )} =\frac{\cos ^2\varphi }{a^2}+\frac{\sin ^2\varphi }{b^2}, \ \text { and }\ \frac{1}{r_q^2(\varphi )} =\frac{1}{r_q^2(0)}, \end{aligned}$$

respectively. Then (3.1) gives

$$\begin{aligned} \Phi _P(P-z{\varvec{u}}_\varphi )&=P+z{\varvec{u}}_\varphi \frac{1}{2F_{\mathcal {M}}(P,z{\varvec{u}}_\varphi )-1} =P+z{\varvec{u}}_\varphi \frac{1}{2\frac{z}{r(\varphi )}-1} , \end{aligned}$$

hence $\Phi _P$ is a real analytic map on $\mathcal {M}^\varepsilon$. It follows in the same way that $\Phi _Q$ is a real analytic map on $\mathcal {M}^\varepsilon$. We conclude that $\Phi :=\Phi _Q\circ \Phi _P$ is also a real analytic map on $\mathcal {M}^\varepsilon$.

(4.6)

Observe that all three convergences $(s,t)\rightarrow (0,0)$, $(u,v)\rightarrow (0,0)$, and $(x,y)\rightarrow (0,0)$ are equivalent.

Then (3.5) gives

$$\begin{aligned} \begin{aligned} u&=s\frac{(1-q)^2}{(1+q)^2} +s^2\frac{2(1-q)^2}{(1+q)^4} - t^2\frac{1-q}{(1+q)^3} +O(s^3)+O(s^2t)+o(t^2)\\&= x\frac{(1-p)^2}{(1+p)^2} -y\frac{2r_p'(0)}{(1+p)^3} +x^2\frac{2(1-p)^2}{(1+p)^4} - xy\frac{r_p'(0)2(3-p)}{(1+p)^5} +\\&\quad + y^2\frac{1}{(1+p)^3}\Big ( -(1-p)+\frac{2(r_p'(0))^2}{(1+p)^3}+\frac{r_p''(0)}{1+p} \Big ) + O(x^3)+O(x^2y)+o(y^2) . \end{aligned} \end{aligned}$$

(4.7)

Further, (3.4) gives

$$\begin{aligned} \begin{aligned} v&=t\frac{1-q}{1+q}\Big (1+\frac{s}{1+q}+O(s^2)\Big )\Big (1-\frac{u}{1-q}\Big )\\&=y\frac{1-p}{1+p}\Big (1+\frac{x}{1+p}+O(x^2)\Big )\Big (1-\frac{u}{1-p}\Big ). \end{aligned} \end{aligned}$$

This immediately implies

$$\begin{aligned} \begin{aligned} \frac{t}{ky}&=\frac{1+\frac{x}{1+p}+O(x^2)}{1+\frac{s}{1+q}+O(s^2)} \frac{1-\frac{u}{1-p}}{1-\frac{u}{1-q}}\\&=1+x\frac{2p}{(1+p)^2}+y\frac{2r_p'(0)}{(1-p^2)(1+p)^2}-s\frac{2q}{(1+q)^2} +\\&+O(x^2)+O(s^2)+O(u^2)+O(xu)+O(su), \end{aligned} \end{aligned}$$

(4.8)

where $k=\frac{1-p}{1+p}\frac{1+q}{1-q}<1$.

Now we are calculating $\Phi$. Lemma 4.1 gives $r_p'(0)=0$, and also $r_q'(0)=r_q''(0)=0$ holds. Equations (4.1), (3.3), and (4.5) give

$$\begin{aligned} r_p''(0)=\Big (\frac{1}{r_p^2(0)}-\frac{1}{r_p^2(\pi /2)}\Big )r_p^3(0) =r_p(0)\Big (1-\frac{r_p^2(0)}{r_p^2(\pi /2)}\Big ) =(1-p^2)\Big (1-\frac{1-p^2}{1-q^2}\Big ). \end{aligned}$$

Thus (4.7) gives

$$\begin{aligned} \begin{aligned} s&\frac{(1-q)^2}{(1+q)^2}+s^2\frac{2(1-q)^2}{(1+q)^4}-t^2\frac{1-q}{(1+q)^3} +O(s^3)+O(s^2t)+o(t^2)\\&= x\frac{(1-p)^2}{(1+p)^2}+x^2\frac{2(1-p)^2}{(1+p)^4} -y^2\frac{(1-p)^2}{(1+p)^2}\frac{1}{1-q^2} +O(x^3)+O(x^2y)+o(y^2) . \end{aligned} \end{aligned}$$

This mutates at $(x,y)=(zy^2,y)$ to

$$\begin{aligned} \begin{aligned} \frac{s}{k^2y^2}&=z\frac{1+\frac{2zy^2}{(1+p)^2} +\frac{1}{z}\big (\frac{t^2}{y^2}\frac{(1+p)^2}{(1-p)^2}\frac{1-q}{(1+q)^3}-\frac{1}{1-q^2}\big ) +O(z^2y^4)+O(zy^3)+o(1)}{1+s^2\frac{2}{(1+q)^2} +O(s^3)+O(s^2t)+o(t^2)}, \end{aligned} \end{aligned}$$

(4.9)

where $y\ne 0$, and z is close to $\kappa _I/2$ by (4.3) and (4.6). Further, (4.8) gives

$$\begin{aligned} \frac{t^2}{y^2}\frac{(1+p)^2}{(1-p)^2}\frac{1-q}{(1+q)^3}-\frac{1}{1-q^2} =\frac{1}{1-q^2}\Big (\frac{t^2}{k^2y^2}-1\Big ) =O(x^2)+O(xs)+O(s^2). \end{aligned}$$

So, after the coordinate-transform $\Psi :(z,y)\mapsto (zy^2,y)$, where $y\ne 0$ and z is close to $\kappa _I/2$, $\Phi$ becomes $\Phi ^\Psi (z,y):=\Psi ^{-1}\circ \Phi \circ \Psi (z,y)=\Psi ^{-1}(\Phi (zy^2,y)),$ hence equations (4.8) and (4.9) give

$$\begin{aligned} \Phi ^\Psi (z,y) =\Psi ^{-1}(zy^2k^2+o(y^2),yk+o(y^2)) =(z+o(1),yk+o(y^2)) . \end{aligned}$$

Therefore, defining $\Phi ^\Psi (z,0):=(z,0)$ extends $\Phi ^\Psi$ to a real analytic mapping in a neighborhood of $(\kappa _I/2,0)$.

Summing up, the analytic map $\Phi ^\Psi$ fixes the points (z, 0) near $(\kappa _I/2,0)$ and has the derivative $\mathsf D\Phi ^\Psi (\kappa _I/2,0)=\left( {\begin{matrix}1&{}0\\ 0&{}k\end{matrix}}\right)$.

Thus $\Phi ^\Psi$ satisfies the conditions in Theorem 2.1 with vectors (1, 0) and (0, 1), so there is a neighborhood $\mathcal {N}$ of $(\kappa _I/2,0)$ such that the set

$$\begin{aligned} \big \{{\varvec{w}}\in \mathcal {N}:\big (\Phi ^\Psi \big )^{(r)}({\varvec{w}})\rightarrow (\kappa _I/2,0) \text { as }r\rightarrow \infty \big \} \end{aligned}$$

is the graph of a $C^1$ function from $\ell _{(0,1)}\cap \mathcal {N}$ to $\ell _{(1,0)}\cap \mathcal {N}$. This proves the statement of the lemma. $\square$

Lemma 4.3

If two Hilbert geometries have two common Riemannian points Q and P, and their borders coincide in some neighborhood of line PQ, then the two Hilbert geometries coincide.

Proof

Let $(\mathcal {L},d_{\mathcal {L}})$ and $(\mathcal {M},d_{\mathcal {M}})$ be Hilbert geometries with common Riemannian points Q and P. Assume that there is a neighborhood $\mathcal {N}$ of line PQ that intersects the border of our Hilbert geometries in two common arcs $\mathcal {I}_0$ and $\mathcal {J}_0$.

Let line PQ intersect $\mathcal {I}_0$ and $\mathcal {J}_0$ in points I and J, respectively. We can assume without loss of generality that the points are ordered as $I\prec Q\prec P\prec J$. So, we can use the notations already introduced in this paper.

Observe that $\mathcal {C}^{\mathcal {L}}_{Q}\equiv \mathcal {C}^{\mathcal {M}}_{Q}$ and $\mathcal {C}^{\mathcal {L}}_{P}\equiv \mathcal {C}^{\mathcal {M}}_{P}$, because the common arcs of $\partial \mathcal {L}$ and $\partial \mathcal {M}$ determine small common arcs of the quadratic infinitesimal circles near line QP. Thus both $\Phi _P$ and $\Phi _Q$ map any common arc of $\partial \mathcal {L}$ and $\partial \mathcal {M}$ to a common arc of $\partial \mathcal {L}$ and $\partial \mathcal {M}$.

We generate common arcs by defining $\mathcal {J}_{k+1}:=\Phi _Q(\mathcal {I}_{k})$ and $\mathcal {I}_{k+1}:=\Phi _P(\mathcal {J}_k)$ for every $k=0,1,\ldots$. Let $\alpha _k$ ($k=0,1,\ldots$) be the angle $\mathcal {I}_{k}$ subtends at Q, and let $\beta _k$ ($k=0,1,\ldots$) be the angle $\mathcal {J}_{k}$ subtends at P.

To show that it is contradictory, assume that every $\alpha _k$ and $\beta _k$ ($k=0,1,\ldots$) is less than $\pi$. Then we clearly have $\beta _0<\alpha _1<\beta _2<\alpha _3<\cdots<\beta _{2k}<\alpha _{2k+1}<\beta _{2k+2}<\cdots <\pi$. So $\mathcal {I}=\lim _{k\rightarrow \infty }\mathcal {I}_{2k+1}$ subtends angle $\alpha =\lim _{k\rightarrow \infty }\alpha _{2k+1}\le \pi$, and $\mathcal {J}=\lim _{k\rightarrow \infty }\mathcal {J}_{2k}$ subtends angle $\beta =\lim _{k\rightarrow \infty }\beta _{2k}\le \pi$. From the sequence of inequalities $\alpha =\beta$ follows, hence $\Phi _Q(\mathcal {I})=\mathcal {J}$ and $\Phi _P(\mathcal {J})=\mathcal {I}$. Then the assumption implies that $\alpha =\beta <\pi$, which contradicts $Q\ne P$. So one of $\alpha _k$ or $\beta _k$ ($k=0,1,\ldots$) is at least $\pi$, say $\alpha _k\ge \pi$. Then $\mathcal {I}_{k}\cup \Phi _Q(\mathcal {I}_{k})$ covers $\partial \mathcal {L}$ and $\partial \mathcal {M}$, and the lemma is proved. $\square$

Theorem 4.4

If a Hilbert geometry has two Riemannian points, and its boundary is twice differentiable where it is intersected by the line joining those Riemannian points, then it is a Cayley–Klein model of the hyperbolic space.

Proof

By Lemma 4.1, there is an ellipse $\mathcal {E}$ touching $\mathcal {M}$ in I, J, such that $\mathcal {C}^{\overline{\mathcal {E}}}_Q \equiv C_Q^{\mathcal {M}}$ and $\mathcal {C}^{\overline{\mathcal {E}}}_P \equiv \mathcal {C}^{\mathcal {M}}_P$. Then Lemma 4.2 shows that $\partial \mathcal {M}$ and $\mathcal {E}$ coincide in a neighborhood of line PQ. Finally Lemma 4.3 proves that $\partial \mathcal {M}$ and $\mathcal {E}$ coincide. $\square$

5 Discussion

Theorem 4.4 can be reformulated in the language of geometric tomography [7]. It generalizes Falconer’s [5, Theorem 3].

Theorem 5.1

Let Q and P be two points of a strictly convex bounded open domain $\mathcal {M}$ in the plane. Assume that the boundary $\partial \mathcal {M}$ is twice differentiable where it intersects line QP. If the $(-1)$-chord functions at Q and P are quadratic, then $\partial \mathcal {M}$ is an ellipse.

Falconer’s [5, Theorem 4] gives that for any two fixed points P, Q several distinct strictly convex bounded open domains $\mathcal {M}$ exist in the plane such that $P,Q\in \mathcal {M}$, the $(-1)$-chord functions at P and Q are equal to 1, the boundary $\partial \mathcal {M}$ is differentiable at $I,J\in PQ\cap \partial \mathcal {M}$ and twice differentiable everywhere else, and $\partial \mathcal {M}$ is not an ellipse. Observe that in such an $\mathcal {M}$ there can not exist a third inner point with quadratic $(-1)$-chord function, because then $\partial \mathcal {M}$ has to be an ellipse by Theorem 5.1. Reformulating these to Hilbert geometries we obtain the following.

Theorem 5.2

Let $d_e$ be a Euclidean metric on the plane, and let $\mathcal {C}_Q$ and $\mathcal {C}_P$ be unit circles with centers Q and P, respectively.

Then there are several distinct non-hyperbolic Hilbert geometries $(\mathcal {M},d)$ such that $\mathcal {C}_Q$ and $\mathcal {C}_P$ are the only quadratical infinitesimal circles in $(\mathcal {M},d)$. The boundary of such a Hilbert geometry is twice differentiable except where it intersects line QP.

How the Hilbert geometries given in this theorem relate to the hyperbolic geometry remains an interesting question.

Theorem 4.4 also raises the problem to determine those pair of ellipses that are infinitesimal circles of a Hilbert geometry. This can be done by following the proof of Lemma 4.1; the details remain to the interested reader for now.

One can specialize [7, Theorem 6.2.14, p. 247] to the following:

This gives the following result which is more general, but weaker for the quadratical case than the combo of the lemmas in the previous section.

Theorem 5.3

If two Hilbert geometries $(\mathcal {L},d_{\mathcal {L}})$ and $(\mathcal {M},d_{\mathcal {M}})$ in the plane $\mathbb {R}^2$ with boundaries of class $C^{2+\delta }(\mathcal {S}^1)$, where $\delta >0$, have two common infinitesimal circles $\mathcal {C}^{\mathcal {L}}_P\equiv \mathcal {C}^{\mathcal {M}}_P$ and $\mathcal {C}^{\mathcal {L}}_Q\equiv \mathcal {C}^{\mathcal {M}}_Q$, and have equal curvatures at the points where line PQ intersects the boundaries, then $\mathcal {M}\equiv \mathcal {K}$.

Notice that this theorem states only a coincidence and therefore implies a weaker version of Theorem 4.4 only together with Lemma 4.1.

It is proved in [8, Theorem 2] that perpendicularity in a Hilbert geometry is reversible for two lines if the perpendicularity of these two lines is also reversible with respect to the local Minkowski geometry at the intersection of the lines³. Calling such points Radon points, the question arises

(5.1)

Kelly and Paige proved in [9] that a Hilbert geometry is a Cayley–Klein model of the hyperbolic geometry if the perpendicularity is symmetric. Since the Riemannian points are Radon points, Theorem 4.4 supports our conjecture that the existence of two Radon points implies the symmetry of the perpendicularity if twice differentiability of the boundary is provided. If not, then Theorem 5.2 proves that even two Riemannian points are not enough to guarantee the symmetry of perpendicularity in Hilbert geometries.

Looking for possible higher dimensional analogs of Theorem 4.4 one can use [3, (16.12), p. 91] which says that

This immediately implies the following generalization of Theorem 4.4.

Theorem 5.4

If a Hilbert geometry has twice differentiable boundary and has a Riemannian point P such that for some fixed $k\in \{2,\ldots ,n-1\}$ on every k-plane through P there is an other Riemannian point, then it is a Cayley–Klein model of the hyperbolic space.