Reflectionless Solutions for Square Matrix NLS with Vanishing Boundary Conditions

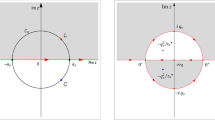
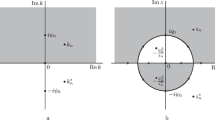
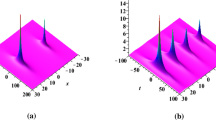
Abstract

In this article we derive the reflectionless solutions of the 2 + 2 matrix NLS equation with vanishing boundary conditions and four different symmetries by using the matrix triplet method of representing the Marchenko integral kernel in separated form. Apart from using the Marchenko method, these solutions are also verified by direct substitution in the 2 + 2 NLS equation.

Appendices

Appendix

A Integral Equations for Kernel Functions

In this appendix we list the integral equations for the auxiliary functions $\overline {K}(x,y,t)$, K(x, y, t), L(x, y, t), and $\overline {L}(x,y,t)$. Their proof can be found in the literature [2, 8, 28]. For the sake of brevity, we omit the time variable in all equations.

We have the following Volterra integral equations for the kernel functions:

$$ \begin{array}{@{}rcl@{}} \overline{K}^{\text{up}}(x,y)&=&-{\int}_{x}^{\infty} dz Q(z)\overline{K}^{{\text{dn}}}(z,z+y-x), \end{array} $$

(A.1a)

$$ \begin{array}{@{}rcl@{}} \overline{K}^{\text{dn}}(x,y)&=&-\tfrac{1}{2}R(\tfrac{1}{2}[x+y])-{\int}_{x}^{\tfrac{1}{2}[x+y]}dz R(z)\overline{K}^{\text{up}}(z,x+y-z), \end{array} $$

(A.1b)

$$ \begin{array}{@{}rcl@{}} K^{\text{up}}(x,y)&=&-\tfrac{1}{2}Q(\tfrac{1}{2}[x+y]) -{\int}_{x}^{\tfrac{1}{2}[x+y]}dz Q(z)K^{{\text{dn}}}(z,x+y-z), \end{array} $$

(A.1c)

$$ \begin{array}{@{}rcl@{}} K^{{\text{dn}}}(x,y)&=&-{\int}_{x}^{\infty} dz R(z)K^{\text{up}}(z,z+y-x), \end{array} $$

(A.1d)

as well as

$$ \begin{array}{@{}rcl@{}} L^{\text{up}}(x,y)&=&{\int}_{-\infty}^{x} dz Q(z)L^{{\text{dn}}}(z,z+y-x), \end{array} $$

(A.2a)

$$ \begin{array}{@{}rcl@{}} L^{{\text{dn}}}(x,y)&=&\tfrac{1}{2}R(\tfrac{1}{2}[x+y]) +{\int}_{x}^{\tfrac{1}{2}[x+y]}dz R(z)L^{\text{up}}(z,x+y-z), \end{array} $$

(A.2b)

$$ \begin{array}{@{}rcl@{}} \overline{L}^{\text{up}}(x,y)&=&\tfrac{1}{2}Q(\tfrac{1}{2}[x+y]) +{\int}_{x}^{\tfrac{1}{2}[x+y]}dz Q(z)\overline{L}^{{\text{dn}}}(z,x+y-z), \end{array} $$

(A.2c)

$$ \begin{array}{@{}rcl@{}} \overline{L}^{{\text{dn}}}(x,y)&=&{\int}_{-\infty}^{x} dz R(z)\overline{L}^{\text{up}}(z,z+y-x). \end{array} $$

(A.2d)

Equations (A.1a) and (A.2a) obviously imply (2.8a).

Suppose that F(y) is a matrix function of y ≥ x ≥ x₀ or a matrix function of y ≤ x ≤ x₀. Then we define

$$\mu(F,x)=\left\{\begin{array}{cc}{\int}_{x}^{\infty} dy \|F(y)\|,&x\ge x_{0},\\ {\int}_{-\infty}^{x} dy \|F(y)\|,&x\le x_{0}. \end{array}\right.$$

Then (A.1a) and (A.2a) imply

$$ \begin{array}{@{}rcl@{}} \mu(\overline{K}^{\text{up}},x)&\le&{\int}_{x}^{\infty} dz \|Q(z)\| \mu(\overline{K}^{{\text{dn}}},z), \end{array} $$

(A.3a)

$$ \begin{array}{@{}rcl@{}} \mu(\overline{K}^{{\text{dn}}},x)&\le&{\int}_{x}^{\infty} dz \|R(z)\|+{\int}_{x}^{\infty} dz \|R(z)\|\mu(\overline{K}^{\text{up}},z), \end{array} $$

(A.3b)

$$ \begin{array}{@{}rcl@{}} \mu(\overline{K}^{\text{up}},x)&\le&{\int}_{x}^{\infty} dz \|Q(z)\|+{\int}_{x}^{\infty} dz \|Q(z)\|\mu(K^{{\text{dn}}},z), \end{array} $$

(A.3c)

$$ \begin{array}{@{}rcl@{}} \mu(\overline{K}^{{\text{dn}}},x)&\le&{\int}_{x}^{\infty} dz \|R(z)\|\mu(K^{\text{up}},z), \end{array} $$

(A.3d)

as well as

$$ \begin{array}{@{}rcl@{}} \mu(L^{\text{up}},x)&\le&{\int}_{-\infty}^{x} dz \|Q(z)\|\mu(L^{{\text{dn}}},x), \end{array} $$

(A.4a)

$$ \begin{array}{@{}rcl@{}} \mu(L^{{\text{dn}}},x)&\le&{\int}_{-\infty}^{x} dz \|R(z)\| +{\int}_{-\infty}^{x} dz \|R(z)\|\mu(L^{\text{up}},x), \end{array} $$

(A.4b)

$$ \begin{array}{@{}rcl@{}} \mu(\overline{L}^{\text{up}},x)&\le&{\int}_{-\infty}^{x} dz \|Q(z)\| +{\int}_{-\infty}^{x} dz \|Q(z)\|\mu(\overline{L}^{{\text{dn}}},z), \end{array} $$

(A.4c)

$$ \begin{array}{@{}rcl@{}} \mu(\overline{L}^{{\text{dn}}},x)&\le&{\int}_{-\infty}^{x} dz \|R(z)\| \mu(\overline{L}^{\text{up}},z). \end{array} $$

(A.4d)

The unique solvability of (A.1a) and (A.2a) now follows immediately by applying Gronwall’s inequality.

Using Gronwall’s inequality we get

$$ \begin{array}{@{}rcl@{}} \mu(\overline{K}^{\text{up}},x)+\mu(\overline{K}^{{\text{dn}}},x)&\le&\left( {\int}_{x}^{\infty} dz \|Q(z)\|\right)\exp\left( {\int}_{x}^{\infty} dz \|Q(z)\|\right), \end{array} $$

(A.5a)

$$ \begin{array}{@{}rcl@{}} \mu(K^{\text{up}},x)+\mu(K^{{\text{dn}}},x)&\le&\left( {\int}_{x}^{\infty} dz \|Q(z)\|\right) \exp\left( {\int}_{x}^{\infty} dz \|Q(z)\|\right), \end{array} $$

(A.5b)

$$ \begin{array}{@{}rcl@{}} \mu(L^{\text{up}},x)+\mu(L^{{\text{dn}}},x)&\le&\left( {\int}_{-\infty}^{x} dz \|Q(z)\|\right) \exp\left( {\int}_{-\infty}^{x} dz \|Q(z)\|\right), \end{array} $$

(A.5c)

$$ \begin{array}{@{}rcl@{}} \mu(\overline{L}^{\text{up}},x)+\mu(\overline{L}^{{\text{dn}}},x) &\le&\left( {\int}_{-\infty}^{x} dz \|Q(z)\|\right)\exp\left( {\int}_{-\infty}^{x} dz \|Q(z)\|\right), \end{array} $$

(A.5d)

where we have used that ∥Q(z)∥≡∥R(z)∥.

Equations (2.8a) and (2.8b) are to be interpreted as follows: The integral terms in (A.1a) and (A.2a) are continuous in $y\in [x,+\infty )$ and in $y\in (-\infty ,x]$, respectively. As a result,

$$ \begin{array}{@{}rcl@{}} \lim_{z\to x^{+}}\left\|2\overline{K}^{{\text{dn}}}(x,2z-x)+R(z)\right\|=0, \end{array} $$

(A.6a)

$$ \begin{array}{@{}rcl@{}} \lim_{z\to x^{+}}\left\|2K^{\text{up}}(x,2z-x)+Q(z)\right\|=0, \end{array} $$

(A.6b)

$$ \begin{array}{@{}rcl@{}} \lim_{z\to x^{-}}\left\|2L^{{\text{dn}}}(x,2z-x)-R(z)\right\|=0, \end{array} $$

(A.6c)

$$ \begin{array}{@{}rcl@{}} \lim_{z\to x^{-}}\left\|2\overline{L}^{\text{up}}(x,2z-x)-Q(z)\right\|=0, \end{array} $$

(A.6d)

where we have substituted $z=\tfrac {1}{2}[x+y]$. If the entries of Q(x) and Q_x both belong to $L^{1}(\mathbb {R},dx)$, then (2.8a) and (2.8b) are valid pointwise.