Coupled shallow-water fluid sloshing in an upright annular vessel

Abstract

The coupled motion of shallow-water sloshing in a horizontally translating upright annular vessel is considered. The vessel’s motion is restricted to a single space dimension, such as for Tuned Liquid Damper systems. For particular parameters, the system is shown to support an internal 1 : 1 resonance, where the frequency of coupled sloshing mode which generates the vessel’s motion is equal to the frequency of a sloshing mode which occurs in a static vessel. Using a Lagrangian Particle Path formation, the fully nonlinear motion of the system is simulated using an efficient numerical symplectic integration scheme. The scheme is based on the implicit-midpoint rule which conserves energy and preserves the energy partition between the fluid and the vessel over many time-steps. Linear and nonlinear results are presented, including those showing the system transitioning to higher-frequency eigenmodes as the fluid depth is reduced.

1 Introduction

Liquid sloshing within a vessel which is prescribed to move in some given time-dependent way has long been a subject of interest within areas of science and technology. One of the original motivations for the study of this topic was to investigate the stability of space craft or rocket propelled missiles [1,2,3]. Other studies have considered engineering motivations such as maritime and terrestrial fluid transport and fuel tank storage under earthquake excitement. For an extensive review of these topics, the reader is directed to [4, 5] and the references therein.

In this article, we focus on the problem of a dynamically coupled vessel/fluid problem. In this case, the vessel’s motion is not given a priori, instead the fluid and vessel’s motions are solved simultaneously, and are intrinsically coupled through the pressure force due to the fluid impacting on the vessel walls. The first investigation of a dynamically coupled sloshing problem was by [6], who considered a vessel partially filled with fluid, attached to a rigid pole anchored at one end about which it rotates, the so called ‘pendulum slosh problem’ [3, 7, 8]. The pendulum provides a restoring force on the vessel, forcing the fluid into motion, which in turn modifies the vessel’s motion via the hydrodynamic force it generates on the vessel walls. However, the rotary motion of the vessel makes the problem difficult to theoretically study. Cooker [9] modified this experiment to a bifilar pendulum attached to a rectangular vessel. Here the difference is that the base of the vessel remains level throughout the motion so the fluid can be considered as irrotational. Cooker constructed a shallow-water theory for this system with linear (small amplitude) vessel displacements in order to determine the natural characteristic frequencies of the system. The experimental and shallow-water theory of this paper were extended by [10,11,12] who studied multi-compartment rectangular vessels, an upright cylindrical vessel and an upright wedge, all suspended as bifilar pendulums. For the rectangular and cylindrical vessel problems, Yu [13] formulated the finite-depth potential theory in order to identify the effect of the evanescent waves on the solution. In the case of an infinite length bifilar pendulum, the vessel becomes free to move due solely to the forces generated by the fluid on the walls, without any additional restoring force. Herczyński and Weidman [14] analytically and experimentally examined this limit for various vessel geometries, including rectangular boxes, upright cylinders, wedges, cones and upright cylindrical annuli.

The upright annular vessel has had little attention in studies when compared to the upright cylindrical vessel, say. However, annular vessels have been associated with tuned liquid dampers (TLDs) which are used in skyscrapers and wind turbines to damp out oscillations caused by strong winds [15]. In a TLD, the vessel is constrained to move in a single horizontal direction with the vessel’s motion restored by a spring-mass-damper model. Neglecting the damping element, the model equations for the TLD are identical to that for the Cooker experiment in the linear, small amplitude limit [16]. Faltinsen et al. [17] considered a nonlinear theoretical and numerical study of the forced annular vessel with resonant forcing frequencies close to the lowest natural sloshing frequency for sloshing in a stationary vessel. They identified bifurcations where the fluid motion changed behaviour between planar sloshing, swirling and irregular sloshing motions. An annular vessel was also considered by [18] who calculated the natural sloshing frequencies in a stationary vessel when a rigid annular baffle is included at the free-surface. The study in this current article is the first such study to consider dynamically coupled sloshing in an annular vessel.

In this current work, we identify two areas of interest, namely we identify the existence of the 1 : 1 resonance between the coupled eigenmodes and the eigenmodes in a stationary vessel, and we perform nonlinear shallow-water simulations. Alemi Ardakani et al. [16] showed for a rectangular vessel that the characteristic equation for the linear system takes the form $\Delta (\omega )=P(\omega )D(\omega )$, where $\omega$ is the characteristic natural frequency, $D(\omega )$ is the characteristic equation for the coupled modes and $P(\omega )$ is the characteristic equation for the natural sloshing frequencies in a stationary vessel. The natural frequencies for the system come from solving $\Delta (\omega )=0$, and if $D(\omega )=P(\omega )=0$ (with $D'(\omega )\ne 0$ and $P'(\omega )\ne 0$) then a 1 : 1 resonance occurs between the coupled modes and the modes in the stationary vessel. Such resonances are of practical interest, as close to these points the nonlinear system has multiple bifurcations of the periodic orbits which can lead to chaotic dynamics, such as in the Faraday problem [19]. Turner and Bridges [20] demonstrated for the Cooker experiment the existence of a heteroclinic orbit, for one fluid depth, which linked the coupled and stationary-vessel modes, allowing them to exchange energy, ultimately producing interesting system dynamics.

In this paper, we present nonlinear simulations of the coupled annular system, assuming that the fluid is a shallow-layer. In this case, we can utilize the Lagrangian Particle Path (LPP) formulation of the problem, first developed by [21] for dynamic sloshing problems, to construct an accurate numerical scheme. The scheme uses the fact that the problem has a Hamiltonian structure, which lends itself to being numerically integrated via a geometric integration scheme, such as the implicit-midpoint-rule [22, 23]. Such schemes conserve the symplectic structure of the system and also preserves the energy partition between the fluid and the vessel, preventing a slow unphysical leaking of energy from the vessel to the fluid over time. This numerical approach has been applied successfully to related coupled sloshing problems [24,25,26].

The current paper is structured as follows. In Sect. 2 we derive the governing nonlinear, finite-depth equations for the system, while in Sect. 3, we take the shallow-water limit of these equations and formulate their LPP representation. In Sect. 4, we investigate the linear modal solutions, derive the characteristic equation, and present results for the characteristic frequencies and the existence of the 1 : 1 resonance. In Sect. 5, we present the symplectic numerical scheme for solving the shallow-water system along with nonlinear results. Conclusions and discussion are given in Sect. 6.

2 Governing nonlinear equations

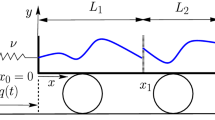
We consider the coupled sloshing motion of an inviscid, incompressible fluid, of density $\rho$, in an upright annular cylinder with mass $m_v$, which is constrained to translate in the horizontal X-direction and is connected to a solid wall by a nonlinear spring. See Fig. 1 for a schematic diagram of the setup. Here (X, Y, Z) is a fixed Cartesian coordinate system with Z pointing vertically upwards, which is related to a cylindrical polar coordinate system $(r,\theta ,z)$ moving with the vessel. The two coordinate systems are related via

$$\begin{aligned} X=R_2+\ell +q(t)+r\cos \theta , \quad Y=r\sin \theta ,\quad Z=z, \end{aligned}$$

(2.1)

where q(t) is the displacement of the vessel from its equilibrium position and $\ell$ is the natural length of the spring. The annular vessel has impermeable walls at $r=R_1$ and $r=R_2>R_1$ and a flat impermeable bottom at $z=0$, such that the fluid occupies the region

$$\begin{aligned} R_1\le r\le R_2,\quad 0\le \theta <2\pi ,\quad 0\le z\le h(r,\theta ,t). \end{aligned}$$

Here $h(r,\theta ,t)$ is the position of the unknown free-surface which needs to be determined as part of the solution, and t is time.

Fig. 1

Schematic diagram of the dynamic coupling between fluid sloshing and the motion of an annular vessel

The governing nonlinear equations for the fluid motion are the Euler equations in the moving frame, coupled to the vessel’s motion which is modelled as a nonlinear Duffing oscillator. The Euler equations for a velocity field with components $(u_r,u_\theta ,u_z)$ relative to the polar coordinates $(r,\theta ,z)$ are

$$\begin{aligned}&\frac{\mathrm{{D}}u_{r}}{\mathrm{{D}}t}-\frac{u_\theta ^2}{r}+\frac{1}{\rho }\frac{\partial p}{\partial r}=-\,{\ddot{q}}\cos \theta , \end{aligned}$$

(2.2)

$$\begin{aligned}&\frac{\mathrm{{D}}u_\theta }{\mathrm{{D}}t}+\frac{u_{r}u_\theta }{r}+\frac{1}{r\rho }\frac{\partial p}{\partial \theta }={\ddot{q}}\sin \theta , \end{aligned}$$

(2.3)

$$\begin{aligned}&\frac{\mathrm{{D}}u_z}{\mathrm{{D}}t}+\frac{1}{\rho }\frac{\partial p}{\partial z}=-g, \end{aligned}$$

(2.4)

$$\begin{aligned}&\frac{1}{r}\frac{\partial }{\partial r}(ru_{r})+\frac{1}{r}\frac{\partial u_\theta }{\partial \theta }+\frac{\partial u_z}{\partial z}=0, \end{aligned}$$

(2.5)

where g is the gravitational acceleration constant acting in the negative z-direction,

$$\begin{aligned} \frac{\mathrm{{D}}}{\mathrm{{D}}t}=\frac{\partial }{\partial t}+u_{r}\frac{\partial }{\partial r}+\frac{u_\theta }{r}\frac{\partial }{\partial \theta }+u_z\frac{\partial }{\partial z}, \end{aligned}$$

and the overdots denote full derivatives with respect to t. Equations (2.2)–(2.5) are the polar, three-dimensional analogue of the equations given in [21], where the $\cos \theta$ and $\sin \theta$ terms on the right-hand side give the projection of the horizontal vessel acceleration in the radial and azimuthal directions, respectively. If one, were to assume an irrotational motion and introduce a streamfunction, then (2.2)–(2.5) reduce to equations (23)–(26) in [13]. The boundary conditions on the impermeable walls are

$$\begin{aligned} u_{r}=0\quad {\mathrm{on}}\quad r=R_1,~R_2\quad {\mathrm{and}}\quad u_z=0\quad {\mathrm{on}}\quad z=0, \end{aligned}$$

(2.6)

while on the free-surface the kinematic and dynamic boundary conditions are

$$\begin{aligned} \frac{\partial h}{\partial t}+u_{r}\frac{\partial h}{\partial r}+\frac{u_\theta }{r}\frac{\partial h}{\partial \theta }=u_z\quad \hbox {and} \quad p=0 \quad \hbox {on} \quad z=h(r,\theta ,t). \end{aligned}$$

(2.7)

The governing equation for the rectilinear translation of the vessel can be derived by considering the reduced Lagrangian approach as outlined in Appendix A of [16]. Via this approach the resulting nonlinear equation is

$$\begin{aligned} (m_v+m_f){\ddot{q}}+\nu q-\mu q^3=-\frac{\mathrm{d}}{\mathrm{d}t}\int _{R_1}^{R_2}\int _0^{2\pi }\int _0^{h(r,\theta ,t)}\rho \left[ u_{r}\cos \theta -u_\theta \sin \theta \right] \,r\,\mathrm{d}z\,\mathrm{d}\theta \,\mathrm{d}r, \end{aligned}$$

(2.8)

where $m_f=\int _{R_1}^{R_2}\int _0^{2\pi }\int _0^{h(r,\theta ,t)}\rho \,r\,\mathrm{d}z\,\mathrm{d}\theta \,\mathrm{d}r=\pi \rho (R_2^2-R_1^2)h$ is the mass of the fluid, and $\nu$ and $\mu$ are the linear and nonlinear spring coefficients, respectively. Note that the RHS of (2.8), together with the $m_f{\ddot{q}}$ term, is equivalent to the hydrodynamic force on the walls $(r=R_1,R_2)$ of the vessel from the fluid, which can be shown using the Reynolds Transport Theorem:

$$\begin{aligned} m_v{\ddot{q}}+\nu q-\mu q^3=\int _0^{2\pi }\int _0^{h(r,\theta ,t)}\cos \theta \left( \left. p\right| _{r=R_2} R_2-\left. p\right| _{r=R_1} R_1\right) \,\mathrm{d}z\; \mathrm{d}\theta . \end{aligned}$$

We reformulate the governing equations in terms of velocities along the free-surface, as Alemi Ardakani and Bridges [21] show that these equations can readily be reduced to a shallow-water system, where the free-surface velocities are new shallow-water variables. On the free-surface, we define the free-surface fluid velocities to be

$$\begin{aligned} U_r=u_{r}(r,\theta ,h(r,\theta ,t),t), \quad U_\theta =u_\theta (r,\theta ,h(r,\theta ,t),t), \quad U_z=u_z(r,\theta ,h(r,\theta ,t),t), \end{aligned}$$

using which, we can form the following identities:

$$\begin{aligned} \frac{\mathrm{{D}}u_{r}}{\mathrm{{D}}t}=\frac{\partial U_r}{\partial t}+U_r\frac{\partial U_r}{\partial r}+\frac{U_\theta }{r}\frac{\partial U_r}{\partial \theta }, \qquad \frac{\mathrm{{D}}u_\theta }{\mathrm{{D}}t}=\frac{\partial U_\theta }{\partial t}+U_r\frac{\partial U_\theta }{\partial r}+\frac{U_\theta }{r}\frac{\partial U_\theta }{\partial \theta }. \end{aligned}$$

Thus, on the free-surface the two horizontal momentum equations become

$$\begin{aligned}&\frac{\partial U_r}{\partial t}+U_r\frac{\partial U_r}{\partial r} +\frac{U_\theta }{r}\frac{\partial U_r}{\partial \theta } -\frac{U_\theta ^2}{r}+\frac{1}{\rho }\frac{\partial p}{\partial r} =-{\ddot{q}}\cos \theta ,\\&\frac{\partial U_\theta }{\partial t}+U_r\frac{\partial U_\theta }{\partial r}+\frac{U_\theta }{r}\frac{\partial U_\theta }{\partial \theta }+\frac{U_rU_\theta }{r} +\frac{1}{r\rho }\frac{\partial p}{\partial \theta }={\ddot{q}}\sin \theta . \end{aligned}$$

The pressure gradients in these equations can be eliminated by integrating the vertical momentum equation between some general point z and the free-surface $h(r,\theta ,t)$ and using (2.7). This leads to

$$\begin{aligned} p(r,\theta ,z,t)=\rho g(h-z)+\rho \int _z^h\frac{\mathrm{{D}}u_z}{\mathrm{{D}}t}\,\mathrm{d}s, \end{aligned}$$

which upon differentiating with respect to r and $\theta$ and evaluating on the free-surface, leads to the internal pressure gradients

$$\begin{aligned} \frac{\partial p}{\partial r}=\rho \left( g+\left. \frac{\mathrm{{D}}u_z}{\mathrm{{D}}t}\right| _{z=h}\right) \frac{\partial h}{\partial r}, \quad \quad \frac{\partial p}{\partial \theta }=\rho \left( g+\left. \frac{\mathrm{{D}}u_z}{\mathrm{{D}}t}\right| _{z=h}\right) \frac{\partial h}{\partial \theta }. \end{aligned}$$

Thus, we have the following exact momentum equations on the free-surface

$$\begin{aligned}&\frac{\partial U_r}{\partial t}+U_r\frac{\partial U_r}{\partial r} +\frac{U_\theta }{r}\frac{\partial U_r}{\partial \theta }-\frac{U_\theta ^2}{r} +g\frac{\partial h}{\partial r}+{\ddot{q}}\cos \theta =-\left. \frac{\mathrm{{D}}u_z}{\mathrm{{D}}t}\right| _{z=h} \frac{\partial h}{\partial r}, \end{aligned}$$

(2.9)

$$\begin{aligned}&\frac{\partial U_\theta }{\partial t}+U_r\frac{\partial U_\theta }{\partial r}+\frac{U_\theta }{r}\frac{\partial U_\theta }{\partial \theta }+\frac{U_rU_\theta }{r} +\frac{g}{r}\frac{\partial h}{\partial \theta }-{\ddot{q}}\sin \theta =-\frac{1}{r}\left. \frac{\mathrm{{D}}u_z}{\mathrm{{D}}t}\right| _{z=h} \frac{\partial h}{\partial \theta }, \end{aligned}$$

(2.10)

while the kinematic condition on the free-surface can be written as

$$\begin{aligned} \frac{\partial h}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}(rhU_r)+\frac{1}{r}\frac{\partial }{\partial \theta }(hU_\theta ) =U_z+\frac{h}{r}\frac{\partial }{\partial r}(rU_r)+\frac{h}{r}\frac{\partial U_\theta }{\partial \theta }. \end{aligned}$$

(2.11)

For the vessel equation, we note that writing the velocities in terms of surface velocities gives

$$\begin{aligned} \int _0^h\rho \left( u_{r}\cos \theta -u_\theta \sin \theta \right) r\,\mathrm{d}z=\rho h\left( U_r\cos \theta -U_\theta \sin \theta \right) r-\int _0^h\rho z\left( \frac{\partial u_{r}}{\partial z}\cos \theta -\frac{\partial u_\theta }{\partial z}\sin \theta \right) r\;\mathrm{d}z, \end{aligned}$$

which leads to an exact vessel equation of the form

$$\begin{aligned}&(m_f+m_v){\ddot{q}}+\nu q+\frac{\mathrm{d}}{\mathrm{d}t}\int _{R_1}^{R_2}\int _0^{2\pi }h\rho \left( U_r\cos \theta -U_\theta \sin \theta \right) r\;\mathrm{d}\theta \; \mathrm{d}r\nonumber \\&\quad =\frac{\mathrm{d}}{\mathrm{d}t}\int _{R_1}^{R_2}\int _0^{2\pi }\int _0^h\rho z\left( \frac{\partial u_{r}}{\partial z}\cos \theta -\frac{\partial u_\theta }{\partial z}\sin \theta \right) r\;\mathrm{d}z \;\mathrm{d}\theta \; \mathrm{d}r. \end{aligned}$$

(2.12)

3 Shallow-water equations and LPP formulation

3.1 Governing shallow-water equations

The exact governing equations (2.9)–(2.12) are not closed since their right-hand sides include terms which involve internal velocities $u_{r}$, $u_\theta$ and $u_z$. A closed set of equations for the shallow-water variables $U_r$, $U_\theta$, q and h can be found by neglecting the right-hand sides of these equations. The principal assumptions required to neglect these terms are

$$\begin{aligned} \left| \frac{\mathrm{{D}}u_z}{\mathrm{{D}}t}\frac{\partial h}{\partial r}\right| \ll 1~~\mathrm{and}~~\left| \frac{1}{r}\frac{\mathrm{{D}}u_z}{\mathrm{{D}}t}\frac{\partial h}{\partial \theta }\right| \ll 1~~\mathrm{on}~~z=h(r,\theta ,t), \end{aligned}$$

along with

$$\begin{aligned}&\left| U_z+\frac{h}{r}\frac{\partial }{\partial r}(rU_r)+\frac{h}{r} \frac{\partial U_\theta }{\partial \theta }\right| \ll 1,\quad \left| \frac{\mathrm{d}}{\mathrm{d}t}\int _{R_1}^{R_2}\int _0^{2\pi }\int _0^h\rho z\left( \frac{\partial u_{r}}{\partial z}\cos \theta -\frac{\partial u_\theta }{\partial z}\sin \theta \right) r\;\mathrm{d}z\; \mathrm{d}\theta \;\mathrm{d}r\right| \ll 1. \end{aligned}$$

It can be shown, based on [21], that these assumptions are equivalent to the usual shallow-water assumptions that the vertical accelerations throughout the fluid are small, that the horizontal velocities $u_r, u_\theta$ are independent of z and that the vertical velocity $u_z$ is, at most, linear in z. Under these assumptions, the motion of the fluid and the vessel can be considered as two-dimensional planar motion only.

The resulting shallow-water equations are then

$$\begin{aligned}&\frac{\partial U_r}{\partial t}+U_r\frac{\partial U_r}{\partial r}+\frac{U_\theta }{r}\frac{\partial U_r}{\partial \theta } -\frac{U_\theta ^2}{r}+g\frac{\partial h}{\partial r}=-{\ddot{q}}\cos \theta , \end{aligned}$$

(3.1)

$$\begin{aligned}&\frac{\partial U_\theta }{\partial t}+U_r\frac{\partial U_\theta }{\partial r} +\frac{U_\theta }{r}\frac{\partial U_\theta }{\partial \theta }+\frac{U_rU_\theta }{r} +\frac{g}{r}\frac{\partial h}{\partial \theta }={\ddot{q}}\sin \theta , \end{aligned}$$

(3.2)

$$\begin{aligned}&\frac{\partial h}{\partial t}+\frac{1}{r}\frac{\partial }{\partial r}(rhU_r) +\frac{1}{r}\frac{\partial }{\partial \theta }(hU_\theta )=0, \end{aligned}$$

(3.3)

$$\begin{aligned}&(m_f+m_v){\ddot{q}}+\nu q+\frac{\mathrm{{d}}}{\mathrm{{d}}t}\int _{R_1}^{R_2}\int _0^{2\pi }h\rho \left( U_r\cos \theta -U_\theta \sin \theta \right) r\;\mathrm{d}\theta \, \mathrm{d}r=0. \end{aligned}$$

(3.4)

We seek numerical solutions of these nonlinear equations, but in their current form the Eulerian convective derivative makes numerical treatment difficult. Hence, we consider a Lagrangian Particle Path (LPP) formulation.

3.2 LPP formulation

To formulate the LPP equations, we seek a solution of the following form:

$$\begin{aligned} r=r(a,b,\tau ),\quad \theta =\theta (a,b,\tau ),\quad t=t(\tau ), \end{aligned}$$

where a, b and $\tau$ are Lagrangian marker coordinates and a Lagrangian time, respectively. The Lagrangian time variable is the same as the physical time, but we use the symbol $\tau =t$ to clearly identify that we are in the Lagrangian framework. The Lagrangian coordinates satisfy $a\in [R_1,R_2]$ and $b\in [0,2\pi ]$, as well as

$$\begin{aligned} \left( \begin{array}{c} \mathrm{d}r \\ \mathrm{d}\theta \\ \mathrm{d}t \end{array}\right) =\left[ \begin{array}{c@{\quad }c@{\quad }c} r_a &{} r_b &{} t_\tau \\ \theta _a &{} \theta _b &{} \theta _\tau \\ 0 &{} 0 &{} t_\tau \end{array}\right] \left( \begin{array}{c} \mathrm{d}a \\ \mathrm{d}b \\ \mathrm{d}\tau \end{array}\right) , \end{aligned}$$

where subscripts denote partial derivatives. Inverting this map gives

$$\begin{aligned} \left( \begin{array}{c} \mathrm{d}a \\ \mathrm{d}b \\ \mathrm{d}\tau \end{array}\right) {=\left[ \begin{array}{c@{\quad }c@{\quad }c} a_r &{} a_\theta &{} a_t \\ b_r &{} b_\theta &{} b_t \\ \tau _r &{} \tau _\theta &{} \tau _t \end{array}\right] \left( \begin{array}{c} \mathrm{d}r \\ \mathrm{d}\theta \\ \mathrm{d}t \end{array}\right) }=\frac{1}{J}\left[ \begin{array}{c@{\quad }c@{\quad }c} \theta _b &{} -r_a &{} \frac{1}{t_\tau }(r_b\theta _\tau -r_\tau \theta _b) \\ -\theta _a &{} \theta _b &{} -\frac{1}{t_\tau }(r_a\theta _\tau -r_\tau \theta _a) \\ 0 &{} 0 &{} \frac{J}{t_\tau } \end{array}\right] \left( \begin{array}{c} \mathrm{d}r \\ \mathrm{d}\theta \\ \mathrm{d}t \end{array}\right) , \end{aligned}$$

(3.5)

where $J=r_a\theta _b-r_b\theta _a$ is the Jacobian of the map. To change from Eulerian to Lagrangian variables, we note that the chain rule for the derivatives are

$$\begin{aligned} \frac{\partial }{\partial t}=\tau _t\frac{\partial }{\partial \tau } +a_t\frac{\partial }{\partial a}+b_t\frac{\partial }{\partial b},\qquad \frac{\partial }{\partial r}= & {} \tau _r\frac{\partial }{\partial \tau } +a_r\frac{\partial }{\partial a}+b_r\frac{\partial }{\partial b},\qquad \frac{\partial }{\partial \theta }=\tau _\theta \frac{\partial }{\partial \tau }+a_\theta \frac{\partial }{\partial a}+b_\theta \frac{\partial }{\partial b}, \end{aligned}$$

which, upon comparing the entries in the equivalent matrices in (3.5), we can write as

$$\begin{aligned} \frac{\partial }{\partial t}= & {} \frac{\partial }{\partial \tau }+\frac{1}{J} (r_b\theta _\tau -r_\tau \theta _b)\frac{\partial }{\partial a}-\frac{1}{J} (r_a\theta _\tau -r_\tau \theta _a)\frac{\partial }{\partial b},\\ \frac{\partial }{\partial r}= & {} \frac{\theta _b}{J}\frac{\partial }{\partial a}-\frac{\theta _a}{J}\frac{\partial }{\partial b},\quad \frac{\partial }{\partial \theta }=-\frac{r_b}{J}\frac{\partial }{\partial a}+\frac{r_a}{J}\frac{\partial }{\partial b}. \end{aligned}$$

Under this change of variables, and by writing $t=\tau$ and $U_r=r_\tau$ and $U_\theta =r\theta _\tau$, the kinematic condition (3.3) becomes

$$\begin{aligned} (rJh)_\tau =0 \quad \Longrightarrow \quad h=\frac{\chi }{rJ}, \end{aligned}$$

(3.6)

where $\chi (a,b)$ is a $\tau$-independent function determined by the initial conditions. The two momentum equations (3.1) and (3.2) reduce to

$$\begin{aligned}&r_{\tau \tau }-r\theta _\tau ^2+\frac{g}{J}\left( \theta _bh_a -\theta _ah_b\right) =-q_{\tau \tau }\cos \theta , \end{aligned}$$

(3.7)

$$\begin{aligned}&r\theta _{\tau \tau }+2r_\tau \theta _\tau +\frac{g}{rJ}\left( -r_bh_a+r_ah_b\right) =q_{\tau \tau }\sin \theta , \end{aligned}$$

(3.8)

while the vessel equation (3.4) becomes

$$\begin{aligned} (m_v+m_f)q_{\tau \tau }+\nu q-\mu q^3=-\frac{\mathrm{d}^2}{\mathrm{d}\tau ^2}\int _{R_1}^{R_2}\int _0^{2\pi }\rho \chi r\cos \theta \;\mathrm{d}a\;\mathrm{d}b. \end{aligned}$$

(3.9)

Before moving on to constructing the numerical scheme to solve (3.6)–(3.9), we first consider the linear form of these equations. This will allow us to identify the natural frequencies of the system and identify whether 1 : 1 resonances are possible between the modes which couple to the vessel’s motion and the ‘stationary-vessel’ modes which occur in the vessel at rest. Note that we use the term ‘stationary-vessel modes’ to refer to those time periodic sloshing modes in a stationary vessel. These modes are frequently referred to as ‘free-sloshing modes’ in the literature; however, this term is also used for sloshing modes in a moving vessel where the vessel is not connected to a spring, i.e. there is no restoring force. Hence, we use the term ‘stationary-vessel’ modes to avoid this ambiguity. The linear solutions also provide a mechanism with which to verify the numerical scheme in Sect. 5.

4 Linear shallow-water modes and internal resonances

In order to identify the characteristic frequencies of the system, and hence any 1 : 1 resonances (where two modes oscillate with the same frequency), we consider solutions of (3.6)–(3.9) linearized about the quiescent solution $r=a$, $\theta =b$, $h=h_0$, $q=0$. Thus, solutions have the form

$$\begin{aligned} r=a+{\widehat{r}}(a,b,\tau ),\quad \theta =b+{\widehat{\theta }}(a,b,\tau ),\quad h=h_0+{\widehat{h}}(a,b,\tau ),\quad q ={\widehat{q}}(\tau ), \end{aligned}$$

where the absolute value of the hatted variables are assumed to be small.

Firstly, we observe that substitution of these expressions into (3.6) gives

$$\begin{aligned} \chi =ah_0,\quad {\mathrm{and}}\quad {\widehat{h}}=-h_0\left( \frac{{\widehat{r}}}{a}+{\widehat{\theta }}_b+{\widehat{r}}_a\right) . \end{aligned}$$

(4.1)

Next, the linear form of the two momentum equations (3.1)–(3.2) become

$$\begin{aligned} {\widehat{r}}_{\tau \tau }-gh_0\left( {\widehat{r}}_{aa}+\frac{{\widehat{r}}_a}{a}-\frac{{\widehat{r}}}{a^2} +{\widehat{\theta }}_{ab}\right) =-Q_{\tau \tau }\cos b,\qquad a{\widehat{\theta }}_{\tau \tau }-\frac{gh_0}{a}\left( {\widehat{r}}_{ab}+\frac{{\widehat{r}}_b}{a} +{\widehat{\theta }}_{bb}\right) =Q_{\tau \tau }\sin b, \end{aligned}$$

after eliminating ${\widehat{h}}$, and the linear vessel equation is

$$\begin{aligned} (m_v+m_f){\widehat{q}}_{\tau \tau }+\nu {\widehat{q}}=-\frac{\mathrm{d}^2}{\mathrm{d}\tau ^2}\int _{R_1}^{R_2}\int _0^{2\pi }\rho \chi \left( {\widehat{r}}\cos b-a{\widehat{\theta }}\sin b\right) \;\mathrm{d}a\;\mathrm{d}b. \end{aligned}$$

To determine the characteristic frequencies for the system, we seek harmonic solutions in terms of an a yet unknown frequency $\omega$, and a given azimuthal wavenumber $m\in \mathbb {Z}$ in the following forms

$$\begin{aligned} {\widehat{r}}(a,b,\tau )=e(a)\cos mb \cos \omega \tau ,\quad {\widehat{\theta }}(a,b,\tau )=f(a)\sin mb \cos \omega \tau ,\quad {\widehat{q}}(\tau )=Q\cos \omega \tau . \end{aligned}$$

(4.2)

The functions e,  f and constant Q then satisfy

$$\begin{aligned}&\left[ \alpha ^2e+e''+a^{-1}e'-a^{-2}e+mf'\right] \cos mb+Q\cos b=0, \end{aligned}$$

(4.3)

$$\begin{aligned}&\left[ \alpha ^2 a^2f-me'-ma^{-1}e-m^2f\right] \sin mb-Q\sin b=0, \end{aligned}$$

(4.4)

$$\begin{aligned}&-\omega ^2(m_v+m_f) Q+\nu Q-\omega ^2\int _{R_1}^{R_2}\int _0^{2\pi }\rho \chi \left( e\cos mb\cos b-af\sin mb\sin b\right) \,\mathrm{d}a\;\mathrm{d}b=0, \end{aligned}$$

(4.5)

where $\alpha =\omega /\sqrt{gh_0}$ and the primes denote derivatives with respect to a. From the form of these equations, it is clear that $m=1$ is required for the coupled modes, in which the fluid motion couples to the vessel’s motion ($Q\ne 0$), while for $m\ne 1$, we require $Q=0$ to find a solution, these correspond to the stationary-vessel modes in a non-moving vessel.

4.1 Case $m=1$: coupled-sloshing modes

In this case, we assume $Q\ne 0$, so that the vessel is moving, and thus (4.3)$+$(4.4)$'$ leads to $e=-(a^2 f)'$. Substituting this back into (4.4) gives the differential equation

$$\begin{aligned} a^2(a^2f)''+a(a^2f)'+(\alpha ^2a^2-1)(a^2f)=\alpha ^2a^2Q, \end{aligned}$$

(4.6)

which has general solution

$$\begin{aligned} f(a)=A\frac{J_1(\alpha a)}{a^2}+B\frac{Y_1(\alpha a)}{a^2}+\frac{Q}{a}, \end{aligned}$$

(4.7)

where $J_1(\alpha a)$ and $Y_1(\alpha a)$ are Bessel functions of the first and second kind respectively, and A and B are constants to be determined. The corresponding solution for e(a) is

$$\begin{aligned} e(a)=-AJ_1'(\alpha a)-BY_1'(\alpha a)-Q, \end{aligned}$$

(4.8)

leading to the general solutions for $r(a,b,\tau )$, $\theta (a,b,\tau )$ and $h(a,b,\tau )$ of the form

$$\begin{aligned} r= & {} a-\left[ AJ_1'(\alpha a)+BY_1'(\alpha a)+Q\right] \cos b\cos \omega t, \end{aligned}$$

(4.9)

$$\begin{aligned} \theta= & {} b+\frac{1}{a^2}\left[ AJ_1(\alpha a)+BY_1(\alpha a)+Q a\right] \sin b\cos \omega t, \end{aligned}$$

(4.10)

$$\begin{aligned} h= & {} h_0-h_0\alpha ^2\left[ AJ_1(\alpha a)+BY_1(\alpha a)\right] \cos b\cos \omega t, \end{aligned}$$

(4.11)

where the form of ${\widehat{h}}$ comes from (4.1).

The values for A and B come from ensuring that $U_r=r_\tau =0$ at $a=R_1$ and $a=R_2$ giving

$$\begin{aligned} A=Q\frac{Y_1'(\alpha R_2)-Y_1'(\alpha R_1)}{\Gamma _1(\alpha )}\quad {\mathrm{and}}\quad B=-Q\frac{J_1'(\alpha R_2)-J_1'(\alpha R_1)}{\Gamma _1(\alpha )}, \end{aligned}$$

where

$$\begin{aligned} \Gamma _m(\alpha )=J_m'(\alpha R_2)Y_m'(\alpha R_1)-J_m'(\alpha R_1)Y_m'(\alpha R_2). \end{aligned}$$

Finally, the characteristic frequencies of the system are then found by substituting (4.7) and (4.8) into (4.5), which after substituting in for the values of A and B can be written as the implicit equation:

$$\begin{aligned} D(\omega ):= & {} \frac{G}{\omega ^2}-\frac{1}{{\widehat{M}}}+\frac{1}{(R_2^2-R_1^2)\Gamma _1(\alpha )}\nonumber \\&\times \,\Big [\frac{4}{\pi }+R_2\left( J_1'(\alpha R_1)Y_1(\alpha R_2)-Y_1'(\alpha R_1)J_1 (\alpha R_2)\right) +R_1\left( J_1'(\alpha R_2)Y_1(\alpha R_1)-Y_1'(\alpha R_2)J_1(\alpha R_1)\right) \Big ]=0,\nonumber \\ \end{aligned}$$

(4.12)

where

$$\begin{aligned} {\widehat{M}}=\frac{m_f}{m_v}\quad \hbox {and}\quad G=\frac{\nu }{m_f}. \end{aligned}$$

(4.13)

Note that the characteristic equation (4.12) is an implicit equation for $\omega$ as $\alpha =\alpha (\omega )$ in the argument of the Bessel functions. This equation has an infinite number of roots.

4.2 Case $m\ne 1$: stationary-vessel-sloshing modes

Following the same approach as for the case $m=1$ but with $Q=0$, we find m(4.3)$+$(4.4)$'$ leads to $e=-\frac{1}{m}(a^2 f)'$, which when substituted back into (4.4) gives

$$\begin{aligned} a^2(a^2f)''+a(a^2f)'+(\alpha ^2a^2-m^2)(a^2f)=0, \end{aligned}$$

(4.14)

and has general solution

$$\begin{aligned} f(a)=A\frac{J_m(\alpha a)}{a^2}+B\frac{Y_m(\alpha a)}{a^2}. \end{aligned}$$

(4.15)

Hence one can show that

$$\begin{aligned} r= & {} a-\left[ AJ_m'(\alpha a)+BY_m'(\alpha a)\right] \cos mb\cos \omega t, \end{aligned}$$

(4.16)

$$\begin{aligned} \theta= & {} b+\frac{1}{a^2}\left[ AJ_m(\alpha a)+BY_m(\alpha a)\right] \sin mb\cos \omega t, \end{aligned}$$

(4.17)

$$\begin{aligned} h= & {} h_0-h_0\alpha ^2\left[ AJ_m(\alpha a)+BY_m(\alpha a)\right] \cos mb\cos \omega t. \end{aligned}$$

(4.18)

This time the characteristic equation for these stationary-vessel sloshing modes comes directly from satisfying the impermeable wall conditions at $a=R_1$ and $a=R_2$ which lead to

$$\begin{aligned} AJ_m'(\alpha R_1)+BY_m'(\alpha R_1)=0 \quad {\mathrm{and}}\quad AJ_m'(\alpha R_2)+BY_m'(\alpha R_2)=0, \end{aligned}$$

which is non-trivially satisfied if

$$\begin{aligned} P_m(\omega ):=\Gamma _m(\alpha )=0. \end{aligned}$$

(4.19)

This again is an implicit equation for $\omega$, with an infinite number of roots.

4.3 Characteristic equation solutions and the 1 : 1 resonance

Using the results above, the full dispersion relation for the annular vessel system is

$$\begin{aligned} \Delta (\omega )=P(\omega )D(\omega ), \end{aligned}$$

(4.20)

where

$$\begin{aligned} P(\omega )=\prod _{\begin{array}{c} m=0\\ m\ne 1 \end{array}}^\infty P_m(\omega ). \end{aligned}$$

This shallow-water form of the dispersion relation has an equivalent finite depth form $\Delta ^{\mathrm{FD}}(\omega )=P^{\mathrm{FD}}(\omega )D^{\mathrm{FD}}(\omega )$ where

$$\begin{aligned} P^{\mathrm{FD}}_m(\omega )= & {} \omega ^2-gk_{mn}\tanh (k_{mn}h_0), \end{aligned}$$

(4.21)

$$\begin{aligned} D^{\mathrm{FD}}(\omega )= & {} \frac{G}{\omega ^2}-\frac{1}{{\widehat{M}}}-1-\frac{\omega ^2}{R_2^2-R_1^2}\sum _{n=1}^\infty \frac{B_n}{k_{1n}h_0} \left[ R_2\widehat{P}(R_2)-R_1\widehat{P}(R_1)\right] \frac{\tanh (k_{1n}h_0)}{gk_{1n} \tanh (k_{1n}h_0)-\omega ^2}, \end{aligned}$$

(4.22)

where $D^{\mathrm{FD}}(\omega )$ can be inferred from the $\nu =0$ limit result in [14] and $P^{\mathrm{FD}}(\omega )$ can be found in [17, 18]. In (4.22)

$$\begin{aligned}&\widehat{P}(r)=Y_1'(k_{1n}R_1)J_1(k_{1n}r)-J_1'(k_{1n}R_1)Y_1(k_{1n}r),\\&B_n=\frac{2k_{1n}\left( Y_1'(k_{1n}R_1)\left[ R_2^2J_2(k_{1n}R_2)-R_1^2J_2(k_{1n}R_1)\right] -J_1'(k_{1n}R_1)\left[ R_2^2Y_2(k_{1n}R_2)-R_1^2Y_2(k_{1n}R_1)\right] \right) }{\left[ \widehat{P}(k_{1n}R_2)\right] ^2\left[ (k_{1n}R_2)^2-1\right] -\left[ \widehat{P}(k_{1n}R_1)\right] ^2\left[ (k_{1n}R_1)^2-1\right] }, \end{aligned}$$

and $k_{mn}$ are the roots of

$$\begin{aligned} J_m'(k_{mn}R_1)Y_m'(k_{mn}R_2)-J_m'(k_{mn}R_2)Y_m'(k_{mn}R_1)=0. \end{aligned}$$

(4.23)

Fig. 2

Plot of the characteristic equations in shallow-water $D(\omega )$ (solid lines) and finite depth $D^{\mathrm{FD}}(\omega )$ (dashed lines) for the case $R_1=0.05\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $\nu =50\,\hbox {kg\,s}^{-2}$. In a$h_0=0.2\,\hbox {m}$ while in b$h_0=0.02\,\hbox {m}$

For the results presented in this section, we consider vessels composed of similar materials to those used in the experiments of [14], thus we consider similar size and weight vessels as this paper. The results in this section are presented for a vessel with $R_1=0.05\,\hbox {m}$, $R_2=0.2\,\hbox {m}$ and $m_v=2\,\hbox {kg}$. The fluid considered is water with $\rho =1000\,\mathrm{kg\,m}^{-3}$, $g=9.81\,\mathrm{ms}^{-2}$, the infinite summation in (4.22) is truncated to 200 terms and we observe qualitatively similar results for other values of the system parameters. In Fig. 2, we consider the forms of $D(\omega )$ (solid line) and $D^{\mathrm{FD}}(\omega )$ (dashed line) for the cases (a) $h_0=0.2$m and (b) $h_0=0.02\,\hbox {m}$. In order to determine these figures the values of $k_{mn}$ from (4.23) are calculated via Newton iterations. The results show that in scenario (a), we are away from the shallow-water limit, with a depth ratio $\delta =h_0/(R_2-R_1)=4/3$ while in (b) $\delta =2/15$ and the shallow-water result for the first 3 roots is in good agreement with the finite-depth results. The interesting feature in this figure is that for both cases the shallow-water result and finite-depth result are in excellent agreement for the first, lowest-frequency mode. Thus, for systems which are dominated by the lowest-frequency-coupled mode, the shallow-water model considered here provides a good model even when considering non-shallow water fluid depths. This same curious behaviour was also observed for a cylindrical vessel by [13], and can be seen also in the characteristic frequency plots in Fig. 3. For the results in Figs. 3, 4 and 5 the values of $\omega$ are found by solving $\Delta (\omega )=0$ via Newton iterations. For the coupled modes in Fig. 3a, the finite-depth and shallow-water results for the lowest-frequency mode agree for the whole range of ${\widehat{M}}=m_f/m_v$ considered, and the difference between the shallow-water and finite-depth results can be shown to be less than $1\%$ at ${\widehat{M}}=10$ for spring coefficients up to $\nu =600\,\mathrm{kg\,s}^{-2}$, and hence, for a wide range of parameter values. For the second coupled mode, the agreement is only good for ${\widehat{M}}\lesssim 1.5$, which is also the case for the lowest-frequency $m=0$ and $m=2$ stationary-vessel-sloshing modes in Fig. 3b. Thus, when considering nonlinear simulations in Sect. 5.4, we should place this restriction on the fluid mass to generate meaningful results, when not considering the lowest-frequency mode.

Fig. 3

Plot of the characteristic frequencies $\omega$ of a the coupled mode characteristic equation $D(\omega )=0$ and b the stationary-vessel mode characteristic equation $P(\omega )=0$ as a function of ${\widehat{M}}{=m_f/m_v}$ for the case $R_1=0.05\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $\nu =50\,\hbox {kg\,s}^{-2}$. In a, results 1 denote the lowest-frequency mode while results 2 denote the second lowest-frequency mode. In b, results 1 denote the first $m=0$ mode while results 2 denote the first $m=2$ mode. In both panels, the solid lines are the finite-depth result, while the dashed lines give the shallow-water result. For result 1 in (a), these two results are indistinguishable

Fig. 4

Plot of the first two characteristic frequencies $\omega$ of $D(\omega )=0$ as a function of $\nu$ for the case $R_1=0.05\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $\nu =50\,\hbox {kg\,s}^{-2}$ and ${\widehat{M}}{=m_f/m_v}=2$

The lowest-frequency-coupled mode, which is well approximated by the shallow-water theory, is particular to the coupled system and is not evident in freely oscillating vessel work of [14]. This can be seen in Fig. 4 where this lowest-frequency mode vanishes in the $\nu =0$ limit and the second mode, given by the dashed line, becomes the observed lowest-frequency mode for that system.

A 1 : 1 internal resonance occurs in the system if there exists an $\omega$ such that $P(\omega )=D(\omega )=0$ and $P_\omega (\omega )\ne 0$ and $D_\omega (\omega )\ne 0$, i.e. if one of the stationary-vessel-sloshing modes resonates with the same frequency as a coupled-sloshing mode. This coupling could lead to interesting vessel motions if a heteroclinic orbit exists which allows energy to be exchanged between the modes, as was observed for the case of a vessel with rectangular cross-section in [20]. In this case, the 1 : 1 resonance condition only exists for a single fluid depth and it was shown that a moving vessel could come to rest with the fluid now oscillating as a stationary-vessel-sloshing mode after the exchange of energy.

Fig. 5

Plot of the value of $\nu$ at which the 1 : 1 resonance occurs between the second lowest frequency of the coupled mode and a the the lowest frequency $m=0$ of the stationary-vessel mode; and b the lowest frequency $m=2$ stationary-vessel mode for the case $R_1=0.05\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$

For the annular vessel, we determined the parameter values at which the 1 : 1 resonance occurs by updating the value of the linear spring coefficient $\nu$ in $D(\omega )=0$ until the value of $\omega$ agrees with that from $P(\omega )=0$, which is independent of $\nu$. We found that in order to obtain a 1 : 1 resonance between the lowest-frequency-coupled mode (result 1 in Fig. 3a) with either of the modes in Fig. 3b, then the value of $\nu$ obtained was unphysically large. Hence, in Fig. 5, we identify $\nu ({\widehat{M}})$ where the 1 : 1 resonance occurs with the second coupled mode (result 2 from Fig. 3a) with the lowest (a) $m=0$ and (b) $m=2$ stationary-vessel modes. In both cases, the shallow-water approximation is valid only for ${\widehat{M}}{=m_f/m_v}\lesssim 1.5$, and this range is also the range for physically realistic values of $\nu$. Hence, a 1 : 1 resonance for the annular cylinder only is likely to be observed for small mass ratios ${\widehat{M}}$. Determining whether the 1 : 1 resonance in this system also possesses a heteroclinic orbit connecting the modes involves an extensive normal mode analysis and is beyond the scope of this paper.

5 Numerical shallow-water simulations

The LPP formulation of the governing equations (3.6)–(3.9) can be solved numerically using a symplectic integration scheme to simulate linear and nonlinear system scenarios. To formulate this approach, we first observe that the kinetic energy, T, and potential energy, V, in shallow-water Eulerian variables are

$$\begin{aligned} T= & {} \int _{R_1}^{R_2}\int _0^{2\pi }\frac{1}{2}\rho h\left[ \left( U_r+q_\tau \cos \theta \right) ^2+\left( U_\theta -q_\tau \sin \theta \right) ^2 \right] \,r\;\mathrm{d}\theta \; \mathrm{d}r+\frac{1}{2}m_v\dot{q}^2,\\ V= & {} \int _{R_1}^{R_2}\int _0^{2\pi }\frac{1}{2}\rho gh^2\,r\;\mathrm{d}\theta \; \mathrm{d}r+\frac{1}{2}\nu q^2-\frac{1}{4}\mu q^4, \end{aligned}$$

which when converted to LPP variables become

$$\begin{aligned} T= & {} \int _{R_1}^{R_2}\int _0^{2\pi }\frac{1}{2}\rho \chi \left[ \left( r_\tau +q_\tau \cos \theta \right) ^2+\left( r\theta _\tau -q_\tau \sin \theta \right) ^2\right] \;\mathrm{d}b \;\mathrm{d}a+\frac{1}{2}m_vq_\tau ^2,\\ V= & {} \int _{R_1}^{R_2}\int _0^{2\pi }\frac{1}{2}\rho g\frac{\chi ^2}{{rJ}}\;\mathrm{d}b\; \mathrm{d}a+\frac{1}{2}\nu q^2-\frac{1}{4}\mu q^4. \end{aligned}$$

Thus, we can construct the Lagrangian ${\mathscr {L}}=\int _{\tau _1}^{\tau _2}L\;\mathrm{d}\tau ,$ where

$$\begin{aligned} L=\frac{1}{2}\int _{R_1}^{R_2}\int _0^{2\pi }\rho \chi \left[ \left( r_\tau +q_\tau \cos \theta \right) ^2 +\left( r\theta _\tau -q_\tau \sin \theta \right) ^2-\frac{g\chi }{rJ}\right] \;\mathrm{d}a \;\mathrm{d}b+\frac{1}{2}m_vq_\tau ^2-\frac{1}{2}\nu q^2+\frac{1}{4}\mu q^4. \end{aligned}$$

(5.1)

Using this Lagrangian, we can construct the Hamiltonian for the system and hence, we can derive the first order system of Hamilton’s equations which can then be integrated using a symplectic integration scheme such as the implicit-midpoint-rule [22].

5.1 Hamilton’s equations for the nonlinear system

To construct the Hamiltonian for the system, we first introduce the momentum variables v, w, p such that

$$\begin{aligned} \frac{\delta {\mathscr {L}}}{\delta r_\tau }= & {} v=r_\tau +q_\tau \cos \theta ,\\ \frac{\delta {\mathscr {L}}}{\delta \theta _\tau }= & {} rw=r\left( r\theta _\tau -q_\tau \sin \theta \right) ,\\ \frac{\delta {\mathscr {L}}}{\delta q_\tau }= & {} p=(m_v+m_f)q_\tau +\int _{R_1}^{R_2} \int _0^{2\pi }\rho \chi \left( r_\tau \cos \theta -r\theta _\tau \sin \theta \right) \;\mathrm{d}a\; \mathrm{d}b\\= & {} m_vq_\tau +\int _{R_1}^{R_2}\int _0^{2\pi }\rho \chi \left( v\cos \theta -w\sin \theta \right) \; \mathrm{d}a \;\mathrm{d}b, \end{aligned}$$

which transforms the Lagrangian (5.1) into

$$\begin{aligned} L=\frac{1}{2}\int _{R_1}^{R_2}\int _0^{2\pi }\rho \chi \left[ v^2 +w^2-\frac{g\chi }{rJ}\right] \;\mathrm{d}a\;\mathrm{d}b+\frac{1}{2m_v}\left( p-I\right) -\frac{1}{2}\nu q^2+\frac{1}{4}\mu q^4, \end{aligned}$$

where $I=\int _{R_1}^{R_2}\int _0^{2\pi }\rho \chi \left( v\cos \theta -w\sin \theta \right) \;\mathrm{d}a\;\mathrm{d}b$. Using the Legendre transformation [27], we then determine the Hamiltonian ${\mathscr {H}}(r,\theta ,q,v,w,p)$ as

$$\begin{aligned} {\mathscr {H}}= & {} \int _{R_1}^{R_2}\int _0^{2\pi }\rho \chi \left[ r_\tau v+r\theta _\tau w\right] \;\mathrm{d}a\;\mathrm{d}b+q_\tau p-L\\= & {} \frac{1}{2}\int _{R_1}^{R_2}\int _0^{2\pi }\rho \chi \left[ v^2+w^2\right] \;\mathrm{d}a\;\mathrm{d}b+\frac{1}{2m_v}\left( p-I\right) ^2+\int _{R_1}^{R_2}\int _0^{2\pi }\frac{1}{2}\rho g\frac{\chi ^2}{rJ}\;\mathrm{d}a\;\mathrm{d}b+\frac{1}{2}\nu q^2+\frac{1}{4}\mu q^4. \end{aligned}$$

Taking variations of the Hamiltonian with respect to the position and momenta variables, we derive Hamilton’s equations for the nonlinear system

$$\begin{aligned} r_\tau= & {} v-\frac{\cos \theta }{m_v}(p-I), \end{aligned}$$

(5.2)

$$\begin{aligned} \theta _\tau= & {} \frac{w}{r}+\frac{\sin \theta }{m_v r}(p-I), \end{aligned}$$

(5.3)

$$\begin{aligned} q_\tau= & {} \frac{1}{m_v}(p-I), \end{aligned}$$

(5.4)

$$\begin{aligned} -v_\tau= & {} -\frac{w^2}{r}-\frac{w\sin \theta }{m_v r}(p-I)+\frac{g}{J} \left[ \theta _b\left( \frac{\chi }{rJ}\right) _a-\theta _a\left( \frac{\chi }{rJ}\right) _b \right] , \end{aligned}$$

(5.5)

$$\begin{aligned} -w_\tau= & {} \frac{v}{r}\left[ w+\frac{\sin \theta }{m_v}(p-I)\right] -\frac{g}{Jr}\left[ r_b \left( \frac{\chi }{rJ}\right) _a-r_a\left( \frac{\chi }{rJ}\right) _b\right] , \end{aligned}$$

(5.6)

$$\begin{aligned} -p_\tau= & {} \nu q+\mu q^3. \end{aligned}$$

(5.7)

The above equations can readily be shown to be consistent with (3.7)–(3.9).

5.2 Spatial and temporal discretization

For the spatial discretization of (5.2)–(5.7), we divide the annular domain by splitting $a\in [R_1,R_2]$ and $b\in [0,\pi ]$ into N and M regularly spaced regions, respectively, via

$$\begin{aligned} a_i= & {} (i-1)\Delta a,\quad i=1,\ldots ,N+1 \quad \hbox {with}\quad \Delta a=\frac{R_2-R_1}{N},\\ b_j= & {} (j-1)\Delta b,\quad j=1,\ldots ,M+1 \quad \hbox {with}\quad \Delta b=\frac{\pi }{M}, \end{aligned}$$

where, for the purposes of computational cost, we have assumed a symmetric solution for $\pi \le b\le 2\pi$. We do this because the focus of this section of the paper is on the flow due to the coupled modes, for which $m=1$ in Sect. 4.1 and these have this required symmetry. Using this discretization we introduce the notation for each variable that $r_{ij}=r(a_i,b_j,\tau )$.

For Hamilton’s equations, the form of the spatial discretization is clear, except within the $v_\tau$ and $w_\tau$ equations where the bracketed terms differentiated with respect to a and b need to be considered with care. Here it is not obvious as regards how to discretize these terms which arise from the term proportional to g in the Hamiltonian. To overcome this issue, we spatially discretize the Hamiltonian directly and then take variations with respect to the discretized position variables and momenta $r_{ij}$ and $\theta _{ij}$. The problematic term in the Hamiltonian is

$$\begin{aligned} {\mathscr {F}}(r,\theta )=\int _{R_1}^{R_2}\int _0^{2\pi }\frac{1}{2}\rho g\frac{\chi ^2(a,b)}{r(r_a\theta _b-r_b\theta _a)}\;\mathrm{d}a\;\mathrm{d}b. \end{aligned}$$

To discretize this term, we express the double integral as an average of four double summations, which allow the spatial derivatives to be discretized via forward or backward differences in the four respective combinations forward-forward, forward-back, back-forward and back-back, where the first part refers to the a derivatives and the second part refers to the b derivatives. Therefore, we write

$$\begin{aligned} {\mathscr {F}}(r,\theta )=\frac{\rho g}{8}\sum _{j=1}^{M}\sum _{i=1}^N\left[ F_{ij}^{FF}+F_{ij}^{FB} +F_{ij}^{BF}+F_{ij}^{BB}\right] , \end{aligned}$$

where

$$\begin{aligned} F_{ij}^{FF}=\frac{\chi _{ij}^2}{r_{ij}J_{ij}^{FF}}, \quad F_{ij}^{FB} =\frac{\chi _{i(j+1)}^2}{r_{i(j+1)}J_{ij}^{FB}}, \quad F_{ij}^{BF}=\frac{\chi _{(i+1)j}^2}{r_{(i+1)j}J_{ij}^{BF}}, \quad F_{ij}^{BB} =\frac{\chi _{(i+1)(j+1)}^2}{r_{(i+1)(j+1)}J_{ij}^{BB}} \end{aligned}$$

and

$$\begin{aligned} J_{ij}^{FF}= & {} (r_{(i+1)j}-r_{ij})(\theta _{i(j+1)}-\theta _{ij})-(r_{i(j+1)}-r_{ij})(\theta _{(i+1)j}-\theta _{ij}),\\ J_{ij}^{BB}= & {} (r_{(i+1)(j+1)}-r_{i(j+1)})(\theta _{(i+1)(j+1)}-\theta _{(i+1)j})-(r_{(i+1)(j+1)}-r_{(i+1)j})(\theta _{(i+1)(j+1)}-\theta _{i(j+1)}),\\ J_{ij}^{FB}= & {} (r_{(i+1)(j+1)}-r_{i(j+1)})(\theta _{i(j+1)}-\theta _{ij})-(r_{i(j+1)}-r_{ij})(\theta _{(i+1)(j+1)}-\theta _{i(j+1)}),\\ J_{ij}^{BF}= & {} (r_{(i+1)j}-r_{ij})(\theta _{(i+1)(j+1)}-\theta _{(i+1)j})-(r_{(i+1)(j+1)}-r_{(i+1)j})(\theta _{(i+1)j}-\theta _{ij}). \end{aligned}$$

The spatially semi-discretized form of Hamilton’s equations are then found to be

$$\begin{aligned} (r_{ij})_\tau= & {} v_{ij}-\frac{\cos \theta _{ij}}{m_v}(p-I), \quad {\mathrm{for}}\quad i=[2,N],~j=[1,M+1], \end{aligned}$$

(5.8)

$$\begin{aligned} (\theta _{ij})_\tau= & {} \frac{w_{ij}}{r_{ij}} +\frac{\sin \theta _{ij}}{m_v r_{ij}}(p-I), \quad {\mathrm{for}}\quad i=[1,N+1],~j=[2,M] \end{aligned}$$

(5.9)

$$\begin{aligned} q_\tau= & {} \frac{1}{m_v}(p-I), \end{aligned}$$

(5.10)

$$\begin{aligned} (v_{ij})_\tau= & {} \frac{w_{ij}^2}{r_{ij}}+\frac{w_{ij}\sin \theta _{ij} }{m_v r_{ij}} (p-I)-\frac{\Delta a\Delta bg}{8\chi _{ij}}\left\{ -\frac{\chi _{ij}^2}{r_{ij}^2} \left[ \frac{1}{J_{ij}^{FF}}+\frac{1}{J_{(i-1)(j-1)}^{BB}}+\frac{1}{J_{i(j-1)}^{FB}} +\frac{1}{J_{(i-1)j}^{BF}}\right] \right. \nonumber \\&+\frac{\chi ^2_{ij}}{r_{ij}}\left[ \frac{(\theta _{i(j+1)}-\theta _{(i+1)j})}{(J_{ij}^{FF})^2}+\frac{(\theta _{i(j-1)}-\theta _{(i-1)j})}{(J_{(i-1)(j-1)}^{BB})^2} +\frac{(\theta _{(i+1)j}-\theta _{i(j-1)})}{(J_{i(j-1)}^{FB})^2}+\frac{(\theta _{(i-1)j} -\theta _{i(j+1)})}{(J_{(i-1)j}^{BF})^2}\right] \nonumber \\&-\frac{\chi _{(i-1)j}^2}{r_{(i-1)j}}\left[ \frac{(\theta _{(i-1)(j+1)} -\theta _{(i-1)j})}{(J_{(i-1)j}^{FF})^2}+\frac{(\theta _{(i-1)j} -\theta _{(i-1)(j-1)})}{(J_{(i-1)(j-1)}^{FB})^2}\right] \nonumber \\&+\frac{\chi _{(i+1)j}^2}{r_{(i+1)j}}\left[ \frac{(\theta _{(i+1)j} -\theta _{(i+1)(j-1)})}{(J_{i(j-1)}^{BB})^2}+\frac{(\theta _{(i+1)(j+1)} -\theta _{(i+1)j})}{(J_{ij}^{BF})^2}\right] \nonumber \\&+\frac{\chi _{i(j-1)}^2}{r_{i(j-1)}}\left[ \frac{(\theta _{(i+1)(j-1)} -\theta _{i(j-1)})}{(J_{i(j-1)}^{FF})^2}+\frac{(\theta _{i(j-1)} -\theta _{(i-1)(j-1)})}{(J_{(i-1)(j-1)}^{BF})^2}\right] \nonumber \\&\left. -\frac{\chi _{i(j+1)}^2}{r_{i(j+1)}}\left[ \frac{(\theta _{i(j+1)} -\theta _{(i-1)(j+1)})}{(J_{(i-1)j}^{BB})^2}+\frac{(\theta _{(i+1)(j+1)} -\theta _{i(j+1)})}{(J_{ij}^{FB})^2}\right] \right\} ,\nonumber \\&\quad \mathrm{for}\quad i=[2,N],~j=[1,M+1] \end{aligned}$$

(5.11)

$$\begin{aligned} (w_{ij})_\tau= & {} -\frac{v_{ij}}{r_{ij}}\left( w_{ij} +\frac{\sin \theta _{ij}}{m_v}(p-I)\right) +\frac{\Delta a\Delta bg}{8\chi _{ij}r_{ij}}\left\{ \frac{\chi ^2_{ij}}{r_{ij}}\left[ \frac{(r_{i(j+1)} -r_{(i+1)j})}{(J_{ij}^{FF})^2}\right. \right. \nonumber \\&\left. +\frac{(r_{i(j-1)} -r_{(i-1)j})}{(J_{(i-1)(j-1)}^{BB})^2}+\frac{(r_{(i+1)j}-r_{i(j-1)})}{(J_{i(j-1)}^{FB})^2}+\frac{(r_{(i-1)j}-r_{i(j+1)})}{(J_{(i-1)j}^{BF})^2}\right] \nonumber \\&-\frac{\chi _{(i-1)j}^2}{r_{(i-1)j}}\left[ \frac{(r_{(i-1)(j+1)}-r_{(i-1)j})}{(J_{(i-1)j}^{FF})^2}+\frac{(r_{(i-1)j}-r_{(i-1)(j-1)})}{(J_{(i-1)(j-1)}^{FB})^2}\right] \nonumber \\&+\frac{\chi _{(i+1)j}^2}{r_{(i+1)j}}\left[ \frac{(r_{(i+1)j} -r_{(i+1)(j-1)})}{(J_{i(j-1)}^{BB})^2}+\frac{(r_{(i+1)(j+1)} -r_{(i+1)j})}{(J_{ij}^{BF})^2}\right] \nonumber \\&+\frac{\chi _{i(j-1)}^2}{r_{i(j-1)}}\left[ \frac{(r_{(i+1)(j-1)} -r_{i(j-1)})}{(J_{i(j-1)}^{FF})^2}+\frac{(r_{i(j-1)} -r_{(i-1)(j-1)})}{(J_{(i-1)(j-1)}^{BF})^2}\right] \nonumber \\&\left. -\frac{\chi _{i(j+1)}^2}{r_{i(j+1)}}\left[ \frac{(r_{i(j+1)} -r_{(i-1)(j+1)})}{(J_{(i-1)j}^{BB})^2}+\frac{(r_{(i+1)(j+1)} -r_{i(j+1)})}{(J_{ij}^{FB})^2}\right] \right\} ,\nonumber \\&\quad \mathrm{for}\quad i=[1,N+1],~j=[2,M] \end{aligned}$$

(5.12)

$$\begin{aligned} p_\tau= & {} -\nu q+\mu q^3. \end{aligned}$$

(5.13)

Here I is discretized using the trapezoidal rule in both the a and b directions.

Note that when (5.11) is evaluated at the boundary points $M=1$ and $M+1$, ghost points for the variables are required ($\theta _{i0}$ and $\theta _{i(M+2)}$, for example) outside the domain. In (5.11) because, we want the flow to be symmetric across $b=0,\pi$, we use the ghost points

$$\begin{aligned} r_{i0}= & {} r_{i2}\quad {\mathrm{and}}\quad r_{i(M+2)}=r_{i(M-1)},\\ \theta _{i0}= & {} -\theta _{i2}\quad \mathrm{and}\quad \theta _{i(M+2)}=\pi +\theta _{i(M-1)}. \end{aligned}$$

Also, when evaluating (5.12) at the boundary points $N=1$ and $N+1$, we again need representations at the ghost points $r_{0j}$ and $r_{(M+2)j}$ etc. In this case, however, the situation is more difficult as we have no symmetry across this boundary, because from Sect. 4 we know the basis functions are Bessel functions in the a direction. Thus, some form of approximation is required. In this paper, we use a 4 grid point Lagrange polynomial extrapolation scheme in order to approximate these values. This choice is examined in Sect. 5.3.

The discretized form of Hamilton’s equations give $4NM-2$ equations for the $4(N+1)(M+1)+2$ unknowns. The remaining $4(N+1)+4(M+1)$ equations come from the impermeable wall boundary conditions at $a=R_1$ and $R_2$ and the symmetry conditions at $b=0$ and $\pi$. These conditions amount to

$$\begin{aligned} r_\tau =0\quad \mathrm{at}\quad a=R_1,~R_2\quad \mathrm{and}\quad \theta _\tau =0\quad \mathrm{at}\quad b=0,~\pi . \end{aligned}$$

Therefore the boundary conditions are

$$\begin{aligned} r_{1j}= & {} R_1\quad \mathrm{and}\quad r_{(N+1)j}=R_2\quad \mathrm{for}\quad j=[1,M+1], \end{aligned}$$

(5.14)

$$\begin{aligned} \theta _{i1}= & {} 0\quad \mathrm{and}\quad \theta _{i(M+1)}=\pi \quad \mathrm{for}\quad i=[1,N+1], \end{aligned}$$

(5.15)

$$\begin{aligned} v_{ij}= & {} \frac{\cos \theta _{ij}}{m_v}(p-I),\quad \mathrm{for}\quad i=1,N+1\quad \mathrm{and}\quad j=[1,M+1], \end{aligned}$$

(5.16)

$$\begin{aligned} w_{ij}= & {} -\frac{\sin \theta _{ij}}{m_v}(p-I),\quad \mathrm{for}\quad j=1,M+1\quad \mathrm{and}\quad i=[1,N+1], \end{aligned}$$

(5.17)

where the final two expressions come from inserting $r_\tau =\theta _\tau =0$ in (5.8) and (5.9).

The semi-discretized equations (5.8)–(5.13), along with the boundary conditions (5.14)–(5.17) can be written as a system of first order ODEs of the form

$$\begin{aligned} \mathbf{p}_\tau =f(\mathbf{p},\mathbf{q}),\quad \mathbf{q}_\tau =g(\mathbf{p},\mathbf{q}), \end{aligned}$$

(5.18)

where

$$\begin{aligned} \mathbf{p} = (v_{11},v_{12},\ldots ,v_{NM},w_{11},\ldots ,w_{NM},p)^\mathrm{T}, \qquad \mathbf{q}=(r_{11},r_{12},\ldots ,r_{NM},\theta _{11},\ldots ,\theta _{NM},q)^\mathrm{T}. \end{aligned}$$

This system of equations can be integrated via the symplectic geometric integration scheme, the implicit-midpoint rule [22]. Using this approach the system of ODEs becomes a system on nonlinear algebraic equations of the form

$$\begin{aligned} \mathbf{p}^{n+1}=\mathbf{p}^n+\Delta \tau f\left( \frac{\mathbf{p}^n+\mathbf{p}^{n+1}}{2},\frac{\mathbf{q}^n+\mathbf{q}^{n+1}}{2}\right) ,\qquad \mathbf{q}^{n+1}=\mathbf{q}^n+\Delta \tau g\left( \frac{\mathbf{p}^n+\mathbf{p}^{n+1}}{2},\frac{\mathbf{q}^n+\mathbf{q}^{n+1}}{2}\right) , \end{aligned}$$

where n denotes the time-step, such that $\mathbf{p}^n=\mathbf{p}(n\Delta \tau )$ and $\Delta \tau$ is the time step. This system of implicit equations are solved at each new time step via Newton–Armijo–GMRES iterations [28].

For the initial conditions, we consider momenta and position conditions from the linear theory of Sect. 4.2. We focus our attention here on non-resonant simulations, because [20] showed for the 2D rectangular vessel that the 1 : 1 resonance occurs at one particular fluid depth, given the system parameters, and this depth was not in the shallow-water limit. Hence, assuming the same is true for the annulus, we are highly unlikely to observe energy transfer between modes by chance. Hence, the initial condition we consider is given by (4.9) and (4.10) with $\tau =0$ and $Q\equiv Q_1$ along with $v(a,b,0)=w(a,b,0)=0$ and $q(0)=Q$ and $p(0)=0$; thus, we have two independent amplitude parameters $Q_1$ and Q. The initial condition when $Q_1=Q$ will allow us to verify our simulations against the exact linear solution of a single coupled mode, but in an experimental setup, it might be difficult to generate such a condition. Hence, we also consider the case when $Q_1=0$ and $Q\ne 0$, which corresponds to a quiescent fluid in a vessel which has been displaced to a distance Q from equilibrium and then is released from rest. This type of condition is more akin to that which can be achieved in a experiment (cf [9, 12] for example), and consists of a superposition of coupled modes.

Fig. 6

Plot of ${\mathscr {H}}(\tau )$ for the lowest frequency-coupled mode ($\omega =2.0255\,\mathrm{s}^{-1}$) with $Q_1=Q=10^{-5}\,\hbox {m}$, $R_1=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $\nu =30\,\hbox {kg\,s}^{-2}$ and $h_0=0.05\,\hbox {m}$. In result 1 the ghost points of (5.12) are found using 4 point Lagrange extrapolation, while in result 2 they are found assuming symmetry about $a=R_1$ and $a=R_2$

Fig. 7

Plot of $h(x,t)-h_0$ for the lowest-frequency-coupled mode ($\omega =2.0255\,\mathrm{s}^{-1}$) with $Q_1=Q=10^{-5}\,\hbox {m}$, $R_1=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $\nu =30\,\hbox {kg\,s}^{-2}$, $h_0=0.05\,\hbox {m}$, where $x=r\cos \theta$, at a$\tau =15.6\,\hbox {s}$, b$\tau =16.2\,\hbox {s}$, c$\tau =16.8\,\hbox {s}$, d$\tau =17.4\,\hbox {s}$, e$\tau =18.0\,\hbox {s}$, f$\tau =18.6\,\hbox {s}$. The dots denote the exact linear solution (4.11)

Fig. 8

Plot of $q(\tau )$ for the lowest-frequency-coupled mode ($\omega =2.0255\,\mathrm{s}^{-1}$) with $Q_1=Q=10^{-5}\,\hbox {m}$, $R_1=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $\nu =30\,\hbox {kg\,s}^{-2}$ and $h_0=0.05\,\hbox {m}$. The dots denote the exact linear solution (4.2). The largest percentage Hamiltonian error for this result is 0.07%

Fig. 9

Plot of a$q(\tau )$ for the second coupled mode ($\omega =6.2951\,\mathrm{s}^{-1}$) with $Q_1=Q=10^{-5}\,\hbox {m}$, $R_1=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $\nu =30\,\hbox {kg\,s}^{-2}$, $h_0=0.05\,\hbox {m}$ and b$h(x,t)-h_0$ at $\tau =1\,\hbox {s}$, 1.1 s, 1.2 s, 1.3 s, 1.4 s and 1.5 s numbered 1, 2, 3, 4, 5, and 6, respectively. The dots denote the exact linear solution (4.2). The largest percentage Hamiltonian error for this result is 0.01%

5.3 Linear simulations

In order to validate the numerical scheme, we compare the numerical solution in the linear amplitude regime with the exact linear solution for one coupled mode given by (4.9)–(4.11). Thus, we choose to set $Q_1=Q=10^{-5}\,\hbox {m}$, and $\mu =0\,\mathrm{kg\,m^{-2}s^{-2}}$ so that the nonlinear terms in the governing equations are negligible. In Figs. 6, 7, 8 and 9, we consider simulations with $R_1=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $\nu =30\,\mathrm{kg\,s}^{-2}$, $m_v=2\,\hbox {kg}$, $h_0=0.05\,\hbox {m}$ along with $(N,M,\Delta \tau )=(100,100,5\times 10^{-3})$ to coincide with the vessel parameters similar to those in Sect. 4.3. For all the results in this section, the resulting system of nonlinear equations are solved with a relative residual of $10^{-8}$.

As discussed in Sect. 5.2, there needs to be some element of approximation when determining r and $\theta$ at the ghost points of (5.12) outside the flow domain. In Fig. 6, we consider the error in the solution when using the 4 point Lagrange extrapolation approximation by plotting ${\mathscr {H}}(\tau )$ when calculating the lowest-frequency-coupled eigenmode. As ${\mathscr {H}}(\tau )$ is equivalent to the total system energy, we wish for this to remain constant for the duration of the simulation. In Fig. 6, we see that this approximation gives only a 0.07% change from its initial value over the duration of the simulation (4000 timesteps). As a comparison, we also plot ${\mathscr {H}}(\tau )$ for a simulation where the variables r and $\theta$ are assumed to have symmetry across these boundaries, i.e. $r_{0j}=2R_1-r_{2j}$, $r_{(N+2)j}=2R_2-r_{Nj}$, $\theta _{0j}=\theta _{2j}$ and $\theta _{(N+2)j}=\theta _{Nj}$. While the energy conservation is good for this approximation, the extrapolation scheme is understandably better. For the remainder of this paper, we highlight the maximum system energy percentage change for each simulation performed, in order to indicate the reliability of the results. In Table 1, we consider the grid dependence of the simulation results using the extrapolation approximation, again simulating the lowest-frequency-coupled eigenmode. We find that this numerical scheme does converge as the grid size is reduced with all maximum energy errors much less than 1% after a 20 s simulation. Hence, the extrapolation approximation is justified for future simulations.

In Figs. 7 and 8, we validate the numerical scheme by comparing the lowest-frequency eigenmode ($\omega =2.0255\,\mathrm{s}^{-1}$) with the exact linear forms of h(x, t) (4.11) and $q(\tau )$ (4.2), given by the black dots. The free surface elevations $h(x,t)-h_0$ in Fig. 7 are plotted along the centre-line plane of the vessel as a function of the Cartesian coordinate $x=r\cos \theta$, with $\theta =0$ and $\theta =\pi$. Agreement between the simulation and the theoretical result is excellent for all times $t\in [0,20]\,\hbox {s}$ for both the free-surface elevation and the vessel displacement $q(\tau )$ in Fig. 8.

In Fig. 9, we observe excellent agreement between the theoretical and numerical simulation results for $q(\tau )$ for the second coupled eigenmode with frequency $\omega =6.2951\,\mathrm{s}^{-1}$. The free-surface profiles in Fig. 9b are taken over half a period of the motion, and as for the lowest-frequency eigenmode, they have almost linear profiles. In this case, however, the magnitude of the motion for the same value of Q is almost 10 times larger than the lowest frequency eigenmode, which is expected due to the $\omega ^2$ factor in (4.11).

Now that the numerical scheme is validated, we consider an initial condition $Q_1=0\,\hbox {m}$, but with $Q=10^{-5}\,\hbox {m}$, again for the parameters $R_1=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$ and $\nu =30\,\mathrm{kg\,s}^{-2}$. This gives a quiescent fluid initially, with a flat free-surface and corresponds to a condition easily generated in an experiment where the vessel is displaced by a distance Q from equilibrum and released from rest. In Fig. 10, we consider the vessel’s motion $q(\tau )$ as the fluid depth is reduced from (a) $h_0=0.05\,\hbox {m}$, (b) $h_0=0.02\,\hbox {m}$ to (c) $h_0=0.005\,\hbox {m}$. For the two-dimensional rectangular vessel, [12] showed that for a fixed set of system parameters, reducing the initial fluid depth $h_0$ (or fluid mass $m_f$) caused the system to ‘transition’ to higher frequency eigenmodes. This was first highlighted by experimental evidence. Here we investigate using numerical simulations whether the same effect is observable in the annular vessel. The results in Fig. 10 show this to be the case, with the system frequency in panel (a) agreeing well with the lowest-frequency eigenmode (dashed line). But as $h_0$ is reduced, the solution becomes a superposition of two modes in (b), before finally becoming solely the higher frequency second coupled mode in (c) at $h_0=0.005\,\hbox {m}$. Re-plotting this result in (d) against the theoretical second coupled mode result (dashed line) shows the system has switched to this frequency. We now go on to consider the annular system in the nonlinear regime.

Table 1 The maximum percentage error between ${\mathscr {H}}(\tau )$ and its initial value for simulations such as result 1 in Fig. 6, for varying numerical grids and fixed $\Delta \tau$

Fig. 10

Plot of $q(\tau )$ (solid lines) for the system $Q_1=0\,\hbox {m}$, $Q=10^{-5}\,\hbox {m}$, $R_0=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $\nu =30\,\mathrm{kg\,s}^{-2}$ and a$h_0=0.05\,\hbox {m}$, b$h_0=0.02\,\hbox {m}$ and c, d$h_0=0.005\,\hbox {m}$. In a–c the dashed lines give the linear result (4.2) for the lowest-frequency-coupled eigenmode, while in (d), it gives the second coupled eigenmode. The largest percentage Hamiltonian error for these results is $0.08\%$

5.4 Nonlinear simulations

In this section, we consider numerical solution results where both nonlinear fluid and nonlinear vessel effects are significant. In this section, we focus on parameter values for which the system is just outside the domain of validity of the linear solution. For the results presented here, we again consider the experimental initial conditions with $Q_1=0\,\hbox {m}$ for the vessel $R_1=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$ and linear spring coefficient $\nu =\,30\,\mathrm{kg\,s}^{-2}$ with the simulation parameters $(N,M,\Delta \tau )=(200,200,5\times 10^{-3})$. Figure 11a considers the vessel displacement $q(\tau )$ for the case $Q=2\times 10^{-2}\,\hbox {m}$ with $\mu =0\,\mathrm{kg\,m^{-2}s^{-2}}$. The linear result for this simulation is given by the solid line in Fig. 10a. The panel contains the nonlinear result (solid line), together with the linear result of Fig. 10a scaled up by a factor 2000. The results are indistinguishable and highlight the same qualitative result as for the rectangular vessel presented in [24]. It means that considering a nonlinear fluid with a linear vessel has little effect on the motion of the vessel (at least for the vessel mass considered). The nonlinear free-surface , on the other hand, are modified, as seen in Fig. 12, which compare the nonlinear and linear results. The main point to note here is that the nonlinearity builds up in the fluid over time so that the free-surface profiles no longer have rotational symmetry about $x=0$ as the linear profiles do. Figure 11b, c shows that by considering nonlinear springs with $\mu =1000\,{\mathrm{kg\,m^{-2}s^{-2}}}$ (dotted line) and $\mu =-1000\,{\mathrm{kg\,m^{-2}\,s^{-2}}}$ (dashed line), the vessel’s motion $q(\tau )$ can be more readily modified. With a hard spring ($\mu >0$), the frequency of the vessel is decreased, while the soft spring ($\mu <0$) increases the frequency of the system. This is in accordance with the results for the rectangular vessel system [24].

Fig. 11

Plot of $q(\tau )$ for the system $Q_1=0\,\hbox {m}$, $R_0=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $h_0=0.05\,\hbox {m}$, $\nu =30\,\mathrm{kg\,s}^{-2}$. In a$\mu =0\,\mathrm{kg\,m^{-2}s^{-2}}$ and $Q=2\times 10^{-2}\,\hbox {m}$ (solid line), while the indistinguishable dashed line represents the linear result with $Q=10^{-5}\,\hbox {m}$ scaled up by a factor of 2000. In b$Q=2\times 10^{-2}\,\hbox {m}$ and $\mu =0\,\mathrm{kg\,m^{-2}s^{-2}}$ (solid line), $\mu =1000\,\mathrm{kg\,m^{-2}s^{-2}}$ (dotted line) and $\mu =-1000\,\mathrm{kg\,m^{-2}s^{-2}}$ (dashed line). c is a blow-up of the end times of (b). The largest percentage Hamiltonian error for these results is $0.8\%$

Fig. 12

Plot of $h(x,t)-h_0$ for the case system $Q=2\times 10^{-2}\,\hbox {m}$, $Q_1=0\,\hbox {m}$, $R_0=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $h_0=0.05\,\hbox {m}$, $\nu =30\,\mathrm{kg\,s}^{-2}$ and $\mu =0\,\mathrm{kg\,m^{-2}s^{-2}}$ (solid lines) given in Fig. 11a, where $x=r\cos \theta$, at a$\tau =15\,\hbox {s}$, b$\tau =30\,\hbox {s}$, c$\tau =45\,\hbox {s}$, d$\tau =60\,\hbox {s}$, e$\tau =75\,\hbox {s}$, f$\tau =90\,\hbox {s}$. The dashed lines give the linear result scaled up by a factor of 2000

Fig. 13

Plot of $q(\tau )$ for the system $Q=10^{-2}\,\hbox {m}$, $Q_1=0\,\hbox {m}$, $R_0=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $h_0=0.02\,\hbox {m}$, $\nu =30\,\mathrm{kg\,s}^{-2}$ and $\mu =0\,\mathrm{kg\,m^{-2}s^{-2}}$ (solid line), while the dashed line represents the linear result with $Q=10^{-5}\,\hbox {m}$ scaled up by a factor of 1000. The largest percentage Hamiltonian error for these results is $0.05\%$

The small effect of nonlinearity on the vessel’s motion due to the fluid for $h_0=0.05\,\hbox {m}$ is likely to be due to the fact that the lowest-frequency eigenmode dominates the solution at this fluid depth. In Fig. 13, we again consider a linear vessel equation with a nonlinear fluid, but this time for $h_0=0.02\,\hbox {m}$, at a depth, as shown in Fig. 10b, where we observed two eigenmodes existing with comparable amplitudes. Here, for a value of $Q=10^{-2}\,\hbox {m}$, we see that the effect of the fluid nonlinearity is greater, with the nonlinear result (solid line) generally having slightly smaller peaks and troughs than the linear result, at least for the time duration considered here. The free-surface profiles for this nonlinear result also show considerable deviation from the linear result in Fig. 14, with more higher frequency oscillations clearly visible in the nonlinear result. Here the broken rotational symmetry of the profiles is more evident than for the $h_0=0.05\,\hbox {m}$ case.

Fig. 14

Plot of $h(x,t)-h_0$ for the case system $Q=10^{-2}\,\hbox {m}$, $Q_1=0\,\hbox {m}$, $R_0=0.1\,\hbox {m}$, $R_2=0.2\,\hbox {m}$, $m_v=2\,\hbox {kg}$, $h_0=0.02\,\hbox {m}$, $\nu =30\,\mathrm{kg\,s}^{-2}$ and $\mu =0\,\mathrm{kg\,m^{-2}\,s^{-2}}$ (solid lines) given in Fig. 13, where $x=r\cos \theta$, at a$\tau =10\,\hbox {s}$, b$\tau =20\,\hbox {s}$, c$\tau =30\,\hbox {s}$, d$\tau =40\,\hbox {s}$, e$\tau =50\,\hbox {s}$, f$\tau =60\,\hbox {s}$. The dashed lines give the linear result scaled up by a factor of 1000

Note, in order to consider larger initial vessel displacements, Q, the numerical model would need to be modified to incorporate some form of numerical filtering to filter out spurious high frequency dispersion waves which occur when shock waves begin to form in the results. This is not considered here, but the interested reader can find out more information in [24], who use such a filtering process for the rectangular vessel.

6 Discussion and conclusions

In this paper, we considered the coupled sloshing system consisting of an incompressible, inviscid fluid within an upright annular vessel, which is attached to a wall by a nonlinear spring. The vessel’s motion was confined to a single space dimension with the nonlinear spring acting as a restoring force. The moving vessel forces the fluid to move, which in turn impacts the rigid walls of the vessel, inducing a force which modifies the vessel’s motion, thus resulting in a coupled fluid/vessel system. This coupling can lead to more interesting and complex motions than that occur in many forced systems, which just consider how the fluid motion is affected by periodically oscillating the vessel with a fixed amplitude and frequency.

Results of the linear system showed that the lowest natural frequency eigenmode of the coupled system is accurately given when both a shallow-water and a non-shallow-water fluid model are considered (for $\nu \lesssim 600\,\mathrm{kg\,s}^{-2}$ where $\nu$ is the linear spring coefficient). Also the frequencies of the higher-frequency eigenmodes are well predicted by a shallow-water fluid model for ${\widehat{M}}=m_f/m_v\lesssim 1.5$, where $m_f$ is the fluid mass and $m_v$ is the vessel mass. It was also observed that as $\nu \rightarrow 0$ (i.e. the freely oscillating vessel limit investigated by [14]), the frequency of the lowest-frequency-coupled mode also tends to zero. Therefore, the lowest frequency freely oscillating eigenmode corresponds to the second lowest-frequency-coupled mode of the spring system in the appropriate limit. These results agree with those observed for the cylindrical vessel in [13].

The characteristic equation for the linear system was shown to support the 1 : 1 resonance where one of the coupled sloshing modes which is linked to the vessel’s motion oscillates with a frequency identical to one of the stationary-vessel-sloshing modes. Turner and Bridges [20] have shown for the rectangular vessel that the existence of a 1 : 1 resonance means that weakly nonlinear solutions close to this point in parameter space can exhibit energy exchange behaviour if a heteroclinic orbit exists between the modes. Thus, it is likely to exhibit similar behaviour for the annular vessel.

The fact that the lowest-frequency mode of the system was excellently approximated by a shallow-water fluid model was exploited by utilizing the Lagrangian Particle Path (LPP) formulation of the governing equations to perform linear and nonlinear numerical simulations. The numerical scheme devised was based on the symplectic implicit-midpoint rule, which conserves the Hamiltonian structure, as well as the system energy, and preserves the energy partition between the fluid and vessel’s motions. Results presented for the linear system showed the system transitioning to successive higher frequency eigenmodes as the fluid mass $m_f$ (or depth $h_0$) was reduced in line with the results found by [12]. This occurs so that the frequency of the system $\omega \rightarrow \omega _0=\sqrt{m_v/\nu }$, which is the frequency of the dry system ($m_f=0$), as $m_f\rightarrow 0$.

The nonlinear simulations showed that for a system dominated by the lowest-frequency mode, including only a nonlinear fluid with a linear vessel does not greatly modify the vessel’s motion, despite the free-surface profile being modified. However, when there exists two modes of similar amplitudes in the solution, then the effect of the nonlinear fluid is greater, leading to an observable modification of the vessel’s motion.