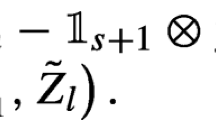Abstract
Computational multi-scale methods capitalize on a large time-scale separation to efficiently simulate slow dynamics over long time intervals. For stochastic systems, one often aims at resolving the statistics of the slowest dynamics. This paper looks at the efficiency of a micro–macro acceleration method that couples short bursts of stochastic path simulation with extrapolation of spatial averages forward in time. To have explicit derivations, we elicit an amenable linear test equation containing multiple time scales. We make derivations and perform numerical experiments in the Gaussian setting, where only the evolution of mean and variance matters. The analysis shows that, for this test model, the stability threshold on the extrapolation step is largely independent of the time-scale separation. In consequence, the micro–macro acceleration method increases the admissible time steps far beyond those for which a direct time discretization becomes unstable.








Similar content being viewed by others
Notes
Not to be confused with numerical stability (necessary for convergence) that measures the robustness of a numerical scheme with respect to perturbations, such as round-of errors, over finite time horizon as step-size tends to zero.
We use \(\varPi \) to unify the notation between this section and the subsequent one, in which we will project onto a lower-dimensional subspace. Here, one can think of \(\varPi \) as the projection from \(\mathbb {R}^d\) onto \(\mathbb {R}^d\).
More generally, the sufficient and necessary condition requires that the pair \((A,\overline{B})\) is controllable, see [24, pp. 355–356]. Assuming controllability only, we may not always be able to reduce (3.3) to (3.2). However, as (3.2) serves as a convenient test equation for asymptotic stability, this discrepancy is of minor importance.
The identity \(P = P^s\otimes P^{f|s}\) means that for every measurable rectangle \(U\times V\subseteq \mathbb {R}^{d_s}\oplus \mathbb {R}^{d_f}\) and Borel function \(g:U\times V\rightarrow \mathbb {R}\), it holds \(\int _{U\times V}g(x)\,P(\text { d}{x})=\int _{U}\int _{V}g(y,z)\,P^{f|s}(\text { d}{z}|y)\,P^s(\text { d}{y})\).
Stating that the matching of a prior \(\mathscr {N}_{\mu ,\varSigma }\) with a slow mean \(\overline{\mu }^s\) and a slow variance \(\overline{\varSigma }^s\) results in the normal distribution with the fast mean \(\overline{\mu }^f=\mu ^f+C^{\!\mathsf {T}}(\varSigma ^s)^{-1}(\overline{\mu }^s-\mu ^s)\) and fast variance \(\overline{\varSigma }^f=\varSigma ^f - C^{\!\mathsf {T}}(\varSigma ^s)^{-1}(C-\overline{C})\) where \(\overline{C}=C^{\!\mathsf {T}}(\varSigma ^s)^{-1}\overline{\varSigma }^s\).
References
Abdulle, A., Blumenthal, A.: Stabilized multilevel Monte Carlo method for stiff stochastic differential equations. J. Comput. Phys. 251, 445–460 (2013). https://doi.org/10.1016/j.jcp.2013.05.039
Abdulle, A., Weinan, E., Engquist, B., Vanden-Eijnden, E.: The heterogeneous multiscale method. Acta Numer. 21(April), 1–87 (2012). https://doi.org/10.1017/S0962492912000025
Andersen, H.H., Hojbjerre, M., Sorensen, D., Eriksen, P.S.: Linear and Graphical Models for the Multivariate Complex Normal Distribution. Lecture Notes in Statistics, vol. 101. Springer, New York (1995)
Blanc, X., Le Bris, C., Legoll, F., Lelièvre, T.: Beyond multiscale and multiphysics: multimaths for model coupling. Netw. Heterog. Media 5(3), 423–460 (2010). https://doi.org/10.3934/nhm.2010.5.423
Buckwar, E., Kelly, C.: Towards a systematic linear stability analysis of numerical methods for systems of stochastic differential equations. SIAM J. Numer. Anal. 48(1), 298–321 (2010). https://doi.org/10.1137/090771843
Buckwar, E., Riedler, M.G., Kloeden, P.E.: The numerical stability of stochastic ordinary differential equations with additive noise. Stoch. Dyn. 11(2 & 3), 265–281 (2011). https://doi.org/10.1142/S0219493711003279
Cover, T.M., Thomas, J.A.: Elements of Information Theory, 2nd edn. Wiley-Interscience, Hoboken (2005). https://doi.org/10.1002/047174882X
de la Cruz Cancino, H.A., Biscay, R.J., Jimenez, J.C., Carbonell, F., Ozaki, T.: High order local linearization methods: an approach for constructing A-stable explicit schemes for stochastic differential equations with additive noise. BIT Numer. Math. 50(3), 509–539 (2010). https://doi.org/10.1007/s10543-010-0272-6
Debrabant, K., Rößler, A.: Diagonally drift-implicit Runge–Kutta methods of weak order one and two for Itô SDEs and stability analysis. Appl. Numer. Math. 59(3–4), 595–607 (2009). https://doi.org/10.1016/j.apnum.2008.03.011
Debrabant, K., Samaey, G., Zieliński, P.: A micro–macro acceleration method for the Monte Carlo simulation of stochastic differential equations. SIAM J. Numer. Anal. 55(6), 2745–2786 (2017). https://doi.org/10.1137/16M1066658
Deisboeck, T.S., Wang, Z., Macklin, P., Cristini, V.: Multiscale cancer modeling. Annu. Rev. Biomed. Eng. 13, 127–55 (2011). https://doi.org/10.1146/annurev-bioeng-071910-124729
Díaz-Infante, S., Jerez, S.: Convergence and asymptotic stability of the explicit Steklov method for stochastic differential equations. J. Comput. Appl. Math. 291, 36–47 (2016). https://doi.org/10.1016/j.cam.2015.01.016
Dudley, R.M.: Real Analysis and Probability, Cambridge Studies in Advanced Mathematics, vol. 74, 2nd edn. Cambridge University Press, Cambridge (2002)
Favino, M., Krause, R., Pivkin, I.: A survey on stochastic multi-scale modeling in biomechanics: computational challenges (2016). https://arxiv.org/abs/1609.07719
Givon, D., Kupferman, R., Stuart, A.M.: Extracting macroscopic dynamics: model problems and algorithms. Nonlinearity 17(6), 55–127 (2004). https://doi.org/10.1088/0951-7715/17/6/R01
Harmandaris, V., Kalligiannaki, E., Katsoulakis, M.A., Plecháč, P.: Path-space variational inference for non-equilibrium coarse-grained systems. J. Comput. Phys. 314, 355–383 (2016). https://doi.org/10.1016/j.jcp.2016.03.021
Hernandez, D.B., Spigler, R.: A-stability of Runge–Kutta methods for systems with additive noise. BIT Numer. Math. 32(4), 620–633 (1992). https://doi.org/10.1007/BF01994846
Higham, D.J.: A-stability and stochastic mean-square stability. BIT Numer. Math. 40(2), 404–409 (2000). https://doi.org/10.1023/A:1022386822865
Horn, R.A., Johnson, C.R.: Topics in Matrix Analysis. Cambridge University Press, New York (1991)
Horn, R.A., Johnson, C.R.: Matrix Analysis, 2nd edn. Cambridge University Press, New York (2013)
Iserles, A.: A First Course in the Numerical Analysis of Differential Equations, Cambridge Texts in Applied Mathematics, vol. 44, 2nd edn. Cambridge University Press, New York (2008). https://doi.org/10.1017/CBO9780511995569
Jørgensen, B., Labouriau, R.S.: Exponential families and theoretical inference (2012). https://pure.au.dk/ws/files/51499534/Mon_52.pdf
Jungers, R.M.: The Joint Spectral Radius: Theory and Applications, Lecture Notes in Control and Information Sciences, vol. 385. Springer, Berlin (2009). https://doi.org/10.1002/oca.4660060112
Karatzas, I., Shreve, S.E.: Brownian Motion and Stochastic Calculus, Graduate Texts in Mathematics, vol. 113, 2nd edn. Springer, New York (1998). https://doi.org/10.1007/BF00046894
Keunings, R.: Micro–macro methods for the multiscale simulation of viscoelastic flow using molecular models of kinetic theory. Rheol. Rev. 67–98 (2004)
Kevrekidis, I.G., Samaey, G.: Equation-free multiscale computation: algorithms and applications. Annu. Rev. Phys. Chem. 60, 321–344 (2009). https://doi.org/10.1146/annurev.physchem.59.032607.093610
Kloeden, P.E., Platen, E.: Numerical Solution of Stochastic Differential Equations, Applications of Mathematics, vol. 23. Springer, Berlin (1999). https://doi.org/10.1007/978-3-662-12616-5
Komori, Y., Mitsui, T.: Stable ROW-type weak scheme for stochastic differential equations. Monte Carlo Methods Appl. 1(4), 279–300 (1995)
Kullback, S.: Information Theory and Statistics. Peter Smith Pub Inc, Gloucester (1978). https://doi.org/10.1109/WITS.1994.513846
Le Bris, C., Lelièvre, T.: Multiscale modelling of complex fluids: a mathematical initiation. In: Engquist, B., Lötstedt, P., Runborg, O. (eds.) Multiscale Modeling and Simulation in Science, pp. 49–137. Springer, Berlin (2009)
Lelièvre, T., Samaey, G., Zieliński, P.: Analysis of a micro–macro acceleration method with minimum relative entropy moment matching (2018). http://arxiv.org/abs/1801.01740
Li, T., Abdulle, A., Weinan, E.: Effectiveness of implicit methods for stiff stochastic differential equations. Commun. Comput. Phys. 3(2), 295–307 (2008)
Liu, W., Mao, X.: Numerical stationary distribution and its convergence for nonlinear stochastic differential equations. J. Comput. Appl. Math. 276, 16–29 (2015). https://doi.org/10.1016/j.cam.2014.08.019
Lunardi, A.: On the Ornstein–Uhlenbeck operator in L2 spaces with respect to invariant measures. Trans. Am. Math. Soc. 349(197), 155–169 (1997)
Metafune, G., Pallara, D., Priola, E.: Spectrum of Ornstein–Uhlenbeck operators in Lp spaces with respect to invariant measures. J. Funct. Anal. 196, 40–60 (2002). https://doi.org/10.1006/jfan.2002.3978
Pinsker, M.S.: Information and Information Stability of Random Variables and Processes. Holden-Day Series in Time Series Analysis. Holden-Day, San Francisco (1964)
Praprotnik, M., Site, L.D., Kremer, K.: Multiscale simulation of soft matter: from scale bridging to adaptive resolution. Annu. Rev. Phys. Chem. 59, 545–71 (2008). https://doi.org/10.1146/annurev.physchem.59.032607.093707
Roberts, A.J.: Normal form transforms separate slow and fast modes in stochastic dynamical systems. Phys. A Stat. Mech. Appl. 387, 12–38 (2008). https://doi.org/10.1016/j.physa.2007.08.023
Roberts, A.J.: Model Emergent Dynamics in Complex Systems, Mathematical Modeling and Computations, vol. 20. SIAM, Philadelphia (2014)
Saito, Y.: Stability analysis of numerical methods for stochastic systems with additive noise. Rev. Econ. Inf. Stud. 8(3–4), 119–123 (2008)
Saito, Y., Shotoku, G.: Mean-square stability of numerical schemes for stochastic differential systems. Vietnam J. Math 30, 1–12 (2002)
Szpruch, Ł., Zhang, X.: V-integrability, asymptotic stability and comparison property of explicit numerical schemes for non-linear SDEs. Math. Comput. 87(310), 755–783 (2018). https://doi.org/10.1090/mcom/3219
Teschl, G.: Ordinary Differential Equations and Dynamical Systems, Graduate Studies in Mathematics, vol. 140. American Mathematical Society, Providence (2012)
Vandecasteele, H., Zieliński, P., Samaey, G.: Efficiency of a micro–macro acceleration method for scale-separated stochastic differential equations (2019). http://arxiv.org/abs/1902.08045
Yuan, C., Mao, X.: Stability in distribution of numerical solutions for stochastic differential equations. Stoch. Anal. Appl. 22(5), 1133–1150 (2004). https://doi.org/10.1081/SAP-200026423
Zhang, W., Hartmann, C., Schütte, C.: Effective dynamics along given reaction coordinates, and reaction rate theory. Faraday Discuss. 195, 365–394 (2016). https://doi.org/10.1039/C6FD00147E
Zielinski, P.: Python code for “Study of micro–macro acceleration schemes for linear slow–fast stochastic differential equations with additive noise” (2018). https://doi.org/10.5281/zenodo.1252982
Zieliński, P., Vandecasteele, H., Samaey, G.: Convergence and stability of a micro–macro acceleration method: linear slow–fast stochastic differential equations with additive noise (2019). http://arxiv.org/abs/1901.07405
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Axel Målqvist.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
GS and PZ acknowledge the support of the Research Council of the University of Leuven through Grant ‘PDEOPT’, and of the Research Foundation—Flanders (FWO—Vlaanderen) under Grant G.A003.13.
Appendices
A Monte-Carlo simulation
Let us discuss in more detail the discretisation in probability of the micro–macro acceleration algorithm presented in Sects. 2.1 and 4.2. We consider an initial distribution given as a random empirical measure
where \(X^j_n\), \(j=1,\dotsc ,J\), are i.i.d. replicas with associated weights \(w^j_n\).
Stage 1: Propagation of microscopic laws In this stage, we freeze the weights and propagate each replica over the K steps of inner integrator \(\mathscr {S}^{\delta t}\) [compare with (4.4)]
where \(\xi ^{\delta t, j}\) are J i.i.d. centered normal variables with variance \(\delta t\) (replicas of \(\delta W_{k+1}\)). In particular, when applying the Euler–Maruyama method to (2.1) we get
The replicas \(X^{\delta t, j}_{n,k}\) are associated to the following empirical measures
Stage 2: Restriction to a finite number of observables In this stage, we evaluate the restriction operator \(\mathscr {R}\) on the empirical measures to obtain K empirical observables as \(\mathbf {m}^{J}_{n,k} = \mathscr {R}(P^{\delta t,J}_{n,k})\). For example, when restricting to the slow mean only as in (4.5), we find K vectors
where \(Y^{\delta t,j}_{n,k}=\varPi ^sX^{\delta t,j}_{n,k}\) and \(\varPi ^s\) is the projection onto the slow variables.
Stage 3: Extrapolation of macroscopic states We apply the extrapolation operator \(\mathscr {E}^{\varDelta t - K\delta t}\) to the empirical macroscopic states \(\mathbf {m}^{J}_{n,0},\dotsc ,\mathbf {m}^{J}_{n,K}\) and obtain \(\mathbf {m}^{s,J}_{n+1}\) as in formula (2.4). In the special case of linear extrapolation one proceeds according to (4.7), with \(\mathbf {m}^{s,J}_{n,0}\) and \(\mathbf {m}^{s,J}_{n,K}\) plugged in the right-hand side.
Stage 4: Matching Finally, the matching amounts to re-weighting the replicas \(X^{\delta t, j}_{n,K}\) using the Lagrange multipliers associated to procedure \((\hbox {ME})^{\mathrm{s}}\) or \((\hbox {MEV})^{\mathrm{s}}\) on page 12. Concentrating on \((\hbox {ME})^{\mathrm{s}}\) only, we approximate the Lagrange multipliers by applying the Newton–Raphson iteration to equation [compare with (2.7)]
In this fashion, we obtain, up to a given tolerance, the vector \(\overline{\lambda }^{s,J}_{n+1}\) of Lagrange multipliers with which, following (2.6), we evaluate weights
The matched empirical distribution reads
B Gap in the drift spectrum and the time scales of (3.2)
To elucidate how Assumption 3.1 influences the time scales present in the stochastic dynamics, recall first that Eq. (3.2) is related to the Ornstein–Uhlenbeck operator
SDE (3.2) and operator (B.1) are connected through the Markov semigroup \((e^{t\mathscr {L}})_{t\ge 0}\), generated by \(\mathscr {L}\), that satisfy
for every \(t\ge 0\) and \(f\in \mathscr {C}_{\mathrm {b}}(\mathbb {R}^d)\), the space of all continuous and bounded functions on \(\mathbb {R}^d\). The assumptions that \(\mathsf {Sp}(A)\subset \mathbb {C}_-\) and B is positive definite ensure the existence of a unique Gaussian invariant measure \(\mathscr {N}_{0,V_\infty }\) for \((e^{t\mathscr {L}})_{t\ge 0}\), where \(V_\infty \) is given by (3.4). To be more precise, the condition for invariance reads
for all \(f\in \mathscr {C}_{\mathrm {b}}(\mathbb {R}^d)\). Moreover, the semigroup \((e^{t\mathscr {L}})_{t\ge 0}\) extends to a strongly continuous semigroup of positive contractions in the complex Hilbert space \(\mathscr {L}^2_{\mathbb {C}}(\mathbb {R}^d, d\mathscr {N}_{0,V_\infty })\) [34].
The time scales induced by the semigroup \((e^{t\mathscr {L}})_{t\ge 0}\) in the space \(\mathscr {L}^2_{\mathbb {C}}(\mathbb {R}^d, d\mathscr {N}_{0,V_\infty })\) are determined by the eigenvalue problem \(\mathscr {L}f = \gamma f\) [46, p. 371]. Every eigenpair \((\gamma ,\phi )\), with \(\mathfrak {R}(\gamma )<0\) and \(\Vert \phi \Vert _2=1\), is related to a decay of \(e^{t\mathscr {L}}\phi \) towards the equilibrium on time scales of order \(|2\gamma |^{-1}\), to wit
where we used condition (B.2) and \(\Vert \cdot \Vert _2\) denotes the associated \(\mathscr {L}^2_{\mathbb {C}}\)-norm. Having a complete orthonormal system \(\{\phi _p\}_{p=1,2\dotsc }\) of eigenfunctions in \(\mathscr {L}^2_{\mathbb {C}}(\mathbb {R}^d, d\mathscr {N}_{0,V_\infty })\), the Fourier expansion
decomposes the trend of \(e^{t\mathscr {L}}f\) towards the equilibrium into separate modes, supported by the invariant subspaces generated by each \(\phi _p\) and exponentially decaying with rates given by \(\mathfrak {R}(\gamma _p)\).
The spectrum of the Ornstein–Uhlenbeck operator (B.1) in \(\mathscr {L}^2_{\mathbb {C}}(\mathbb {R}^d, d\mathscr {N}_{0,V_\infty })\) consists of all complex numbers \(\gamma = \sum _{i=1}^{d}n_i\kappa _i\) with \(n_i\in \mathbb {N}_0, \kappa _i\in \mathsf {Sp}(A)\), and all the (generalised) eigenfunctions are polynomials and form a complete system [35]. Moreover, the invariant subspaces related to each \(\gamma \) consist of homogeneous polynomials in the variables induced by the spectral decomposition of A and with degrees ranging throughout all \(n_i>0\) that appear in the sums generating \(\gamma \) [35, Sect. 4].
There are three main implications of these facts in our setting. First, the spectrum of \(\mathscr {L}\) is independent of the diffusion matrix B. This demonstrates that B has no effect on the time scales of the dynamics and justifies the omission of any assumptions on its spectrum. Second, the eigenvalues of the drift matrix are embedded inside the spectrum of \(\mathscr {L}\) and induce the most prominent time scales. Indeed, every \(\gamma =\kappa _i\) is uniquely determined by \(n_i=1\) and \(n_j=0\) for \(j\ne i\). The associated eigenfunction is a homogeneous polynomial of degree 1 in a variable associated to the invariant subspace of \(\kappa _i\). Therefore, in the Fourier expansion (B.3), all eigenvalues \(\kappa _i\) constitute the first approximation of f. Finally, the dynamics of \(e^{t\mathscr {L}}\) has infinite number of different time scales but the gap in \(\mathsf {Sp}(A)\) reveals itself at the lowest order modes. This can be seen by applying the decomposition of the state space \(\mathbb {R}^d\) into the slow vector variable y, associated to \(\varOmega ^s\), and the fast vector variable z, associated to \(\varOmega ^f\), see the paragraph following Assumption 3.1. This grouping decomposes the first approximation of f into polynomials in y and z that equilibrate under the action of \(e^{t\mathscr {L}}\) on two different time scales with gap given by the gap in \(\mathsf {Sp}(A)\).
Rights and permissions
About this article
Cite this article
Debrabant, K., Samaey, G. & Zieliński, P. Study of micro–macro acceleration schemes for linear slow-fast stochastic differential equations with additive noise. Bit Numer Math 60, 959–998 (2020). https://doi.org/10.1007/s10543-020-00804-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10543-020-00804-5
Keywords
- Micro–macro simulations
- Entropy optimisation
- Stiff stochastic differential equations
- Kullback–Leibler divergence
- Stability