Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-23T21:58:42.264Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of interfaces for the nonlinear parabolic p-Laplacian-type reaction-diffusion equations. II. Fast diffusion vs. absorption

Part of: Parabolic equations and systems

Published online by Cambridge University Press:  18 March 2019

UGUR G. ABDULLA  and
ROQIA JELI
UGUR G. ABDULLA
Affiliation:
Department of Mathematics, Florida Institute of Technology, Melbourne, FL32901, USA emails: abdulla@fit.edu; rjeli2011@my.fit.edu
ROQIA JELI
Affiliation:
Department of Mathematics, Florida Institute of Technology, Melbourne, FL32901, USA emails: abdulla@fit.edu; rjeli2011@my.fit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a full classification of the short-time behaviour of the interfaces and local solutions to the nonlinear parabolic p-Laplacian-type reaction-diffusion equation of non-Newtonian elastic filtration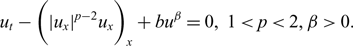

$$u_t-\Big(|u_x|^{p-2}u_x\Big)_x+bu^{\beta}=0, \ 1 \lt p \lt 2, \beta \gt 0.$$
If the interface is finite, it may expand, shrink or remain stationary as a result of the competition of the diffusion and reaction terms near the interface, expressed in terms of the parameters p, β, sign b, and asymptotics of the initial function near its support. In some range of parameters, strong domination of the diffusion causes infinite speed of propagation and interfaces are absent. In all cases with finite interfaces, we prove the explicit formula for the interface and the local solution with accuracy up to constant coefficients. We prove explicit asymptotics of the local solution at infinity in all cases with infinite speed of propagation. The methods of the proof are based on nonlinear scaling laws and a barrier technique using special comparison theorems in irregular domains with characteristic boundary curves. A full description of small-time behaviour of the interfaces and local solutions near the interfaces for slow diffusion case when p>2 is presented in a recent paper by Abdulla and Jeli [(2017) Europ. J. Appl. Math.28(5), 827–853].

Keywords

p-Laplacian-type reaction-diffusion equationsevolution of interfacesfast diffusionnonlinear degenerate parabolic equations

MSC classification

Primary: 35K67: Singular parabolic equations 35K92: Quasilinear parabolic equations with $p$-Laplacian
Secondary: 35K55: Nonlinear parabolic equations 35K57: Reaction-diffusion equations 35K65: Degenerate parabolic equations
Type
Papers
Information
European Journal of Applied Mathematics , Volume 31 , Issue 3 , June 2020 , pp. 385 - 406
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

ABDULLA, U. G. (2000) Reaction–diffusion in irregular domains. J. Differ. Equ. 164, 321–354.CrossRefGoogle Scholar
ABDULLA, U. G. (2001) On the Dirichlet problem for the nonlinear diffusion equation in non-smooth domains. J. Math. Anal. Appl. 260, 384–403.CrossRefGoogle Scholar
ABDULLA, U. G. (2002) Evolution of interfaces and explicit asymptotics at infinity for the fast diffusion equation with absorption. Nonlinear Anal. Theor. Methods Appl. 50, 541–560.CrossRefGoogle Scholar
ABDULLA, U. G. (2005) Well-posedness of the Dirichlet problem for the non-linear diffusion equation in non-smooth domains. Trans. Amer. Math. Soc. 357, 247–265.CrossRefGoogle Scholar
ABDULLA, U. G. & JELI, R. (2017) Evolution of interfaces for the non-linear parabolic p-Laplacian type reaction-diffusion equations. Eur. J. Appl. Math. 28(5), 827–853.CrossRefGoogle Scholar
ABDULLA, U. G. & KING, J. R. (2000) Interface development and local solutions to reaction-diffusion equations. SIAM J. Math. Anal. 32, 235–260.CrossRefGoogle Scholar
ANTONTSEV, S. N., DÍAZ, J. I. & SHMAREV, S. (2012) Energy Methods for Free Boundary Problems: Applications to Nonlinear PDEs and Fluid Mechanics, Vol. 48, Springer Science & Business Media, New York.Google Scholar
BARENBLATT, G. I. (1952) On some unsteady motions of a liquid and gas in a porous medium. Prikl. Mat. Mekh 16, 67–78.Google Scholar
BARENBLATT, G. I. (1996) Scaling, Self-similarity, and Intermediate Asymptotics. Cambridge Texts in Applied Mathematics, Vol. 14, Cambridge University Press, Cambridge, xxii+386 p.Google Scholar
DIAZ, J. I. (1985) Nonlinear Partial Differential Equations and Free Boundaries. Volume I. Research Notes in Mathematics, No. 106, Pitman, Boston, 323 p.Google Scholar
DI BENEDETTO, E. (1986) On the local behaviour of solutions of degenerate parabolic equations with measurable coefficients. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 13(4), 487–535.Google Scholar
DI BENEDETTO, E. (1993) Degenerate Parabolic Equations. Universitext, Springer-Verlag, New York, xvi+387 p.CrossRefGoogle Scholar
DI BENEDETTO, E. & HERRERO, M. A. (1989) On the Cauchy problem and initial traces for a degenerate parabolic equation. Trans. Am. Math. Soc. 314, 187–224.CrossRefGoogle Scholar
DI BENEDETTO, E. & HERRERO, M. A. (1990) Nonnegative solutions of the evolution p-Laplacian equation. Initial traces and Cauchy problem when 1<p<2. Arch. Ration. Mech. Anal. 111, 225–290.CrossRefGoogle Scholar
ESTEBAN, J. R. & VÁZQUEZ, J. L. (1986) On the equation of turbulent filtration in one-dimensional porous media. Nonlinear Anal. Theor. Methods Appl. 10, 1303–1325.CrossRefGoogle Scholar
GRUNDY, R. E. & PELETIER, L. A. (1987) Short time behaviour of a singular solution to the heat equation with absorption. Proc. Roy. Soc. Edinburgh Sect. A 107, 271–288.CrossRefGoogle Scholar
GRUNDY, R. E. & PELETIER, L. A. (1990) The initial interface development for a reaction-diffusion equation with power-law initial data. Q. J. Mech. Appl. Math. 43, 535–559.CrossRefGoogle Scholar
KALASHNIKOV, A. S. (1978) On a nonlinear equation appearing in the theory of non-stationary filtration. Trudy. Sem. Petrovsk 5, 60–68.Google Scholar
KALASHNIKOV, A. S. (1982) Propagation of perturbations in the first boundary value problem for a degenerate parabolic equation with a double nonlinearity. Trudy Sem. Petrovsk. 8.Google Scholar
KALASHNIKOV, A. S. (1987) Some problems of the qualitative theory of non-linear degenerate second-order parabolic equations. Russ. Math. Surv. 42(2), 169–222.CrossRefGoogle Scholar
SHMAREV, S., VDOVIN, V. & VLASOV, A. (2015) Interfaces in diffusion–absorption processes in nonhomogeneous media. Math. Comput. Simul. 118, 360–378.CrossRefGoogle Scholar
TSUTSUMI, M. (1988) On solutions of some doubly nonlinear degenerate parabolic equations with absorption. J. Math. Anal. Appl. 132, 187–212.CrossRefGoogle Scholar