Introduction

With the exponential growth of location-based services, there is a need to improve the positioning accuracy and the capability to resist against external interference in challenging environments such as urban canyons, forested terrains, and indoor areas, in which signal attenuation, interference, and multipath fading can seriously degrade the positioning accuracy of global navigation satellite systems (GNSS) and GNSS-like systems. The positioning accuracy is affected by the orbit determination and time synchronization (ODTS) error, the signal modulation scheme, the receiver processing algorithm, and the receiver working environment (Kaplan and Hegarty 2005). Among these, the modulation scheme has an important impact on positioning accuracy.

The initial modulation scheme developed for GNSS signals was BPSK-R modulation. BPSK-R modulation with a faster-spreading code rate improves accuracy but also requires larger bandwidth and has limited improvement in multipath performance (Betz 2001a, b). Betz (1999) presented the binary offset carrier (BOC) modulation, which has been adopted in the modernized Global Positioning System (GPS) (Betz 2001a, b), the European Galileo System (Galileo 2008), and the BeiDou (Compass) Navigation System (BeiDou 2017) because of its good spectral isolation from heritage signals, high accuracy, multipath interference resistance, and flexibility in signal implementation compared with BPSK-R modulation (Betz 2001a, b). Hegarty et al. (2004) presented the binary code symbol (BCS) modulation, in which a vector is used to shape subcarrier symbols. This scheme is a generalization of BPSK-R and BOC modulation. Hein et al. (2005, 2006) proposed composite BCS (CBCS) and multiplexed BOC (MBOC) modulation to achieve enhanced accuracy and multipath interference resistance by using multilevel subcarrier symbols or combining different subcarrier symbols. MBOC modulation has been adopted for the Galileo E1-B/C and GPS L1C signals. Lestarquit et al. (2008) presented alternate BOC (AltBOC) modulation, which has been adopted for the Galileo E5 signal. This scheme is based on the use of the constant envelope multiplexing (CEM) technique to modulate four signals to improve the high-power amplifier (HPA) efficiency. Yao et al. (2016) presented the asymmetric constant envelope BOC (ACE-BOC) multiplexing, which can be used to modulate four or fewer signals with arbitrary power ratio. These studies on BOC modulation have greatly improved the accuracy and multiplexing efficiency of GNSS signals.

However, for high-order BOC modulation, the main drawback is the ambiguity in tracking due to the multiple side peaks of the autocorrelation function (ACF) (Yao et al. 2010). The receiver may incorrectly lock onto one of these side peaks, causing intolerable measurement bias, and this undesirable behavior limits the application of this modulation scheme in navigation systems. Many methods have been proposed to mitigate or cancel the ACF peak ambiguity during tracking, such as the BPSK-like method (Fishman and Betz 2000), the bump-jump method (Fine and Wilson 1999), the autocorrelation side-peak cancelation technique (Julien et al. 2007; Yao et al. 2010), the double estimator method (Hodgart and Blunt 2007), and the subcarrier cancelation method (Ward and Lillo 2009). These methods can mitigate or even eliminate the ambiguity problem, but they are usually not general and significantly increase the receiver complexity and power consumption.

We present a generalized low-ambiguity anti-interference spread spectrum modulation based on frequency-hopping BOC (FH-BOC), which significantly mitigates the ambiguity problem in BOC modulation. The proposed FH-BOC modulation combines direct-sequence spread spectrum (DSSS) and frequency-hopping spread spectrum (FHSS) techniques. The two techniques are the most practical and dominant spread spectrum techniques. The primary mechanism of external interference suppression in an FHSS system is that of avoidance; it avoids interference by periodic changing of the carrier frequency of a transmitted signal. The FHSS technique has been widely used in mobile communication, radar, and military communication systems because of its many advantages, such as its low probability of intercept, its resistance to narrowband and multipath interference (Simon et al. 1994; Peterson et al. 1995; Torrieri 2015). The new generalized FH-BOC modulation proposed in this research is a BOC-like modulation based on a frequency-hopping square wave subcarrier and a pseudorandom noise (PRN) spreading code for modulating data. Thus, FH-BOC modulation has the advantages of both the DSSS and FHSS techniques. The subcarrier of FH-BOC modulation is implemented by means of BOC frequency hopping while the carrier frequency remains constant, achieving a constant envelope and maintaining flexibility in implementation. Furthermore, we introduce four parameters and a frequency-hopping pattern to shape the ACF and power spectral density (PSD) of FH-BOC and control the hopping of the FH-BOC subcarrier.

We first formulate the mathematical model of FH-BOC modulation and derive analytical expressions for the normalized ACF and PSD. We analyze the time and frequency properties of several representative FH-BOC signals. Next, we present recommended parameter selections, a generation and detection scheme for FH-BOC modulation. Then, we analyze the characteristics of the ACF and PSD, the tracking performance, the spectral separation, and the anti-narrowband interference and multipath interference performance for several specific BOC and FH-BOC signals. Finally, we draw conclusions. In Appendix, we present the detailed derivation of the analytical ACF expressions for FH-BOC modulation.

FH-BOC modulation

Under the assumption that an FH-BOC signal has an ideal spreading code and infinite bandwidth, we construct the mathematical model of the signal and derive its normalized ACF and PSD. Then, we discuss the time and frequency properties of FH-BOC modulation by assigning several sets of representative parameters.

Signal model

An analytical expression for the FH-BOC baseband signal can be constructed as follows:

$$ s(t) = \sum\limits_{k = - \infty }^{ + \infty } {a_{k} \times p\left( {t - kT_{c} ,f_{s}^{k} } \right)} $$
(1)

where \( a_{k} \) denotes a data-modulated PRN spreading code chip, \( p\left( {t,f_{s}^{k} } \right) \) denotes a frequency-hopping square wave subcarrier symbol, \( T_{c} \) is the spreading code chip duration, and \( f_{s}^{k} \) is the subcarrier frequency corresponding to the kth spreading code chip. \( p\left( {t,f_{s}^{k} } \right) \) can be defined in either sine-phased or cosine-phased form as follows:

$$ \begin{aligned} & p_{\sin } \left( {t,f_{s}^{k} } \right) = \left\{ {\begin{array}{*{20}l} {\text{sgn} \left( {\sin \left( {2\pi f_{s}^{k} t} \right)} \right),} \hfill & {0 \le t \le T_{c} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. \\ & p_{\cos } \left( {t,f_{s}^{k} } \right) = \left\{ {\begin{array}{*{20}l} {\text{sgn} \left( {\cos \left( {2\pi f_{s}^{k} t} \right)} \right),} \hfill & {0 \le t \le T_{c} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(2)

Typically, three parameters are essential to define an FHSS signal: (1) The set of M possible carrier frequencies is called hopset; (2) The sequence of carrier frequencies transmitted by an FHSS system is called frequency-hopping pattern; (3) The rate of frequency hopping is called the hopping rate. For an FH-BOC signal, it can be denoted by FH-BOC(\( f_{h}^{M - 1} \):\( f_{d} \):\( f_{h}^{0} \),\( f_{c} \)), where {\( f_{h}^{0} \):\( f_{d} \):\( f_{h}^{M - 1} \)} is the hopset, which includes \( M \) possible single subcarrier frequencies {\( f_{h}^{0} \), \( f_{h}^{1} \),…, \( f_{h}^{M - 1} \)}. The hopset is a monotonically increasing arithmetic sequence; \( f_{d} \) is the common difference, i.e., the minimum frequency-hopping interval, defined by \( f_{d} \) = \( f_{h}^{i} \) − \( f_{h}^{i - 1} \), \( i \) = 1, 2,…, \( M \)-1, and \( f_{c} \) is the spreading code rate, \( f_{c} = { 1\mathord{\left/ {\vphantom { 1{T_{c} }}} \right. \kern-0pt} {T_{c} }} \). The frequency-hopping pattern, denoted by \( \left\{ {C_{k} } \right\} \), is a decimal sequence that controls the frequency hopping of the FH-BOC subcarrier. The hopping rate is denoted by \( f_{v} \),\( f_{c} \) should be an integer multiple of \( f_{v} \). Consistent with the notation for conventional BOC modulation, the abbreviation FH-BOC(\( \alpha_{M - 1} \):\( d \):\( \alpha_{0} \),\( \beta \)) is defined to denote an FH-BOC signal as follows:

$$ \left\{ {\begin{array}{*{20}l} {f_{h}^{M - 1} = \alpha_{M - 1} \times f_{0} } \hfill \\ {f_{d} = d \times f_{0} } \hfill \\ {f_{h}^{0} = \alpha_{0} \times f_{0} } \hfill \\ {f_{c} = \beta \times f_{0} } \hfill \\ \end{array} } \right. $$
(3)

where \( f_{0} \) is the reference frequency, which is typically equal to 1.023 MHz, and {\( \alpha_{0} \):\( d \):\( \alpha_{M - 1} \)} is a monotonically increasing arithmetic sequence {\( \alpha_{0} \), \( \alpha_{1} \),…, \( \alpha_{M - 1} \)} with a common difference \( d \) corresponding to the hopset sequence, i.e., \( \alpha_{i} \) = \( \alpha_{0} \) + \( i \)\( \times \)\( d \), \( i \) = 0, 1, 2, …, M − 1. The parameters should satisfy the definition of FH-BOC modulation; they must be positive integers and \( \alpha_{i} \) should be an integer multiple of \( \beta \). For example, FH-BOC(10:1:1,1) represents a signal whose subcarrier frequency range spans from 1.023 to 10.23 MHz with a minimum frequency-hopping interval of 1.023 MHz and a spreading code rate of 1.023 MHz.

Considering all of the above conditions, we can simplify the time-domain expression for an FH-BOC signal to

$$ \left\{ {\begin{array}{*{20}l} {s(t) = \sum\nolimits_{k = - \infty }^{ + \infty } {a_{k} \times p\left( {t - kT_{c} ,f_{s}^{k} } \right)} } \hfill \\ {f_{h}^{i} = \left( {\alpha_{0} + i \times d} \right) \times f_{0} ,\quad i = 0,1,2, \ldots ,M - 1} \hfill \\ {f_{s}^{k} = f_{h}^{{C_{k} }} } \hfill \\ \end{array} } \right. $$
(4)

In accordance with (4), an example signal FH-BOCsin(10:1:1,1) was implemented. Its waveform is shown in Fig. 1, which illustrates how the subcarrier wave changes with the hopping of the frequency-hopping pattern.

Fig. 1
figure 1

Baseband waveform and frequency-hopping pattern for FH-BOCsin(10:1:1,1)

Full size image

ACF and PSD

The ACF of an FH-BOC signal can be expressed as

$$ \begin{aligned} R\left( {t,t + \tau } \right) & = E\left( {s\left( t \right)s^{*} \left( {t + \tau } \right)} \right) \\ & = E\left( {\sum\limits_{k = - \infty }^{ + \infty } {a_{k} p\left( {t - kT_{c} ,f_{s}^{k} } \right)} \sum\limits_{l = - \infty }^{ + \infty } {a_{l} p^{*} \left( {t + \tau - lT_{c} ,f_{s}^{l} } \right)} } \right) \\ & = \sum\limits_{k = - \infty }^{ + \infty } {\sum\limits_{l = - \infty }^{ + \infty } {R_{a} \left( l \right)} } E\left( {p\left( {t - kT_{c} ,f_{s}^{k} } \right)p^{*} \left( {t + \tau - kT_{c} - lT_{c} ,f_{s}^{k + l} } \right)} \right) \\ \end{aligned} $$
(5)

where \( R_{a} \left( l \right) = E\left( {a_{k} a^{*}_{k + l} } \right) \) denotes the ACF of the spreading code. An ideal spreading code is infinite, aperiodic, independent, and random. Thus, \( R_{a} \left( l \right) \) becomes

$$ R_{a} (l) = \left\{ {\begin{array}{*{20}c} {1,} & {l = 0} \\ {0,} & {l \ne 0} \\ \end{array} } \right. $$
(6)

Accordingly, substituting (6) into (5) yields

$$ R\left( {t,t + \tau } \right) = \sum\limits_{k = - \infty }^{ + \infty } {E\left( {p\left( {t - kT_{c} ,f_{s}^{k} } \right)p^{*} \left( {t + \tau - kT_{c} ,f_{s}^{k} } \right)} \right)} $$
(7)

For an FH-BOC signal, the probability that a frequency channel is used can be expressed as

$$ P\left( {f_{s}^{k} = f_{h}^{i} } \right) = \frac{{l_{i} }}{{L_{c} }},i = 0,1,2, \ldots ,M - 1 $$
(8)

where \( L_{c} \) denotes the total number of occurrences of all frequency channels, \( l_{i} \) denotes the number of occurrences of the channel \( f_{h}^{i} \). Therefore, by substituting (8) into (7), \( R\left( {t,t + \tau } \right) \) can be simplified to

$$ R\left( {t,t + \tau } \right) = \frac{1}{{L_{c} }}\sum\limits_{k = - \infty }^{ + \infty } {\sum\limits_{i = 0}^{M - 1} {p\left( {t - kT_{c} ,f_{h}^{i} } \right)p^{*} \left( {t + \tau - kT_{c} ,f_{h}^{i} } \right) \times l_{i} } } $$
(9)

Notably, an FH-BOC signal is not a wide-sense stationary process but rather has the following characteristics:

$$ \begin{aligned} & E\left( {s\left( {t + T_{c} } \right)} \right) = E\left( {s\left( t \right)} \right) \\ & R\left( {t + T_{c} ,t + \tau + T_{c} } \right) = R\left( {t,t + \tau } \right) \\ \end{aligned} $$
(10)

Thus, this signal is cyclostationary. Its ACF that only depends on \( \tau \) can be obtained by averaging the ACF over the interval \( t \in \left[ {0,T_{c} } \right] \):

$$ R(\tau ) = \frac{1}{{T_{c} }}\int_{0}^{{T_{c} }} {R\left( {t,t + \tau } \right){\text{d}}t} $$
(11)

The detailed derivation of \( R\left( \tau \right) \) can be found in the appendix. For a sine-phased FH-BOC signal, the normalized ACF, \( R_{\sin } \left( \tau \right) \), is

$$ \begin{aligned} R_{\sin } \left( \tau \right) &= \frac{1}{{L_{c} T_{c} }}\sum\limits_{i = 0}^{M - 1} {\sum\limits_{m = 0}^{{2N_{i} - 1}} {\sum\limits_{n = 0}^{{2N_{i} - 1}} {\left( { - 1} \right)^{m + n + 1} l_{i} T_{h}^{i}}}} \\ &\quad {{{\times \varLambda_{{T_{h}^{i} }} \left( {\tau - \left( {m + n + 1 - 2N_{i} } \right)T_{h}^{i} } \right)} } } \end{aligned} $$
(12)

where \( N_{i} = \alpha_{i} /\beta \) and \( \varLambda_{{T_{h}^{i} }} \left( \tau \right) \) is the triangle function with support \( 2T_{h}^{i} ,\;\;T_{h}^{i} = 0.5\left( {f_{h}^{i} } \right)^{ - 1} \), defined as

$$ \varLambda_{{T_{h}^{i} }} \left( \tau \right) = \left\{ {\begin{array}{*{20}l} {1 - \frac{|\tau |}{{T_{h}^{i} }},} \hfill & {|\tau |\; < T_{h}^{i} \;} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(13)

For a cosine-phased FH-BOC signal, the normalized ACF, \( R_{\cos } \left( \tau \right) \), is

$$ \begin{aligned} R_{\cos } \left( \tau \right) &= \frac{1}{{2L_{c} T_{c} }}\sum\limits_{i = 0}^{M - 1} {\sum\limits_{m = 0}^{{4N_{i} - 1}} {\sum\limits_{n = 0}^{{4N_{i} - 1}} {\left( { - 1} \right)^{{m + n + \left\lfloor {\frac{m}{2}} \right\rfloor \text{ + }\left\lfloor {\frac{n}{2}} \right\rfloor }} l_{i} T_{h}^{i} }}}\\&\quad{{{\times \varLambda_{{{{T_{h}^{i} } \mathord{\left/ {\vphantom {{T_{h}^{i} } 2}} \right. \kern-0pt} 2}}} \left( {\tau - \left( {m + n + 1 - 4N_{i} } \right)\frac{{T_{h}^{i} }}{2}} \right)} } } \end{aligned} $$
(14)

where \( \left\lfloor . \right\rfloor \) denotes the floor function (largest integer smaller than or equal to the argument).

According to the Wiener–Khinchin theorem, the PSD of \( s\left( t \right) \) is the Fourier transform of its ACF:

$$ G\left( f \right) = FT\left[ {R\left( \tau \right)} \right] $$
(15)

Thus, by substituting (12) into (15), the PSD of a sine-phased FH-BOC signal can be derived as follows:

$$ \begin{aligned} G_{\sin } \left( f \right) & = \frac{1}{{L_{c} T_{c} }}\sum\limits_{i = 0}^{M - 1} {\sum\limits_{m = 0}^{{2N_{i} - 1}} {\sum\limits_{n = 0}^{{2N_{i} - 1}} {\left( { - 1} \right)^{m + n + 1} T_{h}^{i} l_{i} } } } \\ &\quad\times FT\left( {\varLambda_{{T_{h}^{i} }} \left( {\tau - \left( {m + n + 1 - 2N_{i} } \right)T_{h}^{i} } \right)} \right) \\ & = \frac{1}{{L_{C} T_{c} }}\sum\limits_{i = 0}^{M - 1} {l_{i} \left( {T_{h}^{i} \text{sinc} \left( {fT_{h}^{i} } \right)} \right)}^{2} \frac{{\sin^{2} \left( {2\pi N_{i} fT_{h}^{i} } \right)}}{{\cos^{2} \left( {\pi fT_{h}^{i} } \right)}} \\ \end{aligned} $$
(16)

where \( \text{sinc} \left( {fT_{h}^{i} } \right) = {{\sin \left( {\pi fT_{h}^{i} } \right)} \mathord{\left/ {\vphantom {{\sin \left( {\pi fT_{h}^{i} } \right)} {\pi fT_{h}^{i} }}} \right. \kern-0pt} {\pi fT_{h}^{i} }} \). Similarly, by substituting (14) into (15), the PSD of a cosine-phased FH-BOC signal can be derived:

$$ \begin{aligned} G_{\cos } \left( f \right) & = \frac{1}{{2L_{c} T_{c} }}\sum\limits_{i = 0}^{M - 1} {\sum\limits_{m = 0}^{{4N_{i} - 1}} {\sum\limits_{n = 0}^{{4N_{i} - 1}} {\left( { - 1} \right)^{{m + n + \left\lfloor {\frac{m}{2}} \right\rfloor \text{ + }\left\lfloor {\frac{n}{2}} \right\rfloor }} } } } l_{i} T_{h}^{i} \\ &\quad\times FT\left( {\varLambda_{{{{T_{h}^{i} } \mathord{\left/ {\vphantom {{T_{h}^{i} } 2}} \right. \kern-0pt} 2}}} \left( {\tau - \left( {m + n + 1 - 4N_{i} } \right)\frac{{T_{h}^{i} }}{2}} \right)} \right) \\ & = \frac{{4T_{c} }}{{L_{c} }}\sum\limits_{i = 0}^{M - 1} {l_{i} \text{sinc}^{2} \left( {fT_{c} } \right)\frac{{\sin^{ 4} \left( {\pi f\frac{{T_{h}^{i} }}{2}} \right)}}{{\cos^{2} \left( {\pi fT_{h}^{i} } \right)}}} \\ \end{aligned} $$
(17)

The frequency hopping of the FH-BOC subcarrier determines the similarities and differences in the ACF and PSD between FH-BOC and BOC modulation and potentially endows the signal with certain excellent properties, such as better anti-interception and anti-interference performance. Notably, BOC(kn,n) is a particular case of FH-BOC modulation in which the hopset of FH-BOC modulation includes only one single carrier frequency. Thus, FH-BOC modulation is a more generalized type of modulation.

Time and frequency properties

For an FHSS system, a frequency-hopping pattern with uniform distribution brings better anti-narrowband interference performance (Torrieri 2015); thus, we only discuss FH-BOC modulation with a uniform subcarrier. Both sine-phased and cosine-phased subcarriers are available for FH-BOC modulation. The zero crossings nearest the main peak (ZCNMs) occur at \( \pm T_{c} \times \left( {2\left( {\alpha_{{_{M - 1} }} + \alpha_{ 0} } \right) - \beta } \right)^{ - 1} \) for sine-phased FH-BOC modulation and at approximately \( \pm T_{c} \times \left( {2\left( {\alpha_{{_{M - 1} }} + \alpha_{0} } \right) + 0.5\beta } \right)^{ - 1} \) for cosine-phased FH-BOC modulation. Moreover, the ACF main peak width is twice the time delay corresponding to the ZCNMs. A narrower ACF main peak may provide better code tracking accuracy. For sine-phased BOC modulation, the ZCNMs occur at \( \pm T_{c} \times \left( {4\alpha - \beta } \right)^{ - 1} \) (Betz 2001a, b). Therefore, the ACF main peak width will be the same for both BOC and FH-BOC modulation when the following condition is met:

$$ \alpha = 0.5*\left( {\alpha_{M - 1} + \alpha_{0} } \right) $$
(18)

The ACF main-peak-to-maximum-side-peak ratio (MSR) can be calculated as

$$ R_{\text{MSR}} = 20\lg \left( {\mathop {\hbox{max} }\limits_{{\left| \tau \right| > \tau_{\text{ZCNM}} \;}} \left| {R\left( \tau \right)} \right|} \right) $$
(19)

where \( \tau_{\text{ZCNM}} \) denotes the time delay corresponding to the ZCNMs, \( | \square | \) denotes the absolute value operator, and \( R_{\text{MSR}} \) denotes the MSR of the ACF. A lower MSR can mitigate the ACF peak ambiguity problem (Betz 2001a, b). The PSD main lobe bandwidth (MLB) for FH-BOC modulation is defined as the bandwidth containing the two split spectral lobes and is approximately \( 2\left( {\alpha_{{_{M - 1} }} + \beta } \right) \times f_{0} \). A larger MLB may provide better anti-interception and anti-narrowband interference performance (Peterson et al. 1995). The maximum value of the PSD (MVP) for FH-BOC modulation is defined as

$$ m_{\text{MVP}} = \mathop {\hbox{max} }\limits_{{f \in {\text{MLB}}}} G(f) $$
(20)

A smaller MVP allows higher-power signal transmission without increasing the interference from the noise floor, which is better for self-spectral separation (Betz 1999).

The normalized ACFs and PSDs for sine-phased and cosine-phased FH-BOC(10:1:1,1) signals according to (12) and (14) are presented in Fig. 2, showing narrow peaks and a multimode structure similar to what is observed in BOC modulation. It has been proven that cosine-phased BOC modulation can be treated as two-stage sine-phased BOC modulation, in which the signal is initially equivalent to a sine-phased BOC-modulated signal and the subcarrier chip is then split into two parts (Lohan et al. 2007). Thus, we can guess that cosine-phased FH-BOC modulation can similarly be treated as two-stage sine-phased FH-BOC modulation. Unless otherwise stated, we usually assume the use of a sine-phased subcarrier for FH-BOC modulation by default for convenience of expression.

Fig. 2
figure 2

Normalized ACFs and PSDs for FH-BOC(10:1:1,1)

Full size image

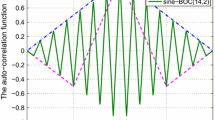
To illustrate the ACF and PSD properties for FH-BOC modulation, a set of specific values, as seen in Fig. 3, was assigned. By comparing several example signals, we present a discussion of the ACFs and PSDs. The normalized ACFs for the example signals are depicted in the top panel, local details of the ACFs are shown in the middle panel, and some ACF properties are listed in Table 1. FH-BOC(20:1:1,1) has the smallest ZCNMs and the largest MSR, implying that it may provide the best code tracking accuracy and lowest ambiguity among the example signals. The ZCNMs and MSR of FH-BOC(10:1:3,1) are smaller than those of FH-BOC(10:1:1,1); thus, FH-BOC(10:1:3,1) may provide better code tracking accuracy but worse ambiguity than FH-BOC(10:1:1,1). The ZCNMs of FH-BOC(10:3:1,1) are the same as those of FH-BOC(10:1:1,1), but the MSR is smaller. The ZCNMs and MSR of FH-BOC(10:2:2,2) are both smaller than those of FH-BOC(10:1:1,1).

Fig. 3
figure 3

Normalized ACFs and PSDs for example FH-BOC signals

Full size image
Table 1 ACF and PSD properties of example FH-BOC signals
Full size table

The normalized PSDs for the example signals are depicted in the bottom panel of Fig. 3, and some PSD properties are listed in Table 1. FH-BOC(20:1:1,1) has the smallest MVP, indicating that it may have the best self-spectral separation. It also has the most subcarrier frequencies, the largest frequency-hopping band, the largest MLB, and the flattest spectral shape, meaning that it has the best anti-interception and anti-narrowband interference performance. FH-BOC(10:1:1,1), FH-BOC(10:1:3,1), and FH-BOC(10:3:1,1) all have the same MLB. The MVP and the number of subcarrier frequencies of FH-BOC(10:1:3,1) are smaller than those of FH-BOC(10:1:1,1). FH-BOC(10:1:3,1) moves more signal power away from the band center, which improves the code tracking accuracy and cross-spectral separation with signals at the center of the band but reduces the anti-narrowband interference performance. For FH-BOC(10:3:1,1), the MVP is larger than for FH-BOC(10:1:1,1), and the number of subcarrier frequencies is smaller. The MLB and MVP of FH-BOC(10:2:2,2) are both larger than those of FH-BOC(10:1:1,1), and the number of subcarrier frequencies is also smaller.

From the discussion above, we can conclude that the FH-BOC(\( \alpha_{M - 1} \):1:1,1) signal has the smallest MSR, the most subcarrier frequencies, the largest frequency-hopping band, and the largest MLB among these FH-BOC signals; therefore, it has the smallest ACF peak ambiguity, the best anti-interception and anti-narrowband interference performance. The top panel of Fig. 4 shows a set of ACFs for FH-BOC(\( \alpha_{M - 1} \):1:1,1) signals; the top panel of Fig. 5 shows the ZCNMs versus the maximum subcarrier frequency and the bottom panel of Fig. 5 shows the MSRs versus the maximum subcarrier frequency. The larger the maximum subcarrier frequency is, the smaller the ZCNMs, and the larger the MSR. The bottom panel of Fig. 4 shows a set of PSDs for FH-BOC(\( \alpha_{M - 1} \):1:1,1) signals. The larger the maximum subcarrier frequency is, the smaller the MVP, and the flatter the spectral shape. By contrast, FH-BOC(\( \alpha_{M - 1} \):1:\( \alpha_{0} \),1), \( \alpha_{0} > 1 \), moves more signal power away from the band center, which improves tracking accuracy and cross-spectral separation with signals at the center of the band but increases the ACF peak ambiguity.

Fig. 4
figure 4

Normalized ACFs and PSDs for FH-BOC(\( \alpha_{M - 1} \):1:1,1) signals

Full size image
Fig. 5
figure 5

ZCNMs and MSRs for FH-BOC(\( \alpha_{M - 1} \):1:1,1) signals

Full size image

Based on the preceding discussion of the ACF and PSD properties for FH-BOC modulation, the use of FH-BOC(\( \alpha_{M - 1} \):1:1,1) signals is proposed, in which the minimum frequency-hopping interval, the minimum subcarrier frequency, and the spreading code rate are fixed to their minimum possible values. The reasons for recommending FH-BOC(\( \alpha_{M - 1} \):1:1,1) signals are that they have the lowest ambiguity, the best anti-interception and anti-narrowband interference performance. If designers want to split signal power to the edge of the allocated band, FH-BOC(\( \alpha_{M - 1} \):1:\( \alpha_{0} \),1), \( \alpha_{0} > 1 \), is proposed. By increasing the minimum subcarrier frequency \( \alpha_{0} \), the signal power will be moved away from the band center, and the ACF main peak will be narrowed, potentially improving the code tracking accuracy. Furthermore, FH-BOC(\( \alpha_{M - 1} \):\( d \):\( \alpha_{0} \),\( \beta \)) is a general and extensive modulation family; for different constraint criteria, the optimal values will be different from those proposed above.

Generation and detection scheme

Since the FH-BOC baseband signal is binary-valued, it can be digitally implemented and processed by a software-defined receiver as long as the sampling rate is twice the frequency-hopping bandwidth, thus, greatly reducing the hardware complexity. Furthermore, the subcarrier frequency can be switched instantaneously, overcoming the shortcomings of frequency synthesizer during frequency switching. The performance for carrier phase measurements and Doppler measurements with FH-BOC signals is not affected relative to that with BOC signals because the frequency hopping is implemented in the baseband. The top panel of Fig. 6 presents a block diagram of FH-BOC signal generation. The data, spreading code, subcarrier, and RF carrier should be generated from a common clock so that they have constant phase offsets. A serial search acquisition scheme for the FH-BOC signal is shown at the bottom of Fig. 6. The decision variable can be expressed as follows:

$$ V = S_{I}^{2} + S_{Q}^{2} $$
(21)

where \( S_{I} \) and \( S_{Q} \) are the outputs of I and Q channels, respectively. \( V \) is the Chi-square random variable with two degrees of freedom. The acquisition threshold can be calculated from noise variance \( \sigma^{2} \) and the desired probability of false alarm \( P_{\text{fa}} \):

Fig. 6
figure 6

Block diagram of FH-BOC signal generation and detection

Full size image
$$ V_{t} = - 2\sigma^{2} \ln P_{\text{fa}} $$
(22)

GNSS signal acquisition is a search process, and the signal match for success is two dimensional, including code dimension and Doppler dimension. However, FH-BOC signal acquisition has an additional search dimension called the frequency-hopping dimension. Therefore, the frequency-hopping pattern has a great effect on the acquisition time and complexity of the FH-BOC signal. For military signals, a pseudorandom frequency-hopping pattern with a large period is proposed, which is difficult for a noncooperative receiver to reproduce and dehop. However, when the period of the frequency-hopping pattern is large, the signal acquisition time and complexity increase, requiring a higher-performance receiver. To eliminate this limitation, we present a frequency-hopping scheme by adjusting the hopping rate \( f_{\nu } \) and the period of the frequency-hopping pattern. Let \( f_{\nu } \) equal to \( f_{c} \) and the period of the frequency-hopping pattern be an integer multiple of spreading code period. The phase of the frequency-hopping pattern can be derived from the spreading code phase because they have a constant phase offset. Thus, we can significantly narrow the search space and the average acquisition time can be estimated as

$$ T_{\text{acq}} = \frac{ 1}{ 2}\frac{{f_{\text{unc}} t_{\text{unc}} N_{T} T_{\text{dwell}} }}{{f_{\text{bin}} t_{\text{bin}} }} $$
(23)

where \( f_{\text{unc}} \) and \( t_{\text{unc}} \) denote the Doppler frequency uncertainty and the spreading code phased uncertainty, respectively. \( f_{\text{bin}} \) and \( t_{\text{bin}} \) denote the Doppler frequency bin and the spreading code bin, respectively; each search increment is a bin. \( N_{T} \) is the ratio of the periods of the frequency-hopping pattern and spreading code, and \( T_{\text{dwell}} \) is the search dwell time. Notably, the acquisition time and complexity of the FH-BOC signal will be the same for the BOC signal with the same MLB when the period of the frequency-hopping pattern is equal to the spreading code period. A BOC receiver can process such a signal with only minor modifications.

For example, let \( f_{\nu } \) equal to \( f_{c} \) and the length of the spreading code and the frequency-hopping pattern be 1023 for FH-BOC(20:1:1,1) and FH-BOC(10:1:3,1) signals generated via this scheme, the simulated and theoretical normalized ACF results are compared in the top panel of Fig. 7, and the simulated and theoretical PSD results are compared in the bottom panel. Consider a receiver front-end bandwidth of 24 MHz, a sampling rate of 64 MHz, an intermediate frequency of 12 MHz, a carrier-to-noise-density ratio (\( {C \mathord{\left/ {\vphantom {C {N_{0} }}} \right. \kern-0pt} {N_{0} }} \)) of 45 dB, and a coherent integration time of 1 ms, Fig. 8 shows the output of FH-BOC(10:1:3,1) from the serial search acquisition scheme; the code and frequency-hopping pattern phase is 581 chips and frequency is 12 MHz.

Fig. 7
figure 7

Simulated and theoretical results for normalized ACFs and PSDs of example signals

Full size image
Fig. 8
figure 8

Output from serial search acquisition for FH-BOC(10:1:3,1) modulated PRN 1

Full size image

Performance analysis

This section focuses on the performance of FH-BOC modulation in comparison with BOC modulation. Several representative signals are selected, including BOC(5,1), BPSK(10), BOC(10,5), FH-BOC(9:1:1,1), FH-BOC(11:1:7,1), and FH-BOC(14:1:1,1). FH-BOC(9:1:1,1) has the same MLB as BPSK(10) and the same ZCNMs as BOC(5,1); FH-BOC(11:1:7,1) has the same ZCNMs as BOC(10,5), and FH-BOC(14:1:1,1) has the same MLB as BOC(10,5). We discuss the properties of the ACFs and PSDs, the tracking performance, the spectral separation, the anti-narrowband interference, and multipath interference for the example signals.

Comparison of ACFs and PSDs

The ACFs and PSDs for the example signals computed over an infinite bandwidth are depicted in Fig. 9, and some properties of the ACFs and PSDs are listed in Table 2. First, the MSR of FH-BOC(14:1:1,1) is the largest among the example signals except for BPSK(10), and the MSRs of the FH-BOC signals are much larger than those of the BOC signals. Therefore, the ACF ambiguity of BOC modulation is mitigated in FH-BOC modulation. Second, the ZCNMs of FH-BOC(11:1:7,1) and BOC(10,5) are the smallest among the example signals. The ZCNMs of FH-BOC(9:1:1,1) and BOC(5,1) are smaller than BPSK(10). Finally, the main lobe of the PSD for BPSK(10) is at the band center, whereas the main lobes of BOC(5,1), BOC(10,5) and FH-BOC(11:1:7,1) are offset from the band center, such that most of the power is allocated to a specific band. The power in the PSD main lobes is evenly distributed within the bands for FH-BOC(9:1:1,1) and FH-BOC(14:1:1,1), and the MVPs are lower than those of the other signals.

Fig. 9
figure 9

Normalized ACFs and PSDs for example signals

Full size image
Table 2 ACF and PSD properties of example signals
Full size table

Suppose that the signals are band-limited to 40 MHz at the transmitter. Figure 10 shows the signal power percentage versus the front-end bandwidth of the receiver, indicating the minimum bandwidth needed to contain a given amount of power for the example signals. Typically, 90 percent of the power should be contained within the front-end bandwidth (Betz 2001a, b). The 90-percent-power bandwidths of FH-BOC(14:1:1,1) and BOC(10,5) are approximately 27.5 MHz and 23.7 MHz, respectively. The 90-percent-power bandwidth of BOC(10,5) is larger than those of FH-BOC(9:1:1,1) and FH-BOC(11:1:7,1), and the 90-percent-power bandwidth of FH-BOC(9:1:1,1) is larger than those of BPSK(10) and BOC(5,1).

Fig. 10
figure 10

Power containment percentages for example signals band-limited to 40 MHz

Full size image

Code tracking accuracy

With the development of receiver processing technology, the signal modulation scheme has become the main factor limiting tracking performance. We compare the ultimate tracking performances for the example signals.

(1) Root mean square (RMS) bandwidth:

The RMS bandwidth \( \beta_{\text{rms}} \) of a band-limited signal is defined by Betz (2001a, b). The higher the RMS bandwidth is, the lower the bound on the code tracking accuracy. Figure 11 shows the RMS bandwidths for the example signals as functions of the front-end bandwidth. When the front-end bandwidth \( \beta_{r} \) is approximately 24 MHz, the \( \beta_{\text{rms}} \) of FH-BOC(11:1:7,1) is the largest, and the \( \beta_{\text{rms}} \) of FH-BOC(9:1:1,1) is larger than those of BOC(5,1) and BPSK(10). When the front-end bandwidth \( \beta_{r} \) is approximately 36 MHz, the \( \beta_{\text{rms}} \) of BOC(10,5) is the largest, and the \( \beta_{\text{rms}} \) of FH-BOC(9:1:1,1) is smaller than that of BOC(5,1) but larger than that of BPSK(10).

Fig. 11
figure 11

RMS bandwidths for example signals band-limited to 40 MHz

Full size image

(2) Lower bound on the code tracking accuracy:

Betz (2001a, b) reported that a lower bound on the code tracking error in white noise could be obtained using the RMS bandwidth:

$$ \sigma_{\text{LB}} = \frac{1}{{2\pi \beta_{\text{rms}} }}\sqrt {\frac{{B_{L} }}{{{C \mathord{\left/ {\vphantom {C {N_{0} }}} \right. \kern-0pt} {N_{0} }}\int_{{ - {{\beta_{r} } \mathord{\left/ {\vphantom {{\beta_{r} } 2}} \right. \kern-0pt} 2}}}^{{{{\beta_{r} } \mathord{\left/ {\vphantom {{\beta_{r} } 2}} \right. \kern-0pt} 2}}} {G_{s} \left( f \right){\text{d}}f} }}} $$
(24)

where \( B_{L} \) denotes the one-sided equivalent rectangular bandwidth of the code tracking loop and \( G_{s} (f) \) is the PSD of the band-limited signal, for an equivalent rectangular bandwidth of the code tracking loop of 1 Hz. The top panels of Fig. 12 shows the lower bounds on the code tracking error for the example signals versus \( {C \mathord{\left/ {\vphantom {C {N_{0} }}} \right. \kern-0pt} {N_{0} }} \). When the front-end bandwidth is 24 MHz, FH-BOC(11:1:7,1) has the lowest code tracking error bound among the example signals, and the bound for FH-BOC(9:1:1,1) is lower than those for BPSK(10), BOC(5,1) and FH-BOC(14:1:1,1). When the front-end bandwidth is 36 MHz, BOC(10,5) has the lowest code tracking error bound, and the bound for FH-BOC(9:1:1,1) is higher than that for BOC(5,1) but lower than that for BPSK(10).

Fig. 12
figure 12

Lower bounds on the code tracking error and NELP code tracking errors for example signals with \( \beta_{r} \) = 24 MHz and \( \beta_{r} \) = 36 MHz

Full size image

Performance of noncoherent early-late processing

The ACF for FH-BOC modulation has a symmetric peak, similar to that for BOC modulation. Thus, code tracking with FH-BOC modulation can rely on a discriminator based on conventional early-late processing. This subsection illustrates noncoherent early-late processing (NELP) for the example signals.

The S-curve produced by a NELP-based discriminator with an early-late spacing of D seconds is given by Betz (2001a, b):

$$ S(\varepsilon ) = \left| {R\left( {\varepsilon - \frac{D}{2}} \right)} \right|^{2} - \left| {R\left( {\varepsilon + \frac{D}{2}} \right)} \right|^{2} $$
(25)

where \( \varepsilon \) is the error on the signal arrival time and \( R(\tau ) \) is the normalized ACF for the signal. An early-late spacing of 40 ns and precorrelation bandwidths (equal to the front-end bandwidth) of 24 MHz and 36 MHz are considered here. The solid lines in Fig. 13 represent the S-curves obtained using the front-end bandwidth of 24 MHz. The S-curve side peaks near the false locking points for FH-BOC(9:1:1,1) and FH-BOC(14:1:1,1) are much smaller than for BOC(5,1), BOC(10,5) and FH-BOC(11:1:7,1), indicating that the ambiguity problem in code tracking is greatly mitigated for FH-BOC(9:1:1,1) and FH-BOC(14:1:1,1). The individual points in Fig. 13 represent the S-curves obtained using the front-end bandwidth of 36 MHz, which are similar to those discussed above.

Fig. 13
figure 13

S-curves for example signals with \( \beta_{r} \) = 24 MHz and \( \beta_{r} \) = 36 MHz

Full size image

The variance of the code tracking error for NELP in white noise is given by Betz and Kolodziejski (2009):

$$ \begin{aligned} \sigma_{\text{NELP}}^{ 2} & { = }\frac{{B_{L} \left( {1 - 0.5B_{L} T} \right)\int_{{ - \beta_{r} /2}}^{{\beta_{r} /2}} {\left( {1 + \frac{{C_{I} }}{{N_{0} }}G_{I} \left( f \right)} \right)} G_{s} \left( f \right)\sin^{2} \left( {\pi f\Delta } \right){\text{d}}f}}{{\frac{{C_{s} }}{{N_{0} }}\left( {2\pi \int_{{ - \beta_{r} /2}}^{{\beta_{r} /2}} f G_{s} \left( f \right)\sin^{2} \left( {\pi f\Delta } \right){\text{d}}f} \right)^{2} }} \\ & \quad \times \left( {1 + \frac{{\int_{{ - \beta_{r} /2}}^{{\beta_{r} /2}} {G_{s} \left( f \right)\cos^{2} \left( {\pi f\Delta } \right){\text{d}}f} }}{{T\frac{{C_{s} }}{{N_{0} }}\left( {\int_{{ - \beta_{r} /2}}^{{\beta_{r} /2}} {G_{s} \left( f \right)\cos \left( {\pi f\Delta } \right){\text{d}}f} } \right)^{2} }}} \right. \\ & \quad \left. { + \frac{{\int_{{ - \beta_{r} /2}}^{{\beta_{r} /2}} {G_{I} \left( f \right)G_{s} \left( f \right)\cos^{2} \left( {\pi f\Delta } \right){\text{d}}f} }}{{T\frac{{C_{s} }}{{C_{I} }}\left( {\int_{{ - \beta_{r} /2}}^{{\beta_{r} /2}} {G_{s} \left( f \right)\cos \left( {\pi f\Delta } \right){\text{d}}f} } \right)^{2} }}} \right) \\ \end{aligned} $$
(26)

where \( {{C_{I} } \mathord{\left/ {\vphantom {{C_{I} } {N_{0} }}} \right. \kern-0pt} {N_{0} }} \) is the ratio of the interference carrier power to the noise density and \( T \) denotes the integration time for code tracking. For an interference carrier power of zero, precorrelation bandwidths (equal to the front-end bandwidth) of 24 MHz and 36 MHz, an integration time \( T \) of 0.02 s, an early-late spacing of 40 ns, and an equivalent rectangular bandwidth of the code tracking loop of 1 Hz, the code tracking errors for the example signals versus \( {C \mathord{\left/ {\vphantom {C {N_{0} }}} \right. \kern-0pt} {N_{0} }} \) are compared in the bottom panels of Fig. 12. The NELP comparison results for the example signals are consistent with the lower bounds on the code tracking error.

Anti-interference performance

The DSSS technique employed by GNSS signals offers strong anti-interference performance. However, GNSS signals are weak, easily suffering interference. A modulation scheme with better anti-interference performance could improve signal tracking performance. We compare the anti-interference performances for spectral separation, narrowband interference, and multipath interference for the example signals.

(1) Spectral separation coefficient (SSC):

SSC quantifies the amount of multiple-access interference among similar signals. The self-SSC quantifies the intrasystem interference, and the cross-SSC quantifies the intersystem interference, which reflects the compatibility among systems (Betz 2001a, b). A lower SSC indicates a better spectral separation between two signals. For a front-end bandwidth of 24 MHz, the cross-SSCs between the example signals and BPSK(1), BPSK(10), MBOC(6,1,1/11), and BOC(10,5) signals are presented in Table 3, along with the self-SSCs of the example signals. FH-BOC(9:1:1,1) and FH-BOC(14:1:1,1) have larger cross-SSCs with the signals listed above than FH-BOC(11:1:7) and BOC(10,5) but have smaller self-SSCs. Thus, FH-BOC(9:1:1,1) and FH-BOC(14:1:1,1) have worse intersystem compatibility but better intrasystem compatibility than FH-BOC(11:1:7) and BOC(10,5).

Table 3 SSCs of example signals with \( \beta_{r} \) =24 MHz
Full size table

(2) Effect of narrowband interference on code tracking:

For a spread spectrum system, the processing gain can reflect the anti-interference performance, especially for narrowband interference. A larger processing gain means better anti-interference performance (Pickholtz et al. 1982). The processing gain for BPSK(n) is

$$ G_{{p - {\text{BPSK}}}} \approx 10\log \left( {n \times \frac{{f_{0} }}{{f_{D} }}} \right) $$
(27)

where \( f_{D} \) is the data rate. The processing gain for BOC(\( \alpha \),\( \beta \)) is

$$ G_{{p - {\text{BOC}}}} \approx 10\log \left( {\beta \times \frac{{f_{0} }}{{f_{D} }}} \right) + 3 $$
(28)

and the processing gain for FH-BOC(\( \alpha_{M - 1} \):\( 1 \):\( \alpha_{0} \),\( \beta \)) is

$$ G_{{p - {\text{FHBOC}}}} \approx 10\log \left( {\beta \times \frac{{f_{0} }}{{f_{D} }}} \right){\text{ + 10log}}\left( {\frac{{\alpha_{M - 1} - \alpha_{0} }}{\beta } + 1} \right) + 3 $$
(29)

A comparison of (27) and (28) reveals that the processing gain for BOC(\( \alpha \),\( \beta \)) is 3 dB higher than that for BPSK(n) with the same spreading code rate. A comparison of (28) and (29) reveals that the processing gain for FH-BOC(\( \alpha_{M - 1} \):\( 1 \):\( \alpha_{0} \),\( \beta \)) is \( 1 0 {\text{log[(}}{{\alpha_{M - 1} - \alpha_{0} )} \mathord{\left/ {\vphantom {{\alpha_{M - 1} - \alpha_{0} )} \beta }} \right. \kern-0pt} \beta } + 1] \) dB higher than that for BOC(\( \alpha \),\( \beta \)), meaning that FH-BOC modulation offers better anti-narrowband interference than the equivalent BOC modulation. Table 4 lists processing gains for the example signals. FH-BOC(14:1:1,1) has the highest processing gain, and BOC(5,1) has the lowest. The processing gain of FH-BOC(9:1:1,1) is 9.6 dB higher than that of BOC(5,1). BPSK(10), BOC(10,5), and FH-BOC(11:1:7,1) have the same processing gain.

Table 4 Processing gains for example signals
Full size table

The effect of interference on a receiver can be measured in terms of the effective carrier-power-to-noise ratio, which is defined as (Betz 2001a, b)

$$ \left( {\frac{C}{{N_{0} }}} \right)_{\text{eff}} = \frac{{\frac{C}{{N_{0} }}\int_{{ - \beta_{r} /2}}^{{\beta_{r} /2}} {G_{s} \left( f \right){\text{d}}f} }}{{\int_{{ - \beta_{r} /2}}^{{\beta_{r} /2}} {G_{s} \left( f \right){\text{d}}f} + \frac{{C_{I} }}{{N_{0} }}K_{\text{SI}} }} $$
(30)

For receivers with precorrelation bandwidths (equal to the front-end bandwidth) of 24 MHz and 36 MHz, a \( C/N_{0} \) of 45 dB, and narrowband interference with a bandwidth of 10 kHz and a center frequency located at the center of one of the main lobes of the signal, Fig. 14 plots the effective \( C/N_{0} \) versus \( {{C_{I} } \mathord{\left/ {\vphantom {{C_{I} } {N_{0} }}} \right. \kern-0pt} {N_{0} }} \) for the example signals. The differences in the processing gains of the example signals for narrowband interference are evident in Fig. 14.

Fig. 14
figure 14

Effective \( C/N_{0} \) values for example signals with \( \beta_{r} \) = 24 MHz and \( \beta_{r} \) = 36 MHz

Full size image

(3) Multipath interference:

Multipath interference is one of the main sources of error in satellite navigation. For a multipath situation with one direct path and one reflected path with a multipath-to-direct ratio of -6 dB, an early-late spacing of 0.5 chip period of the 10.23 MHz spreading code for BPSK(10), 50 ns for BOC(5,1), 40 ns for BOC(10,5), 50 ns for FH-BOC(9:1:1,1), 40 ns for FH-BOC(11:1:7,1), and 50 ns for FH-BOC(14:1:1,1), and receiver front-end bandwidths of 24 MHz and 36 MHz, the top panels of Fig. 15 show the NELP multipath error envelopes versus the multipath delay. FH-BOC(14:1:1,1) has the smallest worst-case bias error. FH-BOC(11:1:7,1) and BOC(10,5) have similar worst-case bias errors. The error envelope for FH-BOC(9:1:1,1) is smaller than those for BPSK(10) and BOC(5,1) when the path delay is less than 30 m, the most common path delay in many urban environments (Hein et al. 2006). The bottom panels show the corresponding average multipath errors. FH-BOC(14:1:1,1) has the smallest average multipath error, and the average multipath error of FH-BOC(9:1:1,1) is smaller than those of BPSK(10) and BOC(5,1).

Fig. 15
figure 15

NELP multipath error envelopes for example signals with \( \beta_{r} \) = 24 MHz and \( \beta_{r} \) = 36 MHz

Full size image

Conclusion

We propose a generalized FH-BOC modulation scheme. Based on theoretical and numerical analyses of the established mathematical model, FH-BOC(\( \alpha_{M - 1} \):1:1,1) is recommended because of its lower ACF ambiguity, better anti-interception performance, and better anti-narrowband interference and multipath interference performance compared with BOC modulation with the same MLB. FH-BOC(\( \alpha_{M - 1} \):1:1,1) has tracking performance similar to that of BOC(\( {{\alpha_{M - 1} } \mathord{\left/ {\vphantom {{\alpha_{M - 1} } 2}} \right. \kern-0pt} 2} + 0.5,1)\), and it can be easily extended to high order with a wider band for better performance. If better spectral separation with signals at the center of the band is needed, one method is to increase the frequency-hopping band of FH-BOC(\( \alpha_{M - 1} \):1:1,1); another is to use FH-BOC(\( \alpha_{M - 1} \):1:\( \alpha_{ 0} \),1), \( \alpha_{ 0} > 1 \). The time and frequency properties of FH-BOC modulation are controlled by four parameters and the frequency-hopping pattern, providing designers with great flexibility for adjustment and optimization. Moreover, a generation and detection scheme and a frequency-hopping scheme are recommended. The acquisition time and complexity of the receiving process for the proposed FH-BOC signal are the same for the BOC signal with the same MLB.

FH-BOC modulation also has the advantages of dual-sideband spectral characteristics. All the information needed for ranging and data demodulation can be obtained by processing one sideband, similar to the case of BOC modulation. The CEM technique can be used to transmit more signal components and maximize HPA efficiency. Furthermore, because the frequency hopping for FH-BOC modulation is implemented in the subcarrier, the performance for carrier phase measurements and Doppler measurements is not affected. FH-BOC modulation enables more multiple accesses than BOC modulation with the same spreading code because it has two-dimensional multiple access space. The new modulation scheme we proposed can serve as a new paradigm for next-generation GNSS signal design, especially military signal design. It can also be used in the signal design for GNSS-like systems, such as systems for indoor positioning, GNSS enhancement, and pseudolite-based positioning.