1 Introduction

Shock-wave/boundary-layer interactions (SBLI) are an important design consideration for many aeronautical applications (Dolling 2001; Gaitonde 2015). Supersonic engine intakes aim to efficiently decelerate incoming flow to subsonic conditions before the entrance to the compressor. Typically this is achieved by creating a sequence of oblique shocks terminated by a weak normal shock to minimise losses within the duct. The shock induced adverse pressure gradient causes unsteadiness, a thickening of the boundary-layer, and, for sufficiently strong SBLI, flow separation can occur. This reduction in flow uniformity can have a detrimental effect on engine performance and reliability.

In this work the reflection of an oblique shock-wave impinging on transitional boundary-layers is investigated via Implicit Large Eddy Simulations (ILES) for a full rectangular duct at Mach 2. In many studies of SBLI a simplified periodic (quasi-2D) span is assumed to reduce computational cost, neglecting complex flow features that arise for internal confined flows. Examples of span-periodic numerical studies of transitional oblique SBLI include (Sansica et al. 2016; Larchevêque 2016) and Quadros and Bernardini (2018). In each case the transitional SBLI was highly unsteady with a range of low and high frequency phenomena arising from the complex coupling between inviscid and viscous effects. Many of the existing works focus on configurations where the flow transitions downstream of the SBLI. In the present contribution the SBLI is exposed to intermittent transition that develops as turbulent spots upstream of the primary shock reflection.

When flow confinement is included the oblique shock interacts with both the sidewall and bottom wall boundary layers, causing multiple regions of flow-reversal not present in quasi-2D simulations. Examples of previous numerical work on confined oblique SBLI include the turbulent SBLI of Bermejo-Moreno et al. (2014) and  Wang et al. (2015), in which wall-modelled and wall-resolved LES were used respectively. In both cases the SBLI was highly three-dimensional and showed a strong dependence on the geometry of the duct. The swept-SBLI of the incident shock with sidewall boundary layers led to a strengthened interaction on the centreline and regions of slender recirculation in the corners. In  Bermejo-Moreno et al. (2014) it was noted that Mach stems were present only in cases where the interaction was strengthened due to the presence of sidewalls. Examples of rectangular duct SBLI focusing on normal-shock interactions include those of Bruce et al. (2011) and  Burton and Babinsky (2012).

Wind tunnel experiments are inherently three-dimensional due to the sidewalls of the test chamber, with large aspect ratios required to make comparison to span-periodic simulations. Some experiments  (Xiang and Babinsky 2019) have proposed that the modified interaction could be predicted by the crossing location of compression waves emitted from corner separations. To demonstrate this effect, blockages were added to the corners of the duct to cause exaggerated corner compressions. It was observed that the topology of the central separation region was sensitive to the size of the corner blockages. The experiments of Giepman et al. (2016) and the complementary numerical study by Quadros and Bernardini (2018) investigated tripped transition of laminar SBLI at \(M=1.7\). It was observed in both cases that, for a given shock strength, the size of the recirculation bubble was highly dependent on the incoming boundary layer state. By placing the boundary layer trips close to the interaction, it was shown experimentally that the recirculation region could be suppressed or removed entirely. While this approach reduces unsteady flow separation, the thicker boundary layer leads to an increase in skin-friction drag downstream of the interaction. A separate numerical study Grébert et al. (2018) looked at the effect of upstream micro Vortex-Generators (mVGs) on a turbulent SBLI at \(M=2.7\). Hairpin vortices shed from the rear of the mVGs led to overall reductions in pressure load fluctuations and separation size of 9% and 20% respectively.

The experimental work of Grossman and Bruce (2017) investigated the role of gaps between the shock generator and sidewalls for a Mach 2 SBLI with a \(12^{\circ }\) flow deflection. The central separation bubble length was sensitive to the size of the sidewall gap, with reduced three-dimensionality and smaller separations seen for larger sidewalls gaps. A further effect was to determine how sensitive the SBLI was to the impingement location of the trailing-edge expansion fan from the end of the shock generator. For impingement points further downstream, a strengthened interaction was observed. The influence of the trailing edge expansion fan was also noted numerically by the laminar duct SBLI of Lusher and Sandham (2019). Similar themes were investigated in the experimental work of  Grossman and Bruce (2018), focusing on regular-irregular transition of SBLI in turbulent duct flows. The strong dependence of effective duct aspect ratio was demonstrated by the transition from regular to irregular (Mach) reflections for a fixed initial flow deflection.

There has also been an interest in the unsteady dynamics of shock-trains that can form within confined flow configurations. The Direct Numerical Simulation (DNS) of Fiévet et al. (2017) attempted to quantify the role of inflow confinement ratio on shock-trains in turbulent duct flows. It was observed that the shock train moved upstream for higher inflow confinement ratios. Temporally varying the inflow boundary-layer thickness led to a dynamic response of the shock-train, dependent on the excitation frequency. Shock-train unsteadiness was also the subject of Hunt and Gamba (2019) for a duct flow at Mach 2. The complex shock-system was shown to be influenced by upstream-propagating acoustic waves from regions of flow separation, and downstream-travelling vortices shed from the separation bubble. The wind tunnel tests of Cheng et al. (2017) looked at the response of an oblique shock-train to downstream pressure perturbations at Mach 2.7. The oblique shock-train was shown to be sensitive to downstream pressure perturbations within the separation bubble and subsonic shear layer. Translational motion of the shock-train was observed at the same frequency as the downstream forcing.

While turbulent duct SBLI has received some attention in recent years, laminar and transitional interactions in ducts are not as well understood. The work of Giepman et al. (2018) also noted experimental difficulties when seeding boundary layers in a laminar case. Numerical simulations are well placed to investigate SBLI for transitional interactions and complement existing experimental literature. The aim of the current work is to investigate oblique SBLI for rectangular ducts containing transitional boundary layers. A tripping method is selected such that intermittent transition develops upstream of the interaction with an imposed asymmetry. Two different aspect ratios are simulated to demonstrate the strong dependence of the cross sectional duct area on the SBLI.

Section 2.1 outlines the governing compressible Navier-Stokes equations to be solved in non-dimensional form. Section 2.2 gives a brief overview of the flux reconstruction and high-order Targeted Essentially Non-Oscillatory (TENO) schemes used for spatial reconstruction of the convective terms. The physical problem is specified in Sect. 3.1; including details of the computational domain and the initialisation of laminar boundary layers within the duct. Section 3.2 introduces the time-dependent blowing/suction strips that generate disturbances upstream of the SBLI. All of the simulations use high-order finite-differencing on structured meshes in the OpenSBLI code (Jacobs et al. 2017; Lusher et al. 2018) as in Sect. 3.3. In Sect. 4.1 the baseline half aspect-ratio results are presented for two different forcing configurations. Instantaneous snapshots of the near-wall region show the response of the separation bubble to intermittent turbulent spots. Finally in Sect. 4.2 the same two forcing configurations are simulated for a wider 1:1 aspect-ratio duct to demonstrate the effects of sidewall confinement.

2 Numerical Method

2.1 Governing Equations

In this work the unsteady compressible Navier-Stokes equations are solved in non-dimensional conservative form. For three spatial directions \(x_i\)\(\left( i=1, 2, 3\right)\) the coupled set of five partial differential equations are given by

$$\begin{aligned}&\frac{\partial \rho }{\partial t} + \frac{\partial }{\partial x_k} \left( \rho u_k \right) = 0, \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial }{\partial t}\left( \rho u_i\right) + \frac{\partial }{\partial x_k} \left( \rho u_i u_k + p \delta _{ik} - \tau _{ik}\right) = 0, \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial }{\partial t}\left( \rho E\right) + \frac{\partial }{\partial x_k} \left( \rho u_k \left( E + \frac{p}{\rho }\right) + q_k - u_i \tau _{ik}\right) = 0, \end{aligned}$$
(3)

with Fourier’s heat flux \(q_k\) and viscous stress tensor \(\tau _{ij}\) defined as

$$\begin{aligned} q_k= & {} \frac{-\mu }{\left( \gamma - 1\right) M_{\infty }^{2} Pr Re}\frac{\partial T}{\partial x_k}, \end{aligned}$$
(4)
$$\begin{aligned} \tau _{ik}= & {} \frac{\mu }{Re} \left( \frac{\partial u_i}{\partial x_k} + \frac{\partial u_k}{\partial x_i} - \frac{2}{3}\frac{\partial u_j}{\partial x_j} \delta _{ik}\right) . \end{aligned}$$
(5)

The coordinates \(x_i\,\left( i=1, 2, 3\right)\) are referred to in this work as \(\left( x,y,z\right)\) for the streamwise, bottom wall-normal and spanwise directions respectively, with corresponding velocity components \(\left( u, v, w\right)\). The equations are non-dimensionalized by freestream velocity, density and temperature \(\left( U^{*}_{\infty }, \rho ^{*}_{\infty }, T^{*}_{\infty }\right)\), with a characteristic length based on the displacement thickness \(\delta ^{*}\) of the boundary layer imposed at the inlet. Pressure is normalised by \(\rho _{\infty }^{*} {U_{\infty }^{*}}^{2}\), to give \(\left( U_{\infty }, \rho _{\infty }, T_{\infty }\right) =1\) in the freestream. Freestream Mach number, Prandtl number and ratio of specific heat capacity for air are taken to be \(M_{\infty } = 2\), \(Pr = 0.72\) and \(\gamma = 1.4\) respectively. Reynolds number based on the inlet displacement thickness is set as \(Re_{\delta ^{*}} = 1500\) throughout. The dynamic viscosity \(\mu \left( T\right)\) is computed by Sutherland’s law

$$\begin{aligned} \mu \left( T\right) = T^{\frac{3}{2}} \left( \frac{1+\frac{T^{*}_{s}}{T^{*}_{\infty }} }{T + \frac{T^{*}_{s}}{T^{*}_{\infty }}}\right) , \end{aligned}$$
(6)

with reference and Sutherland temperatures taken to be \(T_{\infty }^{*} = 288.0\; \text {K}\) and \(T_{s}^{*} = 110.4\). For an ideal Newtonian fluid pressure can be calculated through the equation of state such that

$$\begin{aligned} p = \left( \gamma - 1\right) \left( \rho E - \frac{1}{2} \rho u_i u_i\right) = \frac{1}{\gamma M^{2}_{\infty }} \rho T. \end{aligned}$$
(7)

Throughout this work bottom wall skin friction \(C_f\) is calculated as

$$\begin{aligned} C_f = \frac{\tau _w}{\frac{1}{2} \rho _{\infty } U^{2}_{\infty }}, \quad \tau _w = \mu {\frac{\partial u}{\partial y}\left| \right. }_{y=0}. \end{aligned}$$
(8)

2.2 Targeted Essentially Non-Oscillatory (TENO) Schemes

Simulation of high-speed compressible gas dynamics in a finite-difference framework requires special treatments due to flow discontinuities such as shock waves. Differencing over a discontinuity will create spurious oscillations that contaminate the flow field and cause the solution to diverge. Common methods to deal with shocked flows include adding artificial dissipation to smear the shock over multiple grid points and stabilise the solution. While these classes of shock-capturing schemes are able to resolve shock waves they have the detrimental effect of damping small-scale turbulence. For high-fidelity Large-Eddy Simulations (LES) or Direct Numerical Simulation (DNS) this leads to excessively large grid requirements to adequately resolve turbulence and the transition mechanism (Pirozzoli 2011).

Among the most successful shock-capturing schemes developed in recent times is the family of Weighted Essentially Non-Oscillatory (WENO) schemes introduced by Jiang and Shu (1996), Shu (1997). WENO schemes work by creating a convex combination of smaller candidate stencils that each receive a weighting depending on the local flow smoothness. Stencils containing discontinuities are weighted close to zero to achieve essentially non-oscillatory behaviour around discontinuities. In the work of Brehm et al. (2015) various WENO formulations were shown to be superior to more classical approaches to shock-capturing, albeit at an increased computational cost. A similar study Johnsen et al. (2010) noted that, while WENO schemes were able to robustly capture shock-waves, the induced numerical dissipation made them unsuitable for compressible turbulence, unless paired with a non-dissipative scheme in smooth flow regions. A new class of low-dissipative essentially non-oscillatory schemes were proposed by Fu et al. (2016) to simulate shocked compressible turbulence. Targeted Essentially Non-Oscillatory (TENO) schemes work in a similar manner to previous WENO schemes but achieve lower dissipation due to a modified stencil selection mechanism and re-defined weightings. The family of TENO schemes are a viable alternative to hybrid schemes  (Lusher and Sandham 2019), and have been shown to perform well for a number of compressible flow configurations (Fu et al. 2019).

To illustrate the reconstruction procedure used in TENO schemes we use a simplified 1D advection equation but note that it is easily extended to systems of equations where the procedure is applied for each component of the system in turn. For a simple 1D hyperbolic equation of the form

$$\begin{aligned} U_t + f(U)_x = 0, \end{aligned}$$
(9)

the flux term \(f(U)_x\) at each discrete grid point \(x_i\) can be approximated by computing a flux reconstruction over the half-node locations \([x_{i-\frac{1}{2}}, x_{i+\frac{1}{2}}]\) with grid spacing \(\varDelta x\) such that

$$\begin{aligned} \frac{\partial U}{\partial t} + \frac{1}{\varDelta x} \left( {\hat{f}}_{i+\frac{1}{2}} - {\hat{f}}_{i-\frac{1}{2}}\right) = 0. \end{aligned}$$
(10)

Figure 1 shows a schematic of a full TENO stencil comprised of a set of smaller candidate stencils below. Non-oscillatory behaviour is obtained by measuring the smoothness in each candidate stencil and assigning it a weighting \(\omega _r\) in the final reconstruction. Fluxes at the half-node locations \(f_{i+\frac{1}{2}}\) and \(f_{i-\frac{1}{2}}\) are reconstructed as a weighted sum of essentially non-oscillatory (ENO) interpolations over a set of r candidate stencils

$$\begin{aligned} {\hat{f}}_{i+ \frac{1}{2}} = \sum _{r=0}^{K-3} \omega _r {\hat{f}}^{(r)}_{i+ \frac{1}{2}}, \end{aligned}$$
(11)

where \({\hat{f}}^{(r)}_{i+ \frac{1}{2}}\) are the classic ENO interpolations given in Shu (1997), and \(\omega _r\) are the non-linear weights satisfying the conditions

$$\begin{aligned} \omega _r \ge 0, \quad \text {and} \quad \sum _{r=0}^{K-3} \omega _r = 1, \end{aligned}$$
(12)

for a TENO scheme of order K in smooth regions of the flow. A TENO scheme of order \(K=6\) is used throughout. Flux splitting is applied by summing upwind/downwind biased reconstructions \({\hat{f}} = {\hat{f}}^{+} + {\hat{f}}^{-}\), using the well known local Lax-Friedrichs splitting method

$$\begin{aligned} f^{\pm }(U) = \frac{1}{2} \left( f(U) \pm \alpha U\right) \end{aligned}$$
(13)

for a locally evaluated wave-speed \(\alpha\) over the full numerical stencil. The negative flux contribution is obtained by reflecting the stencils in Fig. 1 about the half-node reconstruction point \(x_{i+\frac{1}{2}}\). The reconstruction is performed in characteristic space as this achieves sharper shock capturing with reduced oscillations (Brehm et al. 2015). For systems of equations the wave-speed \(\alpha\) in the flux splitting (13) is the characteristic wave speed evaluated locally over the stencil.

Fig. 1
figure 1

Staggered candidate stencils for TENO schemes, adapted from Fu et al. (2016)

Full size image

In the standard WENO formulation each candidate stencil is given a non-linear weighting, with candidate stencils crossing discontinuities given a low, albeit non-zero, weight. TENO schemes abandon this approach in favour of a discrete cut-off function that discards candidate stencils completely from the flux reconstruction if they are deemed to be sufficiently non-smooth. Candidate stencils that are considered smooth are included in the reconstruction with their ideal linear weight to further reduce numerical dissipation. In reference to Fig. 1, the 6th order TENO reconstruction uses candidate stencils \(\{S_0, S_1, S_2, S_3\}\). The non-linear weights of Shu (1997) are reformulated with ideal weights \(d_r\) for a scheme of order K to be

$$\begin{aligned} \omega _r = \frac{d_r \delta _r}{\sum _{r=0}^{K-3} d_r \delta _r}, \end{aligned}$$
(14)

where \(\delta _r\) is a discrete cut-off function of the form

$$\begin{aligned} \delta _r = {\left\{ \begin{array}{ll} 0 &\quad{} \text {if} \quad \chi _r < C_T \\ 1 &\quad{} \text {otherwise}\\ \end{array}\right. } \end{aligned}$$

for a tunable cut-off parameter \(C_T\). The smoothness measures \(\chi _r\) are the same as the weight normalization process in WENO

$$\begin{aligned} \chi _r = \frac{\gamma _r}{\sum ^{K-3}_{r=0}\gamma _r}, \end{aligned}$$
(15)

with the WENO-Z (Borges et al. 2008) inspired form of non-linear weights (Fu et al. 2016) given by

$$\begin{aligned} \gamma _r = \left( C + \frac{\tau _K}{\beta _r + \epsilon }\right) ^{q}, \quad r = 0,\dots ,K-3. \end{aligned}$$
(16)

Polynomial smoothness indicators \(\beta _r\) are unchanged from the standard Jiang-Shu formulation (Jiang and Shu 1996), and are given explicitly for the TENO stencils of Fig. 1 in  Fu et al. (2016). The small parameter \(\epsilon \sim 10^{-16}\) is used to avoid division by zero. A global smoothness indicator \(\tau _K\) measures smoothness over the full numerical stencil, and is given for a 6th order TENO scheme as

$$\begin{aligned} \tau _6&= |\beta _3 - \frac{1}{6}\left( \beta _0 + \beta _2 + 4\beta _1\right) |. \end{aligned}$$
(17)

The constants defined in Eq. (16) take the values of \(q = 6\) and \(C=1\), which were shown to significantly enhance the discontinuity detection capability of the scheme  (Fu et al. 2016). The parameter \(C_T\) is a user-specified threshold value that determines whether a given candidate stencil is rejected or contributes to the flux reconstruction. Lower values of \(C_T\) are suitable for compressible turbulence simulations where minimal numerical dissipation is desirable. However, this comes at the cost of increased spurious oscillations around shock-waves. In the following simulations a value of \(C_T = 1.0\times 10^{-6}\) is chosen.

2.3 Explicit Time-Stepping and Viscous Terms

Viscous and heat conduction terms in the momentum (2) and energy (3) equations are computed with standard 4th order central differences inside the domain. At domain boundaries a 4th order one-sided boundary closure  (Carpenter et al. 1998) is used to maintain a consistent order throughout the domain. Metric terms for grid stretching are computed with the same 4th order schemes. For time-advancement a low-storage 3th order explicit Runge-Kutta time-stepping scheme is used in the form proposed by Williamson (1980). The benefit of low-storage schemes is that they only require two storage registers per equation and help to minimise data access within the code. For an m-stage scheme, time advancement of the solution vector u from level \(u^n\) to \(u^{n+1}\) is performed at stage \(i=1, \dots , m\) such that

$$\begin{aligned} du^{(i)}&= A_i du^{(i-1)} + \varDelta t R\left( u^{(i-1)}\right) , \end{aligned}$$
(18)
$$\begin{aligned} u^{(i)}&= u^{(i-1)} + B_i du^{(i)}, \end{aligned}$$
(19)
$$\begin{aligned} u^{n+1}&= u^{(m)}, \end{aligned}$$
(20)

for a constant time-step \(\varDelta t\), initial conditions \(u^{(0)} = u^n\) and \(du^{(0)} = 0\), and residual \(R(u^{(i-1)})\). The constants \(A_i\), \(B_i\) are taken for 3th and 4th order from  Carpenter and Kennedy (1994).

3 Computational Method

3.1 Problem Specification

Fig. 2
figure 2

Non-dimensional computational domain for the rectangular duct. The width of the span \(L_z\) is 87.5 and 175 for the half and one aspect ratio cases respectively

Full size image

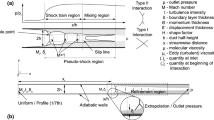
The computational domain consists of a rectangular duct with a finite-length \(\theta _{sg} = 5^{\circ }\) internal shock generator as shown in Fig. 2. The non-dimensional streamwise length and height of the duct are set as \(L_x=800\) and \(L_y = 175\) respectively. Ducts with aspect ratios \(\left( AR=L_z / L_y\right)\) of \(AR=0.5\) and \(AR=1\) are simulated in this work. The shock generator ramp starts at \(x_{sg} = 350\) and has a length of \(L_{sg} = 300\); a trailing edge expansion fan is generated at the end of the ramp and exits through the outlet plane of the computational domain. Following the canonical works of  Hakkinen et al. (1959) and Katzer (1989), a Mach 2 freestream is initialised in the domain with laminar boundary layer profiles imposed on the bottom and sidewalls of the duct. Freestream conditions are maintained on the top portion of the domain upstream of the shock generator. The laminar profiles are obtained via a similarity solution to the compressible boundary layer equations using the Illingworth transformation (White 2006). The initial condition for the integration of the profile uses a recovery factor of \(Pr^{1/2}\). The Reynolds number based on the inlet displacement thickness is \(Re_{\delta ^{*}} = 1500\).

No-slip isothermal wall conditions are enforced on the bottom wall, sidewalls, and on the shock generator for a non-dimensional wall temperature equal to the adiabatic wall condition from the similarity solution of \(T_w = 1.676\) (4 significant figures). A pressure extrapolation is applied at the inlet, with zero gradient conditions enforced on the outlet and upstream of the shock generator. The pressure extrapolation is applied in the subsonic region of the inlet plane. In the corners of the duct flat plate boundary-layer profiles of equal thickness from two adjacent walls are blended together to form a smooth corner profile. The similarity solution streamwise velocity profile for each wall is multiplied by the wall normal velocity component of the adjacent wall to create a combined profile that smoothly tends to zero in the corner. The wall-normal velocity component from the sidewalls is linearly damped with the z coordinate such that they both reach zero on the centreline. For temperature, the profiles \({\hat{T}}(y), {\hat{T}}(z)\) are scaled for a constant wall temperature \(T_{w}\) such that

$$\begin{aligned} {\hat{T}}= & {} \frac{T - T_w}{T_{\infty } - T_{w}}, \end{aligned}$$
(21)

to give \({\hat{T}} \in \left[ 0,1\right]\). The scaled profiles for two intersecting walls are then blended together by

$$\begin{aligned} T(y,z) = T_w + {\hat{T}}(y) {\hat{T}}(z) \left( 1 - T_w\right) , \end{aligned}$$
(22)

giving a smooth profile that varies from \(T=1\) in the freestream to \(T=T_w\) at the wall. The wall normal velocity component w from each of the sidewalls is of equal magnitude but opposite direction, requiring it to be damped with the z coordinate in both directions to create a zero w component of velocity on the centreline.

3.2 Time-Dependent Upstream Disturbances

The aim of the study is to observe the response of oblique duct SBLI for situations where transition occurs upstream of the interaction but the boundary layers are not yet fully turbulent. To induce transition upstream of the shock reflection, disturbances are added to the laminar boundary-layer via strips of wall normal blowing/suction as shown in Fig. 2. Random phases are added to the forcing to observe how asymmetry in the initial disturbances can influence the resulting SBLI flow structures. Further asymmetry can be added to the problem by forcing specific walls within the duct while keeping others laminar. The two configurations considered here are one in which the sidewalls and bottom wall are forced, and one where the bottom wall is kept initially laminar.

For the disturbance strip located on the bottom wall of the domain \(\left( y=0\right)\): the v velocity component is forced using a modified version of the forcing presented in Pirozzoli et al. (2004) such that

$$\begin{aligned} v\left( x, z, t\right) = {\left\{ \begin{array}{ll} A_0 f ( x ) g ( z ) h ( t ) &{} \text {if } x_a< x < x_b \\ 0 &{} \text {otherwise},\\ \end{array}\right. } \end{aligned}$$
(23)

for streamwise \(f \left( x\right)\), spanwise \(g \left( z\right)\) and time \(h\left( t\right)\) dependence

$$\begin{aligned} f(x)&= \exp \left( -\left( \frac{\left( x - (x_b - x_a)\right) ^2}{16}\right) \right) , \end{aligned}$$
(24)
$$\begin{aligned} g (z)&= \sum _ { l = 1 } ^ { l _ { \max } } Z _ { l } \sin \left( 2 \pi l \left( z / L _ { z } + \phi _ { l } \right) \right) , \end{aligned}$$
(25)
$$\begin{aligned} \quad h ( t )&= \sum _ { m = 1 } ^ { m _ { \max } } T _ { m } \sin \left( \omega _m t + 2 \pi \phi _ { m } \right) , \end{aligned}$$
(26)

where the constants \(Z_l\), \(T_m\) are defined by the relations

$$\begin{aligned} \sum _ { l = 1 } ^ { l _ { \max } } Z _ { l } = 1 , \quad Z _ { l } = 1.25 Z _ { l + 1 }, \quad \sum _ { m = 1 } ^ { m _ { \max } } T _ { m } = 1 , \quad T _ { m } = 1.25 T _ { m + 1 }. \end{aligned}$$
(27)

Random phases \(\phi _l, \phi _m\) distributed between \(\left[ 0,1\right]\) are added for each of the \(l,m=20\) terms. The same phases are fixed between different simulations but differ on each of the three forcing strips to create the asymmetry in the initial breakdown. In the corners the forcing is linearly damped to zero within a distance of one boundary layer thickness from the walls. This damping ensures that the forcing from adjacent walls does not introduce discontinuities to the flow. Forcing is applied for a range of evenly spaced frequencies \(\omega _m\) in the interval \(\left[ 0.04, 0.12\right]\), taken from linear stability of compressible boundary-layers (Sansica 2015). The forcing strip is located between \(x_a = 10.0\), \(x_b = 30.0\) with an amplitude of \(A_0 = 0.2\). A high amplitude is selected to trigger transition upstream of the shock reflection. On both sidewalls of the domain the same forcing is applied for the wall-normal velocity w, where the spatial variation g(z) is instead taken over g(y).

Table 1 Overview of the four computational test cases with different forcing configurations. The prefixes (A) and (B) refer to cases with half and one aspect ratio ducts respectively
Full size table

3.3 Computational Method

Fig. 3
figure 3

Comparison of the (left) centreline wall pressure and (right) centreline skin-friction distribution for the baseline grid compared to a 25% coarsened version in each direction. The case A2 is shown

Full size image
Fig. 4
figure 4

Comparison of time-averaged skin-friction contours on the bottom wall for case A2. Showing (top) the baseline grid resolution and (bottom) a grid coarsened by 25% in all directions

Full size image

Two forcing configurations are considered in this work as shown in Table 1: one with disturbances added to both the bottom and sidewalls of the domain (cases A1, B1), and one where the bottom wall is kept laminar, to observe how the transition develops over the span (cases A2, B2). The cases (A) and (B) refer to half and one aspect ratio ducts respectively to assess the effect aspect ratio has on the duct SBLI. Grid stretching is performed symmetrically in the y and z directions to cluster points in the boundary layers of each wall, with a uniform distribution in x. Grid points in y and z are distributed with stretch factors \(s_1, s_2 =1.6, 1.4\) as

$$\begin{aligned} y = \frac{1}{2}L_y \frac{1-\tanh \left( s_1\left( 1-2\xi \right) \right) }{\tanh \left( s_1\right) }, \quad \quad z = \frac{1}{2}L_z \frac{1-\tanh \left( s_2\left( 1-2\xi \right) \right) }{\tanh \left( s_2\right) }, \end{aligned}$$
(28)

for uniformly distributed points \(\xi = \left[ 0,1\right]\). Polynomial smoothing is applied to each of the grid lines in the streamwise x direction to ensure continuity at the start and end locations of the shock generator section of the duct. The baseline half-aspect ratio grid configuration from table 1 has wall units of \(\varDelta x^{+} = 18\), \(2.8< \varDelta y^{+} < 18\) and \(2.2< \varDelta z^{+} < 10\), based on \(C_f\) evaluated in the turbulent region at the outlet. The grid was selected using the LES recommendations of Georgiadis et al. (2010). Grid sensitivity was shown for laminar cases of a similar set-up in figure 3 of Lusher and Sandham (2019), and the performance of the schemes for span-periodic transitional SBLI was reported in Lusher and Sandham (2019). Relatively conservative stretching factors were selected in this study to ensure that the grid was not overly coarse in the middle of the duct. As an example, a more aggressive stretching in y would lead to poor \(\varDelta y\) resolution near the \(z=0, L_z\) sidewalls, in the middle region of the duct at \(y=L_y / 2\).

Figure 3 shows a comparison of the baseline grid for case A2 to a coarser version with a grid of \(\left( 785 \times 285 \times 245\right)\), representing a reduction of about 60% in total grid points. While there is slight discrepancy in the location of the separation bubble, the main flow features are consistent. Notably the sharp rise in \(C_f\) at \(x=600\) agrees well between the meshes, as the flow transitions to turbulence on the centreline. The exit pressure agrees well for both cases, with the coarse grid under-predicting the outlet \(C_f\) by \(5\times 10^{-4}\). Figure 4 shows a comparison of skin-friction on the bottom wall for case A2 between the two grid resolutions. Although the coarser mesh shows a slightly larger separation bubble, the main flow features are consistent between the meshes. The location of the shock-reflection, secondary shock, and transition to turbulence agrees well for the coarser mesh. The asymmetry in the initial breakdown caused by the asymmetric forcing is also clear to see for both meshes. The grid resolution is doubled in the span-wise z direction for the wider \(AR=1\) cases (B1, B2).

Three flow-through times of the domain were simulated to clear the initial transient and let the shock reflection form. Time averaging was applied for a further four flow-through times with statistics collected every time-step. A non-dimensional time-step of \(\varDelta t = 5\times 10^{-3}\) is used throughout. The high-order finite-difference code OpenSBLI (Jacobs et al. 2017;  Lusher et al. 2018) was used to perform the simulations. OpenSBLI is a Python-based finite-difference framework for structured meshes, that generates a C code in the Oxford Parallel Structured (OPS) embedded domain-specific-language (eDSL)  (Reguly et al. 2014; Mudalige et al. 2019). The base code undergoes a source-to-source translation step to a range of computational architectures including CUDA+MPI for multi-GPU clusters. The OpenSBLI code has previously been used to perform supersonic laminar SBLI (Lusher et al. 2018; Lusher and Sandham 2019), transitional SBLI (Lusher and Sandham 2019), and hypersonic roughness-induced transition (Lefieux et al. 2019).

4 Results

4.1 Baseline Half-Aspect Ratio Duct

Fig. 5
figure 5

Time averaged skin friction distributions on the bottom wall. For the cases of (top) forced sidewalls and bottom wall (A1) and (bottom) forced sidewalls only (A2). The dashed white line encloses regions of flow recirculation

Full size image
Fig. 6
figure 6

Time averaged centreline normalised pressure (left) and skin friction (right) on the bottom wall of the duct. For the cases of forced sidewalls and bottom wall (red)(A1) and forced sidewalls only (black)(A2)

Full size image

In this section the baseline \((AR=0.5)\) duct is simulated for the two forcing configurations A1 and A2. Time averaged skin friction on the bottom wall is shown in Fig. 5 for the fully forced (top) and laminar bottom wall cases (bottom). The incident shock is set up to impinge on the bottom wall boundary layer at \(x=580\), which is curved as a result of the swept sidewall SBLI. In the presence of sidewalls the incident shock is strengthened near the centreline and weakened towards the sidewalls (Wang et al. 2015; Lusher and Sandham 2019). For the fully forced case (A1) there is no mean flow separation \(\left( C_f < 0\right)\) at the centreline, the transition develops first in the corners and spreads out in a wedge across the span. In contrast, the laminar bottom wall case shows an oval region of mean flow separation bordered by the turbulence generated in the corners. The latter case also exhibits an asymmetry in the development of the transition, likely caused by the asymmetry in the random phases of the forcing and a relatively short averaging time. The asymmetry can also be observed in the instantaneous density gradients of Fig. 7, showing the asymmetric transitional boundary-layer development along the upper and lower sidewalls. The mean flow does not exhibit flow separation in the corner regions at this moderate shock strength of \(\theta _{sg} = 5.0^{\circ }\). This is in contrast to laminar cases  (Lusher and Sandham 2019) where \(AR=0.5\) ducts were shown to separate for a weaker interaction of \(\theta _{sg} = 2.0^{\circ }\).

At \(x=600\) in Fig. 5 (top) there is a chevron shaped region of high skin friction shown in red followed by a secondary shock in blue at \(x=650\). Comparing this to the centreline pressure plot of Fig. 6 (left) we see that after the initial shock-wave, there is a decrease in pressure corresponding to an expansion before the secondary pressure rise at \(x=650\). Both forcing configurations lead to the same outlet pressure value; however the case with a non-laminar bottom wall (A2) shows a later initial pressure rise. This behaviour can be attributed to compression waves emerging from the front of the mean separation bubble which is only present in case A2.

The flow features immediately downstream of the SBLI are surprisingly similar to the shock-train patterns found in rectangular turbulent ducts of small cross-sectional area. For example the time-averaged contours in figure 8 of Fiévet et al. (2017) show a similar type of alternating expansion-shock pattern. A triangular region of expansion is followed by a curved shock bounded by rapidly growing sidewall boundary layers. It is plausible that the shock-induced transition and subsequent thickening of the sidewall boundary layers in the present study leads to a reduction in cross-sectional area and the formation of a weak shock train. Furthermore, we note that the blue ‘shock-associated’ region in the time averaged contours of Fig. 5 is relatively thick in the streamwise direction. The width of this region suggests that this secondary shock structure is unsteady in time. To reinforce this conclusion Fig. 7 shows the instantaneous logarithm of density gradients \(\log _{10}\left( \nabla \rho ^2\right)\) for case A1 at a height of \(y=25\) above the bottom wall \(\left( \approx 0.15 L_y\right)\). At this height the secondary shock is observed as a thin region of high density gradients between \(x=625\) and \(x=650\). The secondary shock was visible in y planes up until a height of \(\left( \approx 0.5 L_y\right)\) but had no obvious origin. The secondary shock develops as a result of the sudden reduction in cross-sectional area as the flow transitions to turbulence after the SBLI in the lower half of the duct.

Fig. 7
figure 7

Instantaneous logarithm of density gradients \(\log _{10}\left( \nabla \rho ^2\right)\) between \(x=\left[ 450, 800\right]\) for case (A1) at a height of \(y=25\). Red regions correspond to areas of high density gradients showing the shock structure downstream of the SBLI

Full size image

A weaker feature in Fig. 5 is the wave pattern that crosses the centreline at \(x=700\). These crossing structures are a result of the narrow duct (Lusher and Sandham 2019) and would not be present in infinite span simulations. They are associated with shocks that are generated at the top of the domain where the sidewall flow is deflected by the shock generator ramp. The conical shock-waves propagate inwards towards the centreline and cause multiple lateral reflections across the span  (Lusher and Sandham 2019). In the skin friction curve of Fig. 6 (right) the effect of a more developed transition is clear for the fully forced case (A1). Near both sidewalls there is a rise in skin friction signifying that the transition has reached the centreline and is warding off mean flow separation. When only the sidewalls are tripped (A2), incipient centreline separation is reached. The peak in skin friction is about 10% higher in this case, indicating a more energetic breakdown process.

Fig. 8
figure 8

Instantaneous streamwise velocity snapshots above the bottom wall for the half aspect ratio case A2. The solid white line represents the \(u=0\) contour enclosing regions of recirculation. The central recirculation bubble shifts laterally due to oncoming intermittent turbulent spots

Full size image

To further elucidate the response of the central separation bubble to intermittent turbulence, a selection of instantaneous streamwise velocity snapshots are shown in Fig. 8. The snapshots cover one and a half flow-through times after the initial SBLI has formed. The case shown is the one with the unforced bottom wall (A2). The four figures are spaced at intervals of \(\varDelta t=400\), which each correspond to half a flow-through of the freestream. In the top image the transition is relatively symmetric about the centreline and a small region of recirculation is present. At \(t=400\) the transition is stronger on the upper \(z=87.5\) sidewall, pushing the recirculation bubble down towards the \(x=0\) sidewall. By \(t=800\) a corner separation has formed on the lower sidewall at \(x=500\), which is amplifying initial disturbances and causing a breakdown near the corner reattachment point of \(x=525\). At \(x=400\) a turbulent spot has just reached the front of the corner separation and starts interacting with the bubble. Finally by \(t=1200\) the corner separation has been fully removed. The increased mixing rate inside the turbulent spot transfers low-momentum fluid away from the wall. The central separation has contracted and shifts back towards the upper sidewall.

4.2 Aspect-Ratio One Duct

In this section the duct is widened to an aspect ratio of \(AR=1\) to observe how the lateral confinement influences the oblique SBLI. The grid resolution across the span is increased as in Table 1 to compensate for the increase in duct width. Figure 9 shows time-averaged skin friction contours on the bottom wall for cases B1 and B2. In contrast to the \(AR=0.5\) cases both of the \(AR=1\) ducts exhibit mean flow separation on the centreline. This strong dependence of aspect ratio on the SBLI is consistent with previous numerical (Lusher and Sandham 2019; Wang et al. 2015) and experimental (Xiang and Babinsky 2019) studies of confined oblique SBLI. When comparing the central separation bubble length for confined SBLI to span-periodic predictions with an infinitely-wide span, it has been shown (e.g. figure 20 of Xiang and Babinsky (2019), figure 16(a) of  Lusher and Sandham (2019)), that there is a weakened SBLI for narrower ducts \(\left( AR < 1\right)\). As the duct aspect ratio is increased, a stronger interaction is observed with larger regions of flow separation on the centreline. For larger ducts \(\left( AR \gg 2\right)\) the separation sizes reduce again and tend towards the infinite-span predictions. The same asymmetry is observed in the development of the transition front for case B2 as was seen in A2. In case B2 the initially laminar bottom wall leads to a substantially larger separation bubble compared to the forced case B1. For both of the aspect ratios it has been shown that tripping only the sidewalls is not sufficient when attempting to suppress the central flow separation. While case B1 still exhibits mean flow separation, the addition of upstream disturbances to the bottom wall has significantly reduced the extent of flow separation.

The secondary shock that was present in the \(AR=0.5\) case is not seen at \(AR=1\). Despite the same flow conditions and initial disturbances, reducing the lateral flow confinement has suppressed the formation of the structures seen in Fig. 5. Figure 10 shows the time-averaged centreline wall pressure and skin friction distributions at \(AR=1\). In the pressure plot we see the initial pressure rise from the SBLI starts further upstream for case (B2) where the bottom wall remains laminar. The same can be seen in the skin friction curve: the separation point moves much further upstream compared to case B1 despite both having a similar reattachment location. There is a more pronounced pressure plateau at \(x=525\) for case B2, which is characteristic of a laminar SBLI  (Katzer 1989). Similar to the \(AR=0.5\) case there is no mean flow separation in the corner regions, due to the onset of energetic mixing near the sidewalls. This is in contrast to laminar duct SBLI  (Lusher and Sandham 2019) and stronger-shock turbulent SBLI  (Wang et al. 2015), in which long thin corner separations develop.

Fig. 9
figure 9

Time averaged skin friction distributions on the bottom wall. For the cases of (top) forced sidewalls and bottom wall (B1) and (bottom) forced sidewalls only (B2). The dashed white line encloses regions of flow recirculation

Full size image
Fig. 10
figure 10

Time averaged centreline normalised pressure (left) and skin friction (right) on the bottom wall of the duct. For the \(AR=1\) cases of forced sidewalls and bottom wall (red)(B1) and forced sidewalls only (black)(B2)

Full size image
Fig. 11
figure 11

An \(x-z\) plane of instantaneous pressure at a height of \(y=105\) for \(AR=1\). The main incident shock is visible at \(x=450\) and is seen to be strengthened by compressions from both of the sidewalls. The sidewall compressions coalesce into shock-waves that cross at \(x=475\)

Full size image

Figure 11 shows an \(x-z\) plane of pressure evaluated at \(y=105\) for the \(AR=1\) case. The incident oblique shock is visible at \(x=450\) and is curved symmetrically about the centreline. A series of compression waves can be seen upstream of the main shock. These waves pass through and reinforce the incident shock. The compression waves coalesce into weak shock-waves and are observed to cross in this plane at \(x=475\). These features start at the intersection of the sidewall and shock generator ramp at the top of the domain and develop following a conical structure. The result is that there are two regions of the incident shock either side of the centreline that have been strengthened by the sidewall compressions. The crossing location is dependent on which y plane is being observed.

At \(x=710\) the expansion fan generated at the trailing edge of the shock generator is visible. Further downstream there is a shock that is skewed relative to the incident shock. The rotation of the shock is a consequence of the highly unsteady behaviour of the transitional SBLI. As was shown in Fig. 8, the central separation bubble reacts dynamically to oncoming turbulent spots. As the central separation bubble becomes distorted the reflected shock will change in magnitude and orientation. In Fig. 12a instantaneous pressure is shown for a \(z-y\) slice at \(x=450\) where the incident shock is at the same height as in Fig. 11. The two crossing shocks discussed in connection with Fig. 11 correspond to the high pressure regions above the incident shock-wave, with a clear conical form. These conical shocks are the ones that originate in both of the upper corners of the duct as the flow is deflected by the shock generator plate.

Fig. 12
figure 12

a A \(z-y\) plane of instantaneous pressure evaluated at a streamwise location of \(x=450\) for \(AR=1\). Two high pressure regions are observed that originate from the upper corners of the duct at the start of the shock generator. b Dilatation rate \(\left( \nabla \cdot {\mathbf {u}} \right)\) at a height of \(y=105\) for \(AR=1\). Negative and positive regions of dilatation correspond to shock-waves and expansions respectively. c Turbulent kinetic energy at a height of \(y=105\) for \(AR=1\). The sonic line \(\left( M=1\right)\) is shown in dashed black

Full size image
Fig. 13
figure 13

Streamwise pressure profiles at a height of \(y=105\) for (left) \(z=20\) and (right) \(z=87.5\) at \(AR=1\), normalised by the inlet pressure. Near the sidewall \(\left( z=20\right)\) there is an expansion directly after the incident shock. At \(x=475\) on the centreline \(\left( z=87.5\right)\) the crossing point in Fig. 11 is observed as a pressure peak downstream of the incident shock

Full size image

At both sidewalls there are low pressure regions similar to those observed in Fig. 11. Figure 12b shows dilatation rates \(\left( \nabla \cdot {\mathbf {u}} \right)\) for the incident shock near the sidewall at a height of \(y=105\). Expansion fans and shock-waves are characterised by regions of positive (red) and negative (blue) dilatation respectively (Johnsen et al. 2010). The incident shock is curved upstream near the sidewall and is weakened relative to the shock closer to the centreline. Above the sidewall boundary layer there is a small region of expansion as the boundary layer thickens due to the swept sidewall SBLI. Figure 12c shows that the boundary layer rapidly transitions in this region due to upstream disturbances being amplified by the shock-wave. No significant streamwise vorticity generation was observed in these regions.

Streamwise pressure profiles at a height of \(y=105\) are shown in Fig. 13 at span-wise locations (left) \(z=20\) and (right) \(z=87.5\). Between \(x=350\) and \(x=450\) in Fig. 13 (left) there is a steady pressure rise resulting from the sidewall compression waves seen previously in Fig. 11. There is a well-defined discontinuity at the incident shock-wave, followed by a pressure reduction from the sidewall expansion. At the centreline, Fig. 13 (right) shows a stronger incident shock compared to the one at \(z=20\) and no initial pressure rise from sidewall compressions. Furthermore, there is a pressure peak at \(x=475\) corresponding to the crossing of conical structures highlighted in Fig. 11. Differences are also observed between the two forcing configurations downstream of the main interaction due to the unsteady nature of the transitional SBLI, with a delayed pressure rise near \(x=600\) for the case where all of the walls are tripped.

Fig. 14
figure 14

A 3D view of the \(AR=1\) duct for case B2 cut along the \(z=L_z/2\) centreline. Showing time-averaged density contours of the main shock structures within the duct

Full size image

Finally, a three-dimensional view of the shock system is shown in the time-averaged density contours of Fig. 14 for case B2. Half of the duct is shown up to the \(z=L_z/2\) centreline. The corner shock front is observed as the orange region originating from the intersection of the sidewall and upper shock-generator ramp. This corresponds to the crossing structures highlighted in the plane view of Fig. 11. Simulations of SBLI with an infinite-span approximation are unable to capture these three-dimensional effects caused by sidewall flow confinement. Upstream of the incident shockwave, a curved contour surface is observed at the sidewall due to the swept sidewall SBLI. Downstream of the main interaction, the reflected shock can be seen to exit through the computational outlet after interacting with the trailing edge expansion fan at \(x=650\).

5 Conclusions

Oblique shock-wave/boundary-layer interactions (SBLI) have been simulated for a half aspect-ratio rectangular duct at Mach 2. Disturbances were added to a laminar flow via blowing/suction caused intermittent turbulent spots that originated in the low-momentum corners of the duct. The transition spread out in a wedge shape across the width of the span. A pair of conical shock-structures form at the swept sidewall SBLIs and reflect laterally within the duct. Their origin and the height dependence of the crossing point was demonstrated. For a half-aspect ratio case, with disturbances added to both the side and bottom walls, incipient mean separation was not reached for a \(\theta _{sg} = 5.0^{\circ }\) shock generator. When the bottom wall was kept initially laminar a region of shock-induced mean flow recirculation was observed on the centreline. Instantaneous snapshots of the near-wall streamwise velocity showed that the recirculation bubble reacts dynamically to oncoming turbulent spots. Temporary corner separations were seen to develop that caused an earlier streamwise destabilisation of the downstream flow.

A wider aspect-ratio one case was simulated to assess the effect of flow confinement. Both forcing configurations exhibited central mean flow separation. The separation bubble was largest for a case where the bottom wall was kept initially laminar. The strengthened interaction at \(AR=1\) was consistent with previous studies. The orientation of the reflected shock was shown to be skewed due to the unsteady response of the separation bubble to intermittent turbulent spots. For the narrower \(AR=0.5\) cases an additional secondary shock was observed downstream of the interaction. It was attributed to the start of a weak shock train caused by the reducing duct cross-sectional area. A low pressure region was observed on the sidewalls and shown to be related to the transitional behaviour near the sidewall shock. At \(AR=1\) the secondary shock was not observed. The shock structures downstream of the initial SBLI were shown to be highly unsteady in time and influenced by the level of transition on the sidewalls.

The simulations in this work have investigated the effect of duct aspect ratio and upstream boundary-layer state on transitional SBLI, which were identified as two of the critical factors influencing the interaction. Additional parameters such as Reynolds number, shock generator length, and incident shock strength were held fixed in this study. A more systematic parametric study for transitional duct SBLI would be needed to account for these factors. Future work should also include an investigation of the wall-pressure time-series snapshots, to extract the characteristic frequencies present in a transitional duct SBLI. Furthermore, the current study has applied an implicit-LES approach via TENO schemes  (Fu et al. 2019), to focus on the large-scale dynamics of confined shock-induced separation bubbles in the presence of intermittent upstream turbulence. While the location of the sharp \(C_f\) increase at \(x=600\) on the centreline due to the transition was shown to be consistent between two grid resolutions, future DNS studies would be useful to provide fully-resolved data of the small-scale flow structures. While the present contribution has investigated different tripping locations on the flow, a future study with symmetric forcing could be performed to address the asymmetry observed in this work.