Transition from inspiral to plunge into a highly spinning black hole

In the following we consider the probe angular momentum $\ell =\frac{L}{\mu M}$ per unit probe mass μ and rescaled by the central black hole mass M, and the probe energy ${\sim}{e}=\frac{E}{\mu }$ per unit probe mass with respect to the Boyer–Lindquist asymptotic timelike Killing vector ${\partial }_{{\sim}{t}}$. We denote as ${\sim}{r}=r/M$ the adimensional Boyer–Lindquist radial coordinate of Kerr, ã = a/M and the near-extremality parameter $\lambda =\sqrt{1-{\tilde{a}}^{2}}$.

Following Ori–Thorne [6] and subsequent work, we assume the following three simplifying hypotheses:

• The decrease rate of probe angular momentum ℓ per unit dimensionless proper time τ (proper time divided by M) is equal to the rate of a probe on a circular orbit at the ISCO.
• We neglect the radial self-force.
• The proper time ticks as along a circular orbit.

The first hypothesis is equivalent to a linear decay rate of the probe angular momentum,

$$\begin{equation}\ell \left(\tau \right)={\ell }_{{\ast}}-{\kappa }_{{\ast}}\eta \left(\tau -{\tau }_{{\ast}}\right),\quad {\kappa }_{{\ast}}\equiv \frac{8{\sigma }_{{\ast}}}{\sqrt{3}}.\end{equation} \tag{ 1 }$$

Here ℓ_* is the probe angular momentum per unit Mμ at the ISCO, η is the mass ratio, σ_* = σ_∗,∞ + σ_∗,H is a constant determined by the total angular momentum flux emitted from a circular orbit at the ISCO reaching infinity and the horizon, and τ_* is the proper time at which one would reach ℓ = ℓ_*. For the Schwarzschild black hole, σ_* ≈ 0.004 [6] while in the extremely high spin limit [23],

$$\begin{equation}{\sigma }_{{\ast},\infty }\approx 0.987,\quad {\sigma }_{{\ast},H}\approx -0.133.\end{equation} \tag{ 2 }$$

The limitations of the second hypothesis were discussed in [32].

During the transition, we do not assume quasi-circularity, as it was shown to be inconsistent [12]. In [6] the decrease rate of probe energy per proper time was fixed in terms of the corresponding decrease of probe angular momentum after assuming quasi-circularity. Here, the decrease rate of probe energy is fixed by requirement that a potential exists for the radial motion. More precisely, assuming no radial self-force, the first and second order radial geodesic equations take the form

$$\begin{equation}{\left(\frac{\mathrm{d}{\sim}{r}}{\mathrm{d}\tau }\right)}^{2}={{\sim}{e}}^{2}-{\sim}{V}\left({\sim}{r},{\sim}{e},\ell \right),\end{equation} \tag{ 3 }$$

$$\begin{equation}\frac{{\mathrm{d}}^{2}{\sim}{r}}{\mathrm{d}{\tau }^{2}}=-\frac{1}{2}\frac{\partial {\sim}{V}\left({\sim}{r},{\sim}{e},\ell \right)}{\partial {\sim}{r}},\end{equation} \tag{ 4 }$$

where the radial potential is given by

$$\begin{equation}{\sim}{V}\left({\sim}{r},{\sim}{e},\ell \right)=1-\frac{2}{{\sim}{r}}-\frac{2{\left(\ell -\tilde{a}{\sim}{e}\right)}^{2}}{{{\sim}{r}}^{3}}-\frac{{\tilde{a}}^{2}\left({{\sim}{e}}^{2}-1\right)-{\ell }^{2}}{{{\sim}{r}}^{2}}.\end{equation} \tag{ 5 }$$

These equations are compatible given the following constraint equation is obeyed

$$\begin{equation}\frac{\mathrm{d}{\sim}{e}}{\mathrm{d}\tau }\frac{\partial \left({\sim}{V}-{{\sim}{e}}^{2}\right)}{\partial {\sim}{e}}+\frac{\mathrm{d}\ell }{\mathrm{d}\tau }\frac{\partial {\sim}{V}}{\partial \ell }=0.\end{equation} \tag{ 6 }$$

We impose it as the evolution of the probe energy after substituting (1),

$$\begin{equation}\frac{\mathrm{d}{\sim}{e}}{\mathrm{d}\tau }={\kappa }_{{\ast}}\eta \frac{\partial {\sim}{V}/\partial \ell }{\partial \left({\sim}{V}-{{\sim}{e}}^{2}\right)/\partial {\sim}{e}}.\end{equation} \tag{ 7 }$$

In order to describe the transition around the ISCO we define the deviation variables

$$\begin{equation}{\sim}{R}\equiv {\sim}{r}-{{\sim}{r}}_{{\ast}},\end{equation} \tag{ 8 }$$

$$\begin{equation}\chi \equiv {{\sim}{{\Omega}}}_{{\ast}}^{-1}\left({\sim}{e}-{{\sim}{e}}_{{\ast}}\right),\end{equation} \tag{ 9 }$$

$$\begin{equation}\xi \equiv \ell -{\ell }_{{\ast}},\end{equation} \tag{ 10 }$$

where all quantities ${{\sim}{r}}_{{\ast}}$, ${{\sim}{{\Omega}}}_{{\ast}}$, _*, ℓ_* at the ISCO are detailed in appendix. At the ISCO, we have

$$\begin{equation}\frac{{\partial }^{2}{\sim}{V}}{\partial {{\sim}{r}}^{2}}{\vert }_{{\ast}}={{\sim}{e}}_{{\ast}}-\frac{1}{2}\frac{\partial {\sim}{V}}{\partial {\sim}{e}}{\vert }_{{\ast}}-\frac{1}{2}{{\sim}{{\Omega}}}_{{\ast}}^{-1}\frac{\partial {\sim}{V}}{\partial \ell }{\vert }_{{\ast}}=0.\end{equation} \tag{ 11 }$$

We now Taylor expand the potential 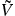at order $O\left({{\sim}{R}}^{4}\right)$ and we truncate to linear order in the deviation parameters ξ, χ. The radial equation (3) and energy evolution equation (7) become

$$\begin{align}\hfill \frac{{\mathrm{d}}^{2}{\sim}{R}}{\mathrm{d}{\tau }^{2}}& =-{\alpha }_{{\ast}}{{\sim}{R}}^{2}+\left({\gamma }_{{\ast}}{\sim}{R}+{\beta }_{{\ast}}\right)\xi -\frac{1}{2}\left(\chi -\xi \right)\left[{c}_{{\ast}}{\sim}{R}+{d}_{{\ast}}\right],\hfill \\ \hfill \frac{\mathrm{d}\left(\chi -\xi \right)}{\mathrm{d}\tau }& ={\kappa }_{{\ast}}\eta \frac{{\gamma }_{{\ast}}{{\sim}{R}}^{2}+2{\beta }_{{\ast}}{\sim}{R}}{-\frac{1}{2}{c}_{{\ast}}{{\sim}{R}}^{2}-{d}_{{\ast}}{\sim}{R}+{\delta }_{{\ast}}},\hfill \end{align} \tag{ 12 }$$

where the Taylor coefficients are defined as

$$\begin{equation}{\alpha }_{{\ast}}=\frac{1}{4}\frac{{\partial }^{3}{\sim}{V}}{\partial {{\sim}{r}}^{3}}{\vert }_{{\ast}},\quad {c}_{{\ast}}={\sim}{{\Omega}}\frac{{\partial }^{3}{\sim}{V}}{\partial {{\sim}{r}}^{2}\partial {\sim}{e}}{\vert }_{{\ast}},\end{equation} \tag{ 13 }$$

$$\begin{equation}{\beta }_{{\ast}}=-\frac{1}{2}\left(\frac{{\partial }^{2}{\sim}{V}}{\partial {\sim}{r}\partial \ell }+{\sim}{{\Omega}}\frac{{\partial }^{2}{\sim}{V}}{\partial {\sim}{r}\partial {\sim}{e}}\right){\vert }_{{\ast}},\quad {d}_{{\ast}}={\sim}{{\Omega}}\frac{{\partial }^{2}{\sim}{V}}{\partial {\sim}{r}\partial {\sim}{e}}{\vert }_{{\ast}},\end{equation} \tag{ 14 }$$

$$\begin{equation}{\gamma }_{{\ast}}=-\frac{1}{2}\left(\frac{{\partial }^{3}{\sim}{V}}{\partial {{\sim}{r}}^{2}\partial \ell }+{\sim}{{\Omega}}\frac{{\partial }^{3}{\sim}{V}}{\partial {{\sim}{r}}^{2}\partial {\sim}{e}}\right){\vert }_{{\ast}},\quad {\delta }_{{\ast}}=\frac{\partial {\sim}{V}}{\partial \ell }{\vert }_{{\ast}}.\end{equation} \tag{ 15 }$$

These equations govern the transition around the ISCO for arbitrary spins. We will check below that all terms neglected in this Taylor expansion asymptote to zero in an appropriate region around the ISCO.

The observation of Ori–Thorne [6] and Kesden [12] is that for standard spins the transition equation (12) are consistent with the scaling

$$\begin{equation}\tau -{\tau }_{{\ast}}\sim {\eta }^{-1/5},\quad {\sim}{R}\sim {\eta }^{2/5},\quad \chi \sim \xi \sim {\eta }^{4/5},\quad \chi -\xi \sim {\eta }^{6/5}.\end{equation} \tag{ 16 }$$

Assuming that scaling, the Taylor terms multiplying γ_*, c_* and d_* are subleading in the small mass ratio limit η → 0 and can be neglected. At leading order in η the equations reduce to

$$\begin{equation}\frac{{\mathrm{d}}^{2}{\sim}{R}}{\mathrm{d}{\tau }^{2}}=-{\alpha }_{{\ast}}{{\sim}{R}}^{2}-{\kappa }_{{\ast}}\eta {\beta }_{{\ast}}\left(\tau -{\tau }_{{\ast}}\right),\end{equation} \tag{ 17 }$$

$$\begin{equation}\frac{\mathrm{d}\left(\chi -\xi \right)}{\mathrm{d}\tau }=2{\kappa }_{{\ast}}\eta \frac{{\beta }_{{\ast}}}{{\delta }_{{\ast}}}{\sim}{R},\end{equation} \tag{ 18 }$$

after using (1). One can set these equations in normalized form including the order of the subleading correction

$$\begin{equation}\frac{{\mathrm{d}}^{2}X}{\mathrm{d}{t}^{2}}=-{X}^{2}-t+O\left({\eta }^{2/5}\right),\quad \frac{\mathrm{d}Y}{\mathrm{d}t}=2X+O\left({\eta }^{2/5}\right),\end{equation} \tag{ 19 }$$

after defining

$$\begin{equation}{\sim}{R}=\frac{{\left({\beta }_{{\ast}}{\kappa }_{{\ast}}\eta \right)}^{2/5}}{{\alpha }_{{\ast}}^{3/5}}X\left(t\right),\end{equation} \tag{ 20 }$$

$$\begin{equation}\tau ={\tau }_{{\ast}}+{\left({\alpha }_{{\ast}}{\beta }_{{\ast}}{\kappa }_{{\ast}}\eta \right)}^{-1/5}t,\end{equation} \tag{ 21 }$$

$$\begin{equation}\chi -\xi =\frac{{\left({\beta }_{{\ast}}{\kappa }_{{\ast}}\eta \right)}^{6/5}}{{\alpha }_{{\ast}}^{4/5}{\delta }_{{\ast}}}Y\left(t\right).\end{equation} \tag{ 22 }$$

By construction, these equations are consistent with the first order radial equation

$$\begin{equation}{\left(\frac{\mathrm{d}X}{\mathrm{d}t}\right)}^{2}=-\frac{2}{3}{X}^{2}-2Xt+Y+O\left({\eta }^{2/5}\right).\end{equation} \tag{ 23 }$$

The first equation of (19) is the Ori–Thorne equation. We identify it here as the Painlevé transcendent equation of the first kind. It is a typical equation in bifurcation phenomena [33]. We will also relate it to the KdV equation (58) later on. It admits a monotonous solution with zero acceleration (d²X/dt² = 0) at t → −∞ given by

$$\begin{equation}X=\sqrt{-t}+\frac{1}{8{t}^{2}}+O\left({t}^{-9/2}\right)+O\left({\eta }^{2/5}\right).\end{equation} \tag{ 24 }$$

The derivation of the equation (19) assumed the scaling (16) and assumed η → 0 with all independent quantities of order unity. However, in the high spin limit, another small parameter exists: $\lambda =\sqrt{1-{\tilde{a}}^{2}}\to 0$. It turns out that the relevant scalings and equations differ depending whether η ≫ λ or λ ≪ η as we now detail.

In the high spin limit, the Taylor coefficients are given up to O(λ^4/3) corrections by

$$\begin{align}\hfill {\alpha }_{{\ast}}& =1-4\cdot {2}^{1/3}{\lambda }^{2/3}, {c}_{{\ast}}=6\sqrt{3}\left(1-\frac{61}{12}\cdot {2}^{1/3}{\lambda }^{2/3}\right),\hfill \\ \hfill {\beta }_{{\ast}}& =\frac{\sqrt{3}{\lambda }^{2/3}}{{2}^{2/3}}, {d}_{{\ast}}=-\frac{4}{\sqrt{3}}\left(1-\frac{17}{4}\cdot {2}^{1/3}{\lambda }^{2/3}\right),\hfill \\ \hfill {\gamma }_{{\ast}}& =\sqrt{3}\left(1-\frac{19}{2}\frac{{\lambda }^{2/3}}{{2}^{2/3}}\right),\quad {\delta }_{{\ast}}=\frac{4\cdot {2}^{1/3}}{\sqrt{3}}{\lambda }^{2/3}.\hfill \end{align} \tag{ 25 }$$

Assuming the scaling (16), the equations of motion are given at leading order in λ and η by the high spin limit of the Ori–Thorne–Kesden equations

$$\begin{equation}\frac{{\mathrm{d}}^{2}{\sim}{R}}{\mathrm{d}{\tau }^{2}}=-{{\sim}{R}}^{2}-\frac{\sqrt{3}}{{2}^{2/3}}{\kappa }_{{\ast}}\eta {\lambda }^{2/3}\left(\tau -{\tau }_{{\ast}}\right),\end{equation} \tag{ 26 }$$

$$\begin{equation}\frac{\mathrm{d}\left(\chi -\xi \right)}{\mathrm{d}\tau }=2\sqrt{3}{\sigma }_{{\ast}}\eta {\sim}{R}.\end{equation} \tag{ 27 }$$

We will now reformulate these equations. Remember that in the high spin regime, the Kerr metric can be written close to the ISCO as the near-horizon extreme Kerr (NHEK) metric with O(λ^1/3) corrections [18], see [25, 34, 35] for reviews:

$$\begin{equation}\mathrm{d}{s}^{2}={M}^{2}\left(1+{\mathrm{cos}}^{2}\;\theta \right)\left(-{R}_{\mathrm{N}}^{2}\mathrm{d}{T}_{\mathrm{N}}^{2}+\frac{\mathrm{d}{R}_{\mathrm{N}}^{2}}{{R}_{\mathrm{N}}^{2}}+\mathrm{d}{\theta }^{2}\right.\left.+\frac{4{\mathrm{sin}}^{2}\;\theta }{{\left(1+{\mathrm{cos}}^{2}\;\theta \right)}^{2}}{\left(\mathrm{d}{{\Phi}}_{\mathrm{N}}+{R}_{\mathrm{N}}\mathrm{d}{T}_{\mathrm{N}}\right)}^{2}\right)+O\left({\lambda }^{1/3}\right).\end{equation} \tag{ 28 }$$

The near-horizon coordinates (T_N, R_N, θ, Φ_N) are related to the Boyer–Lindquist coordinates $\left({\sim}{t},{\sim}{r},\theta ,{\sim}{\phi }\right)$ by

$$\begin{equation}{\sim}{t}=2M{\lambda }^{-2/3}{T}_{\mathrm{N}},\end{equation} \tag{ 29 }$$

$$\begin{equation}{\sim}{r}=1+{\lambda }^{2/3}{R}_{\mathrm{N}},\end{equation} \tag{ 30 }$$

$$\begin{equation}{\sim}{\phi }={{\Phi}}_{\mathrm{N}}+{\lambda }^{-2/3}{T}_{\mathrm{N}}.\end{equation} \tag{ 31 }$$

The ISCO is located at ${R}_{\mathrm{N}}={R}_{\mathrm{N}}^{{\ast}}\equiv {2}^{1/3}+O\left({\lambda }^{1/3}\right)$. The NHEK energy e_N and radius R_N are therefore related to the asymptotically flat energy and Boyer–Lindquist radius as

$$\begin{align}\hfill {\sim}{R}& =\left({R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\right){\lambda }^{2/3},\hfill \\ \hfill {\sim}{e}& =\frac{\ell }{2}+\frac{{\lambda }^{2/3}}{2}{e}_{\mathrm{N}}.\hfill \end{align} \tag{ 32 }$$

This implies

$$\begin{equation}\chi -\xi =\left({e}_{\mathrm{N}}+\frac{3}{4}{2}^{1/3}\xi \right){\lambda }^{2/3}.\end{equation} \tag{ 33 }$$

In terms of the NHEK radius and energy, the high spin Ori–Thorne–Kesden equations can be therefore reformulated as

$$\begin{equation}\frac{{\mathrm{d}}^{2}{R}_{\mathrm{N}}}{\mathrm{d}{\tau }^{2}}=-{\lambda }^{2/3}{\left({R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\right)}^{2}-4{\times}{2}^{1/3}{\sigma }_{{\ast}}\eta \left(\tau -{\tau }_{{\ast}}\right),\end{equation} \tag{ 34 }$$

$$\begin{equation}\frac{\mathrm{d}{e}_{\mathrm{N}}}{\mathrm{d}\tau }=2\sqrt{3}{\sigma }_{{\ast}}\eta {R}_{\mathrm{N}}.\end{equation} \tag{ 35 }$$

So far, we obtained these equations assuming the original scaling (16). More generally, in the presence of a small parameter λ in addition to η, we need to specify how η scales with λ. We define such that

$$\begin{equation}\eta \sim {\lambda }^{1+{\epsilon}}.\end{equation} \tag{ 36 }$$

There are three possible cases:

• Standard high spin: η ≪ λ ( > 0);
• Marginal high spin: η ∼ λ ( = 0);
• Extremely high spin: λ ≪ η (−1 < < 0).

In standard astrophysical settings, the spin obeys the Thorne bound λ > 0.06 while η can be extremely small for extreme mass ratio inspirals. It is therefore natural to consider the standard high spin scaling in order to model astrophysical scenarios. When → ∞, we will recover the Ori–Thorne–Kesden equations as we will detail below. For > 0 finite, we can substitute the coefficients (25) and the redefinition (33) into (12). In order to take the limit λ → 0 of (12) we need to specify the scaling of R_N, e_N and τ in terms of η. The scaling of ξ is then deduced from (1). We find that the equations (34) and (35) are invariant under the following scaling

$$\begin{equation}\tau -{\tau }_{{\ast}}\sim {\eta }^{-\frac{1}{5}-\frac{2}{15\left(1+{\epsilon}\right)}},\end{equation} \tag{ 37a }$$

$$\begin{equation}{R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\sim {\eta }^{\frac{2}{5}-\frac{2}{5\left(1+{\epsilon}\right)}},\end{equation} \tag{ 37b }$$

$$\begin{equation}{e}_{\mathrm{N}}\sim \xi \sim {\eta }^{\frac{4}{5}-\frac{2}{15\left(1+{\epsilon}\right)}},\end{equation} \tag{ 37c }$$

$$\begin{equation}{e}_{\mathrm{N}}+\frac{3}{4}{2}^{1/3}\xi \sim {\eta }^{\frac{6}{5}-\frac{8}{15\left(1+{\epsilon}\right)}}.\end{equation} \tag{ 37d }$$

We now check that (34) and (35) can be also obtained from the full equations (4) and (7) using the scaling (36) and (37). This justifies the neglected terms in the Taylor expansion (12). The Ori–Thorne scaling (16) is recovered in the limit → ∞. We have therefore obtained the Ori–Thorne-Kesden equations in the presence of two small parameters η, λ assuming η ≪ λ.

We found that the scaling (37) applies for all > 0. In the marginal high spin case = 0 of (36), namely η ∼ λ, we also find that the scaling solution (37) holds. It reads explicitly as

$$\begin{equation}\tau -{\tau }_{{\ast}}\sim {\eta }^{-1/3},\quad {R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\sim {\eta }^{0},\quad {e}_{\mathrm{N}}\sim \xi \sim {\eta }^{2/3},\end{equation} \tag{ 38 }$$

or, equivalently,

$$\begin{equation}\tau -{\tau }_{{\ast}}\sim {\eta }^{-1/3},\quad {\sim}{R}\sim {\eta }^{2/3},\quad \chi -\xi \sim {\eta }^{4/3}.\end{equation} \tag{ 39 }$$

The energy equation (35) is unchanged while the radial equation (invariant under (38)) gets modified to the 'marginal extremely high spin radial transition equation'

$$\begin{equation}\frac{{\mathrm{d}}^{2}{R}_{\mathrm{N}}}{\mathrm{d}{\tau }^{2}}=-{\lambda }^{2/3}{\left({R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\right)}^{2}-8{\sigma }_{{\ast}}\eta \left(\tau -{\tau }_{{\ast}}\right){R}_{\mathrm{N}}+\frac{2}{\sqrt{3}}{e}_{\mathrm{N}}.\end{equation} \tag{ 40 }$$

In the extremely high spin case λ ≪ η (−1 < < 0), we find that the scaling (39) remains consistent. It can also be written as

$$\begin{equation}\tau -{\tau }_{{\ast}}\sim {\eta }^{-\frac{1}{3}},\quad {R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\sim {\eta }^{\frac{2}{3}-\frac{2}{3\left(1+{\epsilon}\right)}},\quad {e}_{\mathrm{N}}\sim {\eta }^{\frac{4}{3}-\frac{2}{3\left(1+{\epsilon}\right)}},\quad \xi \sim {\eta }^{\frac{2}{3}}.\end{equation} \tag{ 41 }$$

The radial evolution is now governed by the 'extremely high spin radial transition equation'

$$\begin{equation}\frac{{\mathrm{d}}^{2}{R}_{\mathrm{N}}}{\mathrm{d}{\tau }^{2}}=-{\lambda }^{2/3}{\left({R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\right)}^{2}+4\eta {\sigma }_{{\ast}}\left(\tau -{\tau }_{{\ast}}\right){R}_{\mathrm{N}}^{{\ast}}-8{\sigma }_{{\ast}}\eta \left(\tau -{\tau }_{{\ast}}\right){R}_{\mathrm{N}}+\frac{2}{\sqrt{3}}{e}_{\mathrm{N}},\end{equation} \tag{ 42 }$$

and the equation of motion for the energy is still

$$\begin{equation}\frac{\mathrm{d}{e}_{\mathrm{N}}}{\mathrm{d}\tau }=2\sqrt{3}{\sigma }_{{\ast}}\eta {R}_{\mathrm{N}}.\end{equation} \tag{ 43 }$$

We checked that these equations can be also obtained from the full equations (4) and (7) using the scaling (41), which justifies the neglected terms in the Taylor expansion (12).

The extremely high spin radial transition equation (42) together with the energy equation (43) can only be partly recovered from the NHEK geometry. If we assume the more restricted scaling regime (that probes a smaller range around the ISCO)

$$\begin{equation}\tau -{\tau }_{{\ast}}\sim {\eta }^{-1/3},\quad {R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\sim {\eta }^{0},\quad {e}_{\mathrm{N}}\sim {\eta }^{2/3},\quad \xi \sim {\eta }^{2/3},\end{equation} \tag{ 44 }$$

the energy equation remains unchanged while the radial equation (42) simplifies to the 'NHEK transition equation'

$$\begin{equation}\frac{{\mathrm{d}}^{2}{R}_{\mathrm{N}}}{\mathrm{d}{\tau }^{2}}=-8{\sigma }_{{\ast}}\eta \left(\tau -{\tau }_{{\ast}}\right){R}_{\mathrm{N}}+\frac{2}{\sqrt{3}}{e}_{\mathrm{N}}.\end{equation} \tag{ 45 }$$

This equation can be obtained from NHEK as we now show. Since λ ≪ η, we can take the formal limit λ → 0 first and the O(λ^1/3) corrections to the NHEK geometry (28) are negligible. In the NHEK geometry, the radial geodesic equations read as

$$\begin{equation}{\left(\frac{\mathrm{d}{R}_{\mathrm{N}}}{\mathrm{d}\tau }\right)}^{2}={e}_{\mathrm{N}}^{2}-{V}_{\mathrm{N}}\left({R}_{\mathrm{N}},{e}_{\mathrm{N}},\ell \right),\end{equation} \tag{ 46 }$$

$$\begin{equation}\frac{{\mathrm{d}}^{2}{R}_{\mathrm{N}}}{\mathrm{d}{\tau }^{2}}=-\frac{1}{2}\frac{\partial {V}_{\mathrm{N}}\left({R}_{\mathrm{N}},{e}_{\mathrm{N}},\ell \right)}{\partial {R}_{\mathrm{N}}},\end{equation} \tag{ 47 }$$

where e_N = 2λ^−2/3 − λ^−2/3ℓ is the energy per unit probe mass per unit mass M associated with ${\partial }_{{T}_{\mathrm{N}}}$. Here the radial potential takes a simple exact form,

$$\begin{equation}{V}_{\mathrm{N}}\left({R}_{\mathrm{N}},{e}_{\mathrm{N}},\ell \right)=-2{e}_{\mathrm{N}}\ell {R}_{\mathrm{N}}+\left(1-\frac{3}{4}{\ell }^{2}\right){R}_{\mathrm{N}}^{2}.\end{equation} \tag{ 48 }$$

These equations are compatible given the following constraint equation is obeyed

$$\begin{equation}\frac{\mathrm{d}{e}_{\mathrm{N}}}{\mathrm{d}\tau }\frac{\partial \left({V}_{\mathrm{N}}-{e}_{\mathrm{N}}^{2}\right)}{\partial {e}_{\mathrm{N}}}+\frac{\mathrm{d}\ell }{\mathrm{d}\tau }\frac{\partial {V}_{\mathrm{N}}}{\partial \ell }=0.\end{equation} \tag{ 49 }$$

Up to O(λ^1/3) corrections, the evolution equations are therefore given by

$$\begin{equation}\frac{{\mathrm{d}}^{2}{R}_{\mathrm{N}}}{\mathrm{d}{\tau }^{2}}={e}_{\mathrm{N}}\ell +\left(\frac{3}{4}{\ell }^{2}-1\right){R}_{\mathrm{N}},\end{equation} \tag{ 50 }$$

$$\begin{equation}\frac{\mathrm{d}{e}_{\mathrm{N}}}{\mathrm{d}\tau }={\kappa }_{{\ast}}\eta {R}_{\mathrm{N}}\frac{{e}_{\mathrm{N}}+\frac{3}{4}\ell {R}_{\mathrm{N}}}{{e}_{\mathrm{N}}+\ell {R}_{\mathrm{N}}}.\end{equation} \tag{ 51 }$$

The ISCO has energy, angular momentum and radius ${e}_{\mathrm{N}}={e}_{\mathrm{N}}^{{\ast}}\equiv 0$, $\ell ={\ell }^{{\ast}}\equiv \frac{2}{\sqrt{3}}+O\left({\lambda }^{2/3}\right)$ and ${R}_{\mathrm{N}}={R}_{\mathrm{N}}^{{\ast}}\equiv {2}^{1/3}$. In the linear approximation in e, ℓ around the ISCO values and using (1), we finally obtain the NHEK transition equations (43)–(45).

It is important to note that we cannot obtain either (34), (40) nor (42) from motion in the NHEK geometry since the subleading corrections in λ play a key role in the evolution. This points to a limitation of the near-horizon methods that use only the leading order near-horizon geometry (28). In this case, we can only recover a small subregion of the dynamics (42) when λ ≪ η.

Let us finally discuss the solutions to the equations (40), (42) and (45). The NHEK transition equations can be easily solved analytically. Taking the derivative of (45) with respect to proper time and substituting (43) we obtain the closed-form normalized third-order equation

$$\begin{equation}\frac{{\mathrm{d}}^{3}{R}_{\mathrm{N}}}{\mathrm{d}{t}^{3}}+\left(t-{t}_{{\ast}}\right)\frac{\mathrm{d}{R}_{\mathrm{N}}}{\mathrm{d}t}+\frac{1}{2}{R}_{\mathrm{N}}=0,\end{equation} \tag{ 52 }$$

after defining the rescaled time as $t={\left(8{\sigma }_{{\ast}}\eta \right)}^{1/3}\tau$, ${t}_{{\ast}}={\left(8{\sigma }_{{\ast}}\eta \right)}^{1/3}{\tau }_{{\ast}}$. This equation admits analytic solutions in terms of Airy functions

$$\begin{equation}{R}_{\mathrm{N}}={c}_{1}\text{Ai}{\left(\frac{{t}_{{\ast}}-t}{{2}^{2/3}}\right)}^{2}+{c}_{2}\text{Ai}\left(\frac{{t}_{{\ast}}-t}{{2}^{2/3}}\right)\text{Bi}\left(\frac{{t}_{{\ast}}-t}{{2}^{2/3}}\right)+{c}_{3}\text{Bi}{\left(\frac{{t}_{{\ast}}-t}{{2}^{2/3}}\right)}^{2},\end{equation} \tag{ 53 }$$

with three real integration constants c₁, c₂, c₃. Despite this simplicity and the fact that it can be recovered from NHEK, we will see later that (45) cannot be connected to a quasi-circular inspiral and, more fundamentally, the scaling regime where λ ≪ η is unphysical due to backreaction on the spin of the black hole.

Less obvious is that (40) relates to a well known, integrable nonlinear differential equation. With the same procedure as before, combining (40), (43) gives

$$\begin{equation}\frac{{\mathrm{d}}^{3}{R}_{\mathrm{N}}}{\mathrm{d}{t}^{3}}+\frac{1}{2}{\left(\frac{\lambda }{{\sigma }_{{\ast}}\eta }\right)}^{2/3}\left({R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\right)\frac{\mathrm{d}{R}_{\mathrm{N}}}{\mathrm{d}t}+\left(t-{t}_{{\ast}}\right)\frac{\mathrm{d}{R}_{\mathrm{N}}}{\mathrm{d}t}+\frac{1}{2}{R}_{\mathrm{N}}=0.\end{equation} \tag{ 54 }$$

Similarly, for λ ≪ η, combining (42), (43), one finds instead

$$\begin{equation}\frac{{\mathrm{d}}^{3}{R}_{\mathrm{N}}}{\mathrm{d}{t}^{3}}+\frac{1}{2}{\left(\frac{\lambda }{{\sigma }_{{\ast}}\eta }\right)}^{2/3}\left({R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\right)\frac{\mathrm{d}{R}_{\mathrm{N}}}{\mathrm{d}t}+\left(t-{t}_{{\ast}}\right)\frac{\mathrm{d}{R}_{\mathrm{N}}}{\mathrm{d}t}+\frac{1}{2}\left({R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}\right)=0.\end{equation} \tag{ 55 }$$

We will continue the analysis only for (54) but the result can immediately be applied to (55) by replacing R_N with ${R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}$ and t_* with ${t}_{{\ast}}-{\left(\frac{\lambda }{2{\sigma }_{{\ast}}\eta }\right)}^{2/3}$. We now make the following substitutions

$$\begin{align}\hfill t-{t}_{{\ast}}& =\left(\frac{2}{9}\zeta +{2}^{-2/3}\right){\left(\frac{\lambda }{{\sigma }_{{\ast}}\eta }\right)}^{2/3},\hfill \\ \hfill {R}_{\mathrm{N}}& =\frac{2}{3}\psi \left(\zeta \right)-\frac{2}{3}\zeta ,\hfill \\ \hfill {\omega }^{2}& =\frac{243}{4}{\left(\frac{{\sigma }_{{\ast}}\eta }{\lambda }\right)}^{2},\hfill \end{align} \tag{ 56 }$$

to obtain

$$\begin{equation}-\frac{2}{3}\psi -\frac{1}{3}\zeta \frac{\mathrm{d}\psi }{\mathrm{d}\zeta }+\psi \frac{\mathrm{d}\psi }{\mathrm{d}\zeta }+{\omega }^{2}\frac{{\mathrm{d}}^{3}\psi }{\mathrm{d}{\zeta }^{3}}=0.\end{equation} \tag{ 57 }$$

This equation can be obtained from the Korteweg–de Vries (KdV) equation for Ψ(s, z) [36]

$$\begin{equation}\frac{\partial {\Psi}}{\partial s}+{\Psi}\frac{\partial {\Psi}}{\partial z}+{\omega }^{2}\frac{{\partial }^{3}{\Psi}}{\partial {z}^{3}}=0,\end{equation} \tag{ 58 }$$

by using the self similar variables

$$\begin{equation}\zeta =\frac{z}{{s}^{1/3}},\quad \psi \left(\zeta \right)={s}^{2/3}{\Psi}\left(s,z\right).\end{equation} \tag{ 59 }$$

Note that the first Painlevé equation can also be obtained as a particular reduction of the KdV equation [36]. Indeed set

$$\begin{equation}{\Psi}\left(s,z\right)={\left(8{\omega }^{2}\right)}^{1/5}X\left(t\right)+s,\quad t=2{\left(8{\omega }^{2}\right)}^{-2/5}\left(z-\frac{{s}^{2}}{2}\right).\end{equation} \tag{ 60 }$$

The equation following from (58) can then be integrated to find (19).

The analytic quasi-circular adiabatic evolution in the near-horizon geometry was found in [23]. We are interested in the region between the ISCO and the boundary of the near-horizon region, 2^1/3 < R_N ≪ λ^−2/3. The analysis starts with the result for the gravitational wave emission on a circular orbit in the near-horizon region of Kerr. The total energy radiated per unit Boyer–Lindquist time per probe mass is at leading order in λ given by [19, 22]

$$\begin{equation}-\frac{\mathrm{d}e}{\mathrm{d}\left({\sim}{t}/M\right)}={\sigma }_{{\ast}}\eta \;\left({\sim}{r}-1\right).\end{equation} \tag{ 61 }$$

In terms of near-horizon variables, ${\sim}{r}=1+{\lambda }^{2/3}{R}_{\mathrm{N}}$ and at leading order in λ, the latter equation is equivalent to

$$\begin{equation}\frac{\mathrm{d}\ell }{\mathrm{d}{T}_{\mathrm{N}}}=-4{\sigma }_{{\ast}}\eta {R}_{\mathrm{N}}.\end{equation} \tag{ 62 }$$

For a circular geodesic, the angular momentum and energy are given by

$$\begin{equation}{\ell }_{\mathrm{c}\mathrm{i}\mathrm{r}\mathrm{c}}=\frac{2}{\sqrt{3}}+\frac{4\left(1+{R}_{\mathrm{N}}^{3}\right)}{3\sqrt{3}{R}_{\mathrm{N}}^{2}}{\lambda }^{2/3}+O\left({\lambda }^{4/3}\right),\end{equation} \tag{ 63 }$$

$$\begin{equation}{e}_{\mathrm{N}}^{\mathrm{c}\mathrm{i}\mathrm{r}\mathrm{c}}=-\frac{4+{R}_{\mathrm{N}}^{3}}{2\sqrt{3}{R}_{\mathrm{N}}}{\lambda }^{2/3}+O\left({\lambda }^{4/3}\right).\end{equation} \tag{ 64 }$$

At leading order in λ, a circular geodesic in NHEK obeys

$$\begin{equation}\frac{\mathrm{d}{T}_{\mathrm{N}}}{\mathrm{d}\tau }=\frac{{e}_{\mathrm{N}}}{{R}_{\mathrm{N}}^{2}}+\frac{\ell }{{R}_{\mathrm{N}}}=\frac{2}{\sqrt{3}{R}_{\mathrm{N}}}+O\left({\lambda }^{2/3}\right).\end{equation} \tag{ 65 }$$

The two equation (62)-(65) lead to the linear decay of angular momentum per unit proper time (1), which is also assumed more generally in the transition region. Substituting (63) into (62) we obtain

$$\begin{equation}\frac{\mathrm{d}{R}_{\mathrm{N}}}{\mathrm{d}{T}_{\mathrm{N}}}=-\frac{1}{{T}_{\mathrm{N}}^{\text{in}}}\frac{{R}_{\mathrm{N}}}{1-2{R}_{\mathrm{N}}^{-3}},\quad {T}_{\mathrm{N}}^{\text{in}}\equiv \frac{{\lambda }^{2/3}}{3\sqrt{3}{\sigma }_{{\ast}}\eta }.\end{equation} \tag{ 66 }$$

The explicit solution is given by

$$\begin{equation}{R}_{\mathrm{N}}\left({T}_{\mathrm{N}}\right)={R}_{0}{\mathrm{e}}^{-\frac{{T}_{\mathrm{N}}}{{T}_{\mathrm{N}}^{\text{in}}}}{e}^{\frac{k}{3}+\frac{1}{3}W\left(-k{\mathrm{e}}^{3\frac{{T}_{\mathrm{N}}}{{T}_{\mathrm{N}}^{\text{in}}}-k}\right)},\quad k\equiv \frac{2}{{R}_{0}^{3}},\end{equation} \tag{ 67 }$$

where W is the Lambert or product log function that obeys W(0) = 0 and W(−1/e) = −1. At radii far from the ISCO but still in the near-horizon region, 2^1/3 ≪ R_N ≪ λ^−2/3, the k terms are negligible and we recognize the exponential decay of the early ($-{T}_{\mathrm{N}}\gg {T}_{\mathrm{N}}^{\text{in}}$) near-horizon quasi-circular adiabatic inspiral.

Combining (65) and (66) we also obtain

$$\begin{equation}\left(1-\frac{2}{{R}_{\mathrm{N}}^{3}}\right)\frac{\mathrm{d}{R}_{\mathrm{N}}}{\mathrm{d}\tau }=-\frac{1}{{\tau }^{\text{in}}},\quad {\tau }^{\text{in}}\equiv \frac{\sqrt{3}}{2}{T}_{\mathrm{N}}^{\text{in}}=\frac{{\lambda }^{2/3}}{6{\sigma }_{{\ast}}\eta }\end{equation} \tag{ 68 }$$

which we can integrate to obtain

$$\begin{equation}{R}_{\mathrm{N}}+\frac{1}{{R}_{\mathrm{N}}^{2}}-{R}_{0}-\frac{1}{{R}_{0}^{2}}=\frac{{\tau }_{0}-\tau }{{\tau }^{\text{in}}}\end{equation} \tag{ 69 }$$

where R_N(τ₀) = R₀. The explicit solution for R_N(τ) is the only real cubic root of this equation. Evaluating at τ_*, the proper time elapsed between the initial time and reaching the ISCO is⁴

$$\begin{equation}{\tau }_{{\ast}}-{\tau }_{0}={\tau }^{\text{in}}\left({R}_{0}+{R}_{0}^{-2}-\frac{3}{{2}^{2/3}}\right).\end{equation} \tag{ 70 }$$

It is straightforward to obtain that the inspiral (69) admits around the ISCO the behavior

$$\begin{equation}{R}_{\mathrm{N}}-{R}_{\mathrm{N}}^{{\ast}}=\frac{{2}^{2/3}}{\sqrt{3}}\frac{\sqrt{{\tau }_{{\ast}}-\tau }}{\sqrt{{\tau }^{\text{in}}}}+O\left({\tau }_{{\ast}}-\tau \right).\end{equation} \tag{ 71 }$$

Before presenting the matching with the transition, it is important to first establish to what extent the probe will spin down the central black hole due to superradiance and, more precisely, whether a binary system with λ ≪ η can exist. Heuristic formulae for the spin evolution were derived in [37–41]. Based on these heuristics, it was shown that superradiant scattering slows down the central black hole during the inspiral [41]. A fundamental derivation that takes into account the specificities of the near-extremal behavior is however necessary to quantify this slow down. Such fundamental analysis was performed in [23] using the explicit analytical quasi-circular inspiral evolution but an error occurred on equation (23). We will therefore restart the analysis here.

So far we assumed that M and J (and therefore $\lambda =\sqrt{1-{J}^{2}/{M}^{4}}$) are constant, but in fact they evolve already at first order in the self-force (which is proportional to μ). We would like to derive a lower bound on λ. Let us assume that the black hole is exactly extremal (λ = 0) when the compact object enters the near-horizon region. We further assume that it follows the quasi-circular inspiral (67) or, equivalently, (69), at the entry of the near-horizon region. Thanks to the gravitational wave absorption in the near-horizon region, the central black hole mass evolves as

$$\begin{equation}\frac{\mathrm{d}M}{\mathrm{d}{\sim}{t}}={\sigma }_{{\ast},H}{\eta }^{2}\left({\sim}{r}-1\right).\end{equation} \tag{ 72 }$$

In this case, σ_∗,H < 0, see (2), and energy is extracted from the black hole. This is a consequence of superradiance. The angular momentum obeys

$$\begin{equation}\frac{\mathrm{d}J}{\mathrm{d}{\sim}{t}}={{\sim}{{\Omega}}}^{-1}\frac{\mathrm{d}M}{\mathrm{d}{\sim}{t}},\quad {\sim}{{\Omega}}=\frac{1}{2M}\left(1-\frac{3}{4}{\lambda }^{2/3}{R}_{\mathrm{N}}\right)+O\left(\lambda \right).\end{equation} \tag{ 73 }$$

This leads to the departure from extremality

$$\begin{equation}\frac{\mathrm{d}\lambda }{\mathrm{d}{\sim}{t}}=-\frac{3{\lambda }^{1/3}}{2M}{\sigma }_{{\ast},H}{\eta }^{2}{R}_{\mathrm{N}}^{2}{ >}0.\end{equation} \tag{ 74 }$$

Using ${\sim}{t}=2M{\lambda }^{-2/3}{T}_{\mathrm{N}}$ and (65), the evolution of λ is given in terms of proper time as

$$\begin{equation}\lambda \frac{\mathrm{d}\lambda }{\mathrm{d}\tau }=-2\sqrt{3}{\sigma }_{{\ast},H}{\eta }^{2}\;{\lambda }^{2/3}{R}_{\mathrm{N}}.\end{equation} \tag{ 75 }$$

At the entry of the near-horizon region R_N = R₀ ∼ λ^−2/3. This implies that λ² will develop a linear growth proportional to η² or λ ∼ η, at least. The start of the inspiral evolution therefore rules out extremely high spin binaries with λ ≪ η. The marginal scaling λ ∼ η is not ruled out by this argument.

In the standard high spin case η ≪ λ, the transition motion is given by the high spin limit of the Ori–Thorne–Kesden equations (34) and (35) while the physical quantities scale as (37). The behavior of the inspiral close to the ISCO is given by (71). It exactly corresponds to the asymptotic quasi-circular inspiral condition that cancels at leading order the right-hand side of (34). We can therefore match the transition solution (24) to the τ → −∞ asymptotics (71). The matching can be performed uniquely for any given set of physical parameters η, λ with η ≪ λ.

The result is depicted on figure 1 for η = 10⁻⁶, λ = 10⁻³. We fixed the ambiguity in shifting the proper time by choosing τ_* = 0 (i.e. τ = 0 corresponds to ℓ = ℓ_*). The dotted blue curve is the matching solution

$$\begin{equation}{R}_{\mathrm{N}}={R}_{\mathrm{N}}^{{\ast}}+\frac{{2}^{2/3}}{\sqrt{3}}\frac{\sqrt{{\tau }_{{\ast}}-\tau }}{\sqrt{{\tau }^{\text{in}}}}\end{equation} \tag{ 76 }$$

that asymptotes at τ → 0 to the inspiral (71) and at τ → −∞ to the transition solution (24).

The plunge always occurs at τ > τ_*. The final plunge is therefore a subcritical geodesic in the sense that ℓ < ℓ_*. In [25], only critical (ℓ = ℓ_*) and supercritical (ℓ > ℓ_*) geodesics were described since only geodesics that enter the NHEK region from radial infinity were considered. Instead, subcritical geodesics only exist up to a finite radius within the NHEK region. They can be obtained as analytic continuation of the supercritical orbits, as will be detailed in [31], see also [30].

For the marginal λ ∼ η and extremely high spin case λ ≪ η we find that the solution (76) is not an asymptotic solution at τ → −∞ of the transition equation (40) or (42) combined with (43). If one assumes such an ansatz, an overleading τ^3/2 term appears which invalidates the ansatz. This compounds our earlier observation that the extremely high spin case λ ≪ η is inconsistent with the spin evolution.

Even in the restricted scaling (44) where the NHEK metric is sufficient to describe the motion, the NHEK transition equations are inconsistent with the quasi-circular near-horizon inspiral. Indeed, the NHEK transition equations (43)–(45) do not admit an asymptotic solution without acceleration, which would have been an analogue of (24). Explicitly, imposing that the right-hand side of (45) be zero at τ → −∞ leads to R ∼ (−τ)^−1/2 which is inconsistent since R has to be both positive and monotonous. We deduce that no solution (53) can be matched into the adiabatically evolving quasi-circular inspiral near the ISCO (71) at τ → −∞.⁵

We obtained three sets of non-quasi-circular transition equations in the near-horizon region of the near-extremal Kerr black hole at leading order in the high spin limit that depend upon the relative scaling between the near-extremality parameter λ and the mass ratio η. The Ori–Thorne–Kesden transition equations [6, 12] were derived for arbitrary parameters η ≪ λ ≪ 1 and the radial evolution equation was identified as the Painlevé transcendent equation of the first kind. For these Ori–Thorne–Kesden transition equations, we found a unique match with the near-horizon inspiral of [23]. In contrast, we obtained transition equations for marginal η ∼ λ ≪ 1 and extremely high spin scalings λ ≪ η ≪ 1 that can be written as the KdV equation with self-similar variables. However, we showed that they cannot be matched to the near-horizon quasi-circular inspiral of [23].

In fact, we showed that the spin evolution during the near-horizon inspiral drives the spin of the central black hole away from extremality as λ ∼ η or higher due to superradiant gravitational wave extraction of angular momentum. This rules out the scaling λ ≪ η which compounds the absence of a match between the transition equations and the quasi-circular inspiral for that range of parameters.

While the near-horizon limit was instrumental in formulating the inspiral and transition motion in the high spin limit, we found that the NHEK metric alone is insufficient to describe the transition motion even in the high spin regime. Corrections to the near-horizon metric originating from both the deviation from maximal spin and from the backreaction of the probe play an essential role in the transition motion of extreme mass ratio coalescences.

We thank Samuel Gralla for the suggestion to look at this problem. We thank Matthias Fabry, Thomas Hertog, and Andrew Strominger for useful discussions. We thank Ollie Burke, Jonathan Gair and Joan Simón for sharing their draft. GC is research associate of the F R S-FNRS. GC also acknowledges support from the IISN convention 4.4503.15 and networking support from the COST Action GWverse CA16104. KF is Aspirant FWO-Vlaanderen (ZKD4846-ASP/18). KF also acknowledges support from the C16/16/005 grant of the K U Leuven.

In the final stages of this work, we became aware of overlapping results that were independently obtained in [42].

The angular velocity of circular orbits in Boyer–Lindquist coordinates is given by

$$\begin{equation}{\sim}{{\Omega}}={\left({{\sim}{r}}^{3/2}+\tilde{a}\right)}^{-1}.\end{equation} \tag{ A1 }$$

The angular momentum per unit probe mass and central black hole mass and energy per unit probe mass is given for circular orbits by

$$\begin{equation}{\ell }_{\mathrm{c}\mathrm{i}\mathrm{r}\mathrm{c}}\left({\sim}{r};\lambda \right)=\frac{\sqrt{{\sim}{r}}-2\tilde{a}/{\sim}{r}+{\tilde{a}}^{2}/{{\sim}{r}}^{3/2}}{\sqrt{1-3/{\sim}{r}+2\tilde{a}/{{\sim}{r}}^{3/2}}},\end{equation} \tag{ A2 }$$

$$\begin{equation}{{\sim}{e}}_{\mathrm{c}\mathrm{i}\mathrm{r}\mathrm{c}}\left({\sim}{r};\lambda \right)=\frac{1-2/{\sim}{r}+\tilde{a}/{{\sim}{r}}^{3/2}}{\sqrt{1-3/{\sim}{r}+2\tilde{a}/{{\sim}{r}}^{3/2}}},\end{equation} \tag{ A3 }$$

where $\tilde{a}=\sqrt{1-{\lambda }^{2}}$. The ISCO is located at

$$\begin{align}\hfill {{\sim}{r}}_{{\ast}}& =3+{Z}_{2}-\mathrm{sign}\left(\tilde{a}\right){\left[\left(3-{Z}_{1}\right)\left(3+{Z}_{1}+2{Z}_{2}\right)\right]}^{1/2},\hfill \\ \hfill & =1+{2}^{1/3}{\lambda }^{2/3}+O\left({\lambda }^{4/3}\right)\hfill \end{align} \tag{ A4 }$$

where

$$\begin{align}\hfill {Z}_{1}& \equiv 1+{\left(1-{a}^{2}\right)}^{1/3}\left[{\left(1+\tilde{a}\right)}^{1/3}+{\left(1-\tilde{a}\right)}^{1/3}\right],\hfill \\ \hfill {Z}_{2}& \equiv {\left(3{\tilde{a}}^{2}+{Z}_{1}^{2}\right)}^{1/2}.\hfill \end{align} \tag{ A5 }$$

At the ISCO, the angular velocity is

$$\begin{equation}{{\sim}{{\Omega}}}_{{\ast}}=\frac{1}{{{\sim}{r}}_{{\ast}}^{3/2}+\tilde{a}}=\frac{1}{2}-\frac{3{\lambda }^{2/3}}{4{\times}{2}^{2/3}}+O\left({\lambda }^{4/3}\right)\end{equation} \tag{ A6 }$$

and the probe angular momentum and Boyer–Lindquist energy are

$$\begin{equation}{\ell }_{{\ast}}=\frac{6\sqrt{{{\sim}{r}}_{{\ast}}}-4\tilde{a}}{\sqrt{3{{\sim}{r}}_{{\ast}}}}=\frac{2}{\sqrt{3}}+\frac{{2}^{4/3}}{\sqrt{3}}{\lambda }^{2/3}+O\left({\lambda }^{4/3}\right),\end{equation} \tag{ A7 }$$

$$\begin{equation}{{\sim}{e}}_{{\ast}}=\frac{1-2/{{\sim}{r}}_{{\ast}}+\tilde{a}/{{\sim}{r}}_{{\ast}}^{3/2}}{\sqrt{1-3/{{\sim}{r}}_{{\ast}}+2\tilde{a}/{{\sim}{r}}_{{\ast}}^{3/2}}},\end{equation} \tag{ A8 }$$

$$\begin{equation}=\frac{1}{\sqrt{3}}+\frac{{2}^{1/3}}{\sqrt{3}}{\lambda }^{2/3}+O\left({\lambda }^{4/3}\right)\end{equation} \tag{ A9 }$$