Coupling XFEM and peridynamics for brittle fracture simulation—part I: feasibility and effectiveness

Abstract

A peridynamics (PD)–extended finite element method (XFEM) coupling strategy for brittle fracture simulation is presented. The proposed methodology combines a small PD patch, restricted near the crack tip area, with the XFEM that captures the crack body geometry outside the domain of the localised PD grid. The feasibility and effectiveness of the proposed method on a Mode I crack opening problem is examined. The study focuses on comparisons of the J integral values between the new coupling strategy, full PD grids and the commercial software Abaqus. It is demonstrated that the proposed approach outperforms full PD grids in terms of computational resources required to obtain a certain degree of accuracy. This finding promises significant computational savings when crack propagation problems are considered, as the efficiency of FEM and XFEM is combined with the inherent ability of PD to simulate fracture.

1 Introduction

Significant effort has been devoted to the numerical simulation of crack initiation and propagation in brittle and quasi-brittle media. One of the biggest issues to overcome is the appearance of strong discontinuities in the displacement field. The extended finite element method (XFEM) and the cohesive zone methods (CZM) are two numerical approaches that have been used widely for fracture problems [1, 2]. In CZM, crack propagation can be mesh dependent and, in some cases, remeshing is unavoidable (see [2, 3]). The XFEM was developed to avoid remeshing of the model during crack propagation by introducing special enrichment functions that capture the characteristics of the solution [4, 5].

The Bond-Based PD was introduced by Silling [6] and has been used to simulate a variety of problems [7,8,9,10]. Use of PD is an attractive option for fracture problems as spatial derivatives do not appear in the formulation of the method and thus, no special treatment is required to accommodate discontinuous fields. Furthermore, crack initiation and propagation take place naturally by removing bonds that exceed a predefined stretch threshold without introducing any external criteria [11]. A disadvantage of the Bond Based PD theory is the limitation on the Poisson’s ratio that is enforced due to the particular form of particle interactions ($\nu = 0.25$ for plane strain and 3D problems and $\nu = 0.33$ for plane stress problems, as in a Cauchy crystal). Although this limitation is lifted in the State-Based PD theory [12], here the simpler Bond-Based PD theory is used. For short, when PD is used hereafter, it refers to the Bond-Based PD theory. A special note is given here to the Cracking Particle Method (CPM). CPM is a meshfree method that is able to address crack propagation in 2D and 3D problems by introducing discontinuous enrichment at each particle location and can also deal with complex fracture patterns (see [13,14,15] and the references therein). In this study, the PD model was selected as it does not require additional criteria checks.

The high computational cost associated with the nonlocal PD theory can be restrictive for large scale simulations [16]. Various methods can be found in the literature that aim to improve its computational efficiency. One possible approach is to adopt a refinement procedure. In [17], local refinement was implemented and the convergence of the PD theory to classical elasticity was studied in a 1D bar. The local refinement procedure is extended in [18] to 2D static applications where the quadtree partitioning strategy is used to refine the spatial resolution in specific areas. This method was also used in [19] to study dynamic crack propagation. In order to reduce the spurious reflections that appear due to the horizon change when local refinement is used, Ren et al. [20] introduced the concept of the dual horizon.

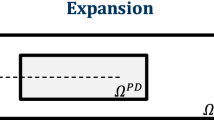
A different approach to reduce the computational burden is to couple PD grids with FE meshes. The purpose of the coupling is to employ the PD theory only in a small area where steep strain gradients or discontinuous displacement fields are expected (e.g. cracks), while the FE method is to be used for the remaining domain. This way, the efficiency of the FE method is combined with the inherent ability of PD to simulate fracture. Thus, the problem domain is divided into two subdomains, $\varOmega^{PD}$ and $\varOmega^{FE}$. In $\varOmega^{PD}$ the solution is approximated by solving the discrete equations from the PD theory, while in $\varOmega^{FE}$ the solution of classical continuum elasticity is approximated using a FE solver. Many coupling methods have been proposed in the literature [16, 21,22,23,24,25,26,27]. A brief synopsis is presented by Zaccariotto et al. [23]. The sheer volume of scientific contributions illustrates the academic interest in the realization of an accurate and efficient FE–PD coupling. It is noted that although this study employs a uniform discretization in $\varOmega^{PD}$, adaptive refinement approaches, similar to the method proposed in [20], could be implemented to further boost the overall efficiency of the final model. The choice of coupling PD with the FE method provides also the opportunity of taking advantage already established FE solvers.

In this study, a methodology is proposed to localise $\varOmega^{PD}$ and to restrict it to the vicinity of the crack tip. Evidently, a portion of the crack remains in $\varOmega^{FE}$, as illustrated in Fig. 1, and treatment of the discontinuous displacement field is required. The aim is to use the XFEM enrichment to capture the displacement jump across the crack. This introduces the following benefits during the numerical simulation: (i) the construction of the underlying FE mesh is independent of the crack location (Fig. 1), (ii) use of the computationally intensive PD theory is limited to a small area and (iii) if $\varOmega^{PD}$ and $\varOmega^{FE}$ are relocated, no remeshing is required. The idea of allowing part of the crack body to appear within $\varOmega^{FE}$ has already been considered in some studies. For instance, in a recent publication [28], Ni et al. used the FE–PD coupling proposed in [22, 23] to study crack propagation problems. The dimensions of $\varOmega^{PD}$ are selected such that both the current and the final locations of the crack tip are included. The part of the crack body that remains within $\varOmega^{FE}$ is modelled as a geometrical boundary and although such implementation is straightforward, if $\varOmega^{PD}$ is relocated, remeshing is required to include the updated crack length. It is envisaged that the XFEM enrichment will circumvent this requirement.

Fig. 1

Schematic of PD–XFEM coupling. Localization of $\varOmega^{PD}$ only near the crack tip. The crack body remains is $\varOmega^{FE}$ and the elements cut are enriched according to XFEM

The two approximations are solved concurrently aiming at a multiscale solution of the problem. The notion of combining different models is not new and various methodologies have been developed to achieve coupling between continuum and discrete models, such as atomistic and molecular dynamics [29, 30]. Multiscale modelling, however, is not broadly available. To address this limitation, Talebi et al. [31], present an open source software that connects different commercially available solvers and allows the user to create multiscale models that are coupled using the Arlequin method [32]. The numerical examples presented in [31] also include cases where XFEM are coupled with FE models and molecular dynamics. Furthermore, the studies presented in [33, 34] are closely related to the present work as they propose a coupling between XFEM and atomistic models. In [33] in particular, an adaptive multiscale method is proposed that can dynamically change the fine scale location. The adaptive process is based on the application of consequent refinement and coarsening steps and is similar to the relocation strategy, presented in Part II of this work. Despite the computational benefits of multiscaling, use of atomistic descriptions impose limitations on the spatial and temporal scales considered (Angstroms and picoseconds respectively).

It is worth noting that, a different way of combining PD with XFEM has been recently presented [35]. In [35] the PD operator derived in [36] is used to augment the XFEM approximation and both models act on the whole computational domain. The PD operator is used to guide the crack during its propagation, alleviating the challenging implementation of external criteria (i.e. level set functions, maximum stress criteria and crack growth criteria). Our proposed methodology differs in that PD and XFEM are used for different parts of the domain and the stress state near the crack tip is exclusively approximated using the PD theory.

This paper is organized as follows: a brief description of the Bond-Based PD and the XFEM formulation is presented in Sect. 2. Section 3 describes the XFEM–PD coupling with the modification of the method presented in [37]. A static and a dynamic example are also included for validation purposes. In Sect. 4, the problem of a double notched plate is solved using three different numerical models: (i) FE only, (ii) PD only and (iii) coupled XFEM–PD. A convergence study is carried out based on the $J$ contour integral to evaluate the accuracy, efficiency and feasibility of the proposed coupling approach. Mode I fracture is simulated for a double cantilever beam using the XFEM–PD and a PD only model in Sect. 5. Lastly, concluding remarks are included in Sect. 6.

2 Definition of the numerical models

2.1 Bond-based peridynamics

According to the PD theory [6], a body consists of material points, or peridynamic particles, that interact with other material points within a finite range called the PD horizon, $\delta$. The PD equation of motion for a material point located at $\varvec{x}^{PD}$ can be expressed as [38]:

$$ \rho \varvec{\ddot{u}} = \mathop \int \nolimits_{{H_{x} }}^{{}} \varvec{f}\left( {\varvec{\eta},\varvec{\xi}} \right)dV_{{x^{\prime}}} + \varvec{b}\left( {\varvec{x}^{PD} } \right), $$

(1)

where $\varvec{x}^{PD} ,\varvec{x}^{{\varvec{'}PD}}$ are the position vectors of two material points, $\varvec{\eta}= \varvec{d}\left( {\varvec{x}^{{\varvec{'}PD}} } \right) - \varvec{d}\left( {\varvec{x}^{PD} } \right)$ is the relative displacement vector and $\varvec{\xi}= \varvec{x}^{{\varvec{'}PD}} - \varvec{x}^{PD}$ is the relative position vector, $\varvec{d}\left( {\varvec{x}^{PD} } \right)$ is the displacement of the PD particles, $\varvec{ f}$ is the pairwise force function, $H_{x}$ is a sphere with radius equal to the PD horizon, $V_{{x^{\prime}}}$ is the volume of the material point $\varvec{x}^{{\varvec{'}PD}}$ and $\varvec{b}$ is the body force per unit volume.

For a microelastic material the pairwise force function $\varvec{f}$ is derivable from a scalar micropotential $w$ as $\varvec{f}\left( {\varvec{\eta},\varvec{\xi}} \right) = \partial w\left( {\varvec{\eta},\varvec{\xi}} \right)/\partial\varvec{\eta}$, $\forall\varvec{\eta},\varvec{\xi}.$ To satisfy the conservation laws of linear and angular momentum, it is required that bond forces between two particles are equal, opposite and collinear leading to $\varvec{f}\left( {\varvec{\eta},\varvec{\xi}} \right) = - \varvec{f}\left( { -\varvec{\eta}, -\varvec{\xi}} \right)\,{\text{and}}\,\left( {\varvec{\eta}+\varvec{\xi}} \right) \times \varvec{f}\left( {\varvec{\eta},\varvec{\xi}} \right) = 0, \forall\varvec{\eta},\varvec{\xi}$ [39]. Using the definition of a microelastic material [38], the pairwise force function can be written in the form:

$$ \varvec{f}\left( {\varvec{\eta},\varvec{\xi}} \right) = c\left(\varvec{\xi}\right)\frac{{\left| {\varvec{\eta}+\varvec{\xi}} \right| - \left|\varvec{\xi}\right|}}{{\left|\varvec{\xi}\right|}}\frac{{\varvec{\eta}+\varvec{\xi}}}{{\left| {\varvec{\eta}+\varvec{\xi}} \right|}} = c\left(\varvec{\xi}\right)s\frac{{\varvec{\eta}+\varvec{\xi}}}{{\left| {\varvec{\eta}+\varvec{\xi}} \right|}}, $$

(2)

where $s$ is the bond stretch, and $c\left(\varvec{\xi}\right)$ is the micromodulus function that can be evaluated by equating the PD strain energy to the strain energy of the continuum model. It is common in the literature to assume that $c\left(\varvec{\xi}\right)$ is either uniform or has a conical variation with respect to $\varvec{\xi}$. If plane stress conditions are assumed and $c\left(\varvec{\xi}\right)$ is uniform, then:

$$ c\left(\varvec{\xi}\right) = c = \frac{9E}{{\pi t\delta^{3} }} $$

(3)

while if a conical variation is assumed, $c\left(\varvec{\xi}\right)$ is computed as:

$$ c\left(\varvec{\xi}\right) = \left( {1 - \frac{\varvec{\xi}}{\delta }} \right)\frac{{24{\rm E}}}{{\pi \delta^{3} \left( {1 - v} \right)}} $$

(4)

In both cases, $c\left(\varvec{\xi}\right) = 0, \,{\text{if}} \left|\varvec{\xi}\right| > \delta$. It is noted that when $c\left(\varvec{\xi}\right)$ is conical, better convergence to classical elasticity has been reported in the literature [17, 40]. Similar expressions can be derived for 1D, plain strain and 3D problems [12]. Here, either the uniform or the conical definition of $c\left(\varvec{\xi}\right)$ is used, and it is explicitly stated in each example. Although the bond constant depends only on the relative position of two particles and describes a linear force-stretch $\left( {\varvec{f} - s} \right)$ interaction relationship, the PD equation of motion leads to a nonlinear system of equations. A linearization of the PD theory has been presented in [6].

The integral expressed in Eq. 1 can be approximated numerically using the collocation method described in [41] as:

$$ \rho \varvec{\ddot{u}}_{i} = \mathop \sum \limits_{j = 1}^{N} \varvec{f}_{i,j} \left( {\varvec{\eta},\varvec{\xi}} \right)V_{j} + \varvec{b}_{i} , $$

(5)

In the work of Kilic and Madenci, a more elaborate approximation has been proposed where the collocation method described in Eq. 5 can be extracted as a special case.

There are two correction factors required for the implementation of the discretized PD equation of motion: (i) the surface and (ii) the volume correction factors. The definitions of the bond constant in Eqs. 3 and 4 assume that the particle is surrounded by other particles and its horizon is uninterrupted. This is violated near the geometric boundaries and the so called ‘skin effect’ of peridynamics manifests itself [42]. To account for this phenomenon, the surface correction based on the volume method presented in [42, 43] is adopted here. The volume correction is required to account for particles that are only partially within the horizon of other particles. The correction procedure suggested in [21] is implemented here.

Material damage in the PD theory is defined at the bond level, as a function of the status of the bond between two particles. If the stretch of a bond exceeds a predefined threshold value, the bond is removed from subsequent computations. The threshold value is commonly termed the critical bond stretch$s_{0}$, and bond breakage takes place when $s \ge s_{0}$. Siling and Askari [38] relate $s_{0}$ to the energy release rate $G_{IC}$ by calculating the energy required to break all bonds per unit of fracture area and equating it to fracture toughness. If a uniform $c\left(\varvec{\xi}\right)$ is used then $s_{0}$ is computed as [38]:

$$ s_{0} = \sqrt {\frac{{4\pi G_{IC} }}{9E\delta }} , $$

(6)

While in the case of a conical $c\left(\varvec{\xi}\right)$ the expression of $s_{0}$ becomes:

$$ s_{0} = \sqrt {\frac{{5\pi G_{IC} }}{9E\delta }} . $$

(7)

Damage is an irreversible process and a history dependent Boolean function $\mu \left( {t,\varvec{\xi}} \right)$ can be introduced in the definition of $\varvec{f}$ to indicate which bonds are broken. Following [44], $\mu \left( {t,\varvec{\xi}} \right)$ is defined as:

$$ \mu \left( {t,\varvec{\xi}} \right) = \left\{ {\begin{array}{*{20}c} {1,} & {s < s_{0} \quad \forall t} \\ {0,} & {\text{otherwise}} \\ \end{array} } \right.. $$

(8)

Thus, the PD theory can naturally incorporate damage by simply removing the bonds whose stretch $s$, exceeds the critical stretch $s_{0}$, through function $\mu \left( {t,\varvec{\xi}} \right)$. There is no need for any additional criteria to trigger damage initiation, or for estimations of the propagation length and direction within the framework. The pointwise evolution of damage in this framework can be monitored using the local damage index $\phi \left( {\varvec{x}^{PD} ,t} \right)$ as [2]:

$$ \phi \left( {\varvec{x}^{PD} ,t} \right) = 1 - \frac{{\int \mu \left( {t,\varvec{\xi}} \right)dV'}}{\int dV'}. $$

(9)

In essence, $\phi \left( {\varvec{x}^{PD} ,t} \right)$ relates the number of healthy bonds to the total number of bonds that are connected at a PD particle. In the present study, an algorithm is developed based on $\phi \left( {\varvec{x}^{PD} ,t} \right)$ to monitor the path and the current location of the crack tip(s).

2.2 The extended finite element method

The standard FE method is not suitable for problems concerning the evolution of strong and weak discontinuities as it is a piecewise differential approximation and the underlying mesh needs to be specifically constructed [1]. The XFEM, introduced in [45, 46], avoid such requirements by adding special enrichment functions to the approximation space. The choice of enrichment functions depends on the problem addressed and they are designed to capture known characteristics of the solution field (e.g. the singular field at the crack tip). Here, the local extrinsic enrichment of the solution field is used where additional nodal degrees-of-freedom (dofs) are introduced for the elements that are cut by the discontinuity. In general, the approximation of the displacement field can be written as [4]:

$$ \varvec{u}\left( \varvec{x} \right) \approx \mathop \sum \limits_{i = 1}^{K} N_{i} \left( {\varvec{x}^{FE} } \right)\varvec{u}_{i} + \mathop \sum \limits_{j = 1}^{M} N_{j} \left( {\varvec{x}^{FE} } \right)\psi \left( {\varvec{x}^{FE} } \right)\varvec{a}_{j} , $$

(10)

where $\varvec{ x}^{FE}$ is the position vector, $K$ is the total number of nodal points, $\varvec{u}_{i}$ are the nodal displacements, $N_{i} \left( {\varvec{x}^{FE} } \right)$ are the standard FE shape functions, $M$ is the number of enriched nodes, $N_{j} \left( {\varvec{x}^{FE} } \right)$ are the shape functions of the enriched part, $\psi \left( {\varvec{x}^{FE} } \right)$ is the enrichment function and $\varvec{a}_{j}$ are the enriched nodal values. In practice, the shape functions $N_{j} \left( {\varvec{x}^{FE} } \right)$ are usually selected to be the same as the standard shape functions $N_{i} \left( {\varvec{x}^{FE} } \right)\varvec{ }$ [4]. This approach is also adopted here. It is noted that the second part of Eq. (10) vanishes if no enrichment takes place and the approximation of the displacement field reduces to the familiar FE approximation. Furthermore, only 2D problems are discussed and the mesh is constructed using 4-noded bilinear elements.

The displacement jump across the crack can be captured using the Heaviside function, defined as:

$$ H\left( {\varvec{x}^{FE} } \right) = \left\{ {\begin{array}{*{20}c} { 1,} & {\varphi \left( {\varvec{x}^{FE} } \right) > 0} \\ { - \,1,} & {\varphi \left( {\varvec{x}^{FE} } \right) < 0} \\ \end{array} \varvec{ }} \right., $$

(11)

where $\varphi \left( {\varvec{x}^{FE} } \right) = \left\| {\varvec{x}^{FE} - \varvec{x}^{FE*} } \right\|sign\big( \varvec{n}_{\varGamma } \cdot \big( \varvec{x}^{FE} - \varvec{x}^{FE*} \big) \big)$ is the signed distance function, $\varvec{x}^{FE*}$ is the closest point to $\varvec{x}$ on the discontinuity and $\varvec{n}_{\varGamma }$ the unit normal on the discontinuity surface [4].

Although the local enrichment of elements is attractive as it limits the additional computational burden, compared to enriching all the FE nodes in the computational domain, unavoidably some of the elements will have only a part of their nodes enriched. These elements are usually termed ‘blending’ or ‘partially enriched’ elements (see [4, 47]). In these elements the partition of unity (PUM) property of the shape functions is violated that can significantly affect the convergence rate of the solution. Here, use of crack tip enrichment is avoided as the area near the crack tip is always within the PD domain. In [48], Belytschko et al. proposed the use of the shifted Heaviside enrichment function that vanishes within the blending elements and thus, the spurious terms that lead to PUM violation are avoided, and no additional treatment is required. Using the shifted enrichment, the displacement approximation from Eq. (10) is re-written as:

$$ \varvec{u}\left( {\varvec{x}^{FE} } \right) \approx \mathop \sum \limits_{{{\text{i}} = 1}}^{K} N_{i} \left( {\varvec{x}^{FE} } \right)\varvec{u}_{i} + \mathop \sum \limits_{j = 1}^{M} N_{j} \left( {\varvec{x}^{FE} } \right)\left( {H\left( {\varvec{x}^{FE} } \right) - H\left( {\varvec{x}_{j}^{FE} } \right)} \right)\varvec{a}_{j} . $$

(12)

Using the displacement approximations described in Eq. 12, the stiffness matrix $\varvec{K}^{FE}$ of the discretized system is given as [4]:

$$ \varvec{K}^{FE} = \left[ {\begin{array}{*{20}c} {\varvec{K}^{std,std} } & {\varvec{K}^{std,enr} } \\ {\varvec{K}^{enr,std} } & {\varvec{K}^{enr,enr} } \\ \end{array} } \right]. $$

(13)

The superscripts $std$ and $enr$ that appear in Eq. 13 refer to the standard and the enriched dofs.

The introduction of the enrichment functions in the approximation necessitates modifications to the numerical integration. The accuracy of the Gauss integration can be improved by [4, 47, 49]: (i) increasing uniformly the number of Gauss points, (ii) partitioning the elements into sub-regions that conform with the discontinuity and (iii) partitioning the elements into regular subregions. Here the numerical integration is performed by dividing the elements into four rectangular sub-regions and performing Gauss integration in each one. For the problems considered here a $32 \times 32$ grid provided adequate accuracy.

3 Coupling methodology

3.1 Formulation

Let $\varOmega$ be the computational domain of the problem and $\partial \varOmega$ its boundary. $\partial_{u} \varOmega$ and $\partial_{F} \varOmega$ are the portions of $\partial \varOmega$ where the prescribed displacements $\varvec{u}_{d}$ and external forces $\varvec{F}_{d}$ are applied. For simplicity, and without loss of generality, we assume absence of body forces and external loads are applied only on $\partial \varOmega$. Then, $\varOmega$ is partitioned into two subdomains, $\varOmega^{PD}$ and $\varOmega^{FE}$ with $\varOmega = \varOmega^{PD} \cup \varOmega^{FE}$ and $\varOmega^{PD} \cap \varOmega^{FE} = \varnothing$. In $\varOmega^{PD}$ the solution is approximated by solving the discrete equations from PD theory, while in $\varOmega^{FE}$ the solution of classical continuum elasticity is approximated using the FE method. The restriction on the Poisson’s ratio due to the implementation of the BB–PD model is also transferred to the coupled XFEM–PD model. In all numerical examples that are presented in the following paragraphs, the Poisson’s ratio of the XFEM is set to match that of the PD model.

Coupling between two different models is usually performed either at a discrete interface or gradually over a zone where both descriptions coexist, often called the ‘overlapping zone’ [22, 29, 50,51,52]. Here the former approach is followed, and the coupling is performed on the boundary $\partial \varOmega_{1}$ that defines the coupling interface between the two models. We limit ourselves to the configuration illustrated in Fig. 2 with the restriction $\partial \varOmega \cap \partial \varOmega_{1} = \varnothing$. This configuration is a desirable situation for our applications because: (i) use of the computationally expensive PD model is reduced, (ii) its application can be focused to specific locations and (iii) the PD model is defined away from the portions $\partial_{u} \varOmega$ and $\partial_{F} \varOmega$ where the boundary conditions are enforced. This circumvents the difficulties associated with the application of boundary conditions on a nonlocal model [6, 23, 53]. Despite being located away from the geometrical boundaries, the PD skin effect still manifests itself. For this reason, use of a surface correction procedure is very important as it will improve the accuracy of the coupling [37].

Fig. 2

Subdivision of $\varOmega$ into $\varOmega^{PD}$ and $\varOmega^{FE}$ and illustration of the discretization near the coupling interface

The coupling is realized at the discrete level of the two models. The PD theory is discretized using a grid of points and a simple collocation method through Eq. 5, to approximate the integral in Eq. 1. The solution of elasticity’s differential equation on the other hand, is approximated by employing the FE method. It is thus termed that this methodology couples PD grids with FE meshes and since the XFEM enrichment is also introduced in $\varOmega^{FE}$ to treat the discontinuous displacement fields, the method is called XFEM–PD coupling hereafter.

The coupling is enforced by introducing additional PD particles in $\varOmega^{FE}$, termed ‘ghost particles’. This terminology is implemented because in the final system of equations the respective dofs can be removed through static condensation. An illustration of the coupling between the two numerical methods with the introduction of the ghost particles is depicted in Fig. 2. The number of the ghost particles introduced is such that the PD horizon $\delta$, of the particles in $\varOmega^{PD}$ is not interrupted near the coupling interface. In Fig. 2, the PD horizon is set to $\delta = 2\varDelta x$ as an illustration. The coupling for different values of $\delta$ can be constructed in a similar manner. In [22, 23], a similar coupling approach has been proposed with the difference that additional FE nodes are introduced in $\varOmega^{PD}$ (termed ‘ghost nodes’).

The introduction of ghost particles allows for the coupling between PD and FE without the requirement of conforming nodes and particles (see Refs. [37, 54]). This property is very attractive for 2D and 3D applications as the discretization lengths of the two models are independent. Furthermore, it has been shown in [37], that coupling approaches like the one described here can minimize the spurious reflections observed in dynamic problems compared to simpler node-to-particle coupling strategies and can lead to comparable accuracy to the computationally more expensive methods that enforce the coupling in a weak sense.

Let $n^{PD}$ be the set of all PD particles in the problem domain $\varOmega$. We denote by $n_{g} = \left\{ {\varvec{x}^{PD} :\varvec{x}^{PD} \in \varOmega^{FE} } \right\}$ the set of ghost particles and by $n_{n} = \left\{ {\varvec{x}^{PD} :\varvec{x}^{PD} \in \varOmega^{PD} } \right\}$ the set of normal particles. Then $n^{PD} = n_{n} \cup n_{g}$ while $n_{n} \cap n_{g} = \varnothing$ since each particle is either normal or ghost. The total number of ghost and normal particles in $\varOmega$ is defined by the cardinality of the sets $\left| {n_{g} } \right|$ and $\left| {n_{n} } \right|$, respectively. Similarly, $n^{FE}$ is the set of all FE nodes and $n_{std}$ and $n_{enr}$ contain the standard and enriched FE nodes. The displacement vectors of the FE nodes and PD particles are given as $\bar{\varvec{u}} = \left\{ {\varvec{u}^{T} ,\varvec{a}^{T} } \right\}^{T}$ and $\varvec{d} = \left\{ {\left( {\varvec{d}^{n} } \right)^{T} , \left( {\varvec{d}^{g} } \right)^{T} } \right\}^{T}$, respectively, where $\varvec{d}^{n}$ and $\varvec{d}^{g}$ refer to the normal and ghost particle dofs, respectively. $\varvec{d}^{g}$ can be computed by interpolating the FE nodal displacements at the location of the ghost particles. If a ghost particle is located within an enriched element, the enrichment part needs to be considered during the interpolation. Thus, $\varvec{d}^{g}$ is computed as:

$$ \varvec{d}_{k}^{g} = \mathop \sum \limits_{{{\text{i}} = 1}}^{K} N_{i} \left( {\varvec{x}_{k}^{PD} } \right)\varvec{u}_{i} + \mathop \sum \limits_{j = 1}^{M} N_{j} \left( {\varvec{x}_{k}^{PD} } \right)\left( {H\left( {\varvec{x}_{k}^{PD} } \right) - H\left( {\varvec{x}_{j}^{FE} } \right)} \right)\varvec{a}_{j} ,\quad k = 1,2, \ldots ,\left| {n_{g} } \right|, $$

(14)

where $K$ and $M$ are the standard and enriched FE nodes, described in the XFEM section. If a ghost particle is located inside an element without enrichment, then the second term in Eq. 14 vanishes and the formula reduces to $\varvec{d}_{k}^{g} = \mathop \sum \limits_{{{\text{i}} = 1}}^{K} N_{i} \left( {\varvec{x}_{k}^{PD} } \right)\varvec{u}_{i}$. The interpolation from Eq. 14 can be re-written using matrix notation as:

$$ \varvec{d}^{g} = \varvec{C}_{g,1} \varvec{u} + \varvec{C}_{g,2} \varvec{a} = \varvec{C}_{g} \bar{\varvec{u}}. $$

(15)

where $\varvec{C}_{g,1}$ and $\varvec{C}_{g,2}$ are the matrices of coefficients that couples the displacements of the ghost particles $\varvec{d}^{g} \varvec{ }$ with the displacements of the standard $\varvec{u}$ and enriched $\varvec{a}$ nodal values, respectively. Similar expressions are derived for the velocity $\dot{\varvec{d}}^{g}$ and the acceleration $\varvec{\ddot{d}}^{g}$ of the ghost particles.

The goal is to develop a coupled XFEM–PD model with the ability to adaptively redefine $\varOmega^{FE}$ and $\varOmega^{PD}$, following the propagation of the crack. Each time $\varOmega^{FE}$ and $\varOmega^{PD}$ are relocated, the location of the coupling interface (e.g. $\partial \varOmega_{1}$ in Fig. 2) is also updated. In the coupling presented in [37], force equilibrium is taken on $\partial \varOmega_{1}$ by computing the intersection of the coupling interface with each bond that connects a ghost with a normal particle. In cases where the location and the shape of $\partial \varOmega_{1}$ is not static during the simulation, re-computation of the bond—interface intersection can be challenging and computationally demanding. Instead, we can assume that the bond force is applied in the interior of the FE, and specifically, at the location of the ghost particle. A comparison of the two idealizations is illustrated schematically in Fig. 3 where a FE and a bond that crosses $\partial \varOmega_{1}$ have been isolated. These two approaches are very similar to the CT and VL coupling schemes presented by Liu and Hong in [52].

Fig. 3

Comparison of the two coupling approaches. On the left, the bond force is applied on the intersection of the bond with the coupling interface and it is effectively distributed on the two nodes that lie on $\partial \varOmega_{1}$ [37]. On the right, the bond force is applied in the interior of the element and the force is distributed to all 4 nodes of the element

The bond force $\varvec{f}_{i,j}$ between particles $i$ and $j$ is computed using Eq. 2. From linear and angular momentum conservation we get that $\varvec{f}_{i,j} = - \,\varvec{f}_{j,i}$. We consider $\varvec{f}_{j,i}$ to be an external concentrated force acting inside the element at the location $\varvec{x}_{j}^{PD}$. The point of application of the concentrated force can be defined using a 2D Dirac delta-function $\delta \left( {x - x_{j}^{PD} ,y - y_{j}^{PD} } \right)$. Let $n$ be the total number of bonds that connect ghost particle $j$ with a normal particle. The total force $\varvec{f}_{j}^{g}$, applied at $\varvec{x}_{j}^{PD}$ is:

$$ \varvec{f}_{j}^{g} = \mathop \sum \limits_{i = 1}^{n} - \varvec{f}_{i,j} V_{i} , \quad j = 1, 2, \ldots ,\left| {n_{g} } \right|. $$

(16)

The force vector $\varvec{f}^{I}$, where $I = 1, 2, 3, 4$ is element nodal numbers (see e.g. Fig. 3), is computed by integrating $\varvec{f}_{j}^{g}$ over the volume of the element as:

$$ \varvec{f}^{I} = \mathop \sum \limits_{j = 1}^{{j_{total} }} \int \varvec{N}^{T} \varvec{f}_{j}^{g} \delta \left( {x - x_{j}^{PD} ,y - y_{j}^{PD} } \right)d\varOmega = \mathop \sum \limits_{j = 1}^{{j_{total} }} \varvec{N}_{{x = x_{j}^{PD} ,y = y_{j}^{PD} }}^{T} \varvec{f}_{j}^{g} , $$

(17)

where $j_{total}$ is the total number of ghost particles in the element. In essence, $\varvec{f}_{j}^{g}$ is distributed to the nodes of the element through the FE shape functions evaluated at the location of the ghost particle. Iterating this procedure over all the FE elements, the vector of forces $\varvec{f}^{C}$, that the PD ghost particles apply on the FE elements can be expressed in the global system as:

$$ \varvec{f}^{C} = \varvec{C}_{F} \varvec{f}^{g} , $$

(18)

where $\varvec{f}^{g}$ is the vector that contains the forces on the ghost particles and $\varvec{C}_{F}$ is the matrix of coefficients that distributes the forces that are applied on the ghost particles to the FE dofs. The interpolation described in Eqs. 15 and 18 is performed by evaluating the FE shape functions at the location of ghost particles. This simplifies the computation of the coupling matrices as $\varvec{C}_{F} = \left( {\varvec{C}_{g} } \right)^{T}$.

Then, the equation of motion in $\varOmega^{FE}$ becomes:

$$ \varvec{M}^{FE} \varvec{\ddot{\bar{u}}} + \varvec{K}^{FE} \bar{\varvec{u}} = \varvec{F}^{FE} + \varvec{f}^{C} , $$

(19)

where $\varvec{M}^{FE}$ is the FE lumped mass matrix. Finally, Eqs. 5, 15 and 19 form the system of equations for the coupled XFEM–PD model.

Under the assumption that the load application is slow, the inertia effects can be neglected. Use of the linearized PD formulation can be more convenient as a global stiffness matrix can be written for the coupled system and linear solvers can be used for its solution [23, 37, 54]. Here the original formulation of the PD theory is used and thus a solver for the nonlinear system of equations needs to be implemented. Various approaches have been used in the literature to obtain an equilibrium solution for the PD theory such as the Adaptive Dynamic Relaxation method (ADR) [24, 55], conjugate gradient solvers [56] and implicit Newton–Raphson [57]. An implicit nonlocal operator formulation for electromagnetic problems that provides that tangent stiffness matrix is also proposed in [58].

In this study the full Newton–Raphson solver is used for the approximation of the solution field. Let $\varvec{U} = \left\{ {\left( {\bar{\varvec{u}}} \right)^{\rm T} ,\left( {\varvec{d}^{n} } \right)^{T} ,\left( {\varvec{d}^{g} } \right)^{T} } \right\}^{T}$ be the vector of displacements for the coupled system. We can then re-write the system of equations more compactly as:

$$ \begin{aligned} & \varvec{g}\left( \varvec{U} \right) = \left[ {\begin{array}{*{20}c} {\varvec{g}^{FE} } \\ {\varvec{g}_{i}^{PD,n} } \\ {\varvec{g}^{PD,g} } \\ \end{array} } \right] = 0,\quad {\text{with }} \\ & \begin{array}{*{20}c} {\varvec{g}^{FE} = \varvec{K}^{FE} \bar{\varvec{u}} - \varvec{F}^{FE} - \varvec{f}^{C} } \\ {\varvec{g}_{i}^{PD,n} = \mathop \sum \limits_{j = 1}^{M} \varvec{f}_{i,j} V_{j} + \varvec{b}_{i} ,\varvec{ }i = 1,2, \ldots ,\left| {n_{n} } \right|} \\ {\varvec{g}^{PD,g} = \varvec{C}_{g} \bar{\varvec{u}} - \varvec{d}^{g} } \\ \end{array} .\end{aligned} $$

(20)

The solution $\varvec{U}$ can be approximated numerically through the iterative procedure:

$$ \varvec{U}^{k + 1} = \varvec{U}^{k} - \left[{{{\mathcal{J}}_{{g\left( \varvec{U} \right)}} }}\right]^{-1} {{g\left( {\varvec{U}^{k} } \right)}}, $$

(21)

where $\varvec{U}^{k + 1}$ and $\varvec{U}^{k}$ are the next and the current approximation of the displacement field, respectively, and ${\mathcal{J}}_{{g\left( \varvec{U} \right)}}$ is the Jacobian of $\varvec{g}\left( \varvec{U} \right)$. The components of ${\mathcal{J}}_{{g\left( \varvec{U} \right)}}$ are defined as:

$$ {\mathcal{J}}_{{g\left( \varvec{U} \right)}} = \frac{{\partial \varvec{g}}}{{\partial \varvec{U}}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \varvec{g}^{FE} }}{{\partial \varvec{U}}}} \\ {\frac{{\partial \varvec{g}_{i}^{PD,n} }}{{\partial \varvec{U}}}} \\ {\frac{{\partial \varvec{g}^{PD,g} }}{{\partial \varvec{U}}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\partial \varvec{g}^{FE} }}{{\partial \bar{\varvec{u}}}}} & {\frac{{\partial \varvec{g}^{FE} }}{{\partial \varvec{d}^{n} }}} & {\frac{{\partial \varvec{g}^{FE} }}{{\partial \varvec{d}^{g} }}} \\ 0 & {\frac{{\partial \varvec{g}^{PD,n} }}{{\partial \varvec{d}^{n} }}} & {\frac{{\partial \varvec{g}^{PD,n} }}{{\partial \varvec{d}^{g} }}} \\ {\frac{{\partial \varvec{g}^{PD,g} }}{{\partial \bar{\varvec{u}}}}} & 0 & {\frac{{\partial \varvec{g}^{PD,g} }}{{\partial \varvec{d}^{g} }}} \\ \end{array} } \right]. $$

(22)

It is easy to show that the following components of ${\mathcal{J}}_{{g\left( \varvec{U} \right)}}$ are computed as:

$$ \frac{{\partial \varvec{g}^{FE} }}{{\partial \bar{\varvec{u}}}} = \varvec{K}^{FE} ,\quad \frac{{\partial \varvec{g}^{PD,g} }}{{\partial \bar{\varvec{u}}}} = \varvec{C}_{g} ,\quad \frac{{\partial \varvec{g}^{PD,g} }}{{\partial \varvec{d}^{g} }} = - \,\varvec{I} $$

(23)

where $\varvec{I}$ is the identity matrix. Then using Eqs. 16, 18 and 20, the remaining entries in Eq. 22 are defined as:

$$ \frac{{\partial \varvec{g}^{FE} }}{{\partial \varvec{d}^{n} }} = - \frac{{\partial \varvec{f}^{C} }}{{\partial \varvec{d}^{n} }} = - \varvec{C}_{F} \frac{{\partial \varvec{f}_{j}^{g} }}{{\partial \varvec{d}_{i}^{n} }} = - \varvec{C}_{F} {\mathcal{J}}_{g,n}^{PD} , \quad j = 1,2, \ldots ,\left| {n_{g} } \right|\quad {\text{and}}\quad i = 1,2, \ldots ,\left| {n_{n} } \right| $$

(24a)

$$ \frac{{\partial \varvec{g}^{FE} }}{{\partial \varvec{d}^{g} }} = - \frac{{\partial \varvec{f}^{C} }}{{\partial \varvec{d}^{g} }} = - \varvec{C}_{F} \frac{{\partial \varvec{f}_{j}^{g} }}{{\partial \varvec{d}_{i}^{g} }} = - \varvec{C}_{F} {\mathcal{J}}_{g,g}^{PD} , \quad j = 1,2, \ldots ,\left| {n_{g} } \right| \quad {\text{and}}\quad i = 1,2, \ldots ,\left| {n_{g} } \right| $$

(24b)

$$ \frac{{\partial \varvec{g}^{PD,n} }}{{\partial \varvec{d}^{n} }} = \frac{\partial }{{\partial \varvec{d}_{j}^{n} }}\left( {\mathop \sum \limits_{k = 1}^{M} \varvec{f}_{i,k} V_{k} } \right) = {\mathcal{J}}_{n,n}^{PD} ,\quad j = 1,2, \ldots ,\left| {n_{n} } \right| \quad {\text{and}}\quad i = 1,2, \ldots ,\left| {n_{n} } \right| $$

(24c)

$$ \frac{{\partial \varvec{g}^{PD,n} }}{{\partial \varvec{d}^{g} }} = \frac{\partial }{{\partial \varvec{d}_{j}^{g} }}\left( {\mathop \sum \limits_{k = 1}^{M} \varvec{f}_{i,k} V_{k} } \right) = {\mathcal{J}}_{n,g}^{PD} , \quad j = 1,2, \ldots ,\left| {n_{g} } \right|\quad {\text{and}}\quad i = 1,2, \ldots ,\left| {n_{g} } \right| $$

(24d)

The matrices ${\mathcal{J}}_{g,n}^{PD}$, ${\mathcal{J}}_{g,g}^{PD}$, ${\mathcal{J}}_{n,n}^{PD}$ and ${\mathcal{J}}_{n,g}^{PD}$ can be computed using Eqs. A.5 and A.6 from “Appendix A” section. Finally, the Jacobian of the coupled system of equations can now be written as:

$$ {\mathcal{J}}_{\varvec{g}} = \left[ {\begin{array}{*{20}c} {\varvec{K}^{FE} } & { - \varvec{C}_{F} {\mathcal{J}}_{g,n}^{PD} } & { - \varvec{C}_{F} {\mathcal{J}}_{g,g}^{PD} } \\ 0 & {{\mathcal{J}}_{n,n}^{PD} } & {{\mathcal{J}}_{n,g}^{PD} } \\ {\varvec{C}_{g} } & 0 & { - \varvec{I}} \\ \end{array} } \right] $$

(25)

One disadvantage that arises when coupled FE meshes and PD grids are used is the appearance of spurious reflections during pulse propagation. A dynamic example is also included in this study to evaluate the amplitude of the reflections. Explicit schemes are generally preferred for dynamic fracture simulations. The central difference, velocity-Verlet algorithm and forward and backward first order differences are some of the methodologies that have been typically employed in the literature for the time integration of the PD equation of motion [24, 38, 40, 59]. In [38], a stability study was carried out using the linearized PD equation of motion. It was shown that the maximum time increment must satisfy:

$$ \varDelta t \le \varDelta t_{critical} = \sqrt {\frac{2\rho }{{\mathop \sum \nolimits_{j = 1}^{N} \frac{c}{{\left|\varvec{\xi}\right|}}V_{j} }}} . $$

(26)

As suggested in [38], for problems that contain nonlinearities or when simulating fracture, to ensure stability, the time step calculated by Eq. 26 is reduced by a factor less than one.

Time integration is performed using the central difference method (Newmark-β with $\beta = 0$ and $\gamma = 0.5$). The displacement and velocity vectors at time increment $t + \varDelta t$ are computed through

$$ \varvec{U}^{t + \varDelta t} = \varvec{U}^{t} + \dot{\varvec{U}}^{t} \varDelta t + \frac{1}{2}\varvec{\ddot{U}}^{t} \varDelta t^{2} , $$

(27a)

$$ \dot{\varvec{U}}^{t + \varDelta t} = \dot{\varvec{U}}^{t} + \frac{1}{2}\left( {\varvec{\ddot{U}}^{t} + \varvec{\ddot{U}}^{t + \varDelta t} } \right)\varDelta t. $$

(27b)

3.2 Static example: plate under multiaxial loading conditions

First a static example is presented to evaluate the error between the solution approximated using the coupled model with the solution approximated using the FE method. Consider a plate under plane stress conditions. The plate is assumed to behave elastically and the variation of $c\left(\varvec{\xi}\right)$ is assumed conical. The geometry of the plate, the boundary conditions and the applied load are illustrated in Fig. 4. This example is used to demonstrate the accuracy of the combined FE–PD model to capture the response of a problem under both normal and shear loads. Application of $\varOmega^{PD}$ is restricted to a small area in the interior of the plate and it is completely enclosed by $\varOmega^{FE}$, a scenario which is desirable in practice as it restricts the use of the computationally expensive model to an area of interest. Thus, in this example, all loads and boundary conditions are applied on the boundary of $\varOmega^{FE}$. The problem parameters are summarized in Table 1.

Fig. 4

Illustration of the problem set-up for the first verification example

Table 1 Summary of the problem parameters for the first verification problem

The same problem is also solved using a FE only model. In both cases, 4-node bilinear elements are used to approximate the solution of classical elasticity. To assess the accuracy of the FE–PD model, the relative error of the displacement magnitude between the FE–PD model and the FE only model is computed at the FE nodal locations. Since the nodal points do not necessarily coincide in $\varOmega^{PD}$, the solution in the PD region is interpolated at the FE nodal locations using linear interpolation. The relative error is computed as:

$$ error = \frac{{\vert|\varvec{u}^{FE only}\vert| - \vert|\varvec{u}^{FE - PD}\vert| }}{{\vert|\varvec{u}^{FE only}\vert| }}$$

(28)

where $\varvec{u}^{FE only}$ and $\varvec{u}^{FE - PD}$ are the displacement fields approximated by the FE only and the FE–PD models, respectively.

The magnitude of the displacement field $\varvec{u}^{FE - PD}$ and the absolute value of the relative error are plotted in Fig. 5, when the fine PD discretization is used (i.e. $\varDelta x^{PD} = \varDelta y^{PD} = 0.01\,{\text{mm}}$). A good agreement can be seen between the results of the two models. The maximum absolute value of the relative error is approximately 0.75%. It can also be seen that the error between the two solutions is mainly concentrated near the interface where the FE and PD coupling is enforced. This observation is also reported in similar coupling approaches [54]. The error is higher at the corners of $\varOmega^{PD}$, where the maximum value is also observed. Changing the discretization in $\varOmega^{PD}$ to a coarser grid with $\varDelta x^{PD} = \varDelta y^{PD} = 0.025\,{\text{mm}}$, the maximum absolute value of the relative error increases to 1.19%. This could be attributed to the PD skin effect. Although a surface correction procedure has been implemented, the softening observed near the boundary of $\varOmega^{PD}$ is reduced but not completely treated [42].

Fig. 5

Left: Magnitude of the displacement field. Right: relative % error between the FE and the FE–PD solutions

3.3 Dynamic example: pulse propagation in a 2D plate

In this example we consider the propagation of a pulse in a plate to investigate, numerically, the spurious reflections that are generated when a pulse crosses the coupling interface. Consider a plate under plane stress conditions. The geometry and boundary conditions are illustrated in Fig. 6. A prescribed displacement with Gaussian shape is enforced on the right side of the plate and the propagation of the pulse is monitored. A summary of the problem parameters is given in Table 2. Similar to the previous example, $c\left(\varvec{\xi}\right)$ is assumed conical.

Fig. 6

Illustration of the geometry and the boundary conditions for the second verification example

Table 2 Summary of the problem parameters for the second verification problem

The aim of this example is to monitor the spurious reflections that are generated when the pulse crosses initially the FE-to-PD interface and subsequently the PD-to-FE interface. The total duration of the simulation is $t_{tot} = 10^{ - 4} \,{\text{s}}$ with $\varDelta t = 5 \times 10^{ - 8} \,{\text{s}}$. The displacement field obtained using the FE–PD model is compared with that obtained using a FE only model. The FE discretization is the same in both modes. Since there is no crack in this problem, there are no enriched terms and the computation of the lumped mass matrix, $\varvec{M}^{FE}$, that appears in Eq. 19 is carried out using a simple row summation on the consistent FE mass matrix.

To compare the two displacement fields the $L_{2}$ norm of error is implemented. The error is defined as:

$$ \left| {error} \right| = \left\| {\varvec{u}^{FE only} - \varvec{u}^{FE - PD} } \right\|_{2} . $$

(29)

Since the discretization is different in $\varOmega^{PD}$ and $\varOmega^{FE}$, the nodal points in $\varOmega^{PD}$ do not necessarily coincide with the FE nodal points. Thus, the solution in $\varOmega^{PD}$ is interpolated on the FE nodal points using linear interpolation.

The propagation of the Gaussian pulse is plotted in Fig. 7 at three time instants, $t_{1} = 0.19 \times 10^{ - 4} \,{\text{s}}$, $t_{2} = 0.56 10^{ - 4} \,{\text{s}}$ and $t_{3} = 0.79 \times 10^{ - 4} \,{\text{s}}$. The evolution of the error between the coupled FE–PD and the FE only models is plotted at the bottom row of Fig. 7. For $t = t_{1}$ the pulse has not reached yet the coupling interface and there is no error between the two models. At time instant $t = t_{2}$ the pulse has crossed the coupling interface and now lies within $\varOmega^{PD}$ in the middle part of the plate. A small reflection appears at the interface with a maximum amplitude of $0.7 \times 10^{ - 6} \,{\text{m}}$. This corresponds to 0.7% of the amplitude of the input pulse. The reflection is captured more accurately in the error plot. Finally, at $t = t_{3}$, the whole pulse has been transferred back to $\varOmega^{FE}$. As the pulse crosses once more the coupling interface, a reflection is generated. In [37], a similar example was used to evaluate the spurious reflections of a similar coupling methodology. Contrary to [37], in this work the nonlinear formulation of the PD theory is implemented in $\varOmega^{PD}$. Still, the reflections due to the coupling are comparable between the two contributions and within an acceptable range.

Fig. 7

Pulse propagation in the coupled FE–PD model captured at three time instants. In the top row $\varvec{u}_{x}$ is plotted for the whole plate, in the middle $\varvec{u}_{x}$ is plotted along the reference line indicated in Fig. 6 and the bottom row indicates the evolution of the relative error between the FE–PD model and a FE only solution

When the pulse crosses the coupling interface $\partial \varOmega_{1}$, part of the total energy is transferred from $\varOmega^{FE}$ to $\varOmega^{PD}$. The total energy, $E_{tot}^{FE}$ and $E_{tot}^{PD}$, is computed within $\varOmega^{FE}$ and $\varOmega^{PD}$, respectively, and plotted versus time in Fig. 8. In the same plot, the time instants illustrated in Fig. 7 are also indicated with dotted lines. At $t_{1} = 0.19 \times 10^{ - 4} \,{\text{s}}$ the pulse has not crossed $\partial \varOmega_{1}$ and $E_{tot}^{PD} = 0$ while at $t_{2} = 0.56 \times 10^{ - 4} \,{\text{s}}$ the pulse is within $\varOmega^{PD}$ and $E_{tot}^{PD}$ takes this maximum value with $E_{tot}^{PD} /E_{prov} = 0.20$. Finally, at $t_{3} = 0.79 \times 10^{ - 4} \,{\text{s}}$ the whole pulse is again within $\varOmega^{FE}$. If no reflections appeared the energy in $\varOmega^{PD}$ should go back to 0. Despite the appearance of spurious reflections, $E_{tot}^{PD}$ at the end of the simulation is low with $E_{tot}^{PD} /E_{prov} = 1.26 \times 10^{ - 5}$. No energy dissipation mechanisms have been incorporated in this analysis and the total energy is conserved.

Fig. 8

Energy distribution between $\varOmega^{FE}$ and $\varOmega^{PD}$

4 Convergence study of the XFEM–PD model

In this section an example featuring a strong discontinuity within the problem domain is considered. Contrary to publications that implement similar coupling methodologies (see e.g. [24, 54]), $\varOmega^{PD}$ is localized near the crack tip only and the discontinuity that appears within $\varOmega^{FE}$ is treated with the incorporation of the XFEM enrichment.

To be able to conduct the comparison with results available in the literature, the example of a double edge-notched plate under plane stress conditions presented in [60] is recreated. The dimensions of the plate are $L = H = 10\,{\text{cm}}$, $h = 0.1\,{\text{cm}}$ and the length of the crack is $a = 5\,{\text{cm}}$ on each side of the plate. The plate is assumed to behave elastically with Young’s modulus $E = 72\,{\text{GPa}}$ and Poison’s ratio $v = 1/3$. A uniform tensile pressure $p = 1\,{\text{MPa}}$ is applied along the top and bottom edges of the specimen. Due to the symmetry of the problem, only the left half of the plate is modelled, with appropriate boundary conditions being applied on the right edge. Following [60], $c\left(\varvec{\xi}\right)$ is conical and computed using Eq. 4. For comparison, three different configurations are used to approximate the resulting displacement fields (see also Fig. 9): (i) Case 1—FE only, (ii) Case 2—PD only, (iii) Case 3—coupled XFEM–PD. In Case 3 the shifted Heaviside enrichment has been employed to treat the displacement jump from the crack body in $\varOmega^{FE}$ and $\varOmega^{PD}$ is constructed as a square patch with $L^{PD} = H^{PD} = 0.04\,{\text{m}}$, centred at the location of the crack tip.

Fig. 9

Schematic illustration of the three models used for the comparison

The commercial software package Abaqus is employed to carry out the FE approximation in Case 1. The FE mesh is defined using 10,662 quadratic elements with 32,451 nodes. Near the crack tip region special crack-tip (collapsed) elements are used. The solution obtained from Case 1 is assumed to be a very close approximation to the exact solution and is used as a benchmark for comparison with the other cases. The numerical approximation of the solution for Cases 2 and 3 is carried out in MATLAB.

The discretization in $\varOmega^{PD}$ for Cases 2 and 3 is $\varDelta x^{PD} = \varDelta y^{PD} = 5 \times 10^{ - 4} \,{\text{m}}$ and the PD horizon is set to $\delta = 4 \times \varDelta x^{PD}$. In Case 3, $\varOmega^{FE}$ is discretized using $\varDelta x^{FE} = \varDelta y^{FE} = 3 \times 10^{ - 3} \,{\text{m}}.$ Furthermore, an additional fictitious material layer of PD particles, of thickness $\delta$, is added in Case 2 for the application of the boundary conditions, as suggested in [24]. In both Cases 2 and 3 the discretization is uniform. In total, the discretization led to 81,600 dof’s for Case 2 (40,800 PD particles) while for Case 3 the total number of dof’s is 17,844 (7744 PD particles and 1156 FE nodes of which 22 are enriched). It is evident that coupling FE with PD can significantly reduce the total number of dof’s compared to using a PD only analysis, while achieving similar discretization near the crack tip.

The simulated displacement fields for each of the cases considered are presented in Fig. 10. In the same figure, a black dotted line is used to indicate the coupling interface $\partial \varOmega_{1}$ in Case 3. For easier comparison the plots have been created using the same colour scales. Additionally, in Fig. 11, the plate is plotted in its deformed state for Case 3. The introduction of the shifted Heaviside enrichment at the elements cut by the crack, enables the FE method to facilitate discontinuous displacement fields and capture the displacement jump at the crack body. It is this property that allows the PD domain to be limited only in the area near the crack tip, without unmerging nodal displacements or specifically constructing the FE mesh to conform to the crack geometry. This will prove invaluable in the following paragraphs were crack propagation problems are considered. Notice also how using the definition from Eq. 14 the ghost particles that are positioned within an enriched element follow its deformation.

Fig. 10

Comparison of the displacement fields approximated using each model. A black dotted line indicates the XFEM–PD boundary $\partial \varGamma_{2}$ in Case 3

Fig. 11

Deformation of the double cantilever beam using Case 3. White squares indicate standard FE, yellow squares the enriched elements, blue dots the normal PD particles and grey dots the ghost particles. Displacements have been magnified by a factor of 1000 for clarity

The aim is to examine the performance and the convergence of the XFEM–PD model more rigorously and systematically. To this end, the $J$ contour integral is employed to allow for the comparison of the stress state near the crack tip. The $J$ contour integral was introduced by Rice [61] and has been used extensively both for linear and nonlinear fracture mechanics [1]. The formulation of the nonlocal $J$-integral for the PD theory can be found in the works of Silling and Lehoucq [39] and Hu et al. [60]. It is defined on a closed contour $\partial R$ that contains the crack tip and separates layers, $R_{1}$ and $R_{2}$, as illustrated in Fig. 12. Here the value of the $J$-integral is used as a tool to study the convergence of the coupled XFEM–PD model to the solution obtained using FE only or a PD only approximation.

Fig. 12

Definition of the contour region for the calculation of the nonlocal $J$-integral according to Hu et al. [60]

Two convergence studies are typically employed in PD [40,41,42, 60] namely (i) $m$-convergence where the PD horizon $\delta$ is kept constant while the discretization length is reduced and the solution converges to the nonlocal solution and (ii) $\delta$-convergence where the ratio $\delta /\varDelta x$ is kept constant and the solution converges to the classical solution as the PD theory converges to classical elasticity theory for $\delta \to 0$. A study on the convergence of the nonlocal $J$-integral using both convergence types can be found in [60].

Following [39, 60], the nonlocal $J$-integral can be approximated as:

$$ J = \mathop \sum \limits_{i = 1}^{{n_{c} }} W_{i} n_{i,x} \varDelta x^{PD} - \mathop \sum \limits_{k = 1}^{{n_{1} }} \mathop \sum \limits_{m = 1}^{{n_{2} }} \varvec{f}\left( {\varvec{\eta}_{k,m} ,\varvec{\xi}_{k,m} } \right) \cdot \left( {\frac{{\partial \varvec{u}_{m} }}{\partial x} + \frac{{\partial \varvec{u}_{k} }}{\partial x}} \right)hA_{k} A_{m} . $$

(30)

where $W_{i}$ is the strain energy density of particle $i$, $n_{c} ,n_{1}$ and $n_{2}$ are the number of particles on $\partial R$, $R_{1}$ and $R_{2}$ respectively, $A_{k}$ is the area associated with particle $k$ and $n_{i,x}$ is the horizontal component of the outward unit normal vector on the contour. To avoid inaccuracies in the approximation of the nonlocal $J$-integral, care must be given to select contours for which the definition of areas $R_{1}$ and $R_{2}$ is possible. The spatial displacement derivatives that appear in Eq. 30, can be approximated numerically using a central difference scheme as:

$$ \frac{{\partial \varvec{u}\left( \varvec{x} \right)}}{\partial x} \approx \frac{{\varvec{u}\left( {x + \varDelta x^{PD} ,y} \right) - \varvec{u}\left( {x - \varDelta x^{PD} ,y} \right)}}{{2\varDelta x^{PD} }}. $$

(31)

Using Case 1, the $J$-integral value for the double notched plate is computed as $J_{A} = 12.89\,{\text{Pa}}\,{\text{m}}$. This value was acquired after convergence tests with local refinement in the vicinity of the crack tip and it matches the one reported in [60] for the same problem. Therefore, it is considered a very close approximation to the analytical solution and will be used subsequently as a benchmarking tool. It is noted that Abaqus computes the $J$-integral using the domain integration method that is considered more robust compared to the direct contour approximation that is used in Eq. 30 [1]. For Cases 2 and 3, the $J$-integral is approximated using Eqs. 30 and $31$. The contour path is defined as a square, centred at the crack tip, with edge length $l^{c}$ (Fig. 12). The path is selected as a square for consistency and for compatibility with Case 3 where $\varOmega^{PD}$ is also square.

Although the path independence of the $J$-integral approximation in Eq. 30 has already been studied in [60], it is important to establish that this property is not affected by the XFEM–PD coupling in Case 3. Using again the same discretization (i.e. $\varDelta x^{FE} = \varDelta y^{FE} = 3 \times 10^{ - 3} \,{\text{m}}$, $\varDelta x^{PD} = \varDelta y^{PD} = 5 \times 10^{ - 4} \,{\text{m}}$ and $\delta = 4 \times \varDelta x^{PD}$), the $J$-integral is evaluated for different values of $l^{c}$. The results are compared with $J_{A}$ in terms of the relative % error.

In both cases we allow $0.004 \le l^{c} \le 0.036$ in order to ensure the feasibility of the contour, i.e. there is adequate clearance to define the areas $R_{1}$ and $R_{2}$ required for Eq. 30. Figure 13 illustrates the relative error for different $l^{c}$ values. The results exemplify that the $J$-integral approximation does not vary significantly for different contour paths. In fact, the maximum variation on the $J$-integral value is approximately 1.06% in both cases. The relative error is higher for paths closer to the crack tip. Typically, paths near the tip are avoided due to numerical inaccuracies. Still, Fig. 13, indicates that the variation is small, and the path independence is satisfied. The results in Fig. 13 also indicate that Case 3 leads to slightly better estimations of the $J$-integral value. This improvement could be due to the different way boundary conditions are applied in the PD theory. In the XFEM–PD model on the other hand, the boundary conditions are applied on $\varOmega^{FE}$.

Fig. 13

Comparison of the relative error between the $J$-integral computed from Cases 2 and 3 with $J^{Abaqus}$ for different contour paths

To illustrate the reduction of the dofs when Case 3 is used instead of Case 2, a convergence study is presented for different values of the discretization length $\varDelta x^{PD}$. The $J$-integral is computed each time using a square contour with $l^{c} = 0.02\,{\text{m}}$. In Case 3 the discretization of $\varOmega^{FE}$ remains unchanged and equal to $\varDelta x^{FE} = \varDelta y^{FE} = 3 \times 10^{ - 3} \,{\text{m}}$. The relative error to $J_{A}$ is plotted versus the total number of dofs in the final system of equations in Fig. 14. Using Case 2 the relative error exhibits a plateau at approximately $1.7\%$. A similar observation was reported in [60] for the same example. Although the convergence rate for Case 3 also deteriorates as the discretization of $\varOmega^{PD}$ becomes finer, the accuracy is improved. As reported in [62], use of XFEM with geometrical enrichment near the crack tip can achieve rates up to $O\left( {h^{2} } \right)$. Although the XFEM–PD does not achieve such rates, the convergence is improved compared to using a PD-only model. On the same figure the total dofs required to achieve $1.75\%$ accuracy is indicated with dotted lines for each case. Case 3 requires less than half the dofs to achieve the same accuracy as Case 2. This increase of performance in Case 3 can be traced back to the fact that for the same number of dofs, Case 3 achieves a finer discretization in $\varOmega^{PD}$.

Fig. 14

Convergence of the J-integral value approximated using Cases 2 and 3 to $J^{Abaqus}$ versus the total number of dofs. Logarithmic scale is used for both axes

The convergence of the J-integral value is also presented for different values of the PD horizon $\delta = n \cdot \varDelta x^{PD}$, $n = 2, 3, \ldots ,6$ and $l^{c} = 0.02\,{\text{m}}$. The results are plotted in Fig. 15 versus the PD discretization length $\varDelta x^{PD}$. When very coarse discretization is used in $\varOmega^{PD}$, the relevant error of Case 3 can be higher compared to Case 2 as the coupling between the two models becomes inaccurate. Higher values of the PD horizon improve the convergence in both cases, while in Case 2, it also affects the value where it exhibits the plateau. As discussed in [60], appropriate selection of $n$ and $\varDelta x^{PD}$ can be made to match exactly the PD solution with classical elasticity. Low values of $\delta$ however, can lead to mesh dependencies during crack propagation while high values induce excessive dispersion and increase the computational cost [38, 63]. For macroscale 2D fracture problems values $n \ge 3$ are typically selected [42]. For the computation of the nonlocal $J$-integral, the value $n = 4$ seems a fair compromise between accuracy and computational cost.

Fig. 15

Convergence of the J-integral value approximated using Cases 2 and 3 for different values of the PD discretization $\varDelta x^{PD}$ and the PD horizon $\delta = n \cdot \varDelta x^{PD}$

Apart from the accuracy improvement the coupled models exhibit compared to the PD-only model, the efficiency of the numerical approximation is also boosted significantly in terms of computational time and memory requirements. This development is directly related to the reduction of the total dofs. To illustrate this improvement, the required time to solve the resulting system of equations was evaluated for each case, using different values of $\varDelta x^{PD}$ in $\varOmega^{PD}$. The analyses were carried out using a system with 16 GB total memory and an i7 8700 K CPU, running at default settings. For all analyses, the PD horizon was set as $\delta = 4\varDelta x^{PD}$ while for Case 3 the discretization of $\varOmega^{FE}$ was also kept constant with $\varDelta x^{FE} = \varDelta y^{FE} = 3 \times 10^{ - 3} \,{\text{m}}$. In both cases, the same Newton–Raphson solver and MATLAB’s backslash operator is used to solve the system of equations described in Eq. 21. The required CPU time for each case as well as the relative speed up between Case 2 and Case 3 are plotted in Fig. 16.

Fig. 16

Comparison of the CPU time needed for each case (left) and the relative speed-up between Case 2 and Case 3 (right). Logarithmic scale is used in all axes

Employing a coupled model can reduce the required computational effort while achieving the same discretization in $\varOmega^{PD}$. For example, the CPU time elapsed when $\varDelta x^{PD} = 5 \times 10^{ - 4} \,{\text{m}}$ is $t^{{{\text{Case}} 2}} = 170.1\,{\text{s}}$ and $t^{{{\text{Case}} 3}} = 34.38\,{\text{s}}$. There are two main reasons that contribute towards the reduction of the CPU time: (i) the reduction in terms of total dofs that lead to a computationally more manageable system of equations and (ii) use of classical elasticity away from the crack tip, assumes a local description, that further boosts the computational efficiency by increasing the sparsity of the equivalent stiffness matrix, i.e. reduces the required algebraic operations in the numerical approximation.

Case 3 entails the additional cost of enforcing the coupling between the two domains. When coarse discretization is implemented in $\varOmega^{PD}$, this additional cost becomes significant compared to the total simulation time and the relative speed up is small, despite the implementation of a local model away from the crack tip. As the PD discretization becomes finer, particularly when $\varDelta x^{PD} < \varDelta x^{FE}$, which is expected to be the typical case for practical applications, the computational gains are highlighted. Compared to Case 2, Case 3 can achieve a speed-up up to $5$ times faster. Thus, coupling of PD grids with FE meshes and the incorporation of XFEM notions can significantly increase the computational efficiency of a coupled model. It is noted here that these results are not meant to be used as a suggestion on the selection of the discretization parameters $\varDelta x^{PD}$ and $\varDelta x^{FE}$. They do offer, however, an indication on the potential gains that a coupled model can offer. Proper selection of the discretization parameters for each domain is particularly important for dynamic problems as they influence the spurious reflections generated when a pulse crosses the coupling interface.

Lastly, the size influence of $\varOmega^{PD}$ on the accuracy of the $J$-integral approximation is evaluated for the XFEM–PD model. The discretization for each model is $\varDelta x^{PD} = \varDelta y^{PD} = 5 \times 10^{ - 4} \,{\text{m}}$ and $\varDelta x^{FE} = \varDelta y^{FE} = 3 \times 10^{ - 3} \,{\text{m}}.$ The PD patch is constructed as a square patch, centred at the crack tip, with side $0.01\,{\text{m}} \le L^{PD} \le 0.94\,{\text{m}}$. The contour used is defined as a square with side $l^{c} = 0.004\,{\text{m}}$, which is the smallest feasible contour. These values are set to allow for at least one layer of FE’s for the application of the loading and boundary conditions and to ensure that computation of the $J$-integral is feasible and is evaluated along the same contour for all cases. The results are plotted in Fig. 17. As $\varOmega^{PD}$ becomes smaller, the PD approximation converges to the $J$-integral value from classical elasticity. Even when $L^{PD} = 5\delta$, the results remain accurate. Obviously, the size of the PD patch affects the computational efficiency of the model and it is desirable to be as small as possible. The results indicate the if the crack tip is covered by a layer of thickness $2.5\delta \sim3\delta$, the $J$-integral approximation will remain accurate. This is important in the current study as during the adaptive relocation of $\varOmega^{PD}$ and $\varOmega^{FE}$, that is presented on the following sections, a criterion is used to ensure that at each time instant the crack tip is sufficiently covered within $\varOmega^{PD} .$

Fig. 17

Influence of the PD patch size on the $J$-integral value. The $x$-axis is plotted in reverse order

5 Static mode I crack propagation example

The XFEM–PD model is used in this section to simulate the crack propagation in a static model I fracture problem. Consider a double cantilever beam with a pre-existing edge breaking crack. The initial crack length is $\alpha = 0.3 \,{\text{mm}}$ and linear elastic material behaviour is assumed under plane stress conditions. The Young’s modulus, Poisson’s ratio and energy release rate are taken as $E = 75 \,{\text{GPa}}$, $v = 1/3$ (due to the PD restriction) and $G_{c} = 5\, {\text{N/m}}$, respectively. To ensure stable crack propagation, a displacement control approach is adopted. Two clamps are fixed at the bottom and top left corners, as illustrated in Fig. 18. It is also assumed that the loading is applied slowly, and the inertia effects can be neglected. The clamps are displaced by $\delta_{y} = 1.5 10^{ - 3} \,{\text{mm}}$ and the reaction force is monitored during the propagation of the crack.

Fig. 18

Illustration of the geometry and boundary conditions for the double cantilever beam

In Fig. 18, the definition of $\varOmega^{PD}$ and $\varOmega^{FE}$ is also illustrated. Specifically, $\varOmega^{PD}$ is constructed in such a way that includes both the initial and the final location of the crack tip. Based on the findings from the previous section, the PD horizon is set to $\delta = 4\varDelta x^{PD}$. Furthermore, a conical micromodulus function is used and the value of $c\left(\varvec{\xi}\right)$ is computed using Eq. 4. The height of $\varOmega^{PD}$, denoted with $L^{PD}$, can be varied to evaluate the size influence of $\varOmega^{PD}$ on the accuracy of the simulation. The prescribed displacement is applied over 200 increments and the solution of the system of equations is approximated using the Newton–Raphson iterative solver. For simplicity only uniform structured grids are used in $\varOmega^{PD}$ and $\varOmega^{FE}$, with $\varDelta x^{PD} = \varDelta y^{PD}$ and $\varDelta x^{FE} = \varDelta y^{FE}$, respectively.

Initially, we set $L^{PD} = 0.15\,{\text{mm}}$ and the discretization parameters are defined as $\varDelta x^{PD} = 2.5 \times 10^{ - 3} \,{\text{mm}}$ and $\varDelta x^{FE} = 10 \times 10^{ - 3} \,{\text{mm }}$ for the PD and FE domains, respectively. In total, 42,196 dofs are used for the discretization of the problem (16,864 PD particles and 4186 FE nodes of which 48 are enriched). The crack is free to propagate within $\varOmega^{PD}$ and its evolution is depicted in Fig. 19 for three different load increments. Since this is a simple Mode I problem, the crack is expected to propagate horizontally, and it is easy to construct $\varOmega^{PD}$, accordingly. The crack is free to propagate in any direction in $\varOmega^{PD}$ but is restricted by its shape. Using this set-up, the simulated peak reaction force is $P = 20.86 \times 10^{ - 4} \,{\text{N}}$ and the final crack length is $a_{f} = 0.6487\,{\text{mm}}$. For validation, the same example is repeated two times, the first time a coarser discretization is used in $\varOmega^{PD}$ with $\varDelta x^{PD} = 3.5 \times 10^{ - 3} \,{\text{mm}}$ while the second time, a PD only model is used, with $\varDelta x^{PD} = 2.5 \times 10^{ - 3} \,{\text{mm}}$. Using the PD only model, the total number of dofs is 131,040 (65,520 PD particles). Use of a coupled model can reduce significantly the total number of dofs for crack propagation problems, compared to a PD-only model with the same discretization. The reaction force $P$, versus the applied displacement $\delta_{y}$ is plotted in Fig. 20 for each case. The results from the XFEM–PD model are in close agreement with those obtained using a PD-only model. The peak reaction force predicted using the PD only model is $P = 20.50 \times 10^{ - 4} \,{\text{N}}$ and the final crack length is $a_{f} = 0.6437\,{\text{mm}}$ and the total CPU time is $t^{PD} = 11{,}986\,{\text{s}}$.

Fig. 19

Crack evolution at three different load increments for $L^{PD} = 0.15\,{\text{mm}}$. White and yellow squares are used to indicate the standard and enriched FE’s, respectively

Fig. 20

Comparison of the reaction force versus the applied displacement using a PD-only model and the XFEM–PD model with $L^{PD} = 0.15 \,{\text{mm}}$

The problem is also repeated with the XFEM–PD model for different values of $\varDelta x^{PD}$, $\varDelta x^{FE}$ and $L^{PD}$ and the results are summarized in Table 3. For all combinations of parameters, the final crack length does not vary considerably, and the differences are of the order of approximately one discretization length, $\varDelta x^{PD}$. Combinations $3$ and $8$ refer to the results of the XFEM–PD model plotted in Fig. 20. For combination numbers $1 - 7$, the discretization parameters $\varDelta x^{PD}$ and $\varDelta x^{FE}$ are kept constant while $L^{PD}$ is increased. As $L^{PD}$ increases, and thus $\varOmega^{PD}$ is used for a larger portion of the plate, $P$ decreases and approaches the value obtained from the PD-only model. The same observation is true for combinations $9$ and $10$ where the discretization in $\varOmega^{FE}$ is refined, with $\varDelta x^{FE} = 5 \times 10^{ - 3} \,{\text{mm}}$. Although from these results it is not easy to infer general guidelines on the size and discretization of $\varOmega^{PD}$ and $\varOmega^{FE}$, it can be seen the final crack length remains almost unaffected. Additionally, the peak force estimation is accurate even when the clearance between the crack and the coupling interface is only $2.5\delta$. This observation is also in agreement with the results plotted in Fig. 17. Finally, the CPU time required for the simulation of the XFEM–PD mode and the relative speed-up compared to the PD-only model is included in the last two columns of Table 3. Obviously, by reducing the size of $\varOmega^{PD}$ the efficiency of the model is improved.

Table 3 Summary of the parameters and the resulting peak force and final crack length obtained from the XFEM–PD model

6 Conclusions and future work

In the present work a methodology for the coupling of two different models, namely Bond-Based peridynamics and classical elasticity, is presented. The aim is to explore possible pathways for the reduction of the computational cost that is associated with the implementation of nonlocal models. The problem domain is subdivided into $\varOmega^{PD}$ and $\varOmega^{FE}$ where the PD theory and elasticity are used, respectively. The coupling methodology used in [37] is modified to allow for the introduction of the XFEM in the coupling region and the use of the original PD formulation. This approach has the benefit of localizing $\varOmega^{PD}$ to a small area that contains the crack tip while at least part of the crack body can appear in $\varOmega^{FE}$. There is no need to construct meshes that conform to the crack geometry as the discontinuous displacement field is captured through the introduction of the Heaviside functions. The area that is modeled using the computationally intensive PD model is thus limited and $\varOmega^{PD}$ is inserted away from boundary conditions and geometrical boundaries that can be cumbersome for PD.

The effectiveness and feasibility of the coupling is evaluated through a series of examples. Two simple problems are solved first to evaluate the coupling under static and dynamic conditions. During pulse propagation specifically, the amplitude of the reflected pulse is comparable to the results presented in [37] while accurate energy transmission is achieved. Then the example of the double edge-notched specimen is solved. In total four different numerical models were used to approximate the solution: a FE only model (Case 1) realized in the commercial software Abaqus, a PD only model (Case 2), and a XFEM–PD model (Case 3) where $\varOmega^{PD}$ is limited near the crack tip only. The $J$-integral value is used to study the performance of the XFEM–PD model. The results indicate that the XFEM–PD model reduces significantly the number of degrees of freedom compared to the PD only, while achieving the same level of accuracy. This leads to a computationally more manageable system both in terms of CPU time needed and required memory resources. Finally, crack propagation is simulated for a model I fracture problem using the XFEM–PD model and the results are compared with the solution obtained from PD. A parametric investigation is also presented to study the size effect of $\varOmega^{PD}$. The results indicate that the solution remains accurate when the crack is covered by approximately $2.5\delta$.

Two disadvantages are highlighted by the crack propagation problem. The first is that in order to construct $\varOmega^{PD}$ in such a way that contains both the initial and the final location of the crack, knowledge of the general crack path is required a priori. In many problems that may contain complex patterns or multiple cracks, this is not possible. The second is that use of the PD theory is unnecessary in certain areas. For example, during the initial and final stages of the simulation, use of PD far from the crack tip is not required. These problems can be circumvented through the introduction of an adaptive relocation strategy for fracture problems that can further boost the efficiency of the method.

Appendix A: Computation of \( {\mathbf{\mathcal{J}}}_{{\varvec{g}\left( \varvec{d} \right)}} \)

In this “Appendix A” the computation of the Jacobian for the PD equation of motion is presented. Assume a uniform 2D grid for the discretization of the problem and let $n^{PD}$ be the set of all particles. Then the total number of particles is $n_{p} = \left| {n^{PD} } \right|$ and since the grid is uniform $V_{i} = V, i = 1, 2, \ldots , n_{p}$. Using Eqs. 2 and 5, we can write:

$$ \varvec{g}_{i} = cV\mathop \sum \limits_{j = 1}^{{M_{i} }} \left( {\frac{{\varvec{d}_{j} - \varvec{d}_{i} +\varvec{\xi}_{i,j} }}{{\vert|\varvec{\xi}_{i,j}\vert| }} - \frac{{\varvec{d}_{j} - \varvec{d}_{i} +\varvec{\xi}_{i,j} }}{{\vert|\varvec{d}_{j} - \varvec{d}_{i} +\varvec{\xi}_{i,j} \vert|}}} \right) + \varvec{b}_{i} = 0, \quad i = 1, 2, \ldots , n_{p} \varvec{ } $$

(A.1)

where $M_{i} \subset n^{PD}$ is a set that contains the particles within the horizon of particle $i$ and for simplicity a constant micromodulus is assumed, i.e. $c\left(\varvec{\xi}\right) = c$. The solution of the system defined in Eq. A.1 using the Newton–Raphson method requires the computation of the Jacobian:

$$ {\mathcal{J}}_{{g\left( \varvec{d} \right)}} = \frac{{\partial \varvec{g}}}{{\partial \varvec{d}}} = \left[ {\begin{array}{*{20}l} {\frac{{\partial g_{1,x} }}{{\partial d_{1,x} }}} \hfill & {\frac{{\partial g_{1,x} }}{{\partial d_{1,y} }}} \hfill & {\frac{{\partial g_{1,x} }}{{\partial d_{2,x} }}} \hfill & {\frac{{\partial g_{1,x} }}{{\partial d_{2,y} }}} \hfill & \cdots \hfill & {\frac{{\partial g_{1,x} }}{{\partial d_{{n_{p} ,x}} }}} \hfill & {\frac{{\partial g_{1,x} }}{{\partial d_{{n_{p} ,y}} }}} \hfill \\ {\frac{{\partial g_{1,y} }}{{\partial d_{1,x} }}} \hfill & {\frac{{\partial g_{1,y} }}{{\partial d_{1,y} }}} \hfill & \ddots \hfill & \ddots \hfill & {} \hfill & \vdots \hfill & \vdots \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \ddots \hfill & {} \hfill & \vdots \hfill & \vdots \hfill \\ {\frac{{\partial g_{{n_{p} ,y}} }}{{\partial d_{1,x} }}} \hfill & {\frac{{\partial g_{{n_{p} ,y}} }}{{\partial d_{1,y} }}} \hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill & {\frac{{\partial g_{{n_{p} ,x}} }}{{\partial d_{{n_{p} ,y}} }}} \hfill & {\frac{{\partial g_{{n_{p} ,y}} }}{{\partial d_{{n_{p} ,y}} }}} \hfill \\ \end{array} } \right] $$

(A.2)

where the notation $\left\langle \cdot \right\rangle_{,x}$ and $\left\langle \cdot \right\rangle_{,y}$ is used to denote the horizontal and the vertical components, respectively. The derivatives in Eq. A.2 can be expressed in a closed form that is convenient for software implementation as:

$$ \begin{aligned} & \frac{{\partial g_{i,\alpha } }}{{\partial d_{k,\beta } }} = cV\mathop \sum \limits_{j = 1}^{{M_{i} }} \frac{\partial }{{\partial d_{k,\beta } }} \\ & \quad \times \left( {\frac{{d_{j,\alpha } - d_{i,\alpha } + \xi_{i,j,\alpha } }}{{\left\| {\varvec{\xi}_{i,j} } \right\|}} - \frac{{d_{j,\alpha } - d_{i,\alpha } + \xi_{i,j,\alpha } }}{{\left\| {\varvec{d}_{j} - \varvec{d}_{i} +\varvec{\xi}_{i,j} } \right\|}}} \right), \\ &\quad \begin{array}{*{20}c} {k,i = 1, 2, \ldots , n_{p} } \\ {\alpha ,\beta = x,y.} \\ \end{array} \end{aligned} $$

(A.3)

The above derivative vanishes when $k \notin M_{i}$ or $k \ne i$.

Let $m \in M_{i}$ and set $k = m$ in Eq. A.3, then:

$$ \frac{{\partial g_{i,\alpha } }}{{\partial d_{m,\beta } }} = cV\frac{\partial }{{\partial d_{m,\beta } }}\left( {\frac{{d_{m,\alpha } - d_{i,\alpha } + \xi_{i,m,\alpha } }}{{\left\| {\varvec{\xi}_{i,m} } \right\|}} - \frac{{d_{m,\alpha } - d_{i,\alpha } + \xi_{i,m,\alpha } }}{{\left\| {\varvec{d}_{m} - \varvec{d}_{i} +\varvec{\xi}_{i,m} } \right\|}}} \right). $$

(A.4)

We can expand Eq. A.4 to arrive to the following expressions:

$$ \frac{{\partial g_{i,x} }}{{\partial d_{m,x} }} = cV\left( {\frac{1}{{\left\| {\varvec{\xi}_{i,m} } \right\|}} - \frac{1}{{a_{i,m} }} + \frac{{\left( {d_{m,x} - d_{i,x} + \xi_{i,m,x} } \right)^{2} }}{{a_{i,m}^{3} }}} \right). $$

(A.5a)

$$ \frac{{\partial g_{i,x} }}{{\partial d_{m,y} }} = \frac{{\partial g_{i,y} }}{{\partial d_{m,x} }} = cV\left( {\frac{{\left( {d_{m,x} - d_{i,x} + \xi_{i,m,x} } \right)\left( {d_{m,y} - d_{i,y} + \xi_{i,m,y} } \right)}}{{a_{i,m}^{3} }}} \right) $$

(A.5b)

$$ \frac{{\partial g_{i,y} }}{{\partial d_{m,y} }} = cV\left( {\frac{1}{{\left\| {\varvec{\xi}_{i,m} } \right\|}} - \frac{1}{{a_{i,m} }} + \frac{{\left( {d_{m,y} - d_{i,y} + \xi_{i,m,y} } \right)^{2} }}{{a_{i,m}^{3} }}} \right). $$

(A.5c)

where $a_{i,j} = \left\| {\varvec{d}_{\varvec{j}} - \varvec{d}_{\varvec{i}} +\varvec{\xi}_{{\varvec{i},\varvec{j}}} } \right\|$ is used for short.

If, on the other hand, we set $k = i$ in Eq. A.3, then we get:

$$ \frac{{\partial g_{i,\alpha } }}{{\partial d_{i,\beta } }} = - \mathop \sum \limits_{j = 1}^{{M_{i} }} \frac{{\partial g_{i,\alpha } }}{{\partial d_{j,\beta } }} $$

(A.6)

Using Eqs. A.5 and A.6 the computation of the Jacobian matrix can be vectorized for efficient computer implementation.