Selective ensemble of uncertain extreme learning machine for pattern classification with missing features

Abstract

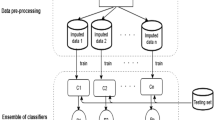
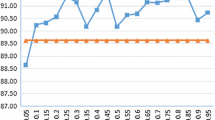
Ensemble learning is an effective technique to improve performance and stability compared to single classifiers. This work proposes a selective ensemble classification strategy to handle missing data classification, where an uncertain extreme learning machine with probability constraints is used as individual (or base) classifiers. Then, three selective ensemble frameworks are developed to optimize ensemble margin distributions and aggregate individual classifiers. The first two are robust ensemble frameworks with the proposed loss functions. The third is a sparse ensemble classification framework with the zero-norm regularization, to automatically select the required individual classifiers. Moreover, the majority voting method is applied to produce ensemble classifier for missing data classification. We demonstrate some important properties of the proposed loss functions such as robustness, convexity and Fisher consistency. To verify the validity of the proposed methods for missing data, numerical experiments are implemented on benchmark datasets with missing feature values. In experiments, missing features are first imputed by using expectation maximization algorithm. Numerical experiments are simulated in filled datasets. With different probability lower bounds of classification accuracy, experimental results under different proportion of missing values show that the proposed ensemble methods have better or comparable generalization compared to the traditional methods in handling missing-value data classifications.

Appendices

Appendix 1

In this appendix, we prove the following triangle inequality holds for $\eta (u)=1-\epsilon ^{-\alpha |u|},(\alpha >0 , u\in R)$:

$$\begin{aligned}&\eta (u_1+u_2)\le \eta (u_1)+\eta (u_2),\forall u_1,u_2\in R \end{aligned}$$

(39)

$$\begin{aligned}&\eta (u_1)+\eta (u_2)-\eta (u_1+u_2) \\&\quad =(1-\epsilon ^{-\alpha |u_1|})+(1-\epsilon ^{-\alpha |u_2|})- (1-\epsilon ^{-\alpha |u_{1}+u_{2}|}) \\&\quad =1-\epsilon ^{-\alpha |u_1|}-\epsilon ^{-\alpha |u_2|}+ \epsilon ^{-\alpha |u_{1}+u_{2}|} \\&\quad \ge 1-\epsilon ^{-\alpha |u_1|}-\epsilon ^{-\alpha |u_2|}+ \epsilon ^{-\alpha (|u_{1}|+|u_{2}|)} \\&\quad =1-\epsilon ^{-\alpha |u_1|}-\epsilon ^{-\alpha |u_2|}+ \epsilon ^{-\alpha |u_1|}\cdot \epsilon ^{-\alpha |u_2|} \\&\quad =1-\epsilon ^{-\alpha |u_2|}+\epsilon ^{-\alpha |u_1|} (\epsilon ^{-\alpha |u_2|}-1) \\&\quad =(1-\epsilon ^{-\alpha |u_2|})\cdot (1-\epsilon ^{-\alpha |u_1|}) \\&\quad \ge 0. \end{aligned}$$

(40)

The first inequality holds for $|u_{1}+u_{2}|\le (|u_{1}|+|u_{2}|)$ accompanied by the monotone decreasing of $f(x)=\epsilon ^{-x}$. The last inequality holds for $\alpha >0$.

Appendix 2

Generally speaking, a DC program takes the form

$$\begin{aligned} \inf \{f(x)=g(x)-h(x),\,\, x\in R^{n}\} ~~~~~(P_{dc}) \end{aligned}$$

(41)

where g and h are lower semicontinuous proper convex functions on $R^{n}$. Such a function f is called a DC function. g and h are the DC components of f. A function $\pi (x)$ is said to be polyhedral convex if

$$\begin{aligned} \pi (x)=max\{\varpi _{i}^{T}x-\sigma _{i},i=1,2,\ldots m\}+\chi _{{\varOmega }}(x),\forall x\in R^{n} \end{aligned}$$

(42)

where $\varpi _{i}\in R^{n},\sigma _{i}\in R,(i=1,2,\ldots m )$. The $\chi _{{\varOmega }}(x)$ is the indicator function of the non-empty convex set ${\varOmega }$, and is defined as: $\chi _{{\varOmega }}=0$ if $x\in {\varOmega }$ and $+\infty$ otherwise. A DC program is called a polyhedral DC program when either g or h is a polyhedral convex function.

A point $x^{*}$ that satisfies the following generalized Kuhn–Tucker condition is called a critical point of $(P_{dc})$

$$\begin{aligned} \partial h(x^{*})\cap \partial g(x^{*})\ne \emptyset \end{aligned}$$

(43)

where $\partial h$ is the subdifferential of the convex function h. It follows that if h is polyhedral convex, then such a critical point for $(P_{dc})$ is almost always a local solution for $(P_{dc})$.

The necessary local optimality condition for $(P_{dc})$ is

$$\begin{aligned} \partial h(x^{*})\subset \partial g(x^{*})\ne \emptyset \end{aligned}$$

(44)

which is also sufficient for many important classes of DC programs, for example, polyhedral DC programs or when f is locally convex at $x^{*}$. We use $g^{*}(y)=\sup \{x^{T}y-g(x),x\in R^{n}\}$ to denote the conjugate function of g. The Fenchel–Rockafellar dual of $(P_{dc})$ is defined as

$$\begin{aligned} \inf \{h^{*}(y)-g^{*}(y),y\in R^{n}\} ~~~~~~~~~~~~~~~~(D_{dc}) \end{aligned}$$

(45)

DCA is an iterative algorithm based on local optimality conditions and duality. The idea of DCA is simple: at each iteration, one replaces the second component h in the primal DC problem $(P_{dc})$ by its affine minorization, $h(x^{k})+(x-x^{k})^{T}y^{k}$, to generate the convex program

$$\begin{aligned} \min \{g(x)-h(x^{k})-(x-x^{k})^{T}y^{k},x\in R^{n},y^{k}\in \partial h(x^{k}) \} \end{aligned}$$

(46)

which is equivalent to determining $x^{k+1} \in \partial g^{*}(y^{k})$. Likewise, the second DC component $g^{*}$ of the dual DC program $(D_{dc})$ is replaced by its affine minorization, $g^{*}(y^{k})+(y-y^{k})^{T}x^{k+1}$, to obtain a convex program that is equivalent to determining $y^{k+1}\in \partial h(x^{k+1})$.

In practice, a simplified form of the DCA is used. Two sequences $\{x^{k}\}$ and $\{y^{k}\}$ satisfying $y^{k}\in \partial h(x^{k})$ are constructed, and $x^{k+1}$ is a solution to the convex program (46). The simplified DCA scheme is described as follows.

Initialization: Choose an initial point $x^{0}\in R^{n}$ and set $k=0$

Repeat

Calculate $y^{k}\in \partial h(x^k)$

Solve convex program (46) to obtain $x^{k+1}$ Let k:=k+1

Until some stopping criterion is satisfied.

DCA is a descent algorithm without linesearch. The following properties are used in next sections :(for simplicity, we omit the dual part of these properties).

• (1) If $g(x^{k+1})-h(x^{k+1}) = g(x^{k})-h(x^{k})$, then $x^{k}$ is a critical point for $(P_{dc})$. In this case, DCA terminates at k-th iteration.

• (2) Let $y^{*}$ be a local solution to the dual of $(P_{dc})$ and $x^{*}\in \partial g^{*}(y^{*})$. If h is differentiable at $x^{*}$, then $x^{*}$ is a local solution to $(P_{dc})$.

• (3) If the optimal value of problem $(P_{dc})$ is finite and the infinite sequence $\{x^{k}\}$ is bounded, then every limit point $x^{*}$ of the sequence $\{x^{k}\}$ is a critical point of $(P_{dc})$.

• (4) DCA converges linearly for general DC programs. Especially, for polyhedral DC programs, the sequence $\{x^{k}\}$ contains finitely many elements, and in a finite number of iterations the algorithm converges to a critical point satisfying the necessary optimality condition.

Moreover, if the second DC component h in $(P_{dc})$ is differentiable , then the subdifferential of the h at point $x^{k}$ is reduced to a singleton, $\partial h(x^{k})=\{\bigtriangledown h(x^{k})\}$. In this case, $x^{k+1}$ is a solution to the following convex program:

$$\begin{aligned} \min \{g(x)-(h(x^{k})+\nabla h(x^{k})^{T}(x-x^{k})),x\in R^{n}\} \end{aligned}$$

(47)