An inviscid model of unsteady separated vortical flow for a moving plate

Abstract

An inviscid vortex shedding model for separated vortices from a solid body is studied. The model describes the separated vortices by vortex sheets and the attached flow via conformal mapping. We develop a computational model to simulate the vortex shedding of a moving body, with varying angle. An unsteady Kutta condition is imposed on the edges of the plate to determine the edge circulations and velocities. The force on the plate is obtained by integrating the unsteady Blasius equation. We apply the model to two representative cases of an accelerated plate, with impulsive start and uniform acceleration, and investigate the dynamics for large angles of attack. For both cases, the vortex force is dominant in the lift over times. The lift coefficients are initially high and decrease in four chord lengths of displacement, in general. For large angles of attack, the appearance of a peak of lift at an early time depends on the power-law velocity, which differs from the behavior for small angles of attack. The lift and drag from the model are in agreement with the Navier–Stokes simulation and experiment for moderate Reynolds numbers. We also demonstrate the vortex shedding of hovering and flapping plates. In the hovering motion, the large increase in lift at the early backward translation is due to the combined effect of the vortex force and added mass force. In the flapping plate, our model provides an improvement in the prediction for the induced force than other shedding models.

1 Introduction

The flight of insects and birds has attracted much attention for the past decades owing to its potential applications to microair vehicles. It has been shown that the conventional aerodynamic theory based on steady flows cannot explain the generation of large lift by small insects, and therefore, unsteady aerodynamics should be considered. Typical flapping-wing animals fly in the regime of Reynolds number 10–10, 000 and employ high angles of attack. Various aerodynamic mechanisms have been proposed for lift generation of hovering flights [1,2,3,4,5].

Unsteady vortex separation during the thrust stroke of the wing motion plays a crucial role in the production of forces in the flapping flight [6]. At high Reynolds numbers, the diffusion of vorticity is negligible compared with its inertial motion; hence, the evolution of the separated flow can be approximated by the inviscid vortex particles. The early vortex models by Wagner [7] and von Karman and Sears [8] included only the trailing-edge vortex. These models admit analytical solutions by assuming that the vortex particles are fixed after deposition, but are applicable to small angles of attack.

The main approaches for modeling of the unsteady separated vortical flow are categorized into two classes: discontinuous models (point vortices) and continuous models (vortex sheets). The former models [9,10,11] release discrete point vortices to model the free shear layers separated from a body and allow the vortices to move according to vortex dynamics. The number of point vortices is increased in time to capture the rich structures of the coherent vortex [12, 13]. Another type of vortex model uses the shedding of point vortices with unsteady intensity, following the Brown–Michael equation [14], which conserves the fluid momentum around the vortex. When a point vortex reaches a maximum intensity, its intensity is frozen and a new vortex is released [15,16,17].

The unsteady separated flows are more accurately modeled by spiral vortex sheets, where a continuous vortex distribution is shed and advected by the flow following the Birkhoff–Rott equation [18]. In this approach, both the solid body and separated vortices are described as vortex sheets [19]. Jones [20] developed the model for a moving rigid body, with large angles of attack. In this model, the kinematic condition (continuity of the normal velocity) on the body gives a Cauchy-type singular integral equation for the sheet strength on the body. The unsteady Kutta condition is imposed to regularize the solution at the edges of the body, which is critical when modelling the shedding process. The several different forms of the unsteady Kutta condition were presented in this model [19,20,21].

The vortex sheet model has been applied to various problems of vortex-body interactions [21, 22] including falling sheets [23, 24], flapping plates and flags [25, 26], hovering and insect flights [27,28,29] and an airfoil [30]. Although this model demonstrated the phenomenon of vortex shedding qualitatively, the validity regime of the model, in terms of the Reynolds number, was not examined, especially for the lift and drag. This model describes the vortex-dominated flow and is expected to be valid for high Reynolds numbers. Recent studies [29, 31] reported that this model is in good agreement with the flows of an impulsively started plate and pitch-up plate for $\text{ Re } \sim 1000$, but the model is in some disagreement with the flow of the clap and fling motion of insect flights (known as the Weis–Fogh mechanism [1]) for $\text{ Re } \sim 100$. This model thus would not be suitable for the study of flight of small insects, because the flow field induced by wing flapping of small insects is in the low Reynolds number regime, $\text{ Re } = O(10^1) - O(10^2)$. For example, small insects such as fruit flies, butterflies and moths fly in the moderate Reynolds numbers, $\text{ Re } = O(10^2)$, while tiny insects such as wasps and thrips fly in the low Reynolds numbers, $\text{ Re } = O(10)$.

A different type of the vortex sheet model for separated vortices from a solid body was proposed by Pullin and Wang [32], for the theoretical study of an accelerated plate. In this model, complex conformal mapping is used to describe the attached flow. Pullin and Wang approximated the free vortex sheets by single point vortices and found a self-similar solution for the unsteady force on an accelerated plate with fixed angles of attack. However, this self-similar solution is valid when the scale of the separated vortex is much smaller than the scale of the plate, and therefore, it is valid only for small times. In this study, by utilizing Pullin and Wang’s theory, we develop a computational model for a moving plate with varying angles, to simulate the vortex shedding phenomena of large structures.

The vortex shedding model based on conformal mapping provides several advantages. The kinematic condition on the body is automatically satisfied in this model, and thus, the model does not need an integral equation for the sheet strength on the body. The unsteady Kutta condition is therefore given in a simple form, with no ambiguity. From the analytic modelling of the flow, the expression for the aerodynamic force on the body is found by integrating the unsteady Blasius equation. Decomposing the force into several parts, the effects of each component of force such as added mass and the separated flow can be monitored. We demonstrate that a prediction for the force on the body is significantly improved than the other vortex shedding models, in a certain situation. We also show that the model is valid for the flow of moderate Reynolds numbers, which is applicable to the flights of small insects. Furthermore, this model is useful for other geometries such as wedge shapes [33, 34], which provides a simple formulation.

We apply the vortex shedding model to various moving plates, mainly focusing on the dynamics of an accelerated plate of the power-law velocity with fixed angles of attack, and conduct longtime simulations. Only a few studies have thoroughly studied the effects of airfoil acceleration on the dynamic forces and vortex structures. Dickinson and Götz [35] performed experiments on a nominally two-dimensional wing, employing impulsively started translations over a wide range of angles of attack. That study revealed a large peak in the lift coefficient after about half a chord length of displacement, which corresponds to the growth and attachment of the start-up leading edge vortex. Pullin and Wang [32] presented a theory that includes any power-law velocity and focused their numerical tests on linear velocities. Li and Wu [36, 37] developed the Wagner model for a starting flow and established vortex force line maps to identify lift enhancing and reducing directions. Chen, Colonius and Taira [38] conducted full numerical simulations for various power-law velocities and highlighted the peak of lift coefficient, mainly for small angles of attack.

In this paper, we apply the vortex shedding model to an impulsive start and uniform acceleration as representative cases and investigate the dynamics of unsteady flows for large angles of attack. We will show that lift for large angles of attack has different characteristics from that for small angles of attack. Additionally, we demonstrate the vortex shedding of hovering and flapping plates and examine the lift and drag forces.

In Sect. 2, the vortex shedding model for a moving flat plate is described. In Sect. 3, the expression of force on the body is derived, and in Sect. 4, a small-time asymptotic solution for the model is found. The numerical method for the vortex sheet evolution is presented in Sect. 5, and the numerical method for small times is validated in Sect. 6. The numerical results for the impulsively started and uniformly accelerated plates and for hovering and flapping plates for long time are presented in Sect. 7. A comparison of the results of our model and the previous vortex shedding model is presented in Sect. 8. Section 9 gives conclusions.

2 Vortex shedding model

In this section, we construct the complex potential for the flow of a plate with translational and rotational motions and provide the evolution equations for free vortex sheets.

2.1 Complex potential

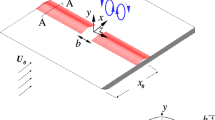
We consider the two-dimensional flow of a flat plate with unsteady translational and rotational motions. Let us assume that the plate is of length L and zero thickness, and the fluid is incompressible and inviscid. As shown in Fig. 1a, the coordinate axes are defined in a fixed laboratory frame of reference such that a general point is denoted by $z=x+ \text {i}y$. At time $t=0$, the center of the plate is located in $x=0$ with an angle $\theta _0 = \theta (t=0)$ with the x-axis. For $t \ge 0$, the plate translates with velocity U(t) and rotates with respect to the center of the plate with angle $\theta (t)$. We assume that free vortex sheets are separated from the edges of the plate. Remind that a vortex sheet is a surface across which the tangential velocity is discontinuous. Figure 1a illustrates the flow of the vortex shedding of a plate in a laboratory frame of reference. The location of the center of the plate is denoted by c(t). A body frame of reference can be introduced for convenience, as shown in Fig. 1b. The free vortex sheets are denoted by $z_{\pm } (\varGamma , t)$ where $\varGamma$ represents the circulation as a Lagrangian parameter. $\varGamma _+$ and $\varGamma _-$ denote the total circulation of the free vortex sheets emanating at the plate edges.

For the unsteady translational motion with fixed angle of attack, Pullin and Wang [32] used a body frame of reference and transformed the physical plane to the exterior of a circle by utilizing conformal mapping, which is a standard procedure for airfoil problems. However, with the rotational motion, the plate has an angular velocity in the body frame and the flow has an instantaneous uniform vorticity. As the flow is rotational and is not a potential flow in this frame, it is difficult to find a complex potential for the flow. Moreover, the plate is no longer a streamline, and Milne–Thomson’s circle theorem cannot be applied. Therefore, we consider a non-inertial frame that is fixed on the plate and rotates with the plate, in order to find a complex potential and to apply the Milne–Thomson circle theorem.

Fig. 1

Schematic of vortex shedding of a plate: a laboratory frame and b body frame

Among various approaches to this problem, we adopt the method proposed by Minotti [39]. The complex potential in the body frame of reference is defined as

$$\begin{aligned} W(z,t) = \phi (z,t) + \text {i} \psi (t), \end{aligned}$$

(1)

where the stream function satisfies

$$\begin{aligned} u_x = \frac{\partial \psi }{\partial y}, \qquad u_y = -\frac{\partial \psi }{\partial x}. \end{aligned}$$

(2)

The flow in the body frame has a uniform vorticity and can be decomposed into an irrotational flow, of potential $\phi$, and a rigid body rotation:

$$\begin{aligned} u_x = \frac{\partial \phi }{\partial x} + \varOmega (t) y, \qquad u_y = \frac{\partial \phi }{\partial y} - \varOmega (t) x, \end{aligned}$$

(3)

where $\varOmega (t)$ is the angular velocity of the rotational motion, $\varOmega (t)= {\dot{\theta }}(t)$. Minotti [39] proposed a non-inertial frame of reference in which the potential and stream function are defined as

$$\begin{aligned} {\bar{\phi }} = \phi - \varOmega xy, \qquad {\bar{\psi }} = \psi + \frac{1}{2} \varOmega (x^2 - y^2). \end{aligned}$$

(4)

The velocity in this non-inertial frame satisfies

$$\begin{aligned} {\bar{u}}_x = u_x - \varOmega y, \qquad {\bar{u}}_y = u_y - \varOmega x, \end{aligned}$$

(5)

which is obviously irrotational. Therefore, the complex potential ${\bar{W}}(z,t)$ is written as

$$\begin{aligned} {\bar{W}}(z,t) = {\bar{\phi }} + \text {i} {\bar{\psi }} = W(z,t) + \frac{\text {i}}{2} \varOmega z^2. \end{aligned}$$

(6)

The plate is at rest in this frame, and the contour immediately adjacent to the plate is a streamline, which means that the stream function over the plate is ${\bar{\psi }} = \text{ const }$.

To construct ${\bar{W}}(z,t)$, we use the Joukowski transformation

$$\begin{aligned} z (\zeta ) = \zeta + \frac{a^2}{\zeta }, \end{aligned}$$

(7)

which maps the z-plane exterior to the plate to the exterior of the circle $|\zeta | = a$ in the $\zeta$-plane. Then, by taking $a=L/4$, we have

$$\begin{aligned} \zeta (z) = \frac{1}{2} \left( z + \sqrt{z^2 - \frac{L^2}{4}} \right) . \end{aligned}$$

(8)

The complex potential in the $\zeta$-plane is written as

$$\begin{aligned} {\bar{W}}(\zeta ,t) = U(t) W_a (\zeta ) + \varOmega (t) {\bar{W}}_r (\zeta ) + W_v (\zeta , t), \end{aligned}$$

(9)

where

$$\begin{aligned} W_a (\zeta )= & {} - \left( e^{\text {i} \theta } \zeta + e^{-\text {i} \theta } \frac{a^2}{\zeta } \right) , \end{aligned}$$

(10)

$$\begin{aligned} {\bar{W}}_r (\zeta )= & {} \frac{\text {i}}{2} \zeta ^2 - \frac{\text {i}}{2} \left( \frac{a^2}{\zeta } \right) ^2. \end{aligned}$$

(11)

The potential $W_a (\zeta )$ describes the attached flow for translation of the plate and ${\bar{W}}_r (\zeta )$ describes the attached flow for rotation of the plate in the non-inertial frame [40]. $W_v (\zeta ,t)$ is the complex potential for vortices separated from the edges of the plate. In the potentials (10) and (11), the second terms are the complex conjugates of image potentials with respect to the circle $| \zeta | = L/4$, to satisfy the boundary condition, ${\bar{\psi }} = \text {const}$, on the plate in the $\zeta$-plane.

The vortices separated from the plate are described by vortex sheets. Let us denote $\zeta _{\pm } = \zeta _{\pm } (\varGamma , t)$ as the vortex sheets mapped onto the $\zeta$-plane,

$$\begin{aligned} \zeta _{\pm } = \frac{1}{2} \left( z_{\pm } + \sqrt{z_{\pm }^2 - \frac{L^2}{4}} \right) . \end{aligned}$$

(12)

The complex potential for the separated free vortex sheets is given by

$$\begin{aligned} W_v (\zeta , t) = \frac{1}{2 \pi \text {i}} \left[ \int _0^{\varGamma _{\pm } (t)} \left( \log [ \zeta - \zeta _{\pm } (\varGamma ,t) ] - \log \left[ \zeta - \frac{L^2}{16 \zeta _{\pm }^* (\varGamma ,t)} \right] \right) \mathrm{d} \varGamma \right] _{-}^{+}, \end{aligned}$$

(13)

where the square bracket denotes a difference $[Q]_-^+ = Q_+ - Q_-$ and the symbol $*$ represents the complex conjugate.

From Eqs. (6) and (7), the resulting complex potential in the $\zeta$-plane is given by

$$\begin{aligned} W(\zeta ,t) = U(t) W_a (\zeta ) + \varOmega (t) W_r (\zeta ) + W_v (\zeta , t), \end{aligned}$$

(14)

where

$$\begin{aligned} W_r (\zeta ) = - \text {i} \left( \frac{L^4}{256 \zeta ^2} + \frac{L^2}{16}\right) . \end{aligned}$$

(15)

Therefore, the complex potential in the z-plane is obtained as

$$\begin{aligned} W(z,t) = U(t) W_a (z) + \varOmega (t) W_r (z) + W_v (\zeta (z), t), \end{aligned}$$

(16)

where

$$\begin{aligned} W_a (z)= & {} -\left( z \cos \theta + \text {i} \sin \theta \sqrt{z^2 - \frac{L^2}{4}} \right) , \end{aligned}$$

(17)

$$\begin{aligned} W_r (z)= & {} - \frac{\text {i}}{4} \left( z - \sqrt{z^2 - \frac{L^2}{4}} \right) ^2 , \end{aligned}$$

(18)

neglecting the constant in $W_r(z)$.

2.2 Evolution equations

The evolution of the free vortex sheets is obtained from the Birkhoff–Rott equation:

$$\begin{aligned} \frac{\partial z_{\pm }^*}{\partial t} (\varGamma ,t) = \frac{\mathrm{d}W}{\mathrm{d}z} (z_{\pm } (\varGamma ,t), t) {:}{=} q (z_{\pm } (\varGamma ,t), t). \end{aligned}$$

(19)

The velocity q(z, t) is then expressed as

$$\begin{aligned} q (z,t)= & {} -U(t) \left( \cos \theta + \frac{\text {i} z \sin \theta }{\sqrt{z^2- L^2/4}} \right) + \text {i} \, \varOmega (t) \left( \frac{L^2}{8} \frac{1}{ \sqrt{z^2 - L^2/4} } -\,z + \sqrt{z^2 - \frac{L^2}{4}} \right) \nonumber \\&+ \frac{1}{2} \left( 1 + \frac{z}{\sqrt{z^2- L^2/4}} \right) w (\zeta , t), \end{aligned}$$

(20)

where $w (\zeta , t)$ is the boundary integral

$$\begin{aligned} w (\zeta , t) = \frac{1}{2 \pi \text {i}} \left[ \int _0^{\varGamma _{\pm } (t)} \left( \frac{1}{\zeta - \zeta _{\pm } (\varGamma ',t) } - \frac{1}{\zeta - L^2/(16 \zeta _{\pm }^* (\varGamma ',t))} \right) \mathrm{d} \varGamma ' \right] _{-}^{+} . \end{aligned}$$

(21)

The edge circulations $\varGamma _{\pm } (t)$ are not known beforehand and should be determined as part of the solution.

To find the edge circulations, we apply the unsteady regularity condition, i.e., Kutta condition. The unsteady Kutta condition is imposed to ensure that the velocity on the bound vortex sheet remains bounded. In Eq. (20), to cancel the singularity by $1/\sqrt{z^2 - L^2/4}$ as $z \rightarrow {\pm } L/2$, the terms with $1/\sqrt{z^2 - L^2/4}$ should vanish:

$$\begin{aligned} - U(t) \sin \theta {\pm } \varOmega (t) \frac{L}{4} - \frac{\text {i}}{2} w (\zeta , t) = 0, \end{aligned}$$

(22)

at $\zeta = {\pm } L/4$. The real part of this equation is

$$\begin{aligned} \text{ Re } \left\{ \frac{\text {i}}{2} w (\zeta , t) \right\} = -U(t) \sin \theta {\pm } \varOmega (t) \frac{L}{4} , \end{aligned}$$

(23)

at $\zeta = {\pm } L/4$. Constraint (23), with Eq. (21), can be solved simultaneously for the unknown circulations $\varGamma _+ (t)$ and $\varGamma _- (t)$ at the edges.

In Eq. (20), the sheet velocities at the edges should be calculated separately, because of the singular term $1/\sqrt{z^2 - L^2/4}$. One can show the limit of the singular term

$$\begin{aligned} \frac{\text {i}}{\sqrt{z^2 - \frac{L^2}{4}}} \left( -U(t) z \sin \theta + \varOmega (t) \frac{L^2}{8} - \frac{\text {i}}{2} z \, w (\zeta , t) \right) \rightarrow {\pm } \frac{L}{8} \frac{\mathrm{d}w}{\mathrm{d} \zeta } ( {\pm } L/4, t), \end{aligned}$$

(24)

as $z \rightarrow {\pm } L/2$. From this limit and the condition (22), the sheet velocities at the edges are obtained by

$$\begin{aligned} q ({\pm } L/2,t)= & {} -U(t) \cos \theta + \text {i} \left( U(t) \sin \theta \mp \varOmega (t) \frac{3L}{4} \right) \nonumber \\&{\pm }\, \frac{\text {i} L}{16 \pi } \left[ \int _0^{\varGamma _{\pm } (t)} \left( \frac{1}{[{\pm } L/4 - \zeta _{\pm } (\varGamma ',t)]^2 } \right. \right. \nonumber \\&\left. \left. -\, \frac{1}{[{\pm } L/4 - L^2/(16 \zeta _{\pm }^* (\varGamma ',t))]^2} \right) \mathrm{d} \varGamma ' \right] _{-}^{+}.~~~~~ \end{aligned}$$

(25)

3 Force on the body

The instantaneous force per unit length exerted by the fluid on the plate can be written as

$$\begin{aligned} F_y - {\text {i}} F_x= & {} -\frac{1}{2} \rho \left( \oint _{C(t)} \left( \frac{{\mathrm{d}}}{{\mathrm{d}z}} [W(z,t) - W_\infty (z,t)] \right) ^2 \mathrm{d}z \right) ^* \nonumber \\&- \rho \frac{{\mathrm{d}}}{{\mathrm{d}t}} \oint _{C(t)} \left( W(z,t) - W_\infty (z,t) \right) \mathrm{d}z , \end{aligned}$$

(26)

from the unsteady Blasius equation [40, 41], where $F_x$ and $F_y$ are the x- and y-components of the force per unit length on the plate, respectively, and $\rho$ is the fluid density. $W_{\infty } (z,t) = -U(t) e^{\text {i} \theta } z$ is the complex potential at the far field and C(t) denotes a closed contour surrounding and immediately adjacent to both the plate and vortex sheets. The integration in Eq. (26) is anticlockwise on the contour C(t).

Let us denote the two integrals in Eq. (26) as $I_1$ and $I_2$, respectively, as follows:

$$\begin{aligned} F_y - \text {i} F_x = -\frac{1}{2} \rho I_1^* - \rho \frac{\text {d} }{\text {dt}} I_2. \end{aligned}$$

(27)

The integrals can be evaluated by stretching the contour C(t) to a large circle at infinity, say $C_\infty$, without changing the value of the integrals. On $C_\infty$, the complex velocity must be expanded as

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}z} [W(z,t) - W_\infty (z,t)] = \frac{a_1}{z^2} + O(z^{-3}), \end{aligned}$$

(28)

to satisfy no momentum flux and pressure force on $C_\infty$. The integral $I_1$ therefore vanishes on $C_\infty$. To calculate $I_2$, we substitute the potential (16) into the integral $I_2$ and split into two parts

$$\begin{aligned} I_2= & {} \oint _{C_\infty } ( U(t) W_a(z) + \varOmega (t) W_r(z) + W_v (\zeta (z),t) - W_\infty (z,t) ) \mathrm{d}z, \nonumber \\= & {} \oint _{C_\infty } \left( U(t) W_a(z) + \varOmega (t) W_r(z) - W_\infty (z,t) \right) dz + \oint _{C_\infty } W_v (\zeta (z),t) \mathrm{d}z,~~~~~ \end{aligned}$$

(29)

The first integral in Eq. (29), of the attached flows, is obtained as

$$\begin{aligned}&\oint _{C_\infty } ( U(t) W_a(z) + \varOmega (t) W_r(z) - W_\infty (z,t) ) \mathrm{d}z \nonumber \\&\quad = U(t) \oint _{C_\infty } ( W_a(z) + e^{\text {i} \theta (t)} z ) \mathrm{d}z + \varOmega (t) \oint _{C_\infty } W_r(z) \mathrm{d}z \nonumber \\&\quad = -\frac{1}{4} \pi L^2 U(t) \sin \theta (t), \end{aligned}$$

(30)

by applying the residue theorem. The second integral in Eq. (29), for the separated flow, can be calculated in the $\zeta$-plane and is evaluated as

$$\begin{aligned} \oint _{C_\infty } W_v (\zeta (z),t) \mathrm{d}z= & {} \oint _{C_\infty } W_v (\zeta (z),t) \frac{\mathrm{d}z}{\mathrm{d} \zeta } \mathrm{d} \zeta \nonumber \\= & {} \left[ \int _0^{\varGamma _{\pm } (t) } \left( -\zeta _{\pm } (\varGamma ,t) + \frac{L^2}{16 \zeta _{\pm }^* (\varGamma ,t)} \right) \mathrm{d} \varGamma \right] _{-}^{+}, \end{aligned}$$

(31)

again by applying the residue theorem.

Combining the results of the integrals $I_1$ and $I_2$ and using Eq. (27), we obtain the final expression of the total force. The forces produced by the attached flows of added mass and of rotation are given by

$$\begin{aligned} F_y^{(a)}&= \frac{1}{4} \pi \rho L^2 \sin \theta (t) \frac{\text {d} U(t)}{\text {dt}},&F_x^{(a)} = 0, ~~~ \end{aligned}$$

(32)

$$\begin{aligned} F_y^{(r)}&= \frac{1}{4} \pi \rho L^2 U(t) \varOmega (t) \cos \theta (t),&F_x^{(r)} = 0. ~~~ \end{aligned}$$

(33)

The force produced by the separated flow, called the vortex force, is

$$\begin{aligned} F_y^{(v)} - \text {i} F_x^{(v)} = \rho \frac{{\text {d}}}{{\text {dt}}} \left[ \int _0^{\varGamma _{\pm } (t) } \left( \zeta _{\pm } (\varGamma ,t) - \frac{L^2}{16 \zeta _{\pm }^* (\varGamma ,t)} \right) \mathrm{d} \varGamma \right] _{-}^{+}. \end{aligned}$$

(34)

When $\varOmega (t)=0$, the result by Pullin and Wang [32] is recovered.

4 Small-time asymptotic solution

We find a small-time asymptotic solution of free vortex sheets from the model, following Pullin and Wang [32]. The small-time solution is used as an initial condition in the computation of the model. For small times, the vortex sheets are expected to have a self-similar structure in time. Assume that initially, the translational and angular velocities of the plate are

$$\begin{aligned} U(t) \sim \alpha t^m, \qquad \varOmega (t) \sim \beta t^m. \end{aligned}$$

(35)

where $m \ge 0$ is a power exponent. The coefficient $\beta =0$ if the leading order of $\varOmega (t)$ is larger than m, and $\alpha =0$ if vice versa.

The terms with U(t) and $\varOmega (t)$ in Eq. (20) are the velocity of the attached flow. If we put ${\bar{z}}_+ = z_+ - L/2$ and expand in powers of ${\bar{z}}_+/L \ll 1$, the leading order term of the velocity is singular and of the form

$$\begin{aligned} q (z_+, t) = - \frac{\text {i}}{2} a_+ t^m {\bar{z}}_+^{-1/2} + \cdots , \end{aligned}$$

(36)

where

$$\begin{aligned} a_+ = L^{\frac{1}{2}} \alpha \sin \theta _0 - \frac{1}{4} L^{\frac{3}{2}} \beta . \end{aligned}$$

(37)

Thus, the appropriate time-independent length scale is

$$\begin{aligned} \delta (t)= & {} K a_+^{2/3} t^{2(m+1)/3}, \end{aligned}$$

(38a)

$$\begin{aligned} K= & {} \left[ \frac{3}{4(1+m)} \right] ^{\frac{2}{3}}, \end{aligned}$$

(38b)

where K is a scaling constant.

We introduce the similarity solution of the form

$$\begin{aligned} z_+ (\varGamma , t)= & {} \frac{L}{2} ( 1 + 2 \epsilon ^2 \omega _0 (\lambda ) + O(\epsilon ^3)), \end{aligned}$$

(39)

$$\begin{aligned} \varGamma _+ (t)= & {} \frac{\delta ^2 (t)}{K^{3/2} t} (J_0 + O(\epsilon ) )(1 - \lambda ), \end{aligned}$$

(40)

where $\epsilon = (\delta (t)/L)^{1/2} \ll 1$ is a time-dependent parameter and $\lambda$ is a dimensionless circulation parameter. $\omega _0 (\lambda )$ is a complex shape function, and the dimensionless constant $J_0$ is to be determined. Substituting Eqs. (39) and (40) in Eq. (19), all terms scale as $\delta (t) t^{-1} \epsilon ^p (t)$, $p=0,1,2, \ldots$. The zeroth-order equation in $\epsilon$ is given by

$$\begin{aligned} \omega _0^* + B (1 - \lambda ) \frac{\mathrm{d} \omega _0^*}{\mathrm{d} \lambda }= & {} \frac{1}{\sqrt{\omega _0}} \left( - \text {i} + \frac{J_0}{2 \pi \text {i}} \int _0^1 F (\omega _0 ; \omega _0') \mathrm{d} \lambda ' \right) , \end{aligned}$$

(41a)

$$\begin{aligned} F (\omega _0 ; \omega _0')= & {} \frac{1}{\sqrt{\omega _0} - \sqrt{\omega _0'} } - \frac{1}{\sqrt{\omega _0} + \sqrt{{\omega _0^*}'} }, \end{aligned}$$

(41b)

where $B = (4m+1)/(2m+2)$. When $\lambda \rightarrow 0$, $\omega _0$ becomes 0, and the right-hand side of Eq. (41a) is unbounded. Satisfaction of the regularity condition follows

$$\begin{aligned} 1 + \frac{J_0}{2 \pi } \int _0^1 F (0 ; \omega _0') \mathrm{d} \lambda ' = 0, \end{aligned}$$

(42)

which determines the constant $J_0$. The zeroth-order equation is found to be the same as that given in Pullin and Wang [32], except the additional term from the plate rotation in the expression of $a_+$.

From Eq. (39) with $\lambda =1$ and Eq. (40) with $\lambda =0$, the self-similar asymptotic solution of the location of the vortex center and the circulation at the leading edge is

$$\begin{aligned} z_+ (0,t)= & {} \frac{L}{2} + K a_+^{2/3} t^{\frac{2}{3} (1+m)} \omega _0 (1) , \end{aligned}$$

(43)

$$\begin{aligned} \varGamma _+ (t)= & {} K^{1/2} a_+^{4/3} t^{\frac{4m+1}{3}} J_0 . \end{aligned}$$

(44)

Similarly, the asymptotic solution of the vortex center and the circulation at the trailing edge is

$$\begin{aligned} z_- (0,t)= & {} -\frac{L}{2} - K a_-^{2/3} t^{\frac{2}{3} (1+m)} \omega _0^* (1) , \end{aligned}$$

(45)

$$\begin{aligned} \varGamma _- (t)= & {} K^{1/2} a_-^{4/3} t^{\frac{4m+1}{3}} J_0 , \end{aligned}$$

(46)

where $a_-$ is defined as

$$\begin{aligned} a_- = L^{\frac{1}{2}} \alpha \sin \theta _0 + \frac{1}{4} L^{\frac{3}{2}} \beta . \end{aligned}$$

(47)

The complex shape function and constant $J_0$ can be obtained by a numerical procedure. By simply replacing the vortex sheet with a single point vortex, they are found as

$$\begin{aligned} \omega _0 = \frac{\text {i}}{2^{1/3}} \left( \frac{1+m}{3+6m} \right) ^{\frac{2}{3}}, \qquad \quad J_0 = \pi \left[ \frac{2(1+m)}{3+6m} \right] ^{\frac{1}{3}}, \end{aligned}$$

(48)

where $\omega _0$ is the leading-order position of the point vortex. Since the purpose of this study is the computation of the model, the high-order solutions are neglected.

5 Numerical method

5.1 Regularization of the equations

The vortex sheet evolution suffers from the Kelvin–Helmholtz instability for all the disturbance wavenumbers. It is well known that in a free shear flow, the vortex sheet develops a singularity at finite time [42]. Numerical computations for the vortex sheet break down when the singularity appears. The singularity could be suppressed by giving a numerical smoothing or physical effects such as viscous diffusion, finite thickness or surface tension. The most common regularization for a vortex sheet is the vortex blob model, in which the singular kernel $K(z)=1/z$ is replaced by a smoothed kernel [43, 44]. A widely used blob regularization is to give a constant parameter $\delta =\delta _0$ in the kernel,

$$\begin{aligned} K_{\delta } (z) = \frac{{\bar{z}}}{ |z|^2 + \delta ^2}. \end{aligned}$$

(49)

However, we have found that in this model, the blob regularization with a constant $\delta _0$ yields oscillations in the solution, which are much more severe than other vortex sheet models [20]. To remove the oscillations, a very small value of $\delta _0$ should be used, but then the computation becomes expensive due to the high resolution of spiral cores.

We here apply a non-uniform regularization for the free vortex sheet

$$\begin{aligned} \delta (s) = \delta _0 \left[ 1 - (1-\tau ) e^{-s(\varGamma )^2/\epsilon ^2}\right] . \end{aligned}$$

(50)

In this approach, $\delta (s)$ gradually decreases to $\delta _0 \tau$ as the arc-length s approaches the plate edge. The parameter $\epsilon$ gives the scale over which $\delta (s)$ decreases. The non-uniform regularization (50) stably calculates separated free vortex sheets of this model. In our simulations, the parameters are set to $\epsilon = 2 \delta _0$ and $\tau =0.05$. Note that the approach of non-uniform regularization in the vortex sheet model was first proposed by Alben [45].

With the blob regularization, the velocity field $q_{\delta } (z,t)$ takes the form,

$$\begin{aligned} q_{\delta } (z,t)= & {} -U(t) \left( \cos \theta + \frac{\text {i} z \sin \theta }{\sqrt{z^2- L^2/4}} \right) + \text {i} \, \varOmega (t) \left( \frac{L^2}{8} \frac{1}{ \sqrt{z^2 - L^2/4} } \right. \nonumber \\&\left. - z + \sqrt{z^2 - \frac{L^2}{4}} \right) + \frac{1}{2} \left( 1 + \frac{z}{\sqrt{z^2- L^2/4}} \right) w_\delta (\zeta , t), \end{aligned}$$

(51)

$$\begin{aligned} w_\delta (\zeta , t)= & {} \frac{1}{2\pi \text {i}} \left[ \int _0^{\varGamma _{\pm } (t)} \left( K_{\delta } (\zeta - \zeta _{\pm } (\varGamma ',t) ) - K_{\delta } \left( \zeta - \frac{L^2}{16 \zeta _{\pm }^* (\varGamma ',t)} \right) \right) \mathrm{d} \varGamma ' \right] _{-}^{+} . \nonumber \\ \end{aligned}$$

(52)

The regularized equation for the evolution of the free vortex sheets is given by

$$\begin{aligned} \frac{\partial z_{\pm }}{\partial t} (\varGamma ,t) = q_{\delta }^* (z_{\pm } (\varGamma ,t), t), \end{aligned}$$

(53)

where $\varGamma _+ (t)$ and $\varGamma _- (t)$ are determined from the Kutta condition

$$\begin{aligned} \text{ Re } \left\{ \frac{\text {i}}{2} w_\delta (\zeta , t) \right\} = -U(t) \sin \theta {\pm } \varOmega (t) \frac{L}{4} \end{aligned}$$

(54)

at $\zeta ={\pm } L/4$. The sheet velocities at the edges, Eq. (25), have the integral kernel of the form $1/z^2$. This can be regularized in a similar manner as K(z). The regularized sheet velocities at the edges are

$$\begin{aligned} q_\delta ({\pm } L/2,t)= & {} -U(t) \cos \theta + \text {i} \left( U(t) \sin \theta \mp \varOmega (t) \frac{3L}{4} \right) \nonumber \\&{\pm } \frac{\text {i} L}{16 \pi } \left[ \int _0^{\varGamma _{\pm } (t)} \left( K_{\delta }^2 \left( {\pm } \frac{L}{4} - \zeta _{\pm } (\varGamma ',t) \right) \right. \right. \nonumber \\&\left. \left. - K_{\delta }^2 \left( {\pm } \frac{L}{4} - \frac{L^2}{16 \zeta _{\pm }^* (\varGamma ',t)} \right) \right) \mathrm{d} \varGamma ' \right] _{-}^{+}. \end{aligned}$$

(55)

5.2 Discretization and time-integration

For numerical computation, we discretize the free vortex sheets by N Lagrangian point vortices. Using the circulation $\varGamma$ as a Lagrangian variable, we denote the locations of the free vortex sheets by $z_j = z_{\pm } (\varGamma _j,t)$ for $1 \le j \le P-1$ and $P+2 \le j \le N$. The integers P and $P+1$ denote the Lagrangian indices of the leading and trailing edges of the plate, respectively. The edge circulations are given by $\varGamma _P = \varGamma _+ (t)$ and $\varGamma _{P+1} = \varGamma _- (t)$. After discretization, Eq. (54) becomes a $2 \times 2$ linear equation for the unknowns $\varGamma _P$ and $\varGamma _{P+1}$.

Once $\varGamma _P$ and $\varGamma _{P+1}$ are determined, we calculate the right-hand side of Eq. (53), for time advancing of the free vortex sheets. In Eq. (51), the integrations over the free vortex sheets are approximated by the trapezoidal rule. The classical fourth-order Runge–Kutta method is employed for time-integration of Eq. (53). The free vortex sheets lack resolution at late times due to the non-uniform distribution of point vortices. To handle this, an adaptive point insertion procedure is applied to maintain the resolution of the free vortex sheets. Third-order local polynomial interpolation is used to insert points whenever the distance between two consecutive points exceeds a given threshold.

The two new point vortices are released from the plate edges at the end of each time step, and their velocities are calculated by using Eq. (55). In the previous vortex shedding models [12, 15, 20], new vortex elements are generally forced to shed tangentially to the plate edges. As this constraint of tangential shedding is reasonable for large angles of attack, it is also enforced in the numerical computation. However, the results are the same even if the constraint of tangential shedding is not applied.

In addition, the shedding process of our model needs a special caution. We have found that the direct use of Eq. (55) produces large oscillations in the solution, particularly in the edge circulations, causing an irregular motion to appear in the core of vortex sheet spirals. This instability is due to the approximation of the initial vortex sheet by a single point vortex, and the mismatch of the $\delta$-parameter between the initial single point vortex and released vortices. In the other vortex sheet model [20], the early-time instability usually damps out after a few time steps, but in our model it does not disappear and deteriorates the solution at late times. This trouble can be overcome by significantly reducing the velocity of new point vortices, specifically, reducing the shedding velocity by 1/3. After this remedy, the early-time instability is greatly decreased and the solution is obtained with high resolution at late times. A similar approach of placing 1/3 distance of the edge and previous vortex was used in the discrete vortex method [12, 13]; however, our method differs from this method in detail.

The solution procedure of the equations requires initial conditions at time $t_1 > 0$. The small-time asymptotic solution of the free vortex sheet separated from a plate, which is presented in Sect. 4, may be used as the initial condition. Initially, two starting point vortices with zero circulation $\varGamma _1 = \varGamma _N = 0$ are placed and their locations, $z_1$ and $z_N$, are given by the small-time asymptotic solutions (43) and (45) with $t=t_1$. The initial estimates for the edge circulation, $\varGamma _P$ and $\varGamma _{P+1}$, for $P=2$ are also given by the small-time solutions (44) and (46) with $t=t_1$.

6 Validation of the numerical method

We first validate the numerical method of the vortex shedding model by comparing with the asymptotic solution for small times.

6.1 Nondimensionalization

We consider a plate velocity of the form $U(t) = \alpha t^m$. The constant $\alpha$ has dimension $\text {Length} \times \text {Time}^{-(1+m)}$. Chord length L gives the length scale, and acceleration constant $\alpha$ gives the velocity scale $U_f$ by setting $\alpha = U_f^{1+m}/L^m$. The velocity profile is then written as

$$\begin{aligned} \frac{U}{U_f} = \left( \frac{t U_f}{L} \right) ^m . \end{aligned}$$

(56)

Therefore, the dimensionless velocity of a plate is

$$\begin{aligned} {\hat{U}} = {\hat{t}}^m, \end{aligned}$$

(57)

where ${\hat{U}} = U/U_f$ and ${\hat{t}} = t U_f/L$. We introduce another time scale, which is appropriate for long time, in Sect. 7.

6.2 Validation

For validation, we take two cases of the velocity profile, an impulsive start ${\hat{U}}(t)=1$ and uniform acceleration ${\hat{U}}(t)={\hat{t}}$. Figure 2 plots the vortex shedding of a plate at the chord length of displacement 0.25 for two regularization parameters, ${\hat{\delta }}_0 = \delta / L = 0.05$ and 0.1. The angle of attack is $\theta = 90^\circ$. The circle denotes the location of the vortex center of the self-similar asymptotic solution. Figure 2a, b shows that for ${\hat{\delta }}_0 = 0.05$, the vortex centers of the numerical solutions are in agreement with the asymptotic solution, for both cases of ${\hat{U}}(t)=1$ and ${\hat{U}}(t)={\hat{t}}$. However, in Fig. 2a$'$, b$'$, for a larger regularization ${\hat{\delta }}_0 = 0.1$, the spirals are smaller and are in relatively poor agreement with the asymptotic solution. The value of the regularization parameter has a large influence on the size of the spiral not only at early times but also at late times, which will be shown at the next section. For this reason, we take a small regularization parameter and set ${\hat{\delta }}_0 = 0.05$ from now on. Figure 2 also shows that the size of the spiral is larger for the plate of impulsive start than that of uniform acceleration, at an early time.

Fig. 2

Vortex of a plate at the chord length of displacement 0.25 for ${\hat{U}}(t)=1$ and ${\hat{U}}(t)={\hat{t}}$ for two regularization parameters. The angle of attack is $\theta = 90^\circ$. The circle denotes the location of the vortex center of the asymptotic solution. a${\hat{U}}(t)=1$, ${\hat{\delta }}_0 =0.05$, b${\hat{U}}(t)={\hat{t}}$, ${\hat{\delta }}_0 =0.05$; a$'$${\hat{U}}(t)=1$, ${\hat{\delta }}_0 =0.1$, b$'$${\hat{U}}(t)={\hat{t}}$, ${\hat{\delta }}_0=0.1$

Fig. 3

Edge circulation ${\hat{\varGamma }}_{\pm }$ of a plate of $\theta = 90^\circ$ at small times for a${\hat{U}}(t)=1$, and b${\hat{U}}(t)={\hat{t}}$. The regularization parameter is ${\hat{\delta }}_0 = 0.05$. The thick (blue) curves correspond to the numerical solution of the model, and the thin (red) curves correspond to the asymptotic solution. a$'$ and b$'$ are log–log plots of a and b (color figure online)

Figure 3 shows the growth of the edge circulation of a plate with $\theta = 90^\circ$ for ${\hat{U}}(t)=1$ and ${\hat{U}}(t)={\hat{t}}$. The thick (blue) curves correspond to the numerical solutions of the model, and the thin (red) curves correspond to the asymptotic solution. At the final time of Fig. 3a, b, the plate travels the same distance 0.5. In the case of $\theta = 90^\circ$, the circulations of the leading and trailing edges are the same. In Fig. 3a, b, the numerical solutions agree with the asymptotic solution at small times, but the difference of the two solutions tends to be large over time, indicating a deviation of the self-similar solution at late times. Figure 3a$'$, b$'$ is log–log plots of Fig. 3a, b and shows that the edge circulations for the impulsive start ($m=0$) and uniform acceleration ($m=1$) grow asymptotically with the rate 1/3 and 5/3, respectively; however, the agreement of the numerical solution with the asymptotic solution is better for $m=1$ than $m=0$.

7 Results for long time

We apply the vortex shedding model to accelerated, hovering and flapping plates and present the results of longtime computations. As commented above, the regularization parameter is set to ${\hat{\delta }}_0 = 0.05$ in all the results in this section, except Fig. 12. The computations use a dimensionless time ${\hat{t}} = t U_f/L$, but it is based on the reference velocity, so the physical time scales in ${\hat{t}}$ are sensitive to the instantaneous velocity of the plate. Chen, Colonius and Taira [38] suggested to use chord lengths for the dimensionless time, in order to be generally insensitive to the instantaneous velocity of the plate. This parameter of dimensionless time is

$$\begin{aligned} {\tilde{t}} = \frac{c(t)}{L}. \end{aligned}$$

(58)

We define lift and drag coefficients as

$$\begin{aligned} C_L = \frac{2 F_L}{\rho U^2 (t) L}, \qquad \quad C_D = \frac{2 F_D}{\rho U^2 (t) L}, \end{aligned}$$

(59)

respectively, where $F_L$ is the lift force per unit length and $F_D$ is the drag force per unit length. These definitions of lift and drag coefficients are more useful in the present study than those scaled by the reference velocity $U_f^2$. The lift and drag forces are written as

$$\begin{aligned} F_L= & {} F_y \cos \theta = ( F_y^{(v)} + F_y^{(a)} + F_y^{(r)} ) \cos \theta , \end{aligned}$$

(60)

$$\begin{aligned} F_D= & {} F_y \sin \theta = ( F_y^{(v)} + F_y^{(a)} + F_y^{(r)} ) \sin \theta . \end{aligned}$$

(61)

For an accelerated plate of the power-law form $U(t) = \alpha t^m$ with fixed angle of attack, Pullin and Wang [32] obtained a small-time asymptotic solution for the vortex normal force and the added mass normal force of the attached flow from the shedding model

$$\begin{aligned} F_y^{(v)}= & {} \, \frac{2 (5m+2)}{3} \left( \frac{3}{4(m+1)} \right) ^{\frac{2}{3}} \rho L^{\frac{4}{3}} J_0 \alpha ^{\frac{5}{3}} \sin ^{\frac{5}{3}} \theta \, \text{ Re } \left\{ \int _0^1 \omega _0^{1/2} (\lambda ) \mathrm{d} \lambda \right\} t^{\frac{5m-1}{3}}, \end{aligned}$$

(62)

$$\begin{aligned} F_y^{(a)}= & {} \frac{\pi m}{4} \rho L^2 \alpha \, \sin \theta \, t^{m-1}. \end{aligned}$$

(63)

Using Eq. (48) from the point vortex approximation, the asymptotic solution for the lift coefficient is given by

$$\begin{aligned} C_L = \frac{2^{\frac{1}{3}} \pi (5m+2)}{3 (m+1)^{\frac{1}{3}} (2m+1)^{\frac{2}{3}} } \sin ^{\frac{5}{3}} \theta \, \cos \theta \, \frac{1}{{\tilde{t}}^{1/3}} + \frac{\pi m}{2(m+1)} \, \sin \theta \cos \theta \, \frac{1}{{\tilde{t}}}.~~ \end{aligned}$$

(64)

The drag coefficient is given by replacing $\cos \theta$ by $\sin \theta$ in Eq. (64). The solution (64) provides useful information and insights to the problem. In the expression of the lift coefficient, the exponent of ${\tilde{t}}$ is independent of m, which suggests appropriate scaling of ${\tilde{t}}$ for lift. We also find that the lift coefficient decreases at early times. The lift is dominated by the $1/{\tilde{t}}$ term initially, which corresponds to the added mass effect; however, it can be shown that the lift is dominated by the vortex force at transient times. The lift coefficient is maximized at an angle between $45^\circ$ and $52.5^\circ$ and decreases to 0 as the angle increases to $90^\circ$ or decreases to $0^\circ$, which explains the phenomenon of dynamical stall.

7.1 Motion of translational acceleration

We consider two cases of translational acceleration: impulsive start and uniform acceleration. Figure 4 shows the evolution of the vortex of a plate for ${\hat{U}}(t)=1$ and ${\hat{U}}(t)={\hat{t}}$ for $\theta = 90^\circ$. The spiral of the impulsively started plate has a larger structure and more turns in the vortex core, whereas the spiral of the uniformly accelerated plate is narrower. The growth of edge circulations for $m=0$ and $m=1$ with $\theta = 90^\circ$ is shown in Fig. 5. The circulation is non-dimensionalized as ${\tilde{\varGamma }}_{\pm }=\varGamma _{\pm }(t)/U(t) L$. The edge circulations increase in time for both cases of $m=0$ and $m=1$, and the edge circulation of $m=0$ is larger than that of $m=1$, which explains the larger size and more turns of the spiral.

Fig. 4

Evolution of vortex of a plate for $\theta = 90^\circ$ at ${\tilde{t}} =0, 0.5, 1.5, 3$ and 4.5 (chord). a$m=0$, and b$m=1$

Fig. 5

Growth of edge circulation ${\tilde{\varGamma }}_{\pm }$ of a plate of $\theta = 90^\circ$, for $m=0$ and 1

Fig. 6

Drag of a plate of $\theta = 90^\circ$, for $m=0$ and $m=1$. a Drag force is normalized by $U_f^2$. b Drag force is normalized by $U(t)^2$. The circles are the numerical result for the Navier–Stokes simulation for $m=0$ and $\text{ Re }=126$ by Koumoutsakos and Shields [46]

Figure 6 plots drag forces for $m=0$ and $m=1$. In Fig. 6a, the drag force is normalized by $U_f^2$ and is plotted with respect to ${\hat{t}}$. The drag force decreases for the impulsive start and increases for the uniform acceleration. In Fig. 6b, the drag force is normalized by $U(t)^2$, which represents the drag coefficient, and is plotted with respect to ${\tilde{t}}$. For $m=0$, the dimensionless time ${\tilde{t}}$ is the same as ${\hat{t}}$, and the curves of Fig. 6a, b are the same. The growths of forces of $m=0$ and $m=1$ are different in Fig. 6a, but are comparable in Fig. 6b. Both the drag coefficients of $m=0$ and $m=1$ decrease in Fig. 6b, and the drag coefficient for $m=1$ is larger than that for $m=0$. For $m=0$, the numerical result of the Navier–Stokes simulation for the Reynolds number $\text{ Re }=126$ by Koumoutsakos and Shields [46] is also given for comparison. It shows an agreement of the vortex shedding model with the Navier–Stokes simulation. We also observe in Fig. 6 that the drag coefficient of $m=0$ has a local minimum and maximum at early times. This behavior will be discussed shortly.

Fig. 7

Evolution of vortex of a plate for $\theta = 67.5^\circ$ and $m=0$. Times are ${\tilde{t}}=0, 0.5, 1, 2$ (top) and ${\tilde{t}}=3, 4$ (bottom)

We decrease the angle of attack to $\theta = 67.5^\circ (=3\pi /8)$. Figure 7 shows the evolution of the vortex of the impulsively started plate for $\theta = 67.5^\circ$. The leading and trailing edge vortices are formed and grow as the plate translates. The leading edge vortex stays near the plate until two chord lengths of displacement. As the leading edge vortex moves away from the plate, the new vortex is produced near the trailing edge and approaches the plate. The evolution of the vortex of the uniformly accelerated plate for $\theta = 67.5^\circ$ is shown in Fig. 8. The vortices of the uniform acceleration are smaller and weaker than those of the impulsive start, but the structures of the vortices are similar to each other.

Fig. 8

Evolution of vortex of a plate of $\theta = 67.5^\circ$ for $m=1$. Times are ${\tilde{t}}=0, 0.5, 1, 2$ (top) and ${\tilde{t}}=3, 4.5$ (bottom)

The circulations and shedding rates at the leading and trailing edges for $\theta = 67.5^\circ$ are plotted in Fig. 9. In Fig. 9a for $m=0$, both the leading and trailing edge circulations grow, and the leading edge circulation is larger than the trailing edge circulation for about ${\tilde{t}}<4$. After ${\tilde{t}}=3$, when the new trailing edge vortex is produced, the circulation of the trailing edge grows rapidly. Finally, the circulations of the leading and trailing edges are crossed over, which exhibits an alternating behavior. In Fig. 9b for $m=1$, the edge circulations grow and the leading edge circulation is larger than the trailing edge circulation. In this case, the edge circulations do not cross over during the observed times, and the edge circulations of $m=1$ are smaller than those of $m=0$. In Fig. 9a$'$, for $m=0$, both the shedding rates of the leading and trailing edges decrease with a similar rate initially, but the shedding rate at the leading edge abruptly changes to increase slightly at early times. We also observe that the difference of the shedding rates between the leading and trailing edges at late times is large for $m=0$, which exhibits a pronounced alternating behavior, while their difference is small for $m=1$.

Fig. 9

Edge circulations and shedding rates of a plate for $\theta = 67.5^\circ$. a${\tilde{\varGamma }}_{\pm }$ for $m=0$, b${\tilde{\varGamma }}_{\pm }$ for $m=1$; (a$'$) $d{\tilde{\varGamma }}_{\pm }/d{\tilde{t}}$ for $m=0$, (b$'$) $d{\tilde{\varGamma }}_{\pm }/d{\tilde{t}}$ for $m=1$. LE represents the leading edge, and TE represents the trailing edge

Figure 10 shows lift on the plate. In Fig. 10a, the lift is normalized by $U_f^2$ and is plotted in ${\hat{t}}$. For $m=0$, the lift decreases for ${\hat{t}}<3.6$, except for a small dip at an early time, and then increases at late times, owing to the new trailing edge vortex. For $m=1$, the lift increases and reaches its peak at ${\hat{t}}=2.8$. The final time of $m=1$ corresponds to five chord lengths of displacement. The initial nonzero force for $m=1$ is the contribution of added mass, and the added mass force remains constant in time. For $m=0$, there is no added mass force. Therefore, for both cases it is found that the vortex force is dominant overall in the lift. In Fig. 10b, the lift is normalized by $U^2(t)$ and is plotted in ${\tilde{t}}$. The lift coefficient of $m=1$ decreases and is larger than that of $m=0$ for ${\tilde{t}} < 4$, but then becomes smaller, which means a more significant role of the trailing edge vortex on the lift at late times in the impulsive start case. The initial high lifts in Fig. 10b indicate that the wing produces an instantaneous nonzero force immediately after the start, in accordance with the asymptotic solution of the lift coefficient (64).

Fig. 10

Lift of a plate for $\theta = 67.5^\circ$, for $m=0$ and $m=1$. a Lift force is normalized by $U_f^2$. b Lift force is normalized by $U^2(t)$. The dashed (green) curve corresponds to the vortex-lift coefficient for $m=1$ (color figure online)

Let us focus on the peak at an early time of the lift coefficient of $m=0$ in Fig. 10b. The dashed (green) curve in Fig. 10b corresponds to the vortex-lift coefficient for $m=1$, where the vortex-lift coefficient is defined as

$$\begin{aligned} C_L^{(v)} = \frac{2 F_L^{(v)}}{\rho U^2 (t) L}, \end{aligned}$$

(65)

and $F_L^{(v)} = F_y^{(v)} \cos \theta$. The vortex-lift coefficient for $m=1$ decreases monotonically and does not have a peak. Chen et al. [38] showed that for small angles of attack $\theta \lesssim 50^\circ$, the vortex-lift coefficient has the peak at a transient time for all values of m, and the curves of the vortex-lift coefficient nearly collapse for $0 \le m \le 1$. The result of Fig. 10b indicates a different characteristic of the vortex-lift coefficient for a large angle of attack, which has a peak only for small m. Moreover, in Fig. 10b, the peak of the lift coefficient for $m=0$ appears soon after the first minimum, whereas their difference is $\varDelta {\tilde{t}} > 1$ for small angles of attack [38]. The appearance of the peak for $m=0$ can be explained by the shedding rate. In Fig. 9a$'$, the shedding rate at the leading edge for $m=0$ also has a minimum and maximum at early times, while the shedding rate at the trailing edge decreases monotonically at early times. In the case of $m=1$ in Fig. 9b$'$, the curve of the shedding rate at the leading edge is merely bent and does not have a dip. Therefore, the appearance of the peak of lift force is attributed to a variation of the shedding rate at the leading edge.

Fig. 11

Lift coefficients of a plate for angles $\theta =67.5^\circ$ and $78.8^\circ$. a$m=0$, and b$m=1$

Lift coefficients for varying angles are plotted in Fig. 11. In Fig. 11a for $m=0$, by increasing the angle to $78.8^\circ ~(=7\pi /16)$, the lift decreases and does not increase at the observed times. This is due to the fact that the new trailing edge vortex forms at later time than $\theta = 67.5^\circ$, although the vortex evolution is not shown here. We find that the peak at an early time is weakened by the increasing angle, and the time difference between the minimum and maximum becomes smaller. In the case of $m=1$ in Fig. 11b, the lift decreases overall with the increasing angle.

We now examine the effect of the regularization parameter ${\hat{\delta }}_0$ on the vortex. Figure 12 shows the vortex at ${\tilde{t}}=2$ for ${\hat{\delta }}_0 =0.05$ and 0.1. The angle of attack is $\theta = 67.5^\circ$, and the velocity of the plate is ${\hat{U}}(t)=1$. The leading edge vortex for ${\hat{\delta }}_0 =0.1$ is considerably smaller and closer to the plate than that of ${\hat{\delta }}_0 =0.05$. This behavior of the location and size of the vortex is related to the asymptotic solution at small times. We have previously shown that the position of the vortex center for ${\hat{\delta }}_0 =0.1$ is in poor agreement with the asymptotic solution, and the size of the vortex for ${\hat{\delta }}_0 =0.1$ is much smaller than that for ${\hat{\delta }}_0 =0.05$. These results indicate that a small $\delta$-value should be used for computation. Nevertheless, the use of an excessively small $\delta$-value makes the computation very expensive and yields an irregular motion on the core of the vortex sheet spiral [44].

Fig. 12

Comparison of vortex at ${\tilde{t}}=2$ for a${\hat{\delta }}_0 =0.05$ and b${\hat{\delta }}_0 =0.1$. Angle of attack is $\theta = 67.5^\circ$ and the velocity of a plate is ${\hat{U}}(t)=1$

We compare our model with the experiment by Dickinson and Götz [35]. The physical settings of the experiment are as follows: The chord length of the plate is 5 cm, and angle of attack is fixed for each test case. The background flow accelerates at a rate of $62.5~ \text{ cm/s }^2$ from the rest and reaches a constant velocity of $10~ \text{ cm/s }$ in 0.16 s. Experiments were run for angles of attack from − 9 to $90^\circ$ in increments of $4.5^\circ$. The Reynolds number for the experiment is $\text{ Re }=192$. For comparison, we conduct the numerical computation of the vortex shedding model for an angle of attack $67.5^\circ$, with the same physical setting for the experiment. The vortex evolution of this computation is similar to Fig. 7, where the only difference is the acceleration at early short times, and thus, the result of the vortex evolution is not shown here. The vortex evolution in Fig. 7 is similar to the flow-visualization image in Fig. 3 in Dickinson and Götz [35], although the angle of attack of the experiment ($45^\circ$) is smaller. Figure 13 shows the comparison of the lift and drag coefficients of the model and the experiment. The lift and drag coefficients are normalized by $U_f^2 = (10~\text{ cm/s })^2$ over all times. The lift and drag of the model are in good agreement with the experimental result after one chord length of travel. The difference in the initial peak may be due to the fact that the physical wing used in the experiment had inertia and would not respond instantly to changes in force.

Fig. 13

Comparison of lift and drag coefficients of the model and the experiment by Dickinson and Götz [35], for $\theta = 67.5^\circ$. The curves are the solutions of the model, and the circles denote the experimental result

Figure 14 shows lift and drag coefficients with respect to the angle of attack. Data are given between $63^\circ$ and $90^\circ$ in the increments of $4.5^\circ$. Filled circles denote the solution of the model, and rectangles denote the experimental result by Dickinson and Götz, at ${\tilde{t}}=2$. The lift coefficients of the model and experiment decrease and are in good agreement. The drag coefficients of the model and experiment have fairly different trends, but are in agreement quantitatively.

Fig. 14

Lift and drag coefficients with respect to the angle of attack. Data are given between $63^\circ$ and $90^\circ$ in the increments of $4.5^\circ$. Filled circles denotes the solution of the model, and rectangles denote the experimental result, at ${\tilde{t}}=2$

7.2 Hovering motion

Next we apply the shedding model to the motion with varying angles. The motion of the plate is given by

$$\begin{aligned} {\hat{c}}(t)= & {} \frac{5}{4} - \frac{1}{32} [ 2 \log 2 + \log \cosh (16 ({\hat{t}}-1)) + \log \cosh (16 ({\hat{t}}-1.5)) ], \\ \theta (t)= & {} \frac{\pi }{2} + \frac{\pi }{128} [ \log \cosh (16 ({\hat{t}}-1)) - \log \cosh (16 ({\hat{t}}-1.5)) ]. \end{aligned}$$

The motion of the plate consists of a forward translation, followed by a smooth stop with rotation, and then a backward translation. This hovering motion was considered in Jones [20].

Figure 15 shows the evolution of vortex of the hovering motion of a plate. The vortices are formed behind the plate at the forward stroke, and the dipole structures are formed both at the leading and trailing edges during the rotation of the plate. Then, the vortices are flipped over at the return stroke. The vortex evolution in Fig. 15 is similar to that in Jones [20]. However, some differences are observed: At ${\hat{t}}=2.5$, the primary leading edge vortex in our model moves backward, while that in the previous model appears to move forward. The location of the trailing edge vortex in our model is also slightly more upward. These differences are not only caused by the difference of the model itself, but also due to the use of non-uniform regularization and a small value of the regularization parameter. The edge circulations and shedding rates of a hovering plate are plotted in Fig. 16.

Fig. 15

Evolution of vortex of a hovering plate at ${\hat{t}}=0,1,1.5,2$ and 2.5

Fig. 16

Edge circulations and shedding rates of a hovering plate

Figure 17 shows the normal force and lift coefficient of a hovering plate. In Fig. 17a, the force components $F_y^{(a)}$, $F_y^{(r)}$, and $F_y^{(v)}$ are also given. Due to decreases in the vortex force and added mass force during the deceleration phase at $0.5< {\hat{t}} < 1$ and the acceleration phase at $1.25< {\hat{t}} < 1.5$, the total normal force has two minima at ${\hat{t}} = 1$ and 1.5. The rotational force has little contribution to the total normal force, as the change of angle is small. At ${\hat{t}} > 1.25$, the plate translates backward, and the angle is greater than $90^\circ$; thus, the signs of the total normal force and lift are opposite. This means that the lift is positive at ${\hat{t}} > 1.25$, as the total normal force acts in the negative direction at the return stroke. In Fig. 17b, the key importance is that the lift coefficient increases greatly at the early return stroke. The reason for this large peak is that at about ${\hat{t}} = 1.5$, the vortex force decreases significantly, and the minima of the added mass force and vortex force nearly overlap at a similar time, and thus, the two forces work together to enhance the lift.

Fig. 17

Force of a hovering plate. a normal force and b lift coefficient. The force components $F_y^{(a)}$, $F_y^{(r)}$ and $F_y^{(v)}$ are also given and $F_y$ represents the total normal force. The normal force and lift coefficients are normalized by $U_f^2$

7.3 Flapping plate

We also consider the vortex wake separating from a flapping plate. This problem has been motivated by the relation to flapping wings and swimming animals. Varying the flapping frequency and amplitude can form a variety of wake patterns such as a von Karman-type wake, reverse von Karman wake and an asymmetric wake [47, 48]. Godoy-Diana et al. [48] showed the transition from drag to thrust producing motions in an experimental study. Considerable research has been carried out on this problem, and a comprehensive review of these works can be found in Wu et al. [49].

Sheng et al. [25] studied the wake of a flapping plate by using the vortex sheet model based on Nitsche and Kransy’s approach [19] and the Brown–Michael model. They compared the results of the vortex sheet model and the Brown–Michael model with the numerical simulation of the Navier–Stokes (NS) equation with $\text{ Re }=1000$. The wake structures of the models and the NS simulation were similar, but there were large differences in the drag force. More significantly, the models predicted thrusts (negative drag) in the mean value, whereas the NS simulation gave a positive mean drag. We here apply our model to the same problem and examine the agreement with the NS simulation.

For this purpose, we adopt the same setting as Sheng et al. [25]. A rigid plate is hinged at the left end of the plate in an oncoming flow with constant velocity U. The plate oscillates with angle $\theta (t)$, with maximal tip displacement A. The angle is given by $\theta (t) = \alpha _m \sin (2 \pi t/\tau )$, where $\theta _m = \sin ^{-1} (A/(2L))$. We define a Strouhal number and dimensionless flapping amplitude $A_L$ as

$$\begin{aligned} \text{ St } = \frac{f A}{U}, \qquad \quad A_L = \frac{A}{L}, \end{aligned}$$

(66)

where f is the frequency of the plate oscillation. The dimensionless parameters are set to $\text{ St }=0.4$ and $A_L = 0.8$ for all the results in this subsection.

The vortex shedding model should be extended to consider the rotation of the plate about an arbitrary fixed point in the plate. Denoting $x_0$ as the position of the rotation center measured from the midpoint of the plate, the complex velocity at $z \rightarrow \infty$ relative to the plate is given by $-U e^{\text {i} \theta } + \text {i} x_0 \varOmega$. Consequently, the term $U \sin \theta$ in the evolution Eqs. (20), (23) and (25) is changed into $U \sin \theta - \text {i} x_0 \varOmega$. In the expression of the added mass force (32), $\sin \theta \, {\dot{U}}(t)$ is also changed to $\sin \theta \, {\dot{U}}(t) - x_0 {\dot{\varOmega }}(t)$.

For comparison with the model, the simulation of the NS equation with the Reynolds number, $\text{ Re }=200$, is performed. This value of the Reynolds number is smaller than $\text{ Re }=1000$ in [25]. We employ a Fourier pseudo-spectral method, with the volume penalization for the solid boundary [50], which is exactly the same used in [25]. The plate is of the thickness 1/(16L). The grid is $8192 \times 4096$ on the computational domain $[-2,22] \times [-6,6]$.

The vorticity contours from the NS simulation with $\text{ Re }=200$ are plotted in Fig. 18. In the first upward sweep, negative vorticity separates from the plate and this leading vortex remains at ${\hat{y}}>0$ in time; its location at $t/\tau =5$ is about ${\hat{x}}=10$ and ${\hat{y}}=1$. With each consecutive down and upward sweep, two vortices of opposite sign are shed and are paired up, except for the leading negative vortex. For example, at $t/\tau =2$, two vortex pairs were observed, i.e., a distinguished one at $3<{\hat{x}}<4$ and a nascent one near the plate. At $t/\tau =5$, we see that vortex pairs travel downwards, forming an asymmetric wake. This behavior of the wake for $\text{ Re }=200$ is similar to that for $\text{ Re }=1000$ in [25]; however, the vortices for $\text{ Re }=200$ become weaker at late times, due to the diffusion of larger viscosity, and travel with a less inclined angle and less downwards than those for $\text{ Re }=1000$. At $t/\tau =5$, the leading vortex pair here is about to reach ${\hat{y}}=-2$, while it is at ${\hat{y}}=-3$ for $\text{ Re }=1000$. Therefore, asymmetry is reduced with a decrease in the Reynolds number. This phenomenon is in accordance with the numerical study by Das et al. [51] over a wide range of Reynolds numbers.

Figure 19 plots the solution of the vortex shedding model at $t/\tau = 1,2,5$. We suppress the vortex shedding at the leading edge, on account of small angles of attack. The location of vortices is in agreement with the NS simulation with $\text{ Re }=200$, but there are some differences between the two results. In Fig. 19, at $t/\tau = 5$, the leading vortex pair is not located downwards, but the other vortex pairs move downwards. Comparing with the solution of the other vortex sheet model [25], we observe that the angle of inclination of vortices in our model is smaller than that.

Fig. 18

Vorticity contours of the flapping plate from the Navier–Stokes simulation for $\text{ Re }=200$, at $t/\tau = 1,2,5$

Fig. 19

Location of the vortex sheet from the shedding model for the flapping plate at $t/\tau = 1,2,5$

Fig. 20

a Shed circulation and b drag coefficient of the flapping plate. The thick (blue) curves correspond to the vortex shedding model, and the thin (red) curves correspond to the Navier–Stokes simulation with $\text{ Re }=200$ (color figure online)

Figure 20 shows the comparison of the shed circulation and drag coefficient of our model and the NS simulation with $\text{ Re }=200$. In Fig. 20a, the circulations of the two results are in excellent agreement. It shows the shedding of negative and positive vortices at each period of sweep. In Fig. 20b, the drag coefficients are relatively in good agreement, although there are some differences in the minima and the drag of the model lags a bit behind the NS simulation. The NS simulation predicts a positive mean drag and the model predicts a negative mean drag, but their difference is not large; the NS simulation is about 0.36 and the model gives -0.19, on average over the interval $1 \le t \le 5$. The mean drag of the NS simulation is 0.49 when the average is taken over the full interval $0 < t \le 5$. However, the previous vortex sheet model [25] predicted a net thrust (negative drag) of -0.72. Therefore, the difference of drag between the vortex shedding model and the NS simulation is significantly reduced, compared to the previous model. Note that there is only a small difference in the drag forces of the NS simulations of $\text{ Re }=200$ and $\text{ Re }=1000$. The drag force of the NS simulation with $\text{ Re }=200$ is slightly larger than that with $\text{ Re }=1000$. In Fig. 20b, the difference of drag may be attributed to the effects of the viscous force and leading edge vortex.

Fig. 21

Comparison of vortex shedding of the two vortex sheet models, for ${\hat{U}} (t)=1$ and $\theta = 90^\circ$. a present model and b Jones model. Times are ${\tilde{t}}=1$ and 3

Fig. 22

Comparison of vortex shedding of the two vortex sheet models, for ${\hat{U}} (t)=1$ and $\theta = 67.5^\circ$. a present model and b Jones model. Times are ${\tilde{t}}=1$ and 3

Fig. 23

Comparison of edge circulations of the two vortex sheet models, for ${\hat{U}} (t)=1$. Angle of attack is a$\theta = 90^\circ$ and b$\theta = 67.5^\circ$. The thick (blue and red) curves correspond to the present model, and the thin (brown and green) curves correspond to the Jones model (color figure online)

8 Comparison with the previous model

We finally compare the results of our model with the previous vortex sheet model by Nitsche and Krasny [19], and Jones [20]. Both Nitsche and Krasny, and Jones described the plate and separated vorices by vortex sheets; however, they implemented different formulations of the unsteady Kutta condition, in order to determine the edge circulations. Nitsche and Krasny used the evolution equation for the edge circulations, whereas Jones explicitly determined the edge circulations by solving an integral equation and removing the singularity. It was shown that those two formulations of the unsteady Kutta condition are mathematically equivalent [20] and numerical results of the two methods are in agreement [27]. Here we compare our model with the Jones model.

We consider an impulsively started plate with angles $\theta = 90^\circ$ and $67.5^\circ$ for comparison. The uniform regularization method is employed to the Jones model, while the non-uniform regularization method is employed to our model. For both methods, the regularization parameter is set to ${\hat{\delta }}_0 = 0.05$. Figure 21 shows the comparison of vortex shedding of our model and the Jones model, for ${\hat{U}} (t)=1$ and $\theta = 90^\circ$. The separated vortices of the two models evolve similarly, but the vortex of the Jones model is slightly larger than that of our model. The vortex center of the Jones model is also located slightly further from the plate than that of our model.

Figure 22 shows the comparison of vortex shedding of our model and the Jones model, for ${\hat{U}} (t)=1$ and $\theta = 67.5^\circ$. The large vortex structures of the two models are similar, but there are more differences between the results of the two models than the case of $\theta = 90^\circ$. At ${\tilde{t}}=1$, the leading edge vortex of the Jones model is larger and travels further from the plate than our model, while the trailing edge vortices of the two models are similar. At ${\tilde{t}}=3$, the leading edge vortex of the Jones model is slightly larger than that of our model, and the trailing edge vortex of the Jones model is located closer to the leading edge vortex than our model. The secondary trailing edge vortex of our model is slightly more evolved than that of the Jones model.

Figure 23 plots the edge circulations of the two models for $\theta = 90^\circ$ and $67.5^\circ$. In Fig. 23a, the edge circulations of the two models grow similarly, but the edge circulation of the Jones model is slightly larger than that of our model. In Fig. 23b, the edge circulations of the two models show the behavior of crossover at late times, but both circulations at the leading and trailing edges of the Jones model are larger than those of our model. These results are consistent with the larger vortices of the Jones model shown in Figs. 21 and 22. We refer to Xu, Nitsche and Krasny [52] for the simulation for the same problem in this section by using the vortex sheet model, in comparison with the Navier–Stokes simulations for varying Reynolds numbers.

9 Conclusions

The main contribution of this work is to develop a new computational model for the vortex shedding of a moving body, using the vortex sheet and conformal mapping. The model does not need an integral equation for the sheet strength on the body, and the Kutta condition is given in a simple form. We also obtain the expression for the aerodynamic force on the body, by integrating the unsteady Blasius equation. The numerical computation of the model gives the solution for the separated flow with high resolution. We show that our model provides not only a qualitative description for the vortex shedding process, but also a quantitative prediction for lift and drag for late times. The lift and drag from the model are in agreement with the Navier–Stokes simulation and experiment for moderate Reynolds numbers, which is consistent with the previous result of the early-time asymptotic solution [32].

We have employed the non-uniform blob regularization for the longtime computation of free vortex sheets. It was shown numerically that the vortex blob method reproduces many features associated with the Navier–Stokes solution with increasing Reynolds number [52, 53]. However, a direct link of the $\delta$-parameter and the physical effects such as viscosity or layer thickness has not yet been established.

We have applied our model mainly to moving bodies with large angles of attack. For small angles of attack, we have suppressed the separation of vortices at the leading edge. If the shedding is allowed at the leading edge for small angles of attack, separated vortices are trapped close to the body, which results in the breakdown of the computation. This problem occurs in most of the inviscid shedding models and limits the application of the models. Darakananda et al. [31, 54] proposed a hybrid vortex shedding model in which the rolled-up cores of free vortex sheets are replaced by point vortices. They reduced the computation cost greatly and succeeded in the simulations for various problems with a wide range of angle of attack. The adoption of this hybrid method to our model is of interest, but is beyond the scope of this paper.

We have considered a plate with impulsive start and uniform acceleration to investigate the unsteady dynamics for large angles of attack. We find that for both cases of $m=0$ and $m=1$, the vortex force is dominant in the lift over time. The lift coefficients are initially high and decrease in four chord lengths of displacement, in general. For the impulsive start, the lift decreases, having a peak at an early time, and increases at late times. The appearance of a peak is explained by the variation of the shedding rate at the leading edge. For the uniformly accelerated plate, the vortex lift decreases monotonically and a peak does not appear. However, for small angles of attack, a peak in the vortex lift appears at a transient time for all power-law velocities and exhibits a universal characteristic [38]. Therefore, the behavior of the lift of the vortex force for large angles of attack differs considerably from that for small angles. In addition, we have demonstrated the separated vortical flows of hovering and flapping plates from the model. In the hovering motion, we show that the large increase in lift at the early return stroke is the combined contribution of the vortex force and added mass force. In the flapping plate, our model provides a good approximation to the wake and the induced force.