Skip to main content
SpringerLink
Log in

Identification of Scale-Independent Material Parameters in the Relaxed Micromorphic Model Through Model-Adapted First Order Homogenization

  • Published:
Journal of Elasticity Aims and scope Submit manuscript

Abstract

We rigorously determine the scale-independent short range elastic parameters in the relaxed micromorphic generalized continuum model for a given periodic microstructure. This is done using both classical periodic homogenization and a new procedure involving the concept of apparent material stiffness of a unit-cell under affine Dirichlet boundary conditions and Neumann’s principle on the overall representation of anisotropy. We explain our idea of “maximal” stiffness of the unit-cell and use state of the art first order numerical homogenization methods to obtain the needed parameters for a given tetragonal unit-cell. These results are used in the accompanying paper (d’Agostino et al. in J. Elast. 2019. Accepted in this volume) to describe the wave propagation including band-gaps in the same tetragonal metamaterial.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Notes

  1. As is well-known, under affine loading, the response of a large periodic structure is periodic up to a vanishing boundary layer.

  2. For the micromorphic model, postulate d) implies a direct interpretation of what the new degrees of freedom (the non symmetric micro-distortion \(P\in \mathbb{R}^{3\times 3}\)) is. While we do not discard such a direct micro-macro relation, we rather believe that any simple relation will fall short of the truth for the relaxed micromorphic model.

  3. For the presentation we have chosen throughout the simplest representation of the curvature energy – a one constant isotropic format.

  4. Despite the name micromorphic model.

  5. The situation is different when one considers homogenization towards a second gradient continuum (or micromorphic approximations thereof) where there is no independent kinematical field. More precisely, the case \(\widehat{\mathbb{C}}_{\textrm{e}}\gg 1\), \(L_{c}\ll 1\) would be consistent with determining \(P\) as some average of the micro-displacements over a unit-cell.

  6. Equation (4)1 and (4)2 together imply \(\textrm{Div} ( \mathbb{C}_{\textrm{micro}}\,\textrm{sym}\,P ) =f\). Constraining \(\textrm{sym}\,P=\textrm{sym}\,\nabla u\) gives \(\textrm{Div} ( \mathbb{C}_{\textrm{micro}}\,\textrm{sym}\,\nabla u ) =f\).

  7. The curvature expression in the Eringen-Mindlin-model or gradient elasticity model would typically include a sixth-order tensor [5], in contrast to the relaxed micromorphic model, which only needs a fourth-order tensor.

  8. Equation (7)1 and (7)2 together imply that \(\textrm{Div} [ \mathbb{C}_{\textrm{micro}}\,\textrm{sym}\,P-\mu \,L_{c}^{2}\Delta P ] =f\). Here \(\mathbb{C}_{\textrm{micro}}\) is invariably coupled to the characteristic length \(L_{c}\). Constraining \(P=\nabla u\) gives \(\textrm{Div} [ \mathbb{C}_{\textrm{micro}}\,\textrm{sym}\,\nabla u-\mu \,L_{c}^{2}\Delta \nabla u ] =f\). This is the fourth-order equilibrium equation of the second gradient formulation (8).

  9. The relaxed micromorphic model cannot be obtained as penalty formulation of gradient elasticity and in a 1-D setting it reduces to linear elasticity with stiffness \(\mathbb{C}_{\textrm{macro}}\).

  10. Letting \(L_{c}\rightarrow 0\) in (7) leads to the algebraic side condition \(\widehat{\mathbb{C}}_{\textrm{e}}\,(\nabla u-P)=\mathbb{C}_{\textrm{micro}}\,\textrm{sym}\,P\). Due to the more general format of \(\widehat{\mathbb{C}}_{\textrm{e}}\) as compared to \(\mathbb{C}_{\textrm{e}}\) and \(\mathbb{C}_{\textrm{c}}\) in (13), it is not possible to analytically solve for \(\textrm{sym}\,P\) and no transparent formula connecting \(\widehat{\mathbb{C}}_{\textrm{e}}\) and \(\mathbb{C}_{\textrm{micro}}\) to \(\mathbb{C}_{\textrm{macro}}\) like (15) results. The formally scale-independent material parameters of the classical Eringen-Mindlin-model are \(\widehat{\mathbb{C}}_{\textrm{e}}\) and \(\mathbb{C}_{\textrm{micro}}\) and the scale-independent parameters of \(W_{\textrm{GE}}\) are \(\mathbb{C}_{\textrm{micro}}=\mathbb{C}_{\textrm{macro}}\). For the Cosserat model, the respective scale-independent stiffness is \(\mathbb{C}_{\textrm{e}}=\mathbb{C}_{\textrm{macro}}\). However, considering (footnote 8) \(\textrm{Div} [ \mathbb{C}_{\textrm{micro}}\,\textrm{sym}\,P-\mu \,L_{c}^{2}\Delta P ] =f\), it is not strictly possible to say that \(\mathbb{C}_{\textrm{micro}}\) is scale-independent in the Eringen-Mindlin model. The identification of \(\mathbb{C}_{\textrm{micro}}\) (and therefore also \(\widehat{\mathbb{C}}_{\textrm{e}}\)) in the Eringen-Mindlin model may be length-scale dependent after all.

  11. It is indeed well known in the field of homogenization techniques (see, e.g., [20, 68]) that the homogenization of a unit-cell on which one imposes periodic boundary conditions mimics the behavior of a very large specimen of the associated equivalent Cauchy continuum. Usually, homogenization techniques only provide a direct transition from the micro to the macro-scale without considering the intermediate (transition) scale in which all relevant microstructure-related phenomena are manifest. Some attempts to introduce a transition scale via the homogenization towards a micromorphic continuum are made in [39, 79], even if it is clear that a definitive answer is far from being provided (see [39, 79] and references cited there). Our relaxed micromorphic model naturally provides the bridge between the micro and macro behavior of the considered homogenized material with the simple and transparent tensor homogenization formulas (15).

  12. In this way, artificial boundary layer effects are avoided.

  13. And not any of the ambiguous extended versions for generalized continua [26, 27, 29, 40].

  14. Since

    $$\begin{aligned} & \frac{1}{2} \bigl\langle \mathbb{C}_{\textrm{KUBC}}^{V} \,\overline{E}, \overline{E} \bigr\rangle \bigl\vert V (x ) \bigr\vert \\ &\quad =\inf \biggl\{ \int _{\xi \in V (x )}\frac{1}{2} \bigl\langle \mathbb{C} (\xi ) \bigl(\textrm{sym}\nabla _{\xi }v (\xi )+ \overline{E} \bigr),\textrm{sym}\nabla _{\xi }v (\xi )+ \overline{E} \bigr\rangle \,d\xi \: |\:v\in C_{0}^{\infty } \bigl(V \! (x ),\mathbb{R}^{3} \bigr) \biggr\} \\ & \quad v\equiv 0\;(\textrm{constant strain assumption: Taylor/Voigt}) \\ &\quad \leq \int _{V}\frac{1}{2} \bigl\langle \mathbb{C}(\xi ) \overline{E}, \overline{E} \bigr\rangle \,d\xi = \frac{1}{2} \biggl\langle \overline{E}, \int _{V} \mathbb{C}(\xi )\,d\xi \,\overline{E} \biggr\rangle = \frac{1}{2} \vert V \vert \biggl\langle \overline{E}, \frac{1}{ \vert V \vert } \int _{V} \mathbb{C}(\xi )\,d\xi \,\overline{E} \biggr\rangle = \frac{1}{2} \vert V \vert \langle \overline{E},\mathbb{C}_{ \textrm{Voigt}} \,\overline{E} \rangle \end{aligned}$$
    (31)

    it is clear that \(\langle \mathbb{C}_{\textrm{KUBC}}^{V}\, \overline{E}, \,\overline{E} \rangle \leq \langle \mathbb{C}_{\textrm{Voigt}} \,\overline{E},\overline{E} \rangle \) for all applied loadings \(\overline{E}\in \textrm{Sym}\left(3\right)\). On the other hand, it is natural to require as well \(\langle \mathbb{C}_{\textrm{micro}}\,\overline{E}, \, \overline{E} \rangle \leq \langle \mathbb{C}_{\textrm{Voigt}} \,\overline{E},\overline{E} \rangle \), where equality will be obtained if and only if the material on the micro-scale is homogeneous, i.e., \(\mathbb{C}(\xi )=\textrm{const}\).

  15. An equivalent, more algorithmic procedure to determine \(\mathbb{C}_{\textrm{KUBC}}^{V}\) is obtained as follows. Consider again (37)

    $$ \langle \overline{\sigma },\overline{\varepsilon } \rangle = \frac{1}{ \vert V \vert } \int _{ V} \bigl\langle \sigma (\xi ), \varepsilon (\xi ) \bigr\rangle \,d\xi = \frac{1}{ \vert V \vert } \int _{V} \bigl\langle \mathbb{C}(\xi )\,\varepsilon (\xi ), \varepsilon (\xi ) \bigr\rangle \,d \xi ,\quad \textrm{Div}\,\sigma \! (\xi )=0, \quad \sigma ^{\,T}\!(\xi )=\sigma (\xi ), $$
    (38)

    and \(\widetilde{v}=\overline{\varepsilon }\cdot \xi \) at the boundary. Let us define the corresponding linear solution operator of the linear elastic problem at the micro-scale \(\mathscr{L}(\xi )\cdot \overline{ \varepsilon }=\varepsilon (\xi )\), (“localization tensor”) and insert this back into (37). This gives

  16. Here, \(\mu \,L^{2}_{c} \langle \mathbb{L}\,\textrm{Curl}\,P,\textrm{Curl}\,P \rangle \) would represent the most general quadratic anisotropic curvature energy in the relaxed micromorphic model, where \(\mathbb{L}\) is a fourth-order tensor mapping non-symmetric second-order tensors to non-symmetric second-order tensors.

  17. \(\mathbb{C}_{\textrm{micro}}\) could be isotropic nevertheless, since isotropy is a subclass of the tetragonal symmetry.

  18. Considering the Voigt upper bound \(\mathbb{C}_{\textrm{Voigt}}:= \frac{1}{ \vert V \vert }\int _{V}\mathbb{C}(\xi )\,d\xi \) as representing the maximal microscopic stiffness is not useful for two reasons: First, \(\mathbb{C}_{\,\textrm{Voigt}}\) will be isotropic and lose the information of the geometry of the microstructure. Second, the actual deformation in any unit-cell will never exhibit constant strain.

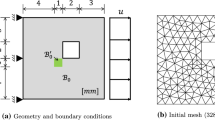
  19. Here, \(x\) is the macro space variable of the continuum, while \(\xi \) is the micro-variable spanning inside the unit-cell.

  20. For a discussion of the non-uniqueness of the unit-cell, see [74].

  21. N.B. the value of \(\lambda _{\textrm{micro}}\) is correctly 5.270 and not 5.981 because of the definition of \(\widehat{\lambda }\) in (47).

References

  1. Abdulle, A.: Analysis of a heterogeneous multiscale FEM for problems in elasticity. Math. Models Methods Appl. Sci. 16(04), 615–635 (2006)

    MathSciNet  MATH  Google Scholar 

  2. Aivaliotis, A., Daouadji, A., Barbagallo, G., Tallarico, D., Neff, P., Madeo, A.: Low-and high-frequency Stoneley waves, reflection and transmission at a Cauchy/relaxed micromorphic interface (2018). arXiv preprint. arXiv:1810.12578

  3. Aivaliotis, A., Daouadji, A., Barbagallo, G., Tallarico, D., Neff, P., Madeo, A.: Microstructure-related Stoneley waves and their effect on the scattering properties of a 2d Cauchy/relaxed-micromorphic interface. Wave Motion 90, 99–120 (2019)

    MathSciNet  Google Scholar 

  4. Aivaliotis, A., Tallarico, D., Daouadji, A., Neff, P., Madeo, A.: Scattering of finite-size anisotropic metastructures via the relaxed micromorphic model (2019). arXiv preprint. arXiv:1905.12297

  5. Auffray, N., Bouchet, R., Brechet, Y.: Derivation of anisotropic matrix for bi-dimensional strain-gradient elasticity behavior. Int. J. Solids Struct. 46(2), 440–454 (2009)

    MATH  Google Scholar 

  6. Barbagallo, G., Madeo, A., d’Agostino, M.V., Abreu, R., Ghiba, I.-D., Neff, P.: Transparent anisotropy for the relaxed micromorphic model: macroscopic consistency conditions and long wave length asymptotics. Int. J. Solids Struct. 120, 7–30 (2017)

    MATH  Google Scholar 

  7. Barbagallo, G., Tallarico, D., d’Agostino, M.V., Aivaliotis, A., Neff, P., Madeo, A.: Relaxed micromorphic model of transient wave propagation in anisotropic band-gap metastructures. Int. J. Solids Struct. 162, 148–163 (2019)

    Google Scholar 

  8. Bauer, S., Neff, P., Pauly, D., Starke, G.: Dev-Div- and DevSym-DevCurl-inequalities for incompatible square tensor fields with mixed boundary conditions. ESAIM Control Optim. Calc. Var. 22(1), 112–133 (2016)

    MathSciNet  MATH  Google Scholar 

  9. Bensoussan, A., Lions, J.-L., Papanicolaou, G.: Asymptotic Analysis for Periodic Structures, vol. 5. North-Holland Publishing Company, Amsterdam (1978)

    MATH  Google Scholar 

  10. Biswas, R., Poh, L.H.: A micromorphic computational homogenization framework for heterogeneous materials. J. Mech. Phys. Solids 102, 187–208 (2017)

    ADS  MathSciNet  Google Scholar 

  11. Boutin, C., Rallu, A., Hans, S.: Large scale modulation of high frequency waves in periodic elastic composites. J. Mech. Phys. Solids 70, 362–381 (2014)

    ADS  MathSciNet  MATH  Google Scholar 

  12. Bouyge, F., Jasiuk, I., Boccara, S., Ostoja-Starzewski, M.: A micromechanically based couple-stress model of an elastic orthotropic two-phase composite. Eur. J. Mech. A, Solids 21(3), 465–481 (2002)

    MATH  Google Scholar 

  13. Braides, A.: A handbook of \({\varGamma }\)-convergence. Handb. Differ. Equ. 3, 101–213 (2006)

    MATH  Google Scholar 

  14. Burgeth, B., Welk, M., Feddern, C., Weickert, J.: Mathematical morphology on tensor data using the Löwner ordering. In: Visualization and Processing of Tensor Fields, pp. 357–368. Springer, Berlin (2006)

    Google Scholar 

  15. Cosserat, E., Cosserat, F.: Théorie des corps déformables (1909). (engl. translation by D. Delphenich, pdf available at http://www.uni-due.de/%7ehm0014/Cosserat_files/Cosserat09_eng.pdf)

    MATH  Google Scholar 

  16. d’Agostino, M.V., Barbagallo, G., Ghiba, I.-D., Eidel, B., Neff, P., Madeo, A.: Effective description of anisotropic wave dispersion in mechanical metamaterials via the relaxed micromorphic model. J. Elast. (2019). Accepted in this volume

  17. Diebels, S., Steeb, H.: Stress and couple stress in foams. Comput. Mater. Sci. 28(3–4), 714–722 (2003)

    Google Scholar 

  18. Weinan, E., Engquist, B.: The heterogeneous multiscale methods. Commun. Math. Sci. 1(1), 87–132 (2003)

    MathSciNet  MATH  Google Scholar 

  19. Ehlers, W., Bidier, S.: From particle mechanics to micromorphic media. Part I: Homogenisation of discrete interactions towards stress quantities. Int. J. Solids Struct. (2018). https://doi.org/10.1016/j.ijsolstr.2018.08.013

    Article  Google Scholar 

  20. Eidel, B., Fischer, A.: The heterogeneous multiscale finite element method for the homogenization of linear elastic solids and a comparison with the FE2 method. Comput. Methods Appl. Mech. Eng. 329, 332–368 (2018)

    ADS  Google Scholar 

  21. Cemal, A.: Eringen. Mechanics of micromorphic materials. In: Applied Mechanics, pp. 131–138. Springer, Berlin (1966)

    Google Scholar 

  22. Eringen, A.C.: Microcontinuum Field Theories. Springer, New York (1999)

    MATH  Google Scholar 

  23. Eringen, A.C., Suhubi, E.S.: Nonlinear theory of simple micro-elastic solids – I. Int. J. Eng. Sci. 2(2), 189–203 (1964)

    MathSciNet  MATH  Google Scholar 

  24. Fischer, A., Eidel, B.: Convergence and error analysis of FE-HMM/FE2 for energetically consistent micro-coupling conditions in linear elastic solids. Eur. J. Mech. A, Solids 77, 103735 (2019)

    ADS  MathSciNet  MATH  Google Scholar 

  25. Forest, S.: Mechanics of generalized continua: construction by homogenizaton. J. Phys. IV 08(4), 39–48 (1998)

    Google Scholar 

  26. Forest, S.: Aufbau und Identifikation von Stoffgleichungen für höhere Kontinua mittels Homogenisierungsmethoden. Tech. Mech. 19(4), 297–306 (1999)

    MathSciNet  Google Scholar 

  27. Forest, S.: Homogenization methods and mechanics of generalized continua – Part 2. Theor. Appl. Mech. 28–29, 113–144 (2002)

    MATH  Google Scholar 

  28. Forest, S., Sab, K.: Cosserat overall modeling of heterogeneous materials. Mech. Res. Commun. 25(4), 449–454 (1998)

    MathSciNet  MATH  Google Scholar 

  29. Forest, S., Trinh, D.K.: Generalized continua and non-homogeneous boundary conditions in homogenisation methods. Z. Angew. Math. Mech. 91(2), 90–109 (2011)

    MathSciNet  MATH  Google Scholar 

  30. Ghiba, I.-D., Neff, P., Madeo, A., Münch, I.: A variant of the linear isotropic indeterminate couple-stress model with symmetric local force-stress, symmetric nonlocal force-stress, symmetric couple-stresses and orthogonal boundary conditions. Math. Mech. Solids 22, 1221–1266 (2016)

    MathSciNet  MATH  Google Scholar 

  31. Ghiba, I.-D., Neff, P., Madeo, A., Placidi, L., Rosi, G.: The relaxed linear micromorphic continuum: existence, uniqueness and continuous dependence in dynamics. Math. Mech. Solids 20(10), 1171–1197 (2014)

    MathSciNet  MATH  Google Scholar 

  32. Gologanu, M., Leblond, J.-B., Perrin, G., Devaux, J.: Recent extensions of Gurson’s model for porous ductile metals Part II: a Gurson-like model including the effect of strong gradients of the macroscopic field. Contin. Micromech. 377, 97–130 (1997)

    MATH  Google Scholar 

  33. Hill, R.: Elastic properties of reinforced solids: some theoretical principles. J. Mech. Phys. Solids 11(5), 357–372 (1963)

    ADS  MATH  Google Scholar 

  34. Hill, R.: On constitutive macro-variables for heterogeneous solids at finite strain. Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci. 326(1565), 131–147 (1972)

    ADS  MATH  Google Scholar 

  35. Hori, M., Nemat-Nasser, S.: Micromechanics: Overall Properties of Heterogeneous Materials, vol. 37. Elsevier, Amsterdam (2013)

    MATH  Google Scholar 

  36. Huet, C.: Application of variational concepts to size effects in elastic heterogeneous bodies. J. Mech. Phys. Solids 38(6), 813–841 (1990)

    ADS  MathSciNet  Google Scholar 

  37. Huet, C.: An integrated micromechanics and statistical continuum thermodynamics approach for studying the fracture behaviour of microcracked heterogeneous materials with delayed response. Eng. Fract. Mech. 58(5–6), 459–556 (1997)

    Google Scholar 

  38. Huet, C.: Coupled size and boundary-condition effects in viscoelastic heterogeneous and composite bodies. Mech. Mater. 31(12), 787–829 (1999)

    Google Scholar 

  39. Hütter, G.: Homogenization of a Cauchy continuum towards a micromorphic continuum. J. Mech. Phys. Solids 99, 394–408 (2017)

    ADS  MathSciNet  Google Scholar 

  40. Hütter, G.: On the micro-macro relation for the microdeformation in the homogenization towards micromorphic and micropolar continua. J. Mech. Phys. Solids 127, 62–79 (2019)

    ADS  MathSciNet  Google Scholar 

  41. Jänicke, R., Diebels, S., Sehlhorst, H.-G., Düster, A.: Two-scale modelling of micromorphic continua. Contin. Mech. Thermodyn. 21(4), 297–315 (2009)

    ADS  MathSciNet  MATH  Google Scholar 

  42. Kanit, T., Forest, S., Galliet, I., Mounoury, V., Jeulin, D.: Determination of the size of the representative volume element for random composites: statistical and numerical approach. Int. J. Solids Struct. 40(13–14), 3647–3679 (2003)

    MATH  Google Scholar 

  43. Kouznetsova, V., Geers, M.G.D., Brekelmans, M.W.A.: Multi-scale constitutive modelling of heterogeneous materials with a gradient-enhanced computational homogenization scheme. Int. J. Numer. Methods Eng. 54(8), 1235–1260 (2002)

    MATH  Google Scholar 

  44. Kouznetsova, V., Geers, M.G.D., Brekelmans, M.W.A.: Multi-scale second-order computational homogenization of multi-phase materials: a nested finite element solution strategy. Comput. Methods Appl. Mech. Eng. 193(48–51), 5525–5550 (2004)

    ADS  MATH  Google Scholar 

  45. Lobos, M., Yuzbasioglu, T., Böhlke, T.: Homogenization and materials design of anisotropic multiphase linear elastic materials using central model functions. J. Elast. 128(1), 17–60 (2017)

    MathSciNet  MATH  Google Scholar 

  46. Love, A.E.H.: A Treatise on the Mathematical Theory of Elasticity. Dover, New York (1944)

    MATH  Google Scholar 

  47. Madeo, A., Collet, M., Miniaci, M., Billon, K., Ouisse, M., Neff, P.: Modeling phononic crystals via the weighted relaxed micromorphic model with free and gradient micro-inertia. J. Elast. 130, 1–25 (2017)

    MathSciNet  MATH  Google Scholar 

  48. Madeo, A., Ghiba, I.-D., Neff, P., Münch, I.: A new view on boundary conditions in the Grioli–Koiter–Mindlin–Toupin indeterminate couple stress model. Eur. J. Mech. A, Solids 59, 294–322 (2016)

    ADS  MathSciNet  MATH  Google Scholar 

  49. Madeo, A., Neff, P., d’Agostino, M.V., Barbagallo, G.: Complete band gaps including non-local effects occur only in the relaxed micromorphic model. C. R., Méc. 344(11), 784–796 (2016)

    ADS  Google Scholar 

  50. Madeo, A., Neff, P., Ghiba, I.-D., Placidi, L., Rosi, G.: Band gaps in the relaxed linear micromorphic continuum. Z. Angew. Math. Mech. 95(9), 880–887 (2014)

    MathSciNet  MATH  Google Scholar 

  51. Madeo, A., Neff, P., Ghiba, I.-D., Rosi, G.: Reflection and transmission of elastic waves in non-local band-gap metamaterials: a comprehensive study via the relaxed micromorphic model. J. Mech. Phys. Solids 95, 441–479 (2016)

    ADS  MathSciNet  Google Scholar 

  52. Mandel, J.: Plasticité classique et viscoplasticité. International Centre for Mechanical Sciences. Courses and Lectures (1971)

    Google Scholar 

  53. Michel, J.-C., Moulinec, H., Suquet, P.M.: Effective properties of composite materials with periodic microstructure: a computational approach. Comput. Methods Appl. Mech. Eng. 172(1–4), 109–143 (1999)

    ADS  MathSciNet  MATH  Google Scholar 

  54. Mindlin, R.D.: Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 16(1), 51–78 (1964)

    MathSciNet  MATH  Google Scholar 

  55. Münch, I., Neff, P., Madeo, A., Ghiba, I.-D.: The modified indeterminate couple stress model: why Yang et al.’s arguments motivating a symmetric couple stress tensor contain a gap and why the couple stress tensor may be chosen symmetric nevertheless. Z. Angew. Math. Mech. 97(12), 1524–1554 (2017)

    MathSciNet  Google Scholar 

  56. Neff, P.: On material constants for micromorphic continua. In: Trends in Applications of Mathematics to Mechanics, STAMM Proceedings, Seeheim, pp. 337–348. Shaker–Verlag, Aachen (2004)

    Google Scholar 

  57. Neff, P.: Existence of minimizers for a finite-strain micromorphic elastic solid. Proc. R. Soc. Edinb., Sect. A, Math. 136(05), 997–1012 (2006)

    MathSciNet  MATH  Google Scholar 

  58. Neff, P., Forest, S.: A geometrically exact micromorphic model for elastic metallic foams accounting for affine microstructure. Modelling, existence of minimizers, identification of moduli and computational results. J. Elast. 87(2–3), 239–276 (2007)

    MathSciNet  MATH  Google Scholar 

  59. Neff, P., Ghiba, I.-D., Lazar, M., Madeo, A.: The relaxed linear micromorphic continuum: well-posedness of the static problem and relations to the gauge theory of dislocations. Q. J. Mech. Appl. Math. 68(1), 53–84 (2014)

    MathSciNet  MATH  Google Scholar 

  60. Neff, P., Ghiba, I.-D., Madeo, A., Placidi, L., Rosi, G.: A unifying perspective: the relaxed linear micromorphic continuum. Contin. Mech. Thermodyn. 26(5), 639–681 (2014)

    ADS  MathSciNet  MATH  Google Scholar 

  61. Neff, P., Jeong, J., Fischle, A.: Stable identification of linear isotropic Cosserat parameters: bounded stiffness in bending and torsion implies conformal invariance of curvature. Acta Mech. 211(3–4), 237–249 (2010)

    MATH  Google Scholar 

  62. Neff, P., Jeong, J., Ramézani, H.: Subgrid interaction and micro-randomness – Novel invariance requirements in infinitesimal gradient elasticity. Int. J. Solids Struct. 46(25–26), 4261–4276 (2009)

    MATH  Google Scholar 

  63. Neff, P., Madeo, A., Barbagallo, G., d’Agostino, M.V., Abreu, R., Ghiba, I.-D.: Real wave propagation in the isotropic-relaxed micromorphic model. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 473(2197) (2017)

  64. Neff, P., Münch, I.: Curl bounds Grad on SO(3). ESAIM Control Optim. Calc. Var. 14(1), 148–159 (2008)

    MathSciNet  MATH  Google Scholar 

  65. Neff, P., Pauly, D., Witsch, K.-J.: Maxwell meets Korn: a new coercive inequality for tensor fields in \(\mathbb{R}^{N\times \,N}\) with square-integrable exterior derivative. Math. Methods Appl. Sci. 35(1), 65–71 (2012)

    ADS  MathSciNet  MATH  Google Scholar 

  66. Neff, P., Pauly, D., Witsch, K.-J.: Poincaré meets Korn via Maxwell: extending Korn’s first inequality to incompatible tensor fields. J. Differ. Equ. 258(4), 1267–1302 (2015)

    ADS  MATH  Google Scholar 

  67. Neumann, F.E.: Vorlesungen über die Theorie der Elasticität der festen Körper und des Lichtäthers. B.G. Teubner, Leipzig (1885)

    MATH  Google Scholar 

  68. Pecullan, S., Gibiansky, L., Torquato, S.: Scale effects on the elastic behavior of periodic and hierarchical two-dimensional composites. J. Mech. Phys. Solids 47(7), 1509–1542 (1999)

    ADS  MathSciNet  MATH  Google Scholar 

  69. Pham, K., Kouznetsova, V.G., Geers, M.G.D.: Transient computational homogenization for heterogeneous materials under dynamic excitation. J. Mech. Phys. Solids 61(11), 2125–2146 (2013)

    ADS  MathSciNet  MATH  Google Scholar 

  70. Reuß, A.: Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 9(1), 49–58 (1929)

    MATH  Google Scholar 

  71. Rokoš, O., Ameen, M.M., Peerlings, R.H.J., Geers, M.G.D.: Micromorphic computational homogenization for mechanical metamaterials with patterning fluctuation fields. J. Mech. Phys. Solids 123, 119–137 (2019)

    ADS  MathSciNet  Google Scholar 

  72. Romano, G., Barretta, R., Diaco, M.: Micromorphic continua: non-redundant formulations. Contin. Mech. Thermodyn. 28(6), 1659–1670 (2016)

    ADS  MathSciNet  MATH  Google Scholar 

  73. Karam, S.: On the homogenization and the simulation of random materials. Eur. J. Mech. A, Solids 5, 585–607 (1992)

    MathSciNet  Google Scholar 

  74. Schröder, J.: A numerical two-scale homogenization scheme: the \(\mathit{FE}^{2}\)-method. Schröder, J., Hackl, K. (eds.) Plasticity and Beyond: Microstructures, Crystal-Plasticity and Phase Transitions, vol. 550, pp. 1–64. Springer, Berlin (2014)

    Google Scholar 

  75. Smyshlyaev, V.P., Cherednichenko, K.D.: On rigorous derivation of strain gradient effects in the overall behaviour of periodic heterogeneous media. J. Mech. Phys. Solids 48(6–7), 1325–1357 (2000)

    ADS  MathSciNet  MATH  Google Scholar 

  76. Sridhar, A., Kouznetsova, V.G., Geers, M.G.D.: Homogenization of locally resonant acoustic metamaterials towards an emergent enriched continuum. Comput. Mech. 57(3), 423–435 (2016)

    MathSciNet  MATH  Google Scholar 

  77. Suquet, P.M.: Local and global aspects in the mathematical theory of plasticity. Plasticity today, 279–309 (1985)

  78. Suquet, P.M.: Effective properties of nonlinear composites. In: Continuum Micromechanics, pp. 197–264. Springer, Berlin (1997)

    MATH  Google Scholar 

  79. Trinh D.K., Janicke, R., Auffray, N., Diebels, S., Forest, S.: Evaluation of generalized continuum substitution models for heterogeneous materials. Int. J. Multiscale Comput. Eng. 10(6), 527–549 (2012)

    Google Scholar 

  80. Voigt, W.: Lehrbuch der Krystallphysik (mit Ausschluss der Krystalloptik). B.G. Teubner, Leipzig (1910)

    Google Scholar 

  81. Wang, C., Feng, L., Jasiuk, I.: Scale and boundary conditions effects on the apparent elastic moduli of trabecular bone modeled as a periodic cellular solid. J. Biomech. Eng. 131(12), 121008 (2009)

    Google Scholar 

  82. Zohdi, T.I.: Homogenization Methods and Multiscale Modeling. Encyclopedia of Computational Mechanics (2004)

    Google Scholar 

Download references

Acknowledgements

Patrizio Neff thanks Samuel Forest (Ecole des Mines, Paris), Geralf Hütter (TU Freiberg) and Jörg Schröder (University of Duisburg-Essen) for helpful discussions. The authors are also indebted to Lev Truskinovsky (ESPCI, Paris) for pertinent remarks which helped improve the paper.

Author information

Authors and Affiliations

  1. Head of Chair for Nonlinear Analysis and Modelling, Fakultät für Mathematik, Universität Duisburg-Essen, Mathematik-Carrée, Thea-Leymann-Straße 9, 45127, Essen, Germany

    Patrizio Neff

  2. Universität Siegen, Institut für Mechanik, Heisenberg-group, Paul-Bonatz-Straße 9-11, 57076, Siegen, Germany

    Bernhard Eidel

  3. GEOMAS, INSA-Lyon, 20 avenue Albert Einstein, 69621, Villeurbanne, France

    Marco Valerio d’Agostino & Angela Madeo

Authors
  1. Patrizio Neff
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bernhard Eidel
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marco Valerio d’Agostino
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Angela Madeo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Patrizio Neff.

Additional information

Dedicated to Prof. Dr. Dr. h. c. Hans-Dieter Alber on the occasion of his 70. birthday with great esteem

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Neff, P., Eidel, B., d’Agostino, M.V. et al. Identification of Scale-Independent Material Parameters in the Relaxed Micromorphic Model Through Model-Adapted First Order Homogenization. J Elast 139, 269–298 (2020). https://doi.org/10.1007/s10659-019-09752-w

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10659-019-09752-w

Keywords

Mathematics Subject Classification (2000)

Search

Navigation