Abstract
An axisymmetric and axially homogenous variational formulation is presented for coupled extension-torsion-inflation deformation in compressible magnetoelastomeric tubes in the presence of azimuthal and axial magnetic fields. The tube’s material is assumed to have a preferred magnetization direction which lie in the radial plane but at an angle from the tube’s axial direction - this imparts helical magnetic anisotropy to the tube. The governing differential equations necessary to solve the above deformation problem are obtained which are shown to reduce to a set of nonlinear algebraic equations in the thin tube limit. This allows us to obtain analytical expressions in terms of the applied magnetic field, preferred magnetization direction and magnetoelastic constants which tell us how these parameters can be tuned to generate unusual coupled deformations such as negative Poisson’s effect. The study can be useful in designing magnetoelastic soft tubular actuators.











Similar content being viewed by others
Notes
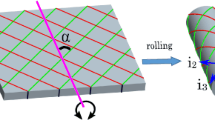
The same figure has also been used by Saxena et al. [29] but the green lines there denote the preferred polarization direction.
The magnetic transverse isotropy also induces elastic transverse isotropy since the former is typically achieved by embedding magnetic particles along the principal direction which automatically alters elastic properties in that direction too.
The intrinsic twist \(\kappa _{0}\) is related to the poling angle as follows: \(R~\kappa _{0}(R)=\tan (\alpha )\).
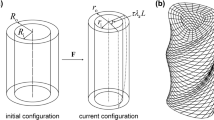
The inflation strain is defined as the ratio of the change in inner radius of the tube to its referential inner radius.
From now on, the quantities corresponding to cases (i) and (ii) will be denoted by putting ‘tilde’ and ‘hat’ respectively as diacritic.
From now on, the quantities evaluated at inner and outer radii will be denoted by putting subscripts 1 and 2 respectively. For example, \(T_{rR}(R_{1})\) will be denoted by \(T_{rR_{1}}\).
The higher order terms in thickness can be neglected when the tube is thin enough.
By overwinding (or unwinding), we mean twisting of a tube in the same (or opposite) direction to that of its intrinsic twist \(\kappa _{0}\).
Abbreviations
- \(\alpha \) :
-
poling angle
- \(\kappa _{0}\) :
-
intrinsic twist
- \(b\) :
-
normalized in-plane displacement
- \(\epsilon \) :
-
imposed axial strain
- \(\kappa \) :
-
imposed twist
- \(\beta \) :
-
imposed inflation
- \(I\) :
-
electric current
- \(\stackrel{*}{\zeta }\) :
-
non-dimensional azimuthal magnetic field
- \(\stackrel {*}{\eta }\) :
-
non-dimensional axial magnetic field
- \(\boldsymbol{\tau }\) :
-
total Cauchy stress tensor
- ℳ:
-
induced twisting moment
- \(\mathcal{P}\) :
-
induced internal pressure
- ℱ:
-
induced axial force
- \(\psi _{\theta } \) :
-
azimuthal magnetic flux per unit deformed length
- \(\psi _{z}\) :
-
axial magnetic flux
- \(\Phi \) :
-
free energy of the cross-section
- \(\phi\) :
-
scalar magnetic potential
- \(\Omega \) :
-
three-dimensional strain energy density
- \(\mathbf{T}\) :
-
total 1st Piola-Kirchhoff stress tensor
- \(\boldsymbol{\tau }^{m}\) :
-
Eulerian Maxwell stress tensor
References
Albanese, A.M., Cunefare, K.A.: Properties of a magnetorheological semi-active vibration absorber. In: Smart Structures and Materials 2003: Damping and Isolation, vol. 5052, pp. 36–44. SPIE, Bellingham (2003, July)
Bustamante, R., Dorfmann, A., Ogden, R.W.: A nonlinear magnetoelastic tube under extension and inflation in an axial magnetic field: numerical solution. J. Eng. Math. 59(1), 139–153 (2007)
Bustamante, R.: Transversely isotropic nonlinear magneto-active elastomers. Acta Mech. 210(3–4), 183–214 (2010)
Brigadnov, I.A., Dorfmann, A.: Mathematical modeling of magneto-sensitive elastomers. Int. J. Solids Struct. 40(18), 4659–4674 (2003)
Brown, W.F.: Magnetoelastic Interactions. Springer, Berlin (1966)
Deng, H.X., Gong, X.L.: Application of magnetorheological elastomer to vibration control. In: Nonlinear Sci. Complex. pp. 462–470 (2007)
Dorfmann, A., Ogden, R.W.: Magnetoelastic modelling of elastomers. Eur. J. Mech. A, Solids 22(4), 497–507 (2003)
Ericksen, J.L.: Magnetizable and polarizable elastic materials. Math. Mech. Solids 13(1), 38–54 (2008)
Ginder, J.M., Nichols, M.E., Elie, L.D., Tardiff, J.L.: Magnetorheological elastomers: properties and applications. In: Smart Structures and Materials 1999: Smart Materials Technologies, vol. 3675, pp. 131–139. SPIE, Bellingham (1999, July)
Gong, X.L., Zhang, X.Z., Zhang, P.Q.: Fabrication and characterization of isotropic magnetorheological elastomers. Polym. Test. 24(5), 669–676 (2005)
Hutter, K.: On thermodynamics and thermostatics of viscous thermoelastic solids in the electromagnetic fields. A Lagrangian formulation. Arch. Ration. Mech. Anal. 58(4), 339–368 (1975)
Hutter, K.: A thermodynamic theory of fluids and solids in electromagnetic fields. Arch. Ration. Mech. Anal. 64(3), 269–298 (1977)
Hu, W., Lum, G.Z., Mastrangeli, M., Sitti, M.: Small-scale soft-bodied robot with multimodal locomotion. Nature 554(7690), 81 (2018)
Jolly, M.R., Carlson, J.D., Munoz, B.C.: A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 5(5), 607 (1996)
Kari, L., Blom, P.: Magneto-sensitive rubber in a noise reduction context–exploring the potential. Plast. Rubber Compos. 34(8), 365–371 (2005)
Kankanala, S.V., Triantafyllidis, N.: On finitely strained magnetorheological elastomers. J. Mech. Phys. Solids 52(12), 2869–2908 (2004)
Kashima, S., Miyasaka, F., Hirata, K.: Novel soft actuator using magnetorheological elastomer. IEEE Trans. Magn. 48(4), 1649–1652 (2012)
Kim, Y., Parada, G.A., Liu, S., Zhao, X.: Ferromagnetic soft continuum robots. Sci. Robot. 4(33), eaax7329 (2019)
Kovetz, A.: Electromagnetic Theory, vol. 975. Oxford University Press, Oxford (2000)
Maugin, G.A.: Continuum Mechanics of Electrodynamics Solids (1988)
Eringen, A.C., Maugin, G.A.: Electrodynamics of Continua I. Foundations and Solid Media. Springer, Berlin (1990)
Mehnert, M., Hossain, M., Steinmann, P.: Towards a thermo-magneto-mechanical coupling framework for magneto-rheological elastomers. Int. J. Solids Struct. 128, 117–132 (2017)
Ogden, R.W., Steigman, D.: Mechanics and Electrodynamics of Magneto-and Electro-Elastic Materials. CISM International Centre for Mechanical Sciences, vol. 527. Springer, Wien (2011)
Pan, E., Heyliger, P.R.: Free vibrations of simply supported and multilayered magneto-electro-elastic plates. J. Sound Vib. 252(3), 429–442 (2002)
Pao, Y.H.: Electromagnetic forces in deformable continua. In: Mechanics Today (A78-35706 14-70), vol. 4, pp. 209–305. Pergamon Press, Inc., New York (1978). NSF-supported research
Pelteret, J.P., Walter, B., Steinmann, P.: Application of metaheuristic algorithms to the identification of nonlinear magneto-viscoelastic constitutive parameters. J. Magn. Magn. Mater. 464, 116–131 (2018)
Ren, Z., Hu, W., Dong, X., Sitti, M.: Multi-functional soft-bodied jellyfish-like swimming. Nat. Commun. 10(1), 1–12 (2019)
Saxena, P.: Finite deformations and incremental axisymmetric motions of a magnetoelastic tube. Math. Mech. Solids 23(6), 950–983 (2018)
Saxena, S., Barreto, D.D., Kumar, A.: Extension-torsion-inflation coupling in compressible electroelastomeric thin tubes. Math. Mech. Solids 25(3), 644–663 (2020)
Santapuri, S., Lowe, R.L., Bechtel, S.E., Dapino, M.J.: Thermodynamic modeling of fully coupled finite-deformation thermo-electro-magneto-mechanical behavior for multifunctional applications. Int. J. Eng. Sci. 72, 117–139 (2013)
Santapuri, S., Steigmann, D.J.: Toward a nonlinear asymptotic model for thin magnetoelastic plates. In: Generalized Models and Non-classical Approaches in Complex Materials 1, pp. 705–716. Springer, Cham (2018)
Shariff, M.H.B.M., Bustamante, R., Hossain, M., Steinmann, P.: A novel spectral formulation for transversely isotropic magneto-elasticity. Math. Mech. Solids 22(5), 1158–1176 (2017)
Soria-Hernández, C.G., Palacios-Pineda, L.M., Elías-Zúñiga, A., Perales-Martínez, I.A., Martínez-Romero, O.: Investigation of the effect of carbonyl iron micro-particles on the mechanical and rheological properties of isotropic and anisotropic MREs: constitutive magneto-mechanical material model. Polymers 11(10), 1705 (2019)
Steigmann, D.J.: On the formulation of balance laws for electromagnetic continua. Math. Mech. Solids 14(4), 390–402 (2009)
Singh, R., Kumar, S., Kumar, A.: Effect of intrinsic twist and orthotropy on extension–twist–inflation coupling in compressible circular tubes. J. Elast. 128(2), 175–201 (2017)
Singh, R., Singh, P., Kumar, A.: Unusual extension-torsion-inflation couplings in pressurized thin circular tubes with helical anisotropy
Walter, B.L., Pelteret, J.P., Kaschta, J., Schubert, D.W., Steinmann, P.: On the wall slip phenomenon of elastomers in oscillatory shear measurements using parallel-plate rotational rheometry: II. Influence of experimental conditions. Polym. Test. 61, 455–463 (2017)
Zhu, J.T., Xu, Z.D., Guo, Y.Q.: Magnetoviscoelasticity parametric model of an MR elastomer vibration mitigation device. Smart Mater. Struct. 21(7), 075034 (2012)
https://www.cse-distributors.co.uk/cable/technical-tables-useful-info/table-4e1a
Acknowledgements
Ajeet Kumar acknowledges funding from JATC (DRDO), IIT Delhi.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Constitutive Relations
In this section, the material models used in this study are discussed.
1.1 A.1 Saint Venant-Kirchhoff Model
For linearly magnetoelastic and orthotropic solid, the constitutive relation can be written as follows in the coordinate system of principal material directions (see Pan and Heyliger [24] for details):
The elastic constants satisfy the following relations:
There are a total of 17 independent constants in the compressible case (3 Young’s moduli, 3 shear moduli, 3 Poisson’s ratios and the remaining 8 are magnetic poling constants). Due to axisymmetric deformation, \(\stackrel{\circ}{\epsilon} _{12}=\stackrel{\circ}{\epsilon} _{13}= \stackrel{\circ}{B}_{1}=0\) which implies that the constants \((G_{12},G_{13},m_{15},\mu _{11})\) do not show up in the formulation. In this paper, we further confine ourselves to transversely isotropic tubes having its principal material direction along \(\mathbf{i}_{3}\) (see Fig. 2). The material constants satisfy the following constraints for the case of transverse isotropy:
Thus, \((E_{2},E_{3},G_{23},\nu _{12},\nu _{32},m_{32},m_{33},m_{24},\mu _{22}, \mu _{33})\) are the only independent constants that show up in the formulation. The elastic constants \((E_{2},\nu _{32},G_{23})\) are represented alternatively using the following parameters:
Here, the notation \(\nu _{iso}\) derives its name from the fact that it would equal \(\nu _{32}\) if the tube were isotropic.
1.2 A.2 Compressible Nonlinear Material Model
To account for compressibility, the incompressible and transversely isotropic energy model of Bustamante [3] is extended to the compressible case in the following way:
Here \(I_{1}: I_{10}\) are the invariants which are defined as
and \(\mathbf{a}_{0}\) is the preferred magnetization direction in the reference configuration. The corresponding incompressible model can be obtained from equation (74) in the limit of \({\nu }\rightarrow 0.5\). Accordingly, \(\nu \) has the physical meaning of the Poisson’s ratio. It is to be noted that for an isotropic material model, only the invariants \(I_{1}:I_{6}\) would be active in equation (74). Two special cases of the above model correspond to the parameter \(\gamma \) being zero and unity. We call the case of \(\gamma =1\) to be the Neo-Hookean model (NH) while \(\gamma =0\) to be the Mooney-Rivlin model (MR). The various constants in equation (74) are taken from Bustamante [3] which are:
\(g_{0}\) | 100 kPa | \(\omega _{0}\) | 1334.296 kPa |
\(g_{1}\) | \(-0.001\ kPa/(kA/m)^{2} \) | \(\omega _{1}\) | \(-0.063748\ kPa/(kA/m)^{2}\) |
\(m_{0}\) | 0.4998 N/(A.m) | \(\omega _{2}\) | \(0.198605\ kPa/(kA/m)^{2}\) |
\(m_{1}\) | 309.3395 kA/m | \(\omega _{3}\) | \(-0.228273\ kPa/(kA/m)^{2}\) |
\(m_{2}\) | 199.1828 kA/m | m | −10 |
\(\mu _{0}\) | \(1.2566\times 10^{-6}\ N/A^{2}\) | \(\zeta _{0} \) | \(0.5\times \mu _{0}\ N/A^{2}\) |
\(h_{0}\) | 0.002881 | \(\zeta _{1}\) | 0 |
\(h_{1}\) | 0.012741 | \(K_{5} \) | \(\frac{\mu _{0}}{2}\) |
It is also noteworthy to mention the work of Shariff et al. [32] who propose a material model for transversely isotropic magnetoelastomers in terms of a different set of spectral invariants. It is noted there that the new set of invariants have better physical meaning and that the experimental characterization of a magnetoelastomer in terms of these new invariants are easier compared to the classical invariants in equation (75).
Appendix B: First Derivatives of \(\tilde{\Phi }\) with Respect to \((\epsilon ,\kappa ,\beta ,\zeta ,\eta )\)
We now obtain the expressions for first derivatives of \(\tilde{\Phi }\) with respect to imposed parameters. Let us suppose \(m\) denotes any of the imposed parameters \((\epsilon ,\kappa ,\beta ,\zeta , \eta )\). We then have
Here \(\boldsymbol{\nabla }\) denotes the Lagrangian gradient operator, \(\boldsymbol{\nabla }\cdot \) the Lagrangian divergence operator and \(\boldsymbol{\nabla }_{\alpha }\cdot \) the Lagrangian divergence operator in the cross-sectional plane. The last equality above was obtained after applying Gauss-divergence theorem in the cross-sectional plane and further using axisymmetry. The quantity \(\mathcal{C} \) in the above equation is given by
The first term arises here due to change in the domain of integration while the second term is due to change in integrand itself.
Let us now set \(m=\epsilon \). We then have \(\frac {\partial \mathbf {x}}{\partial \epsilon }=Z\mathbf{e}_{z} +R \frac {\partial \tilde{b}}{\partial \epsilon }{\mathbf{e}}_{r}\) and \(\frac {\partial \mathbf {H}_{L}}{\partial \epsilon }=\eta {\mathbf{e}}_{Z}\). Substituting this in (76) leads to
In (78a), the first and the fourth terms evaluated at the inner radius vanish as \(\frac {\partial \tilde{b}_{1}}{\partial \epsilon }=0\). Also these two terms when evaluated at the outer radius cancel each other, after using \({T_{rR_{2}}=T^{m*}_{rR_{2}}}\). The quantity \(T_{zZ}\) in the second term of (78b) has also been decomposed into its corresponding mechanical and Maxwell contributions in order to obtain the final expression as shown above.
For \(m=\kappa \), we have \(\frac {\partial \mathbf {x}}{\partial \kappa }=R\frac {\partial \tilde{b}}{\partial \kappa }{\mathbf{e}}_{r} + \left [1+b\right ]RZ\mathbf{e}_{\theta }\) and \(\frac {\partial \mathbf {H}_{L}}{\partial \kappa }=\zeta {\mathbf{e}}_{Z}\). Substituting this in (76) leads to
The boundary terms vanish here for the same reason as in (78) together with the fact that \(T_{\theta R}\) vanishes at the boundaries. Further, the term involving \(T_{rZ}\) becomes zero when axial homogeneity is imposed. We have also decomposed \(T_{\theta Z}\) in the first term of (79b) into its corresponding mechanical and Maxwell contributions.
For m= \(\beta \), we then have \(\displaystyle{ \frac {\partial \mathbf {x}}{\partial \beta }=R\frac {\partial \tilde{b}}{\partial \beta }{\mathbf{e}}_{r}}\) and \(\displaystyle{ \frac {\partial \mathbf {H}_{L}}{\partial \beta }=0}\) which implies
The boundary term at inner radius survives here since \(\tilde{b}_{1}=\beta \) implies \(\frac {\partial \tilde{b}_{1}}{\partial \beta }=1\) whereas the boundary term at outer radius vanishes for the same reason as earlier.
For \(m=\zeta \), we have \(\displaystyle{ \frac {\partial \mathbf{x}}{\partial \zeta }=R\, \frac{\partial \tilde{b}}{\partial \zeta }{\mathbf{e}}_{r}}\) and \(\displaystyle{ \frac {\partial \mathbf {H}_{L}}{\partial \zeta }=\frac{1}{R} {\mathbf{e}}_{\Theta }+ \kappa {\mathbf{e}}_{Z}}\). Substituting this in (76), we obtain:
Again, the boundary terms vanish here for the same reason as in (78). Finally, for \(m=\eta \), we have \(\displaystyle{ \frac {\partial \mathbf{x}}{\partial \eta }=R\, \frac{\partial \tilde{b}}{\partial \eta }{\mathbf{e}}_{r}}\) and \(\displaystyle{ \frac {\partial \mathbf {H}_{L}}{\partial \eta }=[1+\epsilon ] {\mathbf{e}}_{Z}}\). Substituting this in (76), we obtain:
Here again, the boundary terms vanish for the same reason as in (78).
Rights and permissions
About this article
Cite this article
Barreto, D.D., Kumar, A. & Santapuri, S. Extension-Torsion-Inflation Coupling in Compressible Magnetoelastomeric Thin Tubes with Helical Magnetic Anisotropy. J Elast 140, 273–302 (2020). https://doi.org/10.1007/s10659-020-09769-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-020-09769-6