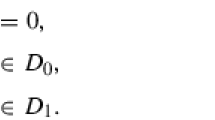Skip to main content
SpringerLink
Log in

New constructions of involutions over finite fields

  • Published:
Cryptography and Communications Aims and scope Submit manuscript

Abstract

Involutions over finite fields are permutations whose compositional inverses are themselves. Involutions especially over \( \mathbb {F}_{q} \) with q is even have been used in many applications, including cryptography and coding theory. The explicit study of involutions (including their fixed points) has started with the paper (Charpin et al. IEEE Trans. Inf. Theory, 62(4), 2266–2276 2016) for binary fields and since then a lot of attention had been made in this direction following it; see for example, Charpin et al. (2016), Coulter and Mesnager (IEEE Trans. Inf. Theory, 64(4), 2979–2986, 2018), Fu and Feng (2017), Wang (Finite Fields Appl., 45, 422–427, 2017) and Zheng et al. (2019). In this paper, we study constructions of involutions over finite fields by proposing an involutory version of the AGW Criterion. We demonstrate our general construction method by considering polynomials of different forms. First, in the multiplicative case, we present some necessary conditions of f(x) = xrh(xs) over \(\mathbb {F}_{q}\) to be involutory on \(\mathbb {F}_{q}\), where s∣(q − 1). Based on this, we provide three explicit classes of involutions of the form xrh(xq− 1) over \(\mathbb {F}_{q^{2}}\). Recently, Zheng et al. (Finite Fields Appl., 56, 1–16 2019) found an equivalent relationship between permutation polynomials of \(g(x)^{q^{i}} - g(x) + cx +(1-c)\delta \) and \(g\left (x^{q^{i}} - x + \delta \right ) +c x\). The other part work of this paper is to consider the involutory property of these two classes of permutation polynomials, which fall into the additive case of the AGW criterion. On one hand, we reveal the relationship of being involutory between the form \( g(x)^{q^{i}} - g(x) + cx +(1-c)\delta \) and the form \( g\left (x^{q^{i}} - x + \delta \right ) +c x \) over \( \mathbb {F}_{q^{m}} \) ; on the other hand, the compositional inverses of permutation polynomials of the form \( g\left (x^{q^{i}} - x + \delta \right ) + cx \) over \( \mathbb {F}_{q^{m}} \) are computed, where \( \delta \in \mathbb {F}_{q^{m}} \), \( g(x) \in \mathbb {F}_{q^{m}}[x] \) and integers m, i satisfy 1 ≤ i ≤ m − 1. In addition, a class of involutions of the form \( g\left (x^{q^{i}} - x + \delta \right ) + cx \) is constructed. Finally, we study the fixed points of constructed involutions and compute the number of all involutions with any given number of fixed points over \( \mathbb {F}_{q} \).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Akbary, A., Ghioca, D., Wang, Q.: On constructing permutations of finite fields. Finite Fields Appl. 17(1), 51–67 (2011)

    Article  MathSciNet  Google Scholar 

  2. Ball, S., Zieve, M.: Symplectic spreads and permutation polynomials. In: Finite Fields and Applications, pp 79–88. Springer (2004)

  3. Barreto, P., Rijmen, V.: The anubis block cipher submission to the nessie project (2000)

  4. Barreto, P.S.L.M., Rijmen, V.: The khazad legacy-level block cipher. Primitive submitted to NESSIE, 97 (2000)

  5. Borghoff, J., Canteaut, A., Güneysu, T., Kavun, E.B., Knezevic, M., Knudsen, L.R., Leander, G., Nikov, V., Paar, C., Rechberger, C., et al.: Prince–a low-latency block cipher for pervasive computing applications. In: International Conference on the Theory and Application of Cryptology and Information Security, pp 208–225. Springer (2012)

  6. Canteaut, A., Roué, J.: On the behaviors of affine equivalent S-boxes regarding differential and linear attacks. In: Annual International Conference on the Theory and Applications of Cryptographic Techniques, pp 45–74. Springer (2015)

  7. Carlet, C., Charpin, P., Zinoviev, V.: Codes, bent functions and permutations suitable for DES-like cryptosystems. Des. Codes Crypt. 15(2), 125–156 (1998)

    Article  MathSciNet  Google Scholar 

  8. Cepak, N., Charpin, P., Pasalic, E.: Permutations via linear translators. Finite Fields Appl. 45, 19–42 (2017)

    Article  MathSciNet  Google Scholar 

  9. Charpin, P., Mesnager, S., Sarkar, S.: Dickson polynomials that are involutions. In: Contemporary Developments in Finite Fields and Applications, pp 22–47. World Scientific (2016)

  10. Charpin, P., Mesnager, S., Sarkar, S.: Involutions over the galois field \(\mathbb {F}_{2^{n}}\). IEEE Trans. Inf. Theory 62(4), 2266–2276 (2016)

    Article  Google Scholar 

  11. Coulter, R.S., Henderson, M.: The compositional inverse of a class of permutation polynomials over a finite field. Bull. Aust. Math. Soc. 65(3), 521–526 (2002)

    Article  MathSciNet  Google Scholar 

  12. Coulter, R.S., Mesnager, S.: Bent functions from involutions over \(\mathbb {F}_{2^{n}}\). IEEE Trans. Inf. Theory 64(4), 2979–2986 (2018)

    Article  Google Scholar 

  13. Daemen, J., Rijmen, V.: The Design of Rijndael: AES-the Advanced Encryption Standard. Springer Science & Business Media (2013)

  14. Dempwolff, U., Müller, P.: Permutation polynomials and translation planes of even order. Adv. Geom. 13(2), 293–313 (2013)

    Article  MathSciNet  Google Scholar 

  15. Ding, C.: Cyclic codes from some monomials and trinomials. SIAM J. Discret. Math. 27(4), 1977–1994 (2013)

    Article  MathSciNet  Google Scholar 

  16. Ding, C., Yuan, J.: A family of skew hadamard difference sets. J. Comb. Theory Series A 113(7), 1526–1535 (2006)

    Article  MathSciNet  Google Scholar 

  17. Ding, C., Qu, L., Wang, Q., Yuan, J., Yuan, P.: Permutation trinomials over finite fields with even characteristic. SIAM J. Discret. Math. 29(1), 79–92 (2015)

    Article  MathSciNet  Google Scholar 

  18. Dobbertin, H.: Almost perfect nonlinear power functions on GF(2n): The Niho case. Inf. Comput. 151(1-2), 57–72 (1999)

    Article  MathSciNet  Google Scholar 

  19. Dobbertin, H.: Almost perfect nonlinear power functions on GF(2n): The Welch case. IEEE Trans. Inf. Theory 45(4), 1271–1275 (1999)

    Article  MathSciNet  Google Scholar 

  20. Feng, X., Lin, D., Wang, L., Wang, Q.: Further results on complete permutation monomials over finite fields. Finite Fields Appl. 57, 47–59 (2019)

    Article  MathSciNet  Google Scholar 

  21. Fu, S., Feng, X.: Involutory differentially 4-uniform permutations from known constructions. Designs, Codes Cryptogr, 1–26. https://doi.org/10.1007/s10623-018-0482-5 (2017)

  22. Gallager, R.: Low-density parity-check codes. IRE Trans Inform Theory 8(1), 21–28 (1962)

    Article  MathSciNet  Google Scholar 

  23. Gupta, R., Sharma, R.K.: Some new classes of permutation trinomials over finite fields with even characteristic. Finite Fields Appl. 41, 89–96 (2016)

    Article  MathSciNet  Google Scholar 

  24. Hou, X.-d.: Determination of a type of permutation trinomials over finite fields, ii. Finite Fields Appl. 35, 16–35 (2015)

    Article  MathSciNet  Google Scholar 

  25. Hou, X.-d.: Permutation polynomials over finite fields—a survey of recent advances. Finite Fields Appl. 32, 82–119 (2015)

    Article  MathSciNet  Google Scholar 

  26. Lee, J.B., Park, Y.H.: Some permuting trinomials over finite fields. Acta Math. Sci. 17(3), 250–254 (1997)

    Article  MathSciNet  Google Scholar 

  27. Li, K., Qu, L., Xi, C.: New classes of permutation binomials and permutation trinomials over finite fields. Finite Fields Appl. 43, 69–85 (2017)

    Article  MathSciNet  Google Scholar 

  28. Li, K., Qu, L., Chen, X., Li, C.: Permutation polynomials of the form \( cx + \text {Tr}_{q^{n}/q}(x^{a}) \) and permutation trinomials over finite fields with even characteristic. Cryptogr. Commun. 10(3), 531–554 (2018)

    Article  MathSciNet  Google Scholar 

  29. Li, K., Qu, L., Wang, Q.: New constructions of permutation polynomials of the form xrh (xq− 1) over \(\mathbb {F}_{q^{2}}\). Des. Codes Cryptogr. 86(10), 2379–2405 (2018)

    Article  MathSciNet  Google Scholar 

  30. Li, K., Qu, L., Wang, Q.: Compositional inverses of permutation polynomials of the form xrh(xs) over finite fields. Cryptogr. Commun. 11 (2), 279–298 (2019). https://doi.org/10.1007/s12095-018-0292-7

    Article  MathSciNet  MATH  Google Scholar 

  31. Li, N., Helleseth, T.: Several classes of permutation trinomials from Niho exponents. Cryptogr. Commun. 9(6), 693–705 (2017)

    Article  MathSciNet  Google Scholar 

  32. Li, N., Zeng, X.: A survey on the applications of Niho exponents. Cryptogr. Commun., 1–40. https://doi.org/10.1007/s12095-018-0305-6 (2018)

  33. Lidl, R., Müller, W.B.: Permutation polynomials in RSA-cryptosystems. In: Advances in Cryptology, pp 293–301. Springer (1984)

  34. Lidl, R., Niederreiter, H.: Finite Fields, vol. 20. Cambridge university press (1997)

  35. Ma, J., Zhang, T., Feng, T., Ge, G.: Some new results on permutation polynomials over finite fields. Des. Codes Crypt. 83(2), 425–443 (2017)

    Article  MathSciNet  Google Scholar 

  36. McFarland, R.L.: A family of difference sets in non-cyclic groups. J. Comb. Theory Series A 15(1), 1–10 (1973)

    Article  MathSciNet  Google Scholar 

  37. Mesnager, S.: On constructions of bent functions from involutions. In: 2016 IEEE International Symposium on Information Theory (ISIT), pp 110–114. IEEE (2016). https://doi.org/10.1109/ISIT.2016.7541271

  38. Mullen, G.L., Wang, Q.: Permutation polynomials of one variable. In: Handbook of Finite Fields, pp 215–230. CRC (2014)

  39. Muller, W.B.: Some remarks on public key cryptography. Studia Sci. Math. Hung. 16, 71–76 (1981)

    MATH  Google Scholar 

  40. Park, Y.H., Lee, J.B.: Permutation polynomials and group permutation polynomials. Bull. Aust. Math. Soc. 63(1), 67–74 (2001)

    Article  MathSciNet  Google Scholar 

  41. Tuxanidy, A., Wang, Q.: On the inverses of some classes of permutations of finite fields. Finite Fields Appl. 28, 244–281 (2014)

    Article  MathSciNet  Google Scholar 

  42. Tuxanidy, A., Wang, Q.: Compositional inverses and complete mappings over finite fields. Discret. Appl. Math. 217, 318–329 (2017)

    Article  MathSciNet  Google Scholar 

  43. Wang, Q.: Cyclotomic mapping permutation polynomials over finite fields. In: Sequences, Subsequences, and Consequences, pp 119–128. Springer (2007)

  44. Wang, Q.: A note on inverses of cyclotomic mapping permutation polynomials over finite fields. Finite Fields Appl. 45, 422–427 (2017)

    Article  MathSciNet  Google Scholar 

  45. Wang, Q.: Polynomials over finite fields: an index approach. In: Combinatorics and Finite Fields. Difference Sets, Polynomials, Pseudorandomness and Applications, pp 1–30. Degruyter (2019)

  46. Wu, B.: The compositional inverse of a class of linearized permutation polynomials over f2n, n odd. Finite Fields Appl. 29, 34–48 (2014)

    Article  MathSciNet  Google Scholar 

  47. Wu, B., Liu, Z.: The compositional inverse of a class of bilinear permutation polynomials over finite fields of characteristic 2. Finite Fields Appl. 24, 136–147 (2013)

    Article  MathSciNet  Google Scholar 

  48. Youssef, A.M., Mister, S., Tavares, S.E.: On the design of linear transformations for substitution permutation encryption networks. In: Workshop on Selected Areas of Cryptography (SAC’96): Workshop Record, pp 40–48 (1997)

  49. Yuan, P., Ding, C.: Permutation polynomials over finite fields from a powerful lemma. Finite Fields Appl. 17(6), 560–574 (2011)

    Article  MathSciNet  Google Scholar 

  50. Zha, Z., Hu, L., Fan, S.: Further results on permutation trinomials over finite fields with even characteristic. Finite Fields Appl. 45, 43–52 (2017)

    Article  MathSciNet  Google Scholar 

  51. Zheng, D., Yuan, M., Li, N., Hu, L., Zeng, X.: Constructions of involutions over finite fields. IEEE Transactions on Information Theory. https://doi.org/10.1109/TIT.2019.2919511 (2019)

  52. Zheng, D., Mu, Y., Yu, L.: Two types of permutation polynomials with special forms. Finite Fields Appl. 56, 1–16 (2019)

    Article  MathSciNet  Google Scholar 

  53. Zieve, M.E.: On some permutation polynomials over \(\mathbb {F}_{q}\) of the form xrh(x(q− 1)/d). Proc. Am. Math. Soc., 2209–2216 (2009)

Download references

Acknowledgements

We thank the associated editor and anonymous referees for their helpful suggestions, in particular, for bringing the reference [51] to our attention.

Author information

Authors and Affiliations

  1. College of Liberal Arts and Sciences, National University of Defense Technology, Changsha, 410073, China

    Tailin Niu, Kangquan Li & Longjiang Qu

  2. State Key Laboratory of Cryptology, Beijing, 100878, China

    Longjiang Qu

  3. School of Mathematics and Statistics, Carleton University, 1125 Colonel By Drive, Ottawa, Ontario, K1S 5B6, Canada

    Qiang Wang

Authors
  1. Tailin Niu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kangquan Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Longjiang Qu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Qiang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Longjiang Qu.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The research of Longjiang Qu is partially supported by the Nature Science Foundation of China (NSFC) under Grant 61722213, 11531002, 11771451, 61772545, and the Open Foundation of State Key Laboratory of Cryptology. The research of Qiang Wang is partially supported by NSERC of Canada.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Niu, T., Li, K., Qu, L. et al. New constructions of involutions over finite fields. Cryptogr. Commun. 12, 165–185 (2020). https://doi.org/10.1007/s12095-019-00386-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12095-019-00386-2

Keywords

Mathematics Subject Classification (2010)

Search

Navigation