Algorithm selection for software validation based on graph kernels

Abstract

Algorithm selection is the task of choosing an algorithm from a given set of candidate algorithms when faced with a particular problem instance. Algorithm selection via machine learning (ML) has recently been successfully applied for various problem classes, including computationally hard problems such as SAT. In this paper, we study algorithm selection for software validation, i.e., the task of choosing a software validation tool for a given validation instance. A validation instance consists of a program plus properties to be checked on it. The application of machine learning techniques to this task first of all requires an appropriate representation of software. To this end, we propose a dedicated kernel function, which compares two programs in terms of their similarity, thus making the algorithm selection task amenable to kernel-based machine learning methods. Our kernel operates on a graph representation of source code mixing elements of control-flow and program-dependence graphs with abstract syntax trees. Thus, given two such representations as input, the kernel function yields a real-valued score that can be interpreted as a degree of similarity. We experimentally evaluate our kernel in two learning scenarios, namely a classification and a ranking problem: (1) selecting between a verification and a testing tool for bug finding (i.e., property violation), and (2) ranking several verification tools, from presumably best to worst, for property proving. The evaluation, which is based on data sets from the annual software verification competition SV-COMP, demonstrates our kernel to generalize well and to achieve rather high prediction accuracy, both for the classification and the ranking task.

1 Introduction

Algorithm selection (Rice 1976) is concerned with choosing a specific algorithm from a set of algorithms for a given instance of a problem class. Algorithm selection is helpful, especially for hard computational problems, because different algorithms exhibit different performance characteristics, and there is normally no single best algorithm that outperforms all others on all problem instances. With the recent advances in machine learning (ML), algorithm selection has been successfully applied in various fields (such as SAT solving, planning and constraint satisfaction, see e.g. Bischl et al. 2016). Algorithm selection is especially beneficial for building portfolio solvers, i.e., solvers in which the (likely) best algorithm is chosen first and then executed on the problem instance. For SAT solving, portfolio solvers often beat standard solvers in competitions (Xu et al. 2008).

Software validation, i.e., the problem of determining whether certain properties are valid for a given software, is another computationally hard (and in general undecidable) problem. Despite this fact, there has recently been enormous progress in software validation, employing diverse techniques ranging from static and dynamic analyses and automata-based methods to abstract interpretations. The annual holding of software verification competitions has furthermore stimulated the development of tools, in particular the tuning of tools towards performance and precision. This offers a software developer faced with the task of showing that her software satisfies a certain property a rather large set of tools (algorithms) to choose from. However, not all tools are equally good at showing a specific property. Due to different validation technologies employed by the tools, they may vary in performance on different programs and properties. To give some examples, there are specialized tools for showing program termination or verifying program properties depending on pointer structures. While competitions like the annual Competition on Software Verification SV-COMP (Beyer 2017) with its rankings provide some a posteriori insight into the particular usefulness of a tool on a validation instance, the software developer rather needs an a priori advice for which tool to choose.

To this end, we propose an approach and present a framework for algorithm selection in software validation. Our framework predicts the (likely) best tool (or even a ranking of tools) for solving a particular validation instance. We assume that validation instances consist of a source code together with properties to be verified. This fits well to the validation instances considered by SV-COMP, and allows us to use the data of the competition for training and evaluation purposes.

Our method builds upon kernel-based machine learning techniques, more specifically support vector machines (Boser et al. 1992). Given a suitable kernel function (Shawe-Taylor and Cristianini 2004), these techniques can be applied in a relatively generic way. Thus, the key challenge in our setting is an appropriate representation of the validation instances, together with the definition of a kernel function that acts as a similarity measure on such instances (viz. programs). On the one side, the representation has to be expressive enough to allow the ML algorithm to identify ways of distinguishing software. On the other side, it should try to avoid confusing the learner by unnecessary details.

So far, two other machine learning methods for selecting tools or algorithms for validation have been proposed (Tulsian et al. 2014; Demyanova et al. 2015, 2017), both of them being based on an explicit feature representation of programs: while Tulsian et al. (2014) only employ structural features of programs (like the number of arrays, loops, recursive functions), Demyanova et al. (2015, 2017) use a number of data-flow analyses to also determine more sophisticated features (e.g., certain loop patterns). Thus, both approaches try to explicitly capture aspects of source code that make validation hard (for some or all tools). With our kernels, we take a different approach, in which we supply the learning algorithm with a more generic representation of source code. Based on this representation, the learner itself should be able to identify the distinguishing patterns. We believe that our kernels are thus more readily usable for other program analysis tasks, for which a machine learning method might be considered (e.g., bad smell or security violation detection).

More specifically, our kernel is constructed on a graph representation of source code. Our graphs are combinations of control-flow graphs (CFGs), program-dependence graphs (PDGs), and abstract syntax trees (ASTs). In these, concrete inscriptions on nodes (like x := y+1) are first of all replaced by abstract labels (e.g., Assign). Such labelled graphs are then used within our specific adaptation of the Weisfeiler–Lehman test for graph isomorphism (Weisfeiler and Lehman 1968). It compares graphs not only according to their labels (and how often they occur) but also according to associations between labels (via edges in the graph). This is achieved by iteratively comparing larger and larger subtrees of nodes, where the maximum depth of subtrees to be considered is a parameter of the framework. The choice of a Weisfeiler–Lehman based kernel is motivated by its better scalability compared to other graph kernels, such as random walk or shortest path kernels (see Shervashidze et al. 2011). However, contrary to Shervashidze et al. (2011), we do not build a linear kernel based on the Weisfeiler–Lehman idea, but employ a generalized Jaccard similarity.

We implemented this technique and carried out experimental studies using data from SV-COMP 2018 and from Beyer and Lemberger’s work on testing versus model checking (Beyer and Lemberger 2017). For the experiments, we considered two settings in which algorithm selection is applied. The first setting uses the kernels for classification of validation instances according to two classes: the first class contains the instances for which a testing tool is better at bug finding, the second class those instances for which a verification tool is better. The second setting considers rank prediction of verification tools, i.e., the prediction of rankings of tools according to their performance on specific problem instances.

The experiments show that our technique can predict rankings with a rather high accuracy, using Spearman’s rank correlation (Spearman 1904) to compare predicted with true rankings. The classifier’s prediction is similarly high. The experiments furthermore show that the overhead associated with prediction is tolerable for practical applications.

Summarizing, this paper makes the following contributions:

• We propose an expressive representation of source code ready for use in machine learning approaches;

• we develop two algorithm selection techniques for software validation based on this representation, one for classification and one for ranking;

• we present an implementation of our approach and extensively evaluate it;

• we experimentally demonstrate our technique—despite being more general and more widely applicable—to compare favorably with existing approaches to the selection of validation tools.

A short description of a first version of our kernel and some ranking experiments have appeared in Czech et al. (2017). This first version is a workshop paper. Here, we give a full account of the learning approach, including the necessary background in machine learning, and present a more thorough evaluation. More concretely, we in addition performed experiments evaluating the learning approach for binary classification (testing vs. verification) and we evaluated the runtime of the approach (both for classification and rank prediction). Apart from that, the data sets have been extended covering an additional category of SV-COMP and taking the data of SV-COMP 2018 instead of 2017 as  Czech et al. (2017) did. All data and software are publicly available¹.

2 Algorithm selection task

Our objective is to carry out algorithm selection in software validation. We start with describing what a validation instance is and how we compare tools with respect to their performance on validation instances.

Definition 1

A validation instance (or short, an instance) $(P,\varphi )$ consists of a program P (in our experiments, we consider C programs) and a property $\varphi$. The latter is also called specification and is typically either given externally or written as an assertion into the program.

We denote by $\mathcal{I}$ the set of all validation instances. We assume that the property to be validated is either part of the program or otherwise fixed, and hence often omit $\varphi$. Figure 1 shows our running example $P_{ SUM }$ of an instance (a program computing n times 2 via addition). In line 10, we find the specification written as an assertion, which is obviously valid. During validation, we expect some validation tool to be run on an instance in order to determine whether the program fulfills the specification. As outcome of such a validation run we consider pairs (a, t), where $t\in \mathbb {R_+}$ is the time in seconds from the start of the validation run to its end, and a is of the following form:

• TRUE, when the tool has concluded that P satisfies $\varphi$,

• FALSE, when the tool has concluded that P violates $\varphi$, and

• UNKNOWN, when no conclusive result was achieved.

We let $A=\{$TRUE, FALSE, UNKNOWN$\}$ be the set of all answers. A validation tool can thus be seen as a function

$$\begin{aligned} tool : \mathcal{I}\rightarrow A \times \mathbb {R}\end{aligned}$$

providing an answer on an instance within some time. The case where the tool does not terminate is covered by the answer UNKNOWN. We let $\mathcal{V}$ be the set of all tools and use $V, V_1, V_2 \in \mathcal{V}$ to refer to specific elements of this set.

Fig. 1

The validation instance $P_{ SUM }$

Assuming that we know the correct answer (i.e., the ground truth TRUE or FALSE), we can judge the tool answer by comparing it to the correct answer. Table 1 provides an overview of the result of such a comparison (Correct, Wrong or Unknown). For comparing tools on validation instances, we define a lexicographic order on pairs of results and runtimes as follows:

$$\begin{aligned} (r,t) \succ (r',t') \quad \text {if } (r \succ r') \quad \text {or}\quad (r = r') \wedge (t < t') , \end{aligned}$$

(1)

where two results r and $r'$ are compared according to the obvious preference order $\text { Correct } \succ \text {Unknown} \succ \text { Wrong }$. In the case where tools do not terminate on a validation instance (i.e., get a timeout), they all share the same result and runtime.

Table 1 Comparison of outcomes of validation runs

The objective of our learning approach is to provide an algorithm selector, i.e., to learn a model which predicts on a given validation instance a tool likely performing well under this ordering. In the following, we present two such selectors. The first one is a simple binary classifier that chooses between a testing tool and a verification tool, whereas the second one chooses among a larger set of verification tools. For the latter, instead of merely predicting the best tool, we propose an approach that predicts a ranking of all tools. In practice, a prediction of that kind is often more useful, especially as it identifies alternatives in cases where the presumably best candidate fails, is not available, or could not be applied for whatever reason. Also, for practical reasons or criteria that have not been considered as training information (e.g., cost), one of the runner-up alternatives might be preferred to the one that is actually predicted the best.

3 Learning algorithms for classification and ranking

The task of choosing a software validation tool for a given validation instance, or of ranking a set of tools according to their appropriateness for a validation problem at hand, requires answering questions like the following: Given a tool and a validation instance, will the former yield a correct result when being applied to the latter? Given two tools, which of them is more appropriate for a specific validation instance?

The idea of algorithm selection via machine learning is to train predictive models that are able to “guess” the answers to these questions. Since all questions are binary in the sense of calling for a simple yes/no answer, the type of machine learning problem that is relevant here is binary classification. As will be seen later on, the problem of ranking can be reduced to binary classification, too (essentially because ranking can be reduced to pairwise comparison).

This section starts with a short description of the necessary background in machine learning. More specifically, we explain the problems of binary classification and label ranking as well as the method of ranking by pairwise comparison for tackling the latter. We also recall support vector machines as a concrete kernel-based machine learning method for binary classification. Although “kernelized” versions of other classification methods exist as well, support vector machines are most commonly used and proved to achieve state-of-the-art performance in many practical domains.

3.1 Binary classification

In the setting of binary classification, we proceed from training data

$$\begin{aligned} \mathbb {D} = \{ (x_i , y_i)\}_{i=1}^N \subset \mathcal {X} \times \mathcal {Y} \end{aligned}$$

(2)

consisting of labeled instances $x_i$. Here, an instance is a formal representation (e.g., a vector, graph, sequence, etc.) of an object of interest, and $\mathcal {X}$ is the set of all representations conceivable, called the instance space. In our concrete application, an instance can be thought of as (the representation of) a validation instance in $\mathcal{I}$, i.e., a program plus properties to be checked. Likewise, $\mathcal {Y} = \{ -1, + 1\}$ is the output space, which in binary classification only comprises two elements representing the positive (answer “yes”) and negative (answer “no”) class, respectively.

Given training data (2), which is typically assumed to be independent and identically distributed according to an underlying probability measure $\mathbf {P}$ on $\mathcal {X} \times \mathcal {Y}$, the task in binary classification is to induce a classifier that generalizes well beyond this data, that is, which is able to assign new instances $x \in \mathcal {X}$ to the correct class. For example, for a given validation tool, we may have seen positive examples $(x_i, +1)$ of validation instances $x_i$ it solved correctly, and negative examples $(x_j,-1)$ of instances it solved incorrectly. For any new query instance x, a classifier trained on this data should then be able to anticipate whether or not the tool will be correct on x.

Formally, a classifier is a mapping $h:\, \mathcal {X} \rightarrow \mathcal {Y}$ taken from a given hypothesis space${\mathcal{H}} \subset {\mathcal{Y}}^{\mathcal{X}}$. A classifier $h \in \mathcal {H}$ is typically evaluated in terms of its risk or expected loss

$$\begin{aligned} R(h) = \int _{\mathcal {X} \times \mathcal {Y}} L(y, h(x)) \, d \, \mathbf {P}(x,y) \, , \end{aligned}$$

where L is a loss function $\mathcal {Y}^2 \rightarrow \mathbb {R}_+$ that specifies a penalty for a prediction $\hat{y} = h(x)$ if the ground truth is y. The simplest loss function of this kind is the 0/1 loss given by $L(y, \hat{y}) = 0$ if $y = \hat{y}$ and $=1$ otherwise, though more general losses are often used in practice. Sometimes, for example, a false positive (e.g., the classifier suggests that a tool will be correct on a validation instance, although it fails) and a false negative (classifier predicts failure, although the tool is correct) cause different costs, which can be modeled by an asymmetric loss function. Regardless of how the loss is defined, the goal of binary classification can be defined as finding a risk-minizing hypothesis

$$\begin{aligned} h^* \in \mathop {{\text {argmin}}}\limits _{h \in \mathcal {H}} R(h) \, . \end{aligned}$$

3.2 Support vector machines

A support vector machine (SVM) is a specific type of binary classifier. More specifically, SVMs are so-called “large margin” classifiers that belong to the class of kernel-based machine learning methods (Schölkopf and Smola 2001). They separate positive from negative training instances in $\mathcal {X} = \mathbb {R}^m$ by means of a linear hyperplane that maximizes the minimum distance of any of the training instances from the hyperplane (decision boundary). Formally, a hyperplane $\{ x \, | \,w^\top x + b = 0 \}$ in $\mathbb {R}^m$ is characterized by the normal vector $w \in \mathbb {R}^m$ and the bias term $b \in \mathbb {R}$. Then, encoding the two classes by $\pm 1$ (as we did above), the margin of a training example $(x_i,y_i) \in \mathbb {R}^m \times \{ -1 , + 1 \}$ is given by $y_i ( w^\top x_i + b)$; thus, a positive margin indicates that $x_i$ is on the right side of the decision boundary, and hence classified correctly, whereas a negative margin corresponds to a mistake on the training data.

The “soft margin” version allows for adding a slack variable $\xi _i \ge 0$ and defines the margin as $y_i ( w^\top x_i + b) + \xi _i$ for each instance $x_i$; this is necessary in the case of data that is not linearly separable. Obviously, the values of the slack variables should be kept small, i.e., the problem comes down to finding a reasonable balance between a large (soft) margin and a small amount of slack. This problem can be formalized in terms of a constrained quadratic optimization problem:

$$\begin{aligned} (w^*, b^*) = \mathop {{\text {argmin}}}\limits _{w, b, \xi } \left\{ \frac{1}{2} \Vert w \Vert ^2 + C \sum _{i=1}^N \xi _i \right\} \end{aligned}$$

(3)

subject to the constraints

$$\begin{aligned} y_i ( w^\top x_i + b) \ge 1- \xi _i \, , \quad \xi _i \ge 0 \, , \end{aligned}$$

(4)

where C is a parameter that controls the penalization of errors on the training data (indicated by a non-zero $\xi _i$). At prediction time, a new instance $x_0 \in \mathbb {R}^m$ is classified positive or negative depending on whether it lies above or below the hyperplane $(w^*, b^*)$. Instead of only returning a binary decision, the distance from the hyperplane is often reported as a kind of measure of certainty (with the idea that the closer an instance to the decision boundary, the less certain the prediction).

As a disadvantage of this measure, note that the distance is not normalized and therefore difficult to interpret and compare. So-called Platt scaling is a post-processing step, in which distances are mapped to [0, 1] via a logistic transformation; thus, each instance is assigned a (pseudo-)probability of belonging to the positive class (Platt 1999).

Instead of solving the problem (3) directly, it is often more convenient to solve its dual. In the dual formulation, training instances $x_i, x_j$ never occur in isolation but always in the form of inner products $\langle x_i , x_j \rangle$. This allows for the “kernelization” of SVMs, simply be replacing such inner products by values $k(x_i, x_j)$ of a so-called kernel function k.

Definition 2

A function $k: {\mathcal {X}}\times {\mathcal {X}}\rightarrow \mathbb {R}$ is a positive semi-definite kernel iff k is symmetric, i.e., $k(x,x') = k(x',x)$, and

$$\begin{aligned} \sum _{i=1}^N \sum _{j=1}^N c_i c_j k(x_i,x_j) \ge 0 \end{aligned}$$

for arbitrary N, arbitrary instances $x_1, \ldots , x_N \in {\mathcal {X}}$ and arbitrary $c_1, \ldots , c_N \in \mathbb {R}$.

If $k(\cdot )$ is a proper kernel function, one can guarantee the existence of an induced feature space $\mathcal {F}$ (which is a Hilbert space) and a feature map $\phi : \, \mathcal {X} \rightarrow \mathcal {F}$ such that $\langle \phi (x) , \phi (x') \rangle = k(x_i, x_j)$. Thus, the computation of inner products in the (typically very high-dimensional) space $\mathcal {F}$ can be replaced by the evaluations of the kernel, which in turn allows a linear model to be fit in $\mathcal {F}$ without ever accessing that space or computing the image $\phi (x_i)$ of a training instance $x_i$—this is called the “kernel trick”. As long as a learning algorithm, which is run in the feature space $\mathcal {F}$, only requires the computation of inner products $\langle \phi (x) , \phi (x') \rangle$, but never individual feature vectors $\phi (x_i)$, it only needs access to the Gram matrix, i.e., the value of the kernel for each pair of training instances:

$$\begin{aligned} G = \left( \begin{array}{cccc} k(x_1, x_1) &{} k(x_1, x_2) &{} \ldots &{} k(x_1, x_N) \\ k(x_2, x_1) &{} k(x_2, x_2) &{} \ldots &{} k(x_2, x_N) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ k(x_N, x_1) &{} k(x_N, x_2) &{} \ldots &{} k(x_N, x_N) \end{array} \right) \end{aligned}$$

Note that the instance space ${\mathcal {X}}$, on which the kernel is defined, is not necessarily a Euclidean space any more. Instead, ${\mathcal {X}}$ can be any space or set of objects. In particular, this allows SVMs to be trained on structured (non-vectorial) objects—in our case, these objects are programs to be validated. In general, a kernel function can be interpreted as a kind of similarity measure on ${\mathcal {X}}$, i.e., the more similar instances $x_i, x_j$, the larger $k(x_i,x_j)$. We will come back to this point in Sect. 5 further below, where we address the question of how to define appropriate kernel functions on validation instances.

3.3 Label ranking

In addition to the problem of classifying, we are interested in the (more complex) problem of ranking. More specifically, the task we would like to tackle is the following: Given a context specified in terms of a representation $x$ (e.g., a validation instance), sort a set of choice alternatives (e.g., a set of validation tools) in descending order of preference. In the machine learning literature, this problem has been studied under the notion of label ranking (Vembu and Gärtner 2010).

More formally, consider a finite set of K alternatives identified by class labels${\mathcal {Y}}= \{ y_1, \ldots , y_K\}$. In our case, ${\mathcal {Y}}$ is the set of validation tools $\mathcal{V}$. We are interested in total order relations $\succ$ on ${\mathcal {Y}}$, that is, complete, transitive, and antisymmetric relations, where $y_i \succ y_j$ indicates that $y_i$ precedes $y_j$ in the order. In our case, the alternatives (labels) correspond to the validation tools, and label preferences are defined in terms of the lexicographic preferences (1) on tools. Formally, a total order $\succ$ can be identified with a permutation $\pi$ of the set $[K]= \{1 , \ldots , K \}$, such that $\pi (i)$ is the position of $y_i$ in the order. We denote the class of permutations of [K] (the symmetric group of order K) by $\mathbb {S}_K$. By abuse of terminology, though justified in light of the above one-to-one correspondence, we refer to elements $\pi \in \mathbb {S}_K$ as both permutations and rankings.

In the setting of label ranking, preferences on ${\mathcal {Y}}$ are “contextualized” by instances $x \in {\mathcal {X}}$, where ${\mathcal {X}}$ is an underlying instance space; in our case, instances are programs (plus properties) to be validated. Thus, each instance $x$ is associated with a ranking $\succ _{x}$ of the label set ${\mathcal {Y}}$ or, equivalently, a permutation $\pi _{x} \in \mathbb {S}_K$. More specifically, since label rankings do not necessarily depend on instances in a deterministic way, each instance $x$ is associated with a probability distribution $\mathbf {P}( \cdot \, \vert \, x)$ on $\mathbb {S}_K$. Thus, for each $\pi \in \mathbb {S}_K$, $\mathbf {P}( \pi \, \vert \, x)$ denotes the probability to observe the ranking $\pi$ in the context specified by $x$.

Just like the goal in binary classification is to learn a classifier, the goal in label ranking is to learn a “label ranker”, i.e., a mapping $\mathcal {M}: \, {\mathcal {X}}\rightarrow \mathbb {S}_K$ that predicts a ranking $\hat{\pi }$ for each instance $x$ given as an input. More specifically, seeking a model with optimal prediction performance, the goal is to find a risk (expected loss) minimizer

$$\begin{aligned} \mathcal {M}^* \in \mathop {{\text {argmin}}}\limits _{\mathcal {M} \in \mathbf {M}} \int _{{\mathcal {X}}\times \mathbb {S}_K} L(\mathcal {M}(x) , \pi ) \, d \, \mathbf {P} , \end{aligned}$$

where $\mathbf {M}$ is the underlying model class, $\mathbf {P}$ is the joint measure $\mathbf {P}(x,\pi ) = \mathbf {P}(x) \mathbf {P}( \pi \, | \,x)$ on ${\mathcal {X}}\times \mathbb {S}_K$ and L is a loss function on $\mathbb {S}_K$. A common example of such a loss is $L(\pi , \hat{\pi } ) = 1 - S(\pi , \hat{\pi } )$, where $S(\pi , \hat{\pi } )$ is the Spearman rank correlation (Spearman 1904):²

$$\begin{aligned} S(\pi , \hat{\pi } ) = 1 - \frac{6\ \sum _{i=1}^K (\pi (i) - \hat{\pi }(i))^2}{K (K^2 -1)} \in [-1,1] \end{aligned}$$

(5)

As can be seen, for each alternative $y_i$, this measure penalizes deviations of the estimated rank $\hat{\pi }(i)$ from its true rank $\pi (i)$; these penalties are added together and normalized so that $S(\pi , \hat{\pi } ) = +1$ if $\hat{\pi } = \pi$ and $S(\pi , \hat{\pi } ) = -1$ if $\hat{\pi }$ is the complete reversal of $\pi$.

As training data $\mathbb {D}$, a label ranker uses a set $\{ (x_i, \pi _i) \}_{i=1}^N$ of instances ${x}_i$ ($i \in [N]$), together with information about the associated rankings $\pi _i$.

3.4 Ranking by pairwise comparison

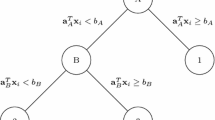
How can a label ranker be represented and trained on a suitable set of data? In this paper, we make use of an established approach to label ranking called ranking by pairwise comparison (RPC), a meta-learning technique that reduces a label ranking task to a set of binary classification problems (Hüllermeier et al. 2008). More specifically, the idea is to train a separate model (base learner) $\mathcal {M}_{i,j}$ for each pair of labels $(y_i, y_j) \in {\mathcal {Y}}$, $1 \le i < j \le K$; thus, a total number of $K(K-1)/2$ models is needed (see Fig. 2 for an illustration). In our case, $\mathcal {M}_{i,j}$ is supposed to compare the ith and jth validation tool.

Fig. 2

Illustration of the RPC approach (for $K=4$). At training time (left), the original data $\mathbb {D}$ is split into $K(K-1)/2$ smaller data sets, one for each pair of labels, and a binary classifier is trained on each of these data sets. If a prediction for a new instance is sought (right), this instance is submitted to each of the binary models, and the pairwise preferences obtained as predictions are combined into a complete ranking $\pi$ via a ranking procedure $\mathcal {P}$

For training, the original data $\mathbb {D}$ is first turned into binary classification data sets $\mathbb {D}_{i,j}$, $1 \le i < j \le K$. To this end, each preference information of the form $y_i \succ _x y_j$ (extracted from full or partial information about a ranking $\pi _x$) is turned into a positive (classification) example $(x,+1)$ for the learner $\mathcal {M}_{i,j}$; likewise, each preference $y_j \succ _x y_i$ is turned into a negative example $(x,-1)$. Thus, $\mathcal {M}_{i,j}$ trained on $\mathbb {D}_{i,j}$ is intended to learn the mapping that outputs $+1$ if $y_i \succ _x y_j$ (the ith tool was better on verification task x than the jth tool) and $-1$ if $y_j \succ _x y_i$ (the ith tool was worse than the jth tool). This mapping can be realized by any binary classifier (of course, like in binary classification, one can also employ a probabilistic classifier that predicts a probability of the preference $y_i \succ _x y_j$). In our approach, we use support vector machines as introduced above as base learners for RPC.

At classification time, a query $x_0 \in {\mathcal {X}}$ is submitted to the complete ensemble of binary learners. Thus, a collection of predicted pairwise preference degrees $\mathcal {M}_{i,j}(x)$, $1 \le i, j \le K$, is obtained. The problem, then, is to turn these pairwise preferences into a ranking of the label set ${\mathcal {Y}}$. To this end, different ranking procedures can be used. The simplest approach is to extend the (weighted) voting procedure that is often applied in pairwise classification (Fürnkranz 2002): For each label $y_i$, a score $s_i \, = \, \sum _{1 \le j \ne i \le K} \mathcal {M}_{i,j}(x_0)$ is obtained, which represents the total preference in favor of that label (the sum of all preferences over all other labels), and then the labels are sorted according to these scores. Despite its simplicity, this ranking procedure has several appealing properties. Apart from its computational efficiency, it turned out to be relatively robust in practice and, moreover, it possesses provable optimality properties³ in the case where Spearman’s rank correlation is used as an underlying accuracy measure (Hüllermeier and Fürnkranz 2010).

4 Representing validation instances

Our approach to algorithm selection involves the use of machine learning methods for inducing binary classifiers. As said before, this requires a suitable representation of the validation instances, both for the training and prediction phase. A core requirement on this representation is its ability to represent various structural relationships between program entities, and to distinguish programs which differ in these structures. The key contribution of our work is the proposal of such a representation.

A common solution is a vectorial representation in the form of a feature vector, as it is supported by a wide range of learning algorithms. Nonetheless, finding suitable features that capture the main characteristics of an instance is often very challenging. In the two approaches existing so far (Tulsian et al. 2014; Demyanova et al. 2015), corresponding features of programs such as the number of loops, conditionals, pointer variables, or arrays in a program are defined in an explicit way. Obviously, this approach requires sufficient domain knowledge (in our case about software validation) to identify features that are important for the prediction problem at hand. Our approach essentially differs in that features are specified in a more indirect way, namely by systematically extracting (a typically large number of) generic features from a suitable representation of the validation instance. Selecting the useful features and combining them appropriately is then basically left to the learner.

But how to represent the validation instances in a more generic way? Pure source code (i.e., strings) is not suitable for this purpose as it does not provide enough structure. The source code of two programs might look very different although the underlying program is actually the same (different variable names, while instead of for loops, etc.). What we need is a representation that abstracts from issues like variable names but still represents the structure of programs, in particular dependencies between elements of the program. These considerations (and some experiments comparing different representations, see Czech et al. 2017) have led to a graph representation of programs combining concepts of three existing program representations:

Control-flow graphs:

CFGs record the control flow in programs and thus the overall structure with loops, conditionals etc.; these are needed, for example, to see loops in programs.

Program-dependence graphs:

PDGs (Horwitz and Reps 1992) represent dependencies between elements in programs. We distinguish control and data dependencies. This information is important, for example, to detect whether a loop boundary depends on an input variable (as is the case in program $P_{ SUM }$).

Abstract syntax trees:

ASTs reflect the syntactical structure of programs according to a given grammar. We only include an abstract syntax tree representation of statements. This can help to reveal the complexity of expressions, in particular the arithmetic operations occuring in expressions.

Unlike CFGs and PDGs but (partly) alike ASTs, we abstract from concrete names occuring in programs. Nodes in the graph will thus not be labeled with statements or variables as occuring in the program, but with abstract identifiers. We let $\varSigma$ be the set of all such labels. Table 2 lists some identifiers and their meaning; the appendix gives the complete list.

Table 2 Some node identifiers and their meaning

The following definition formalizes this graph representation, assuming standard definitions of control-flow and program dependence graphs.

Definition 3

Let P be a validation instance. The graph representation of P is a graph $G =(N,E,s,t,\rho ,\tau ,\nu )$ with

• N a set of nodes (basically, we build an AST for every statement in P, and use the nodes of these ASTs),

• E a set of edges, with $s: E \rightarrow N$ describing the node an edge starts in and $t: E \rightarrow N$ the node an edge terminates in,

• $\rho : N \rightarrow \varSigma$ a labeling function for nodes,

• $\tau : E \rightarrow \{ CD , DD , SD , CF \}$ a labeling function for edges reflecting the type of dependence: $CD$ (control dependency) and $DD$ (data dependency) origin in PDGs, $SD$ (syntactical dependence) is the “consists-of” relationship of ASTs and $CF$ (control flow) the usual control flow in programs, and

• $\nu : N \rightarrow 2^E$ the incoming edge function derived from t by letting

  $$\begin{aligned} \nu (n) = \{ e \in E \mid t(e) = n\} \end{aligned}$$

  for $n \in N$.

We let ${\mathcal {G}}_V$ denote the set of all validation instance graphs.

Figure 3 depicts the graph representation of the validation instance $P_{ SUM }$. The rectangle nodes represent the statements in the program and act as root nodes of small ASTs. For instance, the rectangle labeled Assert at the bottom, middle represents the assertion in line 10. The gray ovals represent the AST parts below statements. We define the depth of nodes n, d(n), as the distance of a node to its root node, i.e. to the statement node it is part of. As an example, the depth of the Assert-node itself is 0, the depth of both ==-nodes is 2.

Fig. 3

Graph representation of $P_{ SUM }$ eliding labeling $\nu$

This graph representation allows us to see the key structural properties of a validation instance, e.g., that the loop (condition) in our example program depends on an assignment where the right-hand side is an input (which makes validation more complicated since it can take arbitrary values). With respect to semantical properties, our graph representation (as well as all feature-based approaches relying on static analyses of programs) is less adequate. To see this, consider the two programs in Fig. 4. They only differ in the assertion at line 5, which from its basic syntax is the same on both sides: a simple boolean expression on two variables of exactly the same type and dependencies. However, validation of the left program is difficult for tools which cannot generate loop invariants. Validation of the program on the right, however, is easy as it is incorrect (which can e.g. be detected by a bounded unrolling of the loop). Here, we clearly see the limits of any learning approach basing its prediction on structural properties of programs.

Fig. 4

Two programs which are difficult to distinguish by our kernel

Since validation instances are now represented by specific graphs, our approach needs to identify meaningful features in graphs. The key idea is that two instances which share common structures should share features and, more importantly, the representation of isomorphic graphs should be identical. With this observation in mind, we have chosen to select our features based on the Weisfeiler–Lehman (WL) test of isomorphism between two discretely labeled, undirected graphs (Weisfeiler and Lehman 1968). Because of its linear runtime (Shervashidze et al. 2011), the WL test is known to scale well to large instances and hence can be applied to programs with several thousands lines of code. Moreover, in our prior work we have already successfully applied a modified Weisfeiler–Lehman subtree kernel (Czech et al. 2017), which is an extension of the WL test.

The Weisfeiler–Lehman test checks isomorphism of two graphs via the following incremental procedure. First, it inspects for every node label $\ell$ whether the two graphs have the same number of nodes labelled $\ell$. For instance, if one graph has three nodes labelled Loop, but the other only two, they cannot be isomorphic. The test then extends this check to subgraphs of consecutively larger size. Again as an example, if one graph contains two nodes labelled Loop which are connected via an edge to a node labelled Assign, but the other graphs contains four such shapes, the graphs cannot be isomorphic.

We apply this idea now to single graphs, i.e., our features are specific subgraph shapes and we count for a given graph how often these features occur. Every subgraph is uniquely identified by a label (which for simplicity will be a number), and in order to get the same label for the same subgraph during feature computation, this labeling follows a fixed scheme. We start with node labels and extend these with information about neighboring nodes in three further steps:

Augmentation:

Concatenate the label of node n with labels of its incoming edges and neighbouring nodes.

Sorting:

Sort this sequence according to a predefined order on labels.

Compression:

Compress the sequences thus obtained into new labels.

These steps are repeated until a predefined bound on the number of iterations is exhausted. This bound is used to regulate the depth of subgraphs considered.

For allowing this WL test to act on validation instances, we made two adaptations to the graph relabeling, giving rise to Algorithm 1:

• (1) Extension to directed multigraphs (to see the direction of relationships betwen nodes), and

• (2) Integration of edge labels (to see the type of relationships between nodes).

In Algorithm 1, we use the notation $\langle \ldots \mid \ldots \rangle$ for list comprehensions, defining a sequence of values, and $\oplus$ for string concatenation. Moreover, z is the compression function compressing sequences of labels into new labels (which for the purpose of unique identification should be injective). In our case, we use integers as labels, i.e., $\varSigma =\mathbb {Z}$ with the usual ordering $\le$. To this end, we first map all node identifiers and edge labels to $\mathbb {Z}$. Every newly arising sequence then simply gets a new number assigned. The functions sort and concat sort sequences of labels (in ascending order) and concatenate sequences, respectively. In Algorithm 1, line 3 represents the augmentation step, line 4 sorting and lines 5 and 6 first concatenate all labels in Aug(n) and then prepend the current node label to this string. Line 7 finally compresses the thus obtained string according to function z.

Figure 5 illustrates these steps on a small subgraph of program $P_{ SUM }$ (also showing z as a function application in order to see the labels being augmented). Figure 5a just depicts the subgraph whereas Fig. 5b shows the graph where every node identifier is replaced by a number and all edge types are replaced by numbers. Note that all three Assign nodes (obviously) have to get the same number. We now specifically look at the two outermost Assign nodes. In the first iteration (result depicted in Fig. 5c), we take the numbers of their predecessor and of the connecting edges, concatenate them, compress them, (sort and concatenate again, which we ignore here), add the node’s own label and compress again. Thereby, both nodes get the label computed by z(0_z(0_0)) which we assume to be mapped to 3. Here, _ is concatenation. The next iteration repeats the same steps for all nodes. In this step (result in Fig. 5d), the leftmost Assign node now is labelled with z(3_z(3_0)) (chosen to be 7) whereas the rightmost Assign node gets z(3_z(0_0)) (chosen to be 6). This is because the predecessors (neighbors with edges going in to this node) of the nodes in the graph have different labels: 3 for the leftmost and 0 for the rightmost node. After this iteration, we can detect the structural difference in the nodes: the node labeled 7 has as a predecessor an Assign node which itself has an Assign node as a predecessor whereas the node labeled 6 has as a predecessor an Assign node which itself has no predecessors.

Fig. 5

Example of two relabel iterations

The $relabel$ algorithm can be used to define our feature representation for validation instances. It is important to notice that every compressed label $\rho (n)$ (after the ith iteration) refers to a subtree pattern of height i rooted at n (Shervashidze et al. 2011). Therefore it is possible to represent a validation instance (graph) by multiple Bags of Subgraphs (BoSs).

Definition 4

Let $G = (N, E, s, t, \rho , \tau , \nu )$, be the graph representations of a validation instance, $z : \varSigma ^* \rightarrow \varSigma$ a compression function, $m \in \mathbb {N}$ an iteration bound and $d\in \mathbb {N}$ a depth for subtrees. Let $G^i= relabel (G, z, i)$ and $\rho ^i$ its node labeling function.

The feature representation$\mathcal {B}^{m}_{G}$ of G consists of a sequence of m feature multisets defined by:

$$\begin{aligned} \mathcal {B}^{m}_{G} = \langle B^{0}_{G}, B^{1}_{G}, \ldots , B^{m}_{G}\rangle \end{aligned}$$

with

$$\begin{aligned} B^{i}_{G} := \{(\sigma , k) \mid \sigma \in \varSigma , k = |\{n \in N \mid d(n) \le d, \rho ^i(n) = \sigma \}| \ \} \end{aligned}$$

Here, we describe bags (or multisets) as pairs of element and its multiplicity. Formally, a multiset $\mathcal {B}$ over a set of elements $\varSigma$ is a mapping $\varGamma : \varSigma \rightarrow \mathbb {N}$, and in the following we will use both notations. Intuitively, each bag of subgraphs counts the number of subgraphs occurring in the graph for a particular iteration value, where this value steers to what extend subgraphs are considered, and the depth d fixes whether an AST node is considered at all. By incorporating the depth, we have the option to consider or ignore details of expressions.

The BoS model is similar to a bag-of-words model (McTear et al. 2016), well known from information retrieval, just that we have subgraphs instead of words. The further difference between these models is that our model in addition stores the iteration in which a subgraph occurs.

5 Graph kernels for verification tasks

As outlined in the previous sections, our idea is to make use of support vector machines as learning algorithms, either directly for binary classification (Sect. 3.1) or as a base learner in the context of learning by pairwise comparison for label ranking (Sect. 3.4). In this regard, the main prerequisite is the definition of a suitable kernel function.

Recalling Definition 4, a validation instance is represented by bags of subgraphs $\langle B^{0}_{G}, B^{1}_{G}, \ldots , B^{m}_{G}\rangle$. To compare such representations $G_1$ and $G_2$ for two validation instances in terms of similarity, our idea is to compare bags $B_{G_1}^{i}$ and $B_{G_2}^{i}$ first and to average over these comparisons afterward. Since a bag is a specific type of set, we make use of Jaccard as an established measure of similarity. For sets A and B, it is defined by $|A \cap B|/|A \cup B|$, i.e., by the cardinality of the intersection over the cardinality of the union. Obviously, it assumes values in the unit interval, with the extremes of 1 for identical and 0 for disjoint sets. Compared to other measures, Jaccard has a number of advantages. In contrast to distance measures on feature vectors (with one entry per subgraph), for example, the simultaneous absence of a subgraph in both $G_1$ and $G_2$ does not contribute to their similarity, which is clearly a desirable property.

We have to keep in mind, however, that the $B_G^i$ are not standard sets but bags that assign multiplicities to the labels $\varSigma$ in the graphs. Therefore, the generalized Jaccard similarity, also known as Ruzicka similarity (Pielou 1984), appears to be a natural choice for a kernel in our case.

Definition 5

(Generalized Jaccard similarity) Let X, Y be bags over some set $\varSigma$ with the multiplicities given by occurrence functions $\varGamma _X: \varSigma \mapsto \mathbb {N}$ and $\varGamma _Y: \varSigma \mapsto \mathbb {N}$, respectively. Then the generalized Jaccard similarity is defined by

$$\begin{aligned} {\text {GJac}}(X, Y) := \frac{\sum _{\sigma \in \varSigma } \min (\varGamma _X(\sigma ), \varGamma _Y(\sigma ))}{\sum _{\sigma \in \varSigma } \max (\varGamma _X(\sigma ), \varGamma _Y(\sigma ))} \end{aligned}$$

The generalized Jaccard similarity compares the size of the (generalized) intersection of the bags X and Y with their (generalized) union. Ralaivola et al. (2005) have proven that the measure is both symmetric and positive semi-definite, so that it can indeed be used as a kernel for bags. Thus, we formally define our kernel function on the representation of validation instances as follows.

Definition 6

Let $G_1$ and $G_2$ be graph representations for validation instances, $m \in \mathbb {N}$ an iteration bound, and $\mathcal {B}_{G_1}^{m},\mathcal {B}_{G_2}^{m}$ the matching validation feature representation. The verification graph kernel$k^m: \mathcal {G}_V \times \mathcal {G}_V \rightarrow \mathbb {R}$ is defined by

$$\begin{aligned} k^m(G_1, G_2) := \frac{1}{m+1}\sum _{i=0}^m {\text {GJac}}(B_{G_1}^{i}, B_{G_2}^{i}) \end{aligned}$$

The kernels are designed with respect to the Weisfeiler Lehmann (WL) test of isomorphism (see Sect. 4). However, instead of testing on uncommon subgraphs in each iteration, we measure the similarity of individual test sets and average over all iterations. In other words, we expect that particular similarity observations may not be representative, while a good estimation can still be achieved on average. Furthermore, the validation graph kernel is positive semi-definite by construction, since kernel functions are closed under addition and multiplication with a positive constant.

6 Implementation

Our approach consists of five major steps: (1) construction of the graph representation of validation instances, (2) bag-of-subgraph computation, (3) kernel computation, (4) learning, and finally (5) prediction.

Construction of graphs To generate the graphs, we employed the configurable software analysis framework CPAchecker (Beyer and Keremoglu 2011). This directly gives us the control-flow graph and AST information by using the integrated C parser of CPAchecker. We implemented the construction of program dependence graphs ourselves, using the technique detailed in Horwitz and Reps (1992). For the sake of simplicity, we ignored complex dependencies introduced by pointers. We furthermore built an extension of CPAchecker which combines all the collected information into one graph.

Computation of bag-of-subgraphs To produce our bag-of-subgraph representation, we further process the graph using NetworkX⁴ 2.1 and our relabeling algorithm as described in Sect. 4. NetworkX is a graph library that makes our program representation accessible. Especially, the support of efficient neighborhood aggregation on large graphs is a convenient property of NetworkX for our use case. During the relabeling process, we make use of MurmurHash3⁵ for our compression function. MurmurHash3 is clearly not injective as we map all possible subgraphs to an element of 0–$2^{128}$. Here, we trade off seldom collisions against a major computational speedup.

Computation of kernel For kernel computation, a large sparse matrix is constructed by collecting information from all bag-of-subgraph models. To store and efficiently process this matrix, we utilize SciPy⁶. SciPy includes a large collection of algorithms for scientific computing. The support of highly efficient sparse matrix operations and compatibility with the linear algebra package NumPy⁷ makes SciPy suitable for calculating our final kernel.

Learning During the learning phase, we need to learn models which—for a pair of tools and a given validation instance—predict the tool performing better on the validation instance according to the ordering defined in Sect. 2. Note that such models are employed both in the binary classification case and for the rankings, as we employ ranking by pairwise comparison (RPC). We integrated the RPC approach and our kernel framework into the scikit-learn library⁸. For learning, we employed the implementation of support vector machines offered by scikit-learn. To select the penalization parameter C of the SVM (see Sect. 3), we tried a standard range of values (0.01, 0.1, 1, 100 and 1000) using internal cross-validation and selected the one with the highest estimated accuracy. We performed this parameter search for each base learner individually.

Prediction For the prediction, we utilized the trained model offered by scikit-learn. Our RPC implementation enables us to infer a ranking from the set of binary predictions. To achieve comparable result for prediction time, the RPC approach is also implemented as an extension to CPAchecker. Our extension allows the utilization of the trained model obtained by and exported from scikit-learn.

All the code is available via GitHub⁹.

7 Experimental evaluation

With the implementation at hand, we extensively evaluated our approach and compared it to existing methods.

7.1 Research questions

For the evaluation, we were interested in the following research questions.

RQ1:

Which parameter choices for the kernels achieve the most accurate prediction? Available options or parameters are the depth d in the AST representation of statements and the iteration bound m in the kernel computation.

RQ2:

What is the relation between the prediction and the validation time? For the binary classifier we—in particular—wanted to find out whether prediction plus consecutive validation with the selected tool can outperform a validation using the testing and the verification tool in sequence.

RQ3:

How does our approach compare to similar existing approaches? Again, for the comparsion we were interested in the accuracy of the prediction.

To study these research questions, we designed a suitable set of experiments. First of all, our general setting with training data and tools was the following. We constructed two data sets: Testing vs. Verification (T/V) for binary classification and Ranking (Rank18) for rank prediction. Tables 3 and 4 provide statistics for both data sets (number of validation instances plus information about the constructed graphs). We used Testing versus Verification as the task for the binary classifier because testing and verification techniques are often complementary, and we wanted to find out whether our prediction can carry out some appropriate classification of programs into ones for which testing and for which verification works better. The choice for employing ranking on verification tools is motivated by the existence of an appropriate data set.

Table 3 Dataset description of Ranking (Rank18)

Table 4 Dataset description of Testing vs. Verification (T/V)

For T/V, we employed results of a recent study by Beyer and Lemberger (2017) about testing and formal verification tools¹⁰ for bug finding. To utilize this data for binary classification, we had to select one testing and one verification tool. In the study by Lemberger and Beyer, the model checker ESBMC-incr (Gadelha et al. 2018) outperforms the competitors in terms of bug finding. The same holds true for the testing tool KLEE (Cadar et al. 2008) compared to other testers. Interestingly, both tools seem to complement each other such that we can expect an improvement by summarizing their findings. Therefore, we chose to evaluate the performance of our base learner for classification on this tool pair.

For Rank18, we used the results of SV-COMP 2018¹¹. SV-COMP is the annual competition on software verification. In the 2018 instance, 21 verification tools participated and were evaluated on 9523 validation instances (written in C) in 5 categories (plus some meta categories). The ground truth for these validation instances is fixed; its computation is a community effort of the SV-COMP participants over the years. The results of SV-COMP are rankings of tools (per category and overall).

For our data set, we excluded concurrent programs (since a large number of verification tools operate on sequential programs only) which left us with 4 categories, namely Safety (reachability properties), MemSafety (memory safety), Termination and Overflow (no overflows). The categories contain programs on which specific properties are to be verified. All categories are summarized into a meta category Overall. We both trained the SVMs on data from individual categories and from Overall to see whether some knowledge about the property to be verified (i.e., the category of the validation instance) might improve the prediction.

With respect to tools, we chose the 10 verification tools participating in all the 4 categories. In this case, these are the tools 2ls (Schrammel and Kroening 2016), CBMC (Kroening and Tautschnig 2014), CPA-Seq (Wendler 2013), DepthK (Rocha et al. 2017), ESBMC-incr (Gadelha et al. 2018), ESBMC-kind (Gadelha et al. 2018), UAutomizer (Heizmann et al. 2013), Symbiotic (Chalupa et al. 2017), Ukojak (Nutz et al. 2015) and UTaipan (Greitschus et al. 2017). Since the prediction for a tool pair $(V_1, V_2)$ is the inverse of $(V_2, V_1)$, we considered only 45 tool pairs¹² during learning. All together, we created 275 datasets for learning based on category and tool combination. To address the research questions, we then set up the following experiments.

For RQ1, we varied the depth of considered ASTs from 1 to 5 (5 because the mean maximum AST depth is 5.16 and we wanted to get close to that). For the iteration bound in the kernel we considered 0, 1 and 2. As criterion for being the “best” parameter choice, we employed the accuracy of the prediction. To this end, we performed a 10-fold cross validation.

We split the experiments into those studying the binary classifier and the rank predictor. In the following, we refer to these as RQ1a and RQ1b, respectively. For RQ1a, the accuracy is the classification rate, i.e. the proportion of correct in all classifications. For RQ1b, we used the Spearman rank correlation to compare observed and predicted rankings.

For both predictions, we furthermore computed the accuracy of a default predictor as a baseline. In the case of binary classification, the default is the majority classifier, which always predicts the same tool, namely the one providing better results in the majority of cases in the training data. Likewise, the default predictor for RQ1b always predicts the same ranking $\hat{\pi }$ which sorts tools $V_i$ according to the well-known Borda rule (de Borda 1781), i.e., according to the number of tools $V_j$ outperformed by $V_i$, summed over all rankings $\pi _k$ in the training data:

$$\begin{aligned} vc(V_i) = \sum _{k=1}^N |\{ V_j \mid V_i \succ _{\pi _k} V_j \}| \end{aligned}$$

By always predicting $\hat{\pi }$, regardless of the validation instance $x$, the default predictor generalizes the majority voting scheme of the binary case. Among all constant predictors of that kind, the Borda rule yields the one that is provably optimal in terms of the Spearman rank correlation as a performance measure (Hüllermeier and Fürnkranz 2010).

For RQ2, we trained the classifier and the rank predictor on our data sets, and then measured the time for prediction for all data instances of T/V and Rank18. The validation times of tools on programs could directly be taken from SV-COMP18 and the study of Beyer and Lemberger (2017).

For RQ3, we searched for approaches carrying out a similar form of prediction on validation tools. To the best of our knowledge, there are just two such approaches: MUX (Tulsian et al. 2014) and Verifolio (Demyanova et al. 2015). As the implementation of MUX is not publicly available, we compared our approach to Verifolio only. The criterion for comparison is again accuracy. We employed the feature computation within Verifolio and used it to train models for binary classification and for ranking by pairwise comparison. We used two kernels in this case: the Jaccard kernel which our own approach employs (in order to have a comparison on equal grounds) and a radial basis function which Verifolio originally used for the support vector machine. These two approaches are denoted by“Verifolio (J)” and “Verifolio (RBF)”.

There are furthermore some tools which employ heuristics to internally decide on which validation technique to run on a given validation instance. For instance, Beyer and Dangl (2018) choose different configurations for the tool CPAchecker based on a simple heuristic. We did not include such tools in the comparison since they cannot make decisions on arbitrary other verification tools.

7.2 Setup

Our experiments were performed on an Intel x86 machine with 4x3.4 GHz CPUs, 8 GB main memory and running openSUSE Leap 42.3. We installed Python 3.6 and Java 8 as our runtime environment. In our second research question we compared the runtime of our prediction against those of the SV-COMP tools. As the exact time behaviour depends on the execution environment, we evaluated our approach on the machines used for the competition. These experiments were performed on an Intel x86 machine with 4x3.4 GHz CPUs, 15 GB main memory running Ubuntu 18.04. More importantly, our approach was executed by the benchmarking tool BenchExec (Beyer et al. 2017).

7.3 Results

In the following we describe the results for all research questions.

RQ1a Table 5 lists the accuracies of binary classification on data set T/V for different kernel parametrizations. The final three rows (Verifolio and Default) can be ignored for now. The performance of a classifier using iteration bound m and AST depth bound d can be found at WLJ$_{(m,d)}$. First of all, we see that the accuracies do not differ a lot and are all relatively high. The best accuracy can be achieved with $m=2$ and $d=2$. When working with lower values of m and d (for performance reasons), the accuracy will only decrease slightly.

Table 5 T/V—accuracy for classification (mean ± standard deviation)

RQ1b Table 6 lists the accuracies of predicted rankings according to Spearman rank correlation. Again, the three final rows can be ignored for the moment. We give the accuracy per category and for Overall and highlight the largest accuracy per (meta-)category in bold. Looking at the different parameters and categories, no clear “winner” can be seen. Within a category, the accuracy values–like for classification–do not differ much. For the category Overall, there is even no iteration of the relabel algorithm necessary in order to achieve the best accuracy.

Table 6 Rank18 – Spearman correlation for rank prediction (mean ± standard deviation)

The table also reveals that category-specific training often pays off. For instance, if our interest is in finding a verification tool for termination checking, then we should train our predictor on the termination examples only.

RQ2 The comparison between prediction and validation time is shown in two figures. For this, we employed the kernel WLJ$_{(1,5)}$ (which is a compromise between the best kernel for binary classification and the best kernel for ranking). First, Fig. 6 depicts the difference between the runtime of prediction plus execution (of the predicted tool) and the sequential execution of both tools. This difference is shown on the y-axis. The x-axis lists the 4270 validation instances of the dataset T/V, ordered with respect to the difference (left to right from smallest to largest). We see that in the majority of cases prediction plus execution outperforms execution of both tools. Moreover, in the cases where the execution of both tools is faster, the difference is usually small.

Fig. 6

Testing vs. Verification: Improvement of prediction + execution time over sequential execution. A value above zero represents an instance that can be processed faster by prediction + execution

Second, Fig. 7 compares the runtimes of the 10 tools of our rankings and the prediction time given in a quantile plot. It shows the number of validation instances n (x-axis) for which a validation or prediction, respectively, can be achieved in t seconds (y-axis). Or slightly rephrased, the figure shows how many instances can be processed if we apply a time limit. We see that prediction has got some base overhead which is above that of the verification tools (left side, line of prediction above tool lines). However, when we increase the time limit the number of instances processable in this limit is (mostly) above that of the verification tools (right side, prediction line below tool lines).

Fig. 7

Rank18: Execution time of the 10 tools and the prediction

This shows that prediction in general does not take so much time that it would be impracticable to employ it. With this observation in mind, we participated in the 2019 edition of SV-COMP with our tool PeSCo (Richter and Wehrheim 2019) to see whether prediction can improve on pure verification. The results can be found at the SV-COMP 2019 website¹³; PeSCo ranked second in the category Overall.

RQ3 Finally, for the comparison with related approaches we studied the accuracy achieved by Verifolio and the majority (default) predictors. The results can again be found in Tables 5 (for classification) and 6 (for ranking), now considering the final rows as well. In terms of rank correlation, our technique is able to outperform the hand-crafted features of Verifolio with both kernels on all the datasets. For overflow problems (category OVERFLOW), our best predictor WLJ$_{(2,4)}$ improves the prediction for more than 0.1. We even have an improvement on category TERMINATION which is particularly surprising since Verifolio has specific hand-crafted features describing different sorts of loops in order to be able to detect termination. Since our generic feature vectors are very high-dimensional, we had furthermore expected that larger training sets would be needed for a support vector machine to generalize well. Still, we are able to outperform Verifolio on the smaller training sets in the categories MemSafety and Overflow. Finally, we see that the default predictor is completely useless for ranking.

For classification (Table 5), our approach again outperforms Verifolio. The comparison with the default majority predictors furthermore shows that learning is always better than taking majority votes, though the default predictor is better here than in the ranking case.

7.4 Threats to validity

There are a number of threats to the validity of the results. First of all, our implementation might contain bugs. In general, machine learning applications are difficult to debug since it is unclear what exactly the outcome of a learning phase should be. To nevertheless find bugs, we carried out a number of sanity checks, like the kernels returning 1 when called with the two arguments being the graphs of the same program.

For the Weisfeiler–Lehman kernel, our implementation uses a non-injective compression function (namely, a hash function). The use of a hash function is motivated by performance reasons. This might—if at all—only have a negative effect on the accuracy of the prediction as this leads to not being able to distinguish (some of) the different label sequences in the graphs anymore.

Our results might furthermore be influenced by the choice of training data. Our prediction might perform worse on other training data, in particular when the programs are written in a language other than C. For training, we however needed validation instances with a known ground truth, and it was beyond the scope of this paper to generate such data ourselves (the SV-COMP community has spent several years for building its benchmark set). Hence our evaluation was restricted to existing data sets.

8 Related work

Our approach applies the idea of algorithm selection to software analysis tools. Algorithm selection is a well-known problem in computer science. Software developers can apply the strategy design pattern (Gamma et al. 1995) to support algorithm selection in their software. In the context of software analysis, algorithm selection is often done manually or heuristically. For example, users can select different solvers (Beyer and Keremoglu 2011; Gurfinkel et al. 2015; Günther and Weissenbacher 2014; Gadelha et al. 2018) or verification approaches (Beyer and Keremoglu 2011; Rakamaric and Emmi 2014; Albarghouthi et al. 2012). Apel et al. (2013) select the domain to use for a variable based on its domain type. Refinement selection (Beyer et al. 2015) uses heuristics to decide which component to refine and which refinement to apply. Recently, a manually created decision model based on boolean program features has been suggested to select the most promising analysis combination (Beyer and Dangl 2018). In contrast, our approach uses machine learning to select an analysis tool for a verification task.

Similar approaches, which also apply machine learning for analysis tool selection, have already been pursued by two other groups of authors, namely by Demyanova et al. (2015) and Tulsian et al. (2014). Both have chosen verification-specific features of source code: while the latter mainly contains features counting program entities (e.g., lines of code, number of array variables, number of recursive functions), the first approach has defined different variable roles (e.g., variable being used as index to array) and loop patterns (e.g., syntactically bounded) as features and employs a light-weight static analysis to extract these features. In contrast to their work, our approach does not require an explicit feature selection, but uses the Weisfeiler–Lehman test of isomorphism as a way to encode structural relationships in programs in our features. An experimental comparison with the approach of Demyanova et al. is contained in Sect. 7; we could not compare to the approach of Tulsian et al., because the authors’ implementation is not publicly available.

Other approaches to algorithm selection via machine learning include approaches for constraint solving and SAT solving (Xu et al. 2008) or planning (Helmert et al. 2011). Kotthoff et al. (2012) have evaluated different machine learning algorithms from the WEKA machine learning library with respect to the purpose of algorithm selection for SAT solving.

The approach most closely connected to ours is that of Habib and Pradel (2018), who use Weisfeiler–Lehman graph kernels for learning the thread-safety of Java classes. Contrary to our approach, they build graphs tailored towards their learning task. The graphs focus on fields of classes, their access in methods and constructors, and concurrency related modifiers like volatile or synchronized. Li et al. (2016) use Weisfeiler–Lehman kernels to detect code similarities. Their graphs mainly reflect call graph structures and interprocedural control flow. Weisfeiler–Lehman subtree kernels (on CFGs only) are also employed for malware detection in Android apps (Wagner et al. 2009; Sahs and Khan 2012).

Allamanis and others (Allamanis et al. 2017) use a graph representation of source code to detect faulty variable usages. Their graphs are built from ASTs with special edges for different sorts of data usage (like “computed from”, “last read” or “last written”). Instead of using these graphs in kernels (like we do) or for extraction of feature vectors, they directly give these graphs as inputs to the learning algorithm (in their case, a neural network).

The work of Alon et al. (2018) and the newly proposed code2vec technique (Alon et al. 2019) also employ an AST representation of programs. These approaches aim at applications like the prediction of names for given method bodies. The technique code2vec first extracts paths of ASTs and then employs a neural network to learn both the representation of paths and their aggregation. The technique is however very sensitive to names used in programs (e.g., variables names). The authors of code2vec have also realized this and have thus proposed a fix to it (Yefet et al. 2019). As we directly replace names by node identifiers in our graph representation, our technique is not vulnerable to adversarial attacks changing variable names.

While the use of kernel functions in software engineering is relatively recent, graph kernels have been applied in other domains much earlier. Indeed, motivated by applications in domains such as bioinformatics, web mining, social networks, etc., where the use of graphs for modeling data is very natural, various types of graph kernels have been proposed in machine learning in the last two decades, for example the random walk and shortest path kernel (Borgwardt and Kriegel 2005). Generally, a distinction can be made between kernels on graphs, which seek to capture the similarity of different nodes in a single graph (Kondor and Lafferty 2002), and kernels between graphs, which compare two graphs with each other (Gärtner et al. 2003; Gärtner 2008). Besides, other types of kernels have been proposed, such as marginalized kernels (Kashima et al. 2003).

Other applications of machine learning to software engineering tasks include the learning of programs from examples ((Raychev et al. 2016; Lau 2001)) and the prediction of properties of programs (e.g., types of program variables (Raychev et al. 2015), fault locations (Le et al. 2016) or bugs (Pradel and Sen 2018)). A survey of different approaches of ML in the area of programming language and software engineering is given in Allamanis et al. (2018). A machine learning approach to software verification itself has recently been proposed in Chen et al. (2016).

9 Conclusion

In this paper, we proposed a novel technique for algorithm selection in the area of software validation. It builds on a graph representation of software and the construction of a kernel function for machine learning, which is based on the Weisfeiler–Lehman test of graph isomorphism and a generalization of the Jaccard measure for determining the similarity between multi-sets (bags) of subgraphs. Thus, data in the form of validation instances (programs plus properties to be checked) becomes amenable to a wide spectrum of kernel-based machine learning methods, including support vector machines as used in this paper.

Despite our concrete application, we like to emphasize that our graphs provide a completely generic representation of software, not specifically tailored to the domain of software validation. As suggested by our extensive experimental studies, our approach can nevertheless outperform custom-build techniques that are fine-tuned to software validation—a result that was not necessarily expected. Our explanation follows a pattern that is commonly observed in practical machine learning applications: Incorporating domain knowledge via hand-crafted features is helpful for the learner, especially if training data is sparse, but comes with the danger of introducing a bias if the features are not sufficiently well chosen or important features are missing. On the other side, offering a large set of generic features to choose from complicates the task of the learner and naturally requires more data (to separate useful from irrelevant features), but reduces the problem of bias. Therefore, a generic approach often outperforms an approach based on hand-crafted features provided enough training data is available.

Since our machine learning approach is readily usable in other applications, we plan to explore its performance for other software engineering problems in future work. Besides, there is of course scope for further improvements on a technical and implementational level, for example by incorporating an alias analysis into the computation of program dependence graphs, by enhancing the kernel function or using learning methods other than support vector machines. We in particular plan to elaborate on a general drawback of standard kernel-based learning methods, namely the difficultly to interpret the predictions: In addition to getting a useful recommendation, it would also be desirable to understand, for example, why one tool is preferred to another one on a specific validation instance. One direction we intend to pursue for this is using graph convolutional networks (Wu et al. 2019; Hamilton et al. 2017; Xu et al. 2019) and representation learning to let a neural network learn appropriate feature vectors for programs.

Node identifiers

Table 7 contains the complete list of node identifiers.

Table 7 All node identifiers and their meaning