Skip to main content
SpringerLink
Log in

Closed-form solutions for elastic tapered parabolic arches under uniform thermal gradients

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

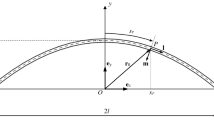
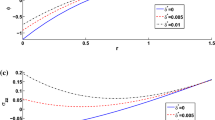
We investigate tapered elastic arches with parabolic axis under uniform thermal gradients. A perturbation of the finite field equations yields a sequence of first-order differential systems, which is turned into a non-dimensional form. If the arch is shallow and slender and its reference shape is stress-free, a closed-form incremental response is found. We comment on the graphics help presenting the results, as a first step towards the investigation of possible non-linear responses superposed on such first-order thermo-elastic state.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Love AEH (1927) A treatise on the mathematical theory of elasticity, 4th edn. The University Press, Cambridge

    MATH  Google Scholar 

  2. Timoshenko SP (1956) Strength of materials, 3rd edn. D. Van Nostrand, Princeton

    MATH  Google Scholar 

  3. Antman SS (1973) The theory of rods. Springer, Berlin

    Google Scholar 

  4. Antman SS (1995) Nonlinear problems of elasticity. Springer, New York

    MATH  Google Scholar 

  5. Tatone A, Rizzi N, Pignataro M (1988) Bifurcation analysis of a circular arch under hydrostatic pressure. Meccanica 23:113–118

    MATH  Google Scholar 

  6. Tufekci A, Arpaci A (1998) Exact solution of in-plane vibrations of circular arches with account taken of axial extension, transverse shear and rotatory inertia effects. J Sound Vib 209:845–856

    ADS  Google Scholar 

  7. Tufekci E, Arpaci A (2006) Analytical solutions of in-plane static problems for non-uniform curved beams including axial and shear deformations. Struct Eng Mech 22(2):131–150

    Google Scholar 

  8. Lin KC, Hsieh CM (2007) The closed form general solutions of 2-D curved laminated beams of variable curvatures. Compos Struct 79(4):606–618

    Google Scholar 

  9. Ruta G (2004) On inner constraints in plane circular arches. Arch Appl Mech (Ingenieur-Archiv) 74:212–222

    ADS  MATH  Google Scholar 

  10. Huang CS, Tseng YP, Leissa AW, Nieh KY (1998) An exact solution for in-plane vibrations of an arch having variable curvature and cross section. Int J Mech Sci 40:1159–1173

    MATH  Google Scholar 

  11. Tufekci E, Ozdemirci O (2006) Exact solution of free in-plane vibration of a stepped circular arch. J Sound Vib 295:725–738

    ADS  Google Scholar 

  12. Gimena L, Gimena FN, Gonzaga P (2008) Structural analysis of a curved beam element defined in global coordinates. Eng Struct 30(2):3355–3364

    MATH  Google Scholar 

  13. Gimena FN, Gonzaga P, Gimena L (2014) Analytical formulation and solution of arches defined in global coordinates. Eng Struct 60:189–198

    MATH  Google Scholar 

  14. Larbi LO, Kaci A, Houari MSA, Tounsi A (2013) An efficient shear deformation beam theory based on neutral surface position for bending and free vibration of functionally graded beams. Mech Based Des Struct Mach 41(4):421–433

    Google Scholar 

  15. Tufekci E, Eroglu U, Aya S (2016) Exact solution for in-plane static problems of circular beams made of functionally graded materials. Mech Based Des Struct Mach 44(4):476–494

    Google Scholar 

  16. Mitchell D, Gau JT (2019) Exact analytical solution to the 3D Navier-Lame equation for a curved beam of constant curvature subject to arbitrary dynamic loading. Eur J Mech A Solids 75:216–224

    MathSciNet  MATH  Google Scholar 

  17. Dawe DJ (1974) Numerical studies using circular arch finite elements. Comput Struct 4:729–740

    Google Scholar 

  18. Kikuchi F (1975) On the validity of the finite element analysis of circular arches represented by an assemblage of beam elements. Comput Methods Appl Mech Eng 5:253–276

    MathSciNet  MATH  Google Scholar 

  19. Marquis JP, Wang TM (1989) Stiffness matrix of parabolic beam element. Comput Struct 31(6):863–870

    MATH  Google Scholar 

  20. Saje M (1991) Finite element formulation of finite planar deformation of curved elastic beams. Comput Struct 39(3):327–337

    MATH  Google Scholar 

  21. Krishnan A, Suresh YJ (1998) A simple cubic linear element for static and free vibration analyses of curved beams. Comput Struct 68:473–489

    MATH  Google Scholar 

  22. Raveendranath P, Singh G, Pradhan B (1999) A two-noded locking free shear deformable curved beam element. Int J Numer Methods Eng 44:265–280

    MATH  Google Scholar 

  23. Raveendranath P, Singh G, Pradhan B (2000) Free vibration of arches using a curved beam element based on a coupled polynomial displacement field. Comput Struct 78:583–590

    Google Scholar 

  24. Raveendranath P, Singh G, Rao GV (2001) A three-noded shear-flexible curved beam element based on coupled displacement field interpolations. Int J Numer Methods Eng 52:85–101

    MATH  Google Scholar 

  25. Wu JS, Chiang LK (2004) A new approach for free vibration analysis of arches with effects of shear deformation and rotary inertia considered. J Sound Vib 277:49–71

    ADS  Google Scholar 

  26. Shahba A, Atternejad R, Semnani SJ (2013) New shape functions for non-uniform curved Timoshenko beams with arbitrarily varying curvature using basic displacement functions. Meccanica 48:159–174

    MathSciNet  MATH  Google Scholar 

  27. Eroglu U, Tufekci E (2018) A new finite element formulation for free vibrations of planar curved beams. Mech Based Des Struct Mach 46(6):730–750

    Google Scholar 

  28. Karami G, Malekzadeh P (2004) In-plane free vibration analysis of circular arches with varying cross-sections using differential quadrature method. J Sound Vib 274:777–799

    ADS  Google Scholar 

  29. Lin W, Qiao N (2008) In-plane vibration analyses of curved pipes conveying fluid using the generalized differential quadrature rule. Comput Struct 86:133–139

    Google Scholar 

  30. Shin YJ, Kwon KM, Yun JH (2008) Vibration analysis of a circular arch with variable cross-section using differential transformation and generalized differential quadrature. J Sound Vib 309:9–19

    ADS  Google Scholar 

  31. Cazzani A, Marcello M, Emilio T (2016) Isogeometric analysis of plane-curved beams. Math Mech Solids 21(5):562–577

    MathSciNet  MATH  Google Scholar 

  32. Luu AT, Kim NI, Lee J (2015) Isogeometric vibration analysis of free-form Timoshenko curved beams. Meccanica 50(1):169–187

    MathSciNet  MATH  Google Scholar 

  33. Huynh TA, Luu AT, Lee J (2017) Bending, buckling and free vibration analyses of functionally graded curved beams with variable curvatures using isogeometric approach. Meccanica 52(11–12):2527–2546

    MathSciNet  Google Scholar 

  34. Kiendl J, Auricchio F, Reali A (2018) A displacement-free formulation for the Timoshenko beam problem and a corresponding isogeometric collocation pproach. Meccanica 53(6):1403–1413

    MathSciNet  MATH  Google Scholar 

  35. Auciello NM, De Rosa MA (1994) Free vibrations of circular arches: a review. J Sound Vib 176:433–458

    ADS  MATH  Google Scholar 

  36. Chidamparam P, Leissa AW (1993) Vibrations of planar curved beams, rings, and arches. Appl Mech Rev 46:467–483

    ADS  Google Scholar 

  37. Karnovsky IA (2012) Theory of arched structures: strength, stability, vibration. Springer, New York

    Google Scholar 

  38. Brownjohn JMW, De Stefano A, Xu YL, Wenzel H, Aktan AE (2011) Vibration-based monitoring of civil infrastructure: challanges and successes. J Civ Struct Health Monit 1:79–95

    Google Scholar 

  39. Yarnold MT, Moon FL, Aktan AE (2015) Temperature-based structural identification of long-span bridges. J Struct Eng 141(11):04015027

    Google Scholar 

  40. DeSilva CN, Whitman AB (1971) Thermodynamical theory of directed curves. J Math Phys 12(8):1603–1609

    ADS  MathSciNet  MATH  Google Scholar 

  41. Bradford MA (2006) In-plane nonlinear behavior of circular pinned arches with elastic restraints under thermal loading. Int J Struct Stab Dyn 6(2):163–177

    MathSciNet  Google Scholar 

  42. Zenkour AM, Mashat DS (2009) Bending analysis of a ceramic-metal arched bridge using a first-order theory. Meccanica 44:721–731

    MathSciNet  MATH  Google Scholar 

  43. Pi YL, Bradford MA (2010) In-plane thermoelastic behaviour and buckling of pin-ended and fixed circular arches. Eng Struct 32:250–260

    Google Scholar 

  44. Rezaiee-Pajand M, Safaei-Rajabzadeh N, Hozhabrossadati SM (2018) Three-dimensional deformations of a curved circular beam subjected to thermo-mechanical loading using green’s function method. Int J Mech Sci 142–143:163–175

    Google Scholar 

  45. Eroğlu U, Ruta G (2018) Fundamental frequencies and buckling in pre-stressed parabolic arches. J Sound Vib 435:104–118

    ADS  Google Scholar 

  46. Lanczos C (1970) The variational principles of mechanics. Toronto University Press, Toronto

    MATH  Google Scholar 

  47. Pignataro M, Rizzi N, Ruta G (2008) A beam model for the flexural–torsional buckling of thin-walled members. Thin Walled Struct 46:816–822

    Google Scholar 

  48. Pease MC (1965) Methods of matrix algebra. Academic Press, New York

    MATH  Google Scholar 

Download references

Acknowledgements

This work was done when U. Eroglu was Visiting Researcher at the Dipartimento di Ingegneria strutturale e geotecnica of University “La Sapienza”, the support of which is gratefully acknowledged. G. Ruta acknowledges the support of institutional grants of the University “La Sapienza” and of PRIN 2015TTJN95 “Identification and monitoring of complex structural systems” from Italian Ministry of University and Research.

Author information

Authors and Affiliations

  1. Mechanical Engineering, Izmir University of Economics, Sakarya Caddesi 156, 35330, Balçova, Izmir, Turkey

    Ugurcan Eroglu

  2. Ingegneria strutturale e geotecnica, University “La Sapienza”, via Eudossiana 18, 00184, Rome, Italy

    Giuseppe Ruta

  3. National Group for Mathematical Physics, Rome, Italy

    Giuseppe Ruta

Authors
  1. Ugurcan Eroglu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Giuseppe Ruta
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Giuseppe Ruta.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Eroglu, U., Ruta, G. Closed-form solutions for elastic tapered parabolic arches under uniform thermal gradients. Meccanica 55, 1135–1152 (2020). https://doi.org/10.1007/s11012-020-01153-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-020-01153-x

Keywords

Search

Navigation