Viscous Sublayer

Abstract

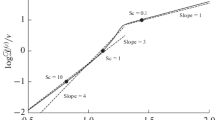
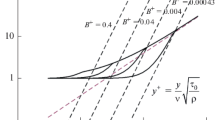
The eddy viscosity and the eddy diffusivity are calculated for the viscous sublayer in turbulent flow near a solid surface by using Fourier transforms of a spectral element of the velocity profiles, the pressure, and the concentration. The different spectral elements are assumed to behave independently of each other in this region, and the magnitudes are plotted as functions of distance from the wall. The tangential velocity profiles show a slope of unity on log–log plots against distance y from the wall, while the normal component shows a slope of 2. The concentration profiles generally show a slope of unity except near the outer limit of the viscous sublayer. There is also a dependence on the value of the Schmidt number as well as the concentration fluctuation assumed to prevail at a distance of δ₀ at the outer limit of the viscous sublayer. When the normal velocity fluctuation is correlated with either the streamwise velocity fluctuation or with the concentration fluctuation, one infers a slope for the eddy viscosity or the eddy diffusivity of 3. The eddy diffusivity shows more structure than the eddy viscosity and can differ substantially from the latter in the depths of the viscous sublayer.

TURBULENT FLOW IN A PIPE

One might be able to approach a valid treatment of fully developed turbulence in a pipe. The steady, fully developed flow has only an axial velocity component, and this depends only on radial position. The average axial pressure drop is the same at each axial and radial position, although there may be a radial average pressure variation as discussed below.

Thus one could express the fluctuations as a sum of a finite number of spectral components of a form similar to that used in the present linear problem:

$${\text{v}}_{r}^{'} = \Sigma [\operatorname{Re} \{ {{V}_{r}}(r)\exp (i{{k}_{\theta }}\theta + i{{k}_{z}}z + i\omega t)\} ],$$

(A.1)

$${\text{v}}_{{\theta }}^{'} = \Sigma [\operatorname{Re} \{ {{V}_{\theta }}(r)\exp (i{{k}_{\theta }}\theta + i{{k}_{z}}z + i\omega t)\} ],$$

(A.2)

$${\text{v}}_{z}^{'} = \Sigma [\operatorname{Re} \{ {{V}_{z}}(r)\exp (i{{k}_{\theta }}\theta + i{{k}_{z}}z + i\omega t)\} ],$$

(A.3)

$$\mathcal{P}{\kern 1pt} ' = \Sigma [\operatorname{Re} \{ P(r)\exp (i{{k}_{\theta }}\theta + i{{k}_{z}}z + i\omega t)\} ].$$

(A.4)

The problem is reduced to finding the radial dependence of V_r, V_θ, V_z, and P for these spectral components. This is a formidable problem, but still simpler than solving directly for fluctuating components in time and space. This method of treating interacting Fourier components could also be used in the present problem for extending the valid range farther into the outer turbulent flow for a single spectral component.

Is there a variation of average pressure with radial position in this pipe flow? I thought I found one in about 1963, but I have lost any notes on it. The averaged radial component of the equation of motion is

$$\begin{gathered} \frac{1}{2}\frac{{\partial \left\langle {{\text{v}}_{r}^{'}{\text{v}}_{r}^{'}} \right\rangle }}{{\partial r}} + \left\langle {\frac{{{\text{v}}_{{\theta }}^{'}}}{r}\frac{{\partial {\text{v}}_{r}^{'}}}{{\partial \theta }}} \right\rangle \\ + \left\langle {{\text{v}}_{z}^{'}\frac{{\partial {\text{v}}_{r}^{'}}}{{\partial z}}} \right\rangle - \,\,\frac{{\partial \left\langle {{\text{v}}_{\theta }^{'}{\text{v}}_{\theta }^{'}} \right\rangle }}{r} = - \frac{1}{\rho }\frac{{\partial \bar {\mathcal{P}}}}{{\partial r}}. \\ \end{gathered} $$

(A.5)

Even if the third term on the left is zero, the fourth term would be expected to generate a nonzero contribution. The first term will generate a zero result overall, since it can be integrated and the correlation should be zero at both the center and the pipe wall. The second term should be zero since the angular fluctuation should not be correlated with the radial fluctuation (fluctuations of the angular velocity should be equally probable in the plus and minus θ directions).