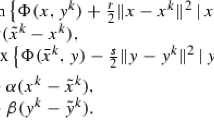Abstract
We investigate the convergence of a recently popular class of first-order primal–dual algorithms for saddle point problems under the presence of errors in the proximal maps and gradients. We study several types of errors and show that, provided a sufficient decay of these errors, the same convergence rates as for the error-free algorithm can be established. More precisely, we prove the (optimal) \(O\left( 1/N\right)\) convergence to a saddle point in finite dimensions for the class of non-smooth problems considered in this paper, and prove a \(O\left( 1/N^2\right)\) or even linear \(O\left( \theta ^N\right)\) convergence rate if either the primal or dual objective respectively both are strongly convex. Moreover we show that also under a slower decay of errors we can establish rates, however slower and directly depending on the decay of the errors. We demonstrate the performance and practical use of the algorithms on the example of nested algorithms and show how they can be used to split the global objective more efficiently.
Similar content being viewed by others
1 Introduction
The numerical solution of nonsmooth optimization problems and the acceleration of their convergence has been regarded a fundamental issue in the past 10–20 years. This is mainly due to the development of image reconstruction and processing, data science and machine learning which require to solve large and highly nonlinear minimization problems. Two of the most popular approaches are forward–backward splittings [22, 23, 42], in particular the FISTA method [7, 8], and first-order primal–dual methods, first introduced in [32, 54] and further studied in [15, 17]. The common thread of all these methods is that they split the global objective into many elementary bricks which, individually, may be “easy” to optimize.
In their original version, all the above mentioned approaches require that the mathematical operations necessary in every step of the respective algorithms can be executed without errors. However, one might stumble over situations in which these operations can only be performed up to a certain precision, e.g. due to an erroneous computation of a gradient or due to the application of a proximal operator lacking a closed-form solution. Examples where this problem arises are TV-type regularized inverse problems [6, 7, 30, 33, 59] or low-rank minimization and matrix completion [14, 44]. To address this issue, there has been a lot of work investigating the convergence of proximal point methods [24, 36, 37, 39, 56, 58], where the latter two also prove rates, and proximal forward–backward splittings [23] under the presence of errors. The objectives of these publications reach from general convergence proofs [21, 34, 43, 53, 64] and convergence up to some accuracy level [26, 27, 47] to convergence rates in dependence of the errors [5, 60, 61] also for the accelerated versions including the FISTA method. The recent paper [9] follows a similar approach to [61], however extending also to nonconvex problems using variable metric strategies and linesearch.
For the recently popular class of first-order primal–dual algorithms mentioned above the list remains short: to the best of our knowledge the only work which considers inaccuracies in the proximal operators for this class of algorithms is the one of Condat [25], who explicitly models errors and proves convergence under mild assumptions on the decay of the errors. However, he does not show any convergence rates. We must also mention Nemirovski’s approach in [48] which is an extension of the extragradient method. This saddle-point optimization algorithm converges with an optimal O(1/N) convergence rate as soon as a particular inequality is satisfied at each iteration, possibly with a controlled error term (cf. Prop 2.2 in [48]).
The goal of this paper is twofold: Most importantly, we investigate the convergence of the primal–dual algorithms presented in [15, 17] for problems of the form
for convex and lower semicontinuous g and h and convex and Lipschitz differentiable f, with errors occurring in the computation of \(\nabla f\) and the proximal operators for g and \(h^*\). Following the line of the preceding works on forward–backward splittings, we consider the different notions of inexact proximal points used in [60] and extended in [5, 58, 61] and, assuming an appropriate decay of the errors, establish the convergence rates of [15, 17] also for perturbed algorithms. More precisely, we prove the well-known \(O\left( 1/N\right)\) rate for the basic version, a \(O\left( 1/N^2\right)\) rate if either f, g or \(h^*\) are strongly convex, and a linear convergence rate in case both the primal and dual objective are strongly convex. Moreover we show that also under a slower decay of errors we can establish rates, however unsurprisingly slower depending on the errors.
In the spirit of [61] for inexact forward–backward algorithms, the second goal of this paper is to provide an interesting application for such inexact primal–dual algorithms. We put the focus on situations where one takes the path of inexactness deliberately in order to split the global objective more efficiently. A particular instance are problems of the form
A popular example is the TV-\(L^1\) model with some imaging operator \(K_1\), where g and h are chosen to be \(L^1\)-norms and \(K_2 = \nabla\) is a gradient. It has e.g been studied analytically by Alliney [2,3,4] and subsequently by Chan and Esedoglu [19], Kärkkäinen et al. [38] and Nikolova [50, 51]. However, due to the nonlinearity and nondifferentiability of the involved terms, solutions of the model are numerically hard to compute. One can find a variety of approaches to solve the TV-\(L^1\) model, reaching from (smoothed) gradient descent [19] over interior point methods [35], primal–dual methods using a semi-smooth Newton method [28] to augmented Lagrangian methods [31, 62]. Interestingly, the inexact framework we propose in this paper provides a very simple and intuitive algorithmic approach to the solution of the TV-\(L^1\) model. More precisely, applying an inexact primal–dual algorithm to formulation (1), we obtain a nested algorithm in the spirit of [6, 7, 20, 30, 33, 59, 61],
where \({{\mathrm {prox}}}_{\sigma h^*}\) denotes the proximal map with respect to \(h^*\) and step size \(\sigma\) (cf. Sect. 2). It requires to solve the inner subproblem of the proximal step with respect to \(g \circ K_2\), i.e. a TV-denoising problem, which does not have a closed-form solution but has to be solved numerically (possibly with an initial guess which improves over the iterates). It has been observed in [7] that, using this strategy on the primal TV-\(L^2\) deblurring problem can cause the FISTA algorithm to diverge if the inner step is not executed with sufficient precision. As a remedy, the authors of [61] demonstrated that the theoretical error bounds they established for inexact FISTA can also serve as a criterion for the necessary precision of the inner proximal problem and hence make the nested approach viable. We show that the bounds for inexact primal–dual algorithms established in this paper can be used to make the nested approach viable for entirely non-differentiable problems such as the TV-\(L^1\) model, while the results of [61] for partly smooth objectives can also be obtained as a special case of the accelerated versions.
In the context of inexact and nested algorithms it is worthwhile mentioning the recent ‘Catalyst’ framework [40, 41], which uses nested inexact proximal point methods to accelerate a large class of generic optimization problems in the context of machine learning. The inexactness criterion applied there is the same as in [5, 60]. Our approach, however, is much closer to [5, 60, 61], stating convergence rates for perturbed algorithms, while [40, 41] focus entirely on nested algorithms, which we only consider as a particular instance of perturbed algorithms in the numerical experiments.
The remainder of the paper is organized as follows: in the next section we introduce the notions of inexact proxima that we will use throughout the paper. In the following Sect. 3 we formulate inexact versions of the primal–dual algorithms presented in [15] and [17] and prove their convergence including rates depending on the decay of the errors. In the numerical Sect. 4 we apply the above splitting idea for nested algorithms to some well-known imaging problems and show how inexact primal–dual algorithms can be used to improve their convergence behavior.
2 Inexact computations of the proximal point
In this section we introduce and discuss the idea of the proximal point and several ways for its approximation. For a proper, convex and lower semicontinuous function \(g :{\mathcal {X}}\rightarrow {(-\infty ,+\infty ]}\) mapping from a Hilbert space \({\mathcal {X}}\) to the real line extended with the value \(+\infty\) and \(y \in {\mathcal {X}}\) the proximal point [45, 46, 55, 56] is given by
Since g is proper we directly obtain \({{\mathrm {prox}}}_{\tau g} (y) \in {{\mathrm {dom}}} g\). The \(1/\tau\)-strongly convex mapping \({{\mathrm {prox}}}_{\tau g} :{\mathcal {X}}\rightarrow {\mathcal {X}}\) is called proximity operator of \(\tau g\). Letting
be the proximity function, the first-order optimality condition for the proximum gives different characterizations of the proximal point:
Based on these equivalences we introduce four different types of inexact computations of the proximal point, which are differently restrictive. Most have already been considered in literature and we give reference next to the definitions. We like to recommend [58, 61] for some illustrations of the different notions in case of a projection. We start with the first expression in (4).
Definition 1
Let \(\varepsilon \ge 0\). We say that \(z \in {\mathcal {X}}\) is a type-0 approximation of the proximal point \({{\mathrm {prox}}}_{\tau g}(y)\) with precision \(\varepsilon\) if
This refers to choosing a proximal point from the \(\sqrt{2\tau \varepsilon }\)-ball around the true proximum. It is important to notice that a type-0 approximation is not necessarily feasible, i.e., it can occur that \(z \notin {{\mathrm {dom}}} g\). This can easily be verified e.g. for g being the indicator function of a convex set, and requires us to treat this approximation slightly differently from the following ones in “Type-0 approximations” section of “Appendix”. Observe that it is easy to check a posteriori the precision of a type-0 approximation provided \(\partial g\) is easy to evaluate. Indeed, if \(e\in \tau \partial g(z)+ z-y\), standard estimates show that \(\Vert z - {{\mathrm {prox}}}_{\tau g}(y) \Vert \le \Vert e\Vert\) and \(z\approx _0^{\varepsilon }{{\mathrm {prox}}}_{\tau g}(y)\) for \(\varepsilon =\Vert e\Vert ^2/(2\tau )\).
In order to relax the second or third expression in (4), we need the notion of an \(\varepsilon\)-subdifferential of \(g :{\mathcal {X}}\rightarrow {(-\infty ,+\infty ]}\) at \(z \in {\mathcal {X}}\):
As a direct consequence of the definition we obtain a notion of \(\varepsilon\)-optimality
Based on this and the second expression in (4), we define a second notion of an inexact proximum. It has e.g. been considered in [5, 60] to prove the convergence of inexact proximal gradient methods under the presence of errors.
Definition 2
Let \(\varepsilon \ge 0\). We say that \(z \in {\mathcal {X}}\) is a type-1 approximation of the proximal point \({{\mathrm {prox}}}_{\tau g}(y)\) with precision \(\varepsilon\) if
Hence, by (5), a type-1 approximation minimizes the energy of the proximity function (3) up to an error of \(\varepsilon\). It turns out that a type-0 approximation is weaker than a type-1 approximation:
Lemma 1
Let\(z \approx _1^{\varepsilon } {{\mathrm {prox}}}_{\tau g}(y)\). Then\(z \in {{\mathrm {dom}}} g\)and
that is\(z \approx _0^{\varepsilon } {{\mathrm {prox}}}_{\tau g}(y)\).
The result is easy to verify and can be found e.g. in [36, 56, 58]. An even morerestrictive version of an inexact proximum can be obtained by relaxing the third expression in (4), which has been introduced in [39] and subsequently been used in [24, 58] in the context of inexact proximalpoint methods.
Definition 3
Let \(\varepsilon \ge 0\). We say that \(z \in {\mathcal {X}}\) is a type-2 approximation of the proximal point \({{\mathrm {prox}}}_{\tau g}(y)\) with precision \(\varepsilon\) if
Letting \(\phi _\tau (z) = \Vert z - y \Vert ^2/(2 \tau )\), the following characterization from [58] of the \(\varepsilon\)-subdifferential of the proximity function \(G_\tau = g + \phi _\tau\) sheds light on the difference between a type-1 and type-2 approximation:
Equation (6) decomposes the error in the \(\varepsilon\)-subdifferential of \(G_\tau\) into two parts related to g respectively \(\phi _\tau\). As a consequence, for a type-1 approximation it is not clear how the error is distributed between g or \(\phi _\tau\), while for a type-2 approximation the error occurs solely in g. Hence a type-2 approximation can be seen as an extreme case of a type-1 approximation with \(\varepsilon _2 = 0\).
In view of the decomposition (6), we define a fourth notion of an inexact proximum as the extreme case \(\varepsilon _1 = 0\), which has been considered in e.g. [36, 56].
Definition 4
Let \(\varepsilon \ge 0\). We say that \(z \in {\mathcal {X}}\) is a type-3 approximation of the proximal point \({{\mathrm {prox}}}_{\tau g}(y)\) with precision \(\varepsilon\) if
Definition 4 gives the notion of a “correct” output for an incorrect input of the proximal operator. Being the two extreme cases, type-2 and type-3 proxima are also proxima of type 1. The decomposition (6) further leads to the following lemma from [60], which allows to treat the type-1, -2 and -3 approximations in the same setting.
Lemma 2
If\(z \in {\mathcal {X}}\)is a type-1 approximation of\({{\mathrm {prox}}}_{\tau g}(y)\)withprecision\(\varepsilon\), then there exists\(r \in {\mathcal {X}}\)with\(\Vert r\Vert \le \sqrt{2 \tau \varepsilon }\)such that
Now note that letting \(r = 0\) in Lemma 2 gives a type-2 approximation, replacing the \(\varepsilon\)-subdifferential by a normal one gives a type-3 approximation. We mention that there exist further notions of approximations of the proximal point, e.g. used in [36], and refer to [61, Section 2.2] for a compact discussion.
Even tough we prove our results for different types of approximations, the most useful in practice seems to be the approximation of type 2. This is due to the following insights obtained by Villa et al. [61]: Without loss of generality let \(g(x) = w(Bx),\) with proper, convex and l.s.c. \(w:{\mathcal {Z}}\rightarrow {(-\infty ,+\infty ]}\) and linear \(B :{\mathcal {X}}\rightarrow {\mathcal {Z}}\). Then the calculation of the proximum requires to solve
Now if there exists \(x_0 \in {\mathcal {X}}\) such that g is continuous in \(Bx_0\), the Fenchel-Moreau-Rockafellar duality formula [63, Corollary 2.8.5] states that
where we refer to the right hand side as the “dual” problem \(W_\tau (z)\). Furthermore we can always recover the primal solution \({\hat{x}}\) from the dual solution \({\hat{z}}\) via the relation \({\hat{x}}= y - B^* {\hat{z}}\). Most importantly, we obtain that \({\hat{x}}\) and \({\hat{z}}\) solve the primal respectively dual problem if and only if the duality gap \({\mathcal {G}}(x,z) := G_\tau (x) + W_\tau (z)\) vanishes, i.e.
The following result in [61] states that the duality gap can also be used as a criterion to assess admissible type-2 approximations of the proximal point:
Proposition 1
Let\(z \in {\mathcal {Z}}\). Then
Proposition 1 has an interesting implication: if one can construct a feasible dual variable z during the solution of (7), it is easy to check the admissibility of the corresponding primal variable x to be a type-2 approximation by evaluating the duality gap. We shall make use of that in the numerical experiments in Sect. 4.
Of course, since a type-2 approximation automatically is a type-1 and type-0 approximation, the above argumentation is also valid to find feasible approximations in these cases. However, since type-1 and type-0 approximations are technically less restrictive, one should need to characterize when an approximation is of such type without already being an approximation of type 2. An example of a type-0 approximation may be found in problems where the desired proximum is the projection onto the intersection of convex sets. The (inexact) proximum may be computed in a straightforward fashion using Dykstra’s algorithm [29], which has e.g. been done in [11] or [1, 17, Ex. 7.7] for Mumford–Shah-type segmentation problems. Depending on the involved sets, one may get an upper bound on the maximal distance of the current iterate of Dykstra’s algorithm to these sets, obtaining a bound on how far the current iterate is from the true proximum. These considerations, however, require to be tested in the respective cases.
3 Inexact primal–dual algorithms
We can now prove the convergence of some primal–dual algorithms under the presence of the respective error. We start with the type-1, -2 and -3 approximations and outline in “Type-0 approximations” section of “Appendix” how to get a grip also on the type-0 approximation. The convergence analysis in this chapter is based on a combination of techniques derived in previous works on the topic: similar results on the convergence of exact primal–dual algorithms can be found e.g. in [15, 17, 18], the techniques to obtain error bounds for the inexact proximum are mainly taken from [5, 60]. We consider the saddle-point problem
where we make the following assumptions:
- 1.
\(K :{\mathcal {X}}\rightarrow {\mathcal {Y}}\) is a linear and bounded operator between Hilbert spaces \({\mathcal {X}}\) and \({\mathcal {Y}}\) with norm \(L = \Vert K\Vert\),
- 2.
\(f :{\mathcal {X}}\rightarrow {(-\infty ,+\infty ]}\) is proper, convex, lower semicontinuous and differentiable with \(L_f\)-Lipschitz gradient,
$$\begin{aligned} \Vert \nabla f(x) - \nabla f(x') \Vert \le L_f \Vert x - x' \Vert \quad {\text { for all }} x,x' \in {{\mathrm {dom}}} f, \end{aligned}$$ - 3.
\(g ,h :{\mathcal {X}}\rightarrow {(-\infty ,+\infty ]}\) are proper, lower semicontinuous and convex functions,
- 4.
problem (8) admits at least one solution \((x^\star ,y^\star ) \in {\mathcal {X}}\times {\mathcal {Y}}\).
It is well-known that taking the supremum over y in \({\mathcal {L}}(x,y)\) leads to the corresponding “primal” formulation of the saddle-point problem (8)
which for a lot of variational problems might be the starting point. Analogously, taking the infimum over x leads to the dual problem. Given an algorithm producing iterates \((x^N,y^N)\) for the solution of (8), the goal of this section is to obtain estimates
for \(\alpha > 0\) and \((x,y) \in {\mathcal {X}}\times {\mathcal {Y}}\). If \((x,y) = (x^\star ,y^\star )\) is a saddle point, the left hand side vanishes if and only if the pair \((x^N,y^N)\) is a saddle point itself, yielding a convergence rate in terms of the primal–dual objective in \(O\left( 1/N^\alpha \right)\). Under mild additional assumptions one can then derive estimates e.g. for the error in the primal objective. If the supremum over y in \({\mathcal {L}}(x^N,y)\) is attained at some \({\tilde{y}}\), one easily sees that
giving a convergence estimate for the primal objective.
In the original versions of primal–dual algorithms (e.g. [15, 18]), the authors require \(h^*\) and g to have a simple structure such that their proximal operators (2) can be sufficiently easily evaluated. A particular feature of most of these operators is that they have a closed-form solution and can hence be evaluated exactly. We study the situation where the proximal operators for g or \(h^*\) can only be evaluated up to a certain precision in the sense of Sect. 2, and as well the gradient of f may contain errors. As opposed to the general iteration of an exact primal–dual algorithm [18]
where \(({\bar{x}},{\bar{y}})\) and \(({\tilde{x}},{\tilde{y}})\) are the previous points, and \(({\hat{x}},{\hat{y}})\) are the updated exact points, we introduce the general iteration of an inexact primal–dual algorithm
Here the updated points \((\check{x},\check{y})\) denote the inexact proximal point , which are only computed up to precision \(\varepsilon\) respectively \(\delta\), in the sense of a type-2 approximation from Sect. 2 for \(\check{y}\) and a type-i approximation for \(i\in \{1,2,3\}\) for \(\check{x}\). The vector \(e \in {\mathcal {X}}\) denotes a possible error in the gradient of f. We use two different pairs of input points \(({\bar{x}},{\bar{y}})\) and \(({\tilde{x}},{\tilde{y}})\) in order to include intermediate overrelaxed input points. It is clear, however, that we require \({\tilde{x}}\) to depend on \(\check{x}\) respectively \({\tilde{y}}\) on \(\check{y}\) in order to couple the primal and dual updates.
At first glance it seems counterintuitive that we allow errors of type 1, 2 and 3 in \(\check{x}\), while only allowing for type-2 errors in \(\check{y}\). The following general descent rule for the iteration (12) sheds some more light on this fact and forms the basis for all the following proofs. It can be derived using simple convexity results and resembles the classical energy descent rules for forward–backward splittings. It can then be used to obtain estimates on the decay of the objective of the form (9). We prove the descent rule for a type-1 approximation of the primal proximum since we always obtain the result for a type-2 or type-3 approximation as a special case.
Lemma 3
Let\(\tau , \sigma > 0\)and \((\check{x},\check{y})\)be obtained from\(({\bar{x}},{\bar{y}})\)and\(({\tilde{x}},{\tilde{y}})\)and the updates (12) for\(i = 1\). Then for every\((x,y) \in {\mathcal {X}}\times {\mathcal {Y}}\)we have
Proof
For the inexact type-2 proximum \(\check{y}\) we have by Definition 3 that \(({\bar{y}} + \sigma K {\tilde{x}} - \check{y})/\sigma \in \partial _\delta h^*(\check{y})\), so by the definition of the subdifferential we find
For the inexact type-1 primal proximum, from Definition 2 and Lemma 2 we have that there exists a vector r with \(\Vert r\Vert \le \sqrt{2 \tau \varepsilon }\) such that
Hence we find that
where we applied the Cauchy–Schwarz inequality to the error term. Further by the Lipschitz property and convexity of f we have (cf. [49])
Now we add the Eqs. (14), (15) and (16), insert
and rearrange to arrive at the result. □
We point out that, as a special case, choosing a type-2 approximation for the primal proximum in Lemma 3 corresponds to dropping the square root in the estimate (13), choosing a type-3 approximation corresponds to dropping the additional \(\varepsilon\) at the end. Also note that the above descent rule is the same as the one in [15, 18] except for the additional error terms in the last line of (13).
Lemma 3 has an immediate implication: in order to control the errors \(\Vert e\Vert\) and \(\varepsilon\) in the last line of Lemma 3 it is obvious that we need to find a useful bound on \(\Vert x - \check{x}\Vert\). We shall obtain this bound using a linear extrapolation in the primal variable x [15]. However, if we allow e.g. a type-1 approximation also in \(\check{y}\), we obtain an additional error term in (13) involving \(\Vert y - \check{y}\Vert\) that we need to bound as well. Even though we shall be able to obtain a bound in most cases, it will be arbitrarily weak due to the asymmetric nature of the used primal–dual algorithms, or go along with severe restrictions on the step sizes. This fact will become more obvious from the proofs in the following.
3.1 The convex case: no acceleration
We start with a proof for a basic version of algorithm (12) using a technical lemma taken from [60] (see “Two technical lemmas” section in "Appendix"). The following inexact primal–dual algorithm corresponds to the choice
in algorithm (12):
Theorem 1
Let\(L = \Vert K\Vert\)and choosesmall\(\beta > 0\)and\(\tau , \sigma > 0\)such that\(\tau L_f + \sigma \tau L^2 + \tau \beta L< 1\), and let the iterates\((x^n, y^n)\)be defined by Algorithm (18) for\(i \in \{1,2,3\}\). Then for any\(N \ge 1\)and\(X^N := \left( \sum _{n=1}^N x^n \right) /N\), \(Y^N := \left( \sum _{n=1}^N y^n \right) /N\)we have for a saddle point\((x^\star ,y^\star ) \in {\mathcal {X}}\times {\mathcal {Y}}\)that
where
Remark 1
The purpose of the parameter\(\beta > 0\)isonly of technical nature and is needed in order to show convergence of the iterates of algorithm (18). In practice, however, we did not observe any issues setting it super small (respectively, to zero). Its role will become obvious in the next Theorem.
Proof
Using the choices (17) in Lemma 3 leads us to
The goal of the proof is, as usual, to manipulate this inequality such that we obtain a recursion where most of the terms cancel when summing the inequality. The starting point is an extension of the scalar product on the right hand side:
where we used (for \(\alpha > 0\)) that by Young’s inequality for every \(x,x' \in {\mathcal {X}}\) and \(y,y' \in {\mathcal {Y}}\),
and \(\alpha = \sigma L + \beta\). This gives
Now we let \(x^0 = x^{-1}\) and sum (22) from \(n = 0, \dots , N-1\) to obtain
where \(\kappa = 1 - \tau L_f - \tau \sigma L^2 - \tau \beta L\). With Young’s inequality on the inner product with \(\alpha = \frac{1 - \tau L_f}{L \tau }\) such that \(L \alpha \tau = 1 - \tau L_f\) and \((L \sigma )/\alpha = (\tau \sigma L^2)/(1 - \tau L_f) < 1\) we obtain
Note that the introduction of the parameter \(\beta > 0\) allowed us to keep an additional term involving the difference of the dual iterates on the right hand side of the inequality. This will allow to prove the convergence of the iterates later on in Theorem 2. The above inequality can now be used to bound the sum on the left hand side as well as \(\Vert x - x^N \Vert\) by only the initialization \((x^0,y^0)\) and the errors \(e^n\), \(\varepsilon _n\) and \(\delta _n\). We start with the latter and let \((x,y) = (x^\star ,y^\star )\) such that the sum on the left hand side is nonnegative, hence with \(\varDelta _0(x,y) := \Vert x - x^0 \Vert ^2/(2\tau ) + \Vert y - y^0 \Vert ^2/(2\sigma )\) we have
(note that the remaining terms on the RHS of (23) are negative). We multiply the equation by \(2 \tau\) and continue with a technical result by Schmidt et al. [60, p.12]. Using Lemma 4 with \(u_N = \Vert x^\star - x^N \Vert\), \(S_N = 2\tau \varDelta _0(x^\star ,y^\star ) + 2 \tau \sum _{n=1}^N (\varepsilon _n + \delta _n)\) and \(\lambda _n = 2 (\tau \Vert e^n \Vert + \sqrt{2 \tau \varepsilon _n})\) we obtain a bound on \(\Vert x^\star - x^N \Vert\):
where we set \(A_N := \sum _{n=1}^N (\tau \Vert e^n \Vert + \sqrt{2 \tau \varepsilon _n})\) and \(B_N := \sum _{n=1}^N \tau (\varepsilon _n + \delta _n)\). Since \(A_N\) and \(B_N\) are increasing we find for all \(n \le N\):
This finally gives
and bounds the error terms. We now obtain from (23) that
which gives the assertion using the convexity of g, f and \(h^*\), the definition of the ergodic sequences \(X^N\) and \(Y^N\) and Jensen’s inequality. It remains to note that for a type-2 approximation the square root in \(A_N\) can be dropped and for a type-3 approximation \(B_N =0\), which gives the different \(A_{N,i}, B_{N,i}\). □
We can immediately deduce the following corollary.
Corollary 1
If\(i \in \{1,2,3\}\), \(\alpha > 0\)and
then
Proof
Under the assumptions of the corollary, if \(\alpha > 1/2\), the sequences \(\{\Vert e^n\Vert \}\), \(\{\varepsilon _n\}\) and \(\{\delta _n\}\) are summable and the error term on the right hand side of Eq. (19) is bounded, hence we obtain a convergence rate of O(1/N). If \(\alpha = 1/2\), all errors behave like O(1/n) (note the square root on \(\varepsilon _n\) for \(i \in \{1,3\}\)), hence \(A_{N,i} = B_{N,i} = O(\ln (N))\), which gives the second assertion. If \(0< \alpha < 1/2\), then by Lemma 5 we obtain \(A_{N,i}^2 = B_{N,i} = O(N^{1-2 \alpha })\), which gives the third assertion. □
Before we establish a convergence result from Theorem 1, respectively Corollary 1, let us comment on this result. In many useful situations it can be quite weak. Exact versions of such primal–dual algorithms [15, 18] guarantee inequality (19) for all \((x,y) \in {\mathcal {X}}\times {\mathcal {Y}}\), rather than for just a saddle point \((x^\star ,y^\star )\). This allows (under some additional assumptions) to both state a rate for the primal and/or dual energy as well as the primal–dual gap and, for infinite dimensional \({\mathcal {X}}\) and \({\mathcal {Y}}\), that the cluster points of the ergodic averages \((X^N,Y^N)\) are saddle points and hence a solution to our initial problem. Theorem 1, however, due to the necessary bound on the error terms, establishes the desired inequality only for a saddle point \((x^\star ,y^\star )\). It only implies a rate in a more degenerate distance, namely a Bregman distance [12, 52]. This is standard and easily seen rewriting the left hand side of (19), adding \(\langle Kx^\star ,y^\star \rangle - \langle x^\star , K^*y^\star \rangle\),
Using
we obtain that (26) is the sum of two Bregman distances,
between the (ergodic) iterates \((X^N,Y^N)\) and the saddle point \((x^\star ,y^\star )\). Hence, Corollary 1 states the rate with respect to this distance.
As shown in, e.g., [13], a vanishing Bregman distance, e.g.,
for some \((x,y) \in {\mathcal {X}}\times {\mathcal {Y}}\), in general does not imply that \(x = x^\star\) or \(y = y^\star\), neither does it imply that the pair (x, y) is even a saddle point. As a matter of fact, without any further assumptions on f, g and \(h^*\), the set of zeros of a Bregman distance can be arbitrarily large and the left-hand side of the inequality in Corollary 1 could vanish even though we have not found a solution to our problem.
On the other hand, it is easy to show that (27) yields that (x, y) is a saddle-point whenever \(f+g\) and \(h^*\) are strictly convex (that is, \(f+g\) strictly convex and h\(C^1\) in the interior of \({{\mathrm {dom}}} h\), with \(\partial h\) empty elsewhere [57, Thm. 26.3]). In that case obviously, (27) yields \((x,y)=(x^\star ,y^\star )\). Other situations might be tricky. One of the worst cases is a simple matrix game (cf. [17]),
where \(A \in {\mathbb {R}}^{k \times l}\) and \(\varDelta _l,\varDelta _k\) denote the unit simplices in \({\mathbb {R}}^l\) respectively \({\mathbb {R}}^k\). Quite obviously, here we have \(f = 0\), \(g = \delta _{\varDelta _l}\) and \(h^* = \delta _{\varDelta _k}\), such that we have to compute the Bregman distances with respect to a characteristic function, which can only be zero or infinity. Hence, every feasible point causes the Bregman distance to vanish such that a rate in this distance is of no use. However, there is a simple workaround in such cases, whenever the primal (or even the dual) variable are restricted to some bounded set D, such that f and/or g have bounded domain. Note that this is a standard assumption also arising in similar works on the topic (e.g. [48]). As can be seen from the proof, one needs a bound on \(\Vert x^n - x^\star \Vert\) in order to control the errors. In this case one can estimate \(\Vert x^n - x^\star \Vert \le {{\mathrm {diam}}}(D)\), and following the line of the proof [cf. inequality (23)] we obtain for all \((x,y) \in {\mathcal {X}}\times {\mathcal {Y}}\) that
Eventually, this again allows deducing a rate for the primal–dual gap (e.g., along the lines in [17]).
Remark 2
Even in bad cases there might exist situations where a rate in a Bregman distance is useful. For instance, the basis pursuit problem aims primarily at finding the support of the solution, rather than its quantitative values (which are then recovered easily). As shown in [13] a Bregman distance with respect to the 1-norm can only vanish if the support of both given arguments agrees. Hence, given a vanishing left-hand side in Corollary 1, we might not have found a saddle point, however, an element with the same support such that our problem is solved.
As we have lined out, a rate in a Bregman distance can be difficult to interpret, and it depends on the particular situation whether it is useful or not. However, we can at least show the convergence of the iterates in case \({\mathcal {X}}\) and \({\mathcal {Y}}\) have finite dimension.
Theorem 2
Let\({\mathcal {X}}\)and\({\mathcal {Y}}\)be finite dimensional and let the sequences\((x^n,y^n)\)and\((X^N,Y^N)\)be defined by Theorem1. If the partial sums\(A_{N,i}\)and\(B_{N,i}\)in Theorem 1converge, there exists a saddlepoint\((x^*,y^*) \in {\mathcal {X}}\times {\mathcal {Y}}\)such that\(x^n \rightarrow x^*\)and\(y^n \rightarrow y^*\).
Proof
Since by assumption \(A_{N,i}\) and \(B_{N,i}\) are summable, plugging \((x^\star ,y^\star )\) into inequality (23) and using (25) establishes the boundedness of the sequence \((x^n,y^n)\) for all \(n \in {\mathbb {N}}\). Hence there exists a subsequence \((x^{n_k},y^{n_k})\) (strongly) converging to a cluster point \((x^*,y^*)\). Using \((x,y) = (x^\star ,x^\star )\) in (23) and the boundedness of the error terms established in (25) we also find that \(\Vert x^{n-1} - x^n \Vert \rightarrow 0\) and \(\Vert y^{n-1} - y^n \Vert \rightarrow 0\) (note that this is precisely the reason for the introduction of \(\beta\) and the strict inequality in \(\tau L_f + \tau \sigma L^2 + \tau \beta L < 1\)). As a consequence we also have \(\Vert x^{n_k-1} - x^{n_k} \Vert \rightarrow 0\) and
i.e. also \(x^{n_k-1} \rightarrow x^*\). Let now T denote the primal update of the exact algorithm (11), i.e. \({\hat{x}}^{n+1} = T({\hat{x}}^n)\), and \(T_{\varepsilon _n}\) denote the primal update of the inexact Algorithm 12, i.e. \(x^{n+1} = T_{\varepsilon _n}(x^n)\). Then, due to the continuity of T, we obtain
We apply the same argumentation to \(y^n\), which together implies that \((x^*,y^*)\) is a fixed point of the (exact) iteration 11 and hence a saddle point of our original problem (8). We now use \((x,y) = (x^*,y^*)\) in inequality (22) and sum from \(n = n_k, \dots , N-1\) (leaving out negative terms on the right hand side) to obtain for \(N > n_k\)
It remains to notice that since \(\Vert e_n\Vert \rightarrow 0, \varepsilon _n \rightarrow 0, \delta _n \rightarrow 0\) and the above observations, the right hand side tends to zero for \(k \rightarrow \infty\), which implies that also \(x^N \rightarrow x^*\) and \(y^N \rightarrow y^*\) for \(N \rightarrow \infty\). □
3.2 The convex case: a stronger version
If we restrict ourselves to type-2 approximations, we can state a stronger version for the reduced problem with \(f=0\):
again assuming it has at least one saddle point \((x^\star ,y^\star )\). We consider the algorithm
which is the inexact analog of the basic exact primal–dual algorithm presented in [15]. Simply speaking, the main difference to the previous section is that, choosing a type-2 approximation and \(f = 0\), there are no errors occurring in the input of the proximal operators, such that we do not need a bound on \(\Vert x-x^n\Vert\), which allows us to obtain a rate for the objective for all \((x,y) \in {\mathcal {X}}\times {\mathcal {Y}}\) instead of only for a saddle point \((x^\star ,y^\star )\) (cf. Theorem 1). Following their line of proof, we can state the following result:
Theorem 3
Let\(L = \Vert K\Vert\)and\(\tau , \sigma > 0\)such that\(\tau \sigma L^2 < 1\), and let the sequence \((x^n,y^n)\)be definedby algorithm (29). Then for\(X^N := \left( \sum _{n=1}^N x^n \right) /N\), \(Y^N := \left( \sum _{n=1}^N y^n \right) /N\)and every\((x,y) \in {\mathcal {X}}\times {\mathcal {Y}}\)we have
Furthermore, if\(\varepsilon _n = O\left( n^{-\alpha }\right)\)and\(\delta _n = O\left( n^{-\alpha }\right)\), then
Proof
The proof can be done exactly along the lines of [15, Theorem 1] (or along the proof of Theorem 1), so we just give the main steps. Letting \(f = 0\) and choosing a type-2 approximation gives \(L_f = 0\) and lets us drop the term \(( \Vert e^{n+1}\Vert + \sqrt{(2 \varepsilon _{n+1})/\tau }) \Vert x - x^{n+1} \Vert\) in inequality (20). This is the essential difference, since we do not have to establish a bound on \(\Vert x - x^{n+1} \Vert\). Choosing \(\alpha = \sqrt{\sigma /\tau }\) in Young’s inequality and proceeding as before the gives
The definition of the ergodic sequences and Jensen’s inequality yield the assertion. □
As before we can state convergence of the iterates if the errors \(\{\varepsilon _n\}\) and \(\{\delta _n\}\) decay fast enough. The proof is the same as for Theorem 2.
Theorem 4
Let the sequences\((x^n,y^n)\)and\((X^N,Y^N)\)be defined by (29) respectively. If the sequences\(\{\varepsilon _n\}\)and\(\{\delta _n\}\)in Theorem3are summable, then every weak cluster point\((x^*,y^*)\)of\((X^N,Y^N)\)is a saddle point ofproblem (28). Moreover, if thedimension of\({\mathcal {X}}\)and\({\mathcal {Y}}\)is finite, there exists a saddle point\((x^*,y^*) \in {\mathcal {X}}\times {\mathcal {Y}}\)such that\(x^n \rightarrow x^*\)and\(y^n \rightarrow y^*\).
Proof
Since by assumption \(A_{N,i}\) and \(B_{N,i}\) are summable, plugging \((x^\star ,y^\star )\) into Eq. (31) establishes the boundedness of the sequence \(x^N\) for all \(N \in {\mathbb {N}}\), which also implies the boundedness of the ergodic average \(X^N\). Note that by the same argumentation as for \(x^N\), this also establish a global bound on \(y^N\) and \(Y^N\). Hence there exists a subsequence \((X^{N_k},Y^{N_k})\) weakly converging to a cluster point \((x^*, y^*)\). Then, since f, g and \(h^*\) are l.s.c. (thus also weakly l.s.c.), we deduce from Eq. (30) that, for every fixed \((x,y) \in {\mathcal {X}}\times {\mathcal {Y}}\),
Taking the supremum over (x, y) then implies that \((x^*,y^*)\) is a saddle point itself and establishes the first assertion. The rest of the proof follows analogously to the proof of Theorem 2. □
Remark 3
The main difference between Theorems 3 and 1 is that inequality (30) bounds the left hand side for all \(x,y \in {\mathcal {X}}\times {\mathcal {Y}}\) and not only for a saddle point \((x^\star ,y^\star )\). Following [15, Remark 2] and if \(\{\varepsilon _n\}, \{\delta _n\}\) are summable we can state the same \(O\left( 1/N\right)\) convergence of the primal energy, dual energy or the global primal–dual gap under the additional assumption that h has full domain, \(g^*\) has full domain or both have full domain. More precisely, if e.g. h has full domain, then it is classical that \(h^*\) is superlinear and that the supremum appearing in the conjugate is attained at some \({\tilde{y}}^N \in \partial h(KX^N)\), which is uniformly bounded in N due to (31) (if \((x,y) = (x^\star ,y^\star )\) then \((X^N,Y^N)\) is globally bounded), such that
Now evoking inequality (30) and proceeding exactly along (10) we can state that
with a constant C depending on \(x^0\), \(y^0\), h and \(\Vert K\Vert\). Analogously we can establish the convergence rates for the dual problem and also the global gap.
Remark 4
If \(h^*\) has bounded domain, e.g. if h is a norm, we can even state “mixed” rates for the primal energy if the errors are not summable. Since in this case \(\Vert y - y^0 \Vert \le {{\mathrm {diam}}}({{\mathrm {dom}}} h^*)\) we may take the supremum over all \(y \in {{\mathrm {dom}}} h^*\) and obtain
for \(\varepsilon _n,\delta _n \in O\left( n^{-\alpha }\right)\). The above result in particular holds for the aforementioned TV-\(L^1\) model, which we shall consider in the numerical section.
3.3 The strongly convex case: primal acceleration
We now turn our focus on possible accelerations of the scheme and consider again the full problem (8) with the additional assumption that g is \(\gamma\)-strongly convex, i.e. for any \(x \in {{\mathrm {dom}}} \partial g\)
As g is \(\gamma\)-strongly convex, its conjugate \(g^*\) has \(1/\gamma\)-Lipschitz gradient, so that acceleration is possible. We mention that we obtain the same result if f (or both g and f) are strongly convex, since it is possible to transfer the strong convexity from f to g and vice versa [18, Section 5]. Hence for simplicity we focus on the case where g is strongly convex. Choosing
in algorithm (12) we define an accelerated inexact primal–dual algorithm:
We prove the following theorem in “Proof of Theorem 5” of “Appendix”.
Theorem 5
Let\(L = \Vert K\Vert\)and\(\tau _n, \sigma _n, \theta _n\)such that
Let\((x^n,y^n) \in {\mathcal {X}}\times {\mathcal {Y}}\)be defined by the above algorithmfor\(i \in \{1,2,3\}\). Then for any saddle point\((x^\star , y^\star ) \in {\mathcal {X}}\times {\mathcal {Y}}\) of (8) and
we have that
and
where
As a direct consequence of Theorem 5 we can state convergence rates of the accelerated algorithm (33) in dependence on the errors \(\{\Vert e^n\Vert \}, \{\delta _n\}\) and \(\{\varepsilon _n\}\).
Corollary 2
Let\(\tau _0 = 1/(2L_f)\), \(\sigma _0 = L_f/L^2\)and\(\tau _n,\sigma _n\)and\(\theta _n\)be given by (33). Let\(\alpha > 0\), \(i \in \{1,2,3\}\)and
Then
Proof
In [15] it has been shown that with this choice we have \(\tau _n \sim 2/(n\gamma )\). Since the product \(\tau _n \sigma _n = \tau _0 \sigma _0 = 1/(2L^2)\) stays constant over the course of the iterations, this implies that \(\sigma _n \sim (n\gamma )/(4L^2)\), from which we directly deduce that \(T_N \sim (\gamma N^2)/(8L_f)\), hence \(T_N = O\left( N^2\right)\). Moreover we find that \(\sqrt{\tau _N/\sigma _N} \sim (\sqrt{8}L)/(\gamma N)\). Now let \(i = 1\) and \(\alpha \in (0,1)\), then we have
Now by assumption \(\Vert e^n\Vert = O\left( n^{-\alpha }\right)\) and \(\varepsilon _n = O\left( n^{-(1+2\alpha )}\right)\) which implies that \(A_{N,1} = O\left( N^{2-\alpha }\right)\). By analogous reasoning we find \(B_{N,1} = O\left( N^{2-2\alpha }\right)\). Summing up we obtain that
yielding the last row of the assertion. For \(\alpha = 1\) we see that \(\sqrt{\tau _N/\sigma _N} A_{N,1}\) is finite and \(B_{N,1} = O\left( \log (N)\right)\), for \(\alpha > 1\) also \(B_{N,1}\) is summable, implying the other two rates. It remains to notice that the cases \(i \in \{2,3\}\) can be obtained as special cases. □
3.4 The strongly convex case: dual acceleration
This section is devoted to the comparison of inexact primal–dual algorithms and inexact forward–backward splittings established in [5, 60, 61], considering the problem
with h having a \(1/\gamma\)-Lipschitz gradient and proximable g. The above mentioned works establish convergence rates for an inexact forward–backward splitting on this problem, where both the computation of the proximal operator with respect to g and the gradient of h might contain errors ([61] only considers errors in the proximum).
The corresponding primal–dual formulation of problem (34) reads
where now \(h^*\) is \(\gamma\)-strongly convex. Hence we know that the algorithm can be accelerated “à la” [15, 18] or as in the previous section, and we shall be able to essentially recover the results on inexact forward–backward splittings/inexact FISTA obtained by [5, 60, 61]. Choosing (note \(f = 0\) and \(e = 0\))
in algorithm (12) we define an accelerated inexact primal–dual algorithm:
We prove the following theorem in “Proof of Theorem 6” of "Appendix".
Theorem 6
Let\(L = \Vert K\Vert\)and\(\tau _n, \sigma _n, \theta _n\)such that
Let\((x^n,y^n) \in {\mathcal {X}}\times {\mathcal {Y}}\)be defined by the above algorithmfor\(i \in \{1,2,3\}\). Then for a saddle point \((x^\star , y^\star ) \in {\mathcal {X}}\times {\mathcal {Y}}\)and
we have that
and
where\(C_N = 1 - \sigma _N \tau _N \theta _N^2 L^2\)and
We can once more establish convergence rates depending on the decay of the errors.
Corollary 3
Let\(\tau _0,\sigma _0\)such that\(\tau _0 \sigma _0 L^2 = 1\). Let\(\alpha > 0\), \(i \in \{1,2,3\}\)and
Then
Proof
We refer to [15] for a proof that using the step sizes in Theorem 6, it can be shown that \(\sigma _n \sim 1/(n\gamma )\) and accordingly \(\tau _n \sim (n\gamma )/L^2\). This directly implies that \(T_N \sim (\gamma N^2)/(2L)\). Now for \(i=1\) and \(\alpha \in (0,1)\) we have that
Now by assumption \(\varepsilon _n = O\left( n^{-1-2\alpha }\right)\), which implies that \(\sqrt{(n-1)\varepsilon _n} = O\left( n^{-\alpha }\right)\) and we deduce \(A_{N,1} = O\left( N^{1-\alpha }\right)\) using Lemma 5. By an analogous argumentation
Now since \(\delta _n = O\left( n^{-2 \alpha }\right)\) we deduce that \(n \delta _n = O\left( n^{1-2\alpha }\right)\) and hence \(B_{N,1} = O\left( N^{2-2 \alpha }\right)\). Using \(T_N = O\left( N^{2}\right)\), we find
which gives the result for \(i=1\) and \(\alpha \in (0,1)\). Choosing \(\alpha > 1\) will yield convergence for \(A_{N,1}\) and \(B_{N,1}\), which implies the fastest overall convergence rate \(O\left( 1/N^2\right)\), the case \(\alpha = 1\) gives \(A_{N,1} = O\left( \log (N)\right)\) and \(B_{N,1} = O\left( \log (N)\right)\). It remains to note that the results for \(i=2,3\) can be obtained as special cases. □
Corollary 3 essentially recovers the results given in [5, 60, 61], though the comparison is not exactly straightforward. For an optimal \(O\left( N^{-2}\right)\) convergence in objective with a type-1 approximation the authors of [60] require \(\varepsilon _n = O\left( 1/n^{4+\kappa }\right)\) for any \(\kappa > 0\), for the error \(d_n\) in the gradient of \(h \circ K\) they need \(\Vert d_n\Vert = O\left( 1/n^{4+\kappa }\right)\). Since a type-2 approximation of the proximum is more demanding, the authors of [61] obtain a weaker dependence of the convergence on the error and only require \(\varepsilon _n = O\left( n^{3+\kappa }\right)\). Note that they only consider the case \(d_n = 0\). The work in [5] essentially refines both results under the same assumptions on the errors. Corollary 3 now states that for an optimal \(O\left( N^{-2}\right)\) convergence we require \(\varepsilon _n = O\left( n^{3 + \kappa }\right)\) in case of a type-1 approximation and \(\varepsilon _n = O\left( n^{2 + \kappa }\right)\) in case of an error of type-2, which seems to be one order less than the other results. We do not have a precise mathematical explanation at this point. The main difference appears to be the changing step sizes \(\tau _n, \sigma _n\) in the proximal operators for the inexact primal–dual algorithm in Theorem 6, which behave like n respectively 1/n, while the step sizes remain fixed for inexact forward–backward. The numerical section, however, indeed confirms the weaker dependence of the inexact primal–dual algorithm on the errors.
Remark 5
We want to highlight that, in the spirit of Sect. 3.2 it is as well possible to state a stronger version in case the approximations are of type-2 in both the primal and dual proximal point, which then bounds the “gap” for all \((x,y) \in {\mathcal {X}}\times {\mathcal {Y}}\) instead of for a saddle point \((x^\star ,y^\star )\) in Theorem 6 [cf. inequality (54)]:
Under some additional assumptions we can then again derive estimates on the primal energy for every fixed \(N \in {\mathbb {N}}\). If again h has full domain, the supremum appearing in the conjugate is attained at some \({\tilde{y}}^N\) and exactly along (10) we derive
In case the errors are summable we again obtain that also \({\tilde{y}}^N\) is globally bounded (cf. Remark 3) and we obtain convergence in \(O\left( 1/N^2\right)\). If the errors are not summable there is no similar argument to obtain the global boundedness of the \({\tilde{y}}^N\), however at least on a heuristic level one can expect a convergence to \(y^*\) at a similar rate as \(X^N\). This is indeed confirmed in the numerical section where we observe the \(O\left( N^{-2\alpha }\right)\) decay from Corollary 3 also for the primal objective for nonsummable errors.
3.5 The smooth case
We finally discuss an accelerated primal–dual algorithm if both g and \(h^*\) are \(\gamma\)- respectively \(\mu\)-strongly convex. In this setting the primal objective is both smooth and strongly convex, and first-order algorithms can be accelerated to linear convergence. We consider the algorithm
and prove the following result in “Proof of Theorem 7” of “Appendix”
Theorem 7
Let\(L = \Vert K\Vert\)and\(\tau ,\sigma , \theta\)such that
Let\((x^n,y^n) \in {\mathcal {X}}\times {\mathcal {Y}}\)be defined by algorithm (37) for\(i \in \{1,2,3\}\). Then for the uniquesaddle-point\((x^\star ,y^\star )\)and
we have
and
where
We can now state convergence rates, if the decay of the errors is also geometric.
Corollary 4
Let\(\alpha > 0\), \(i \in \{1,2,3\}\)and for\(0<q<1\)
Then
Proof
It is clear that we need to investigate the decay of the term
to obtain a convergence rate. In view of the specific form of \(A_{N,i}\) and \(B_{N,i}\) and the rate of \(\varepsilon _n\), \(\delta _n\) and \(\Vert e^n\Vert\) we consider
Now if \(q<\theta <1\), Eq. (39) implies that \(\theta ^N B_{N,i} = O\left( \theta ^N\right)\). For \(A_{N,i}\) we note the factor \(\theta ^{N}\) is squared, as opposed to the factor of \(B_{N,i}\), which implies that the decay of \(\Vert e^n\Vert\) and \(\sqrt{\varepsilon _n}\) can be less restrictive for \(A_{N,i}\) and explains the square root on the constant q for \(\Vert e^n\Vert\). We have to distinguish whether \(\sqrt{q} < \theta\) or \(\sqrt{q} > \theta\). In the former case we have by Eq. (39), now with \(\sqrt{q}\) instead of q, that
while in the latter we obtain \(\theta ^{2N} A_{N,i}^2 = O\left( q^N\right) = O\left( \theta ^N\right)\), which in sum gives \(C_{N,i} = O\left( \theta ^N\right)\). If \(\theta< q<1\), we have by analogous argumentation and (39) that \(\theta ^N B_{N,i} = O\left( q^N\right)\) and since \(\theta< q< \sqrt{q} < 1\) also \(\theta ^{2N} A_{N,i}^2 = O\left( q^N\right)\), which implies \(C_{N,i} = O\left( q^N\right)\). For the case \(\theta = q\) it is sufficient to notice that (39) is in \(O\left( N\theta ^N\right)\). □
It remains to give some explicit formulation of the step sizes that fulfill the conditions (38). Solving (38) for \(\tau ,\sigma\) and \(\theta\) gives [18]
4 Numerical experiments
There exists a large variety of interesting optimization problems, e.g. in imaging, that could be investigated in the context of inexact primal–dual algorithms, and even creating numerical examples for all the discussed notions of inexact proxima and different versions of algorithms clearly goes beyond the scope of this paper. Instead, we want to discuss two different questions on two classical imaging problems and leave further studies to the interested reader. The main goal of this section is to confirm numerically, that the convergence rates we proved above are “sharp” in some sense, meaning that if the errors are close to the upper bounds we obtain the convergence rates predicted by the theory. The second point we want to address is whether one can actually benefit from the theory and employ different splitting strategies in order to obtain nested algorithms, which can then only be solved in an inexact fashion (cf. [61]).
We investigate both questions using problems of the form
\(K_1 :X \rightarrow Y\), \(K_2 :X \rightarrow Z\), where we assume that the proximal operators of both g and \(h^*\) (or \(g^*\) and h by Moreau’s decomposition) have an exact closed form solution. The right hand side of (40) leads to a nested inexact primal–dual algorithm
Hence the dual proximal operator can be evaluated exactly (i.e. \(\delta _n = 0\)), while the inner subproblem has to be computed in an inner loop up to the necessary precision \(\varepsilon _n\). We choose the type-2 approximation since in this case, according to Proposition 1, the precision of the proximum can be assessed by means of the duality gap. In order to be able to evaluate the gap, we solve the \(1/\tau\)-strongly convex dual problem
using FISTA [8]. To distinguish between outer and inner problems for the splittings we denote the iteration number for the outer problem by n, while the iteration number of the inner problem is k. In order to achieve the necessary precision, we iterate the proximal problem until the primal–dual gap (cf. also Sect. 2) satisfies
where \(\varepsilon _n = O\left( 1/n^\alpha \right)\), respectively \(\varepsilon _n = O\left( \theta ^n\right)\) for the last experiment. We vary the parameter \(\alpha\) in order to show the effect of the error decay rate on the algorithm (cf. Remark 4). While for the asymptotic results we proved in the previous section the constant C of the rate does not matter, it indeed does in practice. In order to use Proposition 1 as a criterion, C should correspond to the “natural” size of the duality gap of (41). In order not to choose the constraint too restrictive but still active we follow [61] and choose \(C = {\mathcal {G}}(y^0-\tau B^*y^0,0)\), which is the duality gap of the first proximal subproblem for \(n = 1\) evaluated at \(z = 0\).
For the sake of brevity we discuss only three problems: we start with the non-differentiable TV-\(L^1\) model for deblurring, a problem which cannot be accelerated, and continue with “standard” TV-\(L^2\) deblurring, which also serves as a prototype for a whole list of applications with a general operator instead of a blurring kernel (cf. e.g. [30, 59]). Since in this case the objective is Lipschitz-differentiable, the convex conjugate is strongly convex, which allows to accelerate the algorithm. The third problem we investigate is a “smoothed” version of the TV-\(L^2\) model, which can be accelerated to linear convergence.
We investigate two different setups: as already announced above, we want to confirm the convergence rates predicted by the theory numerically. We hence require the inexact proximal problem (41) to be solved with an error close to the accuracy level \(\varepsilon _n\). To achieve this we, where it is necessary, deliberately solve the inner problem suboptimally, meaning that we use a cold start (random initialization of the algorithm) and reduced step sizes for the inner problem, ensuring that the inner problem is not solved “accidentially” at a higher precision. We shall see that this is indeed necessary for the slow TV-\(L^1\) problem. In a second setup we investigate whether the obtained error bounds can also be used as a criterion to ensure (optimal) convergence of the nested algorithm (41). As observed in e.g. [7] for the TV-\(L^2\) model and the FISTA algorithm, insufficient precision of the inner proximum can cause the algorithm to diverge. Instead of performing a fixed high number of inner iterations as a remedy, we solve the inner problem only up to precision \(\varepsilon _n\) in every step, which by the theory ensures that the algorithm converges with the same rate as the decay of the errors. We then use the best possible step sizes and a warm start strategy (initialization by the previous solution) in order to minimize the computational costs of the inner loop. It has already been observed in [61], that such strategy may significantly speeds up the process. We use a standard primal–dual reconstruction (PDHG) after \(10^5\) iterations as a numerical “ground truth” \(u^*\) to compute the optimal energy \(F^* = F(u^*)\).
Inexact primal–dual on the TV-\(L^1\) problem. a, b loglog plots of the relative objective error versus the outer iteration number for different decay rates \(\alpha\) of the errors. a Cold start, error close to the bound \(O\left( 1/n^\alpha \right)\), b warm start. c, d Number of inner iterations respectively sum of inner iterations versus number of outer iterations for different decay rates \(\alpha\). One can observe in (a) that the predicted rates in the worst case are attained, while in practice the problem also converges for very few inner iterations (b), (c) and (d)
4.1 Nondifferentiable deblurring with the TV-\(L^1\) model
In this section we study the numerical solution of the TV-\(L^1\) model
with a discrete blurring operator \(A :X \rightarrow X\). As already lined out in the introduction, there exist a variety of methods to solve the problem (e.g. [19, 28, 35, 62]), where most of them make use of the fact that the operator A can be written as a convolution. We use an easy strategy which does not rely on the structure of the operator and is hence also applicable to operators different from convolutions. Due to the nondifferentiability of both the data term and regularizer, a very simple approach is to dualize both terms (similar to ADMM [10] or ’PD-Split’ in [17]):
where \(P_\lambda\) denotes the convex set \(P_\lambda = \{ x \in X ~|~ \Vert x \Vert _\infty \le \lambda \}\). One can then employ a standard primal–dual method (PDHG [15]) which reads
Unfortunately one can observe that whenever there is no primal term in the formulation of the problem, the energy tends to oscillate and convergence can be quite slow (even though of course in \(O\left( 1/N\right)\), cf. Fig. 1b). As an alternative we propose to split the problem differently and operate on the following primal–dual formulation:
We employ algorithm (29), i.e. the non-accelerated basic inexact primal–dual algorithm (iPD) with type-2 errors and obtain
Note that the dual proximum in this case can be evaluated error-free.
As a numerical study we perform deblurring on MATLAB’s Lily image in [0, 1] with resolution \(256 \times 192\), which has been corrupted by a Gaussian blur of approximately 12 pixels full width at half maximum (where we assume a pixel size of 1) and 50 percent salt-and-pepper noise, i.e. 50 percent of the pixels have been randomly set to either 0 or 1. Furthermore, we performed power iterations to determine the operator norm of \((A, \nabla )\) as \(L \approx \sqrt{8}\) and set \(\sigma = \tau = 0.99/\sqrt{8}\) for (PDHG). For (iPD) L can be determined analytically as \(L = \Vert A \Vert = 1\), hence \(\tau = \sigma = 0.99\) for (iPD).
At first, we want to confirm the convergence rates predicted by the theory numerically. One can easily observe that the decay of the relative objective is almost exactly as predicted: with higher \(\alpha\) it approaches \(O\left( N^{-1}\right)\), in fact for summable errors it even seems a little better. In the second setup we investigate whether the obtained error bounds can also be used as a criterion to ensure (optimal) convergence of the nested algorithm (44), and results for varying parameter \(\alpha\) can be found in Fig. 1b. Interestingly for this problem, the error bounds from the theory are indeed too pessimistic or, vice versa, the TV-\(L^1\) problem is “easier” than expected. As can be observed in Fig. 1b, the convergence rate for all choices of \(\alpha\) tends towards \(O\left( 1/N\right)\), with slight advantages for higher \(\alpha\), while the number of required inner iterations k (Fig. 1c, d) to reach the necessary precision is remarkably low. In fact, performing just a single inner iteration in every step of the algorithm resulted in a \(O\left( 1/N\right)\) convergence rate (cf. also Fig. 1d). The required number of inner iterations even decreases over the course of the outer iterations which suggests that the dual variable of the inner problem “converges” as well. Note that this does not contradict the theoretical findings of this paper, but the contrary: while the first study clearly confirms that in the worst case the proved worst-case estimates are reached, the second implies that in practice one might as well perform by far better.
4.2 Differentiable deblurring with the TV-\(L^2\) model
The second problem we investigate is the TV-\(L^2\) model for image deblurring
Again, the easiest approach to solve (45) is to write down a primal–dual formulation
Since the above problem is not strongly convex in \(y_2\) it cannot be accelerated, so a basic primal–dual algorithm [15] (PDHG) for the solution reads
We remark that, due to the special relation between the Fourier transform and a convolution, the same problem can be solved without dualizing the data term, since the primal proximal operator admits a closed form solution [15]. The problem however stays non-strongly convex, and in order to keep this a general prototype for \(L^2\)-type problems, we do not use this formulation.
The inexact approach instead operates on a different primal–dual formulation given by
which is now 1-strongly convex in y and can be accelerated. Using the inexact primal–dual algorithm from Sect. 3.4 leads to
with \(\tau _n,\sigma _n,\theta _n\) as given in Theorem 6. We again perform deblurring on MATLAB’s Lily image in [0, 1] with resolution \(256 \times 192\), which has been corrupted by a Gaussian blur of approximately 12 pixels full width at half maximum (where we assume a pixel size of 1), and in this case Gaussian noise with standard deviation \(s = 0.01\) and zero mean. We allow errors of the size \(\varepsilon _n = C/n^{-2\alpha }\) for \(\alpha \in (0,1)\), which by Corollary 3 should result in a \(O\left( N^{-2\alpha }\right)\) rate respectively \(O\left( N^{-2}\right)\) for \(\alpha > 1\). The results can be found in Fig. 2. In contrast to the TV-\(L^1\) problem, in this experiment it was not necessary to employ a cold start strategy and reduced step sizes for the inner problem in order to obtain the worst case rates. Instead also for a warm start and best possible step sizes for the inner problem the bounds for the gap (42) were active for all choices of \(\alpha\). Figure 2 shows the error in relative objective for the ergodic sequence \(U^N\) (a) and the iterates \(u^n\) (b) for increasing \(\alpha\). It can be observed that the rate is almost exactly the one predicted, while the iterates themselves even decay a little faster than the ergodic sequence. The amount of inner iterations necessary to obtain the required precision of the proximum is unsurprisingly higher than in the non-accelerated case, though they stay reasonable for rather low outer iteration numbers.
Inexact primal–dual on the TV-\(L^2\) problem. a and b loglog plots of the relative objective error versus the outer iteration number for different precisions \(C/n^{-2\alpha }\) of the errors. a Ergodic sequence, b iterates. c and d number of inner iterations respectively sum of inner iterations versus number of outer iterations for different decay rates \(\alpha\). One can observe that the predicted rate of \(O\left( N^{-2\alpha }\right)\) is attained both for the ergodic sequence and the single iterates, exactly reflecting the influence of the errors/imprecision
4.3 Smooth deblurring with the TV-\(L^2\) model
The last problem we consider is a smoothed version of the TV-\(L^2\) model from the previous experiments:
for small \(\gamma\), with primal–dual formulation
Since the above problem is \(\gamma\)-strongly convex in u (note that it is also \(L_f = \gamma\)-Lipschitz differentiable in the primal variable), a possible accelerated primal–dual algorithm [18] (PDHGacc) for the solution reads
with \(\tau _n, \sigma _n,\theta _n\) given by Theorem 5 (see also [18]). We choose \(\tau _0 = 0.99 / L\), \(\sigma _0 = (1 - \tau _0 L_f) / \tau _0 L^2\) such that \(\tau _0 L_f + \tau _0 \sigma _0 L^2 = 1\) as required, with \(L = \Vert (A,\nabla ) \Vert \approx \sqrt{8}\) (see also the previous section). We remark that the primal term involving \(\gamma\) could also be handled implicitly, leading to a linear proximal step instead of the explicit evaluation of the gradient which, however, did not substantially affect the results. In the spirit of the previous experiments we employ a different splitting on this problem:
The benefit is that even for small \(\gamma\) this problem is \(\gamma\)-strongly convex in the primal and 1-strongly convex in the dual variable and hence can be accelerated to linear convergence, which provides a huge boost in performance. Note that the same is not possible in formulation (47), since the problem is not strongly convex in \(y_2\). We can handle the smooth primal term in (48) explicitly such that the associated inexact primal–dual algorithm (iPD) from Sect. 3.5 reads
with \(\tau ,\sigma ,\theta\) defined at the end of Sect. 3.5. In this case we have \(\gamma = L_f\), such that the formulas simplify to
We revisit the experimental setting from Sect. 4.3, such that \(L = \Vert A\Vert = 1\), \(\lambda = 0.01\) and choose \(\gamma = 1e-3\). With this size of \(\gamma\) the results were barely distinguishable from the results of the non-smoothed model from Sect. 4.2. This leads to \(\theta \approx 0.96\) for the constant of the linear convergence. Figure 3 shows the results for (PDHGacc) and (iPD) using an error decay rate of \(q = 0.9\), i.e. according to Corollary 4 we expect a linear convergence with constant \(\theta > q\), which is indeed the case. One can observe that already after 250 iterations (iPD) reaches a relative objective error of \(1{\mathrm {e}}{-}10\), while the accelerated PD version has barely reached \(1{\mathrm {e}}{-}2\). It should however be mentioned that also (PDHGacc) reaches the \(O\left( N^{-2}\right)\) rate soon after these 250 iterations. Figure 3c shows the price we pay for the inner loop, i.e. the number of inner iterations which is necessary over the course of the 250 outer iterations. As one expects for linear convergence, the number of inner iterations explodes for high outer iteration numbers, which substantially slows down the algorithm. However, the algorithm reaches an error of \(1{\mathrm {e}}{-}6\) in relative objective already after approximately 100 iterations, in which case the number of inner iterations is still remarkably low (around 10–20), which makes the approach viable in practice. This is in particular interesting for problems with a very costly operator A, where the tradeoff between outer and inner iterations is high.
Inexact primal–dual on the smoothed TV-\(L^2\) problem. a and b Loglog plots of the relative objective error respectively relative error in norm versus the outer iteration numbers for accelerated primal–dual (PDHGacc) and inexact primal–dual (iPD) for \(q = 0.9\), c loglog plot of the inner iteration number vs. outer iteration number for \(q = 0.9\). One can observe that the predicted convergence rate of \(O\left( \theta ^N\right)\) is exactly attained, while for lower outer iteration numbers the necessary amount of inner iterations stays reasonably low
5 Conclusion and outlook
In this paper we investigated the convergence of the class of primal–dual algorithms developed in [15, 18, 54] under the presence of errors occurring in the computation of the proximal points and/or gradients. Following [5, 60, 61] we studied several types of errors and showed that under a sufficiently fast decay of these errors we can establish the same convergence rates as for the error-free algorithms. More precisely we proved the (optimal) \(O\left( 1/N\right)\) convergence to a saddle-point in finite dimensions for the class of non-smooth problems considered in this paper, and proved a \(O\left( 1/N^2\right)\) or even linear \(O\left( \theta ^N\right)\) convergence rate for partly smooth respectively entirely smooth problems. We demonstrated both the performance and the practical use of the approach on the example of nested algorithms, which can be used to split the global objective more efficiently in many situations. A particular example is the nondifferentiable TV-\(L^1\) model which can be very easily solved by our approach. A few questions remain open for the future: A very practical one is whether one can use the idea of nested algorithms to (heuristically) speed up the convergence of real life problems which are not possible to accelerate, such as TV-type methods in medical imaging. As demonstrated in the numerical section, using an inexact primal–dual algorithm one can often “introduce” strong convexity by splitting the problem differently and hence obtain the possibility to accelerate. This can in particular be interesting for problems with operators of very different costs, where the trade-off between inner and outer iterations is high and hence a lot of inner iterations are still feasible. Following the same line, it would furthermore be interesting to combine the convergence results for inexact algorithms with stochastic approaches as done in [16], which are also designed to speed up the convergence for this particular situation, which could provide an additional boost. Another point to investigate is whether one can combine the inexact approach with linesearch and variable metric strategies similar to [9].
References
Alberti, G., Bouchitté, G., Dal Maso, G.: The calibration method for the Mumford–Shah functional and free-discontinuity problems. Calc. Var. Partial. Differ. Equ. 16(3), 299–333 (2003)
Alliney, S.: Digital filters as absolute norm regularizers. IEEE Trans. Signal Process. 40(6), 1548–1562 (1992)
Alliney, S.: Recursive median filters of increasing order: a variational approach. IEEE Trans. Signal Process. 44(6), 1346–1354 (1996)
Alliney, S.: A property of the minimum vectors of a regularizing functional defined by means of the absolute norm. IEEE Trans. Signal Process. 45(4), 913–917 (1997)
Aujol, J.-F., Dossal, C.: Stability of over-relaxations for the forward–backward algorithm, application to FISTA. SIAM J. Optim. 25(4), 2408–2433 (2015)
Barbero, Á., Sra, S.: Fast Newton-type methods for total variation regularization. In: Proceedings of the 28th International Conference on International Conference on Machine Learning, ICML’11, pp. 313–320, USA, 2011. Omnipress (2011)
Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18(11), 2419–2434 (2009)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2(1), 183–202 (2009)
Bonettini, S., Loris, I., Porta, F., Prato, M.: Variable metric inexact line-search-based methods for nonsmooth optimization. SIAM J. Optim. 26(2), 891–921 (2016)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3(1), 1–122 (2011)
Brancolini, A., Rossmanith, C., Wirth, B.: Optimal micropatterns in 2D transport networks and their relation to image inpainting. Arch. Ration. Mech. Anal. 228(1), 279–308 (2018)
Bregman, L.M.: The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 7(3), 200–217 (1967)
Brinkmann, E.-M., Burger, M., Rasch, J., Sutour, C.: Bias reduction in variational regularization. J. Math. Imaging Vis. 59(3), 534–566 (2017)
Cai, J.-F., Candès, E.J., Shen, Z.: A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 20(4), 1956–1982 (2010)
Chambolle, A., Pock, T.: A first-order primal–dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2011)
Chambolle, A., Ehrhardt, M.J., Richtarik, P., Schönlieb, C.-B.: Stochastic primal–dual hybrid gradient algorithm with arbitrary sampling and imaging applications. Working paper or preprint, June (2017)
Chambolle, A., Pock, T.: An introduction to continuous optimization for imaging. Acta Numer. 25, 161–319 (2016)
Chambolle, A., Pock, T.: On the ergodic convergence rates of a first-order primal–dual algorithm. Math. Program. 159(1–2), 253–287 (2016)
Chan, T.F., Esedoglu, S.: Aspects of total variation regularized l1 function approximation. SIAM J. Appl. Math. 65(5), 1817–1837 (2005)
Chaux, C., Pesquet, J.-C., Pustelnik, N.: Nested iterative algorithms for convex constrained image recovery problems. SIAM J. Imaging Sci. 2(2), 730–762 (2009)
Combettes, P.L.: Solving monotone inclusions via compositions of nonexpansive averaged operators. Optimization 53(5–6), 475–504 (2004)
Combettes, P.L., Pesquet, J.-C.: Proximal Splitting Methods in Signal Processing, pp. 185–212. Springer, New York (2011)
Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward–backward splitting. Multiscale Model. Simul. 4(4), 1168–1200 (2005)
Cominetti, R.: Coupling the proximal point algorithm with approximation methods. J. Optim. Theory Appl. 95(3), 581–600 (1997)
Condat, L.: A primal–dual splitting method for convex optimization involving Lipschitzian, proximable and linear composite terms. J. Optim. Theory Appl. 158(2), 460–479 (2013)
d’Aspremont, A.: Smooth optimization with approximate gradient. SIAM J. Optim. 19(3), 1171–1183 (2008)
Devolder, O., Glineur, F., Nesterov, Y.: First-order methods of smooth convex optimization with inexact oracle. Math. Program. 146(1), 37–75 (2014)
Dong, Y., Hintermüller, M., Neri, M.: An efficient primal–dual method for l1-tv image restoration. SIAM J. Imaging Sci. 2(4), 1168–1189 (2009)
Dykstra, R.L.: An algorithm for restricted least squares regression. J. Am. Stat. Assoc. 78(384), 837–842 (1983)
Ehrhardt, M., Betcke, M.: Multicontrast MRI reconstruction with structure-guided total variation. SIAM J. Imaging Sci. 9(3), 1084–1106 (2016)
Esser, E.: Applications of Lagrangian-based alternating direction methods and connections to split Bregman. CAM Rep. 9 (2009)
Esser, E., Zhang, X., Chan, T.F.: A general framework for a class of first order primal–dual algorithms for convex optimization in imaging science. SIAM J. Imaging Sci. 3(4), 1015–1046 (2010)
Fadili, J.M., Peyre, G.: Total variation projection with first order schemes. IEEE Trans. Image Process. 20(3), 657–669 (2011)
Friedlander, M.P., Schmidt, M.: Hybrid deterministic-stochastic methods for data fitting. SIAM J. Sci. Comput. 34(3), A1380–A1405 (2012)
Haoying, F., Ng, M.K., Nikolova, M., Barlow, J.L.: Efficient minimization methods of mixed l2–l1 and l1–l1 norms for image restoration. SIAM J. Sci. Comput. 27(6), 1881–1902 (2006)
Güler, O.: New proximal point algorithms for convex minimization. SIAM J. Optim. 2(4), 649–664 (1992)
He, B., Yuan, X.: An accelerated inexact proximal point algorithm for convex minimization. J. Optim. Theory Appl. 154(2), 536–548 (2012)
Kärkkäinen, T., Kunisch, K., Majava, K.: Denoising of smooth images using l1-fitting. Computing 74(4), 353–376 (2005)
Lemaire, B.: About the convergence of the proximal method. In: Oettli, W., Pallaschke, D. (eds.) Advances in Optimization, pp. 39–51. Springer, Berlin (1992)
Lin, H., Mairal, J., Harchaoui, Z.: Catalyst acceleration for first-order convex optimization: from theory to practice. J. Mach. Learn. Res. 18(1), 7854–7907 (2017)
Lin, H., Mairal, J., Harchaoui, Z.: A universal catalyst for first-order optimization. In: Advances in Neural Information Processing Systems, pp. 3384–3392 (2015)
Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16(6), 964–979 (1979)
Luo, Z.-Q., Tseng, P.: Error bounds and convergence analysis of feasible descent methods: a general approach. Ann. Oper. Res. 46(1), 157–178 (1993)
Ma, S., Goldfarb, D., Chen, L.: Fixed point and Bregman iterative methods for matrix rank minimization. Math. Program. 128(1), 321–353 (2011)
Martinet, B.: Brève communication régularisation d’inéquations variationnelles par approximations successives. ESAIM Math. Model. Numer. Anal. 4(3), 154–158 (1970)
Moreau, J.J.: Proximité et dualité dans un espace hilbertien. Bull. Soc. Math. Fr. 93, 273–299 (1965)
Nedić, A., Bertsekas, D.: Convergence Rate of Incremental Subgradient Algorithms, pp. 223–264. Springer, Boston (2001)
Nemirovski, A.S.: Prox-method with rate of convergence \(O(1/t)\) for variational inequalities with Lipschitz continuous monotone operators and smooth convex–concave saddle point problems. SIAM J. Optim. 15(1), 229–251 (2004). (electronic)
Nesterov, Y.: Introductory Lectures on Convex Optimization: A Basic Course, 1st edn. Springer, Berlin (2014)
Nikolova, M.: Minimizers of cost-functions involving nonsmooth data-fidelity terms. Application to the processing of outliers. SIAM J. Numer. Anal. 40(3), 965–994 (2002)
Nikolova, M.: A variational approach to remove outliers and impulse noise. J. Math. Imaging Vis. 20(1), 99–120 (2004)
Osher, S., Burger, M., Goldfarb, D., Jinjun, X., Yin, W.: An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 4(2), 460–489 (2005)
Patriksson, M.: Cost approximation: a unified framework of descent algorithms for nonlinear programs. SIAM J. Optim. 8, 561–582 (1997)
Pock, T., Cremers, D., Bischof, H., Chambolle, A.: An algorithm for minimizing the Mumford–Shah functional. In: 2009 IEEE 12th International Conference on Computer Vision, pp. 1133–1140, Sept (2009)
Rockafellar, R.T.: Augmented Lagrangians and applications of the proximal point algorithm in convex programming. Math. Oper. Res. 1(2), 97–116 (1976)
Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 14(5), 877–898 (1976)
Rockafellar, R.T.: Convex Analysis. Princeton Landmarks in Mathematics and Physics. Princeton University Press, Princeton (1970)
Salzo, S., Villa, S.: Inexact and accelerated proximal point algorithms. J. Convex Anal. 19(4), 1167–1192 (2012)
Sawatzky, A., Brune, C., Koesters, T., Wübbeling, F., Burger, M.: EM-TV methods for inverse problems with Poisson noise. In: Burger, M., Mennucci, A.C., Osher, S., Rumpf, M. (eds.) Level Set and PDE Based Reconstruction Methods in Imaging. Lecture Notes in Mathematics, vol. 2090, pp. 1–70. Springer, Berlin (2013)
Schmidt, M., Roux, N.L., Bach, F.R.: Convergence rates of inexact proximal-gradient methods for convex optimization. In: Shawe-Taylor, J., Zemel, R.S., Bartlett, P.L., Pereira, F., Weinberger, K.Q. (eds.) Advances in Neural Information Processing Systems, vol. 24, pp. 1458–1466. Curran Associates Inc, Red Hook (2011)
Villa, S., Salzo, S., Baldassarre, L., Verri, A.: Accelerated and inexact forward–backward algorithms. SIAM J. Optim. 23(3), 1607–1633 (2013)
Wu, C., Zhang, J., Duan, Y., Tai, X.-C.: Augmented Lagrangian method for total variation based image restoration and segmentation over triangulated surfaces. J. Sci. Comput. 50(1), 145–166 (2012)
Zalinescu, C.: Convex Analysis in General Vector Spaces. World Scientific, Singapore (2002)
Zaslavski, A.J.: Convergence of a proximal point method in the presence of computational errors in Hilbert spaces. SIAM J. Optim. 20(5), 2413–2421 (2010)
Acknowledgements
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In the “Appendix” we provide two technical results and the proofs for all the accelerated versions of the algorithm, since they basically follow the same line as the basic proof.
1.1 Two technical lemmas
The following lemma is taken from [60].
Lemma 4
[60] Assume that the sequence\(\{ u_N \}\)is nonnegative and satisfies the recursion
for all\(N \ge 1\), where\(\{S_N \}\)is an increasing sequence,\(S_0 \ge u_0^2\), and\(\lambda _n \ge 0\)for all\(n \ge 0\). Then for all\(N \ge 1\)
Lemma 5
For\(\alpha > -1\)let\(s_N := \sum _{n=1}^N n^\alpha\). Then
Proof
Let \(\alpha \in (-1,0)\) and \(n \ge 1\). Then by the monotonicity of \(x \mapsto x^\alpha\) we have for all \(n-1 \le x \le n\) that \(x^\alpha \ge n^\alpha\). Integrating both sides of the inequality from \(n-1\) to n and summing from \(n=1,\dots ,N\) we obtain
We proceed analogously for \(n \le x \le n+1\) to obtain
By computing both integrals we hence find
which implies \(s_N = O(N^{1+ \alpha })\). The proof for \(\alpha > 0\) follows the same idea. Now for every \(n-1 \le x \le n\) we have that \((n-1)^\alpha \le x^\alpha \le n^\alpha\). Integrating the inequality from \(n-1\) to n and summing from \(n=1, \dots , N\) we obtain
Furthermore \(s_{N-1} = s_N - N^\alpha\), so for every \(N\ge 1\)
from which we deduce that \(s_N = O(N^{1+ \alpha })\). □
1.2 Type-0 approximations
It is interesting to consider the notion of a type-0 approximation (cf. Definition 2) as well, since it seems to be the most intuitive one (the authors of [5] mention it but do not explicitly handle the situation). The problem however is that neither the inexact proximal point needs to be feasible, nor do we have an equivalent definition of a type-0 approximation in terms of an (\(\varepsilon\)-) subdifferential. For simplicity we briefly outline a possible strategy on the reduced problem
and consider the algorithm
where again \((\check{x},\check{y})\) are the erroneus proximal points and \(({\tilde{x}},{\tilde{y}})\) and \(({\bar{x}},{\bar{y}})\) are the previous points. A possible way to deal with the type-0 approximation is to “transfer” the error in the primal proximum to the dual proximum. Note that, following the same line as before, by interchanging the order of iterates (starting with the primal variable x) we can now perform the overrelaxation in the dual variable instead of the primal in order to get a bound on y.
So let \({\hat{x}}\) be the true primal proximum and choose \({\tilde{x}}= \check{x}\). Then by the definition of the type-0 approximation there exists \(s \in {\mathcal {X}}\) with \(\Vert s\Vert \le \sqrt{2 \tau \varepsilon }\) such that \(\check{x}= {\hat{x}}+ s\), which implies that
Hence with \(d = Ks\) we can rewrite (49) as
Now
with \(\kappa := (\tau \varepsilon \Vert K\Vert ^2)/\sigma\). This reveals that a type-0 approximation of \({\hat{x}}\) with precision \(\varepsilon\) can essentially be interpreted as a type-3 approximation \(\check{y}\) of \({\hat{y}}\), which in sum with the type-2 approximation gives an overall approximation of type 1 for \(\check{y}\), now however with “mixed” precision \(\kappa\) and \(\delta\). Using the choices
we formally obtain the following algorithm:
This situation can then be treated similarly to the above analysis (cf. Theorem 2) and is summarized in Corollary 5. The main difference here is now that we get an estimate on the true proximum \({\hat{x}}^{n+1}\) while computing \(x^{n+1}\) in practice.
Corollary 5
Let\(L = \Vert K\Vert\)and choose\(\beta > 0\)and\(\tau ,\sigma > 0\)suchthat\(\sigma \tau L^2 + \sigma \beta L< 1\)and let\(({\hat{x}}^n, \check{y}^n)\)be defined by Algorithm (51). Then for\({\hat{X}}^N := \left( \sum _{n=1}^N {\hat{x}}^n \right) /N\)and\(Y^N := \left( \sum _{n=1}^N y^n \right) /N\)we have for any saddle point\((x^\star , y^\star ) \in {\mathcal {X}}\times {\mathcal {Y}}\)that
with\(A_N = \sum _{n=1}^N \sqrt{2 \sigma \kappa _n}\)and\(B_N = \sum _{n=1}^N \sigma \delta _n\).
Proof
We can easily verify the assertion by dropping f and simply interchanging the roles of x and y (and thus \(\tau\) and \(\sigma\)) in Theorem 1. □
As for Theorem 1 we can now state a rate for \(({\hat{X}}^N,Y^N)\) if the partial sums \(A_N\) and\(\sqrt{B_N}\) are in \(o(\sqrt{N})\). Since the result still relies on the unknown true proxima \({\hat{x}}^n\), it then remains to note that for \(\check{X}^N := (\sum _{i=1}^N \check{x}^n) / N\) we have
which implies strong convergence of \(\check{X}^N\) to \({\hat{X}}^N\) with the same rate.
Hence we can essentially handle the situation of a type-0 approximation by the same means as before. The major difference is still that none of the \(\check{x}^n\) need to be feasible, which could impose problems in practice. Since type-0 approximations are the weakest among the introduced notions, they should technically impose the least restrictive error criteria. It however is an open question how to check \(\Vert {\hat{x}}- \check{x}\Vert \le \sqrt{2\tau \varepsilon }\) effectively. It is easy to see that the duality gap bounds this quantity, in which situation Proposition 1 “unfortunately” states that \(\check{x}\) is already a stronger type-2 approximation. Hence it remains to find a different criterion for the precision of a type-0 approximation to make this approach feasible in practice.
1.3 Proof of Theorem 5
Proof
Using Lemma 3, we proceed exactly as in the proof of Theorem 1 (now only including the \(\gamma\)-strong convexity of g as well as \(\tau = \tau _n, \sigma = \sigma _n\) and introducing \(\theta _n\)), to arrive at the basic inequality
where we let \(\varDelta _n(x,y) := \Vert x - x^n \Vert ^2/(2\tau _n) + \Vert y - y^n \Vert ^2/(2\sigma _n)\) for the sake of clarity. The goal of the proof is, again, to manipulate this inequality such that we obtain a recursion where most of the terms cancel when summing the inequality. In order to get a useful recursion in the first line it is clear that we require
such that we obtain the estimate
For a useful recursion for the second line we expand
and compute [cf. Eq. (21) with now \(\alpha = \sigma _n \theta _n L\)]
where we used (52) such that \(\sigma _n \theta _n = \sigma _{n-1}\). We note that since \(\tau _n L_f + \tau _n \sigma _n L^2 \le 1\) we furthermore have
Putting everything together and rearranging we arrive at (note that the terms \(\Vert y^{n+1} - y^n \Vert ^2 /(2 \sigma _n)\) cancel and \(\sigma _{n+1}/\sigma _n = 1/\theta _{n+1}\))
We multiply the inequality by \(\sigma _n / \sigma _0\) to reveal the recursion and sum from \(n=0, \dots , N-1\):
Now, as above, we use that
which gives
This equation can now be use as before to bound all terms on the left hand side. Again for a saddle point \((x^\star ,y^\star ) \in {\mathcal {X}}\times {\mathcal {Y}}\) the sum is nonnegative, hence we obtain the inequality:
For the sake of readability let us denote
Then as before with Lemma 4 we find,
Since \(A_N\) and \(B_N\) are increasing we have for all \(n \le N\)
Now evoking Eq. (53) we obtain
The convexity of \((\xi , \zeta ) \mapsto {\mathcal {L}}(\xi , y^\star ) - {\mathcal {L}}(x^\star , \zeta )\) and the definition of the ergodic averages yields the assertion (cf. the proof of Theorem 6). The estimate on \(\Vert x^\star - x^N \Vert ^2\) follows analogously. It remains to note that for a type-2 approximation the square root in \(A_N\) can be dropped and for a type-3 approximation \(B_N =0\), which gives the different \(A_{N,i}, B_{N,i}\). □
1.4 Proof of Theorem 6
Proof
We proceed exactly as in the proof of Theorem 5 with interchanged roles of \(x,y,\tau _n\) and \(\sigma _n\) to arrive at the basic inequality
where we again let \(\varDelta _n(x,y) := \Vert x - x^n \Vert ^2/(2\tau _n) + \Vert y - y^n \Vert ^2/(2\sigma _n)\). In order to get a useful recursion for the first two lines it is clear that we need to require
such that the second line becomes
For a useful recursion for the third line we expand
and compute with Young’s inequality [cf. Eq. (21) with \(\alpha = 1 / (\tau _n \theta _n L)\)]
In order to obtain a recursion for the first term on the right hand side we note that
in the fourth line. Putting everything together and rearranging we arrive at
Requiring that \(\tau _n \sigma _n \theta _n^2 L^2 \le 1\) we can discard the related term and multiply the inequality by \(\tau _n / \tau _0\) to reveal the recursion:
We now sum the above inequality from \(n=0, \dots , N-1\):
Now, as above, we use that
which gives the first intermediate result:
This equation can now be use as before to bound all terms on the left hand side and hence gives the necessary bound on \(\Vert x - x^N\Vert\) appearing in the error term. For a saddle point \((x^\star ,y^\star ) \in {\mathcal {X}}\times {\mathcal {Y}}\) the sum on the left hand side is nonnegative and:
Hence, again with Lemma 4,
where we denote \(A_N = \sum _{n=1}^N \sqrt{2 \tau _{n-1} \varepsilon _n}\) and \(B_N = \sum _{n=1}^N \tau _{n-1} (\varepsilon _n + \delta _n)\).
Since \(A_N\) and \(B_N\) are increasing we have for all \(n \le N\)
Then we find [again by Eq. (54)]
Using the convexity of \((\xi , \zeta ) \mapsto {\mathcal {L}}(\xi , y^\star ) - {\mathcal {L}}(x^\star , \zeta )\) and Jensen’s inequality as well as the definition of the ergodic averages \((X^N,Y^N)\) yields the first assertion. The estimate on \(\Vert x^\star - x^N\Vert ^2\) and \(\Vert y^\star - y^N \Vert ^2\) then follows analogously from inequality (54). It remains to note that for a type-2 approximation the square root in \(A_N\) can be dropped and for a type-3 approximation \(B_N =0\), which gives the different \(A_{N,i}, B_{N,i}\). □
1.5 Proof of Theorem 7
Proof
We again start with the general descent rule in Lemma 3:
Now we expand and apply Young’s inequality
which gives
Ensuring that \(1+\gamma \tau = 1+\mu \sigma = 1/\theta\) and \((1-\tau L_f)/\tau \ge \sigma \theta ^2 L^2\) we derive
We now multiply by \(\theta ^{-n}\) and sum from \(n = 0, \dots , N-1\):
which again by Young’s inequality implies
For a saddle point \((x^\star ,y^\star )\), the sum on the left hand side is positive, hence we obtain
Evoking Lemma 4 and denoting
we obtain
By monotonicity we have the same bound for all \(n \le N\):
We now again use inequality (55) to obtain a bound for the sum:
Eventually we let
to deduce the assertion by convexity and Jensen’s inequality. By the same argumentation as above we can also use inequality (55) to obtain the convergence of the iterates:
□
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rasch, J., Chambolle, A. Inexact first-order primal–dual algorithms. Comput Optim Appl 76, 381–430 (2020). https://doi.org/10.1007/s10589-020-00186-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-020-00186-y