Novel test section for homogeneous nucleation studies in a pulse expansion wave tube: experimental verification and gasdynamic 2D numerical model

Abstract

A novel design of a pulse expansion wave tube (PEWT) for the study of homogeneous nucleation in mixtures of vapours and gases is presented. The main difference with the previous design consists in a test section with flat walls, which avoid that optical windows and pressure transducers do affect the flow field locally. Additionally, the test section length is reduced by a factor two. The performance of the wave tube is investigated both experimentally and numerically. The thermal insulation of the piezoelectric pressure sensor is proved to be beneficial for accurate measurements. The smallest thickness possible of the diaphragm, initially separating the high- and low-pressure sections of the PEWT, is also shown to be crucial. The flow phenomena are simulated with a 2D numerical model. It is shown to correctly predict the gasdynamic features of the PEWT and the effects of the diaphragm opening process. Nucleation rates for water in helium are determined as a function of supersaturation for two different pressure conditions, 1 MPa and 0.1 MPa, at a temperature of 240 K. The good agreement with results from previous experiments shows that the geometrical mismatch of optical windows and pressure transducers in the original wave tube did not affect the nucleation rates significantly and that both the original and the new wave tube produce reliable measurement data.

Graphic abstract

1 Introduction

Condensation has been actively studied for several decades, but, nevertheless, it remains an active research area with critical implications for many industrial and environmental applications. $\text {CO}_2$ emission and industrial pollution are just two fields in which a profound knowledge of such phase transition plays a crucial role. Effects of condensation are also present in chemical reactors, aircraft, turbines and engine applications (Wyslouzil and Wölk 2016). The oil and gas industry is another important sector interested in condensation phenomena mainly for performance prediction and design improvement of natural gas impurity separators (Kalikmanov et al. 2007), or even for the development of integrated devices to couple the removal of contaminants with the gas liquefaction process. Hence, a full comprehension of this phase transition and more accurate models would lead to beneficial consequences in a wide range of scientific and technological fields. A large variety of measurement techniques was applied in the past (Wyslouzil and Wölk 2016), not only to verify and validate the theory, but also to elaborate corrections for the existing condensation models. The pulse expansion wave tube (PEWT) is one of the expansion based devices. Initially designed to cope with the lack of experimental data related to homogeneous condensation of hydrocarbons, it has been largely and effectively used with water as condensing vapour at a later time. In this paper, we discuss a new PEWT measurement section with flat inner walls to allow a perfectly flush installation of optical windows and pressure sensors. As the rest of the tube remains cylindrical, a square-shape cross-over section is installed as well. Results of first wave experiments with the new gasdynamic facility will be presented including nucleation rate data for water–helium mixtures. Two-dimensional numerical simulations will be compared with experimental wave tube observations.

2 PEWT working principle

Water condensation is considered homogeneous when the vapour-to-liquid transition takes place in the absence of macroscopic surfaces or foreign particles. In heterogeneous condensation, such surfaces or particles act as starting points for the phase transition and a vapour pressure$p_{\mathrm{v}}$ slightly above the saturated vapour pressure$p_{\mathrm{s}}$ is sufficient to trigger the vapour-to-liquid transition. If such surfaces or impurity particles are absent, a gas–vapour mixture can easily become oversaturated ($p_{\mathrm{v}}>p_{\mathrm{s}}$). Nevertheless, due to the stochastic nature of the gas and the vapour molecules, clusters are formed. While the smallest ones dissolve, the largest clusters reach the so-called critical size$n^*$ if adequate supersaturated conditions are met. After that, the critical clusters become stable droplets and grow by collision with the free vapour molecules. The process of critical cluster formation is known as homogeneous nucleation, and it is followed by droplet growth. The number of critical clusters formed per units of volume and time is defined as the nucleation rate J (${\mathrm{m}}^{-3}{\mathrm{s}}^{-1}$). The critical size$n^*$ stands for the number of molecules constituting a critical cluster. A key parameter in nucleation research is the supersaturation S. Its general definition is given in Appendix. Two specific cases are very useful. For an ideal vapour–gas mixture, S becomes:

$$\begin{aligned} S=\frac{p_{\mathrm{v}}(T)}{p_{\mathrm{s}}(p,T)}. \end{aligned}$$

(1)

For a dilute non-ideal vapour–gas mixture, S can be written as:

$$\begin{aligned} S = \frac{y(T)}{y_{\mathrm{eq}}(p,T)} \end{aligned}$$

(2)

with y the molar vapour fraction.

As shown by experimental evidence and confirmed by the Classical Nucleation Theory (Vehkamäki 2006), the nucleation rate has a strong dependency on supersaturation ratio and temperature J(S, T). Exploiting such dependency, the nucleation pulse method (Allard and Kassner 1965) is capable of separating in time the processes of nucleation and droplet growth, enabling an accurate determination of the nucleation rate. The working principle is sketched in Fig. 1.

Fig. 1

Nucleation pulse method: schematic of pressure (p), temperature (T), supersaturation (S) and nucleation rate (J) in time

The initially undersaturated ($S < 1$) vapour–gas mixture is first adiabatically expanded. The corresponding temperature drop causes the saturation level to increase far above unity ($S>> 1$). This is due to the fact that, in the case of homogeneous condensation, the partial vapour pressure $p_{\mathrm{v}}$ decreases with temperature much less than the saturated vapour pressure $p_{\mathrm{s}}$. This state is maintained for a short time, the nucleation pulse, indicated in Fig. 1 with $\varDelta t_p$. The supersaturation level for the pulse is chosen such that an appreciable amount of critical nuclei is formed. At the end of the pulse, the mixture is slightly recompressed, inhibiting the nucleation process to continue, but still keeping a supersaturated level ($S > 1$) for a relatively long period of time, in which the droplets can grow. In order to narrow the size distribution of the clusters, $\varDelta t_p$ must be kept much shorter than the growth time interval. In this way, nucleation and droplet growth are effectively decoupled and the clusters can be assumed to be approximatively monodispersed (Peters 1983).

The first application of the nucleation pulse method dates back to 1965, when Allard and Kassner designed a piston expansion chamber to expand and recompress the test mixture, with a pulse duration of 10 ms. In order to limit vapour depletion, polydispersity and the effect of heat released by the nucleating clusters, it is of fundamental importance to have a sufficiently short pulse duration. Therefore, Wagner and Strey (1981) later improved the design of Allard and Kassner, with a two-piston cloud chamber and a 1 ms nucleation pulse. Peters (1983) was the first to implement the nucleation pulse principle in a gasdynamic facility: the wave tube. The Peters’ tube consists of two sections, the high pressure (driver section—HPS) and the low pressure (driven section—LPS), separated by a diaphragm. A schematic of the Peters’ tube and its corresponding wave diagram is sketched in Fig. 2. After the diaphragm rupture, waves are generated: an expansion fan (E) moving towards the end wall of the HPS and a shock wave (S) in the opposite direction. The idea of Peters was to partially reflect the shock into the HPS, by reducing the LPS cross-sectional area, at position C just a few centimetres behind the diaphragm position D. Doing that, the test mixture at the observation point O is first subjected to an adiabatic expansion E. After a short time interval ($\varDelta t_p$), the shock reflected at the cross-section reduction C reaches the observation point O as a weak shock wave $S_1$. In this way, the mixture undergoes a slight, but sudden, recompression and the nucleation pulse nP ends. The mixture remains at constant pressure, coinciding with the droplet growth stage. The downside of such setup was that E and $S_1$, reflected at the HPS end wall as rE and $\text {rS}_{1c}$ respectively, interact with the cross-section reduction C, generating a second slight expansion $\text {rE}_a$ and a second weak shock r$S_1$. This may lead to a second nucleation stage (sP) at the observation point O, simultaneously with the droplet growth process.

Fig. 2

Schematic $x-t$ wave diagram for the Peters’ tube and the PEWT of Looijmans et al. The waves related to the expansion E are drawn in black ( ), while the waves due to the shock S are represented in green ( ). The resulting pressure–time profiles at the observation point O are sketched in the red box ) on the left side of the wave diagram for both the Peter’ tube ( ) and the PEWT ( ). Below the wave diagram, the geometrical configuration of both tubes is also represented. The observation point O is situated at few mm from the end-wall of the HPS. The length of the HPS for the PEWT of Looijmans et al. is about 125 cm, the distance between D and $W_1$ is about 18 cm, and the widening (W) length is 15 cm. The diameter of the tube is 36 mm, while the widening diameter is 41 mm. For comparison purposes, the Peters’ tube is represented here with the same dimensions of the PEWT, but with a LPS diameter of 31 mm starting from C

The PEWT is a modified version of the Peters’ wave tube by Looijmans et al. (1993). The difference with the Peters’ tube consisted in the elimination of the second nucleation pulse by replacing the cross-sectional area reduction C with a local widening W. In Fig. 2 the PEWT configuration and the corresponding wave diagram are also sketched for comparison with the Peters’ tube. The modifications of Looijmans et al. implied a different way for the shock S to be reflected towards the observation point: at the enlargement $W_1$ as a weak expansion fan $S_1$, at the restriction $W_2$ as a weak shock $S_2$. The outcome was an isolated well-defined nucleation pulse $n_{\mathrm{PEWT}}$. The end-wall reflected waves interact with the cross-sectional area change also in the PEWT case, with the difference that, beside a small recompression $\text {rE}_a$, also a second weak expansion $\text {rE}_{W2}$ at $W_2$ is generated because of rE. Nevertheless, no appreciable disturbance on the droplet growth process is present in this case, since the interference consists of a small positive pressure ripple b after the nucleation pulse. In this way, the resulting PEWT pressure–time profile at the observation point approximates the one prescribed by the nucleation pulse method (Fig. 1) and the decoupling of the nucleation and the droplet growth processes is achieved. Once the droplets grow to a detectable size, they can be measured by optical means (details in Sect. 3).

3 Experimental methodology

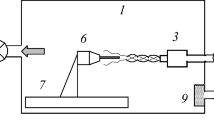
The PEWT overall facility consists of 3 main parts (see Fig. 3): the Mixture Preparation device MPD (Hrubý 1999), the pulse expansion wave tube PEWT, and the Optical Setup. The experimental procedure starts with the PEWT evacuation. The HPS and the LPS are kept separated by means of a polyester (PET) diaphragm placed at the section D. Six possible diaphragm thicknesses ranging from 30 to 250 $\upmu {\mathrm{m}}$ are available. The chosen diaphragm thickness depends on the initial pressure difference between the two sides of the PEWT. The vapour–gas mixture is prepared in the MPD sketched Fig. 3. The pure gas inside the gas bottle $G_1$ flows inside the MPD, where it is split into two molar flow rates $Q_1$ and $Q_2$. The latter remains dry, while $Q_1$ is saturated with the pure water contained inside two saturators $S_1$ and $S_2$. Before exiting the MPD, the fully saturated flow $Q'$ ($Q'=Q_1+Q_{\mathrm{H2O}}$) and the dry one $Q_2$ are mixed together. In this way, the mixture composition can be easily controlled by regulating $Q_1$ and $Q_2$ and by keeping constant the temperature $T_{\mathrm{mpd}}$ and the pressure $p_{\mathrm{mpd}}$ inside the MPD at known values. After that, the HPS is filled with the prepared mixture, while the LPS is pressurized with the pure gas contained into the gas bottle $G_2$. Once the desired pressure levels are reached in both PEWT sides, the so-called flushing procedure starts. In this stage, the pressure level inside the HPS is kept constant and saturation of the tube walls takes place. Such procedure ends when no more net PEWT wall adsorption is present. Doing that, the mixture composition at the test section can be easily derived by calculating $y=y(Q_1,Q_2,T_{\mathrm{mpd}},p_{\mathrm{mpd}})$.

Fig. 3

Layout of the PEWT facility: the test section, the observation point O and the flush mounted optical windows ($A_1$, $A_2$) and pressure transducers (PR, PE) are the modified parts of the new HPS ( )

Once the wall saturation condition is reached, the driver section is isolated from the MPD and the wave experiment can be run. It starts with the fast opening of the diaphragm separating the HPS from the LPS, which leads to the wave pattern described in Sect. 2 and sketched in Fig. 2. The concept and design of the diaphragm section D was first introduced by Looijmans and van Dongen (1997). The present configuration is shown in Fig. 4. The fast opening is triggered by an electrical pulse (200–300 A in 60–80 ms) through a Kanthal ribbon $(150 \times 1.75 \times 0.2\,{\mathrm{mm}})$ positioned in a circumferential groove placed at the section D. The PET diaphragm remains in contact with the 0.2 mm side of the ribbon for the entire experimental procedure, being the LPS clamped to the HPS. The electrical pulse, increasing the Kanthal temperature to about 800 K, weakens the diaphragm, enabling the pressure difference to open it in a short time frame ($\sim$180 $\upmu {\mathrm{s}}$, see Sect. 5.1). It should be noted that the ribbon does not go all the way around the entire diaphragm circumference. At the top, a few millimetres are not wired. There the PET material will remain intact, thus creating a hinge for the diaphragm to rotate around.

Fig. 4

3D view of the PEWT diaphragm section (D)

After the diaphragm rupture, the absolute pressure at the observation point O is shown in Fig. 5. The pressure is measured by means of two transducers, one piezoresistive (PR, Kistler 4073A50) and one piezoelectric (PE, Kistler 603B), placed at the test section wall. Details on the combined PR-PE measuring methodology can be found in Holten et al. (2005). By using such measuring methodology, the uncertainty on the nucleation pulse pressure is less than 0.2%. Although the PE transducer is specifically suited for measuring rapid pressure variations, as in the case of the nucleation pulse technique, the sensor used suffers from a lack of thermal compensation when a temperature gradient is applied to it. Therefore, a coating layer (Dow Corning 732 black sealant) of half a millimetre has been applied to the PE sensing surface in order to insulate it from heat flow from the wall to the expanding gas. In this work, the effect of such coating on the performances of the PE transducer is object of analysis: wave experiments with dry helium have been performed to investigate the contribution of the PE transducer with and without coating layer. The temperature profile is derived from the pressure signal assuming adiabatic conditions (Looijmans and van Dongen 1997). The initial temperature of the mixture is assumed equal to the test section wall temperature, which is measured via two independent thermocouples (Tempcontrol PT-8316) with an accuracy of ± 0.03 K (Fransen et al. 2015).

Fig. 5

Test 1 (see Table 2): PE absolute pressure–time signal

Once the experimental pressure and temperature signals in time are known, it is possible to derive the pulse duration$\varDelta t_p$. The corresponding supersaturation S follows from Eq. 2, with y the initial molar vapour fraction from the MPD and $y_{\mathrm{eq}}=y_{\mathrm{eq}}(p,T)$ the equilibrium molar vapour fraction calculated at the pulse conditions.

Knowing that the experimental form of the nucleation rate is given by the equation

$$\begin{aligned} J=\frac{n_{\mathrm{d}}}{\varDelta t_p}, \end{aligned}$$

(3)

J can be determined if the droplet number density $n_{\mathrm{d}}$ is measured, since $\varDelta t_p$ is already known (Fig. 5).

In order to measure $n_{\mathrm{d}}$, the test section is equipped with the Optical Setup sketched in Fig. 3, based on the light scattering and the light beam attenuation. It consists of

• a linearly polarized 100:1 laser (Lasos Lasnova GLK 3220 T01—wavelength $\lambda =$ 532 nm) probing the test section through the optical window $A_1$ (see Fig. 3),

• a photomultiplier PM (Hamamatsu 1P28A) recording the $90^{\circ }$ scattered irradiance $I_{\mathrm{sca}}(t)$ at the optical window $A_2$ (see Fig. 3),

• a photodiode PD (Telefunken BPW 34) measuring the transmitted laser light I(t) leaving the test section from the optical window $A_3$ (see Fig. 3).

$A_1$, $A_2$ and $A_3$ are three BK7 glass windows. The laser beam interacts with the nearly monodispersed cloud of droplets generated during the nucleation pulse. As the droplets start to grow to an optically detectable size, $I_{\mathrm{sca}}(t)$ and I(t) are detected by the PM and the PD, respectively. During the growth process, $I_{\mathrm{sca}}(t)$ shows a characteristic peaks and valleys pattern of increasing intensity in time (see Fig. 6a). Such pattern is strictly related to the droplet radius r(t) for a fixed refractive indexm of the medium and wavelength$\lambda$ of the laser light. Simultaneously, as r grows in time, I(t) is attenuated proportionally to size and number density of the droplets. In Fig. 6b, a typical attenuated transmitted light $I(t)/I_0$ is shown, with $I_0$ the initial undisturbed value of I(t).

Fig. 6

Test 1 (Table 2): PM $90^{\circ }$ scattered light–time signal (a) and PD relative transmitted light–time signal (b)

The PM output is compared with the theoretical $90^{\circ }$ Mie scattered intensity $I_{{\mathrm{sca}},{\mathrm{th}}}(\alpha )$, which is function of the non-dimensional droplet radius $\alpha = 2\pi r/\lambda$ at a fixed $\lambda$ and m. The $I_{{\mathrm{sca}},{\mathrm{th}}}(\alpha )$ pattern for $\lambda = 532$ nm and $m=1.33$ is shown in Fig. 7a. The almost one-to-one correspondence between experimental (Fig. 6a) and theoretical (Fig. 7a) scatter qualitatively proves that the assumption of nearly monodispersed droplets is well posed for the new PEWT¹ (Wagner and Strey 1981; Wagner 1985; Strey et al. 1994). Therefore, by comparing $I_{\mathrm{sca}}(t)$ in Fig. 6a with the theoretical $I_{{\mathrm{sca}},{\mathrm{th}}}(\alpha )$ in Fig. 7a, the non-dimensional droplet growth rate $\alpha ^2(t)$ in Fig. 7b can be obtained.

Fig. 7

Test 1 (Table 2): a theoretical $90^{\circ }$ Mie scattered intensity as a function of the non-dimensional droplet radius$\alpha = 2\pi r/\lambda$ for a refractive index m = 1.33 and a wavelength $\lambda$ = 532 nm; b non-dimensional droplet growth rate curve $\alpha ^2(t)$ obtained by comparing the experimental $I_{\mathrm{sca}}(t)$ in Fig. 6a with the theoretical $I_{{\mathrm{sca}},{\mathrm{th}}}(\alpha )$ in Fig. 7a

The $n_{\mathrm{d}}$ determination follows from the Lambert–Beer law

$$\begin{aligned} \frac{I}{I_0} = e^{-n_{\mathrm{d}}\pi r^2 Q_{\mathrm{ext}}\cdot l}, \end{aligned}$$

(4)

with the $\alpha$-dependent terms expressed in function of time by means of the calculated $\alpha ^2(t)$. The parameter l stands for the extinction length, and it is taken equal to the inner diameter of the test section ($\sim 32$ mm for the new HPS, see Figs. 9 and 10). The extinction efficiency term $Q_{\mathrm{ext}}(\alpha )$ can be found in the literature and is a function of the non-dimensional droplet radius$\alpha$ for fixed refractive indices m and wavelengths $\lambda$. The reader is referred to Fransen et al. (2014) for a detailed description of this procedure.

3.1 The newly designed HPS

A wide range of experimental conditions, accurate measurements of nucleation rates, droplet growth rates and supersaturation have made the PEWT technique a powerful tool for homogeneous condensation studies. Nucleation rate data have been determined for a wide range of pressures (0.1–4 MPa) and temperatures (220–260 K) and for different binary and ternary vapour–gas mixtures. The nucleation rates have a strong dependence on temperature, pressure and measured optical signals. In the previous version of the PEWT, a slight geometrical mismatch between the cylindrical test section wall and the flat surfaces of $A_1$, $A_3$, PE and PR was present. Such geometrical mismatch might generate local flow disturbances. Therefore, the PEWT high pressure section was redesigned, which also allowed for improved optical alignment.

The new design features a rectangular cross-sectional shape (see Figs. 8 and 9). In this way, flat optical windows and measuring surface of the pressure transducers (PE, PR) have been mounted flush to the HPS wall, without any geometrical mismatch. In order to minimize the intersections between the main laser beam and the secondary reflections, the two optical windows $A_1$ and $A_3$ (see also Fig. 3) have been positioned with the axis mutually parallel and ±2 mm distant from the centre of the HPS. Doing that, the laser beam can enter the test section through $A_1$ with an inclination of 7$^{\circ }$ (see Fig. 9), which prevents any possible optical interference.

Fig. 8

New HPS: sectioned 3D view of the PEWT (all dimensions in mm). The diaphragm section and the widening (internal diameter $\varPhi _w$ = 41 mm) are indicated with the letters D and W, respectively. Details on the observation plane (section A-A) are represented in Fig. 9. The rest of the PEWT is characterized by an internal diameter $\varPhi$ of 36 mm, specified at the plane B-B

Fig. 9

New rectangular test section side view (dimensions in mm). The flush mounted optical windows ($A_1$ and $A_3$) and pressure transducers (PE and PR) can be noted. The laser beam ( ) enters the test section from the left side (window $A_1$) and exits it from the right side (window $A_3$). The secondary reflections are also represented ( )

The PEWT high-pressure section (HPS) has been also shortened from a length of 1.25 m to about 0.66 m, which speeds up the filling procedure (see Sect. 3) and significantly reduces the gas consumption.

Three main parts have been assembled to compose the new HPS: the 0.375 m long test section HPS1 (see Fig. 8), which has a square cross area with rounded off corners (r = 2.67 mm) and a width of 32 mm (see Fig. 9); the outlet and vacuum valve section HPS3 (see Fig. 8) with a circular cross area shape as the LPS, diameter of 36 mm (B-B) and length of 0.167 m; the transition part HPS2, having a length of 0.116 m and designed to facilitate a gradual cross-section transition from the circular shape of HPS3 to the square shape of HPS1 (see Fig. 8).

The test section distance from the HPS end-wall has been increased to 10 mm as shown in Fig. 8. In this way, the thermal boundary layer developing from the walls towards the core of the tube does not represent a possible source of disturbance for the last part of the droplet growth process (Luijten 1998; Luo 2004).

The PEWT performances have been examined with two different experimental campaigns. During the first one, the setup has been tested at 4 different pressure ranges with pure helium, analysing

• the added value brought to the measurement quality by the PE with respect to the PR,

• the effect of the coating on the PE measuring surface, applied to protect it from exchange of heat with the gas during the wave experiment,

• the influence of the diaphragm thickness on the pressure profile at the observation point O.

The above mentioned tests have been exploited as reference to design and verify the 2D numerical model described in Sect. 4.

The second experimental campaign has been executed with the purpose of testing the reliability of the modified PEWT setup by performing homogeneous water nucleation and droplet growth experiments. The tested conditions have been 1 MPa and 240 K as nucleation pressure and temperature, respectively. Helium has been chosen as carrier gas, and the results have been compared to the data obtained by Fransen et al. (2015) in the same experimental conditions by means of the previous PEWT version. Details on both test campaigns will be given in Sect. 5.2.

4 2D numerical model

4.1 Computational domain, numerical settings and grid independence study

The PEWT has been modelled in a two-dimensional manner. Details on the geometrical domain are sketched in Fig. 10. The 3D area variation of the PEWT has been modelled in a 2D manner by changing the widening vertical dimension from 41 to 46.7 mm. This choice allowed to keep the same relative cross-sectional area ratio when passing from the 3D geometry to the 2D model.

Fig. 10

PEWT 2D geometrical domain (all dimensions in mm). The diaphragm opening direction is indicated with the blue arrow ( )

The numerical model is based on non-stationary 2D Euler equations:

$$\begin{aligned} \frac{\partial \mathbf{U} }{\partial t} + \frac{\partial \mathbf{F} }{\partial x} + \frac{\partial \mathbf{G} }{\partial y} = 0, \end{aligned}$$

(5)

with U the vector of unknowns and F and G convective fluxes in x and y direction, respectively:

$$\begin{aligned} \mathbf{U} = \left( \begin{array}{c} \rho \\ \rho u \\ \rho v \\ \rho E \end{array}\right) ; \quad \mathbf{F} = \left( \begin{array}{c} \rho u \\ \rho u^2+p \\ \rho uv \\ (\rho E+p)u \end{array}\right) ; \quad \mathbf{G} = \left( \begin{array}{c} \rho v \\ \rho uv \\ \rho u^2+p \\ (\rho E+p)v \end{array}\right) ; \end{aligned}$$

(6)

Equation 6 has been solved in a coupled manner by means of the density-based explicit solution method present in the commercial software ANSYS$^{{\textregistered }}$ Fluent$^{{\textregistered }}$. The discretization of the convective fluxes F and G has been performed by means of the advection upstream splitting method (AUSM). For the spacial discretization, the least squares cell-based gradient has been employed, while the third order monotone upstream-centred scheme (MUSCL) has been exploited for the flow discretization. The time integration of the governing equations has been performed by means of a second-order implicit formulation. Helium has been chosen as a simulated gas, and it is assumed to behave as a calorically prefect gas.

In order to minimize the numerical errors due to the grid choice, different mesh sizes have been tested for accuracy and computational time ($\varDelta x$ and $\varDelta y$ both decreasing from 6 mm to 1 mm). Instantaneous opening of the diaphragm has been considered at this stage. A mesh size with $\varDelta x$ = 4 mm and $\varDelta y$ = 2 mm has been selected.

Preliminary results of the 2D numerical model are reported in Fig. 11, where the pressure (Fig. 11a) and the temperature (Fig. 11b) profiles in time are compared with the reference experimental results of test 2c$^*$ (Table 1). It should be noticed that the shown numerical results are taken at the observation plane wall $O_{\text {wall}}$ at this stage. Such a choice has been possible only after the verification of a perfect overlapping for the results taken at $O_{\text {wall}}$ and at the observation point O, when the diaphragm opening process is modelled as instantaneous. The simulated pressure and temperature time profiles shown in Fig. 11 differ from the experimental results in three regions: at the first expansion E, at the pulse $n_{\mathrm{PEWT}}$ and at the ripple b. Such differences are due to two main reasons. In the first place, the diaphragm opening process has been simulated as instantaneous at this stage, while such assumption is far from the reality. For this reason, the finite diaphragm opening process will be implemented in the 2D numerical model as explained in the next Sect. 4.2. Secondly, the presence of the contact discontinuity, clearly visible on the wave diagram in Fig. 11b, might have interacted with the reflected expansion rE in the proximity of $W_1$, contributing with a small overshoot to the ripple b. The latter hypothesis has been verified by simulating the exact same conditions, but without widening in the geometrical domain. A small recompression has been observed, caused by the interaction between the expansion E and the only contact discontinuity cd.

Fig. 11

Pressure (a) and temperature (b) map on the $x-t$ wave diagram. The latter is derived from the 2D numerical tool described in this work, with the represented data taken at the tube wall line in time. The simulated initial conditions are the same as for the test 2c$^*$ (Table 1) and the diaphragm opening process is modelled as instantaneous. On the left side of both figures, the pressure (a) and temperature (b) profiles in time ( ) are compared with the reference experimental results ( ) of test 2c$^*$ (Table 1). The simulated profiles are taken at the observation plane wall ($O_w$), where the transducers are placed ( )

4.2 Modelling of the diaphragm opening process

The 3D opening process of the diaphragm, described in Sect. 3, has been simplified for the present 2D model in the following way. It has been assumed that the diaphragm slides away as indicated by the blue arrow sketched in Fig. 10, so that the open area becomes (Arun et al. 2013)

$$\begin{aligned} \dfrac{A}{A_{\text {diaph}}} = \left( \dfrac{d}{d_{\text {diaph}}}\right) ^2 = \left( \frac{t}{t_{\text {diaph}}} \right) ^{1/a}, \end{aligned}$$

(7)

with $t_{\text {diaph}}$ the total opening time of the diaphragm, A the open area of the diaphragm (d the open diaphragm dimension in the 2D model) at the time t and $A_{\text {diaph}}$ the total area of the diaphragm ($d_{\text {diaph}}$ the total diaphragm dimension). The duration of each opening time step has been chosen to be 8 ms. The modelled diaphragm has been divided in 18 segments. The initial boundary condition for the whole diaphragm geometry has been set to be a wall, which perfectly separates the HPS from the LPS side. After that, at each consecutive opening time step, the boundary condition for each piece of the diaphragm has been dynamically changed from wall to interior type, starting from the bottom piece of the diaphragm. In this way, with such discrete piece-wise step function, it has been possible to closely approximate the continuous 3D aperture process of the diaphragm.

A parametric study has been performed on a and $t_{\text {diaph}}$. In first instance, the exponent a has been varied from 1/2 to 1/8 (see Fig. 12), with $t_{\text {diaph}}$ kept fixed at 136 $\upmu {\mathrm{s}}$ (Looijmans et al. 1993). The best agreement with the reference pressure–time profile of test 2c$^*$ (Table 1) has been found for a=3/8. Then, $t_{\text {diaph}}$ has been varied from 136 to 232 $\upmu {\mathrm{s}}$ (see Fig. 13), with a=3/8. A perfect agreement with the experimental reference (test 2c$^*$, Table 1) has been found for $t_{\text {diaph}}$=184 $\upmu {\mathrm{s}}$. The 2D numerical model has been also verified with all the other experimental conditions reported in Table 1 as reference and a perfect agreement has been obtained at any condition.

Fig. 12

Parametric study performed with total opening time $t_{\text {diaph}}$=136 $\upmu {\mathrm{s}}$ and varying the exponent a: $a=1/2$ ( ), $a=3/8$ ( ) and $a=1/8$ ( ). In a the different diaphragm opening function A(t) are shown. In b the reference pressure–time profile (test 2c$^*$ , Table 1) is compared with the simulated p(t) in O. The pressure profile with instantaneous diaphragm opening ( ) is also shown

Fig. 13

Parametric study performed with total opening time $a=3/8$ and varying the $t_{\text {diaph}}$: $t_{\text {diaph}} =$ 136 $\upmu {\mathrm{s}}$ ( ), $t_{\text {diaph}} =$ 184 $\upmu {\mathrm{s}}$ ( ) $t_{\text {diaph}} =$ 232 $\upmu {\mathrm{s}}$ ( ). In a the different diaphragm opening function A(t) are shown. In b the reference p(t) profile (test 2c$^*$ , Table 1) is compared with the simulated ones taken in O. The p(t) profile with instantaneous diaphragm opening ( ) is also shown

5 Results and discussion

5.1 Numerical results

Now that the complete 2D numerical model has been validated, it is possible to analyse the pressure–time profile at the bottom wall of the observation plane (A-A, see Fig. 8), namely $O_{\text {wall}}$ (see Fig. 10), where the pressure transducers are placed. The comparison between the numerical and the reference experimental p(t) and T(t) profiles shows a perfect agreement, when the diaphragm opening process is included in the 2D numerical model (see Fig. 14). It should be also underlined that by modelling the diaphragm opening process the overshoot at the ripple b (see Fig. 11) disappears. This is due to the different position of the contact discontinuity when the reflected expansion wave rE reaches $W_1$ (see Fig. 14b).

Fig. 14

Pressure (a) and temperature (b) map on the $x-t$ wave diagram. The latter is derived from the 2D numerical tool described in this work, with the represented data taken at the tube wall line in time. The simulated initial conditions are the same as for the test 2c$^*$ (Table 1) and the diaphragm opening process is modelled with $a=3/8$ and $t_{\mathrm{diaph}}$ = 184 $\upmu {\mathrm{s}}$. On the left side of both figures, the pressure (a) and temperature (b) profiles in time ( ) are compared with the reference p(t) and T(t) ( ) of test 2c$^*$ (Table 1). The simulated profiles are taken at the observation plane wall $O_w$, where the transducers are placed ( )

Fig. 15

Pressure–time profile at O ( ) and $O_{\text {wall}}$ ( ) with emphasis on the pulse ($t = 1.24\,\div \,1.44$ ms) and the plateau ($t = 1.5\,\div \,2.2$ ms). The experimental pressure measured at $O_{\text {wall}}$ for the test condition 2c$^*$ (Table 1) is used as reference ( )

As evident in Fig. 15, the experimental oscillations present at the plateau ($t = 1.5\,\div \,2.2$ ms) and at the bottom of the pulse ($t = 1.24\,\div \,1.44$ ms) are also appreciable in the numerical results at $O_{\text {wall}}$. On the contrary, such oscillations appears to be damped at the observation point O for the numerical results. An additional proof of such pressure oscillations is reported in Fig. 16. The position and the shape of the $S_2$ front wave are highlighted by narrowing the colour-map around the pressure value in O at the beginning of the pulse recompression $t_A = 1.44$ ms (see Fig. 16b). The evolution in time of such wave is shown by considering the time step before ($t_A\,-\,0.004$ ms, see Fig. 16a) and after ($t_A\,+\,0.004$ ms, see Fig. 16c) $t_A$. Typical oscillation overshoot B and undershoot C of the pressure at $O_w$ are shown in Fig. 16d, e, respectively. In the latter case, the colour-map has been narrowed around the pressure value in O at the time $t_B$ and $t_C$. In this way, it has been possible to make evident that the pressure level in $O_w$ alternatively increases and decreases with respect to the pressure level in O. It has been verified that the s-shape of the waves, visible in Fig. 16a–c, appears to be absent for instantaneous opening of the diaphragm. In the latter case, the waves are parallel to the HPS end-wall and the pressure oscillations are completely absent at $O_w$ (see the wave diagrams in Fig. 11a, b). The ripples of the pressure at $O_w$ in time are more evident in Fig. 17. It can be concluded that the pressure oscillations are caused by the 2D diaphragm opening process. Moreover, such disturbances appear to be sensed by the transducers, placed at the bottom wall of the observation plane A-A, while they are strongly muffled at the observation point O. Therefore, it has been proven that no disturbances are expected to affect the flow field at the observation point O.

Fig. 16

Simulated pressure colour-map of the HPS for different times: a$t_A\,-\,0.004$ ms, b$t_A = 1.44$ ms, c$t_A\,+\,0.004$ ms, d$t_B = 1.564$ ms, e$t_C = 1.604$ ms. A, B and C are highlighted in Fig. 15

Fig. 17

Pressure map of Fig. 14a in 3D form. The z-direction is representative of the pressure level

5.2 Experimental results

The first experimental campaign with the modified version of the PEWT has been performed by running four sets of dry wave experiments with pure dry helium. Each set of tests corresponds to a different pulse pressure level $p_{\text {pulse}}$. Four levels have been checked. The pressure and temperature values, averaged over the pulse duration $\varDelta t_p$, are presented in Table 1. The superscript * indicates the tests performed applying the coating layer to the PE transducer (Sect. 3).

Table 1 Wave experiments overview

The typical temperature profiles with and without coating for PR and PE are shown in Fig. 18. One observes a small but significant difference between the two nucleation temperatures derived from both pressure transducer signals, when the PE is uncoated. It should be noted that a temperature error of 1 K corresponds with a shift in nucleation rate by more than a factor two. The temperature difference disappears when the PE transducer is coated, indicating that the thermal insulation of the coating is effective. Different diaphragm thicknesses have also been tested at 0.5 MPa and 1 MPa, and the results are summarized in Table 1. The 75 $\upmu$m and 125 $\upmu$m diaphragms show an influence on the pulse duration $\varDelta t_{\text {pulse}}$, reducing the available time for the mixture to nucleate. This effect points out the importance of using the thinnest diaphragm possible, provided that it stands the pressure difference existing between HPS and LPS at the beginning of the experiment.

Fig. 18

Temperature profiles at the nucleation pulse obtained from the PR transducer ( ) and from the PE transducer ( ). In a the temperature profiles of the test 2a (Table 1) with uncoated-PE transducer and in b the temperature profiles with the test 2c* (Table 1) with coated-PE

A second experimental campaign has been carried out in order to verify the performances of the novel design. Several homogeneous water nucleation experiments have been run with helium as carrier gas and a pulse temperature of about 240 K. Two nucleation pressures have been tested, 1 MPa and 0.1 MPa, at different supersaturation levels. In Fig. 19 the results for such tests are presented in terms of nucleation rate J - supersaturation S data. A detailed overview of the performed nucleation experiments is given in Table 2. For both pressure conditions, a coating layer has been applied to the PE sensing surface and a diaphragm thickness of 50 $\upmu$m and 40 $\upmu$m has been found to be the optimal choice at 1 MPa and 0.1 MPa, respectively. The measured $J-S$ values are compared with the data obtained by Fransen et al. (2015) in the same conditions as this work, but with the previous version of the PEWT. The main result to be underlined is the substantial agreement with the data of Fransen et al. (2015), which demonstrates the well functioning of the PEWT, in the new version as in the original one of Looijmans et al. (1993).

Table 2 Experimental data overview of the water nucleation experiments performed with the new version of the PEWT discussed in this work and reported in Fig. 19

Fig. 19

Experimental data overview of the water nucleation rates J in function of the supersaturation S at 240 K in helium. The data obtained with the new version of the PEWT at 1 MPa ($\blacksquare$) and 0.1 MPa ($\bullet$) are presented. A detailed overview is reported in Table 2. The data of Fransen et al. (2015) at 1 MPa ($\square$) and 0.1 MPa ($\circ$), with the previous PEWT version, are also shown for comparison. The two trend lines at 1 MPa ( ) and 0.1 MPa ( ) have the only purpose of guiding the eye

6 Conclusions

The High pressure section (HPS) of the PEWT for homogeneous condensation experiments has been redesigned. A square-shape cross-section has been chosen for the test section in order to accommodate, without any geometrical mismatch, the pressure transducers (PR and PE) and two of the three optical windows ($A_1$ and $A_3$). The HPS has been also halved in length with the scope of a faster experimental procedure and a reduced gas consumption. Two test campaigns have been carried out in order to verify, with the first one, the gasdynamic performances of the modified PEWT and, with the second campaign, the nucleation rate (J) - supersaturation (S) data quality when homogeneous condensation experiments are run. The homogeneous water nucleation data $(J-S)$ obtained at 240 K and at two pressure conditions, 1 MPa and 0.1 MPa, in helium with the newly designed PEWT have been shown to be perfectly aligned with previous measurements performed, at the same experimental conditions, by means of the previous version of the PEWT. This means that the modified wave tube is functioning properly. Moreover, it also implies that the quality of the nucleation rate data obtained with the previous version of PEWT is not significantly affected by the slight mismatch of the flat windows and transducers with the circular walls of the previous test section. Both campaigns have demonstrated the combination of piezoresistive (PR) and fast responding coated piezoelectric (PE) transducers to be essential for the purpose of providing a much more accurate measuring of the mixture thermodynamic conditions during the PEWT experiments. The importance of the diaphragm has also been pointed out, proving that the choice of the thinnest diaphragm thickness possible is crucial to minimize the diaphragm opening process intrusiveness during the experiments. Additionally, a 2D numerical model has been successfully developed for the PEWT, representing a powerful support for the design of the forthcoming experiments. Such tool has been shown to correctly predict all the gasdynamic features of the PEWT, including the opening process and the total opening time of the diaphragm and it has been possible to exclude the presence of any disturbance on the flow field at the observation point.

Appendix: Definition of the supersaturation

The supersaturation can be defined for a non-ideal vapour–gas mixture as (Vehkamäki 2006; Holten et al. 2016)

$$\begin{aligned} S_i = \exp \left[ \dfrac{\mu _i^v(p,T,y_i)-\mu _i^v(p,T,y_{i,{\mathrm{eq}}})}{kT} \right] \end{aligned}$$

(8)

and quantifies, relatively to the mixture component i, the deviation of the current state from the corresponding (same p and T) phase equilibrium. In Eq. 8, the term $\mu _i^v(p,T,y_i)$ is the chemical potential of the i-component in the vapour state v at the system conditions p and T, while $\mu _i^v(p,T,y_{i,{\mathrm{eq}}})$ is the chemical potential of the same component, but in the vapour-liquid equilibrium at the same mixture conditions p and T. In case of non-ideal vapour–gas mixture, the exponent of Eq. 8 is defined as

$$\begin{aligned} \dfrac{\mu _i^v-\mu _{i,{\mathrm{eq}}}^v}{kT}=\log \left( \dfrac{f_i}{f_{i,{\mathrm{eq}}}} \right) , \end{aligned}$$

(9)

with $f_i$ and $f_{i,{\mathrm{eq}}}$ the fugacities of the i-component at the vapour state and at the equilibrium state, respectively. In function of the activity f, the fugacity coefficient $\phi$ can be expressed in a general manner as

$$\begin{aligned} \phi = \dfrac{f_i}{y_ip}. \end{aligned}$$

(10)

Moreover, the approximation

$$\begin{aligned} \phi _i \approx \phi _{i,{\mathrm{eq}}}, \end{aligned}$$

(11)

can be made for the present application since y is appreciably small ($\sim$ 500 ppm) and, therefore, almost all molecular interaction can be assumed to take place between the vapour and the gas molecules (dilute gas). In consideration of Eqs. (8, 9, 10 and 11), the supersaturation can now be expressed as

$$\begin{aligned} S_i = \dfrac{\phi _i y_i}{\phi _{i,{\mathrm{eq}}} y_{i,{\mathrm{eq}}}} \approx \dfrac{y_i}{y_{i,{\mathrm{eq}}}} = \dfrac{y_i p}{f_e p_{i,s}} \end{aligned}$$

(12)

with the enhancement factor $f_e$, defined as

$$\begin{aligned} f_e = \dfrac{y_{i,{\mathrm{eq}}}p}{p_{i,s}} = \dfrac{\phi _{i,s}}{\phi _{i,{\mathrm{eq}}}}{\mathrm{exp}}\left( \int _{p_{i,s}}^{p}v^l{\mathrm{d}}p \right) . \end{aligned}$$

(13)

Such factor takes into account two important contributions: the pressure effects on the equilibrium phase by means of the Poynting correction ($\int _{p_{i,s}}^{p}v^l{\mathrm{d}}p$) and the effect of the non-ideal gas behaviour with the ratio $\phi _{i,s} / \phi _{i,{\mathrm{eq}}}$. In the case of ideal vapour–gas mixtures, $f_e\approx$ 1 and the supersaturation definition (Eq. 12) simplifies as follows

$$\begin{aligned} S_i = \dfrac{y_i p}{p_{i,s}} = \dfrac{p_{i,v}}{p_{i,s}}. \end{aligned}$$

(14)

with $p_{i,v} = y_i p$ the partial vapour pressure of the mixture component i.